第19章矩形、菱形与正方形单元测试(含答案)
文档属性
| 名称 | 第19章矩形、菱形与正方形单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 484.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 09:15:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章矩形、菱形与正方形单元测试华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
2.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
3.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.直角三角形中,两直角边长分别为3和4,则斜边上的中线长是( )
A.10 B.5 C.3.5 D.2.5
6.如图,在矩形ABCD中,对角线AC,BD交于点O,若BD=6,则OA的长为( )
A.3 B. C. D.6
7.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若,BD=3,则菱形ABCD的面积为( )
A. B. C. D.
8.如图,在正方形ABCD中,AB=4,CE=DF=1,DE,AF交于点G,点H为AE的中点,连接GH,则GH的长为( )
A. B. C.2 D.
二.填空题(每小题5分,满分20分)
9.将对角线分别为5cm和8cm的菱形改为一个面积不变的正方形,则正方形的边长为 cm.
10.如图,在正方形ABCD中,点E在AB边上,AF⊥DE于点G,交BC于点F.若AE=15,CF=5,则AF的长是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,若AB=6cm,BC=8cm,则△ABO的周长是 cm.
12.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
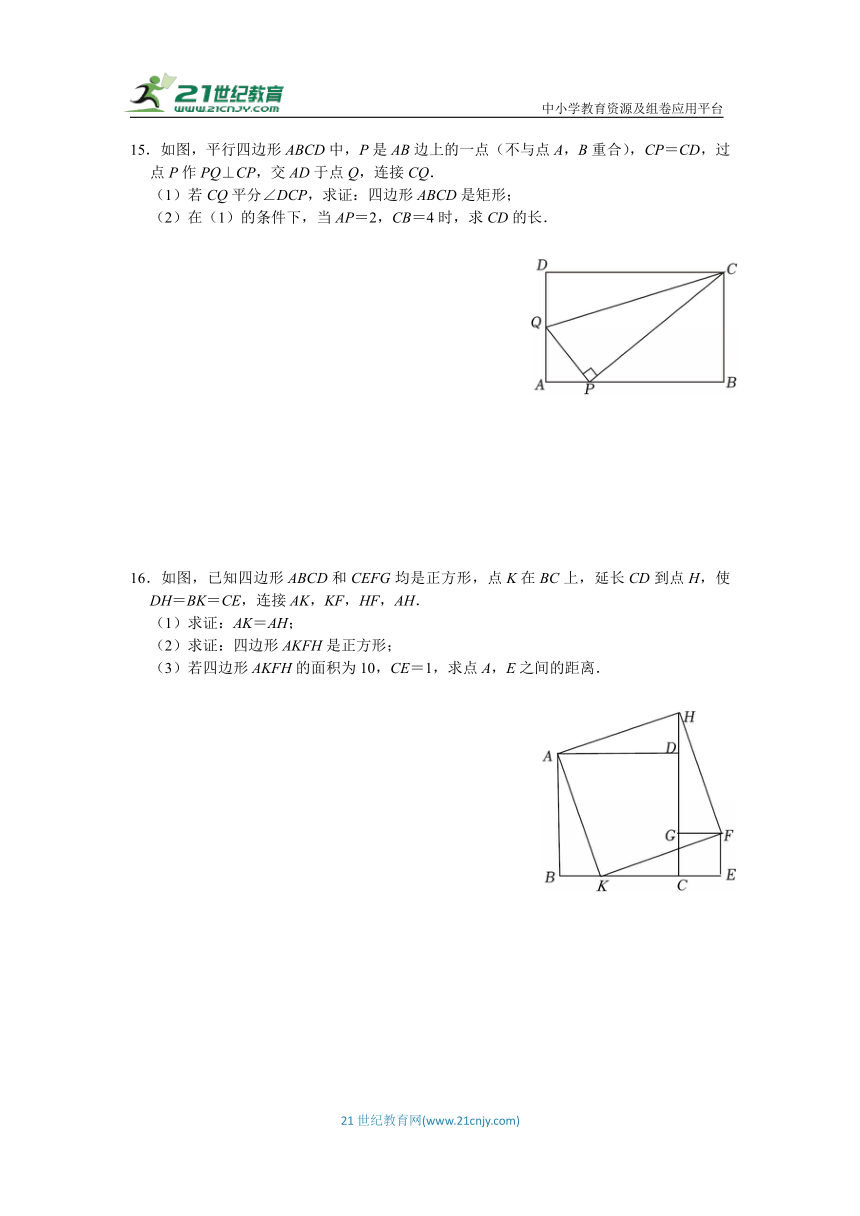
15.如图,平行四边形ABCD中,P是AB边上的一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ.
(1)若CQ平分∠DCP,求证:四边形ABCD是矩形;
(2)在(1)的条件下,当AP=2,CB=4时,求CD的长.
16.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.
(1)求证:AK=AH;
(2)求证:四边形AKFH是正方形;
(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.
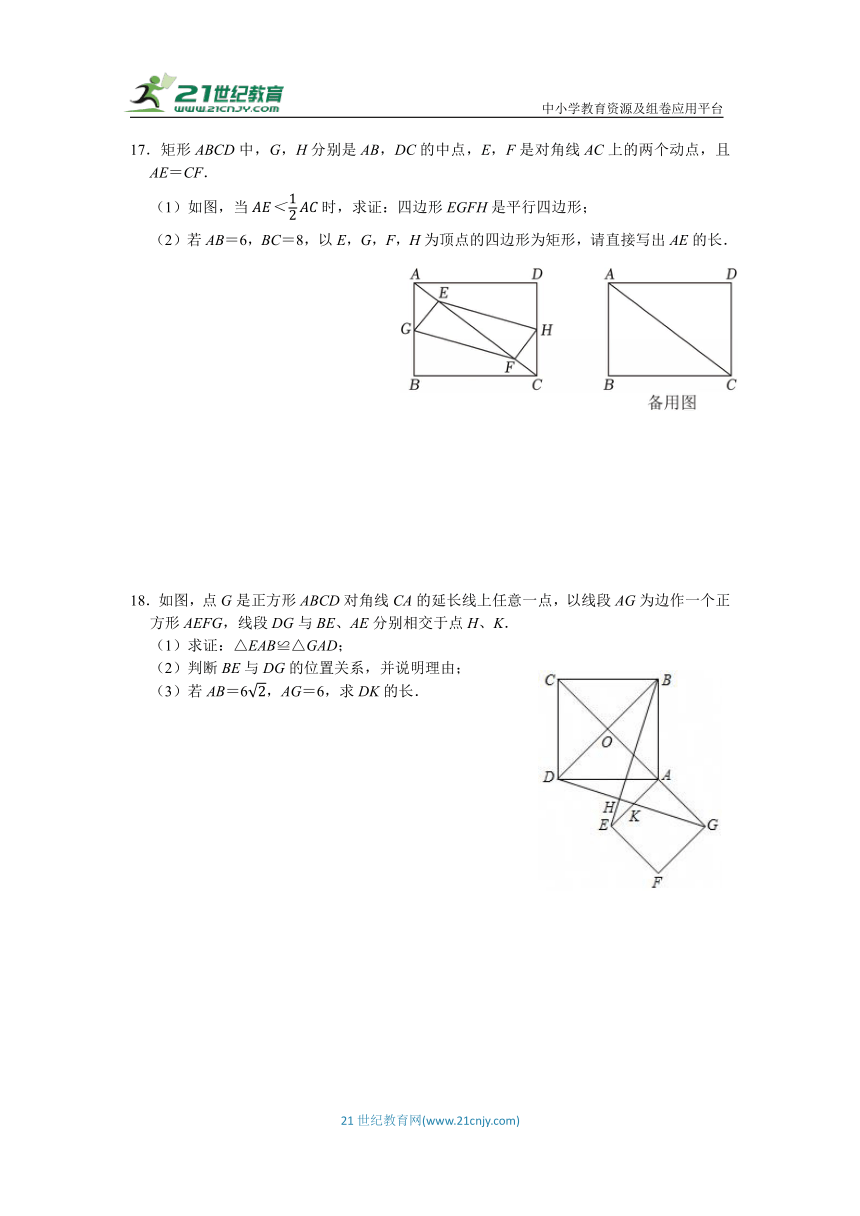
17.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
18.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段DG与BE、AE分别相交于点H、K.
(1)求证:△EAB≌△GAD;
(2)判断BE与DG的位置关系,并说明理由;
(3)若AB=6,AG=6,求DK的长.
参考答案
一、选择题
1—8:CDCBDACD
二、填空题
9.【解答】解:∵菱形的对角线分别为5cm和8cm,
∴菱形的面积S5×8=20cm2,
∴正方形的边长是2(cm).
故答案为:2.
10.【解答】解:∵四边形ABCD是正方形,
∴AB=AD=BC,∠B=DAB=90°,
∴∠BAF+∠FAD=90°,
∵AF⊥DE,
∴∠FAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中,
,
∴△BAF≌△ADE(ASA),
∴BF=AE=15,
∵CF=5,
∴BC=BF+CF=20,
∴AB=BC=20,
在Rt△ABF中,AB=20,BF=15,
由勾股定理得:AF25.
故答案为:25.
11.【解答】解:在矩形ABCD中,对角线AC,BD相交于点O,AB=6cm,BC=8cm,
∴∠ABC=90°,OA=OBAC,
∴AC10(cm),
∴AO=BO=5cm,
∴△ABO的周长为OA+OB+AB=16(cm).
故答案为:16.
12.【解答】解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
13.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
14.【解答】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,对角线AC,BD交于点O,
∴AC⊥BD,OA=OC=,OB=OD=,
∴OB==3,
在Rt△AOB中,∠AOB=90°,
∴OA=,
∵CE⊥AB,
∴∠AEC=90°,
在Rt△AEC中,∠AEC=90°,O为AC中点,
∴=4.
15.【解答】(1)证明:∵PQ⊥CP,
∴∠CPQ=90°,
∵CQ平分∠DCP,
∴∠DCQ=∠PCQ,
又∵CP=CD,CQ=CQ,
∴△DCQ≌△PCQ(SAS),
∴∠D=∠QPC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵CP=CD,
∴设CP=CD=x,则PB=x﹣2,
在Rt△BCP中,BC2+BP2=CP2,
∴(x﹣2)2+42=x2,
∴x=5,
∴CD=5.
16.【解答】(1)证明:∵四边形ABCD和CEFG都是正方形,
∴AB=AD=DC=BC,GC=EC=FG=EF,
∵DH=CE=BK,
∴HG=EK=BC=AD=AB,
在△ADH和△ABK中,
,
∴△ADH≌△ABK(SAS),
∴AK=AH;
(2)证明:∵△ADH≌△ABK,
∴∠HAD=∠BAK.
∴∠HAK=90°,
同理可得:△HGF≌△KEF≌△ABK≌△ADH,
∴AH=AK=HF=FK,
∴四边形AKFH是正方形;
(3)解:∵四边形AKFH的面积为10,
∴KF,
∵EF=CE=1,
∴KE,
∴AB=KE=3,
∵BK=EF=1,
∴BE=BK+KE=4,
∴AE,
故点A,E之间的距离为5.
17.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
18.【解答】(1)证明:∵四边形ABCD、四边形AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠DAB+∠DAE=∠EAG+∠DAE,
∴∠EAB=∠GAD,
∵AB=AD,AE=AG,
∴△EAB≌△GAD(SAS).
(2)解:BE⊥DG,理由如下:
∵△EAB≌△GAD,
∴∠AGD=∠AEB,
∵∠AKG=∠HKE,
在Rt△AGK中,∠AGK+∠AKG=90°
∴∠KEH+∠HKE=90°,
∴∠EHK=180°﹣90°=90°,
∴BE⊥DG.
(3)解:连接DE,如图,
在Rt△ABC中,
∵AB=BC=6,
∴AC12,
∴AO=DOAC=6,
∵AG=AE=AO=DO=6.AO⊥DO,
∴四边形AEDO是正方形,
∵∠DEK=∠GAK=90°,
∵DE=AG=6,∠DKE=∠AKG,
∴△DKE≌△GAK(AAS),
∴EK=AK=3,
在Rt△DKE中,
DK3.
21世纪教育网(www.21cnjy.com)
第19章矩形、菱形与正方形单元测试华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
2.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
3.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.直角三角形中,两直角边长分别为3和4,则斜边上的中线长是( )
A.10 B.5 C.3.5 D.2.5
6.如图,在矩形ABCD中,对角线AC,BD交于点O,若BD=6,则OA的长为( )
A.3 B. C. D.6
7.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若,BD=3,则菱形ABCD的面积为( )
A. B. C. D.
8.如图,在正方形ABCD中,AB=4,CE=DF=1,DE,AF交于点G,点H为AE的中点,连接GH,则GH的长为( )
A. B. C.2 D.
二.填空题(每小题5分,满分20分)
9.将对角线分别为5cm和8cm的菱形改为一个面积不变的正方形,则正方形的边长为 cm.
10.如图,在正方形ABCD中,点E在AB边上,AF⊥DE于点G,交BC于点F.若AE=15,CF=5,则AF的长是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,若AB=6cm,BC=8cm,则△ABO的周长是 cm.
12.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
15.如图,平行四边形ABCD中,P是AB边上的一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ.
(1)若CQ平分∠DCP,求证:四边形ABCD是矩形;
(2)在(1)的条件下,当AP=2,CB=4时,求CD的长.
16.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.
(1)求证:AK=AH;
(2)求证:四边形AKFH是正方形;
(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.
17.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
18.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段DG与BE、AE分别相交于点H、K.
(1)求证:△EAB≌△GAD;
(2)判断BE与DG的位置关系,并说明理由;
(3)若AB=6,AG=6,求DK的长.
参考答案
一、选择题
1—8:CDCBDACD
二、填空题
9.【解答】解:∵菱形的对角线分别为5cm和8cm,
∴菱形的面积S5×8=20cm2,
∴正方形的边长是2(cm).
故答案为:2.
10.【解答】解:∵四边形ABCD是正方形,
∴AB=AD=BC,∠B=DAB=90°,
∴∠BAF+∠FAD=90°,
∵AF⊥DE,
∴∠FAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中,
,
∴△BAF≌△ADE(ASA),
∴BF=AE=15,
∵CF=5,
∴BC=BF+CF=20,
∴AB=BC=20,
在Rt△ABF中,AB=20,BF=15,
由勾股定理得:AF25.
故答案为:25.
11.【解答】解:在矩形ABCD中,对角线AC,BD相交于点O,AB=6cm,BC=8cm,
∴∠ABC=90°,OA=OBAC,
∴AC10(cm),
∴AO=BO=5cm,
∴△ABO的周长为OA+OB+AB=16(cm).
故答案为:16.
12.【解答】解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
13.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
14.【解答】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,对角线AC,BD交于点O,
∴AC⊥BD,OA=OC=,OB=OD=,
∴OB==3,
在Rt△AOB中,∠AOB=90°,
∴OA=,
∵CE⊥AB,
∴∠AEC=90°,
在Rt△AEC中,∠AEC=90°,O为AC中点,
∴=4.
15.【解答】(1)证明:∵PQ⊥CP,
∴∠CPQ=90°,
∵CQ平分∠DCP,
∴∠DCQ=∠PCQ,
又∵CP=CD,CQ=CQ,
∴△DCQ≌△PCQ(SAS),
∴∠D=∠QPC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵CP=CD,
∴设CP=CD=x,则PB=x﹣2,
在Rt△BCP中,BC2+BP2=CP2,
∴(x﹣2)2+42=x2,
∴x=5,
∴CD=5.
16.【解答】(1)证明:∵四边形ABCD和CEFG都是正方形,
∴AB=AD=DC=BC,GC=EC=FG=EF,
∵DH=CE=BK,
∴HG=EK=BC=AD=AB,
在△ADH和△ABK中,
,
∴△ADH≌△ABK(SAS),
∴AK=AH;
(2)证明:∵△ADH≌△ABK,
∴∠HAD=∠BAK.
∴∠HAK=90°,
同理可得:△HGF≌△KEF≌△ABK≌△ADH,
∴AH=AK=HF=FK,
∴四边形AKFH是正方形;
(3)解:∵四边形AKFH的面积为10,
∴KF,
∵EF=CE=1,
∴KE,
∴AB=KE=3,
∵BK=EF=1,
∴BE=BK+KE=4,
∴AE,
故点A,E之间的距离为5.
17.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
18.【解答】(1)证明:∵四边形ABCD、四边形AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠DAB+∠DAE=∠EAG+∠DAE,
∴∠EAB=∠GAD,
∵AB=AD,AE=AG,
∴△EAB≌△GAD(SAS).
(2)解:BE⊥DG,理由如下:
∵△EAB≌△GAD,
∴∠AGD=∠AEB,
∵∠AKG=∠HKE,
在Rt△AGK中,∠AGK+∠AKG=90°
∴∠KEH+∠HKE=90°,
∴∠EHK=180°﹣90°=90°,
∴BE⊥DG.
(3)解:连接DE,如图,
在Rt△ABC中,
∵AB=BC=6,
∴AC12,
∴AO=DOAC=6,
∵AG=AE=AO=DO=6.AO⊥DO,
∴四边形AEDO是正方形,
∵∠DEK=∠GAK=90°,
∵DE=AG=6,∠DKE=∠AKG,
∴△DKE≌△GAK(AAS),
∴EK=AK=3,
在Rt△DKE中,
DK3.
21世纪教育网(www.21cnjy.com)
