第19章矩形、菱形与正方形单元测试A卷(含答案)
文档属性
| 名称 | 第19章矩形、菱形与正方形单元测试A卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 558.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 09:17:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章矩形、菱形与正方形单元测试A卷华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
2.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
3.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
4.如图,在矩形OABC中,OA=9,AB=15,E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.E点坐标是( )
A.(5,15) B.(3,15) C.(15,2) D.(15,4)
5.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1+ B.2+ C.5﹣ D.
6.如图,在正方形ABCD中,E为BC边上一动点(点E、B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接DP.若AB=2时,则△ADP周长的最小值为( )
A. B. C. D.
7.如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
A. B. C. D.
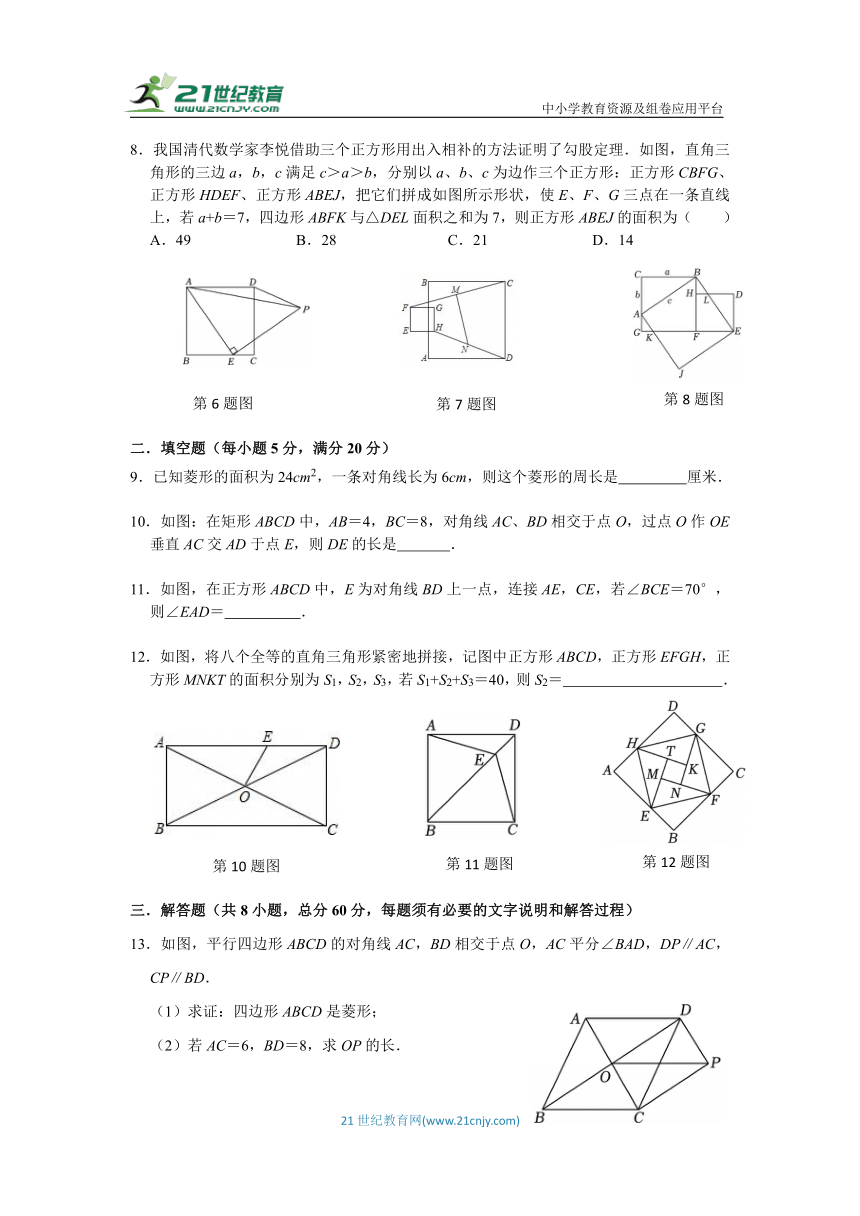
8.我国清代数学家李悦借助三个正方形用出入相补的方法证明了勾股定理.如图,直角三角形的三边a,b,c满足c>a>b,分别以a、b、c为边作三个正方形:正方形CBFG、正方形HDEF、正方形ABEJ,把它们拼成如图所示形状,使E、F、G三点在一条直线上,若a+b=7,四边形ABFK与△DEL面积之和为7,则正方形ABEJ的面积为( )
A.49 B.28 C.21 D.14
二.填空题(每小题5分,满分20分)
9.已知菱形的面积为24cm2,一条对角线长为6cm,则这个菱形的周长是 厘米.
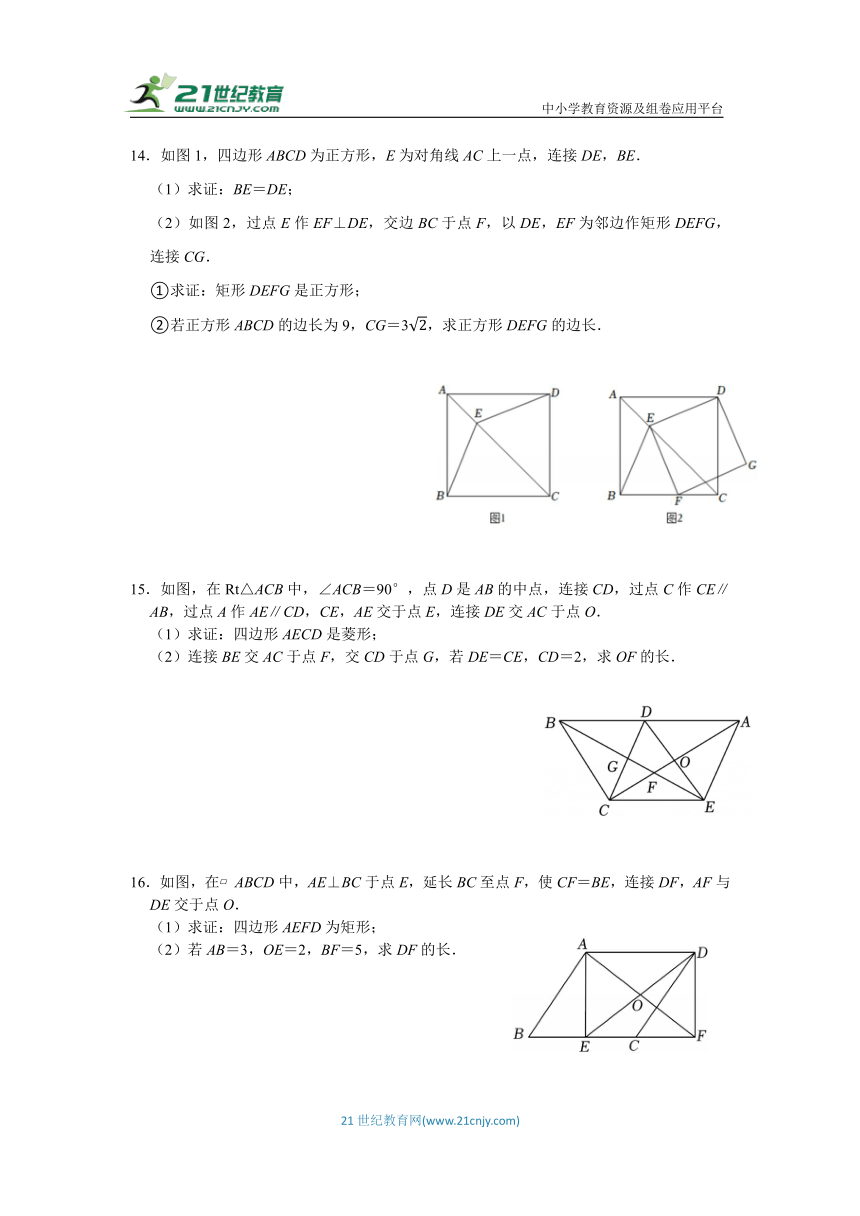
10.如图:在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是 .
11.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,若∠BCE=70°,则∠EAD= .
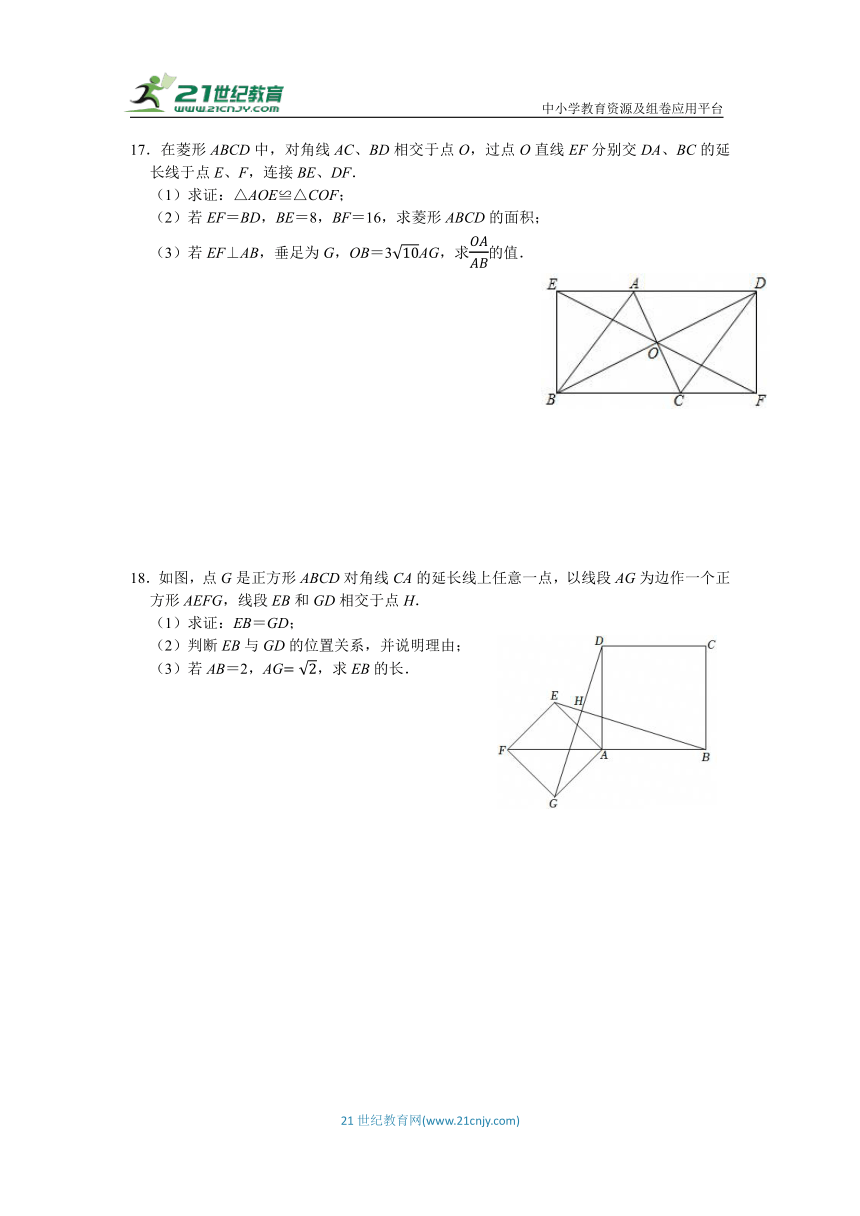
12.如图,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,平行四边形ABCD的对角线AC,BD相交于点O,AC平分∠BAD,DP∥AC,CP∥BD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,求OP的长.
14.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
15.如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,连接CD,过点C作CE∥AB,过点A作AE∥CD,CE,AE交于点E,连接DE交AC于点O.
(1)求证:四边形AECD是菱形;
(2)连接BE交AC于点F,交CD于点G,若DE=CE,CD=2,求OF的长.
16.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=3,OE=2,BF=5,求DF的长.
17.在菱形ABCD中,对角线AC、BD相交于点O,过点O直线EF分别交DA、BC的延长线于点E、F,连接BE、DF.
(1)求证:△AOE≌△COF;
(2)若EF=BD,BE=8,BF=16,求菱形ABCD的面积;
(3)若EF⊥AB,垂足为G,OB=3AG,求的值.
18.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG,求EB的长.
参考答案
一、选择题
1—8:BCCDBCCC
二、填空题
9.【解答】解:如图所示:
∵菱形的面积等于对角线乘积的一半,AC=6cm,S菱形ABCD=24cm2,
∴BD=8cm,AO=3cm,BO=4cm,
在Rt△ABO中,AB2=AO2+BO2,
即有AB2=32+42,
解得:AB=5cm,
∴菱形的周长=4×5=20cm.
故答案为:20.
10.【解答】解:如图,连接CE,
设DE=x,则AE=8﹣x,
∵OE⊥AC,且点O是AC的中点,
∴OE是AC的垂直平分线,
∴CE=AE=8﹣x,
在Rt△CDE中,
x2+42=(8﹣x)2
解得x=3,
∴DE的长是3.
故答案为:3.
11.【解答】解:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,
∵DE=DE,
∴△AED≌△CED(SAS),
∴∠EAD=∠ECD,
又∵∠BCE=70°,
方法1:∴∠EAD=∠BAD﹣∠BCE=20°.
方法2:∴∠BEC=65°,
∵∠BEC=∠CDE+∠ECD,
即65°=45°+∠ECD,
∴∠ECD=20°,
∴∠EAD=20°.
故答案为:20°.
12.【解答】解:本图是由八个全等的直角三角形拼成的,设这个直角三角形两个直角边中较长的长度为a,较短的长度为b,即图中的AE=a,AH=b,
则,,,
∵S1+S2+S3=40,
∴(a+b)2+a2+b2+(a﹣b)2=40,
a2+b2+2ab+a2+b2+a2+b2﹣2ab=40,
3a2+3b2=40,
,
∴.
故答案是:.
三、解答题
13.【解答】(1)证明:∵AC平分∠BAD,
∴∠DAC=∠BAC
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴平行四边形ABCD是菱形;
(2)解:由题意可得:
∴,,AC⊥BD,
∴∠COD=90°,
∵DP∥AC,CP∥BD,∠COD=90°,
∴四边形OCPD是矩形,
∴OP=CD=5.
14.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
15.【解答】(1)证明:∵∠ACB=90°,点D是AB中点,
∴,
∵AE∥CD,CE∥AB,
∴四边形AECD是平行四边形,
∵CD=AD,
∴四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴AC⊥DE,CD=CE,OD=OE,
∵DE=CE,CD=2,
∴DE=CE=CD=2,△CDE为等边三角形,
∴∠AOD=∠ACB=90°,OD=OE=1,∠DEC=60°,
∴BC∥DE,
∵CE∥BD,
∴四边形BCED是平行四边形,
∵DE=CE,
∴四边形BCED是菱形,
∴,
∴EF=2OF,
由勾股定理得OF2=EF2﹣OE2,即OF2=(2OF)2﹣12,
解得.
16.【解答】(1)证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:由(1)知,四边形AEFD为矩形,
∴DF=AE,AF=DE=2OE=4,
∵AB=3,DE=4,BF=5,
∴AB2+AF2=BF2,
∴△BAF为直角三角形,∠BAF=90°,
∴S△ABF,
∴AB×AF=BF×AE,
即3×4=5AE,
∴AE,
∴DF=AE.
17.【解答】证明:(1)∵四边形ABCD是菱形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,又∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2)由△AOE≌△COF,得OE=OF,
∵四边形ABCD是菱形,∴OB=OD
∴四边形EBFD是平行四边形,
∵EF=BD,
∴ EBFE是矩形,∴∠EBF=90°,
设菱形ABCD的边长为x,∴AB=AD=x,∴AE=16﹣x,
在Rt△AEB中,根据勾股定理,得
AB2=AE2+BE2,即x2=(16﹣x)2+82,解得x=10,
∴S菱形=BC BE=10×8=80.
答:菱形ABCD的面积为80.
(3)∵EF⊥AB,垂足为G,
∵四边形ABCD是菱形,
∴OA⊥OB,
∵OG⊥AB,
设AG=a,则OB=3AG=3a,
设OA=x,AB=AD=y,
∵S△AOBAO OBAB OG,
∴3ax=y OG,
∴OG,
在Rt△GOA中,根据勾股定理,得
OG2=OA2﹣AG2,
∴()2=x2﹣a2,
整理,得(y2﹣90a2)x2=a2y2,
∴x2,
在Rt△BOA中,根据勾股定理,得
AB2=OB2+OA2,
∴y2=90a2+x2,
∴x2,
∴x4﹣a2x2﹣90a4=0,
解得x2=10a2或x2=﹣9a2(舍去),
∴xa,
y=10a,
∴OAAG,
∴
答:的值为.
18.【解答】(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠DAB=90°,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:如图1,AD,BE的交点记作点M,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:如图2,连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,OA=OB,
∴BD⊥CG,
∵AB=AD=2,
在Rt△ABD中,DB,
ODDB,
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA,
连接AF,
∵∠FAG=∠CAB=45°,
∴A、G、C三点共线,
即OG=OA+AG,
∴EB=GD.
21世纪教育网(www.21cnjy.com)
第19章矩形、菱形与正方形单元测试A卷华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
2.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
3.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
4.如图,在矩形OABC中,OA=9,AB=15,E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.E点坐标是( )
A.(5,15) B.(3,15) C.(15,2) D.(15,4)
5.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1+ B.2+ C.5﹣ D.
6.如图,在正方形ABCD中,E为BC边上一动点(点E、B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接DP.若AB=2时,则△ADP周长的最小值为( )
A. B. C. D.
7.如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
A. B. C. D.
8.我国清代数学家李悦借助三个正方形用出入相补的方法证明了勾股定理.如图,直角三角形的三边a,b,c满足c>a>b,分别以a、b、c为边作三个正方形:正方形CBFG、正方形HDEF、正方形ABEJ,把它们拼成如图所示形状,使E、F、G三点在一条直线上,若a+b=7,四边形ABFK与△DEL面积之和为7,则正方形ABEJ的面积为( )
A.49 B.28 C.21 D.14
二.填空题(每小题5分,满分20分)
9.已知菱形的面积为24cm2,一条对角线长为6cm,则这个菱形的周长是 厘米.
10.如图:在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是 .
11.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,若∠BCE=70°,则∠EAD= .
12.如图,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,平行四边形ABCD的对角线AC,BD相交于点O,AC平分∠BAD,DP∥AC,CP∥BD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,求OP的长.
14.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
15.如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,连接CD,过点C作CE∥AB,过点A作AE∥CD,CE,AE交于点E,连接DE交AC于点O.
(1)求证:四边形AECD是菱形;
(2)连接BE交AC于点F,交CD于点G,若DE=CE,CD=2,求OF的长.
16.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=3,OE=2,BF=5,求DF的长.
17.在菱形ABCD中,对角线AC、BD相交于点O,过点O直线EF分别交DA、BC的延长线于点E、F,连接BE、DF.
(1)求证:△AOE≌△COF;
(2)若EF=BD,BE=8,BF=16,求菱形ABCD的面积;
(3)若EF⊥AB,垂足为G,OB=3AG,求的值.
18.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG,求EB的长.
参考答案
一、选择题
1—8:BCCDBCCC
二、填空题
9.【解答】解:如图所示:
∵菱形的面积等于对角线乘积的一半,AC=6cm,S菱形ABCD=24cm2,
∴BD=8cm,AO=3cm,BO=4cm,
在Rt△ABO中,AB2=AO2+BO2,
即有AB2=32+42,
解得:AB=5cm,
∴菱形的周长=4×5=20cm.
故答案为:20.
10.【解答】解:如图,连接CE,
设DE=x,则AE=8﹣x,
∵OE⊥AC,且点O是AC的中点,
∴OE是AC的垂直平分线,
∴CE=AE=8﹣x,
在Rt△CDE中,
x2+42=(8﹣x)2
解得x=3,
∴DE的长是3.
故答案为:3.
11.【解答】解:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,
∵DE=DE,
∴△AED≌△CED(SAS),
∴∠EAD=∠ECD,
又∵∠BCE=70°,
方法1:∴∠EAD=∠BAD﹣∠BCE=20°.
方法2:∴∠BEC=65°,
∵∠BEC=∠CDE+∠ECD,
即65°=45°+∠ECD,
∴∠ECD=20°,
∴∠EAD=20°.
故答案为:20°.
12.【解答】解:本图是由八个全等的直角三角形拼成的,设这个直角三角形两个直角边中较长的长度为a,较短的长度为b,即图中的AE=a,AH=b,
则,,,
∵S1+S2+S3=40,
∴(a+b)2+a2+b2+(a﹣b)2=40,
a2+b2+2ab+a2+b2+a2+b2﹣2ab=40,
3a2+3b2=40,
,
∴.
故答案是:.
三、解答题
13.【解答】(1)证明:∵AC平分∠BAD,
∴∠DAC=∠BAC
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴平行四边形ABCD是菱形;
(2)解:由题意可得:
∴,,AC⊥BD,
∴∠COD=90°,
∵DP∥AC,CP∥BD,∠COD=90°,
∴四边形OCPD是矩形,
∴OP=CD=5.
14.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
15.【解答】(1)证明:∵∠ACB=90°,点D是AB中点,
∴,
∵AE∥CD,CE∥AB,
∴四边形AECD是平行四边形,
∵CD=AD,
∴四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴AC⊥DE,CD=CE,OD=OE,
∵DE=CE,CD=2,
∴DE=CE=CD=2,△CDE为等边三角形,
∴∠AOD=∠ACB=90°,OD=OE=1,∠DEC=60°,
∴BC∥DE,
∵CE∥BD,
∴四边形BCED是平行四边形,
∵DE=CE,
∴四边形BCED是菱形,
∴,
∴EF=2OF,
由勾股定理得OF2=EF2﹣OE2,即OF2=(2OF)2﹣12,
解得.
16.【解答】(1)证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:由(1)知,四边形AEFD为矩形,
∴DF=AE,AF=DE=2OE=4,
∵AB=3,DE=4,BF=5,
∴AB2+AF2=BF2,
∴△BAF为直角三角形,∠BAF=90°,
∴S△ABF,
∴AB×AF=BF×AE,
即3×4=5AE,
∴AE,
∴DF=AE.
17.【解答】证明:(1)∵四边形ABCD是菱形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,又∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2)由△AOE≌△COF,得OE=OF,
∵四边形ABCD是菱形,∴OB=OD
∴四边形EBFD是平行四边形,
∵EF=BD,
∴ EBFE是矩形,∴∠EBF=90°,
设菱形ABCD的边长为x,∴AB=AD=x,∴AE=16﹣x,
在Rt△AEB中,根据勾股定理,得
AB2=AE2+BE2,即x2=(16﹣x)2+82,解得x=10,
∴S菱形=BC BE=10×8=80.
答:菱形ABCD的面积为80.
(3)∵EF⊥AB,垂足为G,
∵四边形ABCD是菱形,
∴OA⊥OB,
∵OG⊥AB,
设AG=a,则OB=3AG=3a,
设OA=x,AB=AD=y,
∵S△AOBAO OBAB OG,
∴3ax=y OG,
∴OG,
在Rt△GOA中,根据勾股定理,得
OG2=OA2﹣AG2,
∴()2=x2﹣a2,
整理,得(y2﹣90a2)x2=a2y2,
∴x2,
在Rt△BOA中,根据勾股定理,得
AB2=OB2+OA2,
∴y2=90a2+x2,
∴x2,
∴x4﹣a2x2﹣90a4=0,
解得x2=10a2或x2=﹣9a2(舍去),
∴xa,
y=10a,
∴OAAG,
∴
答:的值为.
18.【解答】(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠DAB=90°,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:如图1,AD,BE的交点记作点M,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:如图2,连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,OA=OB,
∴BD⊥CG,
∵AB=AD=2,
在Rt△ABD中,DB,
ODDB,
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA,
连接AF,
∵∠FAG=∠CAB=45°,
∴A、G、C三点共线,
即OG=OA+AG,
∴EB=GD.
21世纪教育网(www.21cnjy.com)
