第九章中心对称图形—平行四边形期末复习训练(含答案)
文档属性
| 名称 | 第九章中心对称图形—平行四边形期末复习训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 838.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 13:37:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第九章中心对称图形—平行四边形期末复习训练苏科版2024—2025学年八年级下册
一、选择题
1.根据所标数据,不能判断下列四边形是平行四边形的是( )
A. B.
C. D.
2.如图所示为太极图,所谓太极即是阐明宇宙从无极而太极,以至万物化生的过程,下列对太极图的描述中,正确的是(不考虑颜色)( )
A.是中心对称图形
B.是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
3.菱形边长是2cm,一条对角线的长是,则菱形面积是( )
A.4cm2 B. C.2cm2 D.
4.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,OA=9,则BE的长为( )
A. B.9 C. D.12
5.如图,在矩形ABCD中,AB=6,AD=8,动点P从点B出发,沿着BD向点D移动,若过点P作PE⊥AB、PF⊥AD,垂足分别为E、F,连接EF,则EF的长最小为( )
A. B. C.5 D.7
二、填空题
6.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
7.如图,△ODC是由△OAB绕点O顺时针旋转后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,∠BOD的度数为40°,则∠BDC的度数是 .
8.如图,在 ABCD中,BE垂直平分CD于点E,∠BAD=45°,AD=6cm,则 ABCD的对角线AC的长为 cm.
9.如图,矩形ABCD中,∠ACD=30°,边,DM⊥AC于点M,连接BM,则图中阴影部分的面积是 .
10.如图,在正方形ABCD中,E、F、G分别是边AD、BC、CD上的点,BG⊥EF,垂足为H,下列结论中:①H为线段BG的中点;②∠DEF=∠BGC;③BG=EF;④AE+FC=DG,正确的结论有 .
三、解答题
11.如图,在△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,分别连接AD、BE,点M、N、H分别是AD、BE、AB的中点,连接MN、MH、NH.
(1)试猜想△MNH是何特殊三角形,并说明理由;
(2)若AE=4,BD=6,求线段MN的长.
12.如图,等腰△ABC中,AB=AC,AD⊥BC交BC于D点,E点是AB的中点,分别过D,E两点作线段AC的垂线,垂足分别为G,F两点.
(1)求证:四边形DEFG为矩形;
(2)若AB=20,EF=8,求CG的长.
13.如图,矩形ABCD的对角线AC与BD交于点O,点E是CD的中点,连接AE交BD于点F,延长AE到点P,使FP=AF,连接CF,CP,DP.
(1)求证:四边形CFDP是平行四边形;
(2)若四边形CFDP是矩形,且,求AB的长度.
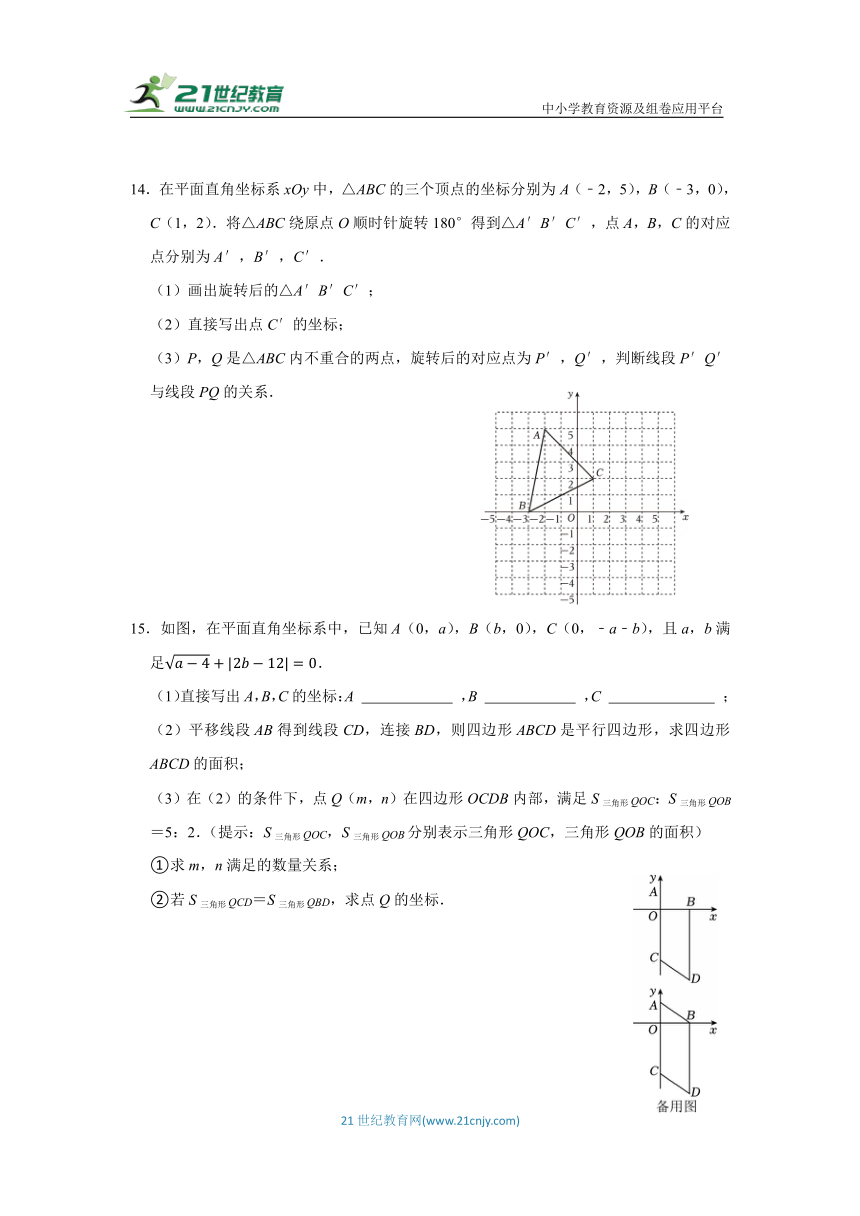
14.在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(﹣2,5),B(﹣3,0),C(1,2).将△ABC绕原点O顺时针旋转180°得到△A′B′C′,点A,B,C的对应点分别为A′,B′,C′.
(1)画出旋转后的△A′B′C′;
(2)直接写出点C′的坐标;
(3)P,Q是△ABC内不重合的两点,旋转后的对应点为P′,Q′,判断线段P′Q′与线段PQ的关系.
15.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(0,﹣a﹣b),且a,b满足.
(1)直接写出A,B,C的坐标:A ,B ,C ;
(2)平移线段AB得到线段CD,连接BD,则四边形ABCD是平行四边形,求四边形ABCD的面积;
(3)在(2)的条件下,点Q(m,n)在四边形OCDB内部,满足S三角形QOC:S三角形QOB=5:2.(提示:S三角形QOC,S三角形QOB分别表示三角形QOC,三角形QOB的面积)
①求m,n满足的数量关系;
②若S三角形QCD=S三角形QBD,求点Q的坐标.
参考答案
一、选择题
1.【解答】解:A、∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,故不符合题意;
B、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故不符合题意;
C、∵∠ACB=∠DAC=40°,
∴AD∥BC,
∵AB=CD,
∴不能判定四边形ABCD是平行四边形,故符合题意;
D、∠ACB=∠CAD=40°,
∴AD∥BC,
∵∠ABD=∠BDC=35°,
∴AB∥CD,
∴四边形ABCD是平行四边形,故不符合题意;
故选:C.
2.【解答】解:该图是中心对称图形,不是轴对称图形,
故选:A.
3.【解答】解:如图,AB=2cm,,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC,
∴,
∴,
∴AC=2OA=2,
∴菱形的面积.
故选:D.
4.【解答】解:在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠EAD=45°,AD∥BC,OA=OB=6,
∴∠AEB=∠EAD=45°,
∴BE=BA.
∵∠CAE=15°,∠BAE=45°,
∴∠BAC=60°,
又∵OA=OB,
∴△OAB为等边三角形,
∴BO=BA=9,
∴BO=BE=9.
故选:B.
5.【解答】解:如图,连接AP,
∵PE⊥AB,PF⊥AD,
∴∠AEP=∠AFP=90°.
∵四边形ABCD是矩形,
∴∠BAD=90°.
∴四边形AEPF为矩形.
∴AP=EF.
∴要求EF的最小值就是要求AP的最小值.
∵点P从B点沿着BD往D点移动,
∴当AP⊥BD时,AP取最小值.
在Rt△BAD中,
∵∠BAD=90°,AB=6,AD=8,
∴BD10,
∵,
∴.
∴EF的长度最小为:.
故选:B.
二、填空题
6.【解答】解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
.
∴△BNA≌△BNE(ASA),
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MNDE.
故答案为:.
7.【解答】解:由条件可知∠AOD=∠BOC,AD=OD,∠A=∠ODC,
∴∠A=∠ADO,
∵∠AOC=100°,∠BOD=40°,
∴,
∴,
∴∠ODC=∠A=75°,
∴∠BDC=180°﹣∠ADO﹣∠ODC=180°﹣75°﹣75°=30°,
故答案为:30°.
8.【解答】解:在 ABCD中,BE垂直平分CD于点E,∠BAD=45°,AD=6cm,如图,连接BD交AC于点F.
∴BD=BC,BC=AD=2,BF=DF,AC=2AF,
∴BD=AD=6cm,
∴DFBD6=3(cm),
∵∠BAD=45°,
∴∠ABD=45°,
∴∠ADB=90°.
在Rt△ADF中,由勾股定理得:AF3(cm),
∴AC=2AF=6cm.
故答案为:6.
9.【解答】解:∵ABCD是矩形,
∴∠DAB=∠ADC=90°,
∵∠ACD=30°,,
∴,
∵DM⊥AC,
∴∠ADM=30°,
∴,
过点M作MH⊥AB,
∴,
则图中阴影部分的面积=S矩形ABCD﹣S△ADM﹣S△ABM﹣S△BCD
,
故答案为:.
10.【解答】解:①如图,当点E,D重合,F,C重合时,
则点G,H与点C重合,
此时BG=BH,故①错误;
②∵BG⊥EF,
∴∠CBG+∠BFH=∠CBG+∠BGC=90°,
∴∠BFH=∠BGC,
∵AD∥BC,
∴∠BFH=∠DEF,
∴∠DEF=∠BGC,故②正确;
③过点E作EM⊥BC于点M,则四边形ABME是矩形,
∴AB=EM,
∵AB=BC,
∴BC=EM,
∵∠CBG+∠BFH=∠FEM+∠BFH=90°,
∴∠CBG=∠FEM,
∵∠C=∠EMF=90°,
∴△BCG≌△EMF(ASA),
∴BG=EF,故③正确;
④∵FM=CG,BM=AE,
∵CD=BC,
∴AE+CF=BC﹣FM,DG=CD﹣CG,
∴AE+FC=DG,故④正确;
故答案为:②③④.
解答题
11.【解答】解:(1)△MNH是直角三角形,理由如下:
∵点M、N、H分别是AD、BE、AB的中点,
∴HM∥BD且HMBD,HN∥AE且HNAE,
∴∠AHM=∠ABC,∠BHN=∠BAC,
∴∠MHN=180°﹣(∠AHM+∠BHN)
=180°﹣(∠ABC+∠BAC),
∵∠ACB=90°,
∴∠ABC+∠BAC=90°,
∴∠AHM=180°﹣(∠ABC+∠BAC)=90°,
∴△MNH是直角三角形.
(2)∵点M、N、H分别是AD、BE、AB的中点,
∴HM∥BD且HMBD=3,HN∥AE且HNAE=2,
∵△MNH是直角三角形,
∴MN2=MH2+NH2=MH2+NH2=9+4=13,
∴MN.
12.【解答】(1)证明:∵AB=AC,AD⊥BC,
∴点D是BC的中点.
∵E点是AB的中点,
∴DE是△ABC 的中位线.
∴DE∥AC.
∵DG⊥AC,EF⊥AC,
∴EF∥DG.
∴四边形DEFG是平行四边形.
又∵∠EFG=90°,
∴四边形DEFG为矩形;
(2)解:∵AD⊥BC交BC于D点,E点是AB的中点,AB=20,
∴DE=AE10,
由(1)知,四边形DEFG为矩形,则GF=DE=10.
在Rt△AEF 中,EF=8,AE=10,由勾股定理得:AF6.
∵AB=AC=20,FG=ED=10,
∴GC=AC﹣FG﹣AF=20﹣10﹣6=4.
13.【解答】(1)证明:∵四边形ABCD是矩形,
∴AO=CO,
∵FP=AF,
∴OF是△ACP的中位线,
∴OF∥CP,
∴∠FDE=∠PCE(两直线平行,内错角相等),
∵点E是CD的中点,
∴DE=CE,
在△DEF和△CEP中,
,
∴△DEF≌△CEP(ASA),
∴EF=EP,
又∵DE=CE,
∴四边形CFDP是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB,∠ADE=90°,
∴根据勾股定理,AD2+DE2=AE2,
若四边形CFDP是矩形,则,
,FP=CD,
∵AF=FP,
∴,
∴,
∴AD2=2CD2,
∴或(不符合题意,舍去),
∵,
∴CD=AB=1,所以AB的长度为1.
14.【解答】解:(1)将△ABC绕原点O顺时针旋转180°得到△A′B′C′,如图1即为所求;
(2)点C′的坐标为(﹣1,﹣2);理由如下:
由图可知,点C′的坐标为(﹣1,﹣2);
(3)P′Q′=PQ.理由如下:
如图2,
设P(a,b),Q(m,n),则P′(﹣a,﹣b),Q′(﹣m,﹣n),
线段P′Q′与线段PQ关于原点对称,
∵,,
∴P′Q′=PQ.
15.【解答】解:(1)∵a,b满足,
∴a﹣4=0,2b﹣12=0,
解得a=4,b=6,
∴A(0,4),B(6,0),C(0,﹣10);
(2)由(1)得AC=4+10=14,OB=6,
∴求平行四边形ABCD的面积为AC OB=14×6=84;
(3)①设Q(m,n),
∵A(0,4),B(6,0),C(0,﹣10),
∴OC=10,OB=6,AC=14,
∵平移线段AB至线段CD,
∴D(6,﹣14),
满足S三角形QOC:S三角形QOB=5:2.
由条件可知,
∴nm,
②由①得Q(m,m),
由图可得:
S△QCD=S梯形OCDB﹣S△QCO﹣S△QBD﹣S△QBC
=72﹣5m﹣(42﹣7m)﹣2m
=30,
∵,
∴m=6,
∴Q(6,﹣4).
21世纪教育网(www.21cnjy.com)
第九章中心对称图形—平行四边形期末复习训练苏科版2024—2025学年八年级下册
一、选择题
1.根据所标数据,不能判断下列四边形是平行四边形的是( )
A. B.
C. D.
2.如图所示为太极图,所谓太极即是阐明宇宙从无极而太极,以至万物化生的过程,下列对太极图的描述中,正确的是(不考虑颜色)( )
A.是中心对称图形
B.是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
3.菱形边长是2cm,一条对角线的长是,则菱形面积是( )
A.4cm2 B. C.2cm2 D.
4.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,OA=9,则BE的长为( )
A. B.9 C. D.12
5.如图,在矩形ABCD中,AB=6,AD=8,动点P从点B出发,沿着BD向点D移动,若过点P作PE⊥AB、PF⊥AD,垂足分别为E、F,连接EF,则EF的长最小为( )
A. B. C.5 D.7
二、填空题
6.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
7.如图,△ODC是由△OAB绕点O顺时针旋转后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,∠BOD的度数为40°,则∠BDC的度数是 .
8.如图,在 ABCD中,BE垂直平分CD于点E,∠BAD=45°,AD=6cm,则 ABCD的对角线AC的长为 cm.
9.如图,矩形ABCD中,∠ACD=30°,边,DM⊥AC于点M,连接BM,则图中阴影部分的面积是 .
10.如图,在正方形ABCD中,E、F、G分别是边AD、BC、CD上的点,BG⊥EF,垂足为H,下列结论中:①H为线段BG的中点;②∠DEF=∠BGC;③BG=EF;④AE+FC=DG,正确的结论有 .
三、解答题
11.如图,在△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,分别连接AD、BE,点M、N、H分别是AD、BE、AB的中点,连接MN、MH、NH.
(1)试猜想△MNH是何特殊三角形,并说明理由;
(2)若AE=4,BD=6,求线段MN的长.
12.如图,等腰△ABC中,AB=AC,AD⊥BC交BC于D点,E点是AB的中点,分别过D,E两点作线段AC的垂线,垂足分别为G,F两点.
(1)求证:四边形DEFG为矩形;
(2)若AB=20,EF=8,求CG的长.
13.如图,矩形ABCD的对角线AC与BD交于点O,点E是CD的中点,连接AE交BD于点F,延长AE到点P,使FP=AF,连接CF,CP,DP.
(1)求证:四边形CFDP是平行四边形;
(2)若四边形CFDP是矩形,且,求AB的长度.
14.在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(﹣2,5),B(﹣3,0),C(1,2).将△ABC绕原点O顺时针旋转180°得到△A′B′C′,点A,B,C的对应点分别为A′,B′,C′.
(1)画出旋转后的△A′B′C′;
(2)直接写出点C′的坐标;
(3)P,Q是△ABC内不重合的两点,旋转后的对应点为P′,Q′,判断线段P′Q′与线段PQ的关系.
15.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(0,﹣a﹣b),且a,b满足.
(1)直接写出A,B,C的坐标:A ,B ,C ;
(2)平移线段AB得到线段CD,连接BD,则四边形ABCD是平行四边形,求四边形ABCD的面积;
(3)在(2)的条件下,点Q(m,n)在四边形OCDB内部,满足S三角形QOC:S三角形QOB=5:2.(提示:S三角形QOC,S三角形QOB分别表示三角形QOC,三角形QOB的面积)
①求m,n满足的数量关系;
②若S三角形QCD=S三角形QBD,求点Q的坐标.
参考答案
一、选择题
1.【解答】解:A、∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,故不符合题意;
B、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故不符合题意;
C、∵∠ACB=∠DAC=40°,
∴AD∥BC,
∵AB=CD,
∴不能判定四边形ABCD是平行四边形,故符合题意;
D、∠ACB=∠CAD=40°,
∴AD∥BC,
∵∠ABD=∠BDC=35°,
∴AB∥CD,
∴四边形ABCD是平行四边形,故不符合题意;
故选:C.
2.【解答】解:该图是中心对称图形,不是轴对称图形,
故选:A.
3.【解答】解:如图,AB=2cm,,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC,
∴,
∴,
∴AC=2OA=2,
∴菱形的面积.
故选:D.
4.【解答】解:在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠EAD=45°,AD∥BC,OA=OB=6,
∴∠AEB=∠EAD=45°,
∴BE=BA.
∵∠CAE=15°,∠BAE=45°,
∴∠BAC=60°,
又∵OA=OB,
∴△OAB为等边三角形,
∴BO=BA=9,
∴BO=BE=9.
故选:B.
5.【解答】解:如图,连接AP,
∵PE⊥AB,PF⊥AD,
∴∠AEP=∠AFP=90°.
∵四边形ABCD是矩形,
∴∠BAD=90°.
∴四边形AEPF为矩形.
∴AP=EF.
∴要求EF的最小值就是要求AP的最小值.
∵点P从B点沿着BD往D点移动,
∴当AP⊥BD时,AP取最小值.
在Rt△BAD中,
∵∠BAD=90°,AB=6,AD=8,
∴BD10,
∵,
∴.
∴EF的长度最小为:.
故选:B.
二、填空题
6.【解答】解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
.
∴△BNA≌△BNE(ASA),
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MNDE.
故答案为:.
7.【解答】解:由条件可知∠AOD=∠BOC,AD=OD,∠A=∠ODC,
∴∠A=∠ADO,
∵∠AOC=100°,∠BOD=40°,
∴,
∴,
∴∠ODC=∠A=75°,
∴∠BDC=180°﹣∠ADO﹣∠ODC=180°﹣75°﹣75°=30°,
故答案为:30°.
8.【解答】解:在 ABCD中,BE垂直平分CD于点E,∠BAD=45°,AD=6cm,如图,连接BD交AC于点F.
∴BD=BC,BC=AD=2,BF=DF,AC=2AF,
∴BD=AD=6cm,
∴DFBD6=3(cm),
∵∠BAD=45°,
∴∠ABD=45°,
∴∠ADB=90°.
在Rt△ADF中,由勾股定理得:AF3(cm),
∴AC=2AF=6cm.
故答案为:6.
9.【解答】解:∵ABCD是矩形,
∴∠DAB=∠ADC=90°,
∵∠ACD=30°,,
∴,
∵DM⊥AC,
∴∠ADM=30°,
∴,
过点M作MH⊥AB,
∴,
则图中阴影部分的面积=S矩形ABCD﹣S△ADM﹣S△ABM﹣S△BCD
,
故答案为:.
10.【解答】解:①如图,当点E,D重合,F,C重合时,
则点G,H与点C重合,
此时BG=BH,故①错误;
②∵BG⊥EF,
∴∠CBG+∠BFH=∠CBG+∠BGC=90°,
∴∠BFH=∠BGC,
∵AD∥BC,
∴∠BFH=∠DEF,
∴∠DEF=∠BGC,故②正确;
③过点E作EM⊥BC于点M,则四边形ABME是矩形,
∴AB=EM,
∵AB=BC,
∴BC=EM,
∵∠CBG+∠BFH=∠FEM+∠BFH=90°,
∴∠CBG=∠FEM,
∵∠C=∠EMF=90°,
∴△BCG≌△EMF(ASA),
∴BG=EF,故③正确;
④∵FM=CG,BM=AE,
∵CD=BC,
∴AE+CF=BC﹣FM,DG=CD﹣CG,
∴AE+FC=DG,故④正确;
故答案为:②③④.
解答题
11.【解答】解:(1)△MNH是直角三角形,理由如下:
∵点M、N、H分别是AD、BE、AB的中点,
∴HM∥BD且HMBD,HN∥AE且HNAE,
∴∠AHM=∠ABC,∠BHN=∠BAC,
∴∠MHN=180°﹣(∠AHM+∠BHN)
=180°﹣(∠ABC+∠BAC),
∵∠ACB=90°,
∴∠ABC+∠BAC=90°,
∴∠AHM=180°﹣(∠ABC+∠BAC)=90°,
∴△MNH是直角三角形.
(2)∵点M、N、H分别是AD、BE、AB的中点,
∴HM∥BD且HMBD=3,HN∥AE且HNAE=2,
∵△MNH是直角三角形,
∴MN2=MH2+NH2=MH2+NH2=9+4=13,
∴MN.
12.【解答】(1)证明:∵AB=AC,AD⊥BC,
∴点D是BC的中点.
∵E点是AB的中点,
∴DE是△ABC 的中位线.
∴DE∥AC.
∵DG⊥AC,EF⊥AC,
∴EF∥DG.
∴四边形DEFG是平行四边形.
又∵∠EFG=90°,
∴四边形DEFG为矩形;
(2)解:∵AD⊥BC交BC于D点,E点是AB的中点,AB=20,
∴DE=AE10,
由(1)知,四边形DEFG为矩形,则GF=DE=10.
在Rt△AEF 中,EF=8,AE=10,由勾股定理得:AF6.
∵AB=AC=20,FG=ED=10,
∴GC=AC﹣FG﹣AF=20﹣10﹣6=4.
13.【解答】(1)证明:∵四边形ABCD是矩形,
∴AO=CO,
∵FP=AF,
∴OF是△ACP的中位线,
∴OF∥CP,
∴∠FDE=∠PCE(两直线平行,内错角相等),
∵点E是CD的中点,
∴DE=CE,
在△DEF和△CEP中,
,
∴△DEF≌△CEP(ASA),
∴EF=EP,
又∵DE=CE,
∴四边形CFDP是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB,∠ADE=90°,
∴根据勾股定理,AD2+DE2=AE2,
若四边形CFDP是矩形,则,
,FP=CD,
∵AF=FP,
∴,
∴,
∴AD2=2CD2,
∴或(不符合题意,舍去),
∵,
∴CD=AB=1,所以AB的长度为1.
14.【解答】解:(1)将△ABC绕原点O顺时针旋转180°得到△A′B′C′,如图1即为所求;
(2)点C′的坐标为(﹣1,﹣2);理由如下:
由图可知,点C′的坐标为(﹣1,﹣2);
(3)P′Q′=PQ.理由如下:
如图2,
设P(a,b),Q(m,n),则P′(﹣a,﹣b),Q′(﹣m,﹣n),
线段P′Q′与线段PQ关于原点对称,
∵,,
∴P′Q′=PQ.
15.【解答】解:(1)∵a,b满足,
∴a﹣4=0,2b﹣12=0,
解得a=4,b=6,
∴A(0,4),B(6,0),C(0,﹣10);
(2)由(1)得AC=4+10=14,OB=6,
∴求平行四边形ABCD的面积为AC OB=14×6=84;
(3)①设Q(m,n),
∵A(0,4),B(6,0),C(0,﹣10),
∴OC=10,OB=6,AC=14,
∵平移线段AB至线段CD,
∴D(6,﹣14),
满足S三角形QOC:S三角形QOB=5:2.
由条件可知,
∴nm,
②由①得Q(m,m),
由图可得:
S△QCD=S梯形OCDB﹣S△QCO﹣S△QBD﹣S△QBC
=72﹣5m﹣(42﹣7m)﹣2m
=30,
∵,
∴m=6,
∴Q(6,﹣4).
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
