第9章中心对称图形—平行四边形单元测试(含答案)
文档属性
| 名称 | 第9章中心对称图形—平行四边形单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 675.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 13:54:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第9章中心对称图形—平行四边形单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
3.如图,在边长为6的正方形ABCD中,点E,F分别是边AB,BC上的动点,且满足AE=BF,AF与DE交于点O,点M是DF的中点,G是边AB上的点,AG=2GB,则OM+FG的最小值是( )
A.4 B.5 C.8 D.10
4.如图,正方形ABCD的对角线交于点O,点E是直线BC上一动点.若AB=4,则AE+OE的最小值是( )
A. B. C. D.
5.如图,矩形ABCD的对角线AC,BD相交于点O,点E是线段AC上一点,连接EB,ED.若△BED的面积等于△BEC的面积,则△ABE和△CDE的E面积比等于( )
A.2:1 B.3:1 C.3:2 D.9:4
6.如图,将△ABC绕B点顺时针方向旋转到△DBE,点A的对应点D恰好落在AC上,且BE∥AC.若∠A=70°,则∠C的度数为( )
A.30° B.40° C.45° D.36°
7.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠BCD=70°,则∠BOE的大小为( )
A.20° B.25° C.35° D.55°
8.如图,在平行四边形ABCD中,AM⊥BC于点M,AN⊥CD于点N,若平行四边形ABCD的周长为22,且AM=4,,则平行四边形ABCD的面积为( )
A.48 B.36 C.24 D.12
二.填空题(每小题5分,满分20分)
9.在 ABCD中,BE,CF分别平分∠ABC,∠BCD,分别交AD于点E,F.若AB=3,BC=5,则EF的长为 .
10.如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线交AC于D.过点A作AE⊥BC于E,交BD于G,过点D作DF⊥BC于F,过点G作GH∥BC,交AC于点H,则下列结论:
①∠BAE=∠C;②S△ABG:S△EBG=AB:BE;③∠ADF=2∠CDF;
④四边形AGFD是菱形;⑤CH=DF.
其中正确的结论是 .
11.如图,将△ABC绕点A逆时针旋转到△ADE,旋转角为α(0°<α<180°),点B的对应点D恰好落在边BC上.若DE⊥AC,∠CAD=24°,则旋转角α的度数为 .
12.如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB,AC、BD的中点,若BC=8,则△PMN的周长是 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
(1)△ABC的形状是 (直接写答案);
(2)将△ABC向右平移3个单位长度得△A1B1C1,在坐标系中画出并求出这个变化过程中△ABC扫过的面积;
(3)画出△ABC绕点C逆时针旋转90°的△CA2B2.
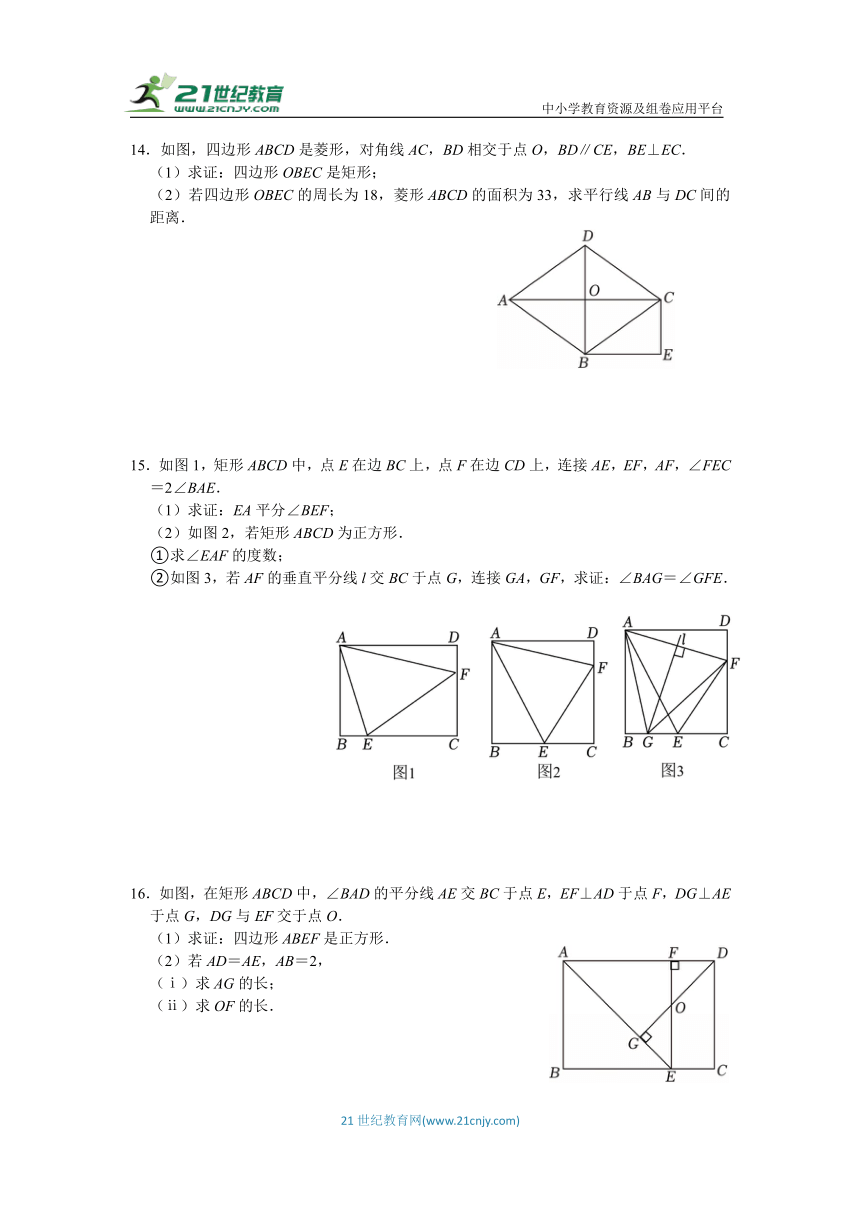
14.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,BD∥CE,BE⊥EC.
(1)求证:四边形OBEC是矩形;
(2)若四边形OBEC的周长为18,菱形ABCD的面积为33,求平行线AB与DC间的距离.
15.如图1,矩形ABCD中,点E在边BC上,点F在边CD上,连接AE,EF,AF,∠FEC=2∠BAE.
(1)求证:EA平分∠BEF;
(2)如图2,若矩形ABCD为正方形.
①求∠EAF的度数;
②如图3,若AF的垂直平分线l交BC于点G,连接GA,GF,求证:∠BAG=∠GFE.
16.如图,在矩形ABCD中,∠BAD的平分线AE交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形.
(2)若AD=AE,AB=2,
(ⅰ)求AG的长;
(ⅱ)求OF的长.
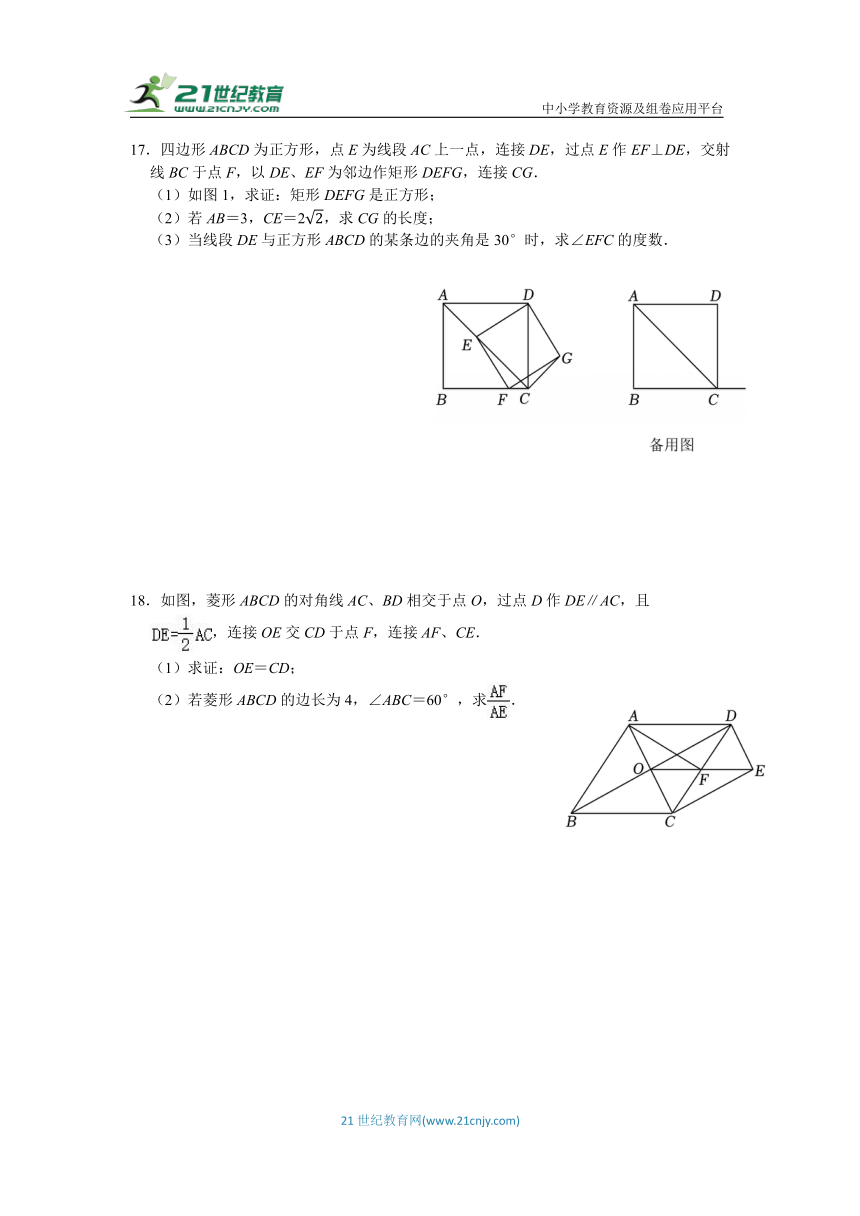
17.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=3,CE=2,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,求∠EFC的度数.
18.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且
,连接OE交CD于点F,连接AF、CE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求.
参考答案
一、选择题
1—8:DCBDABCC
二、填空题
9.解:∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
则∠ABE=∠AEB,
∴AE=AB=3,
同理可证:DF=CD=3,
∴EF=AE+FD﹣AD=3+3﹣5=1.
故答案为:1.
10.解:①∵∠BAC=90°,
∴∠BAE+∠CAE=90°,
∵AE⊥BC,
∴∠C+∠CAE=90°,
∴∠BAE=∠C,①正确;
②作AM∥BD交CB的延长线于M,如图所示:
则∠M=∠CBD,∠BAM=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠M=∠BAM,
∴AB=BM,
∵AM∥BD,
∴AG:GE=BM:BE,
∴AG:GE=AB:BE,
∵S△ABG:S△EBG=AG:GE,
∴S△ABG:S△EBG=AB:BE;②正确;
④∵∠AGD=∠ABD+∠BAE,∠ADG=∠CBD+∠C,∠BAE=∠C,∠CBD=∠ABD,
∴∠AGD=∠ADG,
∴AG=AD,
∵∠BAC=90°,BD平分∠ABC.DF⊥BC,
∴AD=DF,
∴AG=DF,
∵AE⊥BC,
∴AG∥DF,
∴四边形AGFD是平行四边形,
又∵AG=AD,
∴四边形AGFD是菱形;④正确;
⑤∵四边形AGFD是菱形;
∴∠AGD=∠FGD,GF=DF,∠ADB=∠FDB,
∴∠AGB=∠FGB,
在△ABG和△FBG中,
,
∴△ABG≌△FBG(ASA),
∴∠BAE=∠BFG,
∵∠BAE=∠C,
∴∠BFG=∠C,
∴GF∥CH,
∵GH∥BC,
∴四边形GFCH是平行四边形,
∴GF=CH,
∴CH=DF,⑤正确;
③∵∠ADF=2∠ADB,
当∠C=30°,∠CDF=60°,
则∠ADF=120°,
∴∠ADF=2∠CDF;③不正确;
故答案为:①②④⑤.
11.解:如图,
∵DE⊥AC,
∴∠AFD=90°,
∵∠CAD=24°,
∴∠ADE=180°﹣∠CAD﹣∠AFD=180°﹣24°﹣90°=66°,
∵旋转,
∴∠B=∠ADE=66°,AB=AD,
∴∠ADB=∠B=66°,
∴∠BAD=180°﹣∠B﹣∠ABD=180°﹣66°﹣66°=48°,
即旋转角α的度数是48°.
故答案为:48°.
12.解:∵P、N是AB和BD的中点,
∴PNAD8=4,PN∥AD,
∴∠NPB=∠DAB=50°,
同理,PM=4,∠MPA=∠CBA=70°,
∴PM=PN=4,∠MPN=180°﹣50°﹣70°=60°,
∴△PMN是等边三角形.
∴MN=PM=PN=4,
∴△PMN的周长是12.
三、解答题
13.【解答】解:(1)由勾股定理得,AB,AC,BC,
∴AB=AC,AB2+AC2=BC2,
∴∠BAC=90°,
∴△ABC为等腰直角三角形.
故答案为:等腰直角三角形.
(2)如图,△A1B1C1即为所求.
这个变化过程中△ABC扫过的面积为.
(3)如图,△CA2B2即为所求.
14.【解答】(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵BD∥CE,
∴CE⊥AC,
又∵BE⊥EC,
∴∠BOC=∠OCE=∠CEB=90°,
∴四边形OBEC是矩形;
(2)解:∵四边形OBEC的周长为18,四边形OBEC是矩形,
∴OC+OB=9,
∵菱形ABCD的面积为33,
∴AC BD=33,
即2OB×2OC=33,
∴2OB OC=33,
∵OC+OB=9,
∴(OC+OB)2=81,
∴OC2+2OB OC+OB2=81,
∴OC2+OB2=48,
∴BC4,
∵四边形ABCD是菱形,
∴AB=BC=4,
设平行线AB与DC间的距离为x,
则AB x=33,
即4x=33,
解得x,
即平行线AB与DC间的距离为.
15.【解答】(1)证明:作EH平分∠FEC,交CD于点H,
∴,
∵∠FEC=2∠BAE,
∴∠FEH=∠CEH=∠BAE,
∵矩形ABCD中,∠B=90°,
∴∠AEB+∠BAE=90°,
∴∠AEB+∠CEH=90°,
∴∠AEF+∠FEH=90°,
∴∠AEB=∠AEF,即EA平分∠BEF;
(2)①过点A作AR⊥EF于点R,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ARE=90°,
由(1)得∠AEB=∠AEF,
又∵AE=AE,
∴△EAB≌△EAR,
∴AB=AR,∠BAE=∠RAE,
∴AD=AR,
∵AF=AF,∠D=∠FRA=90°,
∴△FAD≌△FAR,
∴∠FAD=∠FAR,
∴;
②过点A作AW⊥EF,在EF上截取ET=EG,
∵ET=EG,∠AEG=∠AET,AE=AE,
∴△AEG≌△AET,
∴∠2=∠3,AG=AT,∠AGE=∠ATE,
∴∠AGB=∠ATW,
∴∠1=∠4
∵AF的垂直平分线l交BC于点G,
∴∠5+∠GAF=90°
∵∠EAF=45°,
∴∠5+∠2=45°,
∴2∠5+2∠2=90°,即∠AGF+∠GAQ=90°,
∴∠AQG=90°,
∴∠AQP=90°=∠AWF,
∵∠APQ=∠FPW,
∴∠PFW=∠4
∴∠GFE=∠1,即∠BAG=∠GFE.
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴∠AFE=∠BAF=∠ABE=90°,
∴四边形ABEF是矩形.
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)(ⅰ)∵AE平分∠BAD,
∴∠DAG=∠BAE.
在△AGD和△ABE中,
∴△AGD≌△ABE(AAS),
∴AB=AG,
∴AG=AB=2;
(ⅱ)由(1)知,四边形ABEF是正方形,
∴AF=AB=2,
由(2)(ⅰ)可知,△AGD≌△ABE,
∴DG=EB=AB=AF=AG=2,
∴,∠DAG=∠ADG=45°,
∴.
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴.
17.【解答】(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA=45°,
∴EQ=EP,
∵∠QEF+∠PEF=90°,∠PED+∠PEF=90°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)解:∵四边形ABCD是正方形,AB=3,
∴AD=CD=3,∠ADC=90°,ACAD=3,
∵CE=2,
∴AE,
∵四边形DEFG是正方形,
∴DE=DG,∠EDG=90°=∠ADC,
∴∠ADE=∠CDG,
∴△ADE≌△CDG(SAS),
∴CG=AE;
(3)解:①当DE与AD的夹角为30°时,
如图2,
∵∠ADE=30°,∠ADC=90°,
∴∠EDC=60°,
∵∠EDC+∠DEF+∠EFC+∠FCD=360°,
∴∠EFC=360°﹣90°﹣90°﹣60°=120°;
②当DE与DC的夹角为30°时,
如图3
∵∠DEF=∠DCF=90°,
∴点D,点E,点C,点F四点共圆,
∴∠EDC=∠EFC=30°,
综上所述:∠EFC=30°或120°.
18.【解答】(1)证明:四边形ABCD是菱形,
∴OA=OC=AC,AD=CD,
∵DE∥AC且DE=AC,
∴DE=OA=OC,
∴四边形OADE、四边形OCED都是平行四边形,
∴OE=AD,
∴OE=CD;
(2)解:连接AE.
∵AC⊥BD,
∴四边形OCED是矩形,
∴CF=DF,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=CD=AD=4,
∴AF⊥CD,
∴AF===2,
在矩形OCED中,CE=OD==2.
在Rt△ACE中,AE===2.
∴==,
21世纪教育网(www.21cnjy.com)
第9章中心对称图形—平行四边形单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
3.如图,在边长为6的正方形ABCD中,点E,F分别是边AB,BC上的动点,且满足AE=BF,AF与DE交于点O,点M是DF的中点,G是边AB上的点,AG=2GB,则OM+FG的最小值是( )
A.4 B.5 C.8 D.10
4.如图,正方形ABCD的对角线交于点O,点E是直线BC上一动点.若AB=4,则AE+OE的最小值是( )
A. B. C. D.
5.如图,矩形ABCD的对角线AC,BD相交于点O,点E是线段AC上一点,连接EB,ED.若△BED的面积等于△BEC的面积,则△ABE和△CDE的E面积比等于( )
A.2:1 B.3:1 C.3:2 D.9:4
6.如图,将△ABC绕B点顺时针方向旋转到△DBE,点A的对应点D恰好落在AC上,且BE∥AC.若∠A=70°,则∠C的度数为( )
A.30° B.40° C.45° D.36°
7.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠BCD=70°,则∠BOE的大小为( )
A.20° B.25° C.35° D.55°
8.如图,在平行四边形ABCD中,AM⊥BC于点M,AN⊥CD于点N,若平行四边形ABCD的周长为22,且AM=4,,则平行四边形ABCD的面积为( )
A.48 B.36 C.24 D.12
二.填空题(每小题5分,满分20分)
9.在 ABCD中,BE,CF分别平分∠ABC,∠BCD,分别交AD于点E,F.若AB=3,BC=5,则EF的长为 .
10.如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线交AC于D.过点A作AE⊥BC于E,交BD于G,过点D作DF⊥BC于F,过点G作GH∥BC,交AC于点H,则下列结论:
①∠BAE=∠C;②S△ABG:S△EBG=AB:BE;③∠ADF=2∠CDF;
④四边形AGFD是菱形;⑤CH=DF.
其中正确的结论是 .
11.如图,将△ABC绕点A逆时针旋转到△ADE,旋转角为α(0°<α<180°),点B的对应点D恰好落在边BC上.若DE⊥AC,∠CAD=24°,则旋转角α的度数为 .
12.如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB,AC、BD的中点,若BC=8,则△PMN的周长是 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
(1)△ABC的形状是 (直接写答案);
(2)将△ABC向右平移3个单位长度得△A1B1C1,在坐标系中画出并求出这个变化过程中△ABC扫过的面积;
(3)画出△ABC绕点C逆时针旋转90°的△CA2B2.
14.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,BD∥CE,BE⊥EC.
(1)求证:四边形OBEC是矩形;
(2)若四边形OBEC的周长为18,菱形ABCD的面积为33,求平行线AB与DC间的距离.
15.如图1,矩形ABCD中,点E在边BC上,点F在边CD上,连接AE,EF,AF,∠FEC=2∠BAE.
(1)求证:EA平分∠BEF;
(2)如图2,若矩形ABCD为正方形.
①求∠EAF的度数;
②如图3,若AF的垂直平分线l交BC于点G,连接GA,GF,求证:∠BAG=∠GFE.
16.如图,在矩形ABCD中,∠BAD的平分线AE交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形.
(2)若AD=AE,AB=2,
(ⅰ)求AG的长;
(ⅱ)求OF的长.
17.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=3,CE=2,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,求∠EFC的度数.
18.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且
,连接OE交CD于点F,连接AF、CE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求.
参考答案
一、选择题
1—8:DCBDABCC
二、填空题
9.解:∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
则∠ABE=∠AEB,
∴AE=AB=3,
同理可证:DF=CD=3,
∴EF=AE+FD﹣AD=3+3﹣5=1.
故答案为:1.
10.解:①∵∠BAC=90°,
∴∠BAE+∠CAE=90°,
∵AE⊥BC,
∴∠C+∠CAE=90°,
∴∠BAE=∠C,①正确;
②作AM∥BD交CB的延长线于M,如图所示:
则∠M=∠CBD,∠BAM=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠M=∠BAM,
∴AB=BM,
∵AM∥BD,
∴AG:GE=BM:BE,
∴AG:GE=AB:BE,
∵S△ABG:S△EBG=AG:GE,
∴S△ABG:S△EBG=AB:BE;②正确;
④∵∠AGD=∠ABD+∠BAE,∠ADG=∠CBD+∠C,∠BAE=∠C,∠CBD=∠ABD,
∴∠AGD=∠ADG,
∴AG=AD,
∵∠BAC=90°,BD平分∠ABC.DF⊥BC,
∴AD=DF,
∴AG=DF,
∵AE⊥BC,
∴AG∥DF,
∴四边形AGFD是平行四边形,
又∵AG=AD,
∴四边形AGFD是菱形;④正确;
⑤∵四边形AGFD是菱形;
∴∠AGD=∠FGD,GF=DF,∠ADB=∠FDB,
∴∠AGB=∠FGB,
在△ABG和△FBG中,
,
∴△ABG≌△FBG(ASA),
∴∠BAE=∠BFG,
∵∠BAE=∠C,
∴∠BFG=∠C,
∴GF∥CH,
∵GH∥BC,
∴四边形GFCH是平行四边形,
∴GF=CH,
∴CH=DF,⑤正确;
③∵∠ADF=2∠ADB,
当∠C=30°,∠CDF=60°,
则∠ADF=120°,
∴∠ADF=2∠CDF;③不正确;
故答案为:①②④⑤.
11.解:如图,
∵DE⊥AC,
∴∠AFD=90°,
∵∠CAD=24°,
∴∠ADE=180°﹣∠CAD﹣∠AFD=180°﹣24°﹣90°=66°,
∵旋转,
∴∠B=∠ADE=66°,AB=AD,
∴∠ADB=∠B=66°,
∴∠BAD=180°﹣∠B﹣∠ABD=180°﹣66°﹣66°=48°,
即旋转角α的度数是48°.
故答案为:48°.
12.解:∵P、N是AB和BD的中点,
∴PNAD8=4,PN∥AD,
∴∠NPB=∠DAB=50°,
同理,PM=4,∠MPA=∠CBA=70°,
∴PM=PN=4,∠MPN=180°﹣50°﹣70°=60°,
∴△PMN是等边三角形.
∴MN=PM=PN=4,
∴△PMN的周长是12.
三、解答题
13.【解答】解:(1)由勾股定理得,AB,AC,BC,
∴AB=AC,AB2+AC2=BC2,
∴∠BAC=90°,
∴△ABC为等腰直角三角形.
故答案为:等腰直角三角形.
(2)如图,△A1B1C1即为所求.
这个变化过程中△ABC扫过的面积为.
(3)如图,△CA2B2即为所求.
14.【解答】(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵BD∥CE,
∴CE⊥AC,
又∵BE⊥EC,
∴∠BOC=∠OCE=∠CEB=90°,
∴四边形OBEC是矩形;
(2)解:∵四边形OBEC的周长为18,四边形OBEC是矩形,
∴OC+OB=9,
∵菱形ABCD的面积为33,
∴AC BD=33,
即2OB×2OC=33,
∴2OB OC=33,
∵OC+OB=9,
∴(OC+OB)2=81,
∴OC2+2OB OC+OB2=81,
∴OC2+OB2=48,
∴BC4,
∵四边形ABCD是菱形,
∴AB=BC=4,
设平行线AB与DC间的距离为x,
则AB x=33,
即4x=33,
解得x,
即平行线AB与DC间的距离为.
15.【解答】(1)证明:作EH平分∠FEC,交CD于点H,
∴,
∵∠FEC=2∠BAE,
∴∠FEH=∠CEH=∠BAE,
∵矩形ABCD中,∠B=90°,
∴∠AEB+∠BAE=90°,
∴∠AEB+∠CEH=90°,
∴∠AEF+∠FEH=90°,
∴∠AEB=∠AEF,即EA平分∠BEF;
(2)①过点A作AR⊥EF于点R,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ARE=90°,
由(1)得∠AEB=∠AEF,
又∵AE=AE,
∴△EAB≌△EAR,
∴AB=AR,∠BAE=∠RAE,
∴AD=AR,
∵AF=AF,∠D=∠FRA=90°,
∴△FAD≌△FAR,
∴∠FAD=∠FAR,
∴;
②过点A作AW⊥EF,在EF上截取ET=EG,
∵ET=EG,∠AEG=∠AET,AE=AE,
∴△AEG≌△AET,
∴∠2=∠3,AG=AT,∠AGE=∠ATE,
∴∠AGB=∠ATW,
∴∠1=∠4
∵AF的垂直平分线l交BC于点G,
∴∠5+∠GAF=90°
∵∠EAF=45°,
∴∠5+∠2=45°,
∴2∠5+2∠2=90°,即∠AGF+∠GAQ=90°,
∴∠AQG=90°,
∴∠AQP=90°=∠AWF,
∵∠APQ=∠FPW,
∴∠PFW=∠4
∴∠GFE=∠1,即∠BAG=∠GFE.
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴∠AFE=∠BAF=∠ABE=90°,
∴四边形ABEF是矩形.
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)(ⅰ)∵AE平分∠BAD,
∴∠DAG=∠BAE.
在△AGD和△ABE中,
∴△AGD≌△ABE(AAS),
∴AB=AG,
∴AG=AB=2;
(ⅱ)由(1)知,四边形ABEF是正方形,
∴AF=AB=2,
由(2)(ⅰ)可知,△AGD≌△ABE,
∴DG=EB=AB=AF=AG=2,
∴,∠DAG=∠ADG=45°,
∴.
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴.
17.【解答】(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA=45°,
∴EQ=EP,
∵∠QEF+∠PEF=90°,∠PED+∠PEF=90°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)解:∵四边形ABCD是正方形,AB=3,
∴AD=CD=3,∠ADC=90°,ACAD=3,
∵CE=2,
∴AE,
∵四边形DEFG是正方形,
∴DE=DG,∠EDG=90°=∠ADC,
∴∠ADE=∠CDG,
∴△ADE≌△CDG(SAS),
∴CG=AE;
(3)解:①当DE与AD的夹角为30°时,
如图2,
∵∠ADE=30°,∠ADC=90°,
∴∠EDC=60°,
∵∠EDC+∠DEF+∠EFC+∠FCD=360°,
∴∠EFC=360°﹣90°﹣90°﹣60°=120°;
②当DE与DC的夹角为30°时,
如图3
∵∠DEF=∠DCF=90°,
∴点D,点E,点C,点F四点共圆,
∴∠EDC=∠EFC=30°,
综上所述:∠EFC=30°或120°.
18.【解答】(1)证明:四边形ABCD是菱形,
∴OA=OC=AC,AD=CD,
∵DE∥AC且DE=AC,
∴DE=OA=OC,
∴四边形OADE、四边形OCED都是平行四边形,
∴OE=AD,
∴OE=CD;
(2)解:连接AE.
∵AC⊥BD,
∴四边形OCED是矩形,
∴CF=DF,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=CD=AD=4,
∴AF⊥CD,
∴AF===2,
在矩形OCED中,CE=OD==2.
在Rt△ACE中,AE===2.
∴==,
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
