苏科版2024—2025学年八年级下学期数学期末考试模拟试卷(含答案)
文档属性
| 名称 | 苏科版2024—2025学年八年级下学期数学期末考试模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 601.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 13:54:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏科版2024—2025学年八年级下学期数学期末考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是红球 B.至少有1个球是白球
C.至少有2个球是红球 D.至少有2个球是白球
2.下列图形既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
3.把分式中的x和y都扩大3倍,分式的值( )
A.不变 B.扩大3倍 C.缩小3倍 D.扩大9倍
4.如图,在四边形ABCD中,已知AD∥BC.添加下列条件不能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AB∥DC C.AB=DC D.∠A=∠C
5.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A. B. C.D.
6.对于反比例函数,下列说法正确的是( )
A.图象经过点(2,﹣3) B.图象位于第一、三象限
C.y随x的增大而增大 D.当0<x<1时,y<﹣5
7.如图,∠CAB=25°,CA、CB是等腰△ABC的两腰,将△ABC绕点A顺时针进行旋转,得到△ADE.当点B恰好在DE的延长线时,则∠EAB的度数为( )
A.155° B.130° C.105° D.75°
8.如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断 ADCE是菱形的是( )
A.∠BAC=90° B.∠DAE=90° C.AB=AC D.AB=AE
9.为了改善生态环境,某社区计划在荒坡上种植600棵树,由于学生志愿者的加入,每日比原计划多种20棵,结果提前1天完成任务.设原计划每天种树x棵,根据题意可列方程为( )
A. B.
C. D.
10.如果实数a满足|2024﹣a|a.那么a﹣20242的值是( )
A.2025 B.2024 C.2023 D.2022
二、填空题(6小题,每题3分,共18分)
11.在分式中,当x= 时,分式的值为零.
12.当2时,的值是 .
13.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
14.在菱形ABCD中,已知对角线DB=10,AC=16,那么菱形ABCD的面积为 .
15.一个不透明的袋子中装有红球、白球共9个,这些球除颜色外都相同.若从中任意摸出一个球,则摸到白球的可能性大,则红球至多有 个.
16.如图,在 ABCD中,∠A=45°,,点M,N分别是边AB,BC上的动点,连接DN,MN,点E,F分别为DN,MN的中点,连接EF,则EF的最小值为 .
苏科版2024—2025学年八年级下学期数学期末考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简再求值:,请你选一个使原代数式有意义的数代入求值.
18.解方程:
(1); (2).
19.计算:
(1)(1)×(1);(2)()2.
20.已知,求下列各式的值.
(1);(2).
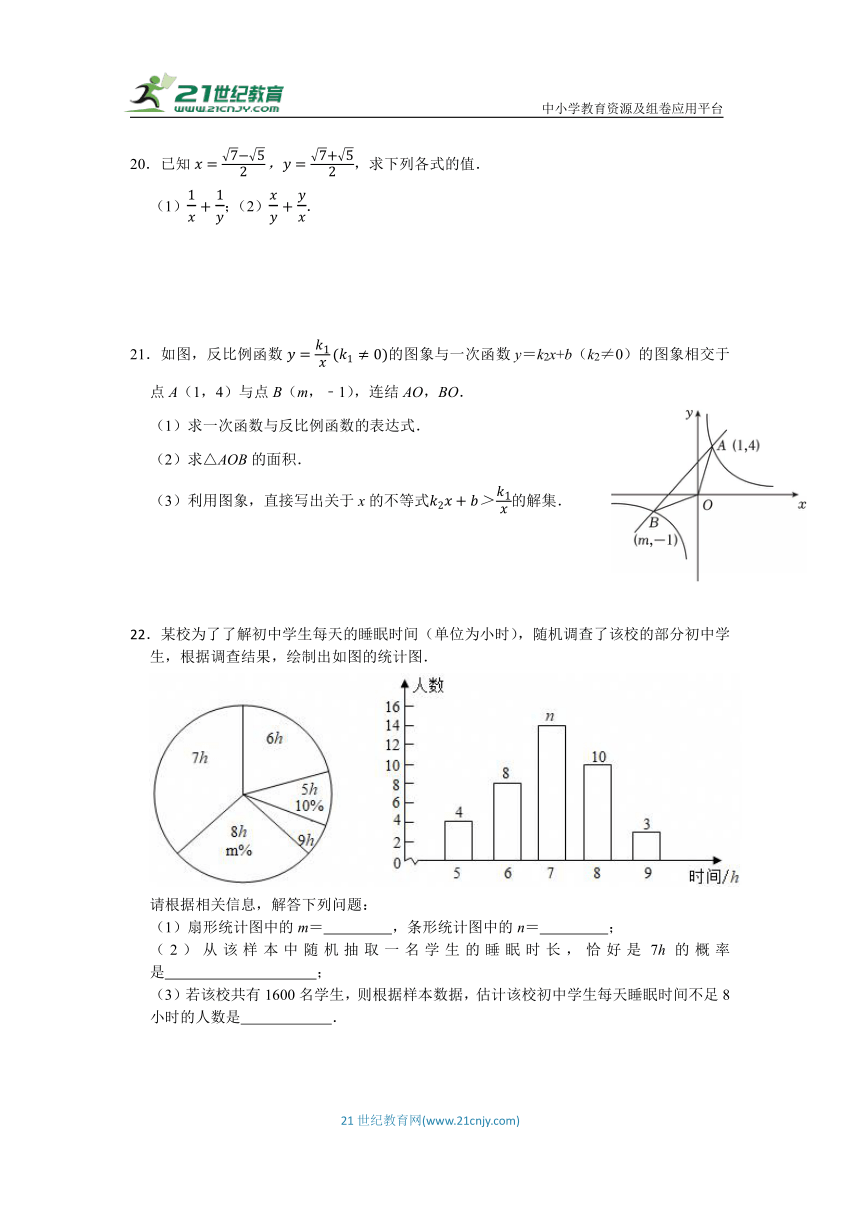
21.如图,反比例函数的图象与一次函数y=k2x+b(k2≠0)的图象相交于点A(1,4)与点B(m,﹣1),连结AO,BO.
(1)求一次函数与反比例函数的表达式.
(2)求△AOB的面积.
(3)利用图象,直接写出关于x的不等式的解集.
22.某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图的统计图.
请根据相关信息,解答下列问题:
(1)扇形统计图中的m= ,条形统计图中的n= ;
(2)从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是 ;
(3)若该校共有1600名学生,则根据样本数据,估计该校初中学生每天睡眠时间不足8小时的人数是 .
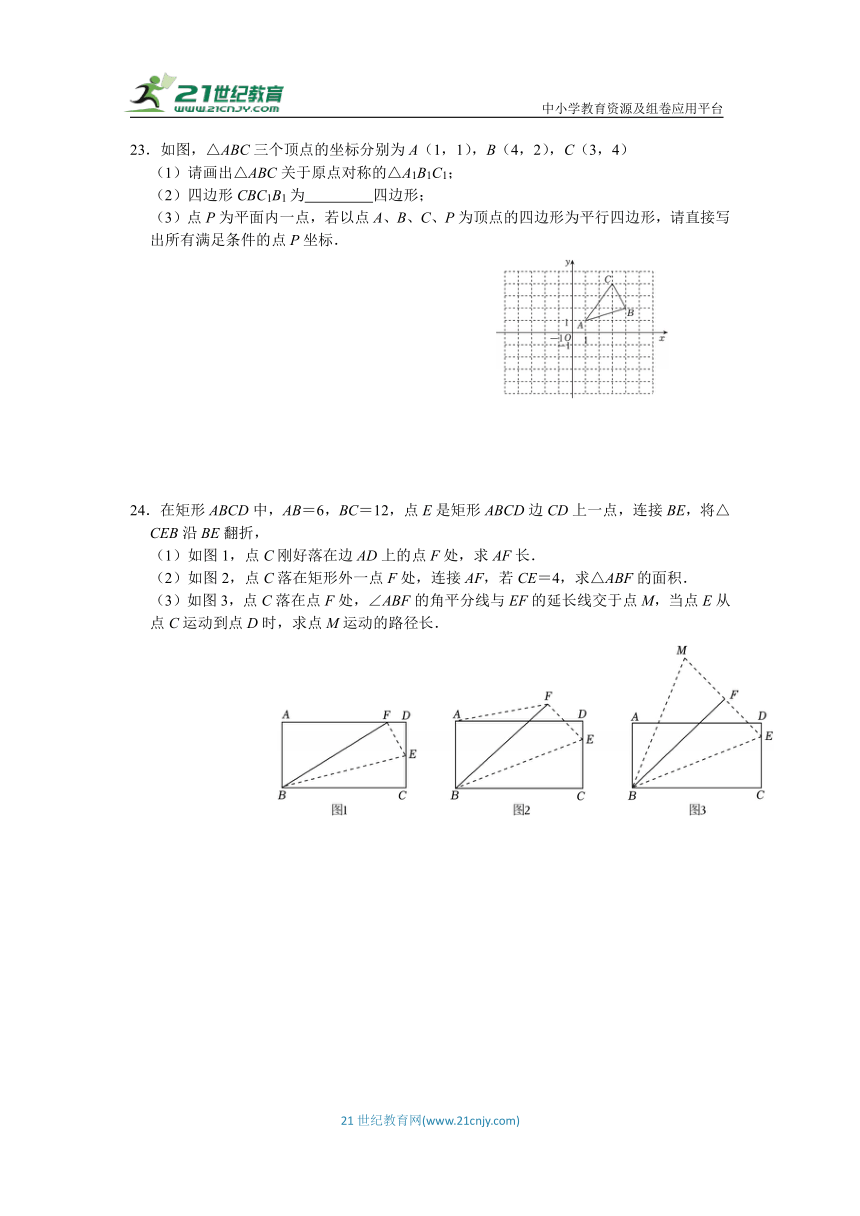
23.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)四边形CBC1B1为 四边形;
(3)点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
24.在矩形ABCD中,AB=6,BC=12,点E是矩形ABCD边CD上一点,连接BE,将△CEB沿BE翻折,
(1)如图1,点C刚好落在边AD上的点F处,求AF长.
(2)如图2,点C落在矩形外一点F处,连接AF,若CE=4,求△ABF的面积.
(3)如图3,点C落在点F处,∠ABF的角平分线与EF的延长线交于点M,当点E从点C运动到点D时,求点M运动的路径长.
25.新定义:如果两个实数a(a≠0)、b使得关于x的分式方程的解是成立,那么我们就把实数a,b组成的数对[a,b]称为关于x的分式方程的一个“友好数对”.
例如:a=2,b=﹣3使得关于x的分式方程的解是成立,所以数对[2,﹣3]就是关于x的分式方程的一个“友好数对”.
(1)判断下列数对是否为关于x的分式方程的“友好数对”,若是,请在括号内打“√”.若不是,打“×”.①[2,1]( );②[3,﹣4]( ).
(2)请判断数对[n,n﹣3]是否有可能是关于x的分式方程的“友好数对”,如果可能,请求出此时的n需满足什么条件?如果不可能,请说明理由.
(3)若数对[﹣3,kn](k<﹣2,n≠0)是关于x的分式方程的“友好数对”,,,试比较M、N的大小.
参考答案
一、选择题
1—10:BDBCCDCADA
二、填空题
11.【解答】解:由题意得:x2﹣1=0且x﹣1≠0,
解得:x=﹣1.
故答案为:﹣1.
12.【解答】解:当2时,
,
故的值是.
故答案为.
13.【解答】解:∵种子粒数5000粒时,种子发芽的频率趋近于0.801,
∴估计种子发芽的概率为0.801,精确到0.1,即为0.8.
故本题答案为:0.8.
14.【解答】解:10×16
=5×16
=80
∴菱形ABCD的面积为80.
故答案为:80.
15.【解答】解:一个不透明的袋子中装有红球、白球共9个,这些球除颜色外都相同.若从中任意摸出一个球,摸到白球的可能性大,
∴白球的数量多于红球的数量,
∴红球至多有4个,
故答案为:4.
16.【解答】解:如图,连接DM,
∵E、F分别为DN、MN的中点,
∴,
∴EF的最小值,就是DM的最小值,当DM⊥AB时,DM最小,
∵在Rt△ADM中,∠A=45°,,
∴DM=AM,DM2+AM2=2DM2=AD2=2,
∴,
∴,
∴EF的最小值是.
故答案为:.
三、解答题
17.【解答】解:原式
,
∵x+3≠0且x+2≠0且x﹣2≠0,
∴x可以取1,
当x=1时,原式1.
18.【解答】解:(1),
方程两边同乘x(x﹣3),得x﹣3=4x,
解得x=﹣1,
检验:当x=﹣1时,x(x﹣3)≠0,
所以分式方程的解是x=﹣1;
(2),
方程两边同乘(x﹣1)(x+2),得x(x+2)=(x﹣1)(x+2)+7,
解得x=5,
检验:当x=5时,(x﹣1)(x+2)≠0,
所以分式方程的解是x=5.
19.【解答】解:(1)原式=323﹣1
2;
(2)原式=(2)
=3
=9
=8.
20.【解答】解:(1)∵,
∴xy ;x+y,
∴原式2;
(2)由(1)知,xy,x+y,
∴原式12.
21.【解答】解:(1)∵A(1,4),
∴k1=4.
∴反比例函数表达式为.
把B(m,﹣1)代入反比例函数,得m=﹣4.
把A(1,4),B(﹣4,﹣1)代入y=k2x+b,
得,
∴,
∴一次函数表达式为y=x+3;
(2)如图,由(1)得C(0,3),又A(1,4),B(﹣4,﹣1),
∴;
(3)由图象可得:不等式的解集为﹣4<x<0或x>1.
22.【解答】解:(1)本次接受调查的初中学生有:4÷10%=40(人),
m%=10÷40×100%=25%,即m=25,
n=40×37.5%=15,
故答案为:25,15;
(2)从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是,
故答案为:;
(3)16001080(人),
答:该校初中学生每天睡眠时间不足8小时的有1080人,
故答案为:1080人.
23.【解答】解:(1)△A1B1C1如图所示.
(2)连接CB1,BC1,
∵BC=B′C′,BC∥B′C′,
∴四边形CBC1B1为平行四边形,
故答案为平行.
(3)如图所示,满足条件的点P的坐标为(2,﹣1),(6,5),(0,3).
24.【解答】解:(1)由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∵四边形ABCD为矩形,
∴∠A=90°,
∴AF6.
(2)过点F作FG⊥AB,交AB的延长线于点G,延长GF交CD的延长线于点H,如图,
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵FG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
设HD=AG=x,则HE=x+2,BG=x+6,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,FE=CE=4.
∴∠EFH+∠GFB=90°.
∵∠GFB+∠GBF=90°,
∴∠EFH=∠GBF.
∵∠H=∠G=90°,
∴GF=3EH=3x+6,FHBGx+2,
∵GH=12,
∴3x+6x+2=12,
∴x.
∴FG=36,
∴△ABF的面积AB FG.
(3)过点M作MG⊥AB,交AB的延长线于点G,延长GM交CD的延长线于点H,如图
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵MG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∴∠G=∠BFM=90°.
∵BM为∠GBF的平分线,
∴∠GBM=∠FBM.
在△BGM和△BFM中,
,
∴△BGM≌△BFM(AAS),
∴BG=BF=12,
∴AG=BG=AB=6,
∵点M在GH上,
∴点M到AD的距离等于AG=6,即点M在GH上运动,
∴点E与点C重合时,点M与点H重合.
当点E与点D重合时,如图,
∵△BGM≌△BFM,
∴MG=MF,
由题意得:△BCE≌△BFE,
∴CD=DF=6.
∵四边形ADHG为矩形,
∴DH=AG=6.
设MG=MF=x,则MD=x+6,MH=GH﹣GM=12﹣x.
∵∠H=90°,
∴MD2=MH2+DH2,
∴(x+6)2=(12﹣x)2+62.
∴x=4.
∴MH=GH﹣GM=8.
∴当点E从点C运动到点D时,点M运动的路径长为线段HM的长等于8.
25.【解答】解:(1)关于x的分式方程,
∵x不是方程的解,
∴数对[2,1]不是关于x的分式方程的“友好数对”;
∵x是方程的解,
∴数对[3,﹣4]是关于x的分式方程的“友好数对”;
故答案为:×,√;
(2)当n=1时,数对[n,n﹣3]是否有可能是关于x的分式方程的“友好数对”,理由如下:
∵x是方程的解,
∴n(n+n﹣3)﹣1=n﹣3,
∴n2﹣2n+1=0,
∴(n﹣1)2=0,
∴n=1,
即n=1时,数对[n,n﹣3]是否有可能是关于x的分式方程的“友好数对”;
(3)∵数对[﹣3,kn](k<﹣2,n≠0)是关于x的分式方程的“友好数对”,
∴x是关于x的分式方程的解,
∴﹣3(﹣3+kn)﹣1=kn,
∴kn=2,
即n,
∴M,
N,
∴M﹣N,
∵k<﹣2,
∴k+2<0,k+1<0,
∴M﹣N>0,
∴M>N.
21世纪教育网(www.21cnjy.com)
苏科版2024—2025学年八年级下学期数学期末考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是红球 B.至少有1个球是白球
C.至少有2个球是红球 D.至少有2个球是白球
2.下列图形既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
3.把分式中的x和y都扩大3倍,分式的值( )
A.不变 B.扩大3倍 C.缩小3倍 D.扩大9倍
4.如图,在四边形ABCD中,已知AD∥BC.添加下列条件不能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AB∥DC C.AB=DC D.∠A=∠C
5.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A. B. C.D.
6.对于反比例函数,下列说法正确的是( )
A.图象经过点(2,﹣3) B.图象位于第一、三象限
C.y随x的增大而增大 D.当0<x<1时,y<﹣5
7.如图,∠CAB=25°,CA、CB是等腰△ABC的两腰,将△ABC绕点A顺时针进行旋转,得到△ADE.当点B恰好在DE的延长线时,则∠EAB的度数为( )
A.155° B.130° C.105° D.75°
8.如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断 ADCE是菱形的是( )
A.∠BAC=90° B.∠DAE=90° C.AB=AC D.AB=AE
9.为了改善生态环境,某社区计划在荒坡上种植600棵树,由于学生志愿者的加入,每日比原计划多种20棵,结果提前1天完成任务.设原计划每天种树x棵,根据题意可列方程为( )
A. B.
C. D.
10.如果实数a满足|2024﹣a|a.那么a﹣20242的值是( )
A.2025 B.2024 C.2023 D.2022
二、填空题(6小题,每题3分,共18分)
11.在分式中,当x= 时,分式的值为零.
12.当2时,的值是 .
13.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
14.在菱形ABCD中,已知对角线DB=10,AC=16,那么菱形ABCD的面积为 .
15.一个不透明的袋子中装有红球、白球共9个,这些球除颜色外都相同.若从中任意摸出一个球,则摸到白球的可能性大,则红球至多有 个.
16.如图,在 ABCD中,∠A=45°,,点M,N分别是边AB,BC上的动点,连接DN,MN,点E,F分别为DN,MN的中点,连接EF,则EF的最小值为 .
苏科版2024—2025学年八年级下学期数学期末考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简再求值:,请你选一个使原代数式有意义的数代入求值.
18.解方程:
(1); (2).
19.计算:
(1)(1)×(1);(2)()2.
20.已知,求下列各式的值.
(1);(2).
21.如图,反比例函数的图象与一次函数y=k2x+b(k2≠0)的图象相交于点A(1,4)与点B(m,﹣1),连结AO,BO.
(1)求一次函数与反比例函数的表达式.
(2)求△AOB的面积.
(3)利用图象,直接写出关于x的不等式的解集.
22.某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图的统计图.
请根据相关信息,解答下列问题:
(1)扇形统计图中的m= ,条形统计图中的n= ;
(2)从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是 ;
(3)若该校共有1600名学生,则根据样本数据,估计该校初中学生每天睡眠时间不足8小时的人数是 .
23.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)四边形CBC1B1为 四边形;
(3)点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
24.在矩形ABCD中,AB=6,BC=12,点E是矩形ABCD边CD上一点,连接BE,将△CEB沿BE翻折,
(1)如图1,点C刚好落在边AD上的点F处,求AF长.
(2)如图2,点C落在矩形外一点F处,连接AF,若CE=4,求△ABF的面积.
(3)如图3,点C落在点F处,∠ABF的角平分线与EF的延长线交于点M,当点E从点C运动到点D时,求点M运动的路径长.
25.新定义:如果两个实数a(a≠0)、b使得关于x的分式方程的解是成立,那么我们就把实数a,b组成的数对[a,b]称为关于x的分式方程的一个“友好数对”.
例如:a=2,b=﹣3使得关于x的分式方程的解是成立,所以数对[2,﹣3]就是关于x的分式方程的一个“友好数对”.
(1)判断下列数对是否为关于x的分式方程的“友好数对”,若是,请在括号内打“√”.若不是,打“×”.①[2,1]( );②[3,﹣4]( ).
(2)请判断数对[n,n﹣3]是否有可能是关于x的分式方程的“友好数对”,如果可能,请求出此时的n需满足什么条件?如果不可能,请说明理由.
(3)若数对[﹣3,kn](k<﹣2,n≠0)是关于x的分式方程的“友好数对”,,,试比较M、N的大小.
参考答案
一、选择题
1—10:BDBCCDCADA
二、填空题
11.【解答】解:由题意得:x2﹣1=0且x﹣1≠0,
解得:x=﹣1.
故答案为:﹣1.
12.【解答】解:当2时,
,
故的值是.
故答案为.
13.【解答】解:∵种子粒数5000粒时,种子发芽的频率趋近于0.801,
∴估计种子发芽的概率为0.801,精确到0.1,即为0.8.
故本题答案为:0.8.
14.【解答】解:10×16
=5×16
=80
∴菱形ABCD的面积为80.
故答案为:80.
15.【解答】解:一个不透明的袋子中装有红球、白球共9个,这些球除颜色外都相同.若从中任意摸出一个球,摸到白球的可能性大,
∴白球的数量多于红球的数量,
∴红球至多有4个,
故答案为:4.
16.【解答】解:如图,连接DM,
∵E、F分别为DN、MN的中点,
∴,
∴EF的最小值,就是DM的最小值,当DM⊥AB时,DM最小,
∵在Rt△ADM中,∠A=45°,,
∴DM=AM,DM2+AM2=2DM2=AD2=2,
∴,
∴,
∴EF的最小值是.
故答案为:.
三、解答题
17.【解答】解:原式
,
∵x+3≠0且x+2≠0且x﹣2≠0,
∴x可以取1,
当x=1时,原式1.
18.【解答】解:(1),
方程两边同乘x(x﹣3),得x﹣3=4x,
解得x=﹣1,
检验:当x=﹣1时,x(x﹣3)≠0,
所以分式方程的解是x=﹣1;
(2),
方程两边同乘(x﹣1)(x+2),得x(x+2)=(x﹣1)(x+2)+7,
解得x=5,
检验:当x=5时,(x﹣1)(x+2)≠0,
所以分式方程的解是x=5.
19.【解答】解:(1)原式=323﹣1
2;
(2)原式=(2)
=3
=9
=8.
20.【解答】解:(1)∵,
∴xy ;x+y,
∴原式2;
(2)由(1)知,xy,x+y,
∴原式12.
21.【解答】解:(1)∵A(1,4),
∴k1=4.
∴反比例函数表达式为.
把B(m,﹣1)代入反比例函数,得m=﹣4.
把A(1,4),B(﹣4,﹣1)代入y=k2x+b,
得,
∴,
∴一次函数表达式为y=x+3;
(2)如图,由(1)得C(0,3),又A(1,4),B(﹣4,﹣1),
∴;
(3)由图象可得:不等式的解集为﹣4<x<0或x>1.
22.【解答】解:(1)本次接受调查的初中学生有:4÷10%=40(人),
m%=10÷40×100%=25%,即m=25,
n=40×37.5%=15,
故答案为:25,15;
(2)从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是,
故答案为:;
(3)16001080(人),
答:该校初中学生每天睡眠时间不足8小时的有1080人,
故答案为:1080人.
23.【解答】解:(1)△A1B1C1如图所示.
(2)连接CB1,BC1,
∵BC=B′C′,BC∥B′C′,
∴四边形CBC1B1为平行四边形,
故答案为平行.
(3)如图所示,满足条件的点P的坐标为(2,﹣1),(6,5),(0,3).
24.【解答】解:(1)由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∵四边形ABCD为矩形,
∴∠A=90°,
∴AF6.
(2)过点F作FG⊥AB,交AB的延长线于点G,延长GF交CD的延长线于点H,如图,
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵FG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
设HD=AG=x,则HE=x+2,BG=x+6,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,FE=CE=4.
∴∠EFH+∠GFB=90°.
∵∠GFB+∠GBF=90°,
∴∠EFH=∠GBF.
∵∠H=∠G=90°,
∴GF=3EH=3x+6,FHBGx+2,
∵GH=12,
∴3x+6x+2=12,
∴x.
∴FG=36,
∴△ABF的面积AB FG.
(3)过点M作MG⊥AB,交AB的延长线于点G,延长GM交CD的延长线于点H,如图
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵MG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∴∠G=∠BFM=90°.
∵BM为∠GBF的平分线,
∴∠GBM=∠FBM.
在△BGM和△BFM中,
,
∴△BGM≌△BFM(AAS),
∴BG=BF=12,
∴AG=BG=AB=6,
∵点M在GH上,
∴点M到AD的距离等于AG=6,即点M在GH上运动,
∴点E与点C重合时,点M与点H重合.
当点E与点D重合时,如图,
∵△BGM≌△BFM,
∴MG=MF,
由题意得:△BCE≌△BFE,
∴CD=DF=6.
∵四边形ADHG为矩形,
∴DH=AG=6.
设MG=MF=x,则MD=x+6,MH=GH﹣GM=12﹣x.
∵∠H=90°,
∴MD2=MH2+DH2,
∴(x+6)2=(12﹣x)2+62.
∴x=4.
∴MH=GH﹣GM=8.
∴当点E从点C运动到点D时,点M运动的路径长为线段HM的长等于8.
25.【解答】解:(1)关于x的分式方程,
∵x不是方程的解,
∴数对[2,1]不是关于x的分式方程的“友好数对”;
∵x是方程的解,
∴数对[3,﹣4]是关于x的分式方程的“友好数对”;
故答案为:×,√;
(2)当n=1时,数对[n,n﹣3]是否有可能是关于x的分式方程的“友好数对”,理由如下:
∵x是方程的解,
∴n(n+n﹣3)﹣1=n﹣3,
∴n2﹣2n+1=0,
∴(n﹣1)2=0,
∴n=1,
即n=1时,数对[n,n﹣3]是否有可能是关于x的分式方程的“友好数对”;
(3)∵数对[﹣3,kn](k<﹣2,n≠0)是关于x的分式方程的“友好数对”,
∴x是关于x的分式方程的解,
∴﹣3(﹣3+kn)﹣1=kn,
∴kn=2,
即n,
∴M,
N,
∴M﹣N,
∵k<﹣2,
∴k+2<0,k+1<0,
∴M﹣N>0,
∴M>N.
21世纪教育网(www.21cnjy.com)
同课章节目录
