义务教育版(2024)五年级全一册信息科技 第23课 兔子增长有规律(2)课件(共22张PPT)
文档属性
| 名称 | 义务教育版(2024)五年级全一册信息科技 第23课 兔子增长有规律(2)课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 义务教育版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2025-05-22 07:55:30 | ||
图片预览






文档简介
(共22张PPT)
第23课 兔子增长有规律(2)
义务教育2024年信息科技身边的算法五年级全一册第六单元
斐波那契数列
说一说:
1.视频中提到的数列叫什么?
2.你能用自然语言说一说什么是斐波那契数列吗?
斐波那契数列
从数列中的第(3)项开始,每(1)项数都是前(2)项数的(相加之和)。
1,1,2,3,5,8,13,21……
发现问题
学习活动一
用流程图描述兔子增长算法
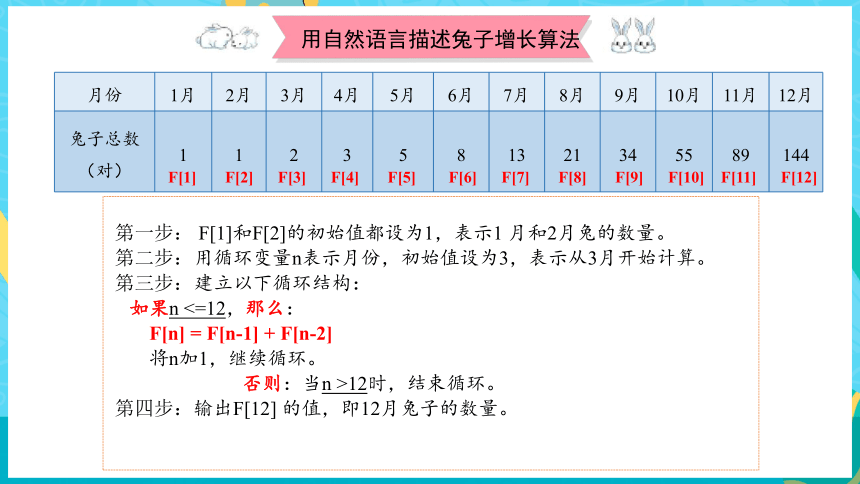
知识回顾:用自然语言描述兔子增长算法
第一步:将F[1]和F[2]的初始值都设为 ,表示1 月和2月兔的数量。
第二步:用循环变量n表示 ,初始值设为 ,表示从3月开始计算。
第三步:建立循环结构:
如果 n <=12,那么:
F[n]= (计算方法)
即F[3] = F[2]+F[1],F[4] = F[3]+F[2]……
将n加1,继续循环。
否则:当 时,结束循环。
第四步:输出 ,即12月兔子的总数。
说一说:依据斐波那契数列的规律,根据给出的句式,用自然语言描述兔子增长的算法。
月份 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月
兔子总数 (对) 1 1 2 3 5 8 13 21 34 55 89 144
1
月份
3
F[n-1] + F[n-2]
n>12
F[12]
处理
输出
初始化
用自然语言描述兔子增长算法
第一步: F[1]和F[2]的初始值都设为1,表示1 月和2月兔的数量。
第二步:用循环变量n表示月份,初始值设为3,表示从3月开始计算。
第三步:建立以下循环结构:
如果n <=12,那么:
F[n] = F[n-1] + F[n-2]
将n加1,继续循环。
否则:当n >12时,结束循环。
第四步:输出F[12] 的值,即12月兔子的数量。
月份 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月
兔子总数(对) 1 1 2 3 5 8 13 21 34 55 89 144
F[1] F[2] F[3] F[4] F[5] F[6] F[7] F[8] F[9] F[10] F[11] F[12]
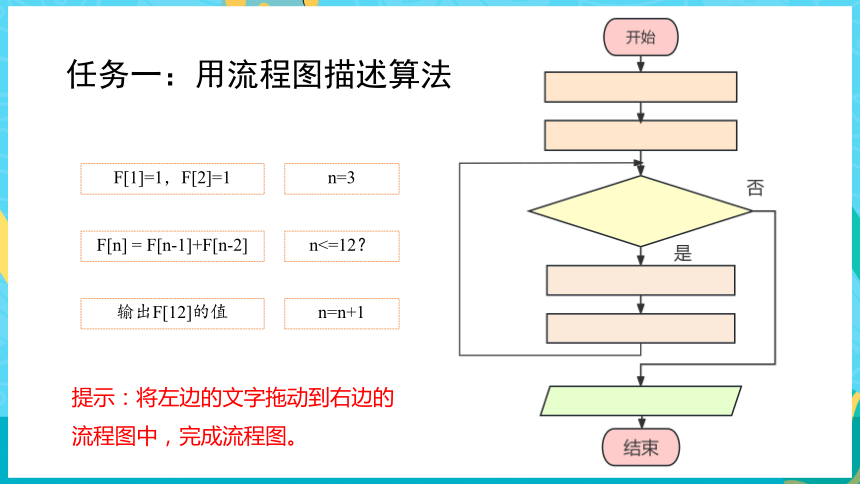
任务一:用流程图描述算法
F[1]=1,F[2]=1
n=3
n<=12?
F[n] = F[n-1]+F[n-2]
n=n+1
输出F[12]的值
提示:将左边的文字拖动到右边的流程图中,完成流程图。
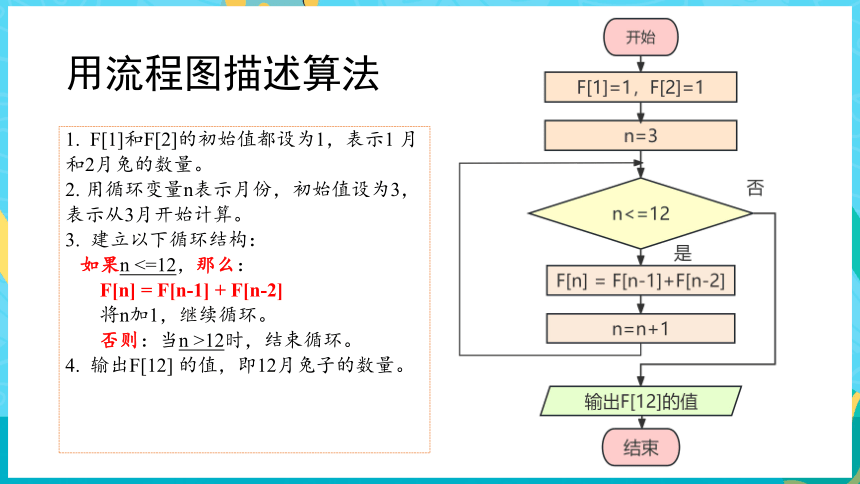
用流程图描述算法
1. F[1]和F[2]的初始值都设为1,表示1 月和2月兔的数量。
2. 用循环变量n表示月份,初始值设为3,表示从3月开始计算。
3. 建立以下循环结构:
如果n <=12,那么:
F[n] = F[n-1] + F[n-2]
将n加1,继续循环。
否则:当n >12时,结束循环。
4. 输出F[12] 的值,即12月兔子的数量。
学习活动二
用两种编程程序验证兔子增长算法
编程程序验证:Python程序
分析编程程序与算法的对应关系
初始项为什么设为0?
列表下标从0开始,而不是从1开始。即列表的第一个数据索引是F[0]。
将“第0项设为0”是为了让列表索引和月份对应。
编程程序验证:Python程序
打开参考程序,观察、运行,分析程序与算法的对应关系
编程程序验证:图形化编程
编程程序验证:图形化编程
打开程序文件,填空完成程序(共有五个地方)
②
③
④
⑤
三个待填写的程序积木也要填入哦
①
编程程序验证
小组讨论:两种编程程序验证兔子增长算法的方法有什么不同?
你更喜欢哪一种?为什么?
我更喜欢用Python程序验证算法,因为……
1.
2.
我更喜欢用图形化编程验证算法,因为……
1.
2.
更简洁
有逻辑
运算更方便
可视化(积木)
容易理解
学习活动三
拓展提升
4人小组合作探究:
搜索更多符合斐波那契数列的植物种子、叶片以及螺旋等实例。
将你的搜索结果填在“任务四”文件中。
提示:可以在网页上搜索,也可以试着询问DeepSeek。
学习活动三:拓展提升
自然界中的斐波那契数列
你最大的收获是?
根据用自然语言描述的算法画出相应的免子增长算法流程图,可以更加直观地理解算法。
日常生活与学习中,只要用心观察,会发现有许多利用递推思维来思考并解决问题的例子。(理论源于生活,用于生活)
依据算法编写编程程序进行验证时,可以采用不同的编程程序语言、不同的实现方法。
1
2
3
课堂总结
结合课件中提到的自然界案例(如树木分枝、向日葵种子排列),查找并描述一个斐波那契数列在生活中的应用实例,分析其与兔子模型的相似性。
作业:
第23课 兔子增长有规律(2)
一、用流程图描述兔子增长算法
循环结构,条件语句
二、编程程序验证兔子增长算法
Python编程程序:while循环
图形化编程程序
附板书:
学生自我评价
打开链接,根据这节课自己的表现,完成自我评价:
谢谢聆听!
第23课 兔子增长有规律(2)
义务教育2024年信息科技身边的算法五年级全一册第六单元
斐波那契数列
说一说:
1.视频中提到的数列叫什么?
2.你能用自然语言说一说什么是斐波那契数列吗?
斐波那契数列
从数列中的第(3)项开始,每(1)项数都是前(2)项数的(相加之和)。
1,1,2,3,5,8,13,21……
发现问题
学习活动一
用流程图描述兔子增长算法
知识回顾:用自然语言描述兔子增长算法
第一步:将F[1]和F[2]的初始值都设为 ,表示1 月和2月兔的数量。
第二步:用循环变量n表示 ,初始值设为 ,表示从3月开始计算。
第三步:建立循环结构:
如果 n <=12,那么:
F[n]= (计算方法)
即F[3] = F[2]+F[1],F[4] = F[3]+F[2]……
将n加1,继续循环。
否则:当 时,结束循环。
第四步:输出 ,即12月兔子的总数。
说一说:依据斐波那契数列的规律,根据给出的句式,用自然语言描述兔子增长的算法。
月份 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月
兔子总数 (对) 1 1 2 3 5 8 13 21 34 55 89 144
1
月份
3
F[n-1] + F[n-2]
n>12
F[12]
处理
输出
初始化
用自然语言描述兔子增长算法
第一步: F[1]和F[2]的初始值都设为1,表示1 月和2月兔的数量。
第二步:用循环变量n表示月份,初始值设为3,表示从3月开始计算。
第三步:建立以下循环结构:
如果n <=12,那么:
F[n] = F[n-1] + F[n-2]
将n加1,继续循环。
否则:当n >12时,结束循环。
第四步:输出F[12] 的值,即12月兔子的数量。
月份 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月
兔子总数(对) 1 1 2 3 5 8 13 21 34 55 89 144
F[1] F[2] F[3] F[4] F[5] F[6] F[7] F[8] F[9] F[10] F[11] F[12]
任务一:用流程图描述算法
F[1]=1,F[2]=1
n=3
n<=12?
F[n] = F[n-1]+F[n-2]
n=n+1
输出F[12]的值
提示:将左边的文字拖动到右边的流程图中,完成流程图。
用流程图描述算法
1. F[1]和F[2]的初始值都设为1,表示1 月和2月兔的数量。
2. 用循环变量n表示月份,初始值设为3,表示从3月开始计算。
3. 建立以下循环结构:
如果n <=12,那么:
F[n] = F[n-1] + F[n-2]
将n加1,继续循环。
否则:当n >12时,结束循环。
4. 输出F[12] 的值,即12月兔子的数量。
学习活动二
用两种编程程序验证兔子增长算法
编程程序验证:Python程序
分析编程程序与算法的对应关系
初始项为什么设为0?
列表下标从0开始,而不是从1开始。即列表的第一个数据索引是F[0]。
将“第0项设为0”是为了让列表索引和月份对应。
编程程序验证:Python程序
打开参考程序,观察、运行,分析程序与算法的对应关系
编程程序验证:图形化编程
编程程序验证:图形化编程
打开程序文件,填空完成程序(共有五个地方)
②
③
④
⑤
三个待填写的程序积木也要填入哦
①
编程程序验证
小组讨论:两种编程程序验证兔子增长算法的方法有什么不同?
你更喜欢哪一种?为什么?
我更喜欢用Python程序验证算法,因为……
1.
2.
我更喜欢用图形化编程验证算法,因为……
1.
2.
更简洁
有逻辑
运算更方便
可视化(积木)
容易理解
学习活动三
拓展提升
4人小组合作探究:
搜索更多符合斐波那契数列的植物种子、叶片以及螺旋等实例。
将你的搜索结果填在“任务四”文件中。
提示:可以在网页上搜索,也可以试着询问DeepSeek。
学习活动三:拓展提升
自然界中的斐波那契数列
你最大的收获是?
根据用自然语言描述的算法画出相应的免子增长算法流程图,可以更加直观地理解算法。
日常生活与学习中,只要用心观察,会发现有许多利用递推思维来思考并解决问题的例子。(理论源于生活,用于生活)
依据算法编写编程程序进行验证时,可以采用不同的编程程序语言、不同的实现方法。
1
2
3
课堂总结
结合课件中提到的自然界案例(如树木分枝、向日葵种子排列),查找并描述一个斐波那契数列在生活中的应用实例,分析其与兔子模型的相似性。
作业:
第23课 兔子增长有规律(2)
一、用流程图描述兔子增长算法
循环结构,条件语句
二、编程程序验证兔子增长算法
Python编程程序:while循环
图形化编程程序
附板书:
学生自我评价
打开链接,根据这节课自己的表现,完成自我评价:
谢谢聆听!
同课章节目录
