1.2第2课时矩形的判定 课件(共28张PPT)
文档属性
| 名称 | 1.2第2课时矩形的判定 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 16:36:26 | ||
图片预览







文档简介
(共28张PPT)
学习目标
1. 经历矩形判定定理的猜想与证明过程,理解并掌握
矩形的判定定理;(重点)
2. 能应用矩形的判定解决简单的证明题和计算题.(难点)
复习引入
导入新课
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
思考 工人师傅在做矩形门窗或零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
讲授新课
对角线相等的平行四边形是矩形
一
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
问题1 除了定义以外,判定矩形的方法还有没有呢?
类似地,那我们研究矩形的性质的逆命题是否成立.
矩形是特殊的平行四边形.
问题2 上节课我们已经知道“矩形的对角线相等”,反过来,小明猜想对角线相等的四边形是矩形,你觉得对吗?
思考 你能证明这一猜想吗?
我猜想:对角线相等的四边形是矩形.
不对,等腰梯形的对角线也相等.
不对,矩形是特殊的平行四边形,所以它的对角线不仅相等且平分.
已知:如图,在□ ABCD中,AC,DB 是它的两条对角线,且 AC = DB. 求证:□ ABCD 是矩形.
证明:∵ AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB.
∴∠ABC = ∠DCB.
∵ AB∥CD,
∴∠ABC + ∠DCB = 180°.
∴ ∠ABC = 90°.
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
证一证
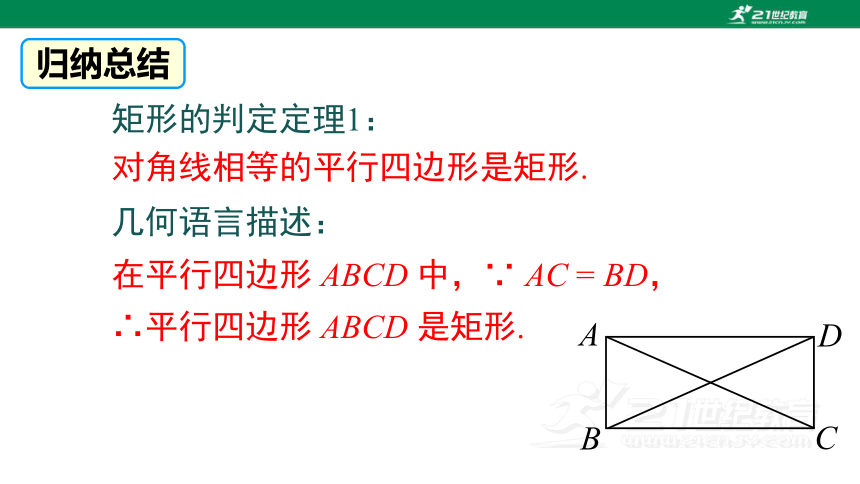
矩形的判定定理1:
对角线相等的平行四边形是矩形.
归纳总结
几何语言描述:
在平行四边形 ABCD 中,∵ AC = BD,
∴平行四边形 ABCD 是矩形.
A
D
C
B
思考 数学来源于生活,事实上工人师傅为了检验两组对边相等的四边形窗框是否成矩形,其中一种方法就是量一量这个四边形的两条对角线长度,如果对角线的长相等,那么窗框一定是矩形,
你现在知道为什么了吗?
对角线相等的平行四边形是矩形.
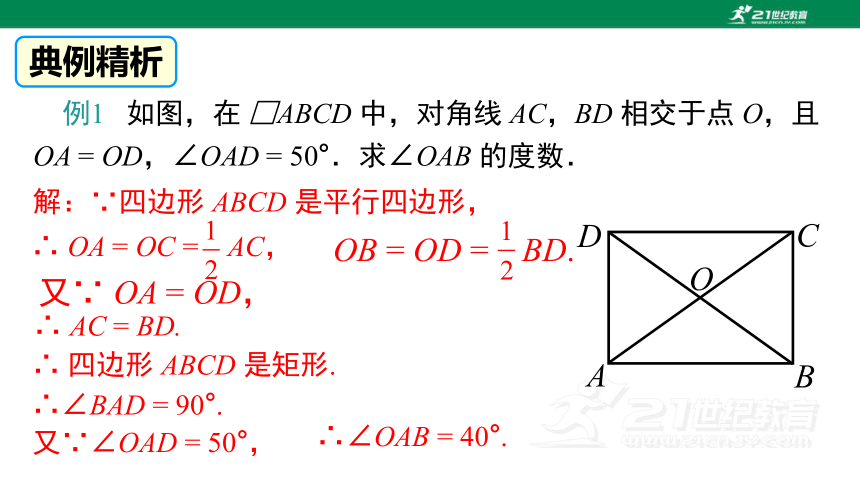
例1 如图,在 □ABCD 中,对角线 AC,BD 相交于点 O,且 OA = OD,∠OAD = 50°.求∠OAB 的度数.
A
B
C
D
O
解:∵四边形 ABCD 是平行四边形,
∴ OA = OC = AC,
OB = OD = BD.
又∵ OA = OD,
∴ AC = BD.
∴ 四边形 ABCD 是矩形.
∴∠BAD = 90°.
又∵∠OAD = 50°,
∴∠OAB = 40°.
典例精析
例2 如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,E、F、G、H 分别是 AO、BO、CO、DO 上的一点,且 AE = BF = CG = DH. 求证:四边形 EFGH 是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵四边形 ABCD 是矩形,
∴ AC = BD(矩形的对角线相等),
AO = BO = CO = DO(矩形的对角线互相平分).
∵ AE = BF = CG = DH,
∴ OE = OF = OG = OH.
∴ 四边形 EFGH 是平行四边形,
且 EG = FH.
∴ 四边形 EFGH 是矩形.
练一练
1. 如图,在 ABCD 中,AC 和 BD 相交于点 O,则下面条件能判定 ABCD 是矩形的是 ( )
A.AC = BD B.AC = BC
C.AD = BC D.AB = AD
A
A
D
C
B
O
2. 如图,□ABCD 中,∠1 = ∠2,此时四边形 ABCD 是矩形吗?为什么?
A
B
C
D
O
1
2
解:四边形 ABCD 是矩形.
理由如下:
∵ 四边形 ABCD 是平行四边形,
∴ AO = CO,DO = BO.
又∵∠1 = ∠2,
∴ AO = BO.
∴ AC = BD.
∴ □ABCD 是矩形.
问题1 上节课我们研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立.
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有两个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
有三个角是直角的四边形是矩形
二
已知:如图,在四边形 ABCD 中,∠A =∠B =∠C = 90°.
求证:四边形 ABCD 是矩形.
证明:∵ ∠A =∠B =∠C = 90°,
∴∠A +∠B = 180°,∠B +∠C = 180°.
∴ AD∥BC,AB∥CD.
∴ 四边形 ABCD 是平行四边形.
∴ 四边形 ABCD 是矩形.
A
B
C
D
证一证
矩形的判定定理:
有三个角是直角的四边形是矩形.
归纳总结
几何语言描述:
在四边形 ABCD 中,∵∠A =∠B =∠C = 90°,
∴ 四边形 ABCD 是矩形.
A
B
C
D
思考 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板.为什么?
有三个角是直角的四边形是矩形.
例3 如图,□ ABCD 的四个内角的平分线分别相交于 E、F、G、H,求证:四边形 EFGH 为矩形.
证明:在□ ABCD 中,AD∥BC,
∴∠DAB +∠ABC = 180°.
∵ AE 与 BG 分别为∠DAB、
∠ABC 的平分线,
A
B
D
C
H
E
F
G
∴ 四边形 EFGH 为矩形.
同理可得∠FEH =∠EHG = 90°,
∴∠AFB = 90°.
∴∠GFE = 90°.
∴∠BAF +∠ABF = ∠DAB + ∠ABC = 90°.
例4 如图,在△ABC 中,AB=AC,AD⊥BC,垂足为 D,AN 是△ABC 的外角∠CAM 的平分线,CE⊥AN,垂足为 E,求证:四边形 ADCE 为矩形.
∴∠MAE=∠CAE= ∠CAM.
= (∠BAC+∠CAM )=90°.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵ AN 是△ABC 外角∠CAM 的平分线,
∴∠DAE=∠DAC+∠CAE
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°.
∴ 四边形 ADCE 为矩形.
练一练
在判断“一个四边形门框是否为矩形”的数学活动课上,一个合作学习小组的 4 位同学分别拟定了如下的方案,其中合理的是 ( )
A.测量对角线是否相等
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个角是否都为直角
D
当堂练习
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(4)有三个角都相等的四边形是矩形;
×
×
×
×
√
√
√
√
(8)一组对角互补的平行四边形是矩形.
2.如图,直线 EF∥MN,PQ 交 EF、MN 于 A、C 两点,AB、CB、CD、AD 分别是∠EAC、∠MCA、∠ ACN、∠CAF 的平分线,则四边形 ABCD 是 ( )
A. 梯形 B. 平行四边形 C. 矩形 D. 不能确定
D
E
F
M
N
Q
P
A
B
C
C
3.如图,在四边形 ABCD 中,AB∥CD,∠BAD = 90°,
AB = 5,BC = 12,AC = 13.求证:四边形 ABCD 是矩形.
证明:四边形 ABCD 中,∵ AB∥CD,∠BAD = 90°,
∴∠D = 90°.
在△ABC 中,∵ AB = 5,BC = 12,AC = 13,
∴ AB2 + BC2 = AC2.
∴△ABC 是直角三角形,且∠B = 90°.
∴ 四边形 ABCD 是矩形.
A
B
C
D
4. 如图,平行四边形 ABCD 中,对角线 AC、BD 相交
于点 O,延长 OA 到 N,使 ON=OB,再延长 OC 至 M,使 CM=AN. 求证:四边形 NDMB 为矩形.
证明:∵四边形 ABCD 为平行四边形,
∴ OA=OC,OD=OB.
∵ AN=CM,ON=OB,
∴ ON=OM=OD=OB.
∴ 四边形 NDMB 为平行四边形,且 MN=BD.
∴ 平行四边形 NDMB 为矩形.
5.如图,△ABC 中,AB=AC,AD 是BC 边上的高,AE 是外角的平分线,DE∥AB 交 AE 于点 E,求证:四边形 ADCE 是矩形.
证明:∵ AB=AC,AD⊥BC,
∴∠B=∠ACB,BD=DC.
∵ AE 是△ABC 的外角平分线,
∴∠FAE=∠EAC.
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴ AE∥BC.
又∵DE∥AB,∴ 四边形 AEDB 是平行四边形.
∴ AE 平行且等于 BD.
又∵ BD=DC,
∴ AE 平行且等于 DC.
故四边形 ADCE 是平行四边形.
又∵∠ADC=90°,
∴ 平行四边形 ADCE 是矩形.
6. 如图,在梯形 ABCD 中,AD∥BC,∠B=90°,AD=24 cm,BC=26 cm,动点 P 从点 A 出发沿 AD 方向向点 D 以 1 cm/s 的速度运动,动点 Q 从点 C 开始沿 CB 方向向点 B 以 3 cm/s 的速度运动.点 P、Q 分别从点 A和点 C 同时出发,当其中一点到达端点时,另一点随之停止运动.
(1) 经过多长时间,四边形 PQCD 是平行四边形?
解:设经过 x s 时四边形 PQCD 是平行四边形,
则 PD = CQ,所以 24-x = 3x,
解得 x = 6.
即经过 6 s 时四边形 PQCD 是平行四边形.
能力提升:
(2)经过多长时间,四边形 PQBA 是矩形?
解:设经过 y s,四边形 PQBA 为矩形,
则 AP = BQ,
∴ y = 26-3y,
解得 y = 6.5.
即经过 6.5 s 时四边形 PQBA 是矩形.
课堂小结
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
学习目标
1. 经历矩形判定定理的猜想与证明过程,理解并掌握
矩形的判定定理;(重点)
2. 能应用矩形的判定解决简单的证明题和计算题.(难点)
复习引入
导入新课
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
思考 工人师傅在做矩形门窗或零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
讲授新课
对角线相等的平行四边形是矩形
一
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
问题1 除了定义以外,判定矩形的方法还有没有呢?
类似地,那我们研究矩形的性质的逆命题是否成立.
矩形是特殊的平行四边形.
问题2 上节课我们已经知道“矩形的对角线相等”,反过来,小明猜想对角线相等的四边形是矩形,你觉得对吗?
思考 你能证明这一猜想吗?
我猜想:对角线相等的四边形是矩形.
不对,等腰梯形的对角线也相等.
不对,矩形是特殊的平行四边形,所以它的对角线不仅相等且平分.
已知:如图,在□ ABCD中,AC,DB 是它的两条对角线,且 AC = DB. 求证:□ ABCD 是矩形.
证明:∵ AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB.
∴∠ABC = ∠DCB.
∵ AB∥CD,
∴∠ABC + ∠DCB = 180°.
∴ ∠ABC = 90°.
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
证一证
矩形的判定定理1:
对角线相等的平行四边形是矩形.
归纳总结
几何语言描述:
在平行四边形 ABCD 中,∵ AC = BD,
∴平行四边形 ABCD 是矩形.
A
D
C
B
思考 数学来源于生活,事实上工人师傅为了检验两组对边相等的四边形窗框是否成矩形,其中一种方法就是量一量这个四边形的两条对角线长度,如果对角线的长相等,那么窗框一定是矩形,
你现在知道为什么了吗?
对角线相等的平行四边形是矩形.
例1 如图,在 □ABCD 中,对角线 AC,BD 相交于点 O,且 OA = OD,∠OAD = 50°.求∠OAB 的度数.
A
B
C
D
O
解:∵四边形 ABCD 是平行四边形,
∴ OA = OC = AC,
OB = OD = BD.
又∵ OA = OD,
∴ AC = BD.
∴ 四边形 ABCD 是矩形.
∴∠BAD = 90°.
又∵∠OAD = 50°,
∴∠OAB = 40°.
典例精析
例2 如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,E、F、G、H 分别是 AO、BO、CO、DO 上的一点,且 AE = BF = CG = DH. 求证:四边形 EFGH 是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵四边形 ABCD 是矩形,
∴ AC = BD(矩形的对角线相等),
AO = BO = CO = DO(矩形的对角线互相平分).
∵ AE = BF = CG = DH,
∴ OE = OF = OG = OH.
∴ 四边形 EFGH 是平行四边形,
且 EG = FH.
∴ 四边形 EFGH 是矩形.
练一练
1. 如图,在 ABCD 中,AC 和 BD 相交于点 O,则下面条件能判定 ABCD 是矩形的是 ( )
A.AC = BD B.AC = BC
C.AD = BC D.AB = AD
A
A
D
C
B
O
2. 如图,□ABCD 中,∠1 = ∠2,此时四边形 ABCD 是矩形吗?为什么?
A
B
C
D
O
1
2
解:四边形 ABCD 是矩形.
理由如下:
∵ 四边形 ABCD 是平行四边形,
∴ AO = CO,DO = BO.
又∵∠1 = ∠2,
∴ AO = BO.
∴ AC = BD.
∴ □ABCD 是矩形.
问题1 上节课我们研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立.
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有两个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
有三个角是直角的四边形是矩形
二
已知:如图,在四边形 ABCD 中,∠A =∠B =∠C = 90°.
求证:四边形 ABCD 是矩形.
证明:∵ ∠A =∠B =∠C = 90°,
∴∠A +∠B = 180°,∠B +∠C = 180°.
∴ AD∥BC,AB∥CD.
∴ 四边形 ABCD 是平行四边形.
∴ 四边形 ABCD 是矩形.
A
B
C
D
证一证
矩形的判定定理:
有三个角是直角的四边形是矩形.
归纳总结
几何语言描述:
在四边形 ABCD 中,∵∠A =∠B =∠C = 90°,
∴ 四边形 ABCD 是矩形.
A
B
C
D
思考 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板.为什么?
有三个角是直角的四边形是矩形.
例3 如图,□ ABCD 的四个内角的平分线分别相交于 E、F、G、H,求证:四边形 EFGH 为矩形.
证明:在□ ABCD 中,AD∥BC,
∴∠DAB +∠ABC = 180°.
∵ AE 与 BG 分别为∠DAB、
∠ABC 的平分线,
A
B
D
C
H
E
F
G
∴ 四边形 EFGH 为矩形.
同理可得∠FEH =∠EHG = 90°,
∴∠AFB = 90°.
∴∠GFE = 90°.
∴∠BAF +∠ABF = ∠DAB + ∠ABC = 90°.
例4 如图,在△ABC 中,AB=AC,AD⊥BC,垂足为 D,AN 是△ABC 的外角∠CAM 的平分线,CE⊥AN,垂足为 E,求证:四边形 ADCE 为矩形.
∴∠MAE=∠CAE= ∠CAM.
= (∠BAC+∠CAM )=90°.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵ AN 是△ABC 外角∠CAM 的平分线,
∴∠DAE=∠DAC+∠CAE
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°.
∴ 四边形 ADCE 为矩形.
练一练
在判断“一个四边形门框是否为矩形”的数学活动课上,一个合作学习小组的 4 位同学分别拟定了如下的方案,其中合理的是 ( )
A.测量对角线是否相等
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个角是否都为直角
D
当堂练习
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(4)有三个角都相等的四边形是矩形;
×
×
×
×
√
√
√
√
(8)一组对角互补的平行四边形是矩形.
2.如图,直线 EF∥MN,PQ 交 EF、MN 于 A、C 两点,AB、CB、CD、AD 分别是∠EAC、∠MCA、∠ ACN、∠CAF 的平分线,则四边形 ABCD 是 ( )
A. 梯形 B. 平行四边形 C. 矩形 D. 不能确定
D
E
F
M
N
Q
P
A
B
C
C
3.如图,在四边形 ABCD 中,AB∥CD,∠BAD = 90°,
AB = 5,BC = 12,AC = 13.求证:四边形 ABCD 是矩形.
证明:四边形 ABCD 中,∵ AB∥CD,∠BAD = 90°,
∴∠D = 90°.
在△ABC 中,∵ AB = 5,BC = 12,AC = 13,
∴ AB2 + BC2 = AC2.
∴△ABC 是直角三角形,且∠B = 90°.
∴ 四边形 ABCD 是矩形.
A
B
C
D
4. 如图,平行四边形 ABCD 中,对角线 AC、BD 相交
于点 O,延长 OA 到 N,使 ON=OB,再延长 OC 至 M,使 CM=AN. 求证:四边形 NDMB 为矩形.
证明:∵四边形 ABCD 为平行四边形,
∴ OA=OC,OD=OB.
∵ AN=CM,ON=OB,
∴ ON=OM=OD=OB.
∴ 四边形 NDMB 为平行四边形,且 MN=BD.
∴ 平行四边形 NDMB 为矩形.
5.如图,△ABC 中,AB=AC,AD 是BC 边上的高,AE 是外角的平分线,DE∥AB 交 AE 于点 E,求证:四边形 ADCE 是矩形.
证明:∵ AB=AC,AD⊥BC,
∴∠B=∠ACB,BD=DC.
∵ AE 是△ABC 的外角平分线,
∴∠FAE=∠EAC.
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴ AE∥BC.
又∵DE∥AB,∴ 四边形 AEDB 是平行四边形.
∴ AE 平行且等于 BD.
又∵ BD=DC,
∴ AE 平行且等于 DC.
故四边形 ADCE 是平行四边形.
又∵∠ADC=90°,
∴ 平行四边形 ADCE 是矩形.
6. 如图,在梯形 ABCD 中,AD∥BC,∠B=90°,AD=24 cm,BC=26 cm,动点 P 从点 A 出发沿 AD 方向向点 D 以 1 cm/s 的速度运动,动点 Q 从点 C 开始沿 CB 方向向点 B 以 3 cm/s 的速度运动.点 P、Q 分别从点 A和点 C 同时出发,当其中一点到达端点时,另一点随之停止运动.
(1) 经过多长时间,四边形 PQCD 是平行四边形?
解:设经过 x s 时四边形 PQCD 是平行四边形,
则 PD = CQ,所以 24-x = 3x,
解得 x = 6.
即经过 6 s 时四边形 PQCD 是平行四边形.
能力提升:
(2)经过多长时间,四边形 PQBA 是矩形?
解:设经过 y s,四边形 PQBA 为矩形,
则 AP = BQ,
∴ y = 26-3y,
解得 y = 6.5.
即经过 6.5 s 时四边形 PQBA 是矩形.
课堂小结
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
