北京市第二中学2024-2025学年高一下学期第五学段数学试题(含答案)
文档属性
| 名称 | 北京市第二中学2024-2025学年高一下学期第五学段数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 726.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 06:41:09 | ||
图片预览




文档简介
2025北京二中高一(下)五学段
数 学
必修第二册
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的选项中,只有一项是符合题目要求的,请将答案填在答题纸上)
1. 已知,是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A. 若,,,则 B. 若,,则
C. 若,,,则 D. 若,,,则
2. 设长方体的长、宽、高分别为,其顶点都在一个球面上,则该球的体积为( )
A. B. C. D.
3. 如图所示,点,,,,为正方体的顶点或所在棱的中点,则下列各图中,不满足的是( )
4. 如图所示,为的直观图,且的面积为,则中最长的边长为( )
A. B.
C. D.
5. 已知单位向量满足,则与的夹角为( )
A. B. C. D.
6. 在中,,则“”是“是钝角三角形”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
7. 在正方体中,为的中点,则直线与所成的角为( )
A. B. C. D.
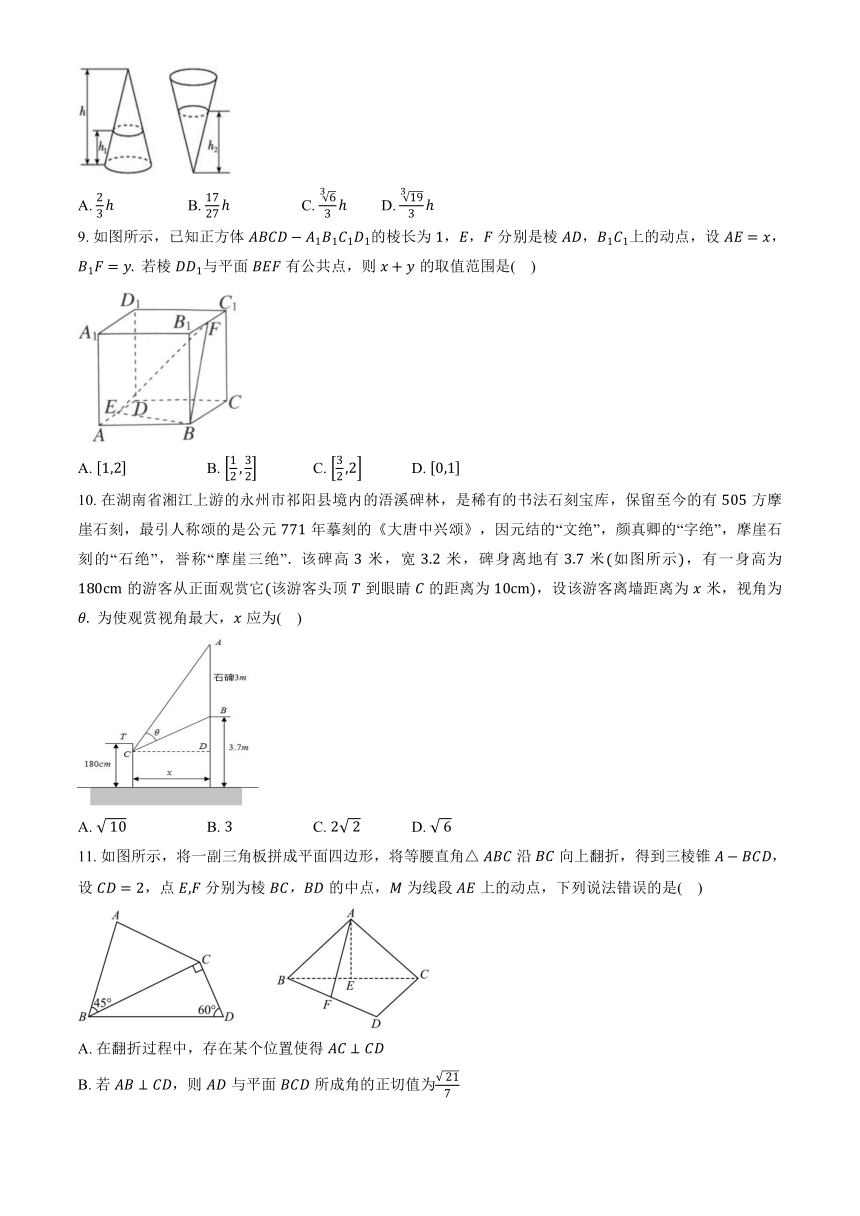
8. 如图所示,圆锥形容器的高为,容器内水面的高为,且,若将容器倒置,水面高为,则等于( )
A. B. C. D.
9. 如图所示,已知正方体的棱长为,,分别是棱,上的动点,设, 若棱与平面有公共点,则的取值范围是( )
A. B. C. D.
10. 在湖南省湘江上游的永州市祁阳县境内的浯溪碑林,是稀有的书法石刻宝库,保留至今的有方摩崖石刻,最引人称颂的是公元年摹刻的《大唐中兴颂》,因元结的“文绝”,颜真卿的“字绝”,摩崖石刻的“石绝”,誉称“摩崖三绝” 该碑高米,宽米,碑身离地有米如图所示,有一身高为的游客从正面观赏它该游客头顶到眼睛的距离为,设该游客离墙距离为米,视角为 为使观赏视角最大,应为( )
A. B. C. D.
11. 如图所示,将一副三角板拼成平面四边形,将等腰直角沿向上翻折,得到,设,点分别为棱的中点,为线段上的动点,下列说法错误的是( )
A. 在翻折过程中,存在某个位置使得
B. 若,则与平面所成角的正切值为
C. 三棱锥体积的最大值为
D. 当时,的最小值为
12. 在单位正方体内任取一个点,过这个点作三个平行于正方体面的平面,将正方体分成个小长方体,则这些小长方体中体积不大于的长方体的个数的最小值是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题5分,共30分. 请将答案填在答题纸上)
13. 在正方体中,二面角的平面角等于 ________.
14. 已知向量,,. 若,则________.
15. 已知圆锥的侧面积为,且它的侧面展开图是一个半圆,则这个圆锥的底面半径是________.
16. 如图所示,在正方体中,是棱的中点,记与的交线为,平面与平面的交线为,若直线分别与所成的角为,则 ________, ________.
17. 已知正四面体中,分别在棱上. 若,,则 ________.
18. 球面三角学是研究球面三角形的边、角关系的一门学科. 如图所示,球的半径为,,,为球面上三点,劣弧的弧长记为,设表示以为圆心,且过,的圆,同理,圆,的劣弧,的弧长分别记为,,阴影部分叫做曲面三角形,若,则称其为曲面等边三角形,线段,,与曲面围成的封闭几何体叫做球面三棱锥,记为球面 设,,.
若平面是面积为的等边三角形,则
若,则
若平面为直角三角形,且,则
若,则球面的体积
其中所有正确结论的序号是________.
三、解答题(本大题共60分,请将答案填在答题纸上)
19(本小题10分)
已知函数.
(1)求的周期和单调递增区间;
(2)若,求的最大值和最小值及取得最值时相应的值.
20(本小题12分)
如图所示,在四棱锥中,底面为矩形,,,,,分别为,的中点.
(1)求证:;
(2)求证:;
(3)求证:
21(本小题12分)
已知的面积为,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)和的值;
(2)的值.
条件①:,;条件②:,.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
22(本小题13分)
如图所示,在三棱柱中,侧棱,为棱的中点.,, .
(1)求证:;
(2)求证:;
(3)在棱上是否存在点,使得?如果存在,求此时的值;如果不存在,请说明理由.
23(本小题13分)
对于行列的数表,定义变换:任选一组其中,对于的第行和第列的个数,将每个数同时加1,或者将每个数同时减1,其余的数不变,得到一个新数表.
(1)已知对依次进行4次变换,如下:写出值;
(2)已知.是否可以依次进行有限次变换,将变换为?说明理由;
(3)已知11行11列的数表,是否可以依次进行次变换,将其变换为?若可以,求的最小值;若不可以,说明理由.
参考答案
选择题
1 2 3 4 5 6 7 8 9 10 11 12
D B D B C A D D A A D B
二、填空题
13.
14.
15. 1
16. ,
17. 3或
【答案】当时,是等边三角形,因此。在中,由余弦定理可得,解得。
当时,不妨设。在中分别使用余弦定理可得
由可知是关于的方程的两个相异正实根,所以
可写为(,因此,解得。
18.①②④
三、解答题
19(本小题10分)已知函数.
(1)求的周期和单调递增区间;
(2)若,求的最大值和最小值及取得最值时相应的值.
【答案】解:函数
,
的单调递增区间为,
由于,
所以,
,
所以当时,,
当时,
20(本小题12分)如图所示,在四棱锥中,底面为矩形,,,,,分别为,的中点.
(1)求证:;
(2)求证:;
(3)求证:
【答案】证明:,E为AD的中点,可得,
底面ABCD为矩形,可得,
则
<法一>如图,取PC中点G,连接FG,
F,G分别为PB,PC的中点,
,且
四边形ABCD为矩形,且E为AD的中点,
,,
,且,
四边形EFGD为平行四边形,
,
又EF不在平面PCD内,GD在平面PCD内,
平面
<法二>:取BC的中点G,连接EG,FG,
F为PB中点,
E为AD中点,
四边形EDCG是平行四边形,
底面ABCD为矩形,
,
平面平面ABCD,,平面ABCD,
平面
,
又,且,,,
平面PAB,
又平面PCD
平面平面
21(本小题12分)已知的面积为,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)和的值;
(2)的值.
条件①:,;条件②:,.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】解:若选择条件①:
解:(Ⅰ)在中,因为,
所以,.
因为,,所以.
由余弦定理,,
所以.
(Ⅱ)由正弦定理,可得.
所以,.
因为,所以,.
所以
.
若选择条件②:
解:(Ⅰ)在中,因为,所以.
因为,所以,.
因为,
所以.
由余弦定理,,所以.
(Ⅱ)由正弦定理得,
所以.
因为,所以.
所以
.
22(本小题13分)如图所示,在三棱柱中,侧棱,为棱的中点.,, .
(1)求证:;
(2)求证:;
(3)在棱上是否存在点,使得?如果存在,求此时的值;如果不存在,请说明理由.
【答案】解:连结交于O,连结
在中,因为M,O分别为AC,中点,
所以
又因为平面,平面,
所以平面
因为侧棱底面ABC,平面ABC,
所以
又因为M为棱AC中点,,所以
因为,,平面
所以平面平面
所以
因为M为棱AC中点,,所以
又因为,所以在和中,
所以,
即
所以
因为,BM,平面
所以平面
当点N为中点时,即,平面平面
设中点为D,连结DM,
因为D,M分别为,AC中点,
所以,且
又因为N为中点,
所以,且,
所以四边形DMBN是平行四边形,
所以,
所以,,
又因为,,
所以平面
又因为平面,
所以平面平面
23(本小题13分)
对于行列的数表,定义变换:任选一组其中,对于的第行和第列的个数,将每个数同时加1,或者将每个数同时减1,其余的数不变,得到一个新数表.
(1)已知对依次进行4次变换,如下:写出值;
(2)已知.是否可以依次进行有限次变换,将变换为?说明理由;
(3)已知11行11列的数表,是否可以依次进行次变换,将其变换为?若可以,求的最小值;若不可以,说明理由.
【答案】(1)根据变换的定义,
可得
(2)不可以,理由如下:
由题可知每次变换T,数表中所有数的和增加或减少5.
因为A中所有数的和为0,所以其经过有限次变换T后各数和为5的倍数.
而 B中所有数的和为9,不符合,故无法通过有限次变换T,将A变换为B.
(3)可以,且k的最小值为 400
当所选时,所有加l的变换T与减1的变换T次数之差设为;
当所选且或者且时,所有加1的变换T与减1的变换T 次数之差设为;
当所选时,加1的变换T与减1的变换T次数之差设为.
考虑变换T 对上述三部分各数之和的影响,
可知,解得,
所以,
其中符合题意的 400 次变换T构造如下:
当所选时,各进行一次减1的变换T;
当所选且或者且时,
各进行10次加l的变换T;
当所选时,进行100次减l的变换T.
数 学
必修第二册
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的选项中,只有一项是符合题目要求的,请将答案填在答题纸上)
1. 已知,是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A. 若,,,则 B. 若,,则
C. 若,,,则 D. 若,,,则
2. 设长方体的长、宽、高分别为,其顶点都在一个球面上,则该球的体积为( )
A. B. C. D.
3. 如图所示,点,,,,为正方体的顶点或所在棱的中点,则下列各图中,不满足的是( )
4. 如图所示,为的直观图,且的面积为,则中最长的边长为( )
A. B.
C. D.
5. 已知单位向量满足,则与的夹角为( )
A. B. C. D.
6. 在中,,则“”是“是钝角三角形”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
7. 在正方体中,为的中点,则直线与所成的角为( )
A. B. C. D.
8. 如图所示,圆锥形容器的高为,容器内水面的高为,且,若将容器倒置,水面高为,则等于( )
A. B. C. D.
9. 如图所示,已知正方体的棱长为,,分别是棱,上的动点,设, 若棱与平面有公共点,则的取值范围是( )
A. B. C. D.
10. 在湖南省湘江上游的永州市祁阳县境内的浯溪碑林,是稀有的书法石刻宝库,保留至今的有方摩崖石刻,最引人称颂的是公元年摹刻的《大唐中兴颂》,因元结的“文绝”,颜真卿的“字绝”,摩崖石刻的“石绝”,誉称“摩崖三绝” 该碑高米,宽米,碑身离地有米如图所示,有一身高为的游客从正面观赏它该游客头顶到眼睛的距离为,设该游客离墙距离为米,视角为 为使观赏视角最大,应为( )
A. B. C. D.
11. 如图所示,将一副三角板拼成平面四边形,将等腰直角沿向上翻折,得到,设,点分别为棱的中点,为线段上的动点,下列说法错误的是( )
A. 在翻折过程中,存在某个位置使得
B. 若,则与平面所成角的正切值为
C. 三棱锥体积的最大值为
D. 当时,的最小值为
12. 在单位正方体内任取一个点,过这个点作三个平行于正方体面的平面,将正方体分成个小长方体,则这些小长方体中体积不大于的长方体的个数的最小值是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题5分,共30分. 请将答案填在答题纸上)
13. 在正方体中,二面角的平面角等于 ________.
14. 已知向量,,. 若,则________.
15. 已知圆锥的侧面积为,且它的侧面展开图是一个半圆,则这个圆锥的底面半径是________.
16. 如图所示,在正方体中,是棱的中点,记与的交线为,平面与平面的交线为,若直线分别与所成的角为,则 ________, ________.
17. 已知正四面体中,分别在棱上. 若,,则 ________.
18. 球面三角学是研究球面三角形的边、角关系的一门学科. 如图所示,球的半径为,,,为球面上三点,劣弧的弧长记为,设表示以为圆心,且过,的圆,同理,圆,的劣弧,的弧长分别记为,,阴影部分叫做曲面三角形,若,则称其为曲面等边三角形,线段,,与曲面围成的封闭几何体叫做球面三棱锥,记为球面 设,,.
若平面是面积为的等边三角形,则
若,则
若平面为直角三角形,且,则
若,则球面的体积
其中所有正确结论的序号是________.
三、解答题(本大题共60分,请将答案填在答题纸上)
19(本小题10分)
已知函数.
(1)求的周期和单调递增区间;
(2)若,求的最大值和最小值及取得最值时相应的值.
20(本小题12分)
如图所示,在四棱锥中,底面为矩形,,,,,分别为,的中点.
(1)求证:;
(2)求证:;
(3)求证:
21(本小题12分)
已知的面积为,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)和的值;
(2)的值.
条件①:,;条件②:,.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
22(本小题13分)
如图所示,在三棱柱中,侧棱,为棱的中点.,, .
(1)求证:;
(2)求证:;
(3)在棱上是否存在点,使得?如果存在,求此时的值;如果不存在,请说明理由.
23(本小题13分)
对于行列的数表,定义变换:任选一组其中,对于的第行和第列的个数,将每个数同时加1,或者将每个数同时减1,其余的数不变,得到一个新数表.
(1)已知对依次进行4次变换,如下:写出值;
(2)已知.是否可以依次进行有限次变换,将变换为?说明理由;
(3)已知11行11列的数表,是否可以依次进行次变换,将其变换为?若可以,求的最小值;若不可以,说明理由.
参考答案
选择题
1 2 3 4 5 6 7 8 9 10 11 12
D B D B C A D D A A D B
二、填空题
13.
14.
15. 1
16. ,
17. 3或
【答案】当时,是等边三角形,因此。在中,由余弦定理可得,解得。
当时,不妨设。在中分别使用余弦定理可得
由可知是关于的方程的两个相异正实根,所以
可写为(,因此,解得。
18.①②④
三、解答题
19(本小题10分)已知函数.
(1)求的周期和单调递增区间;
(2)若,求的最大值和最小值及取得最值时相应的值.
【答案】解:函数
,
的单调递增区间为,
由于,
所以,
,
所以当时,,
当时,
20(本小题12分)如图所示,在四棱锥中,底面为矩形,,,,,分别为,的中点.
(1)求证:;
(2)求证:;
(3)求证:
【答案】证明:,E为AD的中点,可得,
底面ABCD为矩形,可得,
则
<法一>如图,取PC中点G,连接FG,
F,G分别为PB,PC的中点,
,且
四边形ABCD为矩形,且E为AD的中点,
,,
,且,
四边形EFGD为平行四边形,
,
又EF不在平面PCD内,GD在平面PCD内,
平面
<法二>:取BC的中点G,连接EG,FG,
F为PB中点,
E为AD中点,
四边形EDCG是平行四边形,
底面ABCD为矩形,
,
平面平面ABCD,,平面ABCD,
平面
,
又,且,,,
平面PAB,
又平面PCD
平面平面
21(本小题12分)已知的面积为,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)和的值;
(2)的值.
条件①:,;条件②:,.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】解:若选择条件①:
解:(Ⅰ)在中,因为,
所以,.
因为,,所以.
由余弦定理,,
所以.
(Ⅱ)由正弦定理,可得.
所以,.
因为,所以,.
所以
.
若选择条件②:
解:(Ⅰ)在中,因为,所以.
因为,所以,.
因为,
所以.
由余弦定理,,所以.
(Ⅱ)由正弦定理得,
所以.
因为,所以.
所以
.
22(本小题13分)如图所示,在三棱柱中,侧棱,为棱的中点.,, .
(1)求证:;
(2)求证:;
(3)在棱上是否存在点,使得?如果存在,求此时的值;如果不存在,请说明理由.
【答案】解:连结交于O,连结
在中,因为M,O分别为AC,中点,
所以
又因为平面,平面,
所以平面
因为侧棱底面ABC,平面ABC,
所以
又因为M为棱AC中点,,所以
因为,,平面
所以平面平面
所以
因为M为棱AC中点,,所以
又因为,所以在和中,
所以,
即
所以
因为,BM,平面
所以平面
当点N为中点时,即,平面平面
设中点为D,连结DM,
因为D,M分别为,AC中点,
所以,且
又因为N为中点,
所以,且,
所以四边形DMBN是平行四边形,
所以,
所以,,
又因为,,
所以平面
又因为平面,
所以平面平面
23(本小题13分)
对于行列的数表,定义变换:任选一组其中,对于的第行和第列的个数,将每个数同时加1,或者将每个数同时减1,其余的数不变,得到一个新数表.
(1)已知对依次进行4次变换,如下:写出值;
(2)已知.是否可以依次进行有限次变换,将变换为?说明理由;
(3)已知11行11列的数表,是否可以依次进行次变换,将其变换为?若可以,求的最小值;若不可以,说明理由.
【答案】(1)根据变换的定义,
可得
(2)不可以,理由如下:
由题可知每次变换T,数表中所有数的和增加或减少5.
因为A中所有数的和为0,所以其经过有限次变换T后各数和为5的倍数.
而 B中所有数的和为9,不符合,故无法通过有限次变换T,将A变换为B.
(3)可以,且k的最小值为 400
当所选时,所有加l的变换T与减1的变换T次数之差设为;
当所选且或者且时,所有加1的变换T与减1的变换T 次数之差设为;
当所选时,加1的变换T与减1的变换T次数之差设为.
考虑变换T 对上述三部分各数之和的影响,
可知,解得,
所以,
其中符合题意的 400 次变换T构造如下:
当所选时,各进行一次减1的变换T;
当所选且或者且时,
各进行10次加l的变换T;
当所选时,进行100次减l的变换T.
同课章节目录
