2024-2025学年浙教版(2024)七年级数学下册期末真题专项练习 04 解答题(含解析)
文档属性
| 名称 | 2024-2025学年浙教版(2024)七年级数学下册期末真题专项练习 04 解答题(含解析) | 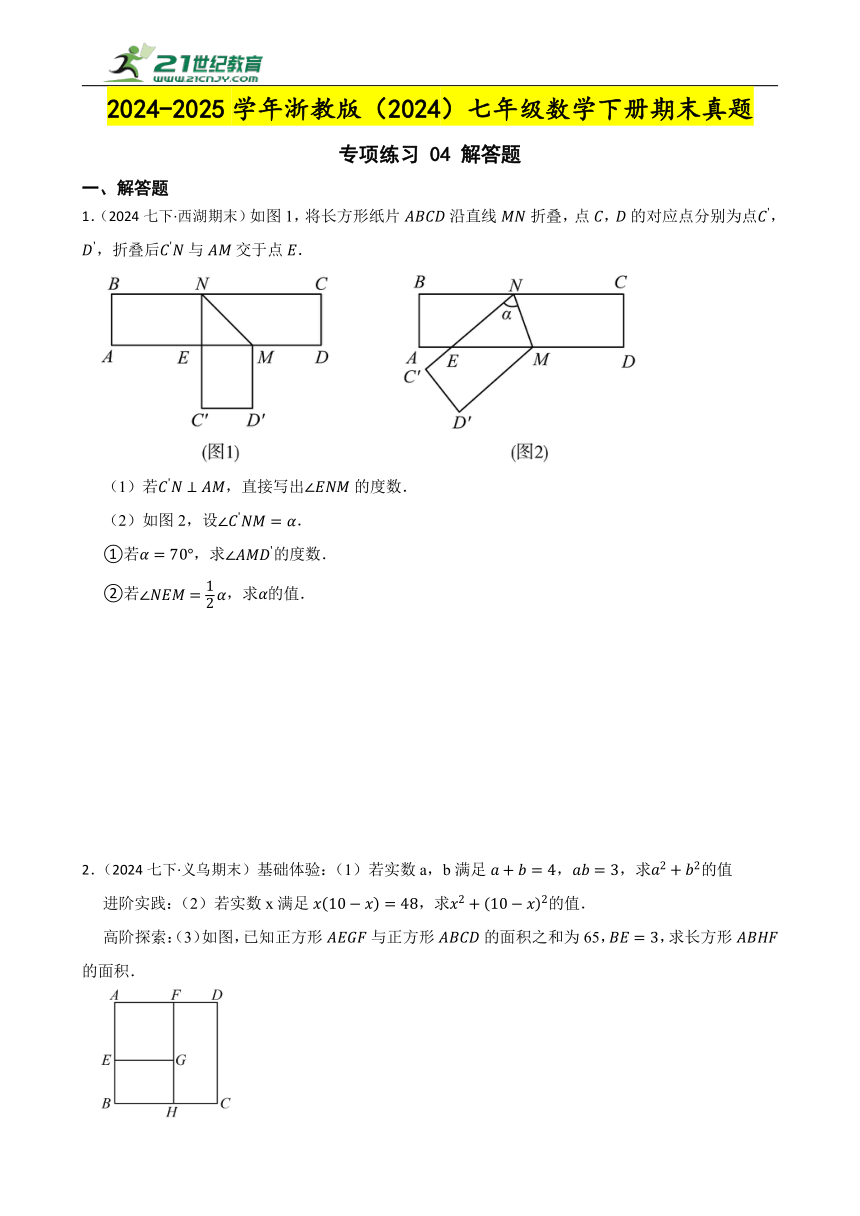 | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 18:14:07 | ||
图片预览




文档简介
2024-2025学年浙教版(2024)七年级数学下册期末真题
专项练习 04 解答题
一、解答题
1.(2024七下·西湖期末)如图1,将长方形纸片沿直线折叠,点,的对应点分别为点,,折叠后与交于点.
(1)若,直接写出的度数.
(2)如图2,设.
①若,求的度数.
②若,求的值.
2.(2024七下·义乌期末)基础体验:(1)若实数a,b满足,,求的值
进阶实践:(2)若实数x满足,求的值.
高阶探索:(3)如图,已知正方形与正方形的面积之和为65,,求长方形的面积.
3.(2024七下·江北期末)已知: 如图点 在 的一边 上, 过点 的直线 , CD 平分 .
(1) 若 , 求 的度数;
(2) 求证: 平分 ;
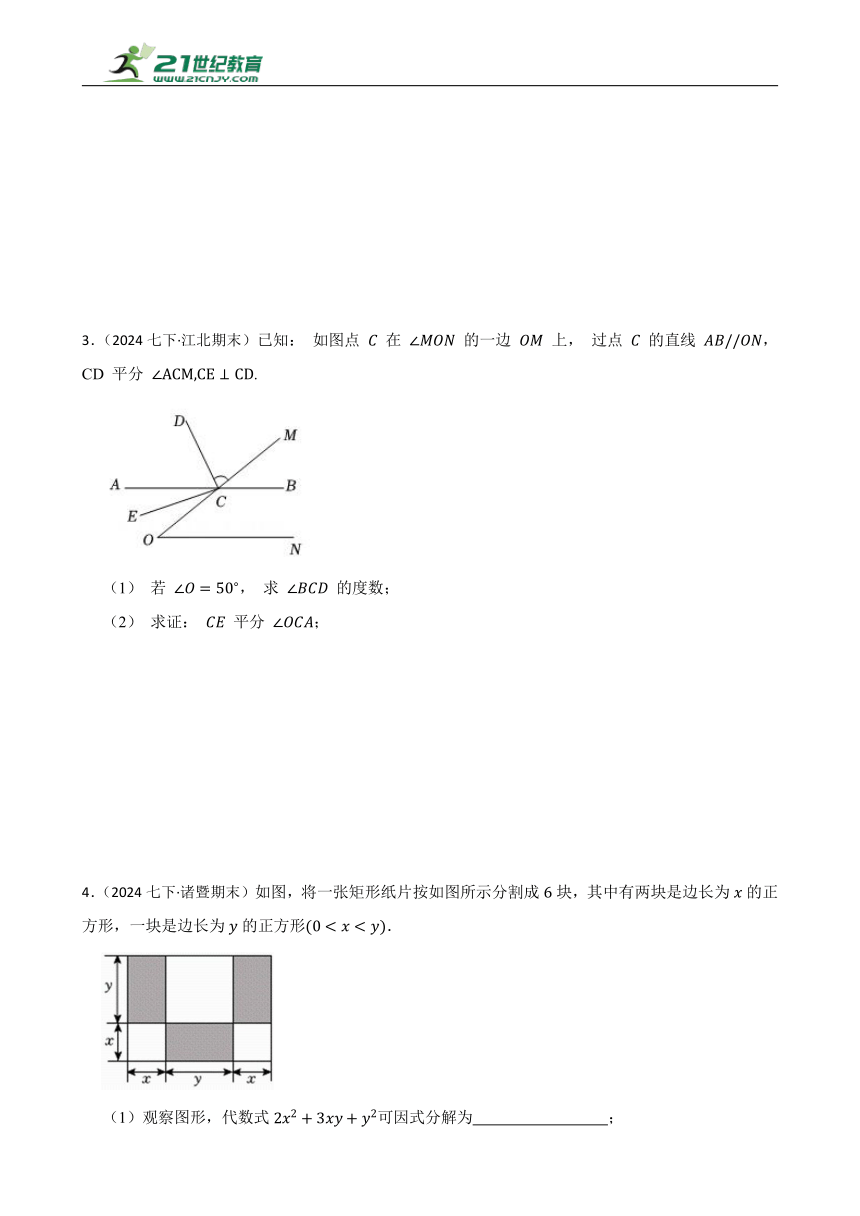
4.(2024七下·诸暨期末)如图,将一张矩形纸片按如图所示分割成块,其中有两块是边长为的正方形,一块是边长为的正方形.
(1)观察图形,代数式可因式分解为 ;
(2)图中阴影部分面积之和记作,非阴影部分面积之和记作.
用含,的代数式表示,;
若,求的值.
5.(2024七下·鄞州期末) 学校举行运动会,由若干名同学组成一个长方形队列.如果原队列中增加54人,就能组成一个正方形队列;如果原队列中减少74人,也能组成一个正方形队列.问原长方形队列有多少名同学?
6.(2024七下·海曙期末)某校七、八年级师生开展 “一日游” 活动, 已知七年级师生共 250 人, 八年级师生共 230 人. 参观某景点时,需要乘船游玩,现有 两种型号的游船,每艘 型船的座位数是每艘 型船的 1.25 倍. 若七年级师生全部乘坐 型船若干艘,刚好坐满; 八年级全部乘坐 型船,要比七年级乘坐的 型船总数多一艘且空 10 个座位.
(1) 两种游船每艘分别有多少个座位;
(2) 若两个年级的师生联合租船, 且每艘游船恰好全部坐满, 请写出所有的租船方案.
7.(2024七下·海曙期末)如图,在三角形 中,点 在边 上,点 分别在边 上,且 .
(1) 试说明: ;
(2) 若 ,求 的度数.
8.(2024七下·海曙期末)2024 年 4 月 25 日中国成功发射神舟十八号载人飞船. 为了弘扬航天精神, 某中学开展了主题为 “理想高于天, 青春梦启航” 的航天知识竞答活动, 学校随机抽取了七年级部分同学的成绩进行整理,分成五组: 组 60 分以下; 组 60 分; 组 70 分; 组 分; 组 分. 每个组都含最小值不含最大值,例如 组包括 60 分,但不包括 70 分,并绘制了如图所示的频数分布直方图、扇形统计图.
根据以上信息, 解答下列问题:
(1) 本次随机抽查 ▲ 名同学, 并补全频数分布直方图.
(2) 扇形统计图中, 组所在扇形的圆心角度数为 .
(3) 该校要对成绩为 组 90 分的学生进行奖励,按成绩从高分到低分设一、二等奖,且一、二等奖的人数比例为 3: 7, 请你估计该校 1500 名学生中获一等奖的学生人数有多少人
9.(2024七下·余姚期末)如图,已知CD∥BE,∠1+∠2=180°.
(1)求证:EF∥BC.
(2)若∠EFA-∠EBA=44°,∠D=2∠AEF,求∠D的度数.
10.(2024七下·金华期末)某校为了解学生一分钟跳绳个数情况,随机抽取了60名学生进行调查,获得每位学生一分钟跳绳个数(单位:个),下面是对数据进行整理、描述和分析后的部分信息.
信息1.一分钟跳绳个数的频数分布直方图如图,数据分成4组:,,,;
信息2.一分钟跳绳个数在这一组的有:182,189,182,180,186,185,183,184,188,185,183,185,186,183,186,184,188,180.根据以上信息,回答下列问题:
(1)求出频数分布直方图中m的值;
(2)求这60个数据的组距及跳绳成绩为“186个”的频率;
(3)该校规定跳绳一分钟180个及以上为良好,若该校有1200名学生,请估计该校学生跳绳达到良好的人数.
11.(2024七下·东阳期末)某校为创建书香校园,倡书风尚,开展了师生“大阅读”活动,并制定“大阅读”星级评选方案,每月评选一次.为了解活动开展情况,学校组织对全校八年级“大阅读”星级评选工作进行抽样调查,随机抽取20名学生阅读的积分(分值为整数)情况进行分析.
【收集数据】20名学生的“大阅读”积分(单位:分):32,43,34,35,15,46,48,24,54,10,25,40,60,42,55,30,47,28,37,42
【整理数据】
积分/分
星级 红 橙 黄 绿 青
频数(人数) 2 3 5
(1)填空:______,______;
(2)根据表格制成如图所示不完整的频数分布直方图,请将其补全.
(3)估计全校1500学生中获得绿星级以上(包括绿星级)的人数共有多少人?
12.(2024七下·越城期末) 某校暑期组织部分学生进行 “明仕遗风” 绍兴站研学游活动。为了提高学生参与活动的积极性, 学校决定在某文创店购买名人徽章和地标冰箱贴作为奖励。已知徽章的单价是冰箱贴的 2 倍, 用 120 元购买冰箱贴的数量比用 160 元购买徽章的数量多8件。
(1)求冰箱贴和徽章的单价.
(2)若购买经费为400元且购买徽章和冰箱贴的数量之比为,求购买徽章和冰箱贴的数量.
13.(2024七下·越城期末) 为了解某校七年级学生体质健康测试项目中的 “仰卧起坐” 情况, 随机抽取该年级部分学生进行了一次 “仰卧起坐” 测试,并根据标准把测试成绩分成 四个等级, 绘制出不完整的统计图:
请根据图中信息解答下列问题:
(1)本次抽取参加测试的学生共 人,扇形统计图中 等级占的百分比是 ;
(2)补全条形统计图;
(3)已知七年级共有学生 800 人,若规定 “仰卧起坐” 测试成绩为 等级属于不合格, 请估计七年级 “仰卧起坐” 测试成绩不合格的人数.
14.(2024七下·玉环期末)已知关于x,y的方程组
(1)请用含的式子表示该方程组的解;
(2)①当取不同值时,,的值也随之变化,取部分数值列表如下:
则表格中的__________,__________;
②不管如何变化,,之间是否存在不变的数量关系?若存在,请写出这个关系式并证明;
(3)根据上述思路,解答下列问题:
①若关于,的方程组中,求的最大值;
②直接写出关于,的方程组与的公共解为__________.
15.(2024七下·定海期末)如图,直线被所截取,直线分别交直线于点与点,已知.
(1)判断直线与是否平行,并说明理由.
(2)计算的度数.
16.(2024七下·钱塘期末)对于实数a,b,定义新运算“*”,规定如下:.
例如:.
(1)若,求的值.
(2)若,求的值.
(3)若,,求的值.
17.(2024七下·钱塘期末)为丰富七年级学生的课间体育活动,某学校准备安排四种球类项目:A.篮球,B.足球,C.排球,D.乒乓球供七年级学生选择(要求每位学生必须选择其中一种球类项目).为了解学生对球类项目的选择情况,该校对七年级的部分学生进行了抽样调查,并根据调查结果制作不完整的统计表图如下:
“学生球类项目选择”情况统计表
球类项目 频数 频率
A.篮球 m 0.40
B.足球 70 0.35
C.排球 40 n
D.乒乓球 10 0.05
“学生球类项目选择”情况条形统计图
(1)求m,n的值,并根据以上信息补全条形统计图.
(2)请根据抽样调查的结果,估计七年级500名同学中选择“足球”项目的人数.
18.(2024七下·长兴期末)美术课上,每位同学都拿到一张正方形纸片,该纸片可看作由4张正方形,1张正方形,4张长方形拼成.小吴同学设计了形如字母Z的图标(如图).
(1)当,时,求阴影部分的面积;
(2)用含,的代数式表示阴影部分的面积;
(3)小吴研究发现:设计图中阴影部分的面积正好等于4张正方形的面积之和,试探索此时,之间的数量关系.
19.(2024七下·吴兴期末)某校为落实“双减”政策及课后服务要求,准备开设乒乓球,素描,书法,篮球,足球五项课后服务项目.为了解学生的需求,学校随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的扇形统计图和条形统计图.请你根据给出的信息解答下列问题:
(1)求报名篮球的学生人数,并补全条形统计图;
(2)求、的值;
(3)若该校有名学生,试估计该校参加“素描”活动的学生有多少人?
20.(2024七下·海曙期末)如图,已知,
(1)判断是否平行,并说明理由.
(2)若,求的度数.
21.(2024七下·西湖期末)设,是实数,定义关于的一种运算:,例如: ,.
(1)求的值.
(2)若,求的值.
(3)是否存在的值,使得成立?若存在请求出的值,若不存在请说明理由.
22.(2024七下·嵊州期末)某水果销售商前往水果批发市场进货,已知苹果的批发价格为每箱40元,橙子的批发价格为每箱50元.他花了3500元购进苹果和橙子共80箱.
(1)问苹果、橙子各购买了多少箱?
(2)该水果销售商有甲、乙两家店铺,因地段不同,每售出一箱苹果和橙子的获利也不同,甲店分别可获利12元和18元,乙店分别可获利10元和15元.现将购进的80箱水果中的a箱苹果和b箱橙子分配到甲店,其余的分配到乙店.由于口碑良好,两家店都很快卖完这批水果.若此次销售过程中销售商在甲店获利600元,那么在乙店获利多少元?
23.(2024七下·嵊州期末)某中学一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,划分等级后的数据整理如下表:
等级 非常了解 比较了解 基本了解 不太了解
频数 50 110 35 5
频率 0.25 m 0.175 0.025
(1)本次问卷调查取样的样本容量为______,表中m的值为______
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数,并补全扇形统计图.
(3)若该校有学生1000人,根据调查结果,估计这些学生中“比较了解”垃圾分类知识的人数.
24.(2024七下·温州期末)分解因式:
(1)
(2)
25.(2024七下·德清期末)已知,直线,A,B,C分别是直线,m,n上的点,连结,,若为锐角,点B在的内部.
(1)如下图,若,,求的度数;
(2)如下图,以为边向左侧作,与直线n交于点D(点D在点C的左侧),作的平分线,交于点E,连结并延长,交直线于点F,记与直线m的夹角为,.若.
①求与的数量关系;
②求的值.
26.(2024七下·柯桥期末)如果两个分式和满足(为整数),则称M,N为“兄弟分式”,整数称为的“信度值”如分式,满足,则称为“兄弟分式”,整数2称为的“信度值”.
(1)已知分式,判断M,N是否为“兄弟分式”,若不是,说明理由;若是,请求出为的“信度值”.
(2)已知x,y均为非零实数,分式属于“兄弟分式”,且两个分式的“信度值”为3,求分式的值.
(3)已知“兄弟分式”M,N,分式为分式的“信度值”是.
①求(用含的代数式表示);
②若的值为正整数,为正整数,求的值.
27.(2024七下·拱墅期末)观察下列等式,可以发现一些规律.
①.左边两项系数之和为2,两项系数之和为3,右边三项系数之和为6,满足算式;
②.左边两个因式各项系数之和分别为3,4,右边各项系数之和为12,满足算式.
(1)任写一个较简单的多项式,把你写的多项式与多项式相乘并计算.类比①或②,写出结论.
(2)若m,n为常数,且,求m,n的值.
(3)根据上面的规律,求的展开式中各项系数的和.
28.(2024七下·平湖期末)已知关于的方程组,其中,为整数.
(1)若方程组有无穷多组解,求实数与的值;
(2)当时,方程组是否有整数解?如有,求出整数解;若没有,请说明理由.
29.(2024七下·平湖期末)交通部门为了安全起见在某道路两旁设置了,两座可旋转探照灯.假定主道路是平行的,即,,为上两点,平分交于点,为上一点,连接,平分交于点.
(1)若,则______;
(2)若点为线段上一点,且满足,当时,试说明:;
(3)在(1)问的条件下,探照灯,射出的光线在道路所在平面旋转.探照灯射出的光线从处开始以每秒的速度绕点逆时针转动,探照灯射出的光线从处开始以每秒的速度绕点逆时针转动,当转至射线后立即以相同速度回转.若它们同时开始转动,当回到出发时的位置时同时停止转动.设转动时间为秒,则在转动过程中,当时,请直接写出此时的值.
30.(2024七下·鄞州期末)给出如下 个平方数∶ ,规定∶ 可以在其中的每个数前任意添上“”号或“”号, 所得的代数和记为 .
(1)当 时,试设计一种可行方案,使得:且最小.
(2)当 时,试设计一种可行方案,使得:且最小.
答案解析部分
1.(1)
(2)解:①∵长方形纸片沿直线折叠,∴
∵,
∵CN∥DM
即70°+70°+∠AMD=180°
∴∠AMD=40°
②由①知:
∵,
在三角形MNE中
∴
解:(1)∵长方形纸片沿直线折叠,
∴AD∥BC,∠MEN=∠ CNE=90°,
∴;
故答案为:45°.
(1)根据垂直的定义,平行线的性质,得到,再根据折痕是角平分线,求出的度数即可;
(2)①折叠的性质,得到,平行得到=,,再根据角的和差关系进行求解即可;
②根据问题①中得到和三角形的内角和定理求解即可.
(1)解:∵长方形纸片沿直线折叠,
∴,
∵,
∴,
∴,
∴;
(2)①∵折叠,
∴,,
∵,
∴,
∴;
②由①知:,
∵,且,
∴,
∴.
2.(1)解:∵, ,
∴,
∴,
∴.
(2)解:设,
∴,
∵,
∴,
∴
;
(3)解:设正方形的边长为a,正方形是边长为b,
∵正方形与正方形的面积之和为65,
∴,
∵,
∴,
∴,
∴
,
∴,
∴,
∴长方形的面积为28.
(1)根据完全平方公式可得,将 代入,即可求解;
(2)设,则,根据题意可得ab=48,根据完全平方公式进行计算,即可求解;
(3)设正方形的边长为a,正方形是边长为b,根据“正方形与正方形的面积之和为65”可得,结合题意可得,根据完全平方公式进行计算,即可求解.
3.(1)解:∵
∴∠O=∠BCM=50°
∴∠ACM=180°-∠BCM=130°
∵ CD 平分 ∠ACM
∴
∴∠BCD=∠BCM+∠DCM=50°+65°=115°
(2)证明:∵
∴∠ACE+∠ACD=90°
由(1)可知:
∴
∵
∴∠BCM=∠O=∠ACO
∴∠ACE=∠ACO
∴ 平分 .
4.(1)(2x+y)(x+y)
(2)解:观察图形,得:,;
,
∴3xy-2x2-y2=2x2-xy,
整理,得:4x2-4xy+y2=0
即(2x-y)2=0,
∴2x-y=0,
,
.
(1)解:观察图形得:长方形纸片分为2块是边长为x的正方形,1块是边长为y的正方形,3块是长为y,宽为x的长方形,
∴长方形纸片的面积为:2x2+3xy+y2,
∵长方形纸片的长为:,宽为,
∴长方形纸片的面积为:(2x+y)(x+y),
∴2x2+3xy+y2=(2x+y)(x+y),
∴代数式2x2+3xy+y2因式分解为(2x+y)(x+y);
故答案为:(2x+y)(x+y).
(1)用两种方式计算长方形纸片的面积,即可得到2x2+3xy+y2=(2x+y)(x+y),即可求解;
(2)①根据图形的特征,直接计算即可;②根据,可得4x2-4xy+y2=0,从而得到y=2x,再代入所求的代数式,即可求解.
5.解:设原队列有m人,
增加54人后组成a×a的正方形队列,减少74人后组成b×b的正方形队列.
根据题意得:
1- ②:
,解得,∴m1=1035;
,解得,∴m2=270;
,解得,∴m3=90;
综上所述,原队列有1035人或270人或90人。
设原队列有m人,增加54人后组成的正方形队列,减少74人后组成的正方形队列.可得:,再利用因式分解的结果建立方程组解题即可;
6.(1)解:设 B型船每艘有 x 个座位,则 A 型船每艘有 1.25x 个座位,根据题意,得
解得, x=40
经检验, 是原分式方程的解,且符合题意。
答: 型船每艘有 50 个座位, 型船每艘有 40 个座位
(2)解:设需租用 型船 m 艘,租用 型船 n 艘
由题意得,
r∴
又 ∵m、n 均为非负整数,
共 3 种租船方案: ①租用 12 艘 B 型船; ②租用 4 艘 A 型船,7 艘 B 型船; ③
租用 8 艘 A 型船, 2 艘 B 型船.
(1)设B型船每艘有x个座位,用x表示A型船的座位,根据七年级师生全部乘坐A型船若干艘,刚好坐满;八年级全部乘坐B型船,要比七年级乘坐的A型船总数多一艘且空10个座位.列出分式方程,解方程即可;
(2)设租用A型船m艘,B型船n艘,根据两个年级的师生联合租船,且每艘游船恰好全部坐满,列出二元一次方程,求出非负整数解即可。.
7.(1)证明:∵BC∥DG,
∴∠DCB=∠1,
,
,
∴DC∥EF。
(2)解:∵EF⊥AB,
∴∠BEF=90°,
∵DC∥EF,
∴ .
,
∴ .
(1)根据两直线平行,内错角相等可得∠DCB=∠1,根据同位角相等可得DC∥EF,据此证明;
(2)根据垂直定义可得∠FEB=90°,根据平行线的性质可得∠CDB=90°,再根据平角的定义,利用角的和差即可求出结果.
8.(1)解:50 名同学.
(2)
(3)解:∴ 一、二等奖的人数比例为 3: 7 ,
∴ 获一等奖的学生占获奖人数的,
(人)
答: 该校 1500 名学生中获一等奖的学生人数有 72 人
解:(1)观察统计图可得,D组人数为15人,所占的百分比为30%,
∴总人数为:(人),
补全频数分布直方图如图所示:
故答案为:50;
(2)观察统计图可得,A组的人数是5人,∴A 组所在扇形的圆心角度数为:,
故答案为:;
(1)基本关系:总数=部分÷部分所占的百分比,利用D组的人数除以其所占的百分比求得随机抽查的总人数,再补全频数分布直方图即可;
(2)基本关系:扇形的圆心角的度数=360°×部分所占的百分比,利用A组的人数除以随机抽查的总人数求得其所占的百分比,再乘以360°即可求解;
(3)利用总人数乘以一等奖人数所占百分比,再乘以E组的人数在样本中所占百分比即可求解.
9.(1)证明:∵,
,
,
同角的补角相等,
∴(内错角相等,两直线平行,
(2)解:∵,
,
,,
,即,
,
(1)先根据得到 ∠1+∠CBE=180 ° ,结合 ∠1+∠2=180 ° ,证明∠2=∠CBE,从而得到;
(2)先证明∠D=2∠AEF,进而证明∠D=2∠2,即可求出∠D的度数.
10.(1)解:根据频数分布直方图可得.
(2)解:由题意可知:组距为170-160=10,
跳绳成绩为“186个”的频率.
(3)解:
答:该校学生跳绳达到良好的估计有640人.
(1)利用频数之和等于总数,求出m的值;
(2)先利用图中分组确定组距,再用频数除以总数求出频率;
(3)用1200乘以良好所占的比例.
11.(1)7,3
(2)解:补全频数分布直方图如下:
(3)解:这1500名学生中获得绿星级以上的人数有.
答:这1500名学生中获得绿星级以上的人数有750人.
(1)解:由样本数据得:的有7人,的有3人,
∴,
故答案为:7,3;
(1)整理样本中的数据得到m和n的值即可;
(2)根据(1)中所得的数据补全统计图即可;
(3)利用中绿星级以上的人数的占比×1500解答即可.
12.(1)解:设冰箱贴的单价为元/件,则徽章的单价为元/件。
由题意得:
解这个方程得:
经检验,是所列方程的根,且符合题意
徽章的单价:(元)
答:冰箱贴的单价为5元/件, 徽章的单价为10元/件.
(2)解:设购买徽章的数量为个,购买冰箱贴的数量为个。
由题意得:
解得:
答:购买徽章的数量为30个,购买冰箱贴的数量为20个。
13.(1)50;
(2)解: 等级的人数为 (人)
补全条形统计图如下:
(3)解:测试成绩不合格的人数为:
答:七年级“仰卧起坐”测试成绩不合格的人数为80人。
14.(1)
(2)①2,2;②存在,;
(3)①的最大值为;②
15.(1)解:平行.理由:由已知可得,
∵,
∴,
∴.
(2)解:∵,∴,
∵,
∴,
∴的度数为.
(1)先利用对顶角相等得到,即可得到,然后根据平行线的判定得到结论即可.
(2)根据两直线平行,内错角相等得到,即可求出的度数解题.
(1)解:平行.
理由:由已知可得,
∵,
∴,
∴.
(2)解:∵,
∴,
∵,
∴,
∴的度数为.
16.(1)解:,
,
,
.
当时,原式
(2)解:,
,
,
.
,
,即,
原式
(3)解:,
,
,
,
,,
∴ (a+b)2=(a+b)2-4ab=9-8=1,
或,
当,时,原式,
当,时,原式,
∴的值为3或-3
(1)先根据新定义运算,再整体代入a+b的值,即可求得;
(2)先根据新定义运算,再将整体代入求值即可;
(3)先根据新定义运算,再利用完全平方公式求出的值,最后代入求值即可.
(1)解:
.
当时,
原式;
(2)
.
,
即.
原式
;
(3)
.
,,
,即.
.
.
.
或.
当,时,
原式;
当,时,
原式.
17.(1)解:此次调查的总人数为(人,
项目的人数(人,
补全条形统计图如下:
(2)(名,
答:估计七年级500名同学中选择“足球”项目的人数为175名
(1)用的频数除以频率求出总人数,再用总人数减去B、C和D的人数求出的人数,即可补全条形统计图;
(2)用总人数乘以样本中的人数所占比例即可求得.
(1)解:此次调查的总人数为(人,
项目的人数(人,
补全条形统计图如下:
(2)(名,
答:估计七年级500名同学中选择“足球”项目的人数为175名.
18.(1)
(2)
(3)
19.(1)解:(人),
,
所以报名篮球的学生有人
补全图形如下:
(2)篮球项目人数所占百分比,即
素描项目人数所占百分比,即;
(3),(人).
估计该校参加“素描”活动的学生有人.
(1)由书法项目人数及其所占百分比可求得总人数,再根据各项目人数之和等于总人数求出篮球人数,从而可补全条形统计图;
(2)分别用篮球、素描人数除以总人数可求得、的值;
(3)总人数乘以样本中素描项目人数所占比例即可求解.
(1)解:(人),
,
所以报名篮球的学生有人
补全图形如下:
(2)篮球项目人数所占百分比,即
素描项目人数所占百分比,即;
(3),
(人).
估计该校参加“素描”活动的学生有人.
20.(1)解:,理由如下:
,
,
,
,
∴;
(2)解:∵,
,
,
∵,
,
,
,
(1)由两直线平行,同位角相等得到,即可得到,然后根据内错角相等,两直线平行解题即可;
(2)根据平行线的性质得到,,即可求出∠DEF的度数解题.
21.(1)解:
(2)解:∴
∴;
经检验,是原方程的解,
∴
(3)存在;
当时,即:,
去分母得
移项合并同类项得
即x(x-1)=0
检验:
当是原方程的根。
当时,,分式无意义,不满足题意,舍去;
故
(1)根据新运算的计算法则,列式计算即可;
(2)根据新运算的计算法则,列出分式方程并解分式方程,记得检验。
(3)根据新运算的计算法则,列出分式方程并解分式方程,记得检验。增根的舍去.
(1)解:;
(2),
∴,
∴;
经检验,是原方程的解,
∴.
(3)存在;
,
当时,即:,
当时,满足题意,
当时,则:,则:,
当时,,分式无意义,不满足题意,舍去;
故.
22.(1)解:设苹果购买了x箱,橙子购买了y箱,
根据题意得,,
解得,,
答:苹果、橙子各购买了50箱、30箱.
(2)解:由题意可得销售商在甲店获利为:12a+18b=600(元),
整理得,2a+3b=100,
销售商在乙店获利为:10(50-a)+15(30-b)
=950-10a-15b
=950-5(2a+3b)
=950-5×100
=450(元),
即在乙店获利450元.
答:在乙店获利450元.
(1)设苹果购买了x箱,橙子购买了y箱,根据“苹果的批发价格为每箱40元,橙子的批发价格为每箱50元.他花了3500元购进苹果和橙子共80箱”,列出二元一次方程组求解即可;
(2)由题意可得销售商在甲店获利,整理后得到2a+3b=100,再表示出在乙店的获利,整理后把2a+3b=100整体代入即可解答.
(1)解:设苹果购买了x箱,橙子购买了y箱,
根据题意得,,
解得,,
答:苹果、橙子各购买了50箱、30箱.
(2)解:由题意可得销售商在甲店获利为:12a+18b=600(元),
整理得,2a+3b=100,
销售商在乙店获利为:10(50-a)+15(30-b)
=950-10a-15b
=950-5(2a+3b)
=950-5×100
=450(元),
即在乙店获利450元.
答:在乙店获利450元.
23.(1)200;
(2)解:等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数为:;补充完整的扇形统计图如下:
(3)解:(人);答:估计这些学生中“比较了解”垃圾分类知识的有550人.
(1)解:本次问卷调查取样的样本容量为;
;
故答案为:200;;
(1)根据“非常了解”的频数与频率,即可求得本次问卷调查取样的样本容量;由频率之和为1即可求得m的值;
(2)由频率与的积即可求得扇形圆心角,进而可补充完整扇形统计图;
(3)样本数据估计总体,用全校人数乘以“比较了解”的频率即可解答.
(1)解:本次问卷调查取样的样本容量为;
;
故答案为:200;;
(2)解:等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数为:;
补充完整的扇形统计图如下:
(3)解:(人);
答:估计这些学生中“比较了解”垃圾分类知识的有550人.
24.解:(1)
=
=;
(2)
=
=
=.
(1)此题多项式各项具有公因式“2”,故先提公因式“2”,再由完全平方公式将商式继续进行因式分解,即可得到答案;
(2)把“x-y”看成一个整体,先从第二项括号内提取出负号放到这一项的前面,然后提公因式“x-y”,再由平方差公式将商式进行分解因式,即可得到答案.
25.(1)
(2)①,
26.(1)是,
(2)1
(3)①②或
27.(1)解:多项式是,
,左边两个因式系数之和分别为2,0,右边各项系数之和为0,满足算式
(2)解: ,
∴ m=2,n=2m-1=3
(3)解:23×11×8=2024
(1)计算左边两个多项式中每个多项式各项系数之和,再求出“系数和”的乘积,即可求得规律;
(2)根据多项式乘多项式展开后,相同的项的系数相同可得m=2,n=2m-1,即可求得;
(3)根据规律直接计算左边三个因式“系数和”的乘积即可.
(1)写的多项式是,;
左边两个因式系数之和分别为2,0,右边各项系数之和为0,满足算式;
(2),为常数,且,
,,
解得,,
(3)由(1)(2)的规律可知,
的展开式中各项系数的和为
.
28.(1)解:依题意,由①得,,③
将③代入②得,
整理得出,④
∵方程组有无穷多组解
∴且时,
即,则,
∴,;
(2)解:没有,
理由如下:由(1)得,
∵,
∴
整理得
①当时,即,
∵
∴此时方程组为
则,
∵为整数,
∴原方程没有整数解;
②当时,即,此时,
若时,显然无解,
若时,,代入得
∵a为整数,
∴不可能为整数,
∴原方程无整数解;
综上:原方程没有整数解.
(1)先把①中的值代入②,使方程变为只含的一元一次方程,再令的系数为零,即可求得a和b的值;
(2)将b=a-1代入可得,再分类讨论和的情况,再结合整数解分析即可求得.
(1)解:依题意,
由①得,,③
将③代入②得,
整理得出,④
∵方程组有无穷多组解
∴且时,
即,则,
∴,
(2)解:没有,理由如下:
由(1)得
∵
∴
整理得
①当时,即,
∵
∴此时方程组为
则
∵为整数
∴原方程没有整数解
②当时,即,此时,
若时,显然无解,
若时,,代入得
∵a为整数,
∴不可能为整数,
∴原方程无整数解;
综上:原方程没有整数解
29.(1)
(2)解:设,则,
∵,
∴,
∵平分,平分,
∴,
∴,
∵,,
∴,
∴,
∴;
(3)解:,
由题意得,
当时,如图,,,
∴,
∴,
∵,
∴,
∴,解得:;
当时,如图,,此时,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,解得:;
综上所述,或.
解:(1)∵,,
∴,解得:,
∵平分,
∴,
∴,
∵,
∴,
故答案为:;
(1)先由平角的定义及角平分线的定义得出,再根据邻补角的意义求出,然后两直线平行,内错角相等求出∠C;
(2)设,先用x表示出,再利用平行线的性质求得,然后利用角平分线的意义求出,,从而可得,再根据内错角相等,两直线平行判定;
(3)分“”、“”两种情况讨论,分别表示出两种情况下相关角的度数,根据直角三角形两锐角互余列出关于t的方程求解.
(1)∵,,
∴,
∵平分,
∴,
∴,
∵,
∴,
故答案为:;
(2)设,则,
∵,
∴,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
∴;
(3),
由题意得,
当时,如图,,此时,,
∴,
∴,
∵,
∴,
∴,
解得;
当当时,如图,,此时,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
解得;
综上,或.
30.(1)解:∵,,
∴8个连续正整数的平方数总可以使得它们的代数和为0,
∴当时,或当时,最小,且最小值为0;
(2)解:当时,
①由题意知,给定的个数中有个奇数,
∴不管如何添置“”号和“”号, 其代数和总为奇数,
∴所求的最终代数和大于等于1,
∴设计最终代数和等于1的可行方案;
②∵,,
∴对于8个连续正整数的平方数总可以使得它们的代数和为0;
③∵,
对 ,根据②中每连续8个一组适当添加“”号和“”号,使每组的代数和为0,
然后对进行设计,但无论如何设计,均无法使它们的代数和为1;
④在对进行设计的过程中,,
又由②知4个连续正整数的平方数总可以使得它们的代数和为4,
∴个连续正整数的平方数总可以使得它们的代数和为;
综上,可行方案为:首先对,根据②每连续8个一组适当添加“”号和“”号,使每组的代数和为0;
其次对,根据④适当添加“”号和“”号,使每组的代数和为;
最后对作的设计,便可以使得给定的个数的代数和为1,即最小.
(1)应该尽量构成互为相反数的两组数,可使2,3,5 ,8项的符号与其他项的符号相反即可;
(2)①由于给定的2045个数中有1023个奇数,因而无论如何设计实施什么方案,即不管如何添置“+”和“-”号,其代数和总为奇数,故所求的最终代数和大于等于1;于是我们寻求最终代数和等于1的可行方案; ②由(1)可知对于8个连续正整数的平方数总可以使得它们的代数和为0;③由2045=8×255+5,对62,72,……,20452,根据②中每连续8个一组适当添加“+”号和“-”号,使每组的代数和为0,然后对12,22,……,52进行设计,但无论如何设计,均无法使它们的代数和为1;④在对12,22,……,52进行设计的过程中,-12+22-32+42-52=-15,又由②知4个连续正整数的平方数总可以使得它们的代数和为4,则16个连续正整数的平方数总可以使得它们的代数和为;进而可得可行方案为:首先对222,232,……,20452,根据②每连续8个一组适当添加“+”号和“-”号,使每组的代数和为0;其次对62,72,……,212根据④适当添加“+”号和“-”号,使每组的代数和为;最后对12,22,……,52,作-12+22-32+42-52=-15的设计,便可以使得给定的2045个数的代数和为1,即|L|最小.
(1)解:∵,,
∴8个连续正整数的平方数总可以使得它们的代数和为0,
∴当时,或当时,最小,且最小值为0;
(2)解:当时,
①由题意知,给定的个数中有个奇数,
∴不管如何添置“”号和“”号, 其代数和总为奇数,
∴所求的最终代数和大于等于1.
∴设计最终代数和等于1的可行方案.
②,
∴对于8个连续正整数的平方数总可以使得它们的代数和为0;
③∵,
对 ,根据②中每连续8个一组适当添加“”号和“”号,使每组的代数和为0,
然后对进行设计,但无论如何设计,均无法使它们的代数和为1.
④在对进行设计的过程中,,
又由②知4个连续正整数的平方数总可以使得它们的代数和为4,
∴个连续正整数的平方数总可以使得它们的代数和为.
综上,可行方案为:首先对,根据②每连续8个一组适当添加“”号和“”号,使每组的代数和为0;其次对,根据④适当添加“”号和“”号,使每组的代数和为;最后对作的设计,便可以使得给定的个数的代数和为1,即最小.
专项练习 04 解答题
一、解答题
1.(2024七下·西湖期末)如图1,将长方形纸片沿直线折叠,点,的对应点分别为点,,折叠后与交于点.
(1)若,直接写出的度数.
(2)如图2,设.
①若,求的度数.
②若,求的值.
2.(2024七下·义乌期末)基础体验:(1)若实数a,b满足,,求的值
进阶实践:(2)若实数x满足,求的值.
高阶探索:(3)如图,已知正方形与正方形的面积之和为65,,求长方形的面积.
3.(2024七下·江北期末)已知: 如图点 在 的一边 上, 过点 的直线 , CD 平分 .
(1) 若 , 求 的度数;
(2) 求证: 平分 ;
4.(2024七下·诸暨期末)如图,将一张矩形纸片按如图所示分割成块,其中有两块是边长为的正方形,一块是边长为的正方形.
(1)观察图形,代数式可因式分解为 ;
(2)图中阴影部分面积之和记作,非阴影部分面积之和记作.
用含,的代数式表示,;
若,求的值.
5.(2024七下·鄞州期末) 学校举行运动会,由若干名同学组成一个长方形队列.如果原队列中增加54人,就能组成一个正方形队列;如果原队列中减少74人,也能组成一个正方形队列.问原长方形队列有多少名同学?
6.(2024七下·海曙期末)某校七、八年级师生开展 “一日游” 活动, 已知七年级师生共 250 人, 八年级师生共 230 人. 参观某景点时,需要乘船游玩,现有 两种型号的游船,每艘 型船的座位数是每艘 型船的 1.25 倍. 若七年级师生全部乘坐 型船若干艘,刚好坐满; 八年级全部乘坐 型船,要比七年级乘坐的 型船总数多一艘且空 10 个座位.
(1) 两种游船每艘分别有多少个座位;
(2) 若两个年级的师生联合租船, 且每艘游船恰好全部坐满, 请写出所有的租船方案.
7.(2024七下·海曙期末)如图,在三角形 中,点 在边 上,点 分别在边 上,且 .
(1) 试说明: ;
(2) 若 ,求 的度数.
8.(2024七下·海曙期末)2024 年 4 月 25 日中国成功发射神舟十八号载人飞船. 为了弘扬航天精神, 某中学开展了主题为 “理想高于天, 青春梦启航” 的航天知识竞答活动, 学校随机抽取了七年级部分同学的成绩进行整理,分成五组: 组 60 分以下; 组 60 分; 组 70 分; 组 分; 组 分. 每个组都含最小值不含最大值,例如 组包括 60 分,但不包括 70 分,并绘制了如图所示的频数分布直方图、扇形统计图.
根据以上信息, 解答下列问题:
(1) 本次随机抽查 ▲ 名同学, 并补全频数分布直方图.
(2) 扇形统计图中, 组所在扇形的圆心角度数为 .
(3) 该校要对成绩为 组 90 分的学生进行奖励,按成绩从高分到低分设一、二等奖,且一、二等奖的人数比例为 3: 7, 请你估计该校 1500 名学生中获一等奖的学生人数有多少人
9.(2024七下·余姚期末)如图,已知CD∥BE,∠1+∠2=180°.
(1)求证:EF∥BC.
(2)若∠EFA-∠EBA=44°,∠D=2∠AEF,求∠D的度数.
10.(2024七下·金华期末)某校为了解学生一分钟跳绳个数情况,随机抽取了60名学生进行调查,获得每位学生一分钟跳绳个数(单位:个),下面是对数据进行整理、描述和分析后的部分信息.
信息1.一分钟跳绳个数的频数分布直方图如图,数据分成4组:,,,;
信息2.一分钟跳绳个数在这一组的有:182,189,182,180,186,185,183,184,188,185,183,185,186,183,186,184,188,180.根据以上信息,回答下列问题:
(1)求出频数分布直方图中m的值;
(2)求这60个数据的组距及跳绳成绩为“186个”的频率;
(3)该校规定跳绳一分钟180个及以上为良好,若该校有1200名学生,请估计该校学生跳绳达到良好的人数.
11.(2024七下·东阳期末)某校为创建书香校园,倡书风尚,开展了师生“大阅读”活动,并制定“大阅读”星级评选方案,每月评选一次.为了解活动开展情况,学校组织对全校八年级“大阅读”星级评选工作进行抽样调查,随机抽取20名学生阅读的积分(分值为整数)情况进行分析.
【收集数据】20名学生的“大阅读”积分(单位:分):32,43,34,35,15,46,48,24,54,10,25,40,60,42,55,30,47,28,37,42
【整理数据】
积分/分
星级 红 橙 黄 绿 青
频数(人数) 2 3 5
(1)填空:______,______;
(2)根据表格制成如图所示不完整的频数分布直方图,请将其补全.
(3)估计全校1500学生中获得绿星级以上(包括绿星级)的人数共有多少人?
12.(2024七下·越城期末) 某校暑期组织部分学生进行 “明仕遗风” 绍兴站研学游活动。为了提高学生参与活动的积极性, 学校决定在某文创店购买名人徽章和地标冰箱贴作为奖励。已知徽章的单价是冰箱贴的 2 倍, 用 120 元购买冰箱贴的数量比用 160 元购买徽章的数量多8件。
(1)求冰箱贴和徽章的单价.
(2)若购买经费为400元且购买徽章和冰箱贴的数量之比为,求购买徽章和冰箱贴的数量.
13.(2024七下·越城期末) 为了解某校七年级学生体质健康测试项目中的 “仰卧起坐” 情况, 随机抽取该年级部分学生进行了一次 “仰卧起坐” 测试,并根据标准把测试成绩分成 四个等级, 绘制出不完整的统计图:
请根据图中信息解答下列问题:
(1)本次抽取参加测试的学生共 人,扇形统计图中 等级占的百分比是 ;
(2)补全条形统计图;
(3)已知七年级共有学生 800 人,若规定 “仰卧起坐” 测试成绩为 等级属于不合格, 请估计七年级 “仰卧起坐” 测试成绩不合格的人数.
14.(2024七下·玉环期末)已知关于x,y的方程组
(1)请用含的式子表示该方程组的解;
(2)①当取不同值时,,的值也随之变化,取部分数值列表如下:
则表格中的__________,__________;
②不管如何变化,,之间是否存在不变的数量关系?若存在,请写出这个关系式并证明;
(3)根据上述思路,解答下列问题:
①若关于,的方程组中,求的最大值;
②直接写出关于,的方程组与的公共解为__________.
15.(2024七下·定海期末)如图,直线被所截取,直线分别交直线于点与点,已知.
(1)判断直线与是否平行,并说明理由.
(2)计算的度数.
16.(2024七下·钱塘期末)对于实数a,b,定义新运算“*”,规定如下:.
例如:.
(1)若,求的值.
(2)若,求的值.
(3)若,,求的值.
17.(2024七下·钱塘期末)为丰富七年级学生的课间体育活动,某学校准备安排四种球类项目:A.篮球,B.足球,C.排球,D.乒乓球供七年级学生选择(要求每位学生必须选择其中一种球类项目).为了解学生对球类项目的选择情况,该校对七年级的部分学生进行了抽样调查,并根据调查结果制作不完整的统计表图如下:
“学生球类项目选择”情况统计表
球类项目 频数 频率
A.篮球 m 0.40
B.足球 70 0.35
C.排球 40 n
D.乒乓球 10 0.05
“学生球类项目选择”情况条形统计图
(1)求m,n的值,并根据以上信息补全条形统计图.
(2)请根据抽样调查的结果,估计七年级500名同学中选择“足球”项目的人数.
18.(2024七下·长兴期末)美术课上,每位同学都拿到一张正方形纸片,该纸片可看作由4张正方形,1张正方形,4张长方形拼成.小吴同学设计了形如字母Z的图标(如图).
(1)当,时,求阴影部分的面积;
(2)用含,的代数式表示阴影部分的面积;
(3)小吴研究发现:设计图中阴影部分的面积正好等于4张正方形的面积之和,试探索此时,之间的数量关系.
19.(2024七下·吴兴期末)某校为落实“双减”政策及课后服务要求,准备开设乒乓球,素描,书法,篮球,足球五项课后服务项目.为了解学生的需求,学校随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的扇形统计图和条形统计图.请你根据给出的信息解答下列问题:
(1)求报名篮球的学生人数,并补全条形统计图;
(2)求、的值;
(3)若该校有名学生,试估计该校参加“素描”活动的学生有多少人?
20.(2024七下·海曙期末)如图,已知,
(1)判断是否平行,并说明理由.
(2)若,求的度数.
21.(2024七下·西湖期末)设,是实数,定义关于的一种运算:,例如: ,.
(1)求的值.
(2)若,求的值.
(3)是否存在的值,使得成立?若存在请求出的值,若不存在请说明理由.
22.(2024七下·嵊州期末)某水果销售商前往水果批发市场进货,已知苹果的批发价格为每箱40元,橙子的批发价格为每箱50元.他花了3500元购进苹果和橙子共80箱.
(1)问苹果、橙子各购买了多少箱?
(2)该水果销售商有甲、乙两家店铺,因地段不同,每售出一箱苹果和橙子的获利也不同,甲店分别可获利12元和18元,乙店分别可获利10元和15元.现将购进的80箱水果中的a箱苹果和b箱橙子分配到甲店,其余的分配到乙店.由于口碑良好,两家店都很快卖完这批水果.若此次销售过程中销售商在甲店获利600元,那么在乙店获利多少元?
23.(2024七下·嵊州期末)某中学一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,划分等级后的数据整理如下表:
等级 非常了解 比较了解 基本了解 不太了解
频数 50 110 35 5
频率 0.25 m 0.175 0.025
(1)本次问卷调查取样的样本容量为______,表中m的值为______
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数,并补全扇形统计图.
(3)若该校有学生1000人,根据调查结果,估计这些学生中“比较了解”垃圾分类知识的人数.
24.(2024七下·温州期末)分解因式:
(1)
(2)
25.(2024七下·德清期末)已知,直线,A,B,C分别是直线,m,n上的点,连结,,若为锐角,点B在的内部.
(1)如下图,若,,求的度数;
(2)如下图,以为边向左侧作,与直线n交于点D(点D在点C的左侧),作的平分线,交于点E,连结并延长,交直线于点F,记与直线m的夹角为,.若.
①求与的数量关系;
②求的值.
26.(2024七下·柯桥期末)如果两个分式和满足(为整数),则称M,N为“兄弟分式”,整数称为的“信度值”如分式,满足,则称为“兄弟分式”,整数2称为的“信度值”.
(1)已知分式,判断M,N是否为“兄弟分式”,若不是,说明理由;若是,请求出为的“信度值”.
(2)已知x,y均为非零实数,分式属于“兄弟分式”,且两个分式的“信度值”为3,求分式的值.
(3)已知“兄弟分式”M,N,分式为分式的“信度值”是.
①求(用含的代数式表示);
②若的值为正整数,为正整数,求的值.
27.(2024七下·拱墅期末)观察下列等式,可以发现一些规律.
①.左边两项系数之和为2,两项系数之和为3,右边三项系数之和为6,满足算式;
②.左边两个因式各项系数之和分别为3,4,右边各项系数之和为12,满足算式.
(1)任写一个较简单的多项式,把你写的多项式与多项式相乘并计算.类比①或②,写出结论.
(2)若m,n为常数,且,求m,n的值.
(3)根据上面的规律,求的展开式中各项系数的和.
28.(2024七下·平湖期末)已知关于的方程组,其中,为整数.
(1)若方程组有无穷多组解,求实数与的值;
(2)当时,方程组是否有整数解?如有,求出整数解;若没有,请说明理由.
29.(2024七下·平湖期末)交通部门为了安全起见在某道路两旁设置了,两座可旋转探照灯.假定主道路是平行的,即,,为上两点,平分交于点,为上一点,连接,平分交于点.
(1)若,则______;
(2)若点为线段上一点,且满足,当时,试说明:;
(3)在(1)问的条件下,探照灯,射出的光线在道路所在平面旋转.探照灯射出的光线从处开始以每秒的速度绕点逆时针转动,探照灯射出的光线从处开始以每秒的速度绕点逆时针转动,当转至射线后立即以相同速度回转.若它们同时开始转动,当回到出发时的位置时同时停止转动.设转动时间为秒,则在转动过程中,当时,请直接写出此时的值.
30.(2024七下·鄞州期末)给出如下 个平方数∶ ,规定∶ 可以在其中的每个数前任意添上“”号或“”号, 所得的代数和记为 .
(1)当 时,试设计一种可行方案,使得:且最小.
(2)当 时,试设计一种可行方案,使得:且最小.
答案解析部分
1.(1)
(2)解:①∵长方形纸片沿直线折叠,∴
∵,
∵CN∥DM
即70°+70°+∠AMD=180°
∴∠AMD=40°
②由①知:
∵,
在三角形MNE中
∴
解:(1)∵长方形纸片沿直线折叠,
∴AD∥BC,∠MEN=∠ CNE=90°,
∴;
故答案为:45°.
(1)根据垂直的定义,平行线的性质,得到,再根据折痕是角平分线,求出的度数即可;
(2)①折叠的性质,得到,平行得到=,,再根据角的和差关系进行求解即可;
②根据问题①中得到和三角形的内角和定理求解即可.
(1)解:∵长方形纸片沿直线折叠,
∴,
∵,
∴,
∴,
∴;
(2)①∵折叠,
∴,,
∵,
∴,
∴;
②由①知:,
∵,且,
∴,
∴.
2.(1)解:∵, ,
∴,
∴,
∴.
(2)解:设,
∴,
∵,
∴,
∴
;
(3)解:设正方形的边长为a,正方形是边长为b,
∵正方形与正方形的面积之和为65,
∴,
∵,
∴,
∴,
∴
,
∴,
∴,
∴长方形的面积为28.
(1)根据完全平方公式可得,将 代入,即可求解;
(2)设,则,根据题意可得ab=48,根据完全平方公式进行计算,即可求解;
(3)设正方形的边长为a,正方形是边长为b,根据“正方形与正方形的面积之和为65”可得,结合题意可得,根据完全平方公式进行计算,即可求解.
3.(1)解:∵
∴∠O=∠BCM=50°
∴∠ACM=180°-∠BCM=130°
∵ CD 平分 ∠ACM
∴
∴∠BCD=∠BCM+∠DCM=50°+65°=115°
(2)证明:∵
∴∠ACE+∠ACD=90°
由(1)可知:
∴
∵
∴∠BCM=∠O=∠ACO
∴∠ACE=∠ACO
∴ 平分 .
4.(1)(2x+y)(x+y)
(2)解:观察图形,得:,;
,
∴3xy-2x2-y2=2x2-xy,
整理,得:4x2-4xy+y2=0
即(2x-y)2=0,
∴2x-y=0,
,
.
(1)解:观察图形得:长方形纸片分为2块是边长为x的正方形,1块是边长为y的正方形,3块是长为y,宽为x的长方形,
∴长方形纸片的面积为:2x2+3xy+y2,
∵长方形纸片的长为:,宽为,
∴长方形纸片的面积为:(2x+y)(x+y),
∴2x2+3xy+y2=(2x+y)(x+y),
∴代数式2x2+3xy+y2因式分解为(2x+y)(x+y);
故答案为:(2x+y)(x+y).
(1)用两种方式计算长方形纸片的面积,即可得到2x2+3xy+y2=(2x+y)(x+y),即可求解;
(2)①根据图形的特征,直接计算即可;②根据,可得4x2-4xy+y2=0,从而得到y=2x,再代入所求的代数式,即可求解.
5.解:设原队列有m人,
增加54人后组成a×a的正方形队列,减少74人后组成b×b的正方形队列.
根据题意得:
1- ②:
,解得,∴m1=1035;
,解得,∴m2=270;
,解得,∴m3=90;
综上所述,原队列有1035人或270人或90人。
设原队列有m人,增加54人后组成的正方形队列,减少74人后组成的正方形队列.可得:,再利用因式分解的结果建立方程组解题即可;
6.(1)解:设 B型船每艘有 x 个座位,则 A 型船每艘有 1.25x 个座位,根据题意,得
解得, x=40
经检验, 是原分式方程的解,且符合题意。
答: 型船每艘有 50 个座位, 型船每艘有 40 个座位
(2)解:设需租用 型船 m 艘,租用 型船 n 艘
由题意得,
r∴
又 ∵m、n 均为非负整数,
共 3 种租船方案: ①租用 12 艘 B 型船; ②租用 4 艘 A 型船,7 艘 B 型船; ③
租用 8 艘 A 型船, 2 艘 B 型船.
(1)设B型船每艘有x个座位,用x表示A型船的座位,根据七年级师生全部乘坐A型船若干艘,刚好坐满;八年级全部乘坐B型船,要比七年级乘坐的A型船总数多一艘且空10个座位.列出分式方程,解方程即可;
(2)设租用A型船m艘,B型船n艘,根据两个年级的师生联合租船,且每艘游船恰好全部坐满,列出二元一次方程,求出非负整数解即可。.
7.(1)证明:∵BC∥DG,
∴∠DCB=∠1,
,
,
∴DC∥EF。
(2)解:∵EF⊥AB,
∴∠BEF=90°,
∵DC∥EF,
∴ .
,
∴ .
(1)根据两直线平行,内错角相等可得∠DCB=∠1,根据同位角相等可得DC∥EF,据此证明;
(2)根据垂直定义可得∠FEB=90°,根据平行线的性质可得∠CDB=90°,再根据平角的定义,利用角的和差即可求出结果.
8.(1)解:50 名同学.
(2)
(3)解:∴ 一、二等奖的人数比例为 3: 7 ,
∴ 获一等奖的学生占获奖人数的,
(人)
答: 该校 1500 名学生中获一等奖的学生人数有 72 人
解:(1)观察统计图可得,D组人数为15人,所占的百分比为30%,
∴总人数为:(人),
补全频数分布直方图如图所示:
故答案为:50;
(2)观察统计图可得,A组的人数是5人,∴A 组所在扇形的圆心角度数为:,
故答案为:;
(1)基本关系:总数=部分÷部分所占的百分比,利用D组的人数除以其所占的百分比求得随机抽查的总人数,再补全频数分布直方图即可;
(2)基本关系:扇形的圆心角的度数=360°×部分所占的百分比,利用A组的人数除以随机抽查的总人数求得其所占的百分比,再乘以360°即可求解;
(3)利用总人数乘以一等奖人数所占百分比,再乘以E组的人数在样本中所占百分比即可求解.
9.(1)证明:∵,
,
,
同角的补角相等,
∴(内错角相等,两直线平行,
(2)解:∵,
,
,,
,即,
,
(1)先根据得到 ∠1+∠CBE=180 ° ,结合 ∠1+∠2=180 ° ,证明∠2=∠CBE,从而得到;
(2)先证明∠D=2∠AEF,进而证明∠D=2∠2,即可求出∠D的度数.
10.(1)解:根据频数分布直方图可得.
(2)解:由题意可知:组距为170-160=10,
跳绳成绩为“186个”的频率.
(3)解:
答:该校学生跳绳达到良好的估计有640人.
(1)利用频数之和等于总数,求出m的值;
(2)先利用图中分组确定组距,再用频数除以总数求出频率;
(3)用1200乘以良好所占的比例.
11.(1)7,3
(2)解:补全频数分布直方图如下:
(3)解:这1500名学生中获得绿星级以上的人数有.
答:这1500名学生中获得绿星级以上的人数有750人.
(1)解:由样本数据得:的有7人,的有3人,
∴,
故答案为:7,3;
(1)整理样本中的数据得到m和n的值即可;
(2)根据(1)中所得的数据补全统计图即可;
(3)利用中绿星级以上的人数的占比×1500解答即可.
12.(1)解:设冰箱贴的单价为元/件,则徽章的单价为元/件。
由题意得:
解这个方程得:
经检验,是所列方程的根,且符合题意
徽章的单价:(元)
答:冰箱贴的单价为5元/件, 徽章的单价为10元/件.
(2)解:设购买徽章的数量为个,购买冰箱贴的数量为个。
由题意得:
解得:
答:购买徽章的数量为30个,购买冰箱贴的数量为20个。
13.(1)50;
(2)解: 等级的人数为 (人)
补全条形统计图如下:
(3)解:测试成绩不合格的人数为:
答:七年级“仰卧起坐”测试成绩不合格的人数为80人。
14.(1)
(2)①2,2;②存在,;
(3)①的最大值为;②
15.(1)解:平行.理由:由已知可得,
∵,
∴,
∴.
(2)解:∵,∴,
∵,
∴,
∴的度数为.
(1)先利用对顶角相等得到,即可得到,然后根据平行线的判定得到结论即可.
(2)根据两直线平行,内错角相等得到,即可求出的度数解题.
(1)解:平行.
理由:由已知可得,
∵,
∴,
∴.
(2)解:∵,
∴,
∵,
∴,
∴的度数为.
16.(1)解:,
,
,
.
当时,原式
(2)解:,
,
,
.
,
,即,
原式
(3)解:,
,
,
,
,,
∴ (a+b)2=(a+b)2-4ab=9-8=1,
或,
当,时,原式,
当,时,原式,
∴的值为3或-3
(1)先根据新定义运算,再整体代入a+b的值,即可求得;
(2)先根据新定义运算,再将整体代入求值即可;
(3)先根据新定义运算,再利用完全平方公式求出的值,最后代入求值即可.
(1)解:
.
当时,
原式;
(2)
.
,
即.
原式
;
(3)
.
,,
,即.
.
.
.
或.
当,时,
原式;
当,时,
原式.
17.(1)解:此次调查的总人数为(人,
项目的人数(人,
补全条形统计图如下:
(2)(名,
答:估计七年级500名同学中选择“足球”项目的人数为175名
(1)用的频数除以频率求出总人数,再用总人数减去B、C和D的人数求出的人数,即可补全条形统计图;
(2)用总人数乘以样本中的人数所占比例即可求得.
(1)解:此次调查的总人数为(人,
项目的人数(人,
补全条形统计图如下:
(2)(名,
答:估计七年级500名同学中选择“足球”项目的人数为175名.
18.(1)
(2)
(3)
19.(1)解:(人),
,
所以报名篮球的学生有人
补全图形如下:
(2)篮球项目人数所占百分比,即
素描项目人数所占百分比,即;
(3),(人).
估计该校参加“素描”活动的学生有人.
(1)由书法项目人数及其所占百分比可求得总人数,再根据各项目人数之和等于总人数求出篮球人数,从而可补全条形统计图;
(2)分别用篮球、素描人数除以总人数可求得、的值;
(3)总人数乘以样本中素描项目人数所占比例即可求解.
(1)解:(人),
,
所以报名篮球的学生有人
补全图形如下:
(2)篮球项目人数所占百分比,即
素描项目人数所占百分比,即;
(3),
(人).
估计该校参加“素描”活动的学生有人.
20.(1)解:,理由如下:
,
,
,
,
∴;
(2)解:∵,
,
,
∵,
,
,
,
(1)由两直线平行,同位角相等得到,即可得到,然后根据内错角相等,两直线平行解题即可;
(2)根据平行线的性质得到,,即可求出∠DEF的度数解题.
21.(1)解:
(2)解:∴
∴;
经检验,是原方程的解,
∴
(3)存在;
当时,即:,
去分母得
移项合并同类项得
即x(x-1)=0
检验:
当是原方程的根。
当时,,分式无意义,不满足题意,舍去;
故
(1)根据新运算的计算法则,列式计算即可;
(2)根据新运算的计算法则,列出分式方程并解分式方程,记得检验。
(3)根据新运算的计算法则,列出分式方程并解分式方程,记得检验。增根的舍去.
(1)解:;
(2),
∴,
∴;
经检验,是原方程的解,
∴.
(3)存在;
,
当时,即:,
当时,满足题意,
当时,则:,则:,
当时,,分式无意义,不满足题意,舍去;
故.
22.(1)解:设苹果购买了x箱,橙子购买了y箱,
根据题意得,,
解得,,
答:苹果、橙子各购买了50箱、30箱.
(2)解:由题意可得销售商在甲店获利为:12a+18b=600(元),
整理得,2a+3b=100,
销售商在乙店获利为:10(50-a)+15(30-b)
=950-10a-15b
=950-5(2a+3b)
=950-5×100
=450(元),
即在乙店获利450元.
答:在乙店获利450元.
(1)设苹果购买了x箱,橙子购买了y箱,根据“苹果的批发价格为每箱40元,橙子的批发价格为每箱50元.他花了3500元购进苹果和橙子共80箱”,列出二元一次方程组求解即可;
(2)由题意可得销售商在甲店获利,整理后得到2a+3b=100,再表示出在乙店的获利,整理后把2a+3b=100整体代入即可解答.
(1)解:设苹果购买了x箱,橙子购买了y箱,
根据题意得,,
解得,,
答:苹果、橙子各购买了50箱、30箱.
(2)解:由题意可得销售商在甲店获利为:12a+18b=600(元),
整理得,2a+3b=100,
销售商在乙店获利为:10(50-a)+15(30-b)
=950-10a-15b
=950-5(2a+3b)
=950-5×100
=450(元),
即在乙店获利450元.
答:在乙店获利450元.
23.(1)200;
(2)解:等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数为:;补充完整的扇形统计图如下:
(3)解:(人);答:估计这些学生中“比较了解”垃圾分类知识的有550人.
(1)解:本次问卷调查取样的样本容量为;
;
故答案为:200;;
(1)根据“非常了解”的频数与频率,即可求得本次问卷调查取样的样本容量;由频率之和为1即可求得m的值;
(2)由频率与的积即可求得扇形圆心角,进而可补充完整扇形统计图;
(3)样本数据估计总体,用全校人数乘以“比较了解”的频率即可解答.
(1)解:本次问卷调查取样的样本容量为;
;
故答案为:200;;
(2)解:等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数为:;
补充完整的扇形统计图如下:
(3)解:(人);
答:估计这些学生中“比较了解”垃圾分类知识的有550人.
24.解:(1)
=
=;
(2)
=
=
=.
(1)此题多项式各项具有公因式“2”,故先提公因式“2”,再由完全平方公式将商式继续进行因式分解,即可得到答案;
(2)把“x-y”看成一个整体,先从第二项括号内提取出负号放到这一项的前面,然后提公因式“x-y”,再由平方差公式将商式进行分解因式,即可得到答案.
25.(1)
(2)①,
26.(1)是,
(2)1
(3)①②或
27.(1)解:多项式是,
,左边两个因式系数之和分别为2,0,右边各项系数之和为0,满足算式
(2)解: ,
∴ m=2,n=2m-1=3
(3)解:23×11×8=2024
(1)计算左边两个多项式中每个多项式各项系数之和,再求出“系数和”的乘积,即可求得规律;
(2)根据多项式乘多项式展开后,相同的项的系数相同可得m=2,n=2m-1,即可求得;
(3)根据规律直接计算左边三个因式“系数和”的乘积即可.
(1)写的多项式是,;
左边两个因式系数之和分别为2,0,右边各项系数之和为0,满足算式;
(2),为常数,且,
,,
解得,,
(3)由(1)(2)的规律可知,
的展开式中各项系数的和为
.
28.(1)解:依题意,由①得,,③
将③代入②得,
整理得出,④
∵方程组有无穷多组解
∴且时,
即,则,
∴,;
(2)解:没有,
理由如下:由(1)得,
∵,
∴
整理得
①当时,即,
∵
∴此时方程组为
则,
∵为整数,
∴原方程没有整数解;
②当时,即,此时,
若时,显然无解,
若时,,代入得
∵a为整数,
∴不可能为整数,
∴原方程无整数解;
综上:原方程没有整数解.
(1)先把①中的值代入②,使方程变为只含的一元一次方程,再令的系数为零,即可求得a和b的值;
(2)将b=a-1代入可得,再分类讨论和的情况,再结合整数解分析即可求得.
(1)解:依题意,
由①得,,③
将③代入②得,
整理得出,④
∵方程组有无穷多组解
∴且时,
即,则,
∴,
(2)解:没有,理由如下:
由(1)得
∵
∴
整理得
①当时,即,
∵
∴此时方程组为
则
∵为整数
∴原方程没有整数解
②当时,即,此时,
若时,显然无解,
若时,,代入得
∵a为整数,
∴不可能为整数,
∴原方程无整数解;
综上:原方程没有整数解
29.(1)
(2)解:设,则,
∵,
∴,
∵平分,平分,
∴,
∴,
∵,,
∴,
∴,
∴;
(3)解:,
由题意得,
当时,如图,,,
∴,
∴,
∵,
∴,
∴,解得:;
当时,如图,,此时,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,解得:;
综上所述,或.
解:(1)∵,,
∴,解得:,
∵平分,
∴,
∴,
∵,
∴,
故答案为:;
(1)先由平角的定义及角平分线的定义得出,再根据邻补角的意义求出,然后两直线平行,内错角相等求出∠C;
(2)设,先用x表示出,再利用平行线的性质求得,然后利用角平分线的意义求出,,从而可得,再根据内错角相等,两直线平行判定;
(3)分“”、“”两种情况讨论,分别表示出两种情况下相关角的度数,根据直角三角形两锐角互余列出关于t的方程求解.
(1)∵,,
∴,
∵平分,
∴,
∴,
∵,
∴,
故答案为:;
(2)设,则,
∵,
∴,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
∴;
(3),
由题意得,
当时,如图,,此时,,
∴,
∴,
∵,
∴,
∴,
解得;
当当时,如图,,此时,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
解得;
综上,或.
30.(1)解:∵,,
∴8个连续正整数的平方数总可以使得它们的代数和为0,
∴当时,或当时,最小,且最小值为0;
(2)解:当时,
①由题意知,给定的个数中有个奇数,
∴不管如何添置“”号和“”号, 其代数和总为奇数,
∴所求的最终代数和大于等于1,
∴设计最终代数和等于1的可行方案;
②∵,,
∴对于8个连续正整数的平方数总可以使得它们的代数和为0;
③∵,
对 ,根据②中每连续8个一组适当添加“”号和“”号,使每组的代数和为0,
然后对进行设计,但无论如何设计,均无法使它们的代数和为1;
④在对进行设计的过程中,,
又由②知4个连续正整数的平方数总可以使得它们的代数和为4,
∴个连续正整数的平方数总可以使得它们的代数和为;
综上,可行方案为:首先对,根据②每连续8个一组适当添加“”号和“”号,使每组的代数和为0;
其次对,根据④适当添加“”号和“”号,使每组的代数和为;
最后对作的设计,便可以使得给定的个数的代数和为1,即最小.
(1)应该尽量构成互为相反数的两组数,可使2,3,5 ,8项的符号与其他项的符号相反即可;
(2)①由于给定的2045个数中有1023个奇数,因而无论如何设计实施什么方案,即不管如何添置“+”和“-”号,其代数和总为奇数,故所求的最终代数和大于等于1;于是我们寻求最终代数和等于1的可行方案; ②由(1)可知对于8个连续正整数的平方数总可以使得它们的代数和为0;③由2045=8×255+5,对62,72,……,20452,根据②中每连续8个一组适当添加“+”号和“-”号,使每组的代数和为0,然后对12,22,……,52进行设计,但无论如何设计,均无法使它们的代数和为1;④在对12,22,……,52进行设计的过程中,-12+22-32+42-52=-15,又由②知4个连续正整数的平方数总可以使得它们的代数和为4,则16个连续正整数的平方数总可以使得它们的代数和为;进而可得可行方案为:首先对222,232,……,20452,根据②每连续8个一组适当添加“+”号和“-”号,使每组的代数和为0;其次对62,72,……,212根据④适当添加“+”号和“-”号,使每组的代数和为;最后对12,22,……,52,作-12+22-32+42-52=-15的设计,便可以使得给定的2045个数的代数和为1,即|L|最小.
(1)解:∵,,
∴8个连续正整数的平方数总可以使得它们的代数和为0,
∴当时,或当时,最小,且最小值为0;
(2)解:当时,
①由题意知,给定的个数中有个奇数,
∴不管如何添置“”号和“”号, 其代数和总为奇数,
∴所求的最终代数和大于等于1.
∴设计最终代数和等于1的可行方案.
②,
∴对于8个连续正整数的平方数总可以使得它们的代数和为0;
③∵,
对 ,根据②中每连续8个一组适当添加“”号和“”号,使每组的代数和为0,
然后对进行设计,但无论如何设计,均无法使它们的代数和为1.
④在对进行设计的过程中,,
又由②知4个连续正整数的平方数总可以使得它们的代数和为4,
∴个连续正整数的平方数总可以使得它们的代数和为.
综上,可行方案为:首先对,根据②每连续8个一组适当添加“”号和“”号,使每组的代数和为0;其次对,根据④适当添加“”号和“”号,使每组的代数和为;最后对作的设计,便可以使得给定的个数的代数和为1,即最小.
同课章节目录
