2024-2025学年湘教版(2024)七年级数学下册期末真题专项练习 02 填空题(含解析)
文档属性
| 名称 | 2024-2025学年湘教版(2024)七年级数学下册期末真题专项练习 02 填空题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 18:13:36 | ||
图片预览




文档简介
2024-2025学年湘教版(2024)七年级数学下册期末真题
专项练习 02 填空题
一、填空题
1.(2024七下·冷水滩期末)图形在平移时,下列特征中不发生改变的有 .(把你认为正确的序号都填上)
①图形的形状;②图形的位置;③线段的长度;④角的大小
2.(2024七下·桑植期末)如图,在三角形中,,,,,则点到直线的距离为 .
3.(2024七下·新田期末) .
4.(2024七下·衡阳期末)不等式组的所有整数解的和是 .
5.(2024七下·衡阳期末)绝对值等于 ;的相反数是 ;的绝对值是 .
6.(2024七下·望城期末)对于x,符号[x]表示不大于x的最大整数.如:[3.14]=3,[一7.59]=一8,则满足关系式的x的整数值有 个.
7.(2024七下·益阳期末)如图所示,把绕点顺时针旋转,得到,交于点,若,则 .
8.(2024七下·永定期末)如图,在四边形中,,对角线交于点,若的面积为,的面积为,则的面积是 .
9.(2024七下·永定期末)如图所示,和是等边三角形,B、C、E在一条直线上,则绕着点 逆时针旋转 度可得到.
10.(2024七下·岳阳期末)如图, , 的面积等于, , ,则的面积是 .
11.(2024七下·岳阳期末)小林乘车进入车库时仔细观察了车库门口的曲臂直杆道闸,已知垂直于水平地面当车牌被自动识别后,曲臂直杆道闸的段绕点缓慢向上旋转,段则一直保持水平状态上升 (即 与始终平行),在该过程中始终等于 .
12.(2024七下·岳阳期末)若 ,,则 .
13.(2024七下·岳阳期末)已知,,则
14.(2024七下·长沙期末)若,则 .
15.(2024七下·邵阳期末)如图,将绕点顺时针旋转后得到,点与点是对应点,点与点是对应点.如果,那么 °.
16.(2024七下·长沙期末)已知实数,满足,并且,,则的最大值是 .
17.(2024七下·长沙期末)某学校七年级三班有名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图如图所示.
根据扇形统计图中提供的信息,给出以下结论:
①最喜欢足球的人数最多,达到了人;
②最喜欢羽毛球的人数最少,只有人;
③最喜欢排球的人数比最喜欢乒乓球的人数少人;
④最喜欢乒乓球的人数比最喜欢篮球的人数多人.
其中正确的结论有 (填序号).
18.(2024七下·长沙期末)不等式的最小整数解为 .
19.(2024七下·长沙期末)若,为实数,且,则的值为 .
20.(2024七下·长沙期末)如图,已知,,则的度数是 .
21.(2024七下·双牌期末)图1为某校七年级两个班级的劳动实践基地,图2是从实践基地抽象出来的几何模型:两块边长为、的正方形,其中重叠部分为池塘,阴影部分、分别表示八(1)(2)两个班级的基地面积.若,,则 .
22.(2024七下·双牌期末)已知在同一平面内,直线,,互相平行,直线与之间的距离是,直线与之间的距离是,那么直线与的距离是 .
23.(2024七下·衡阳期末)如图,把一张长方形纸条沿EF折叠,若,则 °.
24.(2024七下·芙蓉期末)已知x,y,n满足,若,则x的取值范围是 .
25.(2024七下·芙蓉期末)某校开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解六年级学生对每类课程的选择情况,随机抽取了六年级若干名学生进行调查每人只选一类最喜欢的课程,将调查结果绘制成如下统计图,则本次随机调查的学生人数为 人.
26.(2024七下·芙蓉期末)已知点在第三象限.则x的取值范围是 .
27.(2024七下·芙蓉期末)若的算术平方根为,的立方根为,是平方根等于本身的数,则的值为 .
28.(2024七下·邵东期末)已知AB、CD、EF是同一平面内三条互相平行的直线,且AB与CD的距离是8cm,CD与EF的距离是2cm,则AB与EF的距离是 cm.
29.(2024七下·澧县期末)若关于的不等式组有且仅有两个整数解,则的取值范围为 .
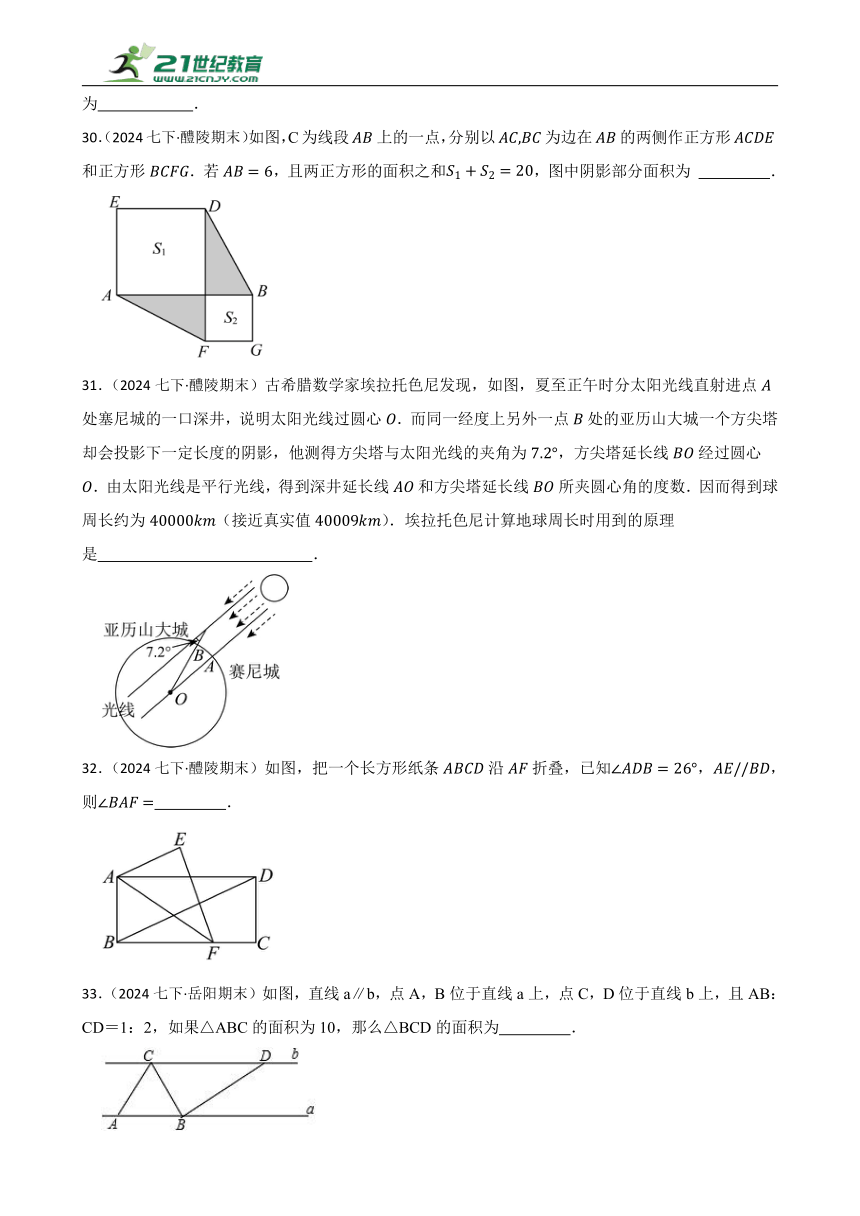
30.(2024七下·醴陵期末)如图,C为线段上的一点,分别以为边在的两侧作正方形和正方形.若,且两正方形的面积之和,图中阴影部分面积为 .
31.(2024七下·醴陵期末)古希腊数学家埃拉托色尼发现,如图,夏至正午时分太阳光线直射进点处塞尼城的一口深井,说明太阳光线过圆心.而同一经度上另外一点处的亚历山大城一个方尖塔却会投影下一定长度的阴影,他测得方尖塔与太阳光线的夹角为,方尖塔延长线经过圆心.由太阳光线是平行光线,得到深井延长线和方尖塔延长线所夹圆心角的度数.因而得到球周长约为(接近真实值).埃拉托色尼计算地球周长时用到的原理是 .
32.(2024七下·醴陵期末)如图,把一个长方形纸条沿折叠,已知,,则 .
33.(2024七下·岳阳期末)如图,直线a∥b,点A,B位于直线a上,点C,D位于直线b上,且AB:CD=1:2,如果△ABC的面积为10,那么△BCD的面积为 .
34.(2024七下·岳阳期末)光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线与表示水底的直线平行,光线从空气射入水中,改变方向后射到水底处,是的延长线,若,则的度数是 .
35.(2024七下·岳阳期末)如图,和关于直线l对称.若,,则的度数为 °.
36.(2024七下·临湘期末)如图,把一块含有角的直角三角板的两个顶点放在直尺的对边上,如果,则 .
37.(2024七下·临湘期末)如图,将绕点A逆时针旋转一定的角度得到,此时边经过点B,若,,则的长是 .
38.(2024七下·永兴期末)如图①,为直线上一点,作射线,使,将一个直角三角尺如图摆放,直角顶点在点处,一条直角边在射线上.将图①中的三角尺绕点以每秒的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第秒时,所在直线恰好平分,则的值为 .
39.(2024七下·永兴期末)计算:
40.(2024七下·娄底期末)如图,已知a∥b,AC⊥AB,AC交直线b于点C,∠1=65°,那么∠2的度数为 .
41.(2024七下·娄底期末)若,则 .
42.(2024七下·黄浦期末)m、n为两个连续的整数,,则m+n= .
43.(2024七下·娄底期末)如图,直线表示一段河道,点表示村庄,现要从河向村庄引水,图中有四种方案,其中沿线段路线开挖的水渠长最短,理由是 .
44.(2024七下·宁乡市期末)我们定义表示不小于实数的最小整数,例如:.现给出下列结论:
①;②若,则;③若,则;④若,,则.
以上选项中,所有正确的序号是 .
45.(2024七下·宁乡市期末)中国古代的数学成就令人敬仰,早在两千多年前,我们的先祖就运用杠杆原理发明了木杆秤,学名叫作戥子.如下图,这是一杆古秤在称物时的状态,已知,则的度数为 .
46.(2024七下·衡南期末)将沿方向平移3个单位得到.若的周长等于8,则四边形的周长为 .
47.(2024七下·赤坎期末)如图,直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=45°,则∠2= .
48.(2024七下·长沙期末)如图,下列结论①与是同位角;②与是内错角;③与是由直线,被直线所截得到的同旁内角.正确的序号是 .
49.(2024七下·长沙期末)某校在对七年级(1)班学生进行调查问卷,学生上学的方式是:A 乘私家车;B乘电动车;C骑自行车;D步行.根据问卷数据绘制如下不完整统计图,扇形统计图中表示 B的扇形圆心角的度数为 .
50.(2024七下·宁乡市期末)如图所示为八年级数学兴趣小组绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线与反射光线平行.如入射光线与镜面的夹角,则的度数为 .(提示:根据光的反射定理知,)
答案解析部分
1.①③④
解:由图形平移的性质,可知图形在平移时,其特征不发生改变的有①③④.
故答案为:①③④.
平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.根据平移的性质直接判断即可.
2.4.8
解:设点B到的距离是h,
∵,
∴,
∴,
∴点B到的距离是.
故答案为:4.8.
根据等面积法得到,据此代值计算即可.
3.9
解:
故填:9.
将底数与指数不同的幂利用乘方定义转化成同指数幂,即逆用积的乘方运算法则计算得出结果.
4.7
解不等式组,
解不等式①得:,
解不等式②得:x≤4,
∴原不等式组的解集是,
故不等式组的所有整数解为:-2,-1,0,1,2,3,4,
∴ 不等式组的所有整数解的和是,
故填:7.
按照解不等式组的一般步骤解不等式组并分析其整数解求和即可.
5.;;
解:绝对值=;
的相反数=;
的绝对值=.
故填:;2;.
结合无理数的估算及绝对值运算法则,立方根及相反数定义逐项计算即可.
6.2
解:,
∴,
解得:,
整数有7,8,9,共3个数.
根据符号[x]的定义即可列出不等式,计算求解即可.
7.
解:由旋转得,∠A'CD=40°,
∵ ∠A'DC=85°,
∴ ∠A'=55°,
∴ ∠A=55°.
故答案为:55°.
根据旋转的性质可得∠A'CD=40°和∠A=∠A',再根据三角形的内角和定理,即可求得.
8.
9.60
10.
11.
12.
13.2
14.
15.
16.
17.①②③④
18.
19.
20.
21.16
22.或
23.
24.
25.
26.
27.
28.10或6
29.
30.8
31.两直线平行,内错角相等
32.58°
33.20
34.
35.105
36.
37.3
38.6或42
39.
40.25°
41.18
42.7
43.垂线段最短
44.①③④
45.
46.14
47.135°
48.③
49.
50.
专项练习 02 填空题
一、填空题
1.(2024七下·冷水滩期末)图形在平移时,下列特征中不发生改变的有 .(把你认为正确的序号都填上)
①图形的形状;②图形的位置;③线段的长度;④角的大小
2.(2024七下·桑植期末)如图,在三角形中,,,,,则点到直线的距离为 .
3.(2024七下·新田期末) .
4.(2024七下·衡阳期末)不等式组的所有整数解的和是 .
5.(2024七下·衡阳期末)绝对值等于 ;的相反数是 ;的绝对值是 .
6.(2024七下·望城期末)对于x,符号[x]表示不大于x的最大整数.如:[3.14]=3,[一7.59]=一8,则满足关系式的x的整数值有 个.
7.(2024七下·益阳期末)如图所示,把绕点顺时针旋转,得到,交于点,若,则 .
8.(2024七下·永定期末)如图,在四边形中,,对角线交于点,若的面积为,的面积为,则的面积是 .
9.(2024七下·永定期末)如图所示,和是等边三角形,B、C、E在一条直线上,则绕着点 逆时针旋转 度可得到.
10.(2024七下·岳阳期末)如图, , 的面积等于, , ,则的面积是 .
11.(2024七下·岳阳期末)小林乘车进入车库时仔细观察了车库门口的曲臂直杆道闸,已知垂直于水平地面当车牌被自动识别后,曲臂直杆道闸的段绕点缓慢向上旋转,段则一直保持水平状态上升 (即 与始终平行),在该过程中始终等于 .
12.(2024七下·岳阳期末)若 ,,则 .
13.(2024七下·岳阳期末)已知,,则
14.(2024七下·长沙期末)若,则 .
15.(2024七下·邵阳期末)如图,将绕点顺时针旋转后得到,点与点是对应点,点与点是对应点.如果,那么 °.
16.(2024七下·长沙期末)已知实数,满足,并且,,则的最大值是 .
17.(2024七下·长沙期末)某学校七年级三班有名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图如图所示.
根据扇形统计图中提供的信息,给出以下结论:
①最喜欢足球的人数最多,达到了人;
②最喜欢羽毛球的人数最少,只有人;
③最喜欢排球的人数比最喜欢乒乓球的人数少人;
④最喜欢乒乓球的人数比最喜欢篮球的人数多人.
其中正确的结论有 (填序号).
18.(2024七下·长沙期末)不等式的最小整数解为 .
19.(2024七下·长沙期末)若,为实数,且,则的值为 .
20.(2024七下·长沙期末)如图,已知,,则的度数是 .
21.(2024七下·双牌期末)图1为某校七年级两个班级的劳动实践基地,图2是从实践基地抽象出来的几何模型:两块边长为、的正方形,其中重叠部分为池塘,阴影部分、分别表示八(1)(2)两个班级的基地面积.若,,则 .
22.(2024七下·双牌期末)已知在同一平面内,直线,,互相平行,直线与之间的距离是,直线与之间的距离是,那么直线与的距离是 .
23.(2024七下·衡阳期末)如图,把一张长方形纸条沿EF折叠,若,则 °.
24.(2024七下·芙蓉期末)已知x,y,n满足,若,则x的取值范围是 .
25.(2024七下·芙蓉期末)某校开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解六年级学生对每类课程的选择情况,随机抽取了六年级若干名学生进行调查每人只选一类最喜欢的课程,将调查结果绘制成如下统计图,则本次随机调查的学生人数为 人.
26.(2024七下·芙蓉期末)已知点在第三象限.则x的取值范围是 .
27.(2024七下·芙蓉期末)若的算术平方根为,的立方根为,是平方根等于本身的数,则的值为 .
28.(2024七下·邵东期末)已知AB、CD、EF是同一平面内三条互相平行的直线,且AB与CD的距离是8cm,CD与EF的距离是2cm,则AB与EF的距离是 cm.
29.(2024七下·澧县期末)若关于的不等式组有且仅有两个整数解,则的取值范围为 .
30.(2024七下·醴陵期末)如图,C为线段上的一点,分别以为边在的两侧作正方形和正方形.若,且两正方形的面积之和,图中阴影部分面积为 .
31.(2024七下·醴陵期末)古希腊数学家埃拉托色尼发现,如图,夏至正午时分太阳光线直射进点处塞尼城的一口深井,说明太阳光线过圆心.而同一经度上另外一点处的亚历山大城一个方尖塔却会投影下一定长度的阴影,他测得方尖塔与太阳光线的夹角为,方尖塔延长线经过圆心.由太阳光线是平行光线,得到深井延长线和方尖塔延长线所夹圆心角的度数.因而得到球周长约为(接近真实值).埃拉托色尼计算地球周长时用到的原理是 .
32.(2024七下·醴陵期末)如图,把一个长方形纸条沿折叠,已知,,则 .
33.(2024七下·岳阳期末)如图,直线a∥b,点A,B位于直线a上,点C,D位于直线b上,且AB:CD=1:2,如果△ABC的面积为10,那么△BCD的面积为 .
34.(2024七下·岳阳期末)光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线与表示水底的直线平行,光线从空气射入水中,改变方向后射到水底处,是的延长线,若,则的度数是 .
35.(2024七下·岳阳期末)如图,和关于直线l对称.若,,则的度数为 °.
36.(2024七下·临湘期末)如图,把一块含有角的直角三角板的两个顶点放在直尺的对边上,如果,则 .
37.(2024七下·临湘期末)如图,将绕点A逆时针旋转一定的角度得到,此时边经过点B,若,,则的长是 .
38.(2024七下·永兴期末)如图①,为直线上一点,作射线,使,将一个直角三角尺如图摆放,直角顶点在点处,一条直角边在射线上.将图①中的三角尺绕点以每秒的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第秒时,所在直线恰好平分,则的值为 .
39.(2024七下·永兴期末)计算:
40.(2024七下·娄底期末)如图,已知a∥b,AC⊥AB,AC交直线b于点C,∠1=65°,那么∠2的度数为 .
41.(2024七下·娄底期末)若,则 .
42.(2024七下·黄浦期末)m、n为两个连续的整数,,则m+n= .
43.(2024七下·娄底期末)如图,直线表示一段河道,点表示村庄,现要从河向村庄引水,图中有四种方案,其中沿线段路线开挖的水渠长最短,理由是 .
44.(2024七下·宁乡市期末)我们定义表示不小于实数的最小整数,例如:.现给出下列结论:
①;②若,则;③若,则;④若,,则.
以上选项中,所有正确的序号是 .
45.(2024七下·宁乡市期末)中国古代的数学成就令人敬仰,早在两千多年前,我们的先祖就运用杠杆原理发明了木杆秤,学名叫作戥子.如下图,这是一杆古秤在称物时的状态,已知,则的度数为 .
46.(2024七下·衡南期末)将沿方向平移3个单位得到.若的周长等于8,则四边形的周长为 .
47.(2024七下·赤坎期末)如图,直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=45°,则∠2= .
48.(2024七下·长沙期末)如图,下列结论①与是同位角;②与是内错角;③与是由直线,被直线所截得到的同旁内角.正确的序号是 .
49.(2024七下·长沙期末)某校在对七年级(1)班学生进行调查问卷,学生上学的方式是:A 乘私家车;B乘电动车;C骑自行车;D步行.根据问卷数据绘制如下不完整统计图,扇形统计图中表示 B的扇形圆心角的度数为 .
50.(2024七下·宁乡市期末)如图所示为八年级数学兴趣小组绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线与反射光线平行.如入射光线与镜面的夹角,则的度数为 .(提示:根据光的反射定理知,)
答案解析部分
1.①③④
解:由图形平移的性质,可知图形在平移时,其特征不发生改变的有①③④.
故答案为:①③④.
平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.根据平移的性质直接判断即可.
2.4.8
解:设点B到的距离是h,
∵,
∴,
∴,
∴点B到的距离是.
故答案为:4.8.
根据等面积法得到,据此代值计算即可.
3.9
解:
故填:9.
将底数与指数不同的幂利用乘方定义转化成同指数幂,即逆用积的乘方运算法则计算得出结果.
4.7
解不等式组,
解不等式①得:,
解不等式②得:x≤4,
∴原不等式组的解集是,
故不等式组的所有整数解为:-2,-1,0,1,2,3,4,
∴ 不等式组的所有整数解的和是,
故填:7.
按照解不等式组的一般步骤解不等式组并分析其整数解求和即可.
5.;;
解:绝对值=;
的相反数=;
的绝对值=.
故填:;2;.
结合无理数的估算及绝对值运算法则,立方根及相反数定义逐项计算即可.
6.2
解:,
∴,
解得:,
整数有7,8,9,共3个数.
根据符号[x]的定义即可列出不等式,计算求解即可.
7.
解:由旋转得,∠A'CD=40°,
∵ ∠A'DC=85°,
∴ ∠A'=55°,
∴ ∠A=55°.
故答案为:55°.
根据旋转的性质可得∠A'CD=40°和∠A=∠A',再根据三角形的内角和定理,即可求得.
8.
9.60
10.
11.
12.
13.2
14.
15.
16.
17.①②③④
18.
19.
20.
21.16
22.或
23.
24.
25.
26.
27.
28.10或6
29.
30.8
31.两直线平行,内错角相等
32.58°
33.20
34.
35.105
36.
37.3
38.6或42
39.
40.25°
41.18
42.7
43.垂线段最短
44.①③④
45.
46.14
47.135°
48.③
49.
50.
同课章节目录
