2024-2025学年湘教版(2024)七年级数学下册期末真题专项练习 04 解答题(含解析)
文档属性
| 名称 | 2024-2025学年湘教版(2024)七年级数学下册期末真题专项练习 04 解答题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 586.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 18:14:42 | ||
图片预览




文档简介
2024-2025学年湘教版(2024)七年级数学下册期末真题
专项练习 04 解答题
一、解答题
1.(2024七下·长沙期末)已知关于、的方程组.
(1)若方程组的解也是方程的一个解,求的值;
(2)若方程组的解满足,求的取值范围.
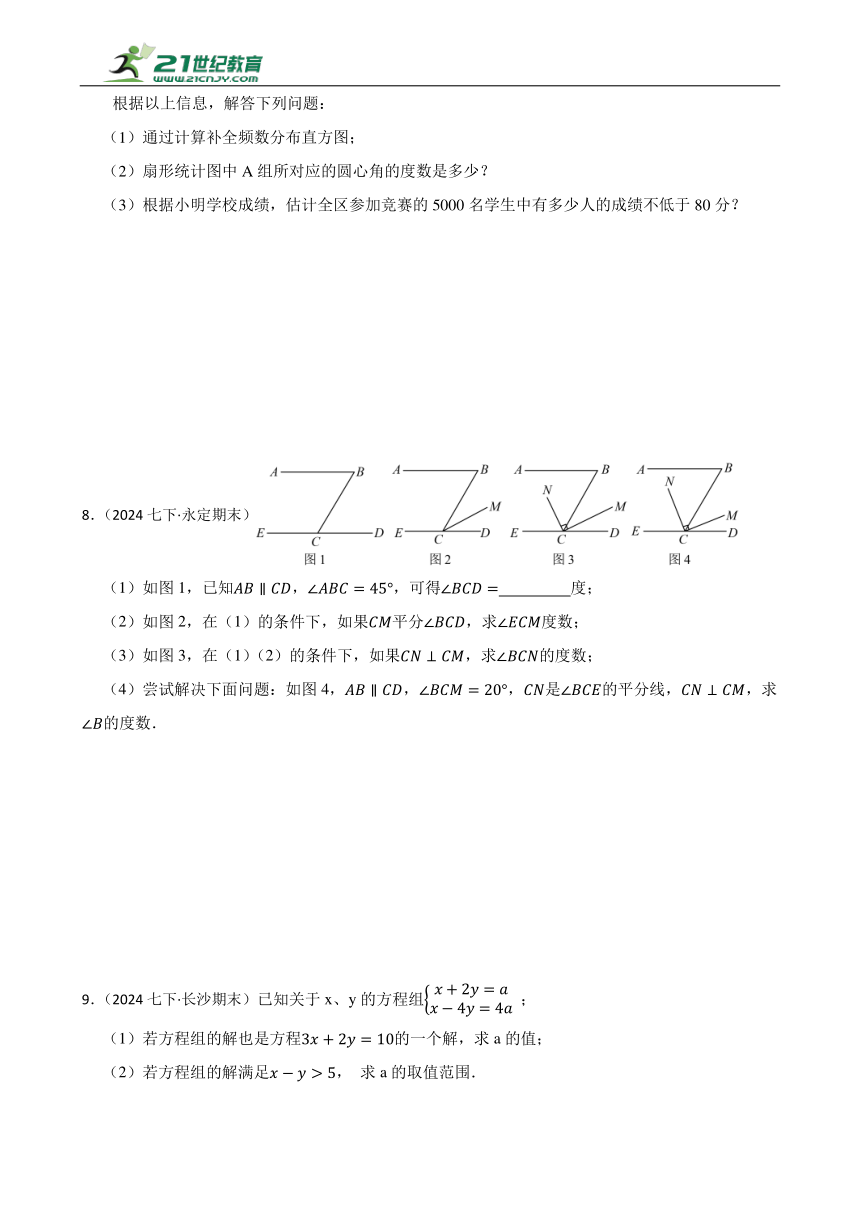
2.(2024七下·衡阳期末)图1是一辆滑轮摄影轨道车,图为其侧面示意图固定在底座于点是轨道车的“手臂”,可通过改变的度数调节车的高度在调节过程中,放摄像机的杆始终平行于.
(1)如图,调节轨道车的“手臂”,使,此时,求的度数.
(2)若图,求的度数之和.
3.(2024七下·长沙期末)体育是长沙市中考的必考科目,某校根据实际情况,决定主要开设:立定跳远;:跑步;:实心球;:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图,请你结合图中解答下列问题:
(1)本次调查学生共______人;将条形图补充完整;
(2)样本中喜欢项目的人数所在扇形统计图中的圆心角的度数是______;
(3)如果该校有学生2000人,请你估计该校选择“立定跳远”这种活动的学生约有多少人?
4.(2024七下·株洲期末)汉江是长江的最大支流,在历史上占居重要地位,常与长江、淮河、 黄河并列,舍称“江海河汉”.每年汛期来临之时,汉江防汛指挥部都会在一危险地带两岸各安置一组探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自顺时针旋转至便立即回转,灯B射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视,已知灯A转动的速度是/秒,灯B转动的速度是/秒,假定这一带汉江两岸河堤是平行的,即,且,转动时间是t秒.
(1)当 秒时,灯A射线第一次平分,此时灯A射线记为射线,当 秒时,灯A射线第一次与射线垂直;
(2)若两灯同时转动,秒时,两束光线所在直线的位置关系是______;(填“平行”或“垂直”)
(3)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,A灯转动几秒,两灯的光束互相平行.
5.(2024七下·衡阳期末)已知方程与不等式,当时,,同时成立,则称“”是方程与不等式的“完美解”.
(1)已知①,②,则方程的解是不等式 (填序号)的“完美解”;
(2)若是方程组与不等式的一组“完美解”,求a的取值范围;
(3)若是方程与不等式组的“完美解”,求的取值范围.
6.(2024七下·长沙期末)为更好组织体育锻炼活动,随机抽取了我区部分七年级学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如图两幅不完整的统计图表.请根据图表信息回答下列问题:
最喜爱体育锻炼项目的统计表
类别 项目 人数(人)
A 跳绳 59
B 健身操
C 俯卧撑 31
D 开合跳
E 其它 22
抽取的学生最喜爱体育锻炼项目的扇形统计图
(1)求参与问卷调查的学生总人数;
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)我区共有七年级学生8000人,估算其中最喜爱“健身操”的人数.
7.(2024七下·望城期末)5月12日是我国“防灾减灾日 .为增强学生防灾减灾意识,某区举行防灾减灾安全知识竞赛.竞赛结束后,发现所有参赛学生的成绩(满分100分)均不低于60分.小明将自己所在学校参加竞赛学生的成绩(用x表示)分为四组:组A(60 ≤x< 70),B组(70 ≤x< 80),C组(80 ≤x< 90),D组(90 ≤x<100)绘制了如下不完整的频数分布直方图和扇形统计图。
根据以上信息,解答下列问题:
(1)通过计算补全频数分布直方图;
(2)扇形统计图中A组所对应的圆心角的度数是多少?
(3)根据小明学校成绩,估计全区参加竞赛的5000名学生中有多少人的成绩不低于80分?
8.(2024七下·永定期末)
(1)如图1,已知,,可得 度;
(2)如图2,在(1)的条件下,如果平分,求度数;
(3)如图3,在(1)(2)的条件下,如果,求的度数;
(4)尝试解决下面问题:如图4,,,是的平分线,,求的度数.
9.(2024七下·长沙期末)已知关于x、y的方程组 ;
(1)若方程组的解也是方程的一个解,求a的值;
(2)若方程组的解满足, 求a的取值范围.
10.(2024七下·耒阳期末)若,求的立方根.
11.(2024七下·长沙期末)我们约定:若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“包含方程”.例如:方程的解为,而不等式组 的解集为,不难发现在的范围内,所以方程 是不等式组 的“包含方程”.请根据约定,解答下列问题.
(1)在一元一次方程;;中,不等式组 的“包含方程”是 (填序号);
(2)若关于 x 的方程 是不等式组 的“包含方程”,求k 的取值范围;
(3)若关于x 的方程 是关于 x 的不等式组 的“包含方程”,且此时该不等式组恰好有7个整数解,试求 m 的取值范围.
12.(2024七下·长沙期末)如图,,在的右侧,平分,平分,所在直线交于点,.
(1)若,求的度数;
(2)将线段沿方向平移,使得点在点的右侧,其他条件不变,若,求的度数.
13.(2024七下·宁乡市期末)临近暑假,我市教育局发布了《夏季安全指南》,某校为了解全校学生对防溺水安全知识的熟悉情况,随机抽查了部分学生进行《防溺水学习手册》题问答测试,并把答对题数制成统计表和扇形统计图(如图所示).
答对题数 6 7 8 9 10
人数(人) 10 14 8 6
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和的值.
(2)求扇形统计图中答对“题”所对的圆心角度数.
(3)若该校共有名学生,根据抽查结果,估计该校学生答对10题的人数.
14.(2024七下·常德期末)完全平方公式经过适当的变形,可以解决很多数学问题.
例如:若,,求的值.
解:∵,,
∴,,
∴,
∴.
根据上面的解题思路与方法解决下列问题:
(1)若,,求的值;
(2)如图,C是线段上的一点,分别以,为边向两边作正方形,设,两正方形的面积和为24,求的面积.
(3)若,求的值.
15.(2024七下·衡阳期末)如图,已知四边形是正方形,点E在上,将经顺时针旋转后与完全重合,再将线段向右平移后与完全重合.
(1)旋转的中心是 ;旋转角度是 ;
(2)试猜想线段和的数量关系和位置关系,并说明理由.
16.(2024七下·益阳期末)为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计表:
身高情况分组表
组别
身高()
根据图表提供的信息,回答下列问题:
(1)抽取的样本中,男生的身高众数在 组,中位数在 组;
(2)抽取的样本中,女生身高在组的人数有多少人?
(3)已知该校共有男生840人,女生820人,请估计身高在组的学生人数.
17.(2024七下·攸县期末)我们在应用整式的乘法公式解题时,经常将乘法公式进行变形,如:,.
(1)根据以上变形填空:
①已知,,则______;
②已知,,则______;
(2)若x满足,求代数式的值;
(3)如图,已知数轴上从左到右依次有点A、B、C三点,它们表示的数分别是m、9、11.以为边在数轴上方作正方形,以为边在数轴上方作正方形,延长交于点P.若正方形与正方形面积的和为96,求长方形的面积.
18.(2024七下·攸县期末)如图所示,已知正方形中的可以经过旋转得到.
(1)图中哪一个点是旋转中心?
(2)按什么方向旋转;旋转角度是多少?
(3)如果.求的长?
19.(2024七下·衡阳期末)【定义】如果两个角的差为,就称这两个角互为“创新角”,其中一个角叫做另一个角的“创新角”.
例如:,,,则和互为“创新角”,即是的“创新角”,也是的“创新角”.
(1)已知和互为“创新角”,且,若和互补,则___________;
(2)如图1所示,在中,,过点作的平行线,的平分线分别交、于、两点.
①若,且和互为“创新角”,则___________;
②如图2所示,过点作的垂线,垂足为,、相交于点.若与互为“创新角”,求的度数;
③如图3所示,的平分线交于点,当和互为“创新角”时,则__________.
20.(2024七下·长沙期末)不妨约定:关于的二元一次方程,
若系数满足,则称这个方程为“开心”方程.例如:方程,其中,满足,且,则方程是“开心”方程,由两个“开心”方程组成的方程组称作“开心”方程组.根据上述规定,回答下列问题:
(1)判断以下方程是不是“开心”方程(填“是”或“不是”);
① ;②______.③______;
(2)若关于的“开心”方程组的解为,求的值.
(3)关于的“开心”方程组满足,其中为整数,为常数且,求的值,并求此“开心方程组”的解.
21.(2024七下·蒸湘期末)如图,在直角三角形中,是斜边上的高,,求:
(1)的度数;
(2)的度数.
22.(2024七下·长沙期末)在平面直角坐标系中,已知点.
(1)如图1,若正数的立方根等于它本身,,则点坐标为______,线段长度为______,的面积为______;
(2)在(1)的条件下,若点为射线上一点,且满足,求此时点的坐标;
(3)点为线段上一点(不与两点重合),点为线段上一点(不与两点重合);
①如图2,若,点是轴上点左侧的一点,连接的角平分线和的角平分线交于点,求与的数量关系;
②如图3,若,连接,交于点,记的面积为的面积为的面积为,那么是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
23.(2024七下·芙蓉期末)解不等式组: ,并写出所有整数解.
24.(2024七下·广水期末)2023年5月30日,神舟十六号载人飞船成功发射,成为我国航天事业的里程碑,某校对全校1500名学生进行了“航空航天知识”了解情况的调查,调查结果分为,,,四个等级(:非常了解;:比较了解;:了解;:不了解).随机抽取了部分学生的调查结果,绘制成两幅不完整的统计图.请结合两幅统计图信息,回答下列问题:
(1)这次调查活动中,一共调查了_____________名学生;
(2)“C”等级所在扇形的圆心角是____________度;
(3)请补上条形统计图中“”等级的信息;
(4)根据本次调查情况,准备进行“航空航天知识”讲座,请你估计七年级名学生中“”等级的人数有多少?
25.(2024七下·邵阳期末)已知,点、分别是、上的点,点在、之间,连接、.
(1)如图,若,求的度数;
(2)如图,若点是下方一点,平分,平分,已知,求的度数;
(3)如图,若点是上方一点,连接、,且的延长线平分,平分,,求的度数.
26.(2024七下·邵东期末)如图,有一副三角板,和,,,,,在同一直线上.
(1)如图1,与点重合.将绕点按顺时针方向进行旋转,当与首次平行,求此时的度数;
(2)如图2,若点在边上(不与、重合),再将绕点按顺时针方向进行旋转(如图3),边交边于,当时,求边旋转的度数;
(3)将从图2初始位置开始,绕点顺时针方向以每秒的速度进行旋转,当第一次与直线平行时停止运动.设运动时间为秒,当线段与的一条边平行,求满足条件的的值(请直接写出结果).
27.(2024七下·长沙期末)如果两个不等式存在公共解,那么称这两个不等式互为“友好不等式”.
(1)在不等式①,②,③中,与不等式互为“友好不等式”的是________;(填序号)
(2)若关于的不等式与不是“友好不等式”,求的取值范围;
(3)若,关于的不等式与不等式互为“友好不等式”,求的取值范围.
28.(2024七下·大祥期末)数形结合是解决数学问题的一种重要的思想方法;借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们进行推理,获得结论.初中数学里的一些代数恒等式,很多都可以借助几何图形进行直观推导和解释.请结合相关知识,解答下列问题:
图①是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)图②中的阴影部分的正方形边长为_________;
(2)观察图②,写出关于代数式,之间的一个代数恒等式:________;
(3)观察图③,请将多项式因式分解:_______﹔
(4)根据(3)题中的等量关系,解决下列问题:若,求的值.
29.(2024七下·醴陵期末)如图,直线相交于点O,,若,试求的度数.
30.(2024七下·双牌期末)小明在学习有关整式的知识时,发现一个有趣的现象:对于关于的多项式,由于,所以当取任意一对互为相反数的数时,多项式的值是相等的,例如,当,即或时,的值均为3;当,即或时,的值均为6.
于是小明给出一个定义:对于关于的多项式,若当取任意一对互为相反数的数时,该多项式的值相等,就称该多项式关于对称.例如:关于对称.
请结合小明的思考过程,运用此定义解决下列问题:
(1)多项式关于________对称;若关于的多项式关于对称,则________;
(2)关于的多项式关于对称,且当时,多项式的值为5,求时,求多项式的值.
31.(2024七下·长沙期末)定义:对于任何有理数,符号表示不大于的最大整数.例如:,,.
(1)填空:=________,=________;
(2)如果,求满足条件的的取值范围;
(3)求方程的整数解.
答案解析部分
1.(1)解:解方程组得:,
方程组的解也是方程的一个解,
,
解得:;
(2)解:,
,
解得:.
(1)先根据加减消元法求解,再将其代入 ,即可求得a的值;
(2)先根据加减消元法求解,再将其代入,解不等式即可.
2.(1)解:如图,过点作,且点在的下方.
,,
.
,
,
,
.
,,
,
.
(2)解:如图,过点作,且点在的下方.
,
.
由可得,
.
,
,
.
(1)通过过拐点C作已知直线的平行线,进而利用平行线的性质将逐一求角往目标角靠拢求解即可;
(2)同理过拐点作平行线联系已知条件角与问题角的关系,此时需推理角度关系,不熟练的情况可以通过设元进行表示角度关系更为直观理解.
3.(1)300人,;
(2)
(3)800人.
4.(1)25;55
(2)平行
(3)当A灯转动15秒或82.5秒,两灯的光束互相平行
5.(1)②
(2)
(3)
6.(1)200人
(2)48人
(3)1600人
7.(1)解:总人数为100÷25%=400
B组人数为400-180-100-40=80人
(2)解:A区所占比1-20%-45%-25%=10%
圆心角360°×10%=36°
(3)解:(人,
答:估计全区参加竞赛的5000名学生中有3500人的成绩不低于80分.
(1)先根据组是100人,占小明所在学校参加竞赛学生的,求出小明所在学校参加竞赛学生人数,由此可求出组的人数,据此可补全频数分布直方图;
(2)由扇形统计图求出组人数占小明所在学校参加竞赛学生人数的百分比,进而可求出组所对应的圆心角的度数;
(3)用5000乘以成绩不低于80分的人数占比即可.
8.(1)45
(2)解:平分,
,
(3)解:,
,
;
(4)解:,
,
,
是的平分线,
,
,
.
解:(1),,
;
故答案为:45.
(1)根据平行线的性质结合已知条件即可求解;
(2)先根据角平分线的定义得到,进而根据补角即可求出∠ECM的度数;
(3)先根据垂直得到∠NCM的度数,进而进行角的运算即可求解;
(4)先根据垂直结合题意求出∠BCN的度数,从而根据角平分线的定义得到∠BCE的度数,再根据平行线的性质即可求解。
9.(1)2
(2)
10.
11.(1)②③
(2)
(3).
12.(1)65°;(2)20°或160°
13.(1)
(2)
(3)人
14.(1);
(2);
(3).
15.(1)点A;
(2);
16.(1)B;C
(2)解:女生身高在组的百分比为:,
∵抽取的样本中,男生、女生人数相同,
∴样本中,女生身高在组的人数有:(人);
(3)解:,
∴估计身高在组的学生约有415人.
解:(1)∵直方图中,组的人数为12,最多,
∴男生的身高的众数在组,
男生总人数为:,按照从低到高的顺序,第20,两人都在组,
∴男生的身高的中位数在组,
故答案为:(1).
(1)根据众数和中位数的定义即可求得;
(2)先根据扇形统计图计算出女生身高在E组的百分比,再计算出总人数×此百分比即可;
(3)利用样本估计总体,即可求得.
17.(1)①17;②2024
(2)
(3)
18.(1)旋转中心为C点
(2)逆时针;旋转角度为
(3)
19.(1)
(2)①;②或;③,或.
20.(1)①不是;②是;③不是;
(2)有.
(3).
21.(1)
(2)
22.(1),5,10;
(2)或
(3)①;②是定值,定值为1,
23.1<x≤4;整数解为2,3,4
24.(1)
(2)
(3)“D”等级名,图形略
(4)名
25.(1)
(2)
(3)
26.(1)
(2)
(3)3或或12.
27.(1)②③
(2)
(3)或
28.(1);
(2);
(3);
(4)
29.
30.(1)2;6
(2)6
31.(1)3,2;(2);(3)
专项练习 04 解答题
一、解答题
1.(2024七下·长沙期末)已知关于、的方程组.
(1)若方程组的解也是方程的一个解,求的值;
(2)若方程组的解满足,求的取值范围.
2.(2024七下·衡阳期末)图1是一辆滑轮摄影轨道车,图为其侧面示意图固定在底座于点是轨道车的“手臂”,可通过改变的度数调节车的高度在调节过程中,放摄像机的杆始终平行于.
(1)如图,调节轨道车的“手臂”,使,此时,求的度数.
(2)若图,求的度数之和.
3.(2024七下·长沙期末)体育是长沙市中考的必考科目,某校根据实际情况,决定主要开设:立定跳远;:跑步;:实心球;:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图,请你结合图中解答下列问题:
(1)本次调查学生共______人;将条形图补充完整;
(2)样本中喜欢项目的人数所在扇形统计图中的圆心角的度数是______;
(3)如果该校有学生2000人,请你估计该校选择“立定跳远”这种活动的学生约有多少人?
4.(2024七下·株洲期末)汉江是长江的最大支流,在历史上占居重要地位,常与长江、淮河、 黄河并列,舍称“江海河汉”.每年汛期来临之时,汉江防汛指挥部都会在一危险地带两岸各安置一组探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自顺时针旋转至便立即回转,灯B射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视,已知灯A转动的速度是/秒,灯B转动的速度是/秒,假定这一带汉江两岸河堤是平行的,即,且,转动时间是t秒.
(1)当 秒时,灯A射线第一次平分,此时灯A射线记为射线,当 秒时,灯A射线第一次与射线垂直;
(2)若两灯同时转动,秒时,两束光线所在直线的位置关系是______;(填“平行”或“垂直”)
(3)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,A灯转动几秒,两灯的光束互相平行.
5.(2024七下·衡阳期末)已知方程与不等式,当时,,同时成立,则称“”是方程与不等式的“完美解”.
(1)已知①,②,则方程的解是不等式 (填序号)的“完美解”;
(2)若是方程组与不等式的一组“完美解”,求a的取值范围;
(3)若是方程与不等式组的“完美解”,求的取值范围.
6.(2024七下·长沙期末)为更好组织体育锻炼活动,随机抽取了我区部分七年级学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如图两幅不完整的统计图表.请根据图表信息回答下列问题:
最喜爱体育锻炼项目的统计表
类别 项目 人数(人)
A 跳绳 59
B 健身操
C 俯卧撑 31
D 开合跳
E 其它 22
抽取的学生最喜爱体育锻炼项目的扇形统计图
(1)求参与问卷调查的学生总人数;
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)我区共有七年级学生8000人,估算其中最喜爱“健身操”的人数.
7.(2024七下·望城期末)5月12日是我国“防灾减灾日 .为增强学生防灾减灾意识,某区举行防灾减灾安全知识竞赛.竞赛结束后,发现所有参赛学生的成绩(满分100分)均不低于60分.小明将自己所在学校参加竞赛学生的成绩(用x表示)分为四组:组A(60 ≤x< 70),B组(70 ≤x< 80),C组(80 ≤x< 90),D组(90 ≤x<100)绘制了如下不完整的频数分布直方图和扇形统计图。
根据以上信息,解答下列问题:
(1)通过计算补全频数分布直方图;
(2)扇形统计图中A组所对应的圆心角的度数是多少?
(3)根据小明学校成绩,估计全区参加竞赛的5000名学生中有多少人的成绩不低于80分?
8.(2024七下·永定期末)
(1)如图1,已知,,可得 度;
(2)如图2,在(1)的条件下,如果平分,求度数;
(3)如图3,在(1)(2)的条件下,如果,求的度数;
(4)尝试解决下面问题:如图4,,,是的平分线,,求的度数.
9.(2024七下·长沙期末)已知关于x、y的方程组 ;
(1)若方程组的解也是方程的一个解,求a的值;
(2)若方程组的解满足, 求a的取值范围.
10.(2024七下·耒阳期末)若,求的立方根.
11.(2024七下·长沙期末)我们约定:若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“包含方程”.例如:方程的解为,而不等式组 的解集为,不难发现在的范围内,所以方程 是不等式组 的“包含方程”.请根据约定,解答下列问题.
(1)在一元一次方程;;中,不等式组 的“包含方程”是 (填序号);
(2)若关于 x 的方程 是不等式组 的“包含方程”,求k 的取值范围;
(3)若关于x 的方程 是关于 x 的不等式组 的“包含方程”,且此时该不等式组恰好有7个整数解,试求 m 的取值范围.
12.(2024七下·长沙期末)如图,,在的右侧,平分,平分,所在直线交于点,.
(1)若,求的度数;
(2)将线段沿方向平移,使得点在点的右侧,其他条件不变,若,求的度数.
13.(2024七下·宁乡市期末)临近暑假,我市教育局发布了《夏季安全指南》,某校为了解全校学生对防溺水安全知识的熟悉情况,随机抽查了部分学生进行《防溺水学习手册》题问答测试,并把答对题数制成统计表和扇形统计图(如图所示).
答对题数 6 7 8 9 10
人数(人) 10 14 8 6
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和的值.
(2)求扇形统计图中答对“题”所对的圆心角度数.
(3)若该校共有名学生,根据抽查结果,估计该校学生答对10题的人数.
14.(2024七下·常德期末)完全平方公式经过适当的变形,可以解决很多数学问题.
例如:若,,求的值.
解:∵,,
∴,,
∴,
∴.
根据上面的解题思路与方法解决下列问题:
(1)若,,求的值;
(2)如图,C是线段上的一点,分别以,为边向两边作正方形,设,两正方形的面积和为24,求的面积.
(3)若,求的值.
15.(2024七下·衡阳期末)如图,已知四边形是正方形,点E在上,将经顺时针旋转后与完全重合,再将线段向右平移后与完全重合.
(1)旋转的中心是 ;旋转角度是 ;
(2)试猜想线段和的数量关系和位置关系,并说明理由.
16.(2024七下·益阳期末)为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计表:
身高情况分组表
组别
身高()
根据图表提供的信息,回答下列问题:
(1)抽取的样本中,男生的身高众数在 组,中位数在 组;
(2)抽取的样本中,女生身高在组的人数有多少人?
(3)已知该校共有男生840人,女生820人,请估计身高在组的学生人数.
17.(2024七下·攸县期末)我们在应用整式的乘法公式解题时,经常将乘法公式进行变形,如:,.
(1)根据以上变形填空:
①已知,,则______;
②已知,,则______;
(2)若x满足,求代数式的值;
(3)如图,已知数轴上从左到右依次有点A、B、C三点,它们表示的数分别是m、9、11.以为边在数轴上方作正方形,以为边在数轴上方作正方形,延长交于点P.若正方形与正方形面积的和为96,求长方形的面积.
18.(2024七下·攸县期末)如图所示,已知正方形中的可以经过旋转得到.
(1)图中哪一个点是旋转中心?
(2)按什么方向旋转;旋转角度是多少?
(3)如果.求的长?
19.(2024七下·衡阳期末)【定义】如果两个角的差为,就称这两个角互为“创新角”,其中一个角叫做另一个角的“创新角”.
例如:,,,则和互为“创新角”,即是的“创新角”,也是的“创新角”.
(1)已知和互为“创新角”,且,若和互补,则___________;
(2)如图1所示,在中,,过点作的平行线,的平分线分别交、于、两点.
①若,且和互为“创新角”,则___________;
②如图2所示,过点作的垂线,垂足为,、相交于点.若与互为“创新角”,求的度数;
③如图3所示,的平分线交于点,当和互为“创新角”时,则__________.
20.(2024七下·长沙期末)不妨约定:关于的二元一次方程,
若系数满足,则称这个方程为“开心”方程.例如:方程,其中,满足,且,则方程是“开心”方程,由两个“开心”方程组成的方程组称作“开心”方程组.根据上述规定,回答下列问题:
(1)判断以下方程是不是“开心”方程(填“是”或“不是”);
① ;②______.③______;
(2)若关于的“开心”方程组的解为,求的值.
(3)关于的“开心”方程组满足,其中为整数,为常数且,求的值,并求此“开心方程组”的解.
21.(2024七下·蒸湘期末)如图,在直角三角形中,是斜边上的高,,求:
(1)的度数;
(2)的度数.
22.(2024七下·长沙期末)在平面直角坐标系中,已知点.
(1)如图1,若正数的立方根等于它本身,,则点坐标为______,线段长度为______,的面积为______;
(2)在(1)的条件下,若点为射线上一点,且满足,求此时点的坐标;
(3)点为线段上一点(不与两点重合),点为线段上一点(不与两点重合);
①如图2,若,点是轴上点左侧的一点,连接的角平分线和的角平分线交于点,求与的数量关系;
②如图3,若,连接,交于点,记的面积为的面积为的面积为,那么是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
23.(2024七下·芙蓉期末)解不等式组: ,并写出所有整数解.
24.(2024七下·广水期末)2023年5月30日,神舟十六号载人飞船成功发射,成为我国航天事业的里程碑,某校对全校1500名学生进行了“航空航天知识”了解情况的调查,调查结果分为,,,四个等级(:非常了解;:比较了解;:了解;:不了解).随机抽取了部分学生的调查结果,绘制成两幅不完整的统计图.请结合两幅统计图信息,回答下列问题:
(1)这次调查活动中,一共调查了_____________名学生;
(2)“C”等级所在扇形的圆心角是____________度;
(3)请补上条形统计图中“”等级的信息;
(4)根据本次调查情况,准备进行“航空航天知识”讲座,请你估计七年级名学生中“”等级的人数有多少?
25.(2024七下·邵阳期末)已知,点、分别是、上的点,点在、之间,连接、.
(1)如图,若,求的度数;
(2)如图,若点是下方一点,平分,平分,已知,求的度数;
(3)如图,若点是上方一点,连接、,且的延长线平分,平分,,求的度数.
26.(2024七下·邵东期末)如图,有一副三角板,和,,,,,在同一直线上.
(1)如图1,与点重合.将绕点按顺时针方向进行旋转,当与首次平行,求此时的度数;
(2)如图2,若点在边上(不与、重合),再将绕点按顺时针方向进行旋转(如图3),边交边于,当时,求边旋转的度数;
(3)将从图2初始位置开始,绕点顺时针方向以每秒的速度进行旋转,当第一次与直线平行时停止运动.设运动时间为秒,当线段与的一条边平行,求满足条件的的值(请直接写出结果).
27.(2024七下·长沙期末)如果两个不等式存在公共解,那么称这两个不等式互为“友好不等式”.
(1)在不等式①,②,③中,与不等式互为“友好不等式”的是________;(填序号)
(2)若关于的不等式与不是“友好不等式”,求的取值范围;
(3)若,关于的不等式与不等式互为“友好不等式”,求的取值范围.
28.(2024七下·大祥期末)数形结合是解决数学问题的一种重要的思想方法;借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们进行推理,获得结论.初中数学里的一些代数恒等式,很多都可以借助几何图形进行直观推导和解释.请结合相关知识,解答下列问题:
图①是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)图②中的阴影部分的正方形边长为_________;
(2)观察图②,写出关于代数式,之间的一个代数恒等式:________;
(3)观察图③,请将多项式因式分解:_______﹔
(4)根据(3)题中的等量关系,解决下列问题:若,求的值.
29.(2024七下·醴陵期末)如图,直线相交于点O,,若,试求的度数.
30.(2024七下·双牌期末)小明在学习有关整式的知识时,发现一个有趣的现象:对于关于的多项式,由于,所以当取任意一对互为相反数的数时,多项式的值是相等的,例如,当,即或时,的值均为3;当,即或时,的值均为6.
于是小明给出一个定义:对于关于的多项式,若当取任意一对互为相反数的数时,该多项式的值相等,就称该多项式关于对称.例如:关于对称.
请结合小明的思考过程,运用此定义解决下列问题:
(1)多项式关于________对称;若关于的多项式关于对称,则________;
(2)关于的多项式关于对称,且当时,多项式的值为5,求时,求多项式的值.
31.(2024七下·长沙期末)定义:对于任何有理数,符号表示不大于的最大整数.例如:,,.
(1)填空:=________,=________;
(2)如果,求满足条件的的取值范围;
(3)求方程的整数解.
答案解析部分
1.(1)解:解方程组得:,
方程组的解也是方程的一个解,
,
解得:;
(2)解:,
,
解得:.
(1)先根据加减消元法求解,再将其代入 ,即可求得a的值;
(2)先根据加减消元法求解,再将其代入,解不等式即可.
2.(1)解:如图,过点作,且点在的下方.
,,
.
,
,
,
.
,,
,
.
(2)解:如图,过点作,且点在的下方.
,
.
由可得,
.
,
,
.
(1)通过过拐点C作已知直线的平行线,进而利用平行线的性质将逐一求角往目标角靠拢求解即可;
(2)同理过拐点作平行线联系已知条件角与问题角的关系,此时需推理角度关系,不熟练的情况可以通过设元进行表示角度关系更为直观理解.
3.(1)300人,;
(2)
(3)800人.
4.(1)25;55
(2)平行
(3)当A灯转动15秒或82.5秒,两灯的光束互相平行
5.(1)②
(2)
(3)
6.(1)200人
(2)48人
(3)1600人
7.(1)解:总人数为100÷25%=400
B组人数为400-180-100-40=80人
(2)解:A区所占比1-20%-45%-25%=10%
圆心角360°×10%=36°
(3)解:(人,
答:估计全区参加竞赛的5000名学生中有3500人的成绩不低于80分.
(1)先根据组是100人,占小明所在学校参加竞赛学生的,求出小明所在学校参加竞赛学生人数,由此可求出组的人数,据此可补全频数分布直方图;
(2)由扇形统计图求出组人数占小明所在学校参加竞赛学生人数的百分比,进而可求出组所对应的圆心角的度数;
(3)用5000乘以成绩不低于80分的人数占比即可.
8.(1)45
(2)解:平分,
,
(3)解:,
,
;
(4)解:,
,
,
是的平分线,
,
,
.
解:(1),,
;
故答案为:45.
(1)根据平行线的性质结合已知条件即可求解;
(2)先根据角平分线的定义得到,进而根据补角即可求出∠ECM的度数;
(3)先根据垂直得到∠NCM的度数,进而进行角的运算即可求解;
(4)先根据垂直结合题意求出∠BCN的度数,从而根据角平分线的定义得到∠BCE的度数,再根据平行线的性质即可求解。
9.(1)2
(2)
10.
11.(1)②③
(2)
(3).
12.(1)65°;(2)20°或160°
13.(1)
(2)
(3)人
14.(1);
(2);
(3).
15.(1)点A;
(2);
16.(1)B;C
(2)解:女生身高在组的百分比为:,
∵抽取的样本中,男生、女生人数相同,
∴样本中,女生身高在组的人数有:(人);
(3)解:,
∴估计身高在组的学生约有415人.
解:(1)∵直方图中,组的人数为12,最多,
∴男生的身高的众数在组,
男生总人数为:,按照从低到高的顺序,第20,两人都在组,
∴男生的身高的中位数在组,
故答案为:(1).
(1)根据众数和中位数的定义即可求得;
(2)先根据扇形统计图计算出女生身高在E组的百分比,再计算出总人数×此百分比即可;
(3)利用样本估计总体,即可求得.
17.(1)①17;②2024
(2)
(3)
18.(1)旋转中心为C点
(2)逆时针;旋转角度为
(3)
19.(1)
(2)①;②或;③,或.
20.(1)①不是;②是;③不是;
(2)有.
(3).
21.(1)
(2)
22.(1),5,10;
(2)或
(3)①;②是定值,定值为1,
23.1<x≤4;整数解为2,3,4
24.(1)
(2)
(3)“D”等级名,图形略
(4)名
25.(1)
(2)
(3)
26.(1)
(2)
(3)3或或12.
27.(1)②③
(2)
(3)或
28.(1);
(2);
(3);
(4)
29.
30.(1)2;6
(2)6
31.(1)3,2;(2);(3)
同课章节目录
