2024-2025学年苏科版(2024)七年级数学下册期末真题专项练习 02 填空题(含解析)
文档属性
| 名称 | 2024-2025学年苏科版(2024)七年级数学下册期末真题专项练习 02 填空题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 383.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 18:17:03 | ||
图片预览




文档简介
2024-2025学年苏科版(2024)七年级数学下册期末真题
专项练习 02 填空题
一、填空题
1.(2024七下·荔湾期末)若关于的不等式的正整数解是1,2,3,则整数的最小值是 .
2.(2024七下·武侯期末)如图,直线,直线c与直线a,b分别相交于点A,B,于点C.若,则 度.
3.(2024七下·东方期末)若,则 .(用“<”、“>”或“=”填空)
4.(2024七下·昌邑期末)将一个含有角的直角三角板按如图所示的方式放置,其中一个角的顶点落在直线a上,含角的顶点落在直线b上,若,,则 度.
5.(2024七下·平南期末)请写出一个二元一次方程,使得它的一个解为 .
6.(2024七下·昌邑期末)已知方程,用含x的代数式表示y为 .
7.(2024七下·隆回期末)下列四幅名车标志设计中能用平移得到的是 (只填序号).
①②③④
8.(2024七下·天河期末)语句“的倍与的和是负数”用不等式可以表示为 .
9.(2024七下·延庆期末)如果关于的方程的解为负数,那么的取值范围是 .
10.(2024七下·门头沟期末)可以用一个a的值说明命题“如果,那么”是假命题,这个值可以是 .
11.(2024七下·廉江期末)若关于的不等式只有3个非负整数解,则的取值范围为
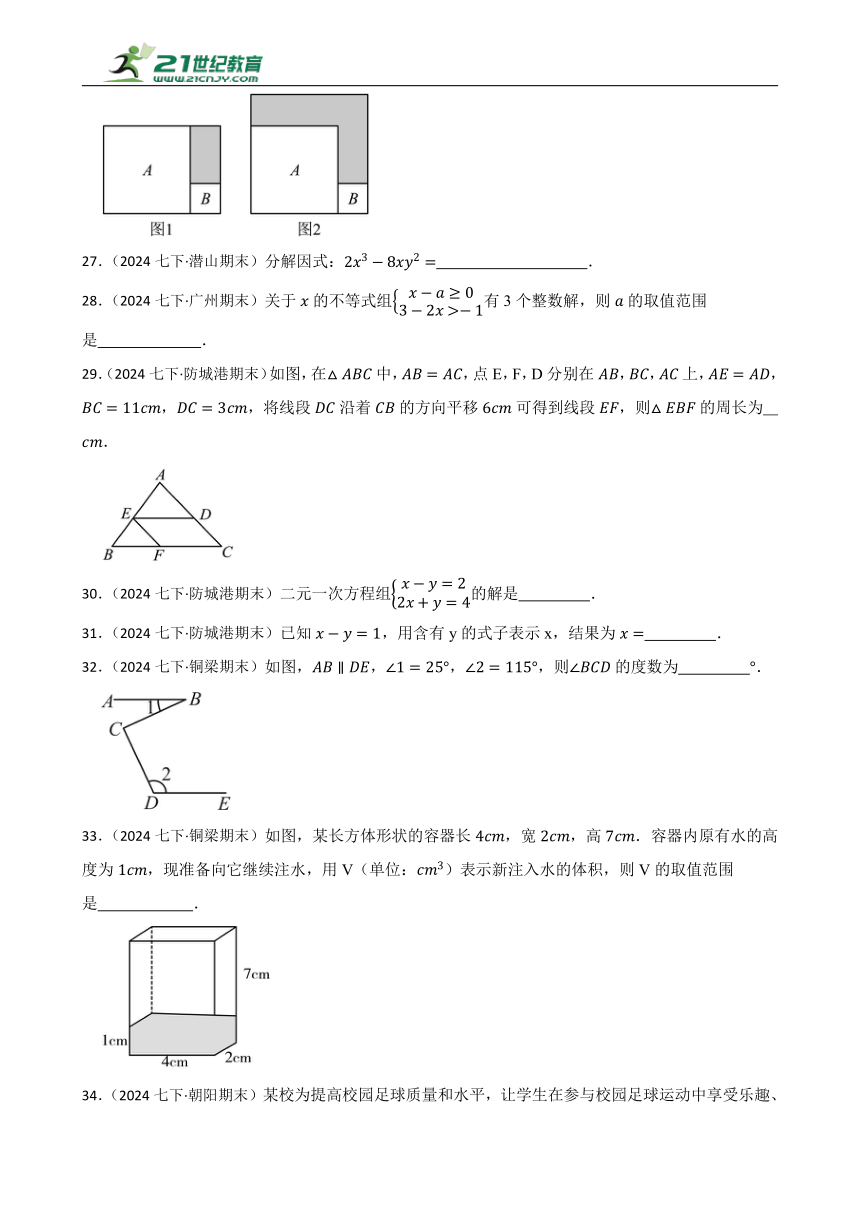
12.(2024七下·廉江期末)如图,已知BO平分∠ABC,过点O作EF∥BC分别交AB于E,交AC于F.且恰好∠FOC=∠FCO,若∠BOC=130°,∠AFE=56°,则∠EOB= .
13.(2024七下·安丘期末)如图,,分别平分和,若,,则 度.
14.(2024七下·安丘期末)如图,在中,是的中线,延长至点E,使,连接,若的面积为2,则的面积是 .
15.(2024七下·安丘期末)计算: .
16.(2024七下·花都期末)如图,点为长方形的边上的点,连接,将三角形沿着翻折得到三角形,三角形翻折得到三角形.此时,点恰好落在线段上,且.以下结论:①;②;③;④,其中结论正确的是 .(填入所有正确的序号)
17.(2024八下·浮梁期末)如图,将沿着点到的方向平移到的位置,此时,,阴影部分面积为40,则平移的距离为
18.(2024七下·永吉期末)不等式组的解集是 .
19.(2024七下·惠阳期末)已知方程组 的解满足x+y=2,则k= .
20.(2024七下·昌平期末)4月23日为世界读书日,小萱从图书馆借来一本共266页的书,计划在10天内读完(包括第10天).如果前4天每天只读15页,若从第5天起平均每天读x页才能按计划完成,则根据题意可列不等式为 .
21.(2024七下·昌平期末)已知命题“同位角相等”,这个命题是 命题.(填“真”或“假”)
22.(2024七下·吴忠期末)“的2倍与3的和不大于35”用不等式表示 .
23.(2024七下·白银期末)如图,在等腰中,,点是边上的中点,,则 .
24.(2024七下·白银期末)计算: .
25.(2024七下·灵璧期末)如图,在中,,,分别以点A,C为圆心,以大于为半径作弧,两弧分别交于点M,N,过点M,N作直线交于点P,连接.若的周长比的周长大,则的周长为 .
26.(2024七下·灵璧期末)如图,有两个正方形A,B,将A,B并列放置后构造新的图形,分别得到长方形图1与正方形图2.若图1、图2中阴影的面积分别为14与36,则正方形B的面积为 .
27.(2024七下·潜山期末)分解因式: .
28.(2024七下·广州期末)关于的不等式组有3个整数解,则的取值范围是 .
29.(2024七下·防城港期末)如图,在中,,点E,F,D分别在,,上,,,,将线段沿着的方向平移可得到线段,则的周长为 .
30.(2024七下·防城港期末)二元一次方程组的解是 .
31.(2024七下·防城港期末)已知,用含有y的式子表示x,结果为 .
32.(2024七下·铜梁期末)如图,,,,则的度数为 .
33.(2024七下·铜梁期末)如图,某长方体形状的容器长,宽,高.容器内原有水的高度为,现准备向它继续注水,用V(单位:)表示新注入水的体积,则V的取值范围是 .
34.(2024七下·朝阳期末)某校为提高校园足球质量和水平,让学生在参与校园足球运动中享受乐趣、增强体质、健全人格、锤炼意志,实现德智体美劳全面发展,举办了校园足球联赛.根据赛事安排,每队均需参赛19场,记分办法如下:胜1场得3分,平1场得1分,负1场得0分.
(1)在这次足球联赛中,若某队得13分,则该队可能负 场;(写出一种情况即可)
(2)在这次足球联赛中,若甲、乙两队都得33分,甲队所有比赛都没有踢平,甲、乙两队负场数不同,则乙队最多胜 场.
35.(2024七下·朝阳期末)不等式的正整数解是 .
36.(2024七下·青山期末)关于,的二元一次方程:,则下列四个结论:
①无论为何值时,该方程都有一组解;
②若,则方程有三组非负整数解;
③若,则不等式的解集为;
④若和是方程的两组解,则.
其中正确的结论是 .(请填写序号)
37.(2016七下·临河期末)小亮解方程组 的解为 ,由于不小心,滴上了两滴墨水,刚好遮住了两个数 和★,请你帮他找回 这个数, = .
38.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起,其中,,,当,且点E在直线的上方时,若这两块三角尺有两条边平行,则
39.(2020八下·大东期末)因式分解:a2﹣4= .
40.(2024七下·陵水期末)方程组的解是 .
41.(2023七下·岚皋期末)已知关于x的不等式组的整数解有且仅有4个,则m的取值范围是 .
42.(2023七下·荣昌期末)“x与4的和不小于x的7倍”用不等式表示为 .
43.(2021七下·赣州期末)已知,在同一平面内,∠ABC=40°,AD∥BC,∠BAD的平分线交直线BC于点E,那么∠AEB的度数为 .
44.某品牌电脑的成本为2400元,售价为2800元,该商店准备举行打折促销活动,要求利润率不低于5%,则这种品牌的电脑最低可打 折销售.
45.(2024七下·长子期末)已知,,则用含的代数式表示为 .
46.(2024七下·环江期末)如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
47.(2024七下·峨山期末)把命题“对顶角相等”改写为“如果……,那么……”的形式为 ,这是一个 命题(填“真”或“假”)
48.(2024七下·铜梁期末)已知方程的一组解为,则m的值是 .
49.(2024七下·淮北期末)如图,,BC平分,设为,点E是射线BC上的一个动点,若,则的度数为 .(用含的代数式表示).
50.(2021七下·江津期末)在平面直角坐标系中,已知点 、 、 ,且三角形 的面积等于8,则a的值是 .
答案解析部分
1.10
解:不等式的解集是:,
∵不等式的正整数解恰是1,2,3,
∴,
∴a的取值范围是.
∴整数a的最小值是10.
故答案为:10.
先求出不等式的解集,再结合“不等式的正整数解恰是1,2,3”可得,求出a的取值范围,最后求出整数a的最小值即可.
2.
3.
4.30
5.(答案不唯一)
解:依题意,是二元一次方程,且满足它的一个解为
故答案为:(答案不唯一).
含有两个未知数,且未知数项的最高次数为1的整式方程就是二元一次方程;能使二元一次方程的左右两边相等的一对未知数的值就是该二元一次方程的解,据此写出一个关于字母x、y的一次二项式,再将x、y的值代入所写的一次二项式计算出结果写在一次二项式的右边即可.
6.
7.②
8.
解:由题意得:,
故答案为:.
根据题意及代数式的表示方法直接求解即可.
9.
10.(答案不唯一).
11.
12.
13.34
14.12
15.4
16.①②④
解:在长方形中,,
∴;
,
,
;
故①正确;
由折叠知,,
;
由长方形性质得,
则,
,
;
故②正确;
,
,,
由折叠知,,
∴,
当时,,
否则;
故③错误;
,
,
故④正确;
综上,正确的有①②④.
利用折叠的性质及等量代换证出,证出AF//EQ,从而可判断出①是否正确;再利用角的运算和等量代换可得,从而可判断出②是否正确;最后利用角的运算和等量代换分析判断出③④是否正确,从而得解.
17.5
18.
由x-1<3,可得x<4,
由x+1<3,可得x<2,
∴不等式组的解集为:,
故答案为:.
利用不等式的性质及不等式组的解法求出解集即可。
19.4
,
①+②,得
3(x+y)=k+2,
由x+y=2,
得3(x+y)=k+2=6,
即k+2=6,
解得k=4,
故答案为:4.
观察方程组,可知两个方程相加后,继而可得关于k的方程,解方程即可得.
20.
21.假
22.
23.65
24.
25.8
26.4
27.
解:2x3-8xy2=2x(x2-4y2)=2x(x+2y)(x-2y)。
故第1空答案为:2x(x+2y)(x-2y)。
先根据提公因式法因式分解,提出公因式2x,再根据平方差公式进一步分解,即可得出最后结果。
28.
解:,
解不等式,得,
解不等式,得,
不等式组的解集为,
不等式组有3个整数解,
,
.
故答案为:.
先分别求得不等式的解,进而得到不等式组的解集,再通过不等式组的整数解确定a的取值范围.
29.11
解:∵线段沿着的方向平移可得到线段,
,,,
,
,
,
,
,
,,
,
∴的周长为:.
故答案为:11.
先利用平移的性质可得,,,再利用平行线的性质及等量代换可得,利用等角对等边的性质可得,利用线段的和差求出,最后利用三角形的周长公式求解即可.
30.
解:
得
解得:
将代入①,得
解得:
二元一次方程组的解是
故答案为:.
利用加减消元法的计算方法及步骤分析求解即可.
31.
解:方程
解得:
故答案为:.
将y当作常数,再利用一元一次方程的计算方法分析求解即可.
32.
33.
34.10(答案不唯一);10
35.1,2
36.①②④.
37.8
解:把x=5代入2x-y=12
得2×5-y=12,
解得y=-2.
把x=5,y=-2代入 ,解得 =8
故答案为:8.
先将x=5代入等式2×5-y=12,求出★=y=-2,再将x、y值代入2 x + y求出 ● =8。
38.30°或45°
解:由题意可得,
∵,
∴或,
当时,
∵,,
∴,
当时,
∵,,
∴,
∴
,
故答案为:或.
分类讨论,结合图形,利用平行线的性质计算求解即可。
39.(a+2)(a﹣2)
解:a2﹣4=(a+2)(a﹣2).
故答案为:(a+2)(a﹣2).
直接利用平方差公式分解因式得出即可.
40.
解:
(1)+(2),得2x=4,解得x=2.
把x=2代入(1),得2+y=3,y=1.
∴原方程组的解为.
故答案为:.
利用加减消元法求出二元一次方程的解即可.
41.
解:,
解不等式,得,
解不等式,得,
不等式组的整数解有且仅有4个,
不等式组的整数解为2,1,0,-1,
,
.
故答案为
先分别解出各个不等式的解集,再根据不等式组的整数解有且仅有4个可得不等式组的整数解为2,1,0,-1, 从而判定,然后求得m的取值范围.
42.
解:根据题意得: ,
故答案为: .
根据 “x与4的和不小于x的7倍” 列出不等式即可.
43.70°或20°
i).如图1,
∵AD∥BC
∴∠BAD+∠ABC=180°
∵∠ABC=40°
∴∠BAD=180°-40°=140°
∵AE是∠BAD的平分线
∴∠BAE= ∠BAD= ×140°=70°
ii).如图2,
∵AD∥BC
∴∠BAD=∠ABC
∵∠ABC=40°
∴∠BAD=40°
∵AE是∠BAD的平分线
∴∠BAE= ∠BAD= ×40°=20°
故∠BAE=70°或20°.
分两种情况:①当点D在点A的左侧时,如图1,②当点D在点A的右侧时,如图2,根据平行线的性质及角平分线的定义分别求解即可.
44.9
解:由题意可知:设x为打折后售出的价钱
则: ,
解得
当按最低折扣出售时, ,
所以最低可打折为 .
则可得最低折扣为九折.
故答案为:9折.
可设x为打折后售出的价钱,则 ,可得x的取值范围,因为按最低折扣出售,则用最低售价x÷2800可得最低折扣.
45.
解:,
,
,
,
,
故答案为:.
本题主要考查了解二元一次方程,根据,把用表示出来,将其代入,进行化简运算,即可求解.
46.10
47.如果两个角是对顶角,那么这两个角相等;真
48.6
49.或
50. 或6
解:分两种情况:①点A在点C的左侧,如图,
∵ 、 ,
∴OB=4,AC=2-a
∵
∴
∴
解得, ;
②当点A在点C的右侧时,如图,
则AC=a-2
∵
∴
∴
解得, ;
综上所述,a的值为:-2或6
故答案为:-2或6
分两种情况:①点A在点C的左侧,②当点A在点C的右侧时,根据三角形面积为8分别列方程求出a值即可.
专项练习 02 填空题
一、填空题
1.(2024七下·荔湾期末)若关于的不等式的正整数解是1,2,3,则整数的最小值是 .
2.(2024七下·武侯期末)如图,直线,直线c与直线a,b分别相交于点A,B,于点C.若,则 度.
3.(2024七下·东方期末)若,则 .(用“<”、“>”或“=”填空)
4.(2024七下·昌邑期末)将一个含有角的直角三角板按如图所示的方式放置,其中一个角的顶点落在直线a上,含角的顶点落在直线b上,若,,则 度.
5.(2024七下·平南期末)请写出一个二元一次方程,使得它的一个解为 .
6.(2024七下·昌邑期末)已知方程,用含x的代数式表示y为 .
7.(2024七下·隆回期末)下列四幅名车标志设计中能用平移得到的是 (只填序号).
①②③④
8.(2024七下·天河期末)语句“的倍与的和是负数”用不等式可以表示为 .
9.(2024七下·延庆期末)如果关于的方程的解为负数,那么的取值范围是 .
10.(2024七下·门头沟期末)可以用一个a的值说明命题“如果,那么”是假命题,这个值可以是 .
11.(2024七下·廉江期末)若关于的不等式只有3个非负整数解,则的取值范围为
12.(2024七下·廉江期末)如图,已知BO平分∠ABC,过点O作EF∥BC分别交AB于E,交AC于F.且恰好∠FOC=∠FCO,若∠BOC=130°,∠AFE=56°,则∠EOB= .
13.(2024七下·安丘期末)如图,,分别平分和,若,,则 度.
14.(2024七下·安丘期末)如图,在中,是的中线,延长至点E,使,连接,若的面积为2,则的面积是 .
15.(2024七下·安丘期末)计算: .
16.(2024七下·花都期末)如图,点为长方形的边上的点,连接,将三角形沿着翻折得到三角形,三角形翻折得到三角形.此时,点恰好落在线段上,且.以下结论:①;②;③;④,其中结论正确的是 .(填入所有正确的序号)
17.(2024八下·浮梁期末)如图,将沿着点到的方向平移到的位置,此时,,阴影部分面积为40,则平移的距离为
18.(2024七下·永吉期末)不等式组的解集是 .
19.(2024七下·惠阳期末)已知方程组 的解满足x+y=2,则k= .
20.(2024七下·昌平期末)4月23日为世界读书日,小萱从图书馆借来一本共266页的书,计划在10天内读完(包括第10天).如果前4天每天只读15页,若从第5天起平均每天读x页才能按计划完成,则根据题意可列不等式为 .
21.(2024七下·昌平期末)已知命题“同位角相等”,这个命题是 命题.(填“真”或“假”)
22.(2024七下·吴忠期末)“的2倍与3的和不大于35”用不等式表示 .
23.(2024七下·白银期末)如图,在等腰中,,点是边上的中点,,则 .
24.(2024七下·白银期末)计算: .
25.(2024七下·灵璧期末)如图,在中,,,分别以点A,C为圆心,以大于为半径作弧,两弧分别交于点M,N,过点M,N作直线交于点P,连接.若的周长比的周长大,则的周长为 .
26.(2024七下·灵璧期末)如图,有两个正方形A,B,将A,B并列放置后构造新的图形,分别得到长方形图1与正方形图2.若图1、图2中阴影的面积分别为14与36,则正方形B的面积为 .
27.(2024七下·潜山期末)分解因式: .
28.(2024七下·广州期末)关于的不等式组有3个整数解,则的取值范围是 .
29.(2024七下·防城港期末)如图,在中,,点E,F,D分别在,,上,,,,将线段沿着的方向平移可得到线段,则的周长为 .
30.(2024七下·防城港期末)二元一次方程组的解是 .
31.(2024七下·防城港期末)已知,用含有y的式子表示x,结果为 .
32.(2024七下·铜梁期末)如图,,,,则的度数为 .
33.(2024七下·铜梁期末)如图,某长方体形状的容器长,宽,高.容器内原有水的高度为,现准备向它继续注水,用V(单位:)表示新注入水的体积,则V的取值范围是 .
34.(2024七下·朝阳期末)某校为提高校园足球质量和水平,让学生在参与校园足球运动中享受乐趣、增强体质、健全人格、锤炼意志,实现德智体美劳全面发展,举办了校园足球联赛.根据赛事安排,每队均需参赛19场,记分办法如下:胜1场得3分,平1场得1分,负1场得0分.
(1)在这次足球联赛中,若某队得13分,则该队可能负 场;(写出一种情况即可)
(2)在这次足球联赛中,若甲、乙两队都得33分,甲队所有比赛都没有踢平,甲、乙两队负场数不同,则乙队最多胜 场.
35.(2024七下·朝阳期末)不等式的正整数解是 .
36.(2024七下·青山期末)关于,的二元一次方程:,则下列四个结论:
①无论为何值时,该方程都有一组解;
②若,则方程有三组非负整数解;
③若,则不等式的解集为;
④若和是方程的两组解,则.
其中正确的结论是 .(请填写序号)
37.(2016七下·临河期末)小亮解方程组 的解为 ,由于不小心,滴上了两滴墨水,刚好遮住了两个数 和★,请你帮他找回 这个数, = .
38.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起,其中,,,当,且点E在直线的上方时,若这两块三角尺有两条边平行,则
39.(2020八下·大东期末)因式分解:a2﹣4= .
40.(2024七下·陵水期末)方程组的解是 .
41.(2023七下·岚皋期末)已知关于x的不等式组的整数解有且仅有4个,则m的取值范围是 .
42.(2023七下·荣昌期末)“x与4的和不小于x的7倍”用不等式表示为 .
43.(2021七下·赣州期末)已知,在同一平面内,∠ABC=40°,AD∥BC,∠BAD的平分线交直线BC于点E,那么∠AEB的度数为 .
44.某品牌电脑的成本为2400元,售价为2800元,该商店准备举行打折促销活动,要求利润率不低于5%,则这种品牌的电脑最低可打 折销售.
45.(2024七下·长子期末)已知,,则用含的代数式表示为 .
46.(2024七下·环江期末)如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
47.(2024七下·峨山期末)把命题“对顶角相等”改写为“如果……,那么……”的形式为 ,这是一个 命题(填“真”或“假”)
48.(2024七下·铜梁期末)已知方程的一组解为,则m的值是 .
49.(2024七下·淮北期末)如图,,BC平分,设为,点E是射线BC上的一个动点,若,则的度数为 .(用含的代数式表示).
50.(2021七下·江津期末)在平面直角坐标系中,已知点 、 、 ,且三角形 的面积等于8,则a的值是 .
答案解析部分
1.10
解:不等式的解集是:,
∵不等式的正整数解恰是1,2,3,
∴,
∴a的取值范围是.
∴整数a的最小值是10.
故答案为:10.
先求出不等式的解集,再结合“不等式的正整数解恰是1,2,3”可得,求出a的取值范围,最后求出整数a的最小值即可.
2.
3.
4.30
5.(答案不唯一)
解:依题意,是二元一次方程,且满足它的一个解为
故答案为:(答案不唯一).
含有两个未知数,且未知数项的最高次数为1的整式方程就是二元一次方程;能使二元一次方程的左右两边相等的一对未知数的值就是该二元一次方程的解,据此写出一个关于字母x、y的一次二项式,再将x、y的值代入所写的一次二项式计算出结果写在一次二项式的右边即可.
6.
7.②
8.
解:由题意得:,
故答案为:.
根据题意及代数式的表示方法直接求解即可.
9.
10.(答案不唯一).
11.
12.
13.34
14.12
15.4
16.①②④
解:在长方形中,,
∴;
,
,
;
故①正确;
由折叠知,,
;
由长方形性质得,
则,
,
;
故②正确;
,
,,
由折叠知,,
∴,
当时,,
否则;
故③错误;
,
,
故④正确;
综上,正确的有①②④.
利用折叠的性质及等量代换证出,证出AF//EQ,从而可判断出①是否正确;再利用角的运算和等量代换可得,从而可判断出②是否正确;最后利用角的运算和等量代换分析判断出③④是否正确,从而得解.
17.5
18.
由x-1<3,可得x<4,
由x+1<3,可得x<2,
∴不等式组的解集为:,
故答案为:.
利用不等式的性质及不等式组的解法求出解集即可。
19.4
,
①+②,得
3(x+y)=k+2,
由x+y=2,
得3(x+y)=k+2=6,
即k+2=6,
解得k=4,
故答案为:4.
观察方程组,可知两个方程相加后,继而可得关于k的方程,解方程即可得.
20.
21.假
22.
23.65
24.
25.8
26.4
27.
解:2x3-8xy2=2x(x2-4y2)=2x(x+2y)(x-2y)。
故第1空答案为:2x(x+2y)(x-2y)。
先根据提公因式法因式分解,提出公因式2x,再根据平方差公式进一步分解,即可得出最后结果。
28.
解:,
解不等式,得,
解不等式,得,
不等式组的解集为,
不等式组有3个整数解,
,
.
故答案为:.
先分别求得不等式的解,进而得到不等式组的解集,再通过不等式组的整数解确定a的取值范围.
29.11
解:∵线段沿着的方向平移可得到线段,
,,,
,
,
,
,
,
,,
,
∴的周长为:.
故答案为:11.
先利用平移的性质可得,,,再利用平行线的性质及等量代换可得,利用等角对等边的性质可得,利用线段的和差求出,最后利用三角形的周长公式求解即可.
30.
解:
得
解得:
将代入①,得
解得:
二元一次方程组的解是
故答案为:.
利用加减消元法的计算方法及步骤分析求解即可.
31.
解:方程
解得:
故答案为:.
将y当作常数,再利用一元一次方程的计算方法分析求解即可.
32.
33.
34.10(答案不唯一);10
35.1,2
36.①②④.
37.8
解:把x=5代入2x-y=12
得2×5-y=12,
解得y=-2.
把x=5,y=-2代入 ,解得 =8
故答案为:8.
先将x=5代入等式2×5-y=12,求出★=y=-2,再将x、y值代入2 x + y求出 ● =8。
38.30°或45°
解:由题意可得,
∵,
∴或,
当时,
∵,,
∴,
当时,
∵,,
∴,
∴
,
故答案为:或.
分类讨论,结合图形,利用平行线的性质计算求解即可。
39.(a+2)(a﹣2)
解:a2﹣4=(a+2)(a﹣2).
故答案为:(a+2)(a﹣2).
直接利用平方差公式分解因式得出即可.
40.
解:
(1)+(2),得2x=4,解得x=2.
把x=2代入(1),得2+y=3,y=1.
∴原方程组的解为.
故答案为:.
利用加减消元法求出二元一次方程的解即可.
41.
解:,
解不等式,得,
解不等式,得,
不等式组的整数解有且仅有4个,
不等式组的整数解为2,1,0,-1,
,
.
故答案为
先分别解出各个不等式的解集,再根据不等式组的整数解有且仅有4个可得不等式组的整数解为2,1,0,-1, 从而判定,然后求得m的取值范围.
42.
解:根据题意得: ,
故答案为: .
根据 “x与4的和不小于x的7倍” 列出不等式即可.
43.70°或20°
i).如图1,
∵AD∥BC
∴∠BAD+∠ABC=180°
∵∠ABC=40°
∴∠BAD=180°-40°=140°
∵AE是∠BAD的平分线
∴∠BAE= ∠BAD= ×140°=70°
ii).如图2,
∵AD∥BC
∴∠BAD=∠ABC
∵∠ABC=40°
∴∠BAD=40°
∵AE是∠BAD的平分线
∴∠BAE= ∠BAD= ×40°=20°
故∠BAE=70°或20°.
分两种情况:①当点D在点A的左侧时,如图1,②当点D在点A的右侧时,如图2,根据平行线的性质及角平分线的定义分别求解即可.
44.9
解:由题意可知:设x为打折后售出的价钱
则: ,
解得
当按最低折扣出售时, ,
所以最低可打折为 .
则可得最低折扣为九折.
故答案为:9折.
可设x为打折后售出的价钱,则 ,可得x的取值范围,因为按最低折扣出售,则用最低售价x÷2800可得最低折扣.
45.
解:,
,
,
,
,
故答案为:.
本题主要考查了解二元一次方程,根据,把用表示出来,将其代入,进行化简运算,即可求解.
46.10
47.如果两个角是对顶角,那么这两个角相等;真
48.6
49.或
50. 或6
解:分两种情况:①点A在点C的左侧,如图,
∵ 、 ,
∴OB=4,AC=2-a
∵
∴
∴
解得, ;
②当点A在点C的右侧时,如图,
则AC=a-2
∵
∴
∴
解得, ;
综上所述,a的值为:-2或6
故答案为:-2或6
分两种情况:①点A在点C的左侧,②当点A在点C的右侧时,根据三角形面积为8分别列方程求出a值即可.
同课章节目录
