2024-2025学年青岛版(2024)七年级数学下册期末真题专项练习 02 填空题(含解析)
文档属性
| 名称 | 2024-2025学年青岛版(2024)七年级数学下册期末真题专项练习 02 填空题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 669.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 18:16:17 | ||
图片预览



文档简介
2024-2025学年青岛版(2024)七年级数学下册期末真题
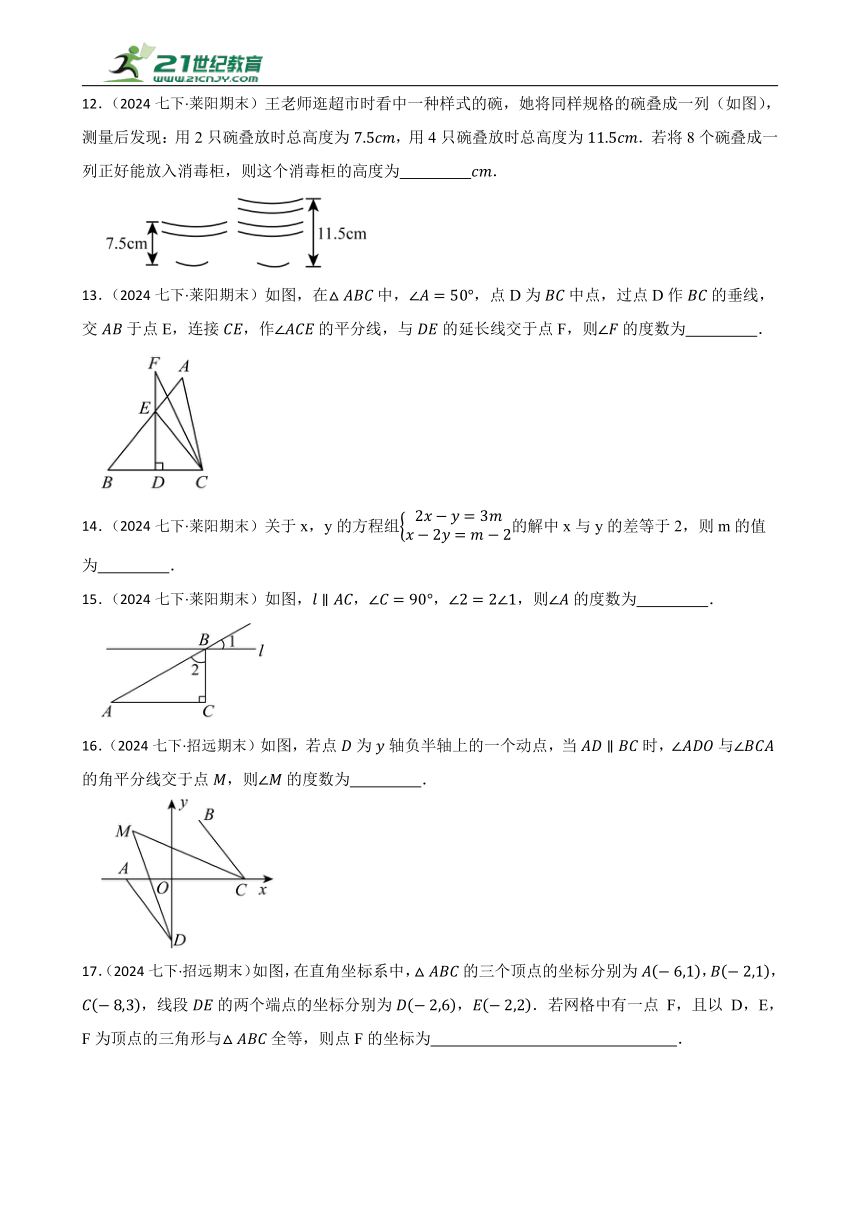
专项练习 02 填空题
一、填空题
1.(2024七下·青岛期末)如图,已知:与交于O点,,请添加一个你认为合适的条件: ,使.
2.(2024七下·青岛期末)如图,在中,边的垂直平分线,分别交,于点D,E两点,连接,,,则的度数是 .
3.(2024七下·青岛期末)如图,在中,点D、点E分别是边、上的点,将和分别沿和折叠至.已知且,则为 °.
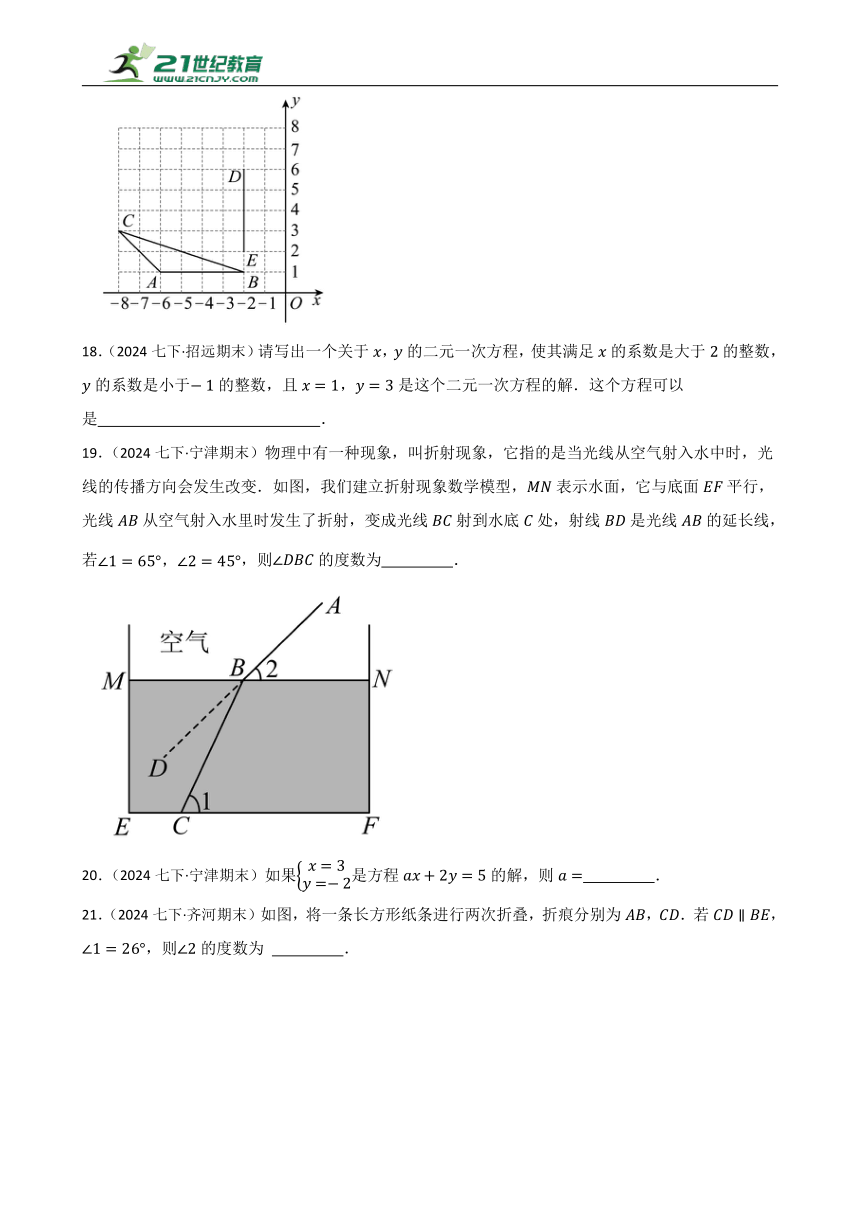
4.(2023七下·青岛高新技术产业开发期末)已知三角形三个内角之比为1∶2∶3,则该三角形最大的内角为 度.
5.(2024七下·济宁期末)如图,在中,的垂直平分线交于点D,,,的度数为 .
6.(2024七下·烟台经济技术开发期末)如图,已知长方形纸片,点E和F分别在边和上,且,H和G分别是边和上的动点,现将点A,B,C,D分别沿,折叠至点N,M,P,K,若与分别在长方形的两侧,且,则的度数为 .
7.(2024七下·蓬莱期末)如图,△EFG的三个顶点E,G和F分别在平行线AB,CD上,FH平分∠EFG,交线段EG于点H,若∠AEF=36°,∠BEG=57°,则∠EHF的大小为 .
8.(2024七下·蓬莱期末)下列命题是假命题的有 .
①若,则;②一个角的余角大于这个角;③若a,b是有理数,则; ④如果,那与是对顶角.
9.(2024七下·德州期末)光从一种介质射向另一种介质时会发生折射.如图,用直线,表示一块玻璃的两个面,且.现有一束光线从空气射向玻璃,是折射光线,为射线延长线上一点.若,,则 .
10.(2024七下·东营期末)若关于x的多项式的乘积化简后不含项,则 .
11.(2024七下·东营期末)若,,则 .
12.(2024七下·莱阳期末)王老师逛超市时看中一种样式的碗,她将同样规格的碗叠成一列(如图),测量后发现:用2只碗叠放时总高度为,用4只碗叠放时总高度为.若将8个碗叠成一列正好能放入消毒柜,则这个消毒柜的高度为 .
13.(2024七下·莱阳期末)如图,在中,,点D为中点,过点D作的垂线,交于点E,连接,作的平分线,与的延长线交于点F,则的度数为 .
14.(2024七下·莱阳期末)关于x,y的方程组的解中x与y的差等于2,则m的值为 .
15.(2024七下·莱阳期末)如图,,,,则的度数为 .
16.(2024七下·招远期末)如图,若点为轴负半轴上的一个动点,当时,与的角平分线交于点,则的度数为 .
17.(2024七下·招远期末)如图,在直角坐标系中,的三个顶点的坐标分别为,,,线段的两个端点的坐标分别为,.若网格中有一点 F,且以 D,E,F为顶点的三角形与全等,则点F的坐标为 .
18.(2024七下·招远期末)请写出一个关于,的二元一次方程,使其满足的系数是大于的整数,的系数是小于的整数,且,是这个二元一次方程的解.这个方程可以是 .
19.(2024七下·宁津期末)物理中有一种现象,叫折射现象,它指的是当光线从空气射入水中时,光线的传播方向会发生改变.如图,我们建立折射现象数学模型,表示水面,它与底面平行,光线从空气射入水里时发生了折射,变成光线射到水底处,射线是光线的延长线,若,则的度数为 .
20.(2024七下·宁津期末)如果是方程的解,则 .
21.(2024七下·齐河期末)如图,将一条长方形纸条进行两次折叠,折痕分别为,.若,,则的度数为 .
22.(2024七下·东平期末)如图,已知,,,若平分,平分,且,则 .
23.(2024七下·东平期末)若方程组的解和满足,则的值为 .
24.(2024七下·庆云期末)如图,,思考解决下列问题:试探究 .
25.(2024七下·莱州期末)如图,,为,的中点,,,则的长为 .
26.(2024七下·莱州期末)已知二元一次方程,用含y的代数式表示x,则 .
27.(2024七下·利津期末)如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,……,( n≥2且n为整数),若∠B=50°,则的度数为 .
28.(2024七下·利津期末)若关于x、y的二元一次方程组的解满足,则整数m的最大值是 .
29.(2024七下·利津期末)如图,在中,,,是的角平分线,是边上的高,则的度数是 .
30.(2024七下·和平期末)如图,在三角形中,,点M是边上的一个动点,连接,则线段长度的最小值是 .
31.(2024七下·淄川期末)计算的结果是 .
32.(2024七下·单县期末)计算: .
33.(2024七下·沂源期末)如图,在边长为1的的正方形网格中,网格线的交点称为格点.已知A,B是格点,在格点上任意放置点C,恰好能使的面积为1的概率是 .
34.(2024七下·海阳期末)在△ABC中,∠A = 105°,∠B -∠C = 15°,则∠C 等于 .
35.(2024七下·聊城期末)已知等腰三角形的一边长为,它的周长为,则它的底边长为 .
36.(2024七下·聊城期末)若,则代数式的值为 .
37.(2024七下·聊城期末)如图,在中,,是高,是中线,是角平分线,交于点,交于点,下面说法:①的面积的面积;②;③;④.正确的是 (把所有正确结论的序号都选上).
38.(2024七下·聊城期末)若n满足,则的值是 .
39.(2024七下·郯城期末)红色沂蒙,时尚临沂,临沂灯光秀照亮了夜空,璀璨夺目.今年春夏打卡临沂灯光秀表演是最热门的网红旅游去处之一,灯光秀以临沂电视塔为中心,依靠沂河岸边,导航前往滨河路篮球广场是最佳的观景地点,把标准地图抽象为几何图形,如图所示,直线表示沂河,直线上点表示电视塔,引两条射线、,分别表示祊河、小涑河且,,在射线上取一点,作,则 .
40.(2024七下·郯城期末)对实数定义一种新的运算,规定,例如:,若,,则 .
41.(2024七下·陵城期末)如图,已知∠1+∠2=180°,∠3=108°,则∠4= °.
42.(2024七下·无棣期末)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点.,,则 .
43.(2024七下·无棣期末)已知:在平面直角坐标系中,线段的两个端点坐标分别是,.当的长度最小时, .
44.(2024七下·无棣期末)已知二元一次方程,用含的代数式表示,则 .
45.(2024七下·章丘期末)若 成立,则 的值为 .
46.(2024七下·章丘期末)如图,在△ABC中,将△ABC沿直线m翻折,点B落在点D的位置,若∠1 ∠2=60°,则∠B的度数是 .
47.(2024七下·崂山期末)如图,在中,和的平分线,相交于点O,,垂足为点F,现给出以下结论:
①点O在的角平分线上;
②;
③
④若,则.
其中正确的是 .(写出所有正确结论的序号)
48.(2024七下·崂山期末)如图,,为的平分线,为的平分线,,,则的度数为 °.
49.(2024七下·崂山期末)如图,在中,,点E,F在,上,沿向内折叠,得到,则图中的和为 .
50.(2024七下·崂山期末)在综合与实践课上,小明设计了如下的运算:,则经过运算可化简为 .
答案解析部分
1.(或或)
2.85
3.51
4.90
解:设三角形三个内角分别为x,2x,3x,
∴x+2x+3x=180°,
解得:x=30°,
∴三个内角的度数分别是30°,60°,90°
故该三角形最大的内角为90度;
故答案为:90.
根据三角形三个内角之比为1∶2∶3设三角形三个内角分别为x,2x,3x; 由三角形内角和为180°可以求出三角形三个内角的具体度数,即可判断出最大的内角为多少度.
5.
6.或
7.75°
8.①②③④
9.
10.
11.
12.
13.
14.2
15.
16.
17.或或或
18.(答案不唯一)
19.
20.3
21.
22.
23.5
24.
25.2
26.
27.
28.-2
29.
30.
解:当时,最短,
∵,
∴,
∴.
故答案为:.
本题考查了垂线段最短和三角形的面积,由时,的值最小,利用面积法,劣势方程,求得CM的值,即可得到答案.
31.
32.
33.
34.30°
35.
36.1
37.①②③
38.0
39.
40.
41.72
42.
43.
44.
45.,,
46.30°
47.①②④
48.57
49.122
50.
专项练习 02 填空题
一、填空题
1.(2024七下·青岛期末)如图,已知:与交于O点,,请添加一个你认为合适的条件: ,使.
2.(2024七下·青岛期末)如图,在中,边的垂直平分线,分别交,于点D,E两点,连接,,,则的度数是 .
3.(2024七下·青岛期末)如图,在中,点D、点E分别是边、上的点,将和分别沿和折叠至.已知且,则为 °.
4.(2023七下·青岛高新技术产业开发期末)已知三角形三个内角之比为1∶2∶3,则该三角形最大的内角为 度.
5.(2024七下·济宁期末)如图,在中,的垂直平分线交于点D,,,的度数为 .
6.(2024七下·烟台经济技术开发期末)如图,已知长方形纸片,点E和F分别在边和上,且,H和G分别是边和上的动点,现将点A,B,C,D分别沿,折叠至点N,M,P,K,若与分别在长方形的两侧,且,则的度数为 .
7.(2024七下·蓬莱期末)如图,△EFG的三个顶点E,G和F分别在平行线AB,CD上,FH平分∠EFG,交线段EG于点H,若∠AEF=36°,∠BEG=57°,则∠EHF的大小为 .
8.(2024七下·蓬莱期末)下列命题是假命题的有 .
①若,则;②一个角的余角大于这个角;③若a,b是有理数,则; ④如果,那与是对顶角.
9.(2024七下·德州期末)光从一种介质射向另一种介质时会发生折射.如图,用直线,表示一块玻璃的两个面,且.现有一束光线从空气射向玻璃,是折射光线,为射线延长线上一点.若,,则 .
10.(2024七下·东营期末)若关于x的多项式的乘积化简后不含项,则 .
11.(2024七下·东营期末)若,,则 .
12.(2024七下·莱阳期末)王老师逛超市时看中一种样式的碗,她将同样规格的碗叠成一列(如图),测量后发现:用2只碗叠放时总高度为,用4只碗叠放时总高度为.若将8个碗叠成一列正好能放入消毒柜,则这个消毒柜的高度为 .
13.(2024七下·莱阳期末)如图,在中,,点D为中点,过点D作的垂线,交于点E,连接,作的平分线,与的延长线交于点F,则的度数为 .
14.(2024七下·莱阳期末)关于x,y的方程组的解中x与y的差等于2,则m的值为 .
15.(2024七下·莱阳期末)如图,,,,则的度数为 .
16.(2024七下·招远期末)如图,若点为轴负半轴上的一个动点,当时,与的角平分线交于点,则的度数为 .
17.(2024七下·招远期末)如图,在直角坐标系中,的三个顶点的坐标分别为,,,线段的两个端点的坐标分别为,.若网格中有一点 F,且以 D,E,F为顶点的三角形与全等,则点F的坐标为 .
18.(2024七下·招远期末)请写出一个关于,的二元一次方程,使其满足的系数是大于的整数,的系数是小于的整数,且,是这个二元一次方程的解.这个方程可以是 .
19.(2024七下·宁津期末)物理中有一种现象,叫折射现象,它指的是当光线从空气射入水中时,光线的传播方向会发生改变.如图,我们建立折射现象数学模型,表示水面,它与底面平行,光线从空气射入水里时发生了折射,变成光线射到水底处,射线是光线的延长线,若,则的度数为 .
20.(2024七下·宁津期末)如果是方程的解,则 .
21.(2024七下·齐河期末)如图,将一条长方形纸条进行两次折叠,折痕分别为,.若,,则的度数为 .
22.(2024七下·东平期末)如图,已知,,,若平分,平分,且,则 .
23.(2024七下·东平期末)若方程组的解和满足,则的值为 .
24.(2024七下·庆云期末)如图,,思考解决下列问题:试探究 .
25.(2024七下·莱州期末)如图,,为,的中点,,,则的长为 .
26.(2024七下·莱州期末)已知二元一次方程,用含y的代数式表示x,则 .
27.(2024七下·利津期末)如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,……,( n≥2且n为整数),若∠B=50°,则的度数为 .
28.(2024七下·利津期末)若关于x、y的二元一次方程组的解满足,则整数m的最大值是 .
29.(2024七下·利津期末)如图,在中,,,是的角平分线,是边上的高,则的度数是 .
30.(2024七下·和平期末)如图,在三角形中,,点M是边上的一个动点,连接,则线段长度的最小值是 .
31.(2024七下·淄川期末)计算的结果是 .
32.(2024七下·单县期末)计算: .
33.(2024七下·沂源期末)如图,在边长为1的的正方形网格中,网格线的交点称为格点.已知A,B是格点,在格点上任意放置点C,恰好能使的面积为1的概率是 .
34.(2024七下·海阳期末)在△ABC中,∠A = 105°,∠B -∠C = 15°,则∠C 等于 .
35.(2024七下·聊城期末)已知等腰三角形的一边长为,它的周长为,则它的底边长为 .
36.(2024七下·聊城期末)若,则代数式的值为 .
37.(2024七下·聊城期末)如图,在中,,是高,是中线,是角平分线,交于点,交于点,下面说法:①的面积的面积;②;③;④.正确的是 (把所有正确结论的序号都选上).
38.(2024七下·聊城期末)若n满足,则的值是 .
39.(2024七下·郯城期末)红色沂蒙,时尚临沂,临沂灯光秀照亮了夜空,璀璨夺目.今年春夏打卡临沂灯光秀表演是最热门的网红旅游去处之一,灯光秀以临沂电视塔为中心,依靠沂河岸边,导航前往滨河路篮球广场是最佳的观景地点,把标准地图抽象为几何图形,如图所示,直线表示沂河,直线上点表示电视塔,引两条射线、,分别表示祊河、小涑河且,,在射线上取一点,作,则 .
40.(2024七下·郯城期末)对实数定义一种新的运算,规定,例如:,若,,则 .
41.(2024七下·陵城期末)如图,已知∠1+∠2=180°,∠3=108°,则∠4= °.
42.(2024七下·无棣期末)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点.,,则 .
43.(2024七下·无棣期末)已知:在平面直角坐标系中,线段的两个端点坐标分别是,.当的长度最小时, .
44.(2024七下·无棣期末)已知二元一次方程,用含的代数式表示,则 .
45.(2024七下·章丘期末)若 成立,则 的值为 .
46.(2024七下·章丘期末)如图,在△ABC中,将△ABC沿直线m翻折,点B落在点D的位置,若∠1 ∠2=60°,则∠B的度数是 .
47.(2024七下·崂山期末)如图,在中,和的平分线,相交于点O,,垂足为点F,现给出以下结论:
①点O在的角平分线上;
②;
③
④若,则.
其中正确的是 .(写出所有正确结论的序号)
48.(2024七下·崂山期末)如图,,为的平分线,为的平分线,,,则的度数为 °.
49.(2024七下·崂山期末)如图,在中,,点E,F在,上,沿向内折叠,得到,则图中的和为 .
50.(2024七下·崂山期末)在综合与实践课上,小明设计了如下的运算:,则经过运算可化简为 .
答案解析部分
1.(或或)
2.85
3.51
4.90
解:设三角形三个内角分别为x,2x,3x,
∴x+2x+3x=180°,
解得:x=30°,
∴三个内角的度数分别是30°,60°,90°
故该三角形最大的内角为90度;
故答案为:90.
根据三角形三个内角之比为1∶2∶3设三角形三个内角分别为x,2x,3x; 由三角形内角和为180°可以求出三角形三个内角的具体度数,即可判断出最大的内角为多少度.
5.
6.或
7.75°
8.①②③④
9.
10.
11.
12.
13.
14.2
15.
16.
17.或或或
18.(答案不唯一)
19.
20.3
21.
22.
23.5
24.
25.2
26.
27.
28.-2
29.
30.
解:当时,最短,
∵,
∴,
∴.
故答案为:.
本题考查了垂线段最短和三角形的面积,由时,的值最小,利用面积法,劣势方程,求得CM的值,即可得到答案.
31.
32.
33.
34.30°
35.
36.1
37.①②③
38.0
39.
40.
41.72
42.
43.
44.
45.,,
46.30°
47.①②④
48.57
49.122
50.
同课章节目录
