2024-2025学年六年级数学下册期末备考真题分类汇编(浙江专版)解决问题(二)【答案+解析】
文档属性
| 名称 | 2024-2025学年六年级数学下册期末备考真题分类汇编(浙江专版)解决问题(二)【答案+解析】 |

|
|
| 格式 | docx | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 00:00:00 | ||
图片预览




文档简介
2024-2025学年六年级数学下册期末备考真题分类汇编(浙江专版)
解决问题(二)
一、解决问题
1.(2024六下·南湖期末)小红骑车从甲地去乙地,小明步行从乙地去甲地,两人同时出发。当两人相遇时,小明走了全程的。相遇后两人继续前行,当小红到达乙地后,小明离甲地还有12千米。甲乙两地相距多少千米?
2.(2024六下·钱塘期末)一个长8dm、宽5dm、高4dm的水槽,里面装有100升水。在这个水槽中放入一底面积为10dm,高2dm的圆柱形物体,水将上升到几分米
3.(2024六下·钱塘期末)唐僧师徒仨,西行路迢迢。偶遇一大树,树顶冲九霄。八戒问悟空,此树几许高 “看我变戏法!”悟空微微笑。取出金箍棒,化作10米高。量得地上影,仅有8分米。复量大树影,恰与棒齐高。试问小朋友,此树高多少 (用比例解答)
4.(2024六下·钱塘期末)我国古代著名的数学典籍《九章算术》上有这么一道题:今有三人共车,二车空:二人共车,九人步。问:人与车各几何 意思是:有一些人一起坐车。如果3个人共坐一辆车,则有2辆车是空的;如果改成2个人共坐一辆车,那么就有9个人需要步行。问:人与车各多少
聪明的小朋友,请你试着解一解。(可用方程解)
5.(2024六下·钱塘期末)数学思考
欧洲的吉普赛人有一种神秘的读心术,据称能测算人内心的感应。具体做法是:被测者在心里想一个两位数,再用这个两位数依次减去它自己十位上和个位上的数字,算出所得的差(如:所想两位数是37,则用37-3-7,得27),然后在“读心大师”所提供的图表上找到与这个差相对应的图形,并牢记这个图形。最后,点一下“大师”手中的水晶球,水晶球上就会出现刚刚所记的那个图形。
其实这只是吉普赛人玩的一个小把戏。因为,不管被测者一开始想的是哪个两位数,最后所得的差一定是9的倍数。而“读心大师”的图表上,所有9的倍数相对应的图形都是同一个,也就是水晶球上会显示的那唯一的一个图形。
聪明的小朋友,你能根据所学知识,说明一下为什么任意一个两位数依次减去十位和个位计的数字后,所得的差三定是9的倍数可
6.(2024六下·钱塘期末)甲、乙、丙三个工程队合修一条长70km的公路。甲、乙两个工程队修路的长度之比是2:3,乙、丙两个工程队修路的长度之比是4:5。这三个工程队分别修了多少千米
7.(2024六下·钱塘期末)甲、乙、丙、丁四人向希望工程捐款。甲的捐款数占其余三人捐款总数的,乙的捐款数占其余三人捐款总数的,丙的捐款数占其余三人捐款总数的,丁的捐款数是780元。他们四人共捐款多少元
8.(2024六下·钱塘期末)一段长1850米长的路,甲工程队需要4天可以修完,乙工程队需要5天才能修完,丙工程队需要6天才能修完。现在三队合修,怎样分配工作最合理
9.(2024六下·南湖期末)红星汽配厂甲车间的人数是乙车间的30%。如果从乙车间调70人到甲车间,那么两车间人数相等。甲、乙两车间各有多少人?
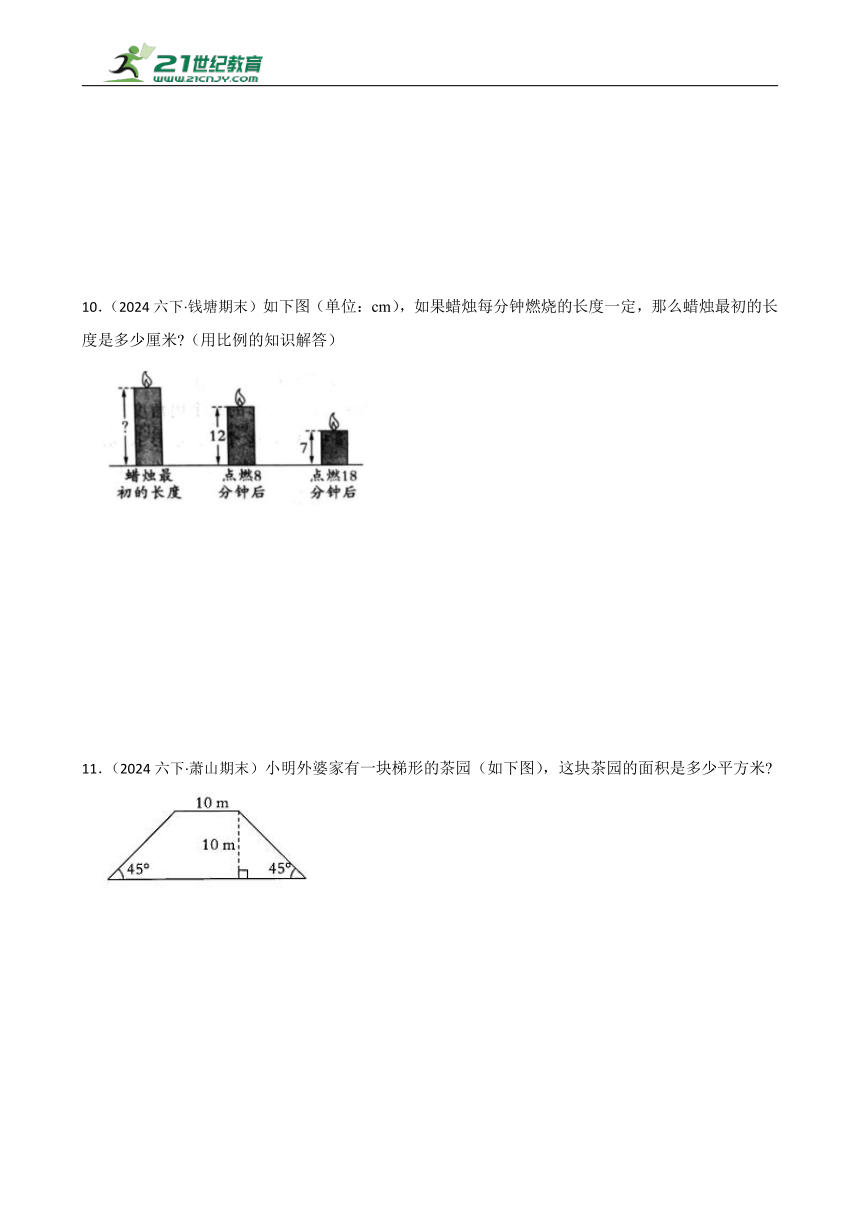
10.(2024六下·钱塘期末)如下图(单位:cm),如果蜡烛每分钟燃烧的长度一定,那么蜡烛最初的长度是多少厘米 (用比例的知识解答)
11.(2024六下·萧山期末)小明外婆家有一块梯形的茶园(如下图),这块茶园的面积是多少平方米
12.(2024六下·萧山期末)“谷雨”过后的双休日,小明和爸爸帮外婆采茶。
(1)第一天,爸爸采了450克茶,比小明采的3倍还多15克。小明第一天采了多少克茶 (用方程解答)
(2)第二天,小明改进了采茶技术,竟然比爸爸多采了。小明采了550克,爸爸第二天采了多少克
13.(2024六下·萧山期末)下图是一个由长方形和半圆组成的图形,请按照要求提出数学问题,并解答。
(1) 用两步或三步计算的问题:( )
(2) 用四步或四步以上计算的问题:( )
14.(2023六下·温岭期末)一个圆柱形容器里面装有60cm深的水,该容器里面的底面直径为2dm,调皮的弟弟将一个底面半径为6cm的圆锥形玩具完全浸没在水中,这时水面上升了3cm(水未溢出)。这个圆锥形玩具的高是多少厘米?
15.(2024六下·萧山期末)某小学在“春分”那天进行“立鸡蛋”比赛,经过选拔,最终有60人进入决赛,其中六⑴班和六⑵班进入决赛的人数一样多。若各班进入决赛人数统计如下图,则六⑴班有多少人进入决赛
16.(2024·期末)(江苏南通市)某商场在促销期间规定:商场内所有商品按标价的80%出售。若消费金额不足1000元,则按如下方案获得相应金额的奖券:
消费金额a/元 a<400 400≤a<600 600≤a<800 800≤a<1 000
获得奖券的金额/元 0 60 120 180
若消费金额不小于1000元,则在现有优惠的条件下再打七五折。
根据上述促销方法,顾客在商场内购物可以获得双重优惠。例如:购买标价为600元的商品,则消费金额为600× 80% = 480(元),获得的优惠额为600×(1-80%) + 60=180(元) ,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)在双重优惠下,当购买标价是多少元的商品时,可以得到的优惠率?
17.(2023六下·南湖期末)高度适宜的书桌对孩子良好体姿的养成很重要。科学研究发现,当学生的身高大约比书桌高度的3倍少40厘米时,最合适学生良好体姿的养成。照此推算,身高为 155 厘米的学生,所用书桌的高度应是多少厘米?
18.(2024六下·南湖期末)李叔叔买了3盆兰花和2盆绿萝,一共用去185元。已知一盆兰花比一盆绿萝贵20元。兰花和绿萝每盆各多少元?
19.(2024六下·萧山期末)外婆炒的茶叶小有名气,去年每千克售价80元,今年由于成本提高,单价提高了25%。今年买8千克茶的钱,去年可以买多少千克 (用比例解答)
20.(2024六下·南湖期末)小强用橡皮泥做了一个圆锥形学具,圆锥的底面周长是12.56厘米,高是9厘米。他又做一个长方体纸盒,正好能把圆锥形橡皮泥装进去。
(1)橡皮泥学具的体积是多少立方厘米?
(2)做这个纸盒至少用了多少平方厘米硬纸?
21.(2024六下·南湖期末)超市运进200千克大米,进价是2.4元/千克,大米全部售出后,共获得利润120元。
(1)每千克大米售价是多少元?
(2)售价比进价高百分之几?
22.(2024六下·桐乡市期末)一个带有容积刻度的圆柱形容器,里面水平放置着一个由圆柱和圆锥两部分组成的几何体铁块。以同样的速度往容器中注水(如左下图),注水时间与水面对应刻度的关系如右下图所示。
(1)图中铁块圆柱部分的高是圆锥高的( )倍。
(2)每秒注水多少毫升?
(3)铁块圆柱部分的体积是多少立方厘米。
23.(2024六下·桐乡市期末)把一块底面积是64平方分米,高是8分米的圆柱形铁块熔铸成一个长16分米,宽8分米的长方体。长方体高多少分米?
24.(2024六下·钱塘期末)如图,一个蔬菜大棚,长30m,横截面是半径2m的半圆,顶部和两端使用塑料薄膜。
(1)这个大棚的种植面积是多少m2
(2)制作这个大棚用塑料薄膜约多少m2?(得数保留整数)
25.(2024六下·钱塘期末)学校食堂采购一批大米,计划每天用450千克,可以用40天。响应“光盘行动”,实际用了45天,实际每天比计划少用多少千克
26.(2024六下·钱塘期末)某电视机厂去年生产电视机108万台,其中上半年产量是下半年的80%。这个电视机厂去年上半年和下半年的产量分别是多少万台
27.(2024六下·钱塘期末)客车与货车同时从A、B两地相对开出,两车在距离中点10km处相遇。已知客车和货车的速度比是5:4,求A、B两地距离。
28.(2024六下·钱塘期末)在比例尺是1:500的图纸上,一个圆形花坛的周长是9.42cm。这个花坛的实际面积是多少
29.(2024六下·钱塘期末)营养学家建议,儿童每天水的摄入量应不少于1500毫升,小刚每天用底面直径6厘米,高10厘米的圆柱形水杯喝6杯水,小刚水的摄入量达到要求了吗 (π取3.14)
30.(2024六下·钱塘期末)一间教室,长9米,宽6米,高3米,门窗13.5平方米.要把教室四周和屋顶粉刷一遍,每平方米付材料和工资费用10.5元,一共要付多少元
31.(2024六下·钱塘期末)在一次数学活动中,同学们把一个圆沿半径剪成若干等份,然后拼成一个近似的长方形(如下图), 量得这个长方形的周长是 41.4 厘米。这个圆的面积是多少平方厘米
32.(2024六下·钱塘期末)一瓶葡萄酒,瓶子的容积是1050 毫升,瓶子中酒高15 厘米。小强把瓶子倒过来,这时瓶底空出的高度为6厘米。你能求出瓶中有多少毫升?
33.(2024六下·钱塘期末)把1.5米长的竹竿直立在地面上,量得它的影长是1.2米,同时量得同一地的一根旗杆的影长是6.4米。这根旗杆高多少米 (用比例解答)
34.(2024六下·钱塘期末)妈妈让小明去复印店里复印两页资料,每页各复印25份。复印店里有两种价格,小明怎样复印比较划算 (通过计算说明)
“复印机”印 每页复印一份0.50元
“一体机”印 每页印一份0.15元,30份起印,每印一页资料需另加制版费5元。
35.(2024六下·钱塘期末)为了宣传“绿色奥运”,李叔叔和王叔叔分别从黄龙体育中心和武林广场骑车出发,沿同一条路线相向而行,骑车情况如下图所示。如果他们同时出发,经过多少时间就能相遇 (得数保留一位小数)
36.(2024六下·钱塘期末)如下图是一个上部为圆柱,下部为圆锥的密封容器,圆锥的高是18cm,圆柱的高是20cm,此时水面高度为24cm。若将容器倒立放置,水面的高度是多少厘米
37.(2024六下·钱塘期末)一个服装厂原来生产一套服装的成本是160元,由于扩大生产规模,每套服装的成本降低了20%。原来生产20套服装的钱,现在可以生产多少套 (用比例解答)
38.(2024六下·钱塘期末)为倡导合理利用电资源,电力局推行了居民申请使用“峰谷”电制度,具体如右下图所示。已知一个家庭使用峰谷电的某月电费为95.2元,经测算,比不使用峰谷电节约10.8元,该家庭当月使用峰电和谷电各多少千瓦时?
8: 00---22:00:每千瓦时0.56元(峰电价格)
22: 00---8: 00:每千瓦时0.28元(谷电价格)
不使用峰谷电:每千瓦时0.53元
39.(2024六下·钱塘期末)小钱和小塘是同班同学且住在同一幢楼。早上7:40分,小钱出发骑车去学校,7:46分时追上一直匀速步行的小塘,这时想起未带马克笔,立即将速度提高到原来的2倍返回,到家拿好笔之后继续出发去学校,结果两人在8:00同时到达学校,已知小钱在家找笔花了36分钟,那么小塘是几时从家出发的
40.(2024六下·钱塘期末)甲、乙、丙三名志愿者合租一辆车往上海运送疫情物资。从A地到B地,甲在全程化处卸货,乙在全程刚好一半的地方卸货,只有丙运到终点。共付运费760元,他们该怎样支付运费最合理
41.(2024六下·钱塘期末)一块蛋糕如右图,在它的表面涂上奶油,需要涂多少平方厘米的奶油 这块蛋糕体积多大
42.(2024六下·钱塘期末)2022年参加北京冬奥会的总人数为2892人,比第一届夏蒙尼冬奥会的12倍少204人,第一届冬奥会参加人数是多少人 (两种方法计算)
43.(2024六下·钱塘期末)杭州出租车的计费标准是:起步价(3千米以内,包括3千米)13元,以后每超过1千米另加价2.5元,超过起步里程10千米以上的部分加收50%,即每千米3.75元,(不足1千米的按1千米计算)由于油价持续上涨,出租车另收取每车次1元燃油附加费。
(1)欢欢一次乘坐出租车行驶了5.2千米,应付车费多少元
(2)欢欢家距离图书馆有15.7千米,欢欢身上有50元,周末欢欢从图书馆坐出租车到家
的钱够吗 如果够,还剩多少钱 如果不够,还差多少钱
44.(2024六下·钱塘期末)为迎接亚运会,杭州围绕“城市承接力明显提高、老百姓获得感明显提升”这一目标,大力建设城市轨道,每段城市轨道铺轨面原计划每天铺100米,35天完成,实际由于时间紧迫,要求25天完成,那么实际平均每天要铺多少米 (用比例解)
45.(2024六下·钱塘期末)小明看一本课外书,看了一部分后,已看页数与未看页数的比是3:5,接着他又看了34页,这时已看的页数是全书的80%,这本课外书共有多少页
46.(2024六下·钱塘期末)如下图,在一个棱长1dm的正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞,已知侧面洞口是边长dm的正方形,上下底面是直径为dm的圆,求这个正方体剩余部分的体积。(得数保留两位小数)
47.(2024六下·钱塘期末)如下图,长方体容器内装有水,从里面量,容器的底面长20cm,宽12cm。现把一个圆柱和一个圆锥浸没于水中,水面上升了1cm,且水没有溢出。如果圆锥和圆柱的底面积相等,高也相等,那么圆柱和圆锥的体积各是多少
48.(2024六下·钱塘期末)为迎接杭州亚运会,钱塘区一高校进行10000米长跑比赛,当小军到达终点时,小丁离终点还有1000米,小强离终点还有3250米,照这样的速度,当小丁到达终点时,小强离终点还有多少米
49.(2024六下·钱塘期末)如下图所示,一个长方体礼盒刚好能容纳6个圆柱形茶叶罐。
(1)一个圆柱形茶叶罐的体积是多少立方厘米
(2)做一个长方体礼盒至少需要多少平方厘米的包装材料?(接口处不计)
(3)能容纳这6个条叶罐的长方体礼盒还可以设计出不同的方案,请你设计一种方案,并算出需多少包装材料。
50.(2024六下·萧山期末)如下图,一个底面直径是5厘米的圆锥,过顶点沿底面直径纵切成两半,表面积将增加30平方厘米。这个圆锥的体积是多少立方厘米?
答案解析部分
1.18千米
2.解:100÷(8×5)=2.5(dm)
10×2÷(8×5)=0.5(dm)
2.5+0.5=3(dm)
答:水将上升到3分米。
先根据长方体的高=长方体的体积÷(长×宽),求出水槽中水的高度;根据圆柱的体积=底面积×高,算出圆柱的体积,再用圆柱形物体的体积除以长方体水槽的底面求出水槽中水面增加的高度;最后用水槽中水的高度加上水槽中水面增加的高度,即可求出水将上升到几分米。
3.解:设此树高x米
10:0.8=x:10
0.8x=100
0.8x÷0.8=100÷0.8
x=125
答:此树高125米。
同一时间、同一地点测得的物体高度与影子长度成正比例,即金箍棒高度:金箍棒影长=树的高度:树的影长,设树高x米,列方程求解即可。
4.解:设共有x辆车。
3(x-2)=2x+9
3x-6=2x+9
x=15
2x+9=39
答:共有39个人,15辆车。
根据题意,假设共有x辆车,再根据3个人共坐一辆车,则有2辆车是空的与2个人共坐一辆车,有9个人需要步行的总人数不变的条件,列出方程:3(x-2)=2x+9,再将方程求解即可。
5.解:设任意两位数为,则,所以题中所得之差为9的倍数。
根据题意,假设任意两位数为,再根据题目的要求进行计算,这时任意两位数为中的a在十位上表示的是10a,b在个位上表示的是b,则,9a是9的倍数,所以任意一个两位数依次减去十位和个位计的数字后,所得的差三定是9的倍数。
6.解:先根据比的基本性质把两个比写成甲:乙:丙的形式;
甲:乙=2:3=8:12
乙:丙=4:5=12:15
甲:乙:丙=8:12:15
甲队修了:70×=70×=16(km)
乙队修了:70×=70×=24(km)
丙队修了:70×=70×=30(km)
答:甲、乙、丙三个工程队分别干了16千米、24千米、30千米。
总工作量被平均分成35份,甲队修了总工作量的,乙队修了总工作量的,甲队修了总工作量的,总工作量×这个队修的长度占总长度的分率=这个队修的长度,据此解答。
7.解:甲捐的是其他三人捐款总数的,即甲捐款数量:其他三人的捐款总数=1:2,甲捐款数量占捐款总数的;
同理:乙捐款占捐款总数的
丙捐款占捐款总数的
丁捐款占捐款总数的1---=
780÷=780×=3600(元)
答:他们四人共捐款3600元。
丁的捐款数÷丁的捐款数对应四人共捐款的分率=四人共捐款的钱数,据此解答。
8.解:
甲:=750(米)
乙:=600(米)
丙:=500(米)
答:现在三队合修,甲队修750米,乙队修600米,丙队修500米。
先算出每队的工作效率,然后根据工作效率求出三队的工作效率之比;根据工作效率比,分别求出甲、乙、丙三队需要修的路长。
9.甲车间:60人;乙车间:200人
10.解:设蜡烛最初的长度是xcm。
2(x-12)=8
2x-24=8
2x=32
x=16
答:蜡烛最初的长度是16cm。
8分钟燃烧的长度=蜡烛原来的长度-点燃8分钟后的长度;
10分钟燃烧的长度=点燃8分钟后的长度-点燃18分钟后的长度;
8分钟燃烧的长度:8分钟=10分钟燃烧的长度:10分钟;据此比例关系列比例,根据比例的基本性质解比例。
11.解:10+10+10
=20+10
=30(米)
(10+30)×10÷2
=40×10÷2
=400÷2
=200(平方米)
答:这块茶园的面积是200平方米。
由题意可知,等腰直角三角形的两条直角边相等,所以梯形的下底为10+10+10=30米;梯形的面积公式:S=(a+b)×h÷2,代入数值计算即可。
12.(1)解:设小明第一天采了x克茶。
3x+15=450
x=145
答:小明第一天采了145克茶。
(2)解:设爸爸第二天采了y克。
(1+)y=550
y=550
y÷=550÷
y=500
答:爸爸第二天采了500克。
⑴根据题意可知,小明采茶的质量×3+15=爸爸采茶的质量,设小明第一天采了x克的茶,据此列方程解答。
(2)根据题意可知,爸爸第二天采茶的质量× (1+)=小明第二天采茶的质量,设爸爸第二天采了y克的茶,据此列方程解答。
13.(1)解:半圆的面积是多少平方厘米
3.14×(10÷2)2÷2
=3.14×25÷2
=78.5÷2
=39.25(平方厘米)
答:半圆的面积是39.25平方厘米。
(2)解:长方形的面积比半圆的面积大多少平方厘米
10×(10÷2)-3.14×(10÷2)2÷2
=10×5-3.14×25÷2
=50-78.5÷2
=50-39.25
=10.75(平方厘米)
答:长方形的面积比半圆的面积大10.75平方厘米。
提的问题要联系题目所给出的信息,不要自己创造条件。
(1)可以提出:半圆的面积是多少平方厘米?
然后根据半圆面积=πr2÷2,进行求解;
(2)可以提出:长方形的面积比半圆的面积大多少平方厘米
可以根据长方形面积-半圆面积=长×宽-πr2÷2,进行求解。
14.解:2dm=20cm
20÷2=10(cm)
3.14×102×3×3÷(3.14×62)
=314×9÷3.14÷36
=900÷36
=25(cm)
答:这个圆锥形玩具的高是25cm。
这个圆锥形玩具的高=这个圆锥形玩具的体积×3÷底面积;其中,这个圆锥形玩具的体积=上升水的体积=圆柱的底面积×上升水的高度。
15.解:(1-30%)÷2
=70%÷2
=35%
60×35%=21(人)
答:六⑴班有21人进入决赛。
把进入决赛的人数看作单位“1”,先求出六⑴班进人决赛的人数占总人数的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。
16.(1)解:1000×(1- 80%)+180
=1000×20%+180
=200+180
=380(元)
380÷1000=38%
答:顾客得到的优惠率是38%。
(2)解:设标价是x元,则优惠总金额为x元,消费金额为0.8x元。
当消费金额不小于1000元时,优惠率为1-80%×75%=40%,40%> ,所以消费金额一定小于1000元。
①当800≤0.8x<1000时:
x(1- 80%)+180=x
0.2x+180=x
x=180
x=1350
不符合800≤0.8x<1000的设定。
②当600≤0.8x<800时:
x(1- 80%)+120=x
0.2x+120=x
x=120
x=900
符合600≤0.8x<800的设定。
③当400≤0.8x<600时:
x(1- 80%)+60=x
0.2x+60=x
x=60
x=450
不符合400≤0.8x<600的设定。
答:当购买标价为900元的商品时,可以得到的优惠率。
(1)把标价为1000元代入题中规定的计算方法计算即可;
(2)本体可以设标价是x元,则优惠总金额为x元,消费金额为0.8x元;
若消费金额不小于1000元,则在现有优惠的条件下再打七五折,所以先算出消费金额,然后根据表中消费金额的范围,列出相对应的方程,最后找到符合规定的结果即可。
17.解:(155+40)÷3
=195÷3
=65(厘米)
答:所用书桌的高度应是65厘米。
根据题意可得数量关系:学生的身高=书桌高度×3-40,已知学生身高,所以书桌高度=(学生身高+40)÷3,依据此数量关系即可解答。
18.兰花:45元;绿萝:25元
19.解:设今年买8千克茶的钱,去年可以买x千克。
80x=80×(1+25%)×8
80x=800
80x÷80=800÷80
x=10
答:去年可以买10千克。
根据“去年每千克售价80元,今年由于成本提高,单价提高了25%"可知,今年的茶叶每千克[80×(1+25%)]元,根据总价不变,即茶叶的质量和茶叶的单价的乘积一定,两者成反比例关系。
20.(1)37.68立方厘米
(2)176平方厘米
21.(1)3元
(2)25%
22.(1)2
(2)10毫升
(3)30立方厘米
23.4分米
24.(1)解:圆的直径:2×2=4(米)
30×4=120(平方米)
答:这个大棚的种植面积是120平方米。
(2)解:3.14×2×2+3.14×2×2×30÷2
=12.56+188.4
=200.96(平方米)
≈201(平方米)
答:制作这个大棚用塑料薄膜约201平方米。
(1)大棚的长×圆的直径=这个大棚的种植面积;
(2)圆的面积+圆柱的侧面积÷2=制作这个大棚用塑料薄膜的面积。
25.解:450×40÷45
=18000÷45
=400(千克)
450-400=50(千克)
答:实际每天比计划少用50千克。
计划每天用的质量×用的天数=大米的质量,大米的质量÷实际用的天数=实际每天用的质量,实际每天用的质量-计划每天用的质量=实际每天比计划少用的质量。
26.解:下半年生产的台数看做单位1,上半年生产的台数是80%,
108÷(1+80%)
=108÷1.8
=60(万台)
108-60=48(万台)
答:下半年的产量是60万台,上半年的产量是48万台。
去年生产电视机的台数÷对应的百分率=下半年生产的台数,去年生产电视机的台数-下半年生产的台数=上半年生产的台数。
27.解:(5+4)÷2=4.5(份)
5-4.5=0.5(份)
10÷0.5=20(km/份)
20×(5+4)=180(km)
答:两地相距180km。
客车和货车的速度比是5:4,路程比也是5:4,把路程看做9份,中点处是4.5份;
货车行驶了4份,少行驶0.5份,0.5份是10千米,1份就是20千米;
A、B两地的距离一共是9份,1份的长度×9份=A、B两地的距离。
28.解:9.42÷3.14÷2=1.5(cm)
1.5×500=750(cm)=7.5(m)
3.14×7.5×7.5=176.625(m2)
答:花坛面积为176.625m2。
圆的周长÷π÷2=圆的半径,圆的半径×500=花坛的半径,π×花坛半径的平方=花坛的面积。
29.解:底面半径:6÷2=3(厘米)
3.14×3×3×10=28.26×10=282.6(毫升)
282.6×6=1695.6(毫升)
1695.6毫升>1500毫升
答:够。
π×底面半径的平方×高=圆柱的体积;圆柱的体积×6=小刚一天喝水的体积,小刚一天喝水的体积>1500毫升,说明够。
30.解:9×6+6×3×2+9×3×2
=54+36+54
=144(m2)
144-13.5=130.5(m2)
130.5×10.5=1370.25(元)
答:一共要付1370.25元。
教室的长×宽+长×高×2+宽×高×2-门窗和黑板的面积=需要粉刷的面积,需要粉刷的面积×每平方米付材料和工资费用 =粉刷这个教室共需要的钱数。
31.解:长方形的周长:πd+d=41.4cm
即:(π+1)×d=41.4
d=41.4÷(3.14+1)
d=41.4÷4.14
d =10
圆的半径:r=10÷2=5(厘米)
S=πr2=3.14×52=3.14×25=78.5(cm2)
答: 这个圆的面积是78.5平方厘米。
把一个圆沿半径剪成若干等份,然后拼成一个近似的长方形,长方形的周长=圆的的周长+2个半径,据此求出圆的直径,再求出圆的半径,最后用π×半径的平方求出圆的面积
32.解:1050÷(15+6)
=1050÷21
=50(平方厘米)
50×15=750(mL)
答: 瓶中有750毫升酒。
瓶子中酒高+瓶底空出的高度=酒瓶看做圆柱时的高度,瓶子的容积÷酒瓶看做圆柱时的高度=酒瓶的底面积,酒瓶的底面积×酒瓶中酒的高度=酒瓶中酒的容积。
33.解: 设这根旗杆高x米。
1.5: 1.2=x: 6.4
1.2x=6.4×1.5
1.2x=9.6
x=9.6÷1.2
x=8
答: 这根旗杆高8米。
竹竿的长度:影长=旗杆的长度:影长,据此比例关系列比例,根据比例的基本性质解比例。
34.解:复印机印:
0.5×25×2=25(元)
一体机印:
(0.15×30+5)×2
=9.5×2
=19(元)
25元>19元
答:用一体机复印比较划算。
复印机印:一页的钱数×复印的份数=复印一页一共需要的钱数,复印一页一共需要的钱数×2=复印两页一共需要的钱数;
一体机印:每页印一份的钱数×30页+5元的制版费=复印一页需要的钱数,复印一页需要的钱数×2=复印两页一共需要的钱数;
哪个计算的钱数少,用哪个复印划算。
35.解:4200÷[4200÷40+4200÷(35-5)]
=4200÷(105+140)
=4200÷245
≈17.1(分)
答:经过17.1分就能相遇。
王叔叔骑行的路程÷骑行的时间=王叔叔骑行的速度,李叔叔骑行的路程÷骑行的时间=李叔叔骑行的速度,总路程÷两人的速度和=相遇时间。
36.解:(24-18)+18÷3
=6+6
=12(厘米)
答:水面的高是12厘米。
水的高度-圆锥的高=圆柱内水的高度,圆锥内水的高度÷3=放入圆柱后水的高度,两个高度的和就是容器倒立放置水面的高度。
37.解:设现在可以生产x套。
160×(1-20%)x=160×20
160×80%x=3200
128x=3200
x=3200÷128
x=25
答:现在可以生产25套。
原来生产一套服装的成本×(1-20%)=现在生产一套服装的成本;现在生产一套服装的成本×生产的套数=原来生产一套服装的成本×生产的套数,据此反比例关系列比例,根据比例的基本性质解比例。
38.解:(95.2+10.8)÷0.53
=106÷0.53
=200(千瓦时)
谷:(200×0.56-95.2)÷(0.56-0.28)
=16.8÷0.28
=60(千瓦时)
峰:200-60=140(千瓦时)
答:该家庭当月使用峰电140千瓦时,谷电60千瓦时。
使用峰谷电的某月电费+比不使用峰谷电节约的钱数=不使用峰谷电的电费,不使用峰谷电的电费÷不使用峰谷电的电价=用电的度数,用电的度数×峰电价格-95.2元=全用峰电的钱数和使用峰谷电的钱数差,全用峰电的钱数和使用峰谷电的钱数差÷峰电谷电价格差=使用谷电的度数,用电的度数-使用谷电的度数=使用峰电的度数。
39.解:(46-40)÷2×1
=6÷2×1
=3(分钟)
在路上的时间:60-40-6=14(分钟)
拿好笔回学校的时间:14-6-3=5(分钟)
第一次遇见小塘的地方到学校的时间:5-3=2(分钟)
小塘从第一次遇见小塘到学校的时间:60-46=14(分钟)
14÷2=7(分钟)
5×7=35(分钟)
60-35=25(分钟)
答:小塘是7:25分从家里出发的。
原来小钱的速度:现在小钱的速度=1:2,原来用的时间:现在用的时间=2:1;在路上的时间:60-40-6=14,拿好笔回学校的时间:14-6-3=5,一次遇见小塘的地方到学校的时间:5-3=2,小塘从第一次遇见小塘到学校的时间:60-46=14,小塘从家里出发的时间60-35=25分,即7:25。
40.解:甲:乙:丙=::1=4:5:10
甲:(元)
乙:(元)
丙:(元)
答:甲付160元,乙付200元,丙付400元。
先求出甲乙丙的路程比,共付运费×甲走的路程占总路程的分率=甲应付运费,共付运费×乙走的路程占总路程的分率=乙应付运费,共付运费×丙走的路程占总路程的分率=丙应付运费。
41.解:两个长方形的面积和:8×10×2=160(cm2)
两个扇形面积和:102×π÷2=50π=157(cm2)
侧面积:2π×10×8÷4=40π=125.6(cm2)
160+157+125.6=442.6(dm2)
底面积:10×10×π÷4=25π=78.5(cm2)
体积:78.5×8=628(cm3)
答:需要涂442.6平方厘米的奶油,体积是628立方厘米。
两个长方形的面积和+两个扇形面积和+圆柱的侧面积=需要涂奶油的面积,蛋糕的底面积×高=蛋糕的体积。
42.解:方法一:
(2892+204)÷12
=3096÷12
=258(人)
答:第一届冬奥会参加的人数是258人。
方法二:
设第一届冬奥会的参加的人数是x人。
12x-204=2892
12x=2892+204
12x=3096
x=3096÷12
x=258
答:第一届冬奥会参加的人数是258人。
方法一:(2022年参加北京冬奥会的总人数+204人)÷12=第一届冬奥会参加的人数;
方法二:等量关系:第一届冬奥会参加的人数×12倍-204人=2022年参加北京冬奥会的总人数,根据等量关系列方程,根据等式性质解方程。
43.(1)解:5.2千米按6千米收费
13+(6-3)×2.5+1
=13+7.5+1
=21.5(元)
答:应付车费21.5元。
(2)解:15.7千米按16千米收费
16-10=6(千米)
13+(10-3)×2.5+6×3.75+1
=13+17.5+22.5+1
=54(元)
54-50=4(元)
答:不够,还差4元。
(1)3千米以内的收费+超过部分的收费+燃油附加费=应付车费;
(2)分三段收费,3千米以内的收费+10千米以内超过部分的收费+10千米以上部分的收费+燃油附加费=应付车费。
44.解:设实际每天铺x米。
25x=100×35
25x=3500
x=3500÷25
x=140
答:实际每天铺140米。
原计划每天铺的长度×铺完需要的天数=实际每天铺的长度×铺完需要的天数,据此反比例关系列比例,根据比例的基本性质解比例。
45.解:已看页数看做3,未看页数看做5,全书的页数是8,
已看页数是全书的:3÷8=0.375=37.5%
34页对应的百分率:80%-37.5%=42.5%
课外书总页数:34÷42.5%=80(页)
答:课外书共80页。
34页÷34页对应全书页数的百分率=全书的页数。
46.解:
=1-0.32+0.064-3.14×
=0.744-0.07536
≈0.67(dm3)
答:这个正方体剩余部分的体积是0.67立方分米。
中间去掉了2个底面边长为dm的长方体,两个长方体重叠的部分是棱长dm的正方体。上下面挖去的圆柱与长方体也有重叠的部分,没有重叠的部分实际就是高是(1-)dm的圆柱。用大正方体的体积减去挖去的2个长方体的体积,加上重叠部分正方体的体积,再减去高是(1-)dm的圆柱的体积就是剩余部分的体积。
47.解:圆锥的体积:20×12×1÷(3+1)
=240×1÷4
=60(立方厘米)
圆柱的体积:60×3=180(立方厘米)
答:圆柱的体积四180立方厘米,圆锥的体积是60立方厘米。
上升部分水的体积等于圆柱与圆锥的体积和,根据等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3 +1)倍,根据已知一个数的几倍是多少,求这个数,用除法求出圆锥的体积,进而求出圆柱的体积。
48.解:设当小丁到达终点时,小强离终点还有x米。
x=2500
答:设当小丁到达终点时,小强离终点还有2500米。
小军、小丁、小强三人的速度是恒定的,所以它们跑的距离之比等于它们跑的时间之比,所以,可以建立比例关系:小军跑完全程与小丁还剩1000米的距离之比,等于小丁跑完全程与小强还剩x米的距离之比,最后解出未知数即可。
49.(1)解:3.14×(8÷2)2×10
=3.14×16×10
=502.4(立方厘米)
答:一个圆柱形茶叶罐的体积是502.4立方厘米。
(2)解:8×3=24(厘米),8×2=16(厘米)
(24×16+24×10+16×10)×2
=(384+240+160)×2
=784×2
=1568(平方厘米)
答:做一个长方体礼盒至少需要1568平方厘米的包装材料。
(3)解:可以每排放3罐,放两层。
长:8×3=24(厘米)
高:10×2=20(厘米)
宽:8厘米
(24×8+24×20+8×20)×2
=(192+480+160)×2
=832×2
=1664(平方厘米)
答:需1664平方厘米包装材料。
圆柱体的底面积=3.14×r2,圆柱的体积公式:V=Sh;长方体的表面积=(长×宽+长×高+宽×高)×2
(1)圆柱体的半径是(8÷2),高是10,根据圆柱体的底面积和体积公式即得出茶叶罐的体积。
(2)长方体礼盒的长是圆柱形茶叶罐3个直径的长度,宽是两个直径的长度,高等于茶叶罐的高度,根据长方体的表面积公式即可求出;
(3)可以每排放3罐,放两层。长方体礼盒的长是圆柱形茶叶罐3个直径的长度,宽是1个直径的长度,高是2个茶叶罐的高度,根据长方体的表面积公式即可求出。
50.解:30÷2=15(平方厘米)
15×2÷5=6(厘米)
×3.14×(5÷2)2×6
=×3.14×6.25×6
=39.25(立方厘米)
答:这个圆锥的体积是39.25立方厘米。
通过现察图形可知,把这个圆锥过顶点沿底面直径纵切成两半,表面积将增加2个等腰三角形的面积,三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高。可以先根据表面积增加30平方厘米求出圆锥的高,再根据圆锥的体积公式求出圆锥的体积。
解决问题(二)
一、解决问题
1.(2024六下·南湖期末)小红骑车从甲地去乙地,小明步行从乙地去甲地,两人同时出发。当两人相遇时,小明走了全程的。相遇后两人继续前行,当小红到达乙地后,小明离甲地还有12千米。甲乙两地相距多少千米?
2.(2024六下·钱塘期末)一个长8dm、宽5dm、高4dm的水槽,里面装有100升水。在这个水槽中放入一底面积为10dm,高2dm的圆柱形物体,水将上升到几分米
3.(2024六下·钱塘期末)唐僧师徒仨,西行路迢迢。偶遇一大树,树顶冲九霄。八戒问悟空,此树几许高 “看我变戏法!”悟空微微笑。取出金箍棒,化作10米高。量得地上影,仅有8分米。复量大树影,恰与棒齐高。试问小朋友,此树高多少 (用比例解答)
4.(2024六下·钱塘期末)我国古代著名的数学典籍《九章算术》上有这么一道题:今有三人共车,二车空:二人共车,九人步。问:人与车各几何 意思是:有一些人一起坐车。如果3个人共坐一辆车,则有2辆车是空的;如果改成2个人共坐一辆车,那么就有9个人需要步行。问:人与车各多少
聪明的小朋友,请你试着解一解。(可用方程解)
5.(2024六下·钱塘期末)数学思考
欧洲的吉普赛人有一种神秘的读心术,据称能测算人内心的感应。具体做法是:被测者在心里想一个两位数,再用这个两位数依次减去它自己十位上和个位上的数字,算出所得的差(如:所想两位数是37,则用37-3-7,得27),然后在“读心大师”所提供的图表上找到与这个差相对应的图形,并牢记这个图形。最后,点一下“大师”手中的水晶球,水晶球上就会出现刚刚所记的那个图形。
其实这只是吉普赛人玩的一个小把戏。因为,不管被测者一开始想的是哪个两位数,最后所得的差一定是9的倍数。而“读心大师”的图表上,所有9的倍数相对应的图形都是同一个,也就是水晶球上会显示的那唯一的一个图形。
聪明的小朋友,你能根据所学知识,说明一下为什么任意一个两位数依次减去十位和个位计的数字后,所得的差三定是9的倍数可
6.(2024六下·钱塘期末)甲、乙、丙三个工程队合修一条长70km的公路。甲、乙两个工程队修路的长度之比是2:3,乙、丙两个工程队修路的长度之比是4:5。这三个工程队分别修了多少千米
7.(2024六下·钱塘期末)甲、乙、丙、丁四人向希望工程捐款。甲的捐款数占其余三人捐款总数的,乙的捐款数占其余三人捐款总数的,丙的捐款数占其余三人捐款总数的,丁的捐款数是780元。他们四人共捐款多少元
8.(2024六下·钱塘期末)一段长1850米长的路,甲工程队需要4天可以修完,乙工程队需要5天才能修完,丙工程队需要6天才能修完。现在三队合修,怎样分配工作最合理
9.(2024六下·南湖期末)红星汽配厂甲车间的人数是乙车间的30%。如果从乙车间调70人到甲车间,那么两车间人数相等。甲、乙两车间各有多少人?
10.(2024六下·钱塘期末)如下图(单位:cm),如果蜡烛每分钟燃烧的长度一定,那么蜡烛最初的长度是多少厘米 (用比例的知识解答)
11.(2024六下·萧山期末)小明外婆家有一块梯形的茶园(如下图),这块茶园的面积是多少平方米
12.(2024六下·萧山期末)“谷雨”过后的双休日,小明和爸爸帮外婆采茶。
(1)第一天,爸爸采了450克茶,比小明采的3倍还多15克。小明第一天采了多少克茶 (用方程解答)
(2)第二天,小明改进了采茶技术,竟然比爸爸多采了。小明采了550克,爸爸第二天采了多少克
13.(2024六下·萧山期末)下图是一个由长方形和半圆组成的图形,请按照要求提出数学问题,并解答。
(1) 用两步或三步计算的问题:( )
(2) 用四步或四步以上计算的问题:( )
14.(2023六下·温岭期末)一个圆柱形容器里面装有60cm深的水,该容器里面的底面直径为2dm,调皮的弟弟将一个底面半径为6cm的圆锥形玩具完全浸没在水中,这时水面上升了3cm(水未溢出)。这个圆锥形玩具的高是多少厘米?
15.(2024六下·萧山期末)某小学在“春分”那天进行“立鸡蛋”比赛,经过选拔,最终有60人进入决赛,其中六⑴班和六⑵班进入决赛的人数一样多。若各班进入决赛人数统计如下图,则六⑴班有多少人进入决赛
16.(2024·期末)(江苏南通市)某商场在促销期间规定:商场内所有商品按标价的80%出售。若消费金额不足1000元,则按如下方案获得相应金额的奖券:
消费金额a/元 a<400 400≤a<600 600≤a<800 800≤a<1 000
获得奖券的金额/元 0 60 120 180
若消费金额不小于1000元,则在现有优惠的条件下再打七五折。
根据上述促销方法,顾客在商场内购物可以获得双重优惠。例如:购买标价为600元的商品,则消费金额为600× 80% = 480(元),获得的优惠额为600×(1-80%) + 60=180(元) ,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)在双重优惠下,当购买标价是多少元的商品时,可以得到的优惠率?
17.(2023六下·南湖期末)高度适宜的书桌对孩子良好体姿的养成很重要。科学研究发现,当学生的身高大约比书桌高度的3倍少40厘米时,最合适学生良好体姿的养成。照此推算,身高为 155 厘米的学生,所用书桌的高度应是多少厘米?
18.(2024六下·南湖期末)李叔叔买了3盆兰花和2盆绿萝,一共用去185元。已知一盆兰花比一盆绿萝贵20元。兰花和绿萝每盆各多少元?
19.(2024六下·萧山期末)外婆炒的茶叶小有名气,去年每千克售价80元,今年由于成本提高,单价提高了25%。今年买8千克茶的钱,去年可以买多少千克 (用比例解答)
20.(2024六下·南湖期末)小强用橡皮泥做了一个圆锥形学具,圆锥的底面周长是12.56厘米,高是9厘米。他又做一个长方体纸盒,正好能把圆锥形橡皮泥装进去。
(1)橡皮泥学具的体积是多少立方厘米?
(2)做这个纸盒至少用了多少平方厘米硬纸?
21.(2024六下·南湖期末)超市运进200千克大米,进价是2.4元/千克,大米全部售出后,共获得利润120元。
(1)每千克大米售价是多少元?
(2)售价比进价高百分之几?
22.(2024六下·桐乡市期末)一个带有容积刻度的圆柱形容器,里面水平放置着一个由圆柱和圆锥两部分组成的几何体铁块。以同样的速度往容器中注水(如左下图),注水时间与水面对应刻度的关系如右下图所示。
(1)图中铁块圆柱部分的高是圆锥高的( )倍。
(2)每秒注水多少毫升?
(3)铁块圆柱部分的体积是多少立方厘米。
23.(2024六下·桐乡市期末)把一块底面积是64平方分米,高是8分米的圆柱形铁块熔铸成一个长16分米,宽8分米的长方体。长方体高多少分米?
24.(2024六下·钱塘期末)如图,一个蔬菜大棚,长30m,横截面是半径2m的半圆,顶部和两端使用塑料薄膜。
(1)这个大棚的种植面积是多少m2
(2)制作这个大棚用塑料薄膜约多少m2?(得数保留整数)
25.(2024六下·钱塘期末)学校食堂采购一批大米,计划每天用450千克,可以用40天。响应“光盘行动”,实际用了45天,实际每天比计划少用多少千克
26.(2024六下·钱塘期末)某电视机厂去年生产电视机108万台,其中上半年产量是下半年的80%。这个电视机厂去年上半年和下半年的产量分别是多少万台
27.(2024六下·钱塘期末)客车与货车同时从A、B两地相对开出,两车在距离中点10km处相遇。已知客车和货车的速度比是5:4,求A、B两地距离。
28.(2024六下·钱塘期末)在比例尺是1:500的图纸上,一个圆形花坛的周长是9.42cm。这个花坛的实际面积是多少
29.(2024六下·钱塘期末)营养学家建议,儿童每天水的摄入量应不少于1500毫升,小刚每天用底面直径6厘米,高10厘米的圆柱形水杯喝6杯水,小刚水的摄入量达到要求了吗 (π取3.14)
30.(2024六下·钱塘期末)一间教室,长9米,宽6米,高3米,门窗13.5平方米.要把教室四周和屋顶粉刷一遍,每平方米付材料和工资费用10.5元,一共要付多少元
31.(2024六下·钱塘期末)在一次数学活动中,同学们把一个圆沿半径剪成若干等份,然后拼成一个近似的长方形(如下图), 量得这个长方形的周长是 41.4 厘米。这个圆的面积是多少平方厘米
32.(2024六下·钱塘期末)一瓶葡萄酒,瓶子的容积是1050 毫升,瓶子中酒高15 厘米。小强把瓶子倒过来,这时瓶底空出的高度为6厘米。你能求出瓶中有多少毫升?
33.(2024六下·钱塘期末)把1.5米长的竹竿直立在地面上,量得它的影长是1.2米,同时量得同一地的一根旗杆的影长是6.4米。这根旗杆高多少米 (用比例解答)
34.(2024六下·钱塘期末)妈妈让小明去复印店里复印两页资料,每页各复印25份。复印店里有两种价格,小明怎样复印比较划算 (通过计算说明)
“复印机”印 每页复印一份0.50元
“一体机”印 每页印一份0.15元,30份起印,每印一页资料需另加制版费5元。
35.(2024六下·钱塘期末)为了宣传“绿色奥运”,李叔叔和王叔叔分别从黄龙体育中心和武林广场骑车出发,沿同一条路线相向而行,骑车情况如下图所示。如果他们同时出发,经过多少时间就能相遇 (得数保留一位小数)
36.(2024六下·钱塘期末)如下图是一个上部为圆柱,下部为圆锥的密封容器,圆锥的高是18cm,圆柱的高是20cm,此时水面高度为24cm。若将容器倒立放置,水面的高度是多少厘米
37.(2024六下·钱塘期末)一个服装厂原来生产一套服装的成本是160元,由于扩大生产规模,每套服装的成本降低了20%。原来生产20套服装的钱,现在可以生产多少套 (用比例解答)
38.(2024六下·钱塘期末)为倡导合理利用电资源,电力局推行了居民申请使用“峰谷”电制度,具体如右下图所示。已知一个家庭使用峰谷电的某月电费为95.2元,经测算,比不使用峰谷电节约10.8元,该家庭当月使用峰电和谷电各多少千瓦时?
8: 00---22:00:每千瓦时0.56元(峰电价格)
22: 00---8: 00:每千瓦时0.28元(谷电价格)
不使用峰谷电:每千瓦时0.53元
39.(2024六下·钱塘期末)小钱和小塘是同班同学且住在同一幢楼。早上7:40分,小钱出发骑车去学校,7:46分时追上一直匀速步行的小塘,这时想起未带马克笔,立即将速度提高到原来的2倍返回,到家拿好笔之后继续出发去学校,结果两人在8:00同时到达学校,已知小钱在家找笔花了36分钟,那么小塘是几时从家出发的
40.(2024六下·钱塘期末)甲、乙、丙三名志愿者合租一辆车往上海运送疫情物资。从A地到B地,甲在全程化处卸货,乙在全程刚好一半的地方卸货,只有丙运到终点。共付运费760元,他们该怎样支付运费最合理
41.(2024六下·钱塘期末)一块蛋糕如右图,在它的表面涂上奶油,需要涂多少平方厘米的奶油 这块蛋糕体积多大
42.(2024六下·钱塘期末)2022年参加北京冬奥会的总人数为2892人,比第一届夏蒙尼冬奥会的12倍少204人,第一届冬奥会参加人数是多少人 (两种方法计算)
43.(2024六下·钱塘期末)杭州出租车的计费标准是:起步价(3千米以内,包括3千米)13元,以后每超过1千米另加价2.5元,超过起步里程10千米以上的部分加收50%,即每千米3.75元,(不足1千米的按1千米计算)由于油价持续上涨,出租车另收取每车次1元燃油附加费。
(1)欢欢一次乘坐出租车行驶了5.2千米,应付车费多少元
(2)欢欢家距离图书馆有15.7千米,欢欢身上有50元,周末欢欢从图书馆坐出租车到家
的钱够吗 如果够,还剩多少钱 如果不够,还差多少钱
44.(2024六下·钱塘期末)为迎接亚运会,杭州围绕“城市承接力明显提高、老百姓获得感明显提升”这一目标,大力建设城市轨道,每段城市轨道铺轨面原计划每天铺100米,35天完成,实际由于时间紧迫,要求25天完成,那么实际平均每天要铺多少米 (用比例解)
45.(2024六下·钱塘期末)小明看一本课外书,看了一部分后,已看页数与未看页数的比是3:5,接着他又看了34页,这时已看的页数是全书的80%,这本课外书共有多少页
46.(2024六下·钱塘期末)如下图,在一个棱长1dm的正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞,已知侧面洞口是边长dm的正方形,上下底面是直径为dm的圆,求这个正方体剩余部分的体积。(得数保留两位小数)
47.(2024六下·钱塘期末)如下图,长方体容器内装有水,从里面量,容器的底面长20cm,宽12cm。现把一个圆柱和一个圆锥浸没于水中,水面上升了1cm,且水没有溢出。如果圆锥和圆柱的底面积相等,高也相等,那么圆柱和圆锥的体积各是多少
48.(2024六下·钱塘期末)为迎接杭州亚运会,钱塘区一高校进行10000米长跑比赛,当小军到达终点时,小丁离终点还有1000米,小强离终点还有3250米,照这样的速度,当小丁到达终点时,小强离终点还有多少米
49.(2024六下·钱塘期末)如下图所示,一个长方体礼盒刚好能容纳6个圆柱形茶叶罐。
(1)一个圆柱形茶叶罐的体积是多少立方厘米
(2)做一个长方体礼盒至少需要多少平方厘米的包装材料?(接口处不计)
(3)能容纳这6个条叶罐的长方体礼盒还可以设计出不同的方案,请你设计一种方案,并算出需多少包装材料。
50.(2024六下·萧山期末)如下图,一个底面直径是5厘米的圆锥,过顶点沿底面直径纵切成两半,表面积将增加30平方厘米。这个圆锥的体积是多少立方厘米?
答案解析部分
1.18千米
2.解:100÷(8×5)=2.5(dm)
10×2÷(8×5)=0.5(dm)
2.5+0.5=3(dm)
答:水将上升到3分米。
先根据长方体的高=长方体的体积÷(长×宽),求出水槽中水的高度;根据圆柱的体积=底面积×高,算出圆柱的体积,再用圆柱形物体的体积除以长方体水槽的底面求出水槽中水面增加的高度;最后用水槽中水的高度加上水槽中水面增加的高度,即可求出水将上升到几分米。
3.解:设此树高x米
10:0.8=x:10
0.8x=100
0.8x÷0.8=100÷0.8
x=125
答:此树高125米。
同一时间、同一地点测得的物体高度与影子长度成正比例,即金箍棒高度:金箍棒影长=树的高度:树的影长,设树高x米,列方程求解即可。
4.解:设共有x辆车。
3(x-2)=2x+9
3x-6=2x+9
x=15
2x+9=39
答:共有39个人,15辆车。
根据题意,假设共有x辆车,再根据3个人共坐一辆车,则有2辆车是空的与2个人共坐一辆车,有9个人需要步行的总人数不变的条件,列出方程:3(x-2)=2x+9,再将方程求解即可。
5.解:设任意两位数为,则,所以题中所得之差为9的倍数。
根据题意,假设任意两位数为,再根据题目的要求进行计算,这时任意两位数为中的a在十位上表示的是10a,b在个位上表示的是b,则,9a是9的倍数,所以任意一个两位数依次减去十位和个位计的数字后,所得的差三定是9的倍数。
6.解:先根据比的基本性质把两个比写成甲:乙:丙的形式;
甲:乙=2:3=8:12
乙:丙=4:5=12:15
甲:乙:丙=8:12:15
甲队修了:70×=70×=16(km)
乙队修了:70×=70×=24(km)
丙队修了:70×=70×=30(km)
答:甲、乙、丙三个工程队分别干了16千米、24千米、30千米。
总工作量被平均分成35份,甲队修了总工作量的,乙队修了总工作量的,甲队修了总工作量的,总工作量×这个队修的长度占总长度的分率=这个队修的长度,据此解答。
7.解:甲捐的是其他三人捐款总数的,即甲捐款数量:其他三人的捐款总数=1:2,甲捐款数量占捐款总数的;
同理:乙捐款占捐款总数的
丙捐款占捐款总数的
丁捐款占捐款总数的1---=
780÷=780×=3600(元)
答:他们四人共捐款3600元。
丁的捐款数÷丁的捐款数对应四人共捐款的分率=四人共捐款的钱数,据此解答。
8.解:
甲:=750(米)
乙:=600(米)
丙:=500(米)
答:现在三队合修,甲队修750米,乙队修600米,丙队修500米。
先算出每队的工作效率,然后根据工作效率求出三队的工作效率之比;根据工作效率比,分别求出甲、乙、丙三队需要修的路长。
9.甲车间:60人;乙车间:200人
10.解:设蜡烛最初的长度是xcm。
2(x-12)=8
2x-24=8
2x=32
x=16
答:蜡烛最初的长度是16cm。
8分钟燃烧的长度=蜡烛原来的长度-点燃8分钟后的长度;
10分钟燃烧的长度=点燃8分钟后的长度-点燃18分钟后的长度;
8分钟燃烧的长度:8分钟=10分钟燃烧的长度:10分钟;据此比例关系列比例,根据比例的基本性质解比例。
11.解:10+10+10
=20+10
=30(米)
(10+30)×10÷2
=40×10÷2
=400÷2
=200(平方米)
答:这块茶园的面积是200平方米。
由题意可知,等腰直角三角形的两条直角边相等,所以梯形的下底为10+10+10=30米;梯形的面积公式:S=(a+b)×h÷2,代入数值计算即可。
12.(1)解:设小明第一天采了x克茶。
3x+15=450
x=145
答:小明第一天采了145克茶。
(2)解:设爸爸第二天采了y克。
(1+)y=550
y=550
y÷=550÷
y=500
答:爸爸第二天采了500克。
⑴根据题意可知,小明采茶的质量×3+15=爸爸采茶的质量,设小明第一天采了x克的茶,据此列方程解答。
(2)根据题意可知,爸爸第二天采茶的质量× (1+)=小明第二天采茶的质量,设爸爸第二天采了y克的茶,据此列方程解答。
13.(1)解:半圆的面积是多少平方厘米
3.14×(10÷2)2÷2
=3.14×25÷2
=78.5÷2
=39.25(平方厘米)
答:半圆的面积是39.25平方厘米。
(2)解:长方形的面积比半圆的面积大多少平方厘米
10×(10÷2)-3.14×(10÷2)2÷2
=10×5-3.14×25÷2
=50-78.5÷2
=50-39.25
=10.75(平方厘米)
答:长方形的面积比半圆的面积大10.75平方厘米。
提的问题要联系题目所给出的信息,不要自己创造条件。
(1)可以提出:半圆的面积是多少平方厘米?
然后根据半圆面积=πr2÷2,进行求解;
(2)可以提出:长方形的面积比半圆的面积大多少平方厘米
可以根据长方形面积-半圆面积=长×宽-πr2÷2,进行求解。
14.解:2dm=20cm
20÷2=10(cm)
3.14×102×3×3÷(3.14×62)
=314×9÷3.14÷36
=900÷36
=25(cm)
答:这个圆锥形玩具的高是25cm。
这个圆锥形玩具的高=这个圆锥形玩具的体积×3÷底面积;其中,这个圆锥形玩具的体积=上升水的体积=圆柱的底面积×上升水的高度。
15.解:(1-30%)÷2
=70%÷2
=35%
60×35%=21(人)
答:六⑴班有21人进入决赛。
把进入决赛的人数看作单位“1”,先求出六⑴班进人决赛的人数占总人数的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。
16.(1)解:1000×(1- 80%)+180
=1000×20%+180
=200+180
=380(元)
380÷1000=38%
答:顾客得到的优惠率是38%。
(2)解:设标价是x元,则优惠总金额为x元,消费金额为0.8x元。
当消费金额不小于1000元时,优惠率为1-80%×75%=40%,40%> ,所以消费金额一定小于1000元。
①当800≤0.8x<1000时:
x(1- 80%)+180=x
0.2x+180=x
x=180
x=1350
不符合800≤0.8x<1000的设定。
②当600≤0.8x<800时:
x(1- 80%)+120=x
0.2x+120=x
x=120
x=900
符合600≤0.8x<800的设定。
③当400≤0.8x<600时:
x(1- 80%)+60=x
0.2x+60=x
x=60
x=450
不符合400≤0.8x<600的设定。
答:当购买标价为900元的商品时,可以得到的优惠率。
(1)把标价为1000元代入题中规定的计算方法计算即可;
(2)本体可以设标价是x元,则优惠总金额为x元,消费金额为0.8x元;
若消费金额不小于1000元,则在现有优惠的条件下再打七五折,所以先算出消费金额,然后根据表中消费金额的范围,列出相对应的方程,最后找到符合规定的结果即可。
17.解:(155+40)÷3
=195÷3
=65(厘米)
答:所用书桌的高度应是65厘米。
根据题意可得数量关系:学生的身高=书桌高度×3-40,已知学生身高,所以书桌高度=(学生身高+40)÷3,依据此数量关系即可解答。
18.兰花:45元;绿萝:25元
19.解:设今年买8千克茶的钱,去年可以买x千克。
80x=80×(1+25%)×8
80x=800
80x÷80=800÷80
x=10
答:去年可以买10千克。
根据“去年每千克售价80元,今年由于成本提高,单价提高了25%"可知,今年的茶叶每千克[80×(1+25%)]元,根据总价不变,即茶叶的质量和茶叶的单价的乘积一定,两者成反比例关系。
20.(1)37.68立方厘米
(2)176平方厘米
21.(1)3元
(2)25%
22.(1)2
(2)10毫升
(3)30立方厘米
23.4分米
24.(1)解:圆的直径:2×2=4(米)
30×4=120(平方米)
答:这个大棚的种植面积是120平方米。
(2)解:3.14×2×2+3.14×2×2×30÷2
=12.56+188.4
=200.96(平方米)
≈201(平方米)
答:制作这个大棚用塑料薄膜约201平方米。
(1)大棚的长×圆的直径=这个大棚的种植面积;
(2)圆的面积+圆柱的侧面积÷2=制作这个大棚用塑料薄膜的面积。
25.解:450×40÷45
=18000÷45
=400(千克)
450-400=50(千克)
答:实际每天比计划少用50千克。
计划每天用的质量×用的天数=大米的质量,大米的质量÷实际用的天数=实际每天用的质量,实际每天用的质量-计划每天用的质量=实际每天比计划少用的质量。
26.解:下半年生产的台数看做单位1,上半年生产的台数是80%,
108÷(1+80%)
=108÷1.8
=60(万台)
108-60=48(万台)
答:下半年的产量是60万台,上半年的产量是48万台。
去年生产电视机的台数÷对应的百分率=下半年生产的台数,去年生产电视机的台数-下半年生产的台数=上半年生产的台数。
27.解:(5+4)÷2=4.5(份)
5-4.5=0.5(份)
10÷0.5=20(km/份)
20×(5+4)=180(km)
答:两地相距180km。
客车和货车的速度比是5:4,路程比也是5:4,把路程看做9份,中点处是4.5份;
货车行驶了4份,少行驶0.5份,0.5份是10千米,1份就是20千米;
A、B两地的距离一共是9份,1份的长度×9份=A、B两地的距离。
28.解:9.42÷3.14÷2=1.5(cm)
1.5×500=750(cm)=7.5(m)
3.14×7.5×7.5=176.625(m2)
答:花坛面积为176.625m2。
圆的周长÷π÷2=圆的半径,圆的半径×500=花坛的半径,π×花坛半径的平方=花坛的面积。
29.解:底面半径:6÷2=3(厘米)
3.14×3×3×10=28.26×10=282.6(毫升)
282.6×6=1695.6(毫升)
1695.6毫升>1500毫升
答:够。
π×底面半径的平方×高=圆柱的体积;圆柱的体积×6=小刚一天喝水的体积,小刚一天喝水的体积>1500毫升,说明够。
30.解:9×6+6×3×2+9×3×2
=54+36+54
=144(m2)
144-13.5=130.5(m2)
130.5×10.5=1370.25(元)
答:一共要付1370.25元。
教室的长×宽+长×高×2+宽×高×2-门窗和黑板的面积=需要粉刷的面积,需要粉刷的面积×每平方米付材料和工资费用 =粉刷这个教室共需要的钱数。
31.解:长方形的周长:πd+d=41.4cm
即:(π+1)×d=41.4
d=41.4÷(3.14+1)
d=41.4÷4.14
d =10
圆的半径:r=10÷2=5(厘米)
S=πr2=3.14×52=3.14×25=78.5(cm2)
答: 这个圆的面积是78.5平方厘米。
把一个圆沿半径剪成若干等份,然后拼成一个近似的长方形,长方形的周长=圆的的周长+2个半径,据此求出圆的直径,再求出圆的半径,最后用π×半径的平方求出圆的面积
32.解:1050÷(15+6)
=1050÷21
=50(平方厘米)
50×15=750(mL)
答: 瓶中有750毫升酒。
瓶子中酒高+瓶底空出的高度=酒瓶看做圆柱时的高度,瓶子的容积÷酒瓶看做圆柱时的高度=酒瓶的底面积,酒瓶的底面积×酒瓶中酒的高度=酒瓶中酒的容积。
33.解: 设这根旗杆高x米。
1.5: 1.2=x: 6.4
1.2x=6.4×1.5
1.2x=9.6
x=9.6÷1.2
x=8
答: 这根旗杆高8米。
竹竿的长度:影长=旗杆的长度:影长,据此比例关系列比例,根据比例的基本性质解比例。
34.解:复印机印:
0.5×25×2=25(元)
一体机印:
(0.15×30+5)×2
=9.5×2
=19(元)
25元>19元
答:用一体机复印比较划算。
复印机印:一页的钱数×复印的份数=复印一页一共需要的钱数,复印一页一共需要的钱数×2=复印两页一共需要的钱数;
一体机印:每页印一份的钱数×30页+5元的制版费=复印一页需要的钱数,复印一页需要的钱数×2=复印两页一共需要的钱数;
哪个计算的钱数少,用哪个复印划算。
35.解:4200÷[4200÷40+4200÷(35-5)]
=4200÷(105+140)
=4200÷245
≈17.1(分)
答:经过17.1分就能相遇。
王叔叔骑行的路程÷骑行的时间=王叔叔骑行的速度,李叔叔骑行的路程÷骑行的时间=李叔叔骑行的速度,总路程÷两人的速度和=相遇时间。
36.解:(24-18)+18÷3
=6+6
=12(厘米)
答:水面的高是12厘米。
水的高度-圆锥的高=圆柱内水的高度,圆锥内水的高度÷3=放入圆柱后水的高度,两个高度的和就是容器倒立放置水面的高度。
37.解:设现在可以生产x套。
160×(1-20%)x=160×20
160×80%x=3200
128x=3200
x=3200÷128
x=25
答:现在可以生产25套。
原来生产一套服装的成本×(1-20%)=现在生产一套服装的成本;现在生产一套服装的成本×生产的套数=原来生产一套服装的成本×生产的套数,据此反比例关系列比例,根据比例的基本性质解比例。
38.解:(95.2+10.8)÷0.53
=106÷0.53
=200(千瓦时)
谷:(200×0.56-95.2)÷(0.56-0.28)
=16.8÷0.28
=60(千瓦时)
峰:200-60=140(千瓦时)
答:该家庭当月使用峰电140千瓦时,谷电60千瓦时。
使用峰谷电的某月电费+比不使用峰谷电节约的钱数=不使用峰谷电的电费,不使用峰谷电的电费÷不使用峰谷电的电价=用电的度数,用电的度数×峰电价格-95.2元=全用峰电的钱数和使用峰谷电的钱数差,全用峰电的钱数和使用峰谷电的钱数差÷峰电谷电价格差=使用谷电的度数,用电的度数-使用谷电的度数=使用峰电的度数。
39.解:(46-40)÷2×1
=6÷2×1
=3(分钟)
在路上的时间:60-40-6=14(分钟)
拿好笔回学校的时间:14-6-3=5(分钟)
第一次遇见小塘的地方到学校的时间:5-3=2(分钟)
小塘从第一次遇见小塘到学校的时间:60-46=14(分钟)
14÷2=7(分钟)
5×7=35(分钟)
60-35=25(分钟)
答:小塘是7:25分从家里出发的。
原来小钱的速度:现在小钱的速度=1:2,原来用的时间:现在用的时间=2:1;在路上的时间:60-40-6=14,拿好笔回学校的时间:14-6-3=5,一次遇见小塘的地方到学校的时间:5-3=2,小塘从第一次遇见小塘到学校的时间:60-46=14,小塘从家里出发的时间60-35=25分,即7:25。
40.解:甲:乙:丙=::1=4:5:10
甲:(元)
乙:(元)
丙:(元)
答:甲付160元,乙付200元,丙付400元。
先求出甲乙丙的路程比,共付运费×甲走的路程占总路程的分率=甲应付运费,共付运费×乙走的路程占总路程的分率=乙应付运费,共付运费×丙走的路程占总路程的分率=丙应付运费。
41.解:两个长方形的面积和:8×10×2=160(cm2)
两个扇形面积和:102×π÷2=50π=157(cm2)
侧面积:2π×10×8÷4=40π=125.6(cm2)
160+157+125.6=442.6(dm2)
底面积:10×10×π÷4=25π=78.5(cm2)
体积:78.5×8=628(cm3)
答:需要涂442.6平方厘米的奶油,体积是628立方厘米。
两个长方形的面积和+两个扇形面积和+圆柱的侧面积=需要涂奶油的面积,蛋糕的底面积×高=蛋糕的体积。
42.解:方法一:
(2892+204)÷12
=3096÷12
=258(人)
答:第一届冬奥会参加的人数是258人。
方法二:
设第一届冬奥会的参加的人数是x人。
12x-204=2892
12x=2892+204
12x=3096
x=3096÷12
x=258
答:第一届冬奥会参加的人数是258人。
方法一:(2022年参加北京冬奥会的总人数+204人)÷12=第一届冬奥会参加的人数;
方法二:等量关系:第一届冬奥会参加的人数×12倍-204人=2022年参加北京冬奥会的总人数,根据等量关系列方程,根据等式性质解方程。
43.(1)解:5.2千米按6千米收费
13+(6-3)×2.5+1
=13+7.5+1
=21.5(元)
答:应付车费21.5元。
(2)解:15.7千米按16千米收费
16-10=6(千米)
13+(10-3)×2.5+6×3.75+1
=13+17.5+22.5+1
=54(元)
54-50=4(元)
答:不够,还差4元。
(1)3千米以内的收费+超过部分的收费+燃油附加费=应付车费;
(2)分三段收费,3千米以内的收费+10千米以内超过部分的收费+10千米以上部分的收费+燃油附加费=应付车费。
44.解:设实际每天铺x米。
25x=100×35
25x=3500
x=3500÷25
x=140
答:实际每天铺140米。
原计划每天铺的长度×铺完需要的天数=实际每天铺的长度×铺完需要的天数,据此反比例关系列比例,根据比例的基本性质解比例。
45.解:已看页数看做3,未看页数看做5,全书的页数是8,
已看页数是全书的:3÷8=0.375=37.5%
34页对应的百分率:80%-37.5%=42.5%
课外书总页数:34÷42.5%=80(页)
答:课外书共80页。
34页÷34页对应全书页数的百分率=全书的页数。
46.解:
=1-0.32+0.064-3.14×
=0.744-0.07536
≈0.67(dm3)
答:这个正方体剩余部分的体积是0.67立方分米。
中间去掉了2个底面边长为dm的长方体,两个长方体重叠的部分是棱长dm的正方体。上下面挖去的圆柱与长方体也有重叠的部分,没有重叠的部分实际就是高是(1-)dm的圆柱。用大正方体的体积减去挖去的2个长方体的体积,加上重叠部分正方体的体积,再减去高是(1-)dm的圆柱的体积就是剩余部分的体积。
47.解:圆锥的体积:20×12×1÷(3+1)
=240×1÷4
=60(立方厘米)
圆柱的体积:60×3=180(立方厘米)
答:圆柱的体积四180立方厘米,圆锥的体积是60立方厘米。
上升部分水的体积等于圆柱与圆锥的体积和,根据等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3 +1)倍,根据已知一个数的几倍是多少,求这个数,用除法求出圆锥的体积,进而求出圆柱的体积。
48.解:设当小丁到达终点时,小强离终点还有x米。
x=2500
答:设当小丁到达终点时,小强离终点还有2500米。
小军、小丁、小强三人的速度是恒定的,所以它们跑的距离之比等于它们跑的时间之比,所以,可以建立比例关系:小军跑完全程与小丁还剩1000米的距离之比,等于小丁跑完全程与小强还剩x米的距离之比,最后解出未知数即可。
49.(1)解:3.14×(8÷2)2×10
=3.14×16×10
=502.4(立方厘米)
答:一个圆柱形茶叶罐的体积是502.4立方厘米。
(2)解:8×3=24(厘米),8×2=16(厘米)
(24×16+24×10+16×10)×2
=(384+240+160)×2
=784×2
=1568(平方厘米)
答:做一个长方体礼盒至少需要1568平方厘米的包装材料。
(3)解:可以每排放3罐,放两层。
长:8×3=24(厘米)
高:10×2=20(厘米)
宽:8厘米
(24×8+24×20+8×20)×2
=(192+480+160)×2
=832×2
=1664(平方厘米)
答:需1664平方厘米包装材料。
圆柱体的底面积=3.14×r2,圆柱的体积公式:V=Sh;长方体的表面积=(长×宽+长×高+宽×高)×2
(1)圆柱体的半径是(8÷2),高是10,根据圆柱体的底面积和体积公式即得出茶叶罐的体积。
(2)长方体礼盒的长是圆柱形茶叶罐3个直径的长度,宽是两个直径的长度,高等于茶叶罐的高度,根据长方体的表面积公式即可求出;
(3)可以每排放3罐,放两层。长方体礼盒的长是圆柱形茶叶罐3个直径的长度,宽是1个直径的长度,高是2个茶叶罐的高度,根据长方体的表面积公式即可求出。
50.解:30÷2=15(平方厘米)
15×2÷5=6(厘米)
×3.14×(5÷2)2×6
=×3.14×6.25×6
=39.25(立方厘米)
答:这个圆锥的体积是39.25立方厘米。
通过现察图形可知,把这个圆锥过顶点沿底面直径纵切成两半,表面积将增加2个等腰三角形的面积,三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高。可以先根据表面积增加30平方厘米求出圆锥的高,再根据圆锥的体积公式求出圆锥的体积。
同课章节目录
