2024-2025学年六年级数学下册期末备考真题分类汇编(浙江专版)选择题(二)【答案+解析】
文档属性
| 名称 | 2024-2025学年六年级数学下册期末备考真题分类汇编(浙江专版)选择题(二)【答案+解析】 |

|
|
| 格式 | docx | ||
| 文件大小 | 622.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 07:48:12 | ||
图片预览


文档简介
2024-2025学年六年级数学下册期末备考真题分类汇编(浙江专版)
选择题(二)
一、单选题
1.(2024六下·温岭期末)如图,一个长方体的底面周长是56厘米,高是8厘米,它的棱长总和是( )厘米。
A.64 B.88 C.256 D.144
2.(2024六下·温岭期末)甲数的与乙数的相等,乙数的20%与丙数的25%相等。下列结果正确的是( )。(甲、乙、丙均不为0)
A.甲>乙>丙 B.乙>甲>丙 C.甲>丙>乙 D.丙>甲>乙
3.(2024六下·温岭期末)在数学学习中,我们学习了很多的数或数量,下面表达正确的是( ).
A. B.
C. D.
4.(2024六下·温岭期末)植树节种树,陈明已经种了x棵,比未种棵数的4倍少7棵,未种的有( )棵。
A.4x-7 B.4x+7 C.(x+7)÷4 D.4(x+7)
5.(2024六下·永康期末)一个立体图形,从上面看到是,从左面看到:。要搭成这样的立体图形,至少用( )个小正方体。
A.5 B.6 C.7 D.8
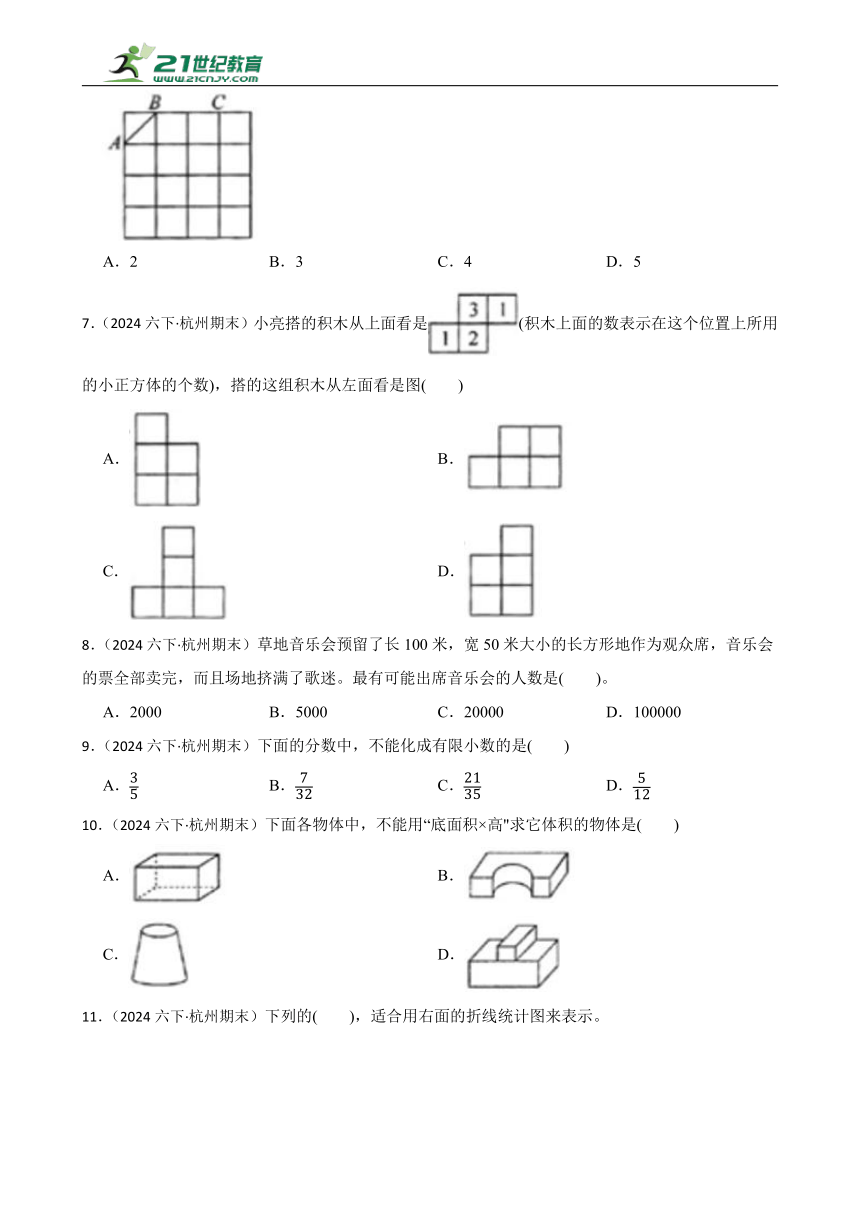
6.(2024六下·杭州期末)★如图,在正方形的点子图上,找一点 D,使 ABCD 是一个梯形。D点共有( )种不同的选法。
A.2 B.3 C.4 D.5
7.(2024六下·杭州期末)小亮搭的积木从上面看是(积木上面的数表示在这个位置上所用的小正方体的个数),搭的这组积木从左面看是图( )
A. B.
C. D.
8.(2024六下·杭州期末)草地音乐会预留了长100米,宽50米大小的长方形地作为观众席,音乐会的票全部卖完,而且场地挤满了歌迷。最有可能出席音乐会的人数是( )。
A.2000 B.5000 C.20000 D.100000
9.(2024六下·杭州期末)下面的分数中,不能化成有限小数的是( )
A. B. C. D.
10.(2024六下·杭州期末)下面各物体中,不能用“底面积×高"求它体积的物体是( )
A. B.
C. D.
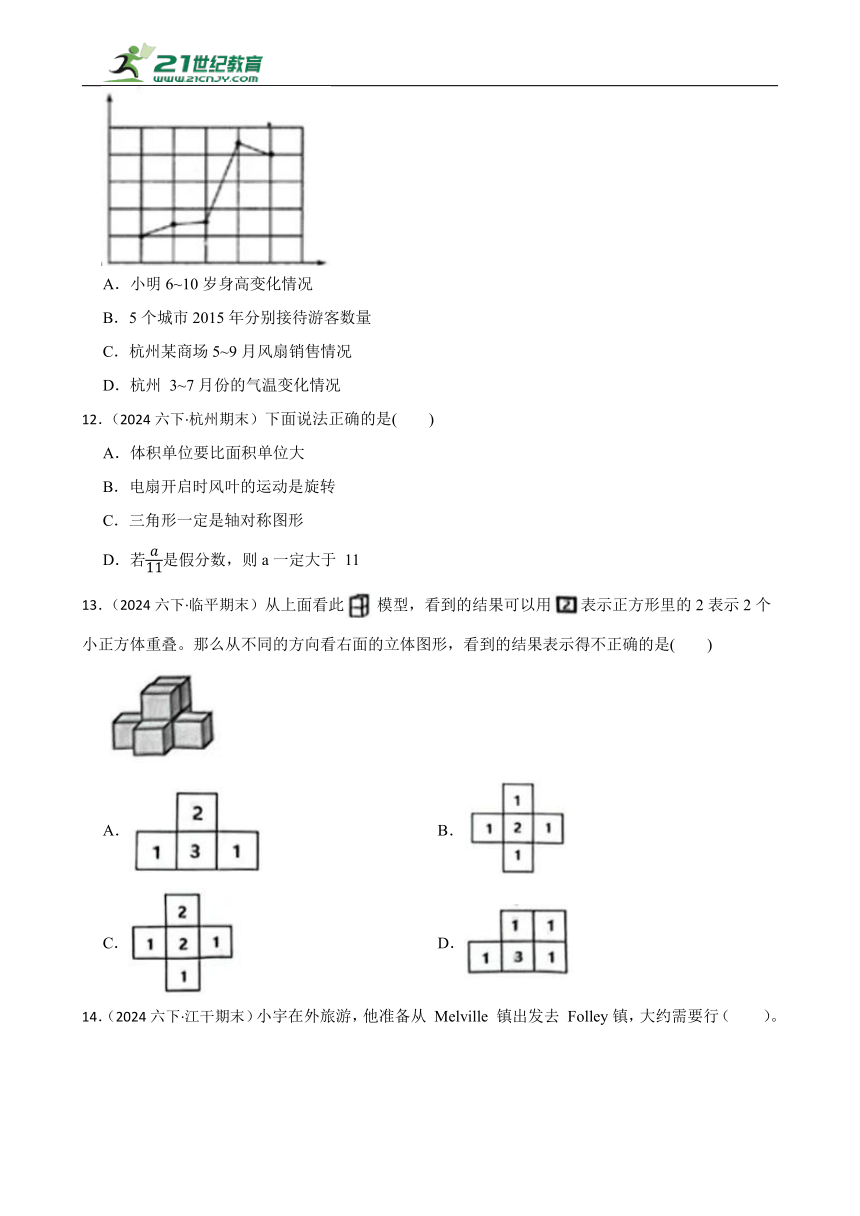
11.(2024六下·杭州期末)下列的( ),适合用右面的折线统计图来表示。
A.小明6~10岁身高变化情况
B.5个城市2015年分别接待游客数量
C.杭州某商场5~9月风扇销售情况
D.杭州 3~7月份的气温变化情况
12.(2024六下·杭州期末)下面说法正确的是( )
A.体积单位要比面积单位大
B.电扇开启时风叶的运动是旋转
C.三角形一定是轴对称图形
D.若是假分数,则a一定大于 11
13.(2024六下·临平期末)从上面看此模型,看到的结果可以用表示正方形里的2表示2个小正方体重叠。那么从不同的方向看右面的立体图形,看到的结果表示得不正确的是( )
A. B.
C. D.
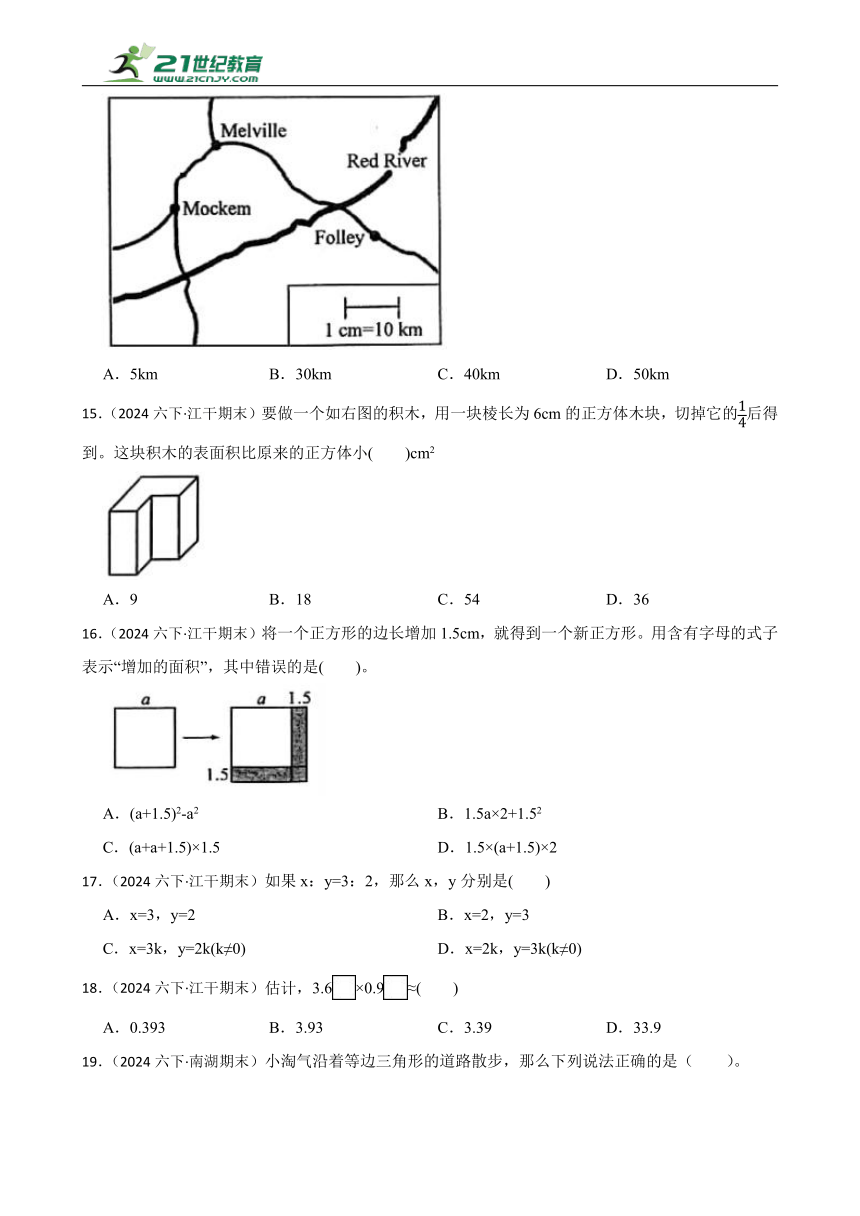
14.(2024六下·江干期末)小宇在外旅游,他准备从 Melville 镇出发去 Folley镇,大约需要行( )。
A.5km B.30km C.40km D.50km
15.(2024六下·江干期末)要做一个如右图的积木,用一块棱长为6cm的正方体木块,切掉它的后得到。这块积木的表面积比原来的正方体小( )cm2
A.9 B.18 C.54 D.36
16.(2024六下·江干期末)将一个正方形的边长增加1.5cm,就得到一个新正方形。用含有字母的式子表示“增加的面积”,其中错误的是( )。
A.(a+1.5)2-a2 B.1.5a×2+1.52
C.(a+a+1.5)×1.5 D.1.5×(a+1.5)×2
17.(2024六下·江干期末)如果x:y=3:2,那么x,y分别是( )
A.x=3,y=2 B.x=2,y=3
C.x=3k,y=2k(k≠0) D.x=2k,y=3k(k≠0)
18.(2024六下·江干期末)估计,3.6×0.9≈( )
A.0.393 B.3.93 C.3.39 D.33.9
19.(2024六下·南湖期末)小淘气沿着等边三角形的道路散步,那么下列说法正确的是( )。
A.从点A向东偏北30°方向可以走到点C
B.从点A向西可以走到点B
C.从点B向北偏西60°方向可以走到点C
D.从点C向南偏西30°方向可以走到点A
20.(2024六下·南湖期末)如图,平行四边形ABCD的面积是10cm2,圆的面积是多少?( )
A.10cm2 B.15.7cm2 C.20cm2 D.31.4cm2
21.(2024六下·南湖期末)甲杯中有200毫升水,乙杯中有400毫升水。把12克糖放入甲、乙两个杯中,使两杯糖水的含糖率相同。那么应该在甲杯中放入多少克糖?( )
A.6克 B.4克 C.3克 D.2克
22.(2024六下·南湖期末)下面哪一组中的两种量成反比例关系?( )
A.小汽车行驶的速度和时间。
B.订阅《小学生数学报》,订阅的数量和总价。
C.步测一段距离,每步的平均长度和走的步数。
D.正方形的周长和边长。
23.(2024六下·桐乡市期末)盒子里有黑白两色的棋子若干枚,黑色棋子和白色棋子数量的比是4∶5,那么,以下四句话中表述正确的是( )。
①黑色棋子是白色棋子的②黑色棋子比白色棋子少
③白色棋子比黑色棋子多20% ④白色棋子数是整盒棋子数的
A.① B.①② C.①②③ D.①②④
24.(2024六下·桐乡市期末)如下图,李叔叔将两块完全相同的长方体钢坯分别加工成2个和8个的圆柱形的钢模。比一比两种加工方法削去的钢材体积,( )。
A.①大 B.②大 C.一样大 D.不能比较
25.(2024六下·桐乡市期末)数学上把相差2的两个质数叫“孪生质数”。下列符合孪生质数的是( )。
A.4和6 B.7和9 C.15和17 D.17和19
26.(2024六下·桐乡市期末)下列式子中,“5”和“2”可以直接相加减的是( )。
A. B.345+2.06 C. D.8.75-4.2
27.(2024六下·瑞安期末)如图,在数学课上同学们准备把一根长12厘米的吸管剪成三段,首尾相接围成三角形。如果第一次在2厘米处剪了一刀,第二次在( )处剪才能围成三角形。
A.① B.② C.③ D.④
28.(2024六下·瑞安期末)下列各图的阴影部分表达不正确的是( )。
A. B.
C. D.
29.(2024六下·瑞安期末)关于算式0.8□×1.6□的积,下列选项可能正确的是( )。
A.① B.② C.③ D.④
30.(2024六下·瑞安期末)下面四杯糖水中,最甜的一杯是( )。
A.糖和水的质量比是1∶9 B.20g糖配成200g糖水
C.200g水中加入20g糖 D.含糖率为11%
31.(2024六下·瑞安期末)温州市的陆地面积约12103平方千米,如图,瑞安市的陆地面积大约是( )平方千米。
A.6000 B.3000 C.1300 D.600
32.(2024六下·瑞安期末)下面四杯糖水中,最甜的一杯是( )。
A.糖和水的质量比是1:9 B.20g糖配成 200g糖水
C.200g水中加入20g糖 D.含糖率为 11%
33.(2024六下·温岭期末)如图所示为一个正方体的展开图,若相对两个面上标的数字刚好互为倒数,则axb的值为( )
A.1 B. C. D.
34.(2024六下·义乌期末)如下图,将一张长方形的纸绕指定的这条宽旋转一周,形成的阴影部分不规则的立体图形,这个立体图形的体积是多少( )
A.12cm2 B.12cm3 C.48 πcm3 D.144 πcm3
35.(2024六下·慈溪期末)观察下图,按规律画下去,当某幅图中○的个数有 25 个时,□的个数为( )
A.144 B.121 C.100 D.81
36.(2024六下·慈溪期末)在右面的几何图形中再添1个,从左面观察不可能看到( )。
A. B.
C. D.
37.(2024六下·慈溪期末)50÷8=6……2,如果把被除数、除数同时扩大到原来的 100倍,那么它的结果是( )
A.商6余2 B.商600余8 C.商6余200 D.商600余200
38.(2024六下·钱塘期末)下列叙述其中正确的说法有( )个.
①甲数比乙数多20%,那么乙数比甲数少20%;
②a2一定大于a;
③2与任何质数相乘得到的都是合数;
④负数都比0小。
A.1 B.2 C.3 D.4
39.(2024六下·钱塘期末)如下图,梯形ABCD的两条对角线相交于点O。三角形AOB的面积是4cm2,三角形AOD的面积是10cm2,那么三角形AOB与三角形COD的面积比是( )。
A.2:5 B.4:15 C.4:25 D.无法确定
40.(2024六下·钱塘期末)如果x:y=3:2,那么x,y分别是( )。
A. B.x=2,y=3
C.x=3k,y=2k(k≠0) D.x=2k,y=3k(k≠0)
41.(2024六下·钱塘期末)小明走的路程比小军少,小军走的时间比小明少,小明与小军的速度比是( )。
A.3:5 B.2:3 C.5:4 D.3:3
42.(2024六下·钱塘期末)下列说法错误的是( ).
A.三角形各边长度确定以后,它的周长和面积就确定了。
B.假分数的倒数一定是真分数。
C.在直线上,-2和4之间的距离是6格。
D.6个人坐4把椅子,总有一把椅子上至少坐2人。
43.(2024六下·钱塘期末)估计8.5□×0.9□≈( )
A.0.839 B.8.39
C.83.9 D.8.93
44.(2024六下·钱塘期末)用若干个同样的小正方体摆成一个立体图形,从正面和左面看到的分别是和,要搭成这样的立体图形最多用( )个小正方体。
A.4 B.5 C.7 D.8
45.(2024六下·钱塘期末)甲数÷乙数=5……3,如果甲数、乙数同时扩大到原来的100倍,那么余数是( )。
A.3 B.30 C.0.03 D.300
46.(2024六下·钱塘期末)估计,6.5□×0.9□≈( )。
A.0.639 B.6.39 C.63.9 D.6.93
47.(2024六下·钱塘期末)如下图, 在正方形铁皮上剪下一个圆和一个扇形, 恰好围成一个圆锥,如果圆的直径为 a 厘米, 扇形的半径为b厘米, 那么a: b=( )。
A.1: 2 B.1: 3 C.1: 4 D.1: 5
48.(2024六下·钱塘期末)如下图直角三角形, 两直角边 AB: BC=a:b,将其绕AB和BC 为轴旋转分别得到圆锥甲和乙, 则甲、乙两个圆锥的体积比是( )。
A.b:1 B.a:b C.b:a D.a:1
49.(2024六下·钱塘期末)小斌一周练习4 天慢跑,一天中最远跑3.3 千米, 最近跑2.4 千米, 那么4
天中小斌一共跑了( )千米。
A.4~8千米 B.10~13千米 C.13~16千米 D.多于16千米
50.(2024六下·钱塘期末)如果3、5、9、x, 能够组成一个比例, 则x不可能是( )。
A. B.5.4 C.15 D.
答案解析部分
1.D
解:(56÷2+8)×4
=36×4
=144(厘米)。
故答案为:D。
它的棱长总和=(长+宽+高)×4;其中,长+宽=长方体的底面周长÷2。
2.B
解:甲×=乙×,乙×20%=丙×25%
甲:乙=:=5:6
乙:丙=25%:20%=5:4
甲:乙:丙=25:30:24,则乙>甲>丙。
故答案为:B。
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质写出甲、乙、丙的比,然后比较大小。
3.A
解:A项:4÷5=0.8,原题干说法正确;
B项:3÷4×1=(吨),原题干说法错误;
C项:1÷100×1=0.01(平方厘米),原题干说法错误;
D项:7÷4=,原题干说法错误。
故答案为:A。
A项:4份的长度=4份÷平均分的份数;
B项:涂色部分的质量=总质量÷总份数×涂色部分占的份数;
C项:涂色部分的面积=总面积÷总份数×涂色部分占的份数;
D项:涂色部分占的分率=涂色部分占的份数÷把单位“1”平均分的份数。
4.C
解:(x+7)÷4(棵)。
故答案为:C。
未种树的棵数=(已经种树的棵数+少的棵数)÷4。
5.A
解:4+1=5(个)。
故答案为:A。
至少需要小正方体的个数=下面一层的4个+上面1层的1个。
6.D
解:如图有梯形ABCF、梯形ABCD、梯形ABCG、梯形ABCH、梯形ABCF。共5种。
故答案为:D。
只有一组对边平行的四边形是梯形,据此画一画。
7.A
解:搭的这组积木从左面看,看到两排3层,并且第三层在左边一个的上面,是 。
故答案为:A。
从左面看,看到三层,下面、中间一层各有2个正方形,上面一层一个正方形,并且左侧对齐。
8.C
解:100×50=5000(平方米)
4×5000=20000(人)。
故答案为:C。
草地音乐会预留长方形观众席的面积=长×宽,每平方米大约可以容纳4人,最有可能出席音乐会的人数=4×草地音乐会预留长方形观众席的面积。
9.D
解:A项:能化成有限小数;
B项:32=2×2×2×2×2,能化成有限小数;
C项:=,能化成有限小数;
D项:12=2×2×3,不能化成有限小数。
故答案为:D。
一个最简分数,如果分母中除了有质因数2和5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中除了有质因数2和5以外,还有其它的质因数,这个分数就不能化成有限小数。
10.C
解:A、长方体是柱体,可以利用公式求体积;
B、是柱体,可以利用公式求体积;
C、是柱体,但不能用底面积×高计算体积;
D、长方体是柱体,可以利用公式求体积。
故答案为:C。
本题考查柱体的体积的公式,解题的关键是了解柱体的体积通项公式的运用条件。
11.D
解:A项:小明6~10岁身高变化情况不会降低,所以错误;
B项:适合用条形统计图;
C项:适合用条形统计图;
D项:气温变化情况高低不定,所以适合用右面的折线统计图来表示。
故答案为:D。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况;扇形统计图能反应各个部分占总体的百分之几。
12.B
解:A项:体积单位与面积单位不是同一类的的单位,不能比较大小,原题干说法错误;
B项:电扇开启时风叶的运动是旋转,原题干说法正确;
C项:三角形不一定是轴对称图形,原题干说法错误;
D项:若是假分数,则a大于或者等于11 ,原题干说法错误。
故答案为:B。
A项:体积单位与面积单位不是同一类的的单位,不能比较大小;
B项:比如像在平面上推东西、开关抽屉······这些物体都是沿着直线移动,这样的现象叫做平移;像转动方向盘、电扇的转动、旋转木马······这些物体都是绕着一个点或一个轴移动,这样的现象我们把它叫做旋转;
C项:等边三角形、等腰三角形是轴对称图形,其它三角形不是轴对称图形,所以三角形不一定是轴对称图形;
D项:分子比分母小的分数是真分数;分子大于或等于分母的分数是假分数。
13.B
解:A项:从正面看,原题干说法正确;
B项:从上面看是,原题干说法错误;
C项:从上面看,原题干说法正确;
D项:从右面看,原题干说法正确。
故答案为:B。
从上面看,看到“+”字型,并且中间和上面是两个正方体,剩余都是一个正方体。
14.C
解:测量得,从Melville镇到Folley镇大约是4厘米,
图上1厘米表示实际距离10千米,图上4厘米表示实际距离40千米。
故答案为:C。
实际距离=图上距离÷比例尺。
15.B
解:6×6÷2=36÷2=18(平方厘米)
这块积木的表面积比原来的正方体小18cm2
故答案为:B。
通过平移可以看出,这块积木的表面积比原来的正方体的表面积一共小正方体一个面的面积的一半,据此解答。
16.D
解:A:表示大正方形的面积-小正方形的面积=增加的面积,正确;
B:表示两个长方形阴影的面积+右下角小正方形的面积=增加的面积,正确;
C:表示两个长方形阴影的面积+右下角小正方形的面积=增加的面积,正确;
D:1.5×(a+1.5)×2比增加的面积多了1个1.5×1.5的面积,错误。
故答案为:D。
长方形的面积=长×宽,正方形的面积=边长×边长,据此解答。
17.C
解:如果x:y=3:2,那么x=3k,y=2k(k≠0) 。
故答案为:C。
化简比的方法:单位不统一的,先统一单位,再根据比的基本性质,比的前项和后项同时乘以或除以同一个不为0的数,把比化为最简单的整数比。据此解答。
18.C
解:因为0.9<1,所以3.6×0.9得积比3.6小一点点,是3.39。
故答案为:C。
一个非0数乘小于1的数,积小于这个数;据此解答。
19.D
20.B
21.B
22.C
23.D
24.C
25.D
26.B
27.C
28.B
29.C
30.D
31.C
32.D
解:A项:1÷(1+9)=10%;
B项:20÷200=10%;
C项:20÷(20+200)≈9.1%;
D项:11%;
11%>10%>9.1%,则最甜的是含糖率为11%。
故答案为:D。
含糖率=糖的质量÷糖水的质量,然后比较大小。
33.B
解:这个正方体展开图的4和c相对,5和b相对,3和a相对;
5×b=1,则b=1÷5=
3×a=1,则a=1÷3=
ab=×= 。
故答案为:B。
正方体相对的面不相邻,据此找出4和c相对,5和b相对,3和a相对;又因为乘积是1的两数互为倒数,分别求出b=1÷5=,a=1÷3=,然后再把a与b相乘。
34.C
解:π×62×1÷3+π×62×3÷3
=π×(12+36)
=π×48
=48π(立方厘米)。
故答案为:C。
这个立体图形的体积=上面圆锥的体积+下面圆锥的体积;其中,圆锥的体积=π×半径2×高÷3。
35.A
解:(25-1)÷2
=24÷2
=12(个)
12×12=144(个)。
故答案为:A。
第n个图形中,□的个数=[(○的个数-1)÷2]2。
36.D
解:因为从左面看,左边是两层,右边是一层,所以再添1个,从左面观察不可能看到 。
故答案为:D。
当放在这个立体图形的右边是A项,当放在这个立体图形第二层的上面是B项,当放在这个立体图形的左边是C项,不可能得到D项。
37.C
解:2×100=200,结果是商6······200。
故答案为:C。
在有余数的整数除法里,被除数和除数同时扩大或缩小相同的倍数(0除外),商不变,但是余数也扩大或缩小相同的倍数(0除外)。
38.B
解:①两次的比较量不同,结果不会一样,原题说法错误;
②当a=1时,a2等于a,原题说法错误;
③2与任何质数相乘得到的都是合数,原题说法正确;
④负数都比0小,原题说法正确。
故答案为:B。
①一个比较量是甲数,一个比较量是乙数,比较量不同,结果不会一样;
②当a等于1或0时,a2和a都相等;
③2与任何质数相乘得到的积,都至少有1、它本身、2这三个因数,所以一定是合数;
④负数都小于0,正数都大于0。
39.A
解:由于O点是对角线的交点,所以△AOB与△BOC的面积相等,△AOD与△COD的面积相等(因为它们有相同的底和高)。
因为S△AOB=4平方厘米,S△AOD=10平方厘米,所以S△BOC=4平方厘米,S△COD=10平方厘米。
所以,S△AOB:S△COD=4:10=2:5。
故答案为:A。
在解决这类问题时,理解梯形和三角形的性质是关键。特别是需要知道对角线如何将梯形分为四个三角形,以及这些三角形如何具有相同的底和高,因此具有相同的面积。通过这些性质,可以有效地计算和比较不同三角形的面积,从而解决题目。
40.C
解::=2:3,A错误;
x=2,y=3 时,x:y=2:3,B错误;
x=3k,y=2k时,x:y=3:2,C正确;
x=2k,y=3k是,x:y=2:3,D错误。
故答案为:C。
先代入,再化简比,根据化简后的结果判断。
41.A
解:[(1-)÷1]:[1÷(1-)]
=[:1]:[1÷]
=:
=3:5。
故答案为:A。
把小军走的路程看作单位“1”,则小明走的路程是1-=,把小明用的时间看作单位“1”,小军用的时间是1-=,速度=路程÷时间,然后写出比 ,并且依据比的基本性质化简比。
42.B
解:假分数的倒数可能是真分数或假分数,所以B项错误。
故答案为:B。
A项中,三角形的各边长度确定后,周长就确定了,面积也就确定了;
B项中,假分数的倒数可能是真分数或假分数;
C项中,4-(-2)=6(格),所以它们之间的距离是6格;
D项中,6-4=2(人),所以总有一把椅子上至少坐2人。
43.B
解:8.5□×0.9□≈8.39。
故答案为:B。
一个小数乘0.9□是比这个小数小一点的数,所以选8.39合适。
44.C
解:如图:
要搭成这样的立体图形最多用7个小正方体。
故答案为:C。
根据从不同方向看到的图形,倒推出来搭成这样的立体图形最多需要的小正方体数量。
45.D
解:甲数、乙数同时扩大到原来的100倍,余数也扩大100倍,是300。
故答案为:D。
商不变规律中余数变化规律:除数、被除数扩大或缩小几倍,余数就随着扩大或缩小几倍。
46.B
解:因为0.9□<1,
所以6.5□×0.9□的结果比6.5要小一点,是6.39。
故答案为:B。
一个非0数乘小于1的数,积小于这个数;据此解答。
47.A
解:扇形的半径为b厘米,扇形的底面周长是π×b×2÷4=π×b÷2(厘米),
圆的周长:π×(a÷2)×2=πa(厘米)
因为扇形的底面周长=圆的周长,
所以π×b÷2=πa,
b÷2=a
b÷a=2
b:a=2:1
a:b=1:2
故答案为:A。
根据图可以看出,扇形的底面周长=圆的周长,据此先分别求出扇形的底面周长和圆的周长,在求出a: b的比。
48.C
解:直角边AB的长度看做a, BC的长度看做b
AB为轴旋转得到圆锥甲,甲的底面半径是b,高是a,体积是π×b×b×a÷3
BC为轴旋转得到圆锥乙,乙的底面半径是a,高是b,体积是π×a×a×b÷3
甲、乙两个圆锥的体积比是:(π×b×b×a÷3):(π×a×a×b÷3)=b:a
故答案为:C。
π×底面半径的平方×高÷3=圆锥的体积;化简比的方法:根据比的基本性质,比的前项和后项同时乘以或除以同一个不为0的数,把比化为最简单的整数比。
49.B
解:最远跑:3.3×4=13.2(千米)
最近跑:2.4×4=9.6(千米)
4天中小斌一共跑的路程在9.6~13.2千米之间,包括9.6千米和13.2千米
符合条件的是10~13千米 。
故答案为:B。
一天中最远跑的路程×4=4天最远跑的路程,一天中最近跑的路程×4=4天最近跑的路程,
实际4天跑的路程在这两个数之间,也包括这两个数。
50.D
解:A:3×5=9×,x可能是;
B:3×9=5×5.4,x可能是5.4;
C:9:3=15:5,x可能是15;
D:即组不成积相等,也组不成比值相等,所以x不可能是。
故答案为:D。
组成比例的主要条件是两个比的比值相等或外项积等于内项积。
选择题(二)
一、单选题
1.(2024六下·温岭期末)如图,一个长方体的底面周长是56厘米,高是8厘米,它的棱长总和是( )厘米。
A.64 B.88 C.256 D.144
2.(2024六下·温岭期末)甲数的与乙数的相等,乙数的20%与丙数的25%相等。下列结果正确的是( )。(甲、乙、丙均不为0)
A.甲>乙>丙 B.乙>甲>丙 C.甲>丙>乙 D.丙>甲>乙
3.(2024六下·温岭期末)在数学学习中,我们学习了很多的数或数量,下面表达正确的是( ).
A. B.
C. D.
4.(2024六下·温岭期末)植树节种树,陈明已经种了x棵,比未种棵数的4倍少7棵,未种的有( )棵。
A.4x-7 B.4x+7 C.(x+7)÷4 D.4(x+7)
5.(2024六下·永康期末)一个立体图形,从上面看到是,从左面看到:。要搭成这样的立体图形,至少用( )个小正方体。
A.5 B.6 C.7 D.8
6.(2024六下·杭州期末)★如图,在正方形的点子图上,找一点 D,使 ABCD 是一个梯形。D点共有( )种不同的选法。
A.2 B.3 C.4 D.5
7.(2024六下·杭州期末)小亮搭的积木从上面看是(积木上面的数表示在这个位置上所用的小正方体的个数),搭的这组积木从左面看是图( )
A. B.
C. D.
8.(2024六下·杭州期末)草地音乐会预留了长100米,宽50米大小的长方形地作为观众席,音乐会的票全部卖完,而且场地挤满了歌迷。最有可能出席音乐会的人数是( )。
A.2000 B.5000 C.20000 D.100000
9.(2024六下·杭州期末)下面的分数中,不能化成有限小数的是( )
A. B. C. D.
10.(2024六下·杭州期末)下面各物体中,不能用“底面积×高"求它体积的物体是( )
A. B.
C. D.
11.(2024六下·杭州期末)下列的( ),适合用右面的折线统计图来表示。
A.小明6~10岁身高变化情况
B.5个城市2015年分别接待游客数量
C.杭州某商场5~9月风扇销售情况
D.杭州 3~7月份的气温变化情况
12.(2024六下·杭州期末)下面说法正确的是( )
A.体积单位要比面积单位大
B.电扇开启时风叶的运动是旋转
C.三角形一定是轴对称图形
D.若是假分数,则a一定大于 11
13.(2024六下·临平期末)从上面看此模型,看到的结果可以用表示正方形里的2表示2个小正方体重叠。那么从不同的方向看右面的立体图形,看到的结果表示得不正确的是( )
A. B.
C. D.
14.(2024六下·江干期末)小宇在外旅游,他准备从 Melville 镇出发去 Folley镇,大约需要行( )。
A.5km B.30km C.40km D.50km
15.(2024六下·江干期末)要做一个如右图的积木,用一块棱长为6cm的正方体木块,切掉它的后得到。这块积木的表面积比原来的正方体小( )cm2
A.9 B.18 C.54 D.36
16.(2024六下·江干期末)将一个正方形的边长增加1.5cm,就得到一个新正方形。用含有字母的式子表示“增加的面积”,其中错误的是( )。
A.(a+1.5)2-a2 B.1.5a×2+1.52
C.(a+a+1.5)×1.5 D.1.5×(a+1.5)×2
17.(2024六下·江干期末)如果x:y=3:2,那么x,y分别是( )
A.x=3,y=2 B.x=2,y=3
C.x=3k,y=2k(k≠0) D.x=2k,y=3k(k≠0)
18.(2024六下·江干期末)估计,3.6×0.9≈( )
A.0.393 B.3.93 C.3.39 D.33.9
19.(2024六下·南湖期末)小淘气沿着等边三角形的道路散步,那么下列说法正确的是( )。
A.从点A向东偏北30°方向可以走到点C
B.从点A向西可以走到点B
C.从点B向北偏西60°方向可以走到点C
D.从点C向南偏西30°方向可以走到点A
20.(2024六下·南湖期末)如图,平行四边形ABCD的面积是10cm2,圆的面积是多少?( )
A.10cm2 B.15.7cm2 C.20cm2 D.31.4cm2
21.(2024六下·南湖期末)甲杯中有200毫升水,乙杯中有400毫升水。把12克糖放入甲、乙两个杯中,使两杯糖水的含糖率相同。那么应该在甲杯中放入多少克糖?( )
A.6克 B.4克 C.3克 D.2克
22.(2024六下·南湖期末)下面哪一组中的两种量成反比例关系?( )
A.小汽车行驶的速度和时间。
B.订阅《小学生数学报》,订阅的数量和总价。
C.步测一段距离,每步的平均长度和走的步数。
D.正方形的周长和边长。
23.(2024六下·桐乡市期末)盒子里有黑白两色的棋子若干枚,黑色棋子和白色棋子数量的比是4∶5,那么,以下四句话中表述正确的是( )。
①黑色棋子是白色棋子的②黑色棋子比白色棋子少
③白色棋子比黑色棋子多20% ④白色棋子数是整盒棋子数的
A.① B.①② C.①②③ D.①②④
24.(2024六下·桐乡市期末)如下图,李叔叔将两块完全相同的长方体钢坯分别加工成2个和8个的圆柱形的钢模。比一比两种加工方法削去的钢材体积,( )。
A.①大 B.②大 C.一样大 D.不能比较
25.(2024六下·桐乡市期末)数学上把相差2的两个质数叫“孪生质数”。下列符合孪生质数的是( )。
A.4和6 B.7和9 C.15和17 D.17和19
26.(2024六下·桐乡市期末)下列式子中,“5”和“2”可以直接相加减的是( )。
A. B.345+2.06 C. D.8.75-4.2
27.(2024六下·瑞安期末)如图,在数学课上同学们准备把一根长12厘米的吸管剪成三段,首尾相接围成三角形。如果第一次在2厘米处剪了一刀,第二次在( )处剪才能围成三角形。
A.① B.② C.③ D.④
28.(2024六下·瑞安期末)下列各图的阴影部分表达不正确的是( )。
A. B.
C. D.
29.(2024六下·瑞安期末)关于算式0.8□×1.6□的积,下列选项可能正确的是( )。
A.① B.② C.③ D.④
30.(2024六下·瑞安期末)下面四杯糖水中,最甜的一杯是( )。
A.糖和水的质量比是1∶9 B.20g糖配成200g糖水
C.200g水中加入20g糖 D.含糖率为11%
31.(2024六下·瑞安期末)温州市的陆地面积约12103平方千米,如图,瑞安市的陆地面积大约是( )平方千米。
A.6000 B.3000 C.1300 D.600
32.(2024六下·瑞安期末)下面四杯糖水中,最甜的一杯是( )。
A.糖和水的质量比是1:9 B.20g糖配成 200g糖水
C.200g水中加入20g糖 D.含糖率为 11%
33.(2024六下·温岭期末)如图所示为一个正方体的展开图,若相对两个面上标的数字刚好互为倒数,则axb的值为( )
A.1 B. C. D.
34.(2024六下·义乌期末)如下图,将一张长方形的纸绕指定的这条宽旋转一周,形成的阴影部分不规则的立体图形,这个立体图形的体积是多少( )
A.12cm2 B.12cm3 C.48 πcm3 D.144 πcm3
35.(2024六下·慈溪期末)观察下图,按规律画下去,当某幅图中○的个数有 25 个时,□的个数为( )
A.144 B.121 C.100 D.81
36.(2024六下·慈溪期末)在右面的几何图形中再添1个,从左面观察不可能看到( )。
A. B.
C. D.
37.(2024六下·慈溪期末)50÷8=6……2,如果把被除数、除数同时扩大到原来的 100倍,那么它的结果是( )
A.商6余2 B.商600余8 C.商6余200 D.商600余200
38.(2024六下·钱塘期末)下列叙述其中正确的说法有( )个.
①甲数比乙数多20%,那么乙数比甲数少20%;
②a2一定大于a;
③2与任何质数相乘得到的都是合数;
④负数都比0小。
A.1 B.2 C.3 D.4
39.(2024六下·钱塘期末)如下图,梯形ABCD的两条对角线相交于点O。三角形AOB的面积是4cm2,三角形AOD的面积是10cm2,那么三角形AOB与三角形COD的面积比是( )。
A.2:5 B.4:15 C.4:25 D.无法确定
40.(2024六下·钱塘期末)如果x:y=3:2,那么x,y分别是( )。
A. B.x=2,y=3
C.x=3k,y=2k(k≠0) D.x=2k,y=3k(k≠0)
41.(2024六下·钱塘期末)小明走的路程比小军少,小军走的时间比小明少,小明与小军的速度比是( )。
A.3:5 B.2:3 C.5:4 D.3:3
42.(2024六下·钱塘期末)下列说法错误的是( ).
A.三角形各边长度确定以后,它的周长和面积就确定了。
B.假分数的倒数一定是真分数。
C.在直线上,-2和4之间的距离是6格。
D.6个人坐4把椅子,总有一把椅子上至少坐2人。
43.(2024六下·钱塘期末)估计8.5□×0.9□≈( )
A.0.839 B.8.39
C.83.9 D.8.93
44.(2024六下·钱塘期末)用若干个同样的小正方体摆成一个立体图形,从正面和左面看到的分别是和,要搭成这样的立体图形最多用( )个小正方体。
A.4 B.5 C.7 D.8
45.(2024六下·钱塘期末)甲数÷乙数=5……3,如果甲数、乙数同时扩大到原来的100倍,那么余数是( )。
A.3 B.30 C.0.03 D.300
46.(2024六下·钱塘期末)估计,6.5□×0.9□≈( )。
A.0.639 B.6.39 C.63.9 D.6.93
47.(2024六下·钱塘期末)如下图, 在正方形铁皮上剪下一个圆和一个扇形, 恰好围成一个圆锥,如果圆的直径为 a 厘米, 扇形的半径为b厘米, 那么a: b=( )。
A.1: 2 B.1: 3 C.1: 4 D.1: 5
48.(2024六下·钱塘期末)如下图直角三角形, 两直角边 AB: BC=a:b,将其绕AB和BC 为轴旋转分别得到圆锥甲和乙, 则甲、乙两个圆锥的体积比是( )。
A.b:1 B.a:b C.b:a D.a:1
49.(2024六下·钱塘期末)小斌一周练习4 天慢跑,一天中最远跑3.3 千米, 最近跑2.4 千米, 那么4
天中小斌一共跑了( )千米。
A.4~8千米 B.10~13千米 C.13~16千米 D.多于16千米
50.(2024六下·钱塘期末)如果3、5、9、x, 能够组成一个比例, 则x不可能是( )。
A. B.5.4 C.15 D.
答案解析部分
1.D
解:(56÷2+8)×4
=36×4
=144(厘米)。
故答案为:D。
它的棱长总和=(长+宽+高)×4;其中,长+宽=长方体的底面周长÷2。
2.B
解:甲×=乙×,乙×20%=丙×25%
甲:乙=:=5:6
乙:丙=25%:20%=5:4
甲:乙:丙=25:30:24,则乙>甲>丙。
故答案为:B。
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质写出甲、乙、丙的比,然后比较大小。
3.A
解:A项:4÷5=0.8,原题干说法正确;
B项:3÷4×1=(吨),原题干说法错误;
C项:1÷100×1=0.01(平方厘米),原题干说法错误;
D项:7÷4=,原题干说法错误。
故答案为:A。
A项:4份的长度=4份÷平均分的份数;
B项:涂色部分的质量=总质量÷总份数×涂色部分占的份数;
C项:涂色部分的面积=总面积÷总份数×涂色部分占的份数;
D项:涂色部分占的分率=涂色部分占的份数÷把单位“1”平均分的份数。
4.C
解:(x+7)÷4(棵)。
故答案为:C。
未种树的棵数=(已经种树的棵数+少的棵数)÷4。
5.A
解:4+1=5(个)。
故答案为:A。
至少需要小正方体的个数=下面一层的4个+上面1层的1个。
6.D
解:如图有梯形ABCF、梯形ABCD、梯形ABCG、梯形ABCH、梯形ABCF。共5种。
故答案为:D。
只有一组对边平行的四边形是梯形,据此画一画。
7.A
解:搭的这组积木从左面看,看到两排3层,并且第三层在左边一个的上面,是 。
故答案为:A。
从左面看,看到三层,下面、中间一层各有2个正方形,上面一层一个正方形,并且左侧对齐。
8.C
解:100×50=5000(平方米)
4×5000=20000(人)。
故答案为:C。
草地音乐会预留长方形观众席的面积=长×宽,每平方米大约可以容纳4人,最有可能出席音乐会的人数=4×草地音乐会预留长方形观众席的面积。
9.D
解:A项:能化成有限小数;
B项:32=2×2×2×2×2,能化成有限小数;
C项:=,能化成有限小数;
D项:12=2×2×3,不能化成有限小数。
故答案为:D。
一个最简分数,如果分母中除了有质因数2和5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中除了有质因数2和5以外,还有其它的质因数,这个分数就不能化成有限小数。
10.C
解:A、长方体是柱体,可以利用公式求体积;
B、是柱体,可以利用公式求体积;
C、是柱体,但不能用底面积×高计算体积;
D、长方体是柱体,可以利用公式求体积。
故答案为:C。
本题考查柱体的体积的公式,解题的关键是了解柱体的体积通项公式的运用条件。
11.D
解:A项:小明6~10岁身高变化情况不会降低,所以错误;
B项:适合用条形统计图;
C项:适合用条形统计图;
D项:气温变化情况高低不定,所以适合用右面的折线统计图来表示。
故答案为:D。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况;扇形统计图能反应各个部分占总体的百分之几。
12.B
解:A项:体积单位与面积单位不是同一类的的单位,不能比较大小,原题干说法错误;
B项:电扇开启时风叶的运动是旋转,原题干说法正确;
C项:三角形不一定是轴对称图形,原题干说法错误;
D项:若是假分数,则a大于或者等于11 ,原题干说法错误。
故答案为:B。
A项:体积单位与面积单位不是同一类的的单位,不能比较大小;
B项:比如像在平面上推东西、开关抽屉······这些物体都是沿着直线移动,这样的现象叫做平移;像转动方向盘、电扇的转动、旋转木马······这些物体都是绕着一个点或一个轴移动,这样的现象我们把它叫做旋转;
C项:等边三角形、等腰三角形是轴对称图形,其它三角形不是轴对称图形,所以三角形不一定是轴对称图形;
D项:分子比分母小的分数是真分数;分子大于或等于分母的分数是假分数。
13.B
解:A项:从正面看,原题干说法正确;
B项:从上面看是,原题干说法错误;
C项:从上面看,原题干说法正确;
D项:从右面看,原题干说法正确。
故答案为:B。
从上面看,看到“+”字型,并且中间和上面是两个正方体,剩余都是一个正方体。
14.C
解:测量得,从Melville镇到Folley镇大约是4厘米,
图上1厘米表示实际距离10千米,图上4厘米表示实际距离40千米。
故答案为:C。
实际距离=图上距离÷比例尺。
15.B
解:6×6÷2=36÷2=18(平方厘米)
这块积木的表面积比原来的正方体小18cm2
故答案为:B。
通过平移可以看出,这块积木的表面积比原来的正方体的表面积一共小正方体一个面的面积的一半,据此解答。
16.D
解:A:表示大正方形的面积-小正方形的面积=增加的面积,正确;
B:表示两个长方形阴影的面积+右下角小正方形的面积=增加的面积,正确;
C:表示两个长方形阴影的面积+右下角小正方形的面积=增加的面积,正确;
D:1.5×(a+1.5)×2比增加的面积多了1个1.5×1.5的面积,错误。
故答案为:D。
长方形的面积=长×宽,正方形的面积=边长×边长,据此解答。
17.C
解:如果x:y=3:2,那么x=3k,y=2k(k≠0) 。
故答案为:C。
化简比的方法:单位不统一的,先统一单位,再根据比的基本性质,比的前项和后项同时乘以或除以同一个不为0的数,把比化为最简单的整数比。据此解答。
18.C
解:因为0.9<1,所以3.6×0.9得积比3.6小一点点,是3.39。
故答案为:C。
一个非0数乘小于1的数,积小于这个数;据此解答。
19.D
20.B
21.B
22.C
23.D
24.C
25.D
26.B
27.C
28.B
29.C
30.D
31.C
32.D
解:A项:1÷(1+9)=10%;
B项:20÷200=10%;
C项:20÷(20+200)≈9.1%;
D项:11%;
11%>10%>9.1%,则最甜的是含糖率为11%。
故答案为:D。
含糖率=糖的质量÷糖水的质量,然后比较大小。
33.B
解:这个正方体展开图的4和c相对,5和b相对,3和a相对;
5×b=1,则b=1÷5=
3×a=1,则a=1÷3=
ab=×= 。
故答案为:B。
正方体相对的面不相邻,据此找出4和c相对,5和b相对,3和a相对;又因为乘积是1的两数互为倒数,分别求出b=1÷5=,a=1÷3=,然后再把a与b相乘。
34.C
解:π×62×1÷3+π×62×3÷3
=π×(12+36)
=π×48
=48π(立方厘米)。
故答案为:C。
这个立体图形的体积=上面圆锥的体积+下面圆锥的体积;其中,圆锥的体积=π×半径2×高÷3。
35.A
解:(25-1)÷2
=24÷2
=12(个)
12×12=144(个)。
故答案为:A。
第n个图形中,□的个数=[(○的个数-1)÷2]2。
36.D
解:因为从左面看,左边是两层,右边是一层,所以再添1个,从左面观察不可能看到 。
故答案为:D。
当放在这个立体图形的右边是A项,当放在这个立体图形第二层的上面是B项,当放在这个立体图形的左边是C项,不可能得到D项。
37.C
解:2×100=200,结果是商6······200。
故答案为:C。
在有余数的整数除法里,被除数和除数同时扩大或缩小相同的倍数(0除外),商不变,但是余数也扩大或缩小相同的倍数(0除外)。
38.B
解:①两次的比较量不同,结果不会一样,原题说法错误;
②当a=1时,a2等于a,原题说法错误;
③2与任何质数相乘得到的都是合数,原题说法正确;
④负数都比0小,原题说法正确。
故答案为:B。
①一个比较量是甲数,一个比较量是乙数,比较量不同,结果不会一样;
②当a等于1或0时,a2和a都相等;
③2与任何质数相乘得到的积,都至少有1、它本身、2这三个因数,所以一定是合数;
④负数都小于0,正数都大于0。
39.A
解:由于O点是对角线的交点,所以△AOB与△BOC的面积相等,△AOD与△COD的面积相等(因为它们有相同的底和高)。
因为S△AOB=4平方厘米,S△AOD=10平方厘米,所以S△BOC=4平方厘米,S△COD=10平方厘米。
所以,S△AOB:S△COD=4:10=2:5。
故答案为:A。
在解决这类问题时,理解梯形和三角形的性质是关键。特别是需要知道对角线如何将梯形分为四个三角形,以及这些三角形如何具有相同的底和高,因此具有相同的面积。通过这些性质,可以有效地计算和比较不同三角形的面积,从而解决题目。
40.C
解::=2:3,A错误;
x=2,y=3 时,x:y=2:3,B错误;
x=3k,y=2k时,x:y=3:2,C正确;
x=2k,y=3k是,x:y=2:3,D错误。
故答案为:C。
先代入,再化简比,根据化简后的结果判断。
41.A
解:[(1-)÷1]:[1÷(1-)]
=[:1]:[1÷]
=:
=3:5。
故答案为:A。
把小军走的路程看作单位“1”,则小明走的路程是1-=,把小明用的时间看作单位“1”,小军用的时间是1-=,速度=路程÷时间,然后写出比 ,并且依据比的基本性质化简比。
42.B
解:假分数的倒数可能是真分数或假分数,所以B项错误。
故答案为:B。
A项中,三角形的各边长度确定后,周长就确定了,面积也就确定了;
B项中,假分数的倒数可能是真分数或假分数;
C项中,4-(-2)=6(格),所以它们之间的距离是6格;
D项中,6-4=2(人),所以总有一把椅子上至少坐2人。
43.B
解:8.5□×0.9□≈8.39。
故答案为:B。
一个小数乘0.9□是比这个小数小一点的数,所以选8.39合适。
44.C
解:如图:
要搭成这样的立体图形最多用7个小正方体。
故答案为:C。
根据从不同方向看到的图形,倒推出来搭成这样的立体图形最多需要的小正方体数量。
45.D
解:甲数、乙数同时扩大到原来的100倍,余数也扩大100倍,是300。
故答案为:D。
商不变规律中余数变化规律:除数、被除数扩大或缩小几倍,余数就随着扩大或缩小几倍。
46.B
解:因为0.9□<1,
所以6.5□×0.9□的结果比6.5要小一点,是6.39。
故答案为:B。
一个非0数乘小于1的数,积小于这个数;据此解答。
47.A
解:扇形的半径为b厘米,扇形的底面周长是π×b×2÷4=π×b÷2(厘米),
圆的周长:π×(a÷2)×2=πa(厘米)
因为扇形的底面周长=圆的周长,
所以π×b÷2=πa,
b÷2=a
b÷a=2
b:a=2:1
a:b=1:2
故答案为:A。
根据图可以看出,扇形的底面周长=圆的周长,据此先分别求出扇形的底面周长和圆的周长,在求出a: b的比。
48.C
解:直角边AB的长度看做a, BC的长度看做b
AB为轴旋转得到圆锥甲,甲的底面半径是b,高是a,体积是π×b×b×a÷3
BC为轴旋转得到圆锥乙,乙的底面半径是a,高是b,体积是π×a×a×b÷3
甲、乙两个圆锥的体积比是:(π×b×b×a÷3):(π×a×a×b÷3)=b:a
故答案为:C。
π×底面半径的平方×高÷3=圆锥的体积;化简比的方法:根据比的基本性质,比的前项和后项同时乘以或除以同一个不为0的数,把比化为最简单的整数比。
49.B
解:最远跑:3.3×4=13.2(千米)
最近跑:2.4×4=9.6(千米)
4天中小斌一共跑的路程在9.6~13.2千米之间,包括9.6千米和13.2千米
符合条件的是10~13千米 。
故答案为:B。
一天中最远跑的路程×4=4天最远跑的路程,一天中最近跑的路程×4=4天最近跑的路程,
实际4天跑的路程在这两个数之间,也包括这两个数。
50.D
解:A:3×5=9×,x可能是;
B:3×9=5×5.4,x可能是5.4;
C:9:3=15:5,x可能是15;
D:即组不成积相等,也组不成比值相等,所以x不可能是。
故答案为:D。
组成比例的主要条件是两个比的比值相等或外项积等于内项积。
同课章节目录
