8.1 成对数据的统计相关性 同步练习(2课时,含答案) 2024~2025学年高二数学人教A版(2019)选择性必修3
文档属性
| 名称 | 8.1 成对数据的统计相关性 同步练习(2课时,含答案) 2024~2025学年高二数学人教A版(2019)选择性必修3 |  | |
| 格式 | docx | ||
| 文件大小 | 251.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 20:07:27 | ||
图片预览




文档简介
8.1 成对数据的统计相关性
8.1.1 变量的相关关系
一、 单项选择题
1 对于散点图,下列说法中正确的是( )
A. 一定可以看出变量之间的变化规律
B. 一定不可以看出变量之间的变化规律
C. 可以看出正相关与负相关有明显区别
D. 看不出正相关与负相关有什么区别
2 (2024钦州期末)变量x与y的成对样本数据的散点图如下图所示,据此可以推断变量x与y之间( )
A. 可能存在负相关
B. 可能存在正相关
C. 一定存在正相关
D. 一定存在负相关
3 (2024辽宁期中)下列变量之间的关系中,不是相关关系的是( )
A. 光照时间与大棚内蔬菜的产量
B. 举重运动员所能举起的最大重量与他的体重
C. 某正方形的边长与此正方形的面积
D. 人的身高与体重
4 下列变量具有线性相关关系的是( )
A. 人的身高与视力
B. 角的大小与所对的圆弧长
C. 家庭的支出与收入
D. 匀速行驶的车辆的行驶距离与时间
5 某商家去年上半年各月的人均销售额(单位:千元)与利润率的统计表如下:
月份 人均销售额 利润率(%)
1 6 12.6
2 5 10.4
3 8 18.5
4 3 3.0
5 4 8.1
6 7 16.3
根据表中数据,下列说法中正确的是( )
A. 利润率与人均销售额成正相关关系
B. 利润率与人均销售额成负相关关系
C. 利润率与人均销售额成正比例函数关系
D. 利润率与人均销售额成反比例函数关系
6 对变量x,y由观测数据得散点图1,对变量y,z由观测数据得散点图2,则下列结论中正确的是( )
图1 图2
A. 变量x与y负相关,变量x与z正相关
B. 变量x与y负相关,变量x与z负相关
C. 变量x与y正相关,变量x与z正相关
D. 变量x与y正相关,变量x与z负相关
二、 多项选择题
7 (2023北海期末)下列各组的两个变量中,是正相关关系的是( )
A. 学生的身高与学生的化学成绩
B. 汽车行驶的里程与它的耗油量
C. 人的年龄与年收入
D. 水果的重量与它的总价
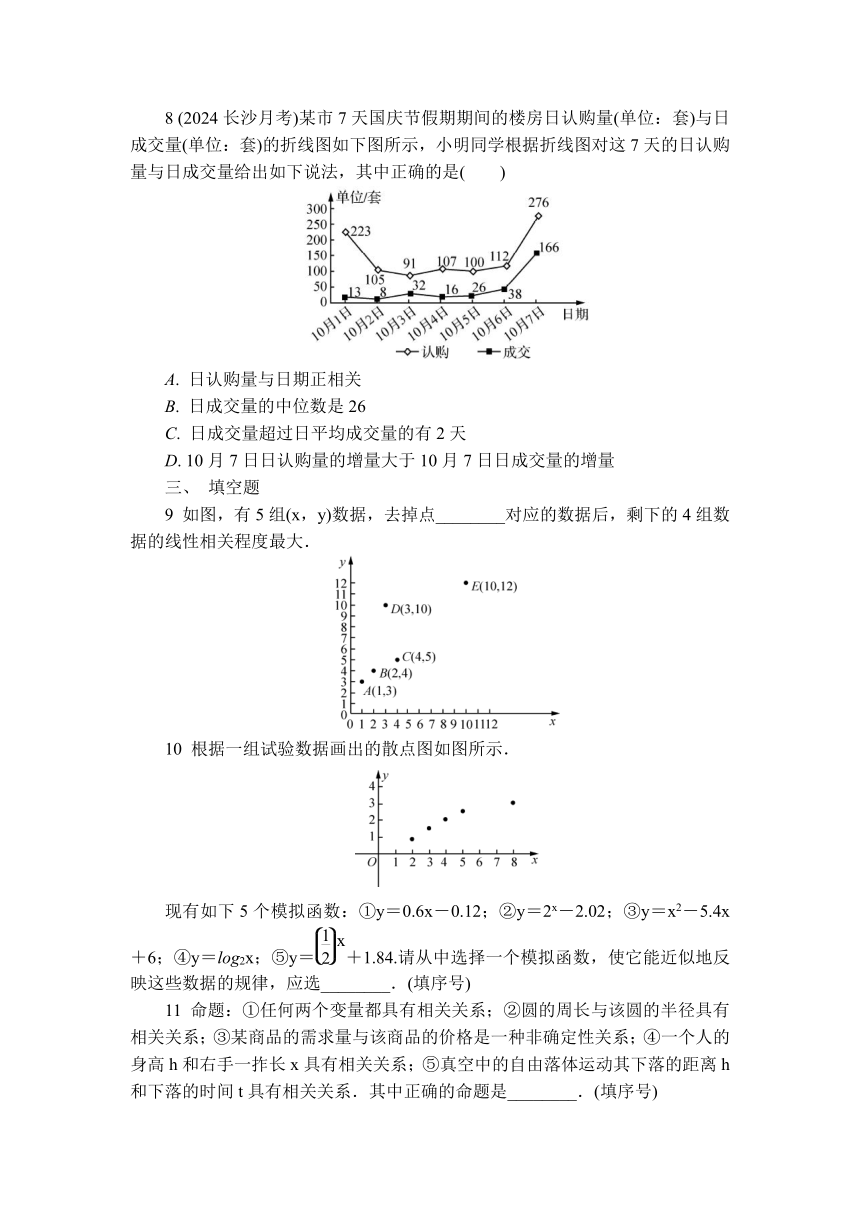
8 (2024长沙月考)某市7天国庆节假期期间的楼房日认购量(单位:套)与日成交量(单位:套)的折线图如下图所示,小明同学根据折线图对这7天的日认购量与日成交量给出如下说法,其中正确的是( )
A. 日认购量与日期正相关
B. 日成交量的中位数是26
C. 日成交量超过日平均成交量的有2天
D. 10月7日日认购量的增量大于10月7日日成交量的增量
三、 填空题
9 如图,有5组(x,y)数据,去掉点________对应的数据后,剩下的4组数据的线性相关程度最大.
10 根据一组试验数据画出的散点图如图所示.
现有如下5个模拟函数:①y=0.6x-0.12;②y=2x-2.02;③y=x2-5.4x+6;④y=log2x;⑤y=+1.84.请从中选择一个模拟函数,使它能近似地反映这些数据的规律,应选________.(填序号)
11 命题:①任何两个变量都具有相关关系;②圆的周长与该圆的半径具有相关关系;③某商品的需求量与该商品的价格是一种非确定性关系;④一个人的身高h和右手一拃长x具有相关关系;⑤真空中的自由落体运动其下落的距离h和下落的时间t具有相关关系.其中正确的命题是________.(填序号)
四、 解答题
12 某零售店近5个月的销售额和利润额资料如下表所示:
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
(1) 根据上表数据作出散点图;
(2) 观察散点判断利润额y与销售额x是否具有线性相关关系.如果具有线性相关关系,那么是正相关还是负相关?
13 两对变量A和B,C和D的取值分别对应如表1和表2,画出散点图,分别判断它们是否具有相关关系.若具有相关关系,说出它们相关关系的区别.
表1
A 26 18 13 10 4 -1
B 20 24 34 38 50 64
表2
C 0 5 10 15 20 25 30 35
D 541.67 602.66 672.09 704.99 806.71 908.59 975.42 1 034.75
8.1.2 样本相关系数
一、 单项选择题
1 (2024清远期末)通过计算样本相关系数r可以反映两个随机变量之间的线性相关程度,以下四个选项中分别计算出四个样本的相关系数r,则反映样本数据成正相关,并且线性相关程度最强的是( )
A. r=0.93 B. r=0.82
C. r=0.04 D. r=-0.05
2 在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=x+1上,则这组样本数据的样本相关系数为( )
A. -1 B. 0 C. D. 1
3 变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4)(11.8,3),(12.5,2),(13,1),r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则下列结论中正确的是( )
A. r2C. r2<04 (2024凉山州三模)调查某校高三学生的身高x和体重y得到如图所示的散点图,其中身高x和体重y的样本相关系数r=0.825 5,则下列说法中正确的是( )
A. 学生的身高和体重没有相关性
B. 学生的身高和体重正相关
C. 学生的身高和体重负相关
D. 若从样本中抽取一部分,则这部分的样本相关系数一定是0.825 5
5 (2024上海浦东新区期中)通过随机抽样,我们绘制了如图所示的某种商品每千克价格(单位:百元)与该商品消费者年需求量(单位:kg)的散点图.若去掉图中右下方的点A,则下列说法中正确的是( )
A. “每千克价格”与“年需求量”这两个变量由负相关变为正相关
B. “每千克价格”与“年需求量”这两个变量的样本相关程度不变
C. “每千克价格”与“年需求量”这两个变量的样本相关系数变大
D. “每千克价格”与“年需求量”这两个变量的样本相关系数变小
6 如图是相关变量x,y的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到样本,相关系数为r1;方案二:剔除点(10,21),根据剩下的数据,得到样本相关系数为r2,则下列结论中正确的是( )
A. 0C. -1二、 多项选择题
7 下列有关样本相关系数的说法中,正确的是( )
A. |r|≥1,且|r|越接近1,相关程度越大
B. |r|≤1,且|r|越接近0,相关程度越小
C. |r|≤1,且|r|越接近1,相关程度越大
D. 样本相关系数用来衡量变量x与y的线性相关程度
8 (2024山西部分学校月考)对四组样本数据进行统计,获得以下散点图,关于其样本相关系数的比较,其中正确的是( )
A. r3<0 B. r4<0 C. r1>r4 D. r2>r3
三、 填空题
9 (2024赣州期中)甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的样本相关系数分别为r1=0.66,r2=-0.97,r3=0.92,r4=0.89,则这四人中,________研究的两个随机变量的线性相关程度最高.
10 (2024随州月考)已知是的4倍,是的1.5倍,则样本相关系数r的值为________.
11 某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x 2 4 5 6 8
y 30 40 60 50 70
这两个变量的线性相关性是________.(填“强”或“弱”)
四、 解答题
12 某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区,依据抽样数据计算得到相应的样本相关系数r=0.81;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(xi,yi)(i=1,2,…,30),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得=60,=1 200,=90,=8 000,=800.
(1) 求该地区这种野生动物数量的估计值(该地区这种野生动物数量的估计值等于样本区这种野生动物数量的平均数乘以地块数);
(2) 求方案二抽取的样本(xi,yi)(i=1,2,…,30)的相关系数(精确到0.01),并判定哪种抽样方法更能准确地估计.
附:相关系数r=,≈1.414,相关系数|r|∈[0.75,1],则相关性很强,|r|的值越大,相关性越强.
13 互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分.某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下称外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 2日 3日 4日 5日
外卖甲日接单x(百单) 5 2 9 8 11
外卖乙日接单y(百单) 2 3 10 5 15
(1) 试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2) 据统计表明,y与x之间具有线性相关关系.请用相关系数r对y与x之间的相关性强弱进行判断(若|r|>0.75,则可认为y与x有较强的线性相关关系,r值精确到0.001).
参考数据:=66,≈77.
参考公式:r=.
8.1 成对数据的统计相关性
8.1.1 变量的相关关系
1. C 给出一组样本数据,总可以作出相应的散点图,但不一定能分析出两个变量的关系,但是通过散点图可以看出正相关与负相关有明显区别.
2. A 从散点图看,这些点在一条直线的附近,且从左上角到右下角呈递减的趋势,所以据此可以推断变量x与y之间可能存在负相关.
3. C C中的两个变量之间是确定的函数关系,A,B,D中的两个变量之间的关系都是相关关系.
4. C 人的身高与视力之间没有相关的关系,故A错误;角的大小α与所对的圆弧长l之间的关系为l=α·r,其中r为所对圆弧的半径,它们之间是确定的函数关系,故B错误;收入多时,支出也相应多,故家庭的支出与收入之间的关系是相关关系,故C正确;匀速行驶的车辆的行驶距离s与时间t之间的关系为s=vt,其中v为匀速速度,它们之间是确定的函数关系,故D错误.
5. A 如图,画出利润率与人均销售额的散点图.由图可知利润率与人均销售额成正相关关系.
6. B 由散点图可知,变量x与y负相关,变量y与z正相关,所以变量x与z负相关.
7. BD 学生的身高与学生的化学成绩没有必然联系,故A错误;汽车行驶的里程与它的耗油量正相关,故B正确;人的年龄与年收入没有必然联系,故C错误;水果的重量与它的总价正相关,故D正确.故选BD.
8. BD 由题图可以看出,样本点并不是从左下至右上分布,故A错误;将日成交量的数据按从小到大的顺序排列,中位数为26,故B正确;日平均成交量为≈42.7,超过42.7的只有一天,故C错误;10月7日日认购量的增量为276-112=164,日成交量的增量为166-38=128,故D正确.故选BD.
9. D 去掉点D对应的数据后,其余四点大致在一条直线附近,相关性最强.
10. ④ 由题图可知散点大体在函数y=log2x的图象上,故选择y=log2x可以近似地反映这些数据的规律.
11. ③④ 客观现象之间存在的相互依存关系叫相关关系,是一种不确定的关系,函数关系是一种确定的关系.对于①,任何两个变量不一定都具有相关关系,故①错误;对于②,圆的周长与该圆的半径是函数关系,而不是相关关系,故②错误;对于③,某商品的需求量与该商品的价格是一种非确定性关系,故③正确;对于④,一般情况下,一个人的身高h和右手一拃长x是正相关关系,故④正确;对于⑤,真空中的自由落体运动其下落的距离h和下落的时间t是函数关系,不是相关关系,故⑤不正确.故正确的命题为③④.
12. (1) 散点图如图所示:
(2) 由散点图可知,所有散点接近一条直线排列,所以利润额y与销售额x具有线性相关关系.
由图可知当销售额x增加时,利润额y呈现增加的趋势,所以是正相关.
13. 散点图分别如图1和图2.
从图中可以看出两图中的点各自分布在一条直线附近,因此两对变量都具有相关关系.
在图1中,当A的值由小变大时,B的值却是由大变小,故A和B成负相关;
在图2中,当C的值由小变大时,D的值也是由小变大,故C和D成正相关.
图1 图2
8.1.2 样本相关系数
1. A 因为样本相关系数的绝对值越大,线性相关程度越强,且r>0为正相关,又0.93>0.82>|-0.05|>0.04,所以r=0.93时,线性相关程度最强,且为正相关.
2. D 因为所有样本点均在直线y=x+1上,所以这组数据完全正相关,则样本相关系数为1.
3. C 根据题中提供的数据,变量Y随X的增大而增大,故Y与X正相关,即r1>0;变量V随U的增大而减小,故V与U负相关,即r2<0,故r2<04. B 由散点图可知,散点的分布集中在一条直线附近,所以学生的身高和体重具有相关性,故A错误;又身高x和体重y的样本相关系数r=0.825 5>0,所以学生的身高和体重正相关,故B正确,C错误;从样本中抽取一部分,相关性可能变强,也可能变弱,所以这部分的样本相关系数不一定是0.825 5,故D错误.
5. D 对于A,去掉图中右下方的点A后,根据图象,两个变量还是负相关,故A错误;对于B,C,D,去掉图中右下方的点A后,相对来说数据会集中,相关程度会更高,但因为是负相关,样本相关系数会更接近-1,即样本相关系数会变小,故D正确,B,C错误.
6. D 根据相关变量 x,y的散点图知,变量x,y负相关,且点(10,21)是离群值.方案一中,没剔除离群值,线性相关性弱些,成负相关;方案二中,剔除离群值,线性相关性强些,也是负相关,所以-17. BCD 由相关系数的定义可得|r|≤1,故A错误;|r|越接近0,相关程度越小,|r|越接近1,相关程度越大,故B,C正确;相关系数和x与y的线性相关程度有关,故D正确.故选BCD.
8. BD 由题图可知,r1,r4对应的样本数据都是负相关,所以r1,r4都是负数.又r1对应的样本数据比r4对应的样本数据的线性相关程度更强,所以r19. 乙 因为|r2|>|r3|>|r4|>|r1|,所以这四人中,乙研究的两个随机变量的线性相关程度最高.
10. r===.
11. 强 因为r=≈0.92,所以有把握认为该产品的广告费支出与销售额之间具有强的线性相关关系.
12. (1) 由题意,得样本区野生的动物平均数为=×1 200=40,
又地块数为300,所以该地区这种野生动物数量的估计值为300×40=12 000.
(2) 由题中数据可得,样本(xi,yi)(i=1,2,…,30)的相关系数为r===≈0.94.
因为0.81<0.94,
所以方案二的分层抽样方法更能准确地估计.
13. (1) 由表格中的数据,可得==7,==7,
外卖甲的日接单量的方差s=×[(5-7)2+(2-7)2+(9-7)2+(8-7)2+(11-7)2]=10,
外卖乙的日接单量的方差s=×[(2-7)2+(3-7)2+(10-7)2+(5-7)2+(15-7)2]=23.6.
因为=,s(2) 因为r=≈≈0.857>0.75,
所以可认为y与x之间有较强的线性相关关系.
8.1.1 变量的相关关系
一、 单项选择题
1 对于散点图,下列说法中正确的是( )
A. 一定可以看出变量之间的变化规律
B. 一定不可以看出变量之间的变化规律
C. 可以看出正相关与负相关有明显区别
D. 看不出正相关与负相关有什么区别
2 (2024钦州期末)变量x与y的成对样本数据的散点图如下图所示,据此可以推断变量x与y之间( )
A. 可能存在负相关
B. 可能存在正相关
C. 一定存在正相关
D. 一定存在负相关
3 (2024辽宁期中)下列变量之间的关系中,不是相关关系的是( )
A. 光照时间与大棚内蔬菜的产量
B. 举重运动员所能举起的最大重量与他的体重
C. 某正方形的边长与此正方形的面积
D. 人的身高与体重
4 下列变量具有线性相关关系的是( )
A. 人的身高与视力
B. 角的大小与所对的圆弧长
C. 家庭的支出与收入
D. 匀速行驶的车辆的行驶距离与时间
5 某商家去年上半年各月的人均销售额(单位:千元)与利润率的统计表如下:
月份 人均销售额 利润率(%)
1 6 12.6
2 5 10.4
3 8 18.5
4 3 3.0
5 4 8.1
6 7 16.3
根据表中数据,下列说法中正确的是( )
A. 利润率与人均销售额成正相关关系
B. 利润率与人均销售额成负相关关系
C. 利润率与人均销售额成正比例函数关系
D. 利润率与人均销售额成反比例函数关系
6 对变量x,y由观测数据得散点图1,对变量y,z由观测数据得散点图2,则下列结论中正确的是( )
图1 图2
A. 变量x与y负相关,变量x与z正相关
B. 变量x与y负相关,变量x与z负相关
C. 变量x与y正相关,变量x与z正相关
D. 变量x与y正相关,变量x与z负相关
二、 多项选择题
7 (2023北海期末)下列各组的两个变量中,是正相关关系的是( )
A. 学生的身高与学生的化学成绩
B. 汽车行驶的里程与它的耗油量
C. 人的年龄与年收入
D. 水果的重量与它的总价
8 (2024长沙月考)某市7天国庆节假期期间的楼房日认购量(单位:套)与日成交量(单位:套)的折线图如下图所示,小明同学根据折线图对这7天的日认购量与日成交量给出如下说法,其中正确的是( )
A. 日认购量与日期正相关
B. 日成交量的中位数是26
C. 日成交量超过日平均成交量的有2天
D. 10月7日日认购量的增量大于10月7日日成交量的增量
三、 填空题
9 如图,有5组(x,y)数据,去掉点________对应的数据后,剩下的4组数据的线性相关程度最大.
10 根据一组试验数据画出的散点图如图所示.
现有如下5个模拟函数:①y=0.6x-0.12;②y=2x-2.02;③y=x2-5.4x+6;④y=log2x;⑤y=+1.84.请从中选择一个模拟函数,使它能近似地反映这些数据的规律,应选________.(填序号)
11 命题:①任何两个变量都具有相关关系;②圆的周长与该圆的半径具有相关关系;③某商品的需求量与该商品的价格是一种非确定性关系;④一个人的身高h和右手一拃长x具有相关关系;⑤真空中的自由落体运动其下落的距离h和下落的时间t具有相关关系.其中正确的命题是________.(填序号)
四、 解答题
12 某零售店近5个月的销售额和利润额资料如下表所示:
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
(1) 根据上表数据作出散点图;
(2) 观察散点判断利润额y与销售额x是否具有线性相关关系.如果具有线性相关关系,那么是正相关还是负相关?
13 两对变量A和B,C和D的取值分别对应如表1和表2,画出散点图,分别判断它们是否具有相关关系.若具有相关关系,说出它们相关关系的区别.
表1
A 26 18 13 10 4 -1
B 20 24 34 38 50 64
表2
C 0 5 10 15 20 25 30 35
D 541.67 602.66 672.09 704.99 806.71 908.59 975.42 1 034.75
8.1.2 样本相关系数
一、 单项选择题
1 (2024清远期末)通过计算样本相关系数r可以反映两个随机变量之间的线性相关程度,以下四个选项中分别计算出四个样本的相关系数r,则反映样本数据成正相关,并且线性相关程度最强的是( )
A. r=0.93 B. r=0.82
C. r=0.04 D. r=-0.05
2 在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=x+1上,则这组样本数据的样本相关系数为( )
A. -1 B. 0 C. D. 1
3 变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4)(11.8,3),(12.5,2),(13,1),r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则下列结论中正确的是( )
A. r2
A. 学生的身高和体重没有相关性
B. 学生的身高和体重正相关
C. 学生的身高和体重负相关
D. 若从样本中抽取一部分,则这部分的样本相关系数一定是0.825 5
5 (2024上海浦东新区期中)通过随机抽样,我们绘制了如图所示的某种商品每千克价格(单位:百元)与该商品消费者年需求量(单位:kg)的散点图.若去掉图中右下方的点A,则下列说法中正确的是( )
A. “每千克价格”与“年需求量”这两个变量由负相关变为正相关
B. “每千克价格”与“年需求量”这两个变量的样本相关程度不变
C. “每千克价格”与“年需求量”这两个变量的样本相关系数变大
D. “每千克价格”与“年需求量”这两个变量的样本相关系数变小
6 如图是相关变量x,y的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到样本,相关系数为r1;方案二:剔除点(10,21),根据剩下的数据,得到样本相关系数为r2,则下列结论中正确的是( )
A. 0
7 下列有关样本相关系数的说法中,正确的是( )
A. |r|≥1,且|r|越接近1,相关程度越大
B. |r|≤1,且|r|越接近0,相关程度越小
C. |r|≤1,且|r|越接近1,相关程度越大
D. 样本相关系数用来衡量变量x与y的线性相关程度
8 (2024山西部分学校月考)对四组样本数据进行统计,获得以下散点图,关于其样本相关系数的比较,其中正确的是( )
A. r3<0 B. r4<0 C. r1>r4 D. r2>r3
三、 填空题
9 (2024赣州期中)甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的样本相关系数分别为r1=0.66,r2=-0.97,r3=0.92,r4=0.89,则这四人中,________研究的两个随机变量的线性相关程度最高.
10 (2024随州月考)已知是的4倍,是的1.5倍,则样本相关系数r的值为________.
11 某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x 2 4 5 6 8
y 30 40 60 50 70
这两个变量的线性相关性是________.(填“强”或“弱”)
四、 解答题
12 某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区,依据抽样数据计算得到相应的样本相关系数r=0.81;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(xi,yi)(i=1,2,…,30),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得=60,=1 200,=90,=8 000,=800.
(1) 求该地区这种野生动物数量的估计值(该地区这种野生动物数量的估计值等于样本区这种野生动物数量的平均数乘以地块数);
(2) 求方案二抽取的样本(xi,yi)(i=1,2,…,30)的相关系数(精确到0.01),并判定哪种抽样方法更能准确地估计.
附:相关系数r=,≈1.414,相关系数|r|∈[0.75,1],则相关性很强,|r|的值越大,相关性越强.
13 互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分.某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下称外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 2日 3日 4日 5日
外卖甲日接单x(百单) 5 2 9 8 11
外卖乙日接单y(百单) 2 3 10 5 15
(1) 试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2) 据统计表明,y与x之间具有线性相关关系.请用相关系数r对y与x之间的相关性强弱进行判断(若|r|>0.75,则可认为y与x有较强的线性相关关系,r值精确到0.001).
参考数据:=66,≈77.
参考公式:r=.
8.1 成对数据的统计相关性
8.1.1 变量的相关关系
1. C 给出一组样本数据,总可以作出相应的散点图,但不一定能分析出两个变量的关系,但是通过散点图可以看出正相关与负相关有明显区别.
2. A 从散点图看,这些点在一条直线的附近,且从左上角到右下角呈递减的趋势,所以据此可以推断变量x与y之间可能存在负相关.
3. C C中的两个变量之间是确定的函数关系,A,B,D中的两个变量之间的关系都是相关关系.
4. C 人的身高与视力之间没有相关的关系,故A错误;角的大小α与所对的圆弧长l之间的关系为l=α·r,其中r为所对圆弧的半径,它们之间是确定的函数关系,故B错误;收入多时,支出也相应多,故家庭的支出与收入之间的关系是相关关系,故C正确;匀速行驶的车辆的行驶距离s与时间t之间的关系为s=vt,其中v为匀速速度,它们之间是确定的函数关系,故D错误.
5. A 如图,画出利润率与人均销售额的散点图.由图可知利润率与人均销售额成正相关关系.
6. B 由散点图可知,变量x与y负相关,变量y与z正相关,所以变量x与z负相关.
7. BD 学生的身高与学生的化学成绩没有必然联系,故A错误;汽车行驶的里程与它的耗油量正相关,故B正确;人的年龄与年收入没有必然联系,故C错误;水果的重量与它的总价正相关,故D正确.故选BD.
8. BD 由题图可以看出,样本点并不是从左下至右上分布,故A错误;将日成交量的数据按从小到大的顺序排列,中位数为26,故B正确;日平均成交量为≈42.7,超过42.7的只有一天,故C错误;10月7日日认购量的增量为276-112=164,日成交量的增量为166-38=128,故D正确.故选BD.
9. D 去掉点D对应的数据后,其余四点大致在一条直线附近,相关性最强.
10. ④ 由题图可知散点大体在函数y=log2x的图象上,故选择y=log2x可以近似地反映这些数据的规律.
11. ③④ 客观现象之间存在的相互依存关系叫相关关系,是一种不确定的关系,函数关系是一种确定的关系.对于①,任何两个变量不一定都具有相关关系,故①错误;对于②,圆的周长与该圆的半径是函数关系,而不是相关关系,故②错误;对于③,某商品的需求量与该商品的价格是一种非确定性关系,故③正确;对于④,一般情况下,一个人的身高h和右手一拃长x是正相关关系,故④正确;对于⑤,真空中的自由落体运动其下落的距离h和下落的时间t是函数关系,不是相关关系,故⑤不正确.故正确的命题为③④.
12. (1) 散点图如图所示:
(2) 由散点图可知,所有散点接近一条直线排列,所以利润额y与销售额x具有线性相关关系.
由图可知当销售额x增加时,利润额y呈现增加的趋势,所以是正相关.
13. 散点图分别如图1和图2.
从图中可以看出两图中的点各自分布在一条直线附近,因此两对变量都具有相关关系.
在图1中,当A的值由小变大时,B的值却是由大变小,故A和B成负相关;
在图2中,当C的值由小变大时,D的值也是由小变大,故C和D成正相关.
图1 图2
8.1.2 样本相关系数
1. A 因为样本相关系数的绝对值越大,线性相关程度越强,且r>0为正相关,又0.93>0.82>|-0.05|>0.04,所以r=0.93时,线性相关程度最强,且为正相关.
2. D 因为所有样本点均在直线y=x+1上,所以这组数据完全正相关,则样本相关系数为1.
3. C 根据题中提供的数据,变量Y随X的增大而增大,故Y与X正相关,即r1>0;变量V随U的增大而减小,故V与U负相关,即r2<0,故r2<0
5. D 对于A,去掉图中右下方的点A后,根据图象,两个变量还是负相关,故A错误;对于B,C,D,去掉图中右下方的点A后,相对来说数据会集中,相关程度会更高,但因为是负相关,样本相关系数会更接近-1,即样本相关系数会变小,故D正确,B,C错误.
6. D 根据相关变量 x,y的散点图知,变量x,y负相关,且点(10,21)是离群值.方案一中,没剔除离群值,线性相关性弱些,成负相关;方案二中,剔除离群值,线性相关性强些,也是负相关,所以-1
8. BD 由题图可知,r1,r4对应的样本数据都是负相关,所以r1,r4都是负数.又r1对应的样本数据比r4对应的样本数据的线性相关程度更强,所以r1
10. r===.
11. 强 因为r=≈0.92,所以有把握认为该产品的广告费支出与销售额之间具有强的线性相关关系.
12. (1) 由题意,得样本区野生的动物平均数为=×1 200=40,
又地块数为300,所以该地区这种野生动物数量的估计值为300×40=12 000.
(2) 由题中数据可得,样本(xi,yi)(i=1,2,…,30)的相关系数为r===≈0.94.
因为0.81<0.94,
所以方案二的分层抽样方法更能准确地估计.
13. (1) 由表格中的数据,可得==7,==7,
外卖甲的日接单量的方差s=×[(5-7)2+(2-7)2+(9-7)2+(8-7)2+(11-7)2]=10,
外卖乙的日接单量的方差s=×[(2-7)2+(3-7)2+(10-7)2+(5-7)2+(15-7)2]=23.6.
因为=,s
所以可认为y与x之间有较强的线性相关关系.
