5.1 第2课时 平行投影与正投影 课件(共29张PPT)
文档属性
| 名称 | 5.1 第2课时 平行投影与正投影 课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
1.知道平行投影和正投影的含义.(重点)
2.了解不同时刻物体在太阳光下形成的影子的特点.
(重点)
3.会利用平行投影的性质进行相关计算.(难点)
学习目标
问题引入
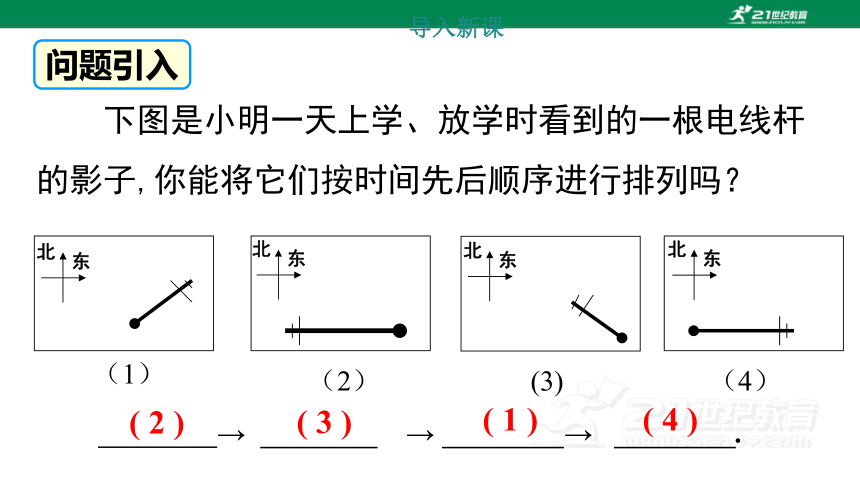
下图是小明一天上学、放学时看到的一根电线杆的影子,你能将它们按时间先后顺序进行排列吗?
东
北
(1)
(2)
(3)
(4)
东
北
东
北
东
北
→ → → .
( 2 )
( 3 )
( 1 )
( 4 )
导入新课
平行投影与正投影
一
观察下列图片,你认为太阳光线有什么特征?
太阳离我们很遥远,其光线可以看成平行光线.
观察与思考
讲授新课
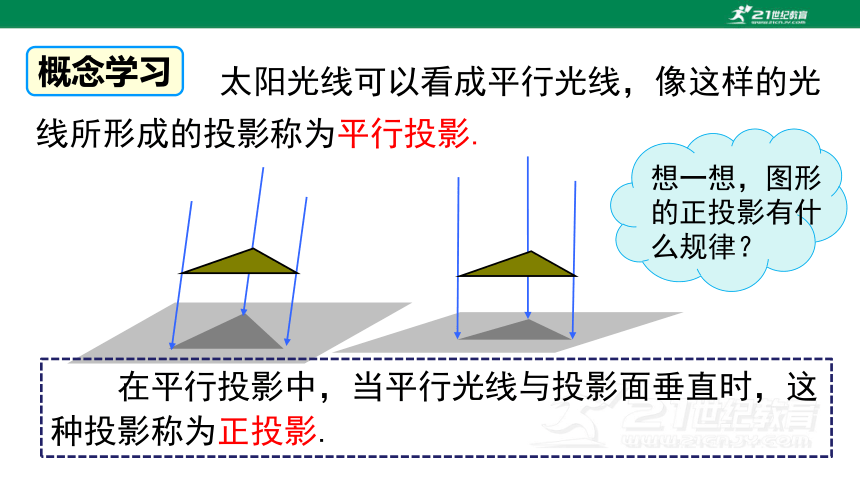
太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影.
概念学行投影中,当平行光线与投影面垂直时,这种投影称为正投影.
想一想,图形的正投影有什么规律?
例如,物体在太阳光的照射下形成的影子 (简称日影) 就是平行投影.
日影的方向可以反映时间,我国古代的计时器日晷,就是根据日影来观测时间的.
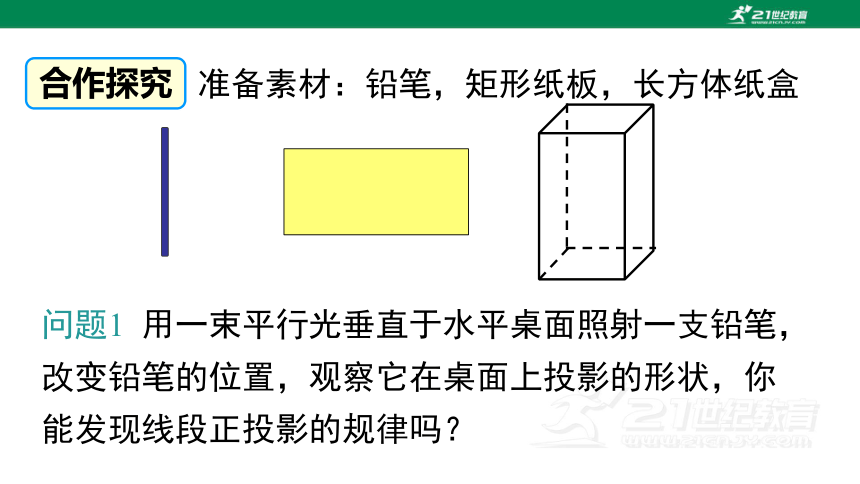
准备素材:铅笔,矩形纸板,长方体纸盒
问题1 用一束平行光垂直于水平桌面照射一支铅笔,改变铅笔的位置,观察它在桌面上投影的形状,你能发现线段正投影的规律吗?
合作探究
H
A
B
A
B
A
B
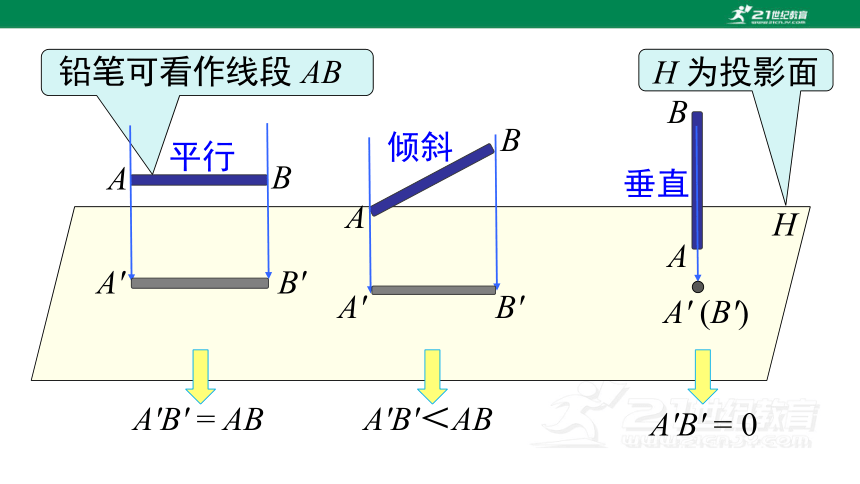
铅笔可看作线段 AB
A'
B'
A'
B'
A' (B')
H 为投影面
A'B' = AB
A'B'<AB
A'B' = 0
平行
倾斜
垂直
线段正投影有如下规律:
知识要点
2. 在同一时刻,两根长度不等的木杆置于阳光下,但
它们的影长相等,则它们的相对位置是 ( )
A.两根垂直于地面 B.两根都平行斜插在地面上
C.两根木杆不平行 D.一根倒在地上
C
1. 木棒长为 1 m,则它的正投影的长一定 ( )
A.大于 1 m B.小于 1 m
C.等于 1 m D.小于或等于 1 m
D
练一练
H
问题2 用一束平行光垂直于水平桌面照射一张矩形纸板 ABCD,改变纸板的位置,观察它在桌面上投影的形状,你能发现矩形 ABCD 正投影的规律吗?
A
B
D
C
H
A
B
D
C
A'
B'
C'
D'
A'
B'
C'
D'
A
B
D
C
平行
倾斜
垂直
D'(A')
C'(B')
A
B
D
C
四边形 ABCD 与四边形 A'B'C'D' 重合
四边形 A'B'C'D' 在大小和形状上已发生改变
四边形 A'B'C'D'变为线段 C'D'
(或 A'B')
平面图形的正投影有如下规律:
平行形不变,倾斜形改变,垂直成线段.
知识要点
1. 皮皮拿着一块正方形纸板在阳光下做投影实验,该
纸板在投影面上形成的投影不可能是 ( )
A
B
C
D
D
练一练
2. 小明同学拿着一个三角形木架在太阳光下玩,他不断
变换着木架的位置,则该木架在地上出现的影子可能
是 ______(填序号).
①点;②线段;③三角形;④四边形.
②③
H
问题3 根据平面图形正投影的规律,你能说出长方体ABCD-A1B1C1D1 在投影面 H 上的正投影是什么图形?
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
长方体在投影面
H 上的正投影就是矩形 A'B'C'D'
H
A1
B1
C1
D1
A
B
C
D
想一想:若将长方体 ABCD-A1B1C1D1 倾斜放置,它在投影面 H 上的正投影是什么图形?
长方体的两个面 ABB1A1 与 DCC1D1 垂直于投影面,故这两个面在投影面上的投影为两条线段.
长方体的另外四个面在投影面上的投影都是平面图形.
几何体的正投影有如下规律:
一般地,一个几何体在一个平面上的正投影是一个平面图形.
一个几何体在一个平面上的正投影叫做这个几何体的视图.(下节课学习)
知识要点
1. 如图,箭头表示投射的方向,则图中圆柱的正
投影是 ( )
A.圆 B.圆柱
C.梯形 D.矩形
D
2. 底面与投影面垂直的圆锥的正投影是 ( )
A.圆 B.三角形 C.矩形 D.正方形
B
练一练
例1 下图中三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄.
(1)在三个不同时刻,同一棵树的影子长度不同,请将它们按拍摄的先后顺序进行排列,并说明你的理由.
(甲)
(乙)
(丙)
→ → .
( 乙 )
( 甲 )
( 丙 )
(2)在同一时刻,大树和小树的影子与它们的高度之间有什么关系?与同伴交流.
在同一时刻,大树和小树的影子与它们的高度成比例.
例2 某校墙边有甲、乙两根木杆.已知乙杆的高度为 1.5 m.
(1)某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
(甲)
(乙)
A
D
D
B
E
E
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D'
B
E
E'
(3)在(2)的情况下,如果测得甲、乙木杆的影子长分别为 1.24 m 和 1 m,那么你能求出甲木杆的高度吗
(甲)
(乙)
A
D
D'
B
E
E'
解:因为△ADD'∽△BEE',所以
即,甲木杆的高度为 1.86 m.
1.5 m
例 圆柱的轴截面平行于投影面,它的正投影是边长为 4 的正方形,则这个圆柱的表面积是______.
4
4
圆柱的底面直径为 4
圆柱的高为 4
练一练
1.圆形物体在阳光下的投影不可能是( )
A.圆形 B.线段 C.矩形 D.椭圆形
C
2.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则AB_____CD
(填“=”“<”“>”“≥”或“≤”).
≥
当堂练习
3. 下列说法正确的有 ( )
①线段 a 垂直于投影面 P,则线段 a 在投影面 P 上的
正投影是一个点;②长方形的对角线垂直于投影面,
则长方形在投影面上的正投影是一条线段;③正方体
的一侧面与投影面平行,则该正方体有 4 个面的正投
影是线段;④圆锥的轴截面与投影面平行,则圆锥在
投影面上的正投影是等腰三角形.
A.1 个 B.2 个 C.3 个 D.4 个
D
4.一位同学想利用树影测树高,已知在某一时刻直立于地面的长 1.5 m 的竹竿的影长为 3 m,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高 CD = 1.2 m,地面部分影长 BD = 5.4 m,求树高 AB.
A
B
D
C
E
解:过点 D 作 DE∥AC 交 AB 于点 E.
∴四边形 AEDC 为平行四边形,
∴AE = CD = 1.2.
∴AB = AE + EB = 3.9.
∴树高 AB 为 3.9 m.
A
B
D
C
方法二:
解:延长 AC 交 BD 的延长线于点 E.
∴BE = BD + DE = 7.8 .
∴树高 AB 为 3.9 m.
E
平行投影
与
正投影
概念:平行光线所形成的投影
平行投影
正
投
影
画法
计算
课堂小结
线段的
正投影
平面图形的正投影
几何体的正投影
平行长不变,倾斜长变短,垂直成一点
影长≤线段长
平行形不变,倾斜形改变,垂直成线段
平面图形
1.知道平行投影和正投影的含义.(重点)
2.了解不同时刻物体在太阳光下形成的影子的特点.
(重点)
3.会利用平行投影的性质进行相关计算.(难点)
学习目标
问题引入
下图是小明一天上学、放学时看到的一根电线杆的影子,你能将它们按时间先后顺序进行排列吗?
东
北
(1)
(2)
(3)
(4)
东
北
东
北
东
北
→ → → .
( 2 )
( 3 )
( 1 )
( 4 )
导入新课
平行投影与正投影
一
观察下列图片,你认为太阳光线有什么特征?
太阳离我们很遥远,其光线可以看成平行光线.
观察与思考
讲授新课
太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影.
概念学行投影中,当平行光线与投影面垂直时,这种投影称为正投影.
想一想,图形的正投影有什么规律?
例如,物体在太阳光的照射下形成的影子 (简称日影) 就是平行投影.
日影的方向可以反映时间,我国古代的计时器日晷,就是根据日影来观测时间的.
准备素材:铅笔,矩形纸板,长方体纸盒
问题1 用一束平行光垂直于水平桌面照射一支铅笔,改变铅笔的位置,观察它在桌面上投影的形状,你能发现线段正投影的规律吗?
合作探究
H
A
B
A
B
A
B
铅笔可看作线段 AB
A'
B'
A'
B'
A' (B')
H 为投影面
A'B' = AB
A'B'<AB
A'B' = 0
平行
倾斜
垂直
线段正投影有如下规律:
知识要点
2. 在同一时刻,两根长度不等的木杆置于阳光下,但
它们的影长相等,则它们的相对位置是 ( )
A.两根垂直于地面 B.两根都平行斜插在地面上
C.两根木杆不平行 D.一根倒在地上
C
1. 木棒长为 1 m,则它的正投影的长一定 ( )
A.大于 1 m B.小于 1 m
C.等于 1 m D.小于或等于 1 m
D
练一练
H
问题2 用一束平行光垂直于水平桌面照射一张矩形纸板 ABCD,改变纸板的位置,观察它在桌面上投影的形状,你能发现矩形 ABCD 正投影的规律吗?
A
B
D
C
H
A
B
D
C
A'
B'
C'
D'
A'
B'
C'
D'
A
B
D
C
平行
倾斜
垂直
D'(A')
C'(B')
A
B
D
C
四边形 ABCD 与四边形 A'B'C'D' 重合
四边形 A'B'C'D' 在大小和形状上已发生改变
四边形 A'B'C'D'变为线段 C'D'
(或 A'B')
平面图形的正投影有如下规律:
平行形不变,倾斜形改变,垂直成线段.
知识要点
1. 皮皮拿着一块正方形纸板在阳光下做投影实验,该
纸板在投影面上形成的投影不可能是 ( )
A
B
C
D
D
练一练
2. 小明同学拿着一个三角形木架在太阳光下玩,他不断
变换着木架的位置,则该木架在地上出现的影子可能
是 ______(填序号).
①点;②线段;③三角形;④四边形.
②③
H
问题3 根据平面图形正投影的规律,你能说出长方体ABCD-A1B1C1D1 在投影面 H 上的正投影是什么图形?
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
长方体在投影面
H 上的正投影就是矩形 A'B'C'D'
H
A1
B1
C1
D1
A
B
C
D
想一想:若将长方体 ABCD-A1B1C1D1 倾斜放置,它在投影面 H 上的正投影是什么图形?
长方体的两个面 ABB1A1 与 DCC1D1 垂直于投影面,故这两个面在投影面上的投影为两条线段.
长方体的另外四个面在投影面上的投影都是平面图形.
几何体的正投影有如下规律:
一般地,一个几何体在一个平面上的正投影是一个平面图形.
一个几何体在一个平面上的正投影叫做这个几何体的视图.(下节课学习)
知识要点
1. 如图,箭头表示投射的方向,则图中圆柱的正
投影是 ( )
A.圆 B.圆柱
C.梯形 D.矩形
D
2. 底面与投影面垂直的圆锥的正投影是 ( )
A.圆 B.三角形 C.矩形 D.正方形
B
练一练
例1 下图中三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄.
(1)在三个不同时刻,同一棵树的影子长度不同,请将它们按拍摄的先后顺序进行排列,并说明你的理由.
(甲)
(乙)
(丙)
→ → .
( 乙 )
( 甲 )
( 丙 )
(2)在同一时刻,大树和小树的影子与它们的高度之间有什么关系?与同伴交流.
在同一时刻,大树和小树的影子与它们的高度成比例.
例2 某校墙边有甲、乙两根木杆.已知乙杆的高度为 1.5 m.
(1)某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
(甲)
(乙)
A
D
D
B
E
E
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D'
B
E
E'
(3)在(2)的情况下,如果测得甲、乙木杆的影子长分别为 1.24 m 和 1 m,那么你能求出甲木杆的高度吗
(甲)
(乙)
A
D
D'
B
E
E'
解:因为△ADD'∽△BEE',所以
即,甲木杆的高度为 1.86 m.
1.5 m
例 圆柱的轴截面平行于投影面,它的正投影是边长为 4 的正方形,则这个圆柱的表面积是______.
4
4
圆柱的底面直径为 4
圆柱的高为 4
练一练
1.圆形物体在阳光下的投影不可能是( )
A.圆形 B.线段 C.矩形 D.椭圆形
C
2.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则AB_____CD
(填“=”“<”“>”“≥”或“≤”).
≥
当堂练习
3. 下列说法正确的有 ( )
①线段 a 垂直于投影面 P,则线段 a 在投影面 P 上的
正投影是一个点;②长方形的对角线垂直于投影面,
则长方形在投影面上的正投影是一条线段;③正方体
的一侧面与投影面平行,则该正方体有 4 个面的正投
影是线段;④圆锥的轴截面与投影面平行,则圆锥在
投影面上的正投影是等腰三角形.
A.1 个 B.2 个 C.3 个 D.4 个
D
4.一位同学想利用树影测树高,已知在某一时刻直立于地面的长 1.5 m 的竹竿的影长为 3 m,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高 CD = 1.2 m,地面部分影长 BD = 5.4 m,求树高 AB.
A
B
D
C
E
解:过点 D 作 DE∥AC 交 AB 于点 E.
∴四边形 AEDC 为平行四边形,
∴AE = CD = 1.2.
∴AB = AE + EB = 3.9.
∴树高 AB 为 3.9 m.
A
B
D
C
方法二:
解:延长 AC 交 BD 的延长线于点 E.
∴BE = BD + DE = 7.8 .
∴树高 AB 为 3.9 m.
E
平行投影
与
正投影
概念:平行光线所形成的投影
平行投影
正
投
影
画法
计算
课堂小结
线段的
正投影
平面图形的正投影
几何体的正投影
平行长不变,倾斜长变短,垂直成一点
影长≤线段长
平行形不变,倾斜形改变,垂直成线段
平面图形
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
