2024-2025学年北师大版九年级数学下册 3.2 圆的对称性 课件(共27张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册 3.2 圆的对称性 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 781.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 10:54:20 | ||
图片预览







文档简介
(共27张PPT)
第三章 圆
3.2 圆的对称性
1.圆的对称性
2.圆心角与所对的弧、弦之间的关系
3.相等圆心角、弧、弦之间的关系. (重点、难点)
学习目标
新课导入
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
新课讲解
1.一个圆绕着它的圆心旋转任意一个角度,都能与原来
的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,
所以圆是中心对称图形,对称中心为圆心.
新课讲解
利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1) 是轴对称图形但不是中心对称图形;
(2) 是中心对称图形但不是轴对称图形;
(3) 既是轴对称图形又是中心对称图形.
解: (1)如图①②是轴对称图形但不是中心对称图形;
(2)如图③是中心对称图形但不是轴对称图形;
(3)如图④既是轴对称图形又是中心对称图形.
新课讲解
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?你是怎么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么结论?
新课讲解
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
新课讲解
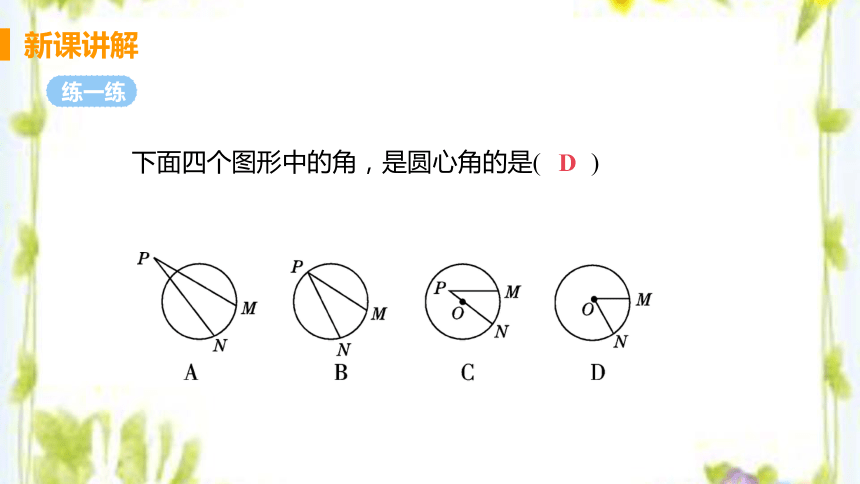
下面四个图形中的角,是圆心角的是( )
D
练一练
新课讲解
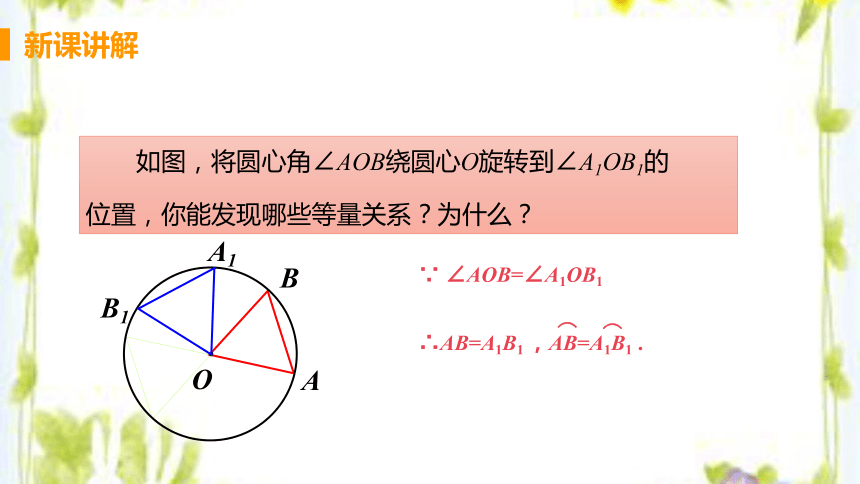
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的
位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
新课讲解
如图,⊙O与⊙O1是等圆,∠AOB=∠A1OB1=60°,请问上述结论还成立吗?为什么
·
O
A
B
A1
·
O1
B1
·
新课讲解
弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
课堂小结
1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
当堂小练
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
D
当堂小练
2.如图,AB为⊙O的弦,∠A=40°,则AB所对的圆心角等于( )
A.40°
B.80°
C.100°
D.120°
C
拓展与延伸
如图,在⊙O中,弦AB>CD,OM⊥AB,ON⊥CD,M,N分别为垂足,那么OM,ON的大小关系是( )
A.OM>ON
B.OM=ON
C.OMD.无法确定
C
1.如图是两个同心圆,其中两条直径互相垂直,大圆的半径是2,则阴影部分的面积之和为 (结果保留π).
2π
课后练习
3.如图,在☉O中,若AC=BC,∠OAB=50°,则∠BOC= .
2.(2023珠海期中改编)如图,AB是☉O的直径,,∠COD=34°.
(1)∠BOC= °,∠DOE= °;
(2)∠AOE= °;
(3)∠AEO= °.
40°
51
78
34
34
4.【例1】(人教9上P89改编)如图,在☉O中,,∠A=36°,则∠C= .
72°
5.【例2】(北师9下P104、人教9上P123)如图,在☉O中,,点D,E分别是☉O的半径OA与OB的中点,求证:CD=CE.
证明:如图,连接CO,
∵OA=OB,且D,E分别是OA,OB的中点,
∴OD=OE,
又,∴∠COD=∠COE,
在△COD和△COE中,,
∴△COD≌△COE(SAS),∴CD=CE.
6.【例3】(北师9下P73、人教9上P85)如图,在☉O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)若∠AOB=∠COD,求证:OE=OF;
(2)若OE=OF,求证:
(1)若∠AOB=∠COD,求证:OE=OF;
证明:(1)∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=AOB,∠FOD=COD,
∵∠AOB=∠COD,∴∠EOB=∠FOD,
在△EOB和△FOD中,,
∴△EOB≌△FOD(AAS),∴OE=OF.
(2)若OE=OF,求证:
(2)∵OE⊥AB,OF⊥CD,
∴∠OEB=∠OFD=90°,
在Rt△BEO和Rt△DFO中,,
∴Rt△BEO≌Rt△DFO(HL),∴BE=DF,
∵OA=OB,OC=OD,∴AB=2BE,CD=2DF,
∴AB=CD,
7.如图,AB是☉O的直径,C,D是☉O上两点,弦BC=CD=DA,则∠BCD= .
120°
8.(北师9下P72、人教9上P90)如图,A,B是☉O上的两点,∠AOB=120°,C是的中点.求证:四边形OACB是菱形.
证明:连接OC,
∵C是的中点,∠AOB=120°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,∴四边形OACB是菱形.
★9. 0.55 (人教9上P85改编)如图,AB,CD是☉O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且,求证:OE=OF.
证明:连接OA,OB,OC,OD.
,
AB=CD.
∵OE⊥AB,OF⊥CD,OA=OB=OC=OD,
∴AE=AB,CF=CD,
∴AE=CF(设为λ),设☉O的半径为μ,
由勾股定理得OE=,OF=,∴OE=OF.
请完成课本本节对应习题
布置作业
感谢大家关注
第三章 圆
3.2 圆的对称性
1.圆的对称性
2.圆心角与所对的弧、弦之间的关系
3.相等圆心角、弧、弦之间的关系. (重点、难点)
学习目标
新课导入
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
新课讲解
1.一个圆绕着它的圆心旋转任意一个角度,都能与原来
的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,
所以圆是中心对称图形,对称中心为圆心.
新课讲解
利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1) 是轴对称图形但不是中心对称图形;
(2) 是中心对称图形但不是轴对称图形;
(3) 既是轴对称图形又是中心对称图形.
解: (1)如图①②是轴对称图形但不是中心对称图形;
(2)如图③是中心对称图形但不是轴对称图形;
(3)如图④既是轴对称图形又是中心对称图形.
新课讲解
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?你是怎么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么结论?
新课讲解
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
新课讲解
下面四个图形中的角,是圆心角的是( )
D
练一练
新课讲解
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的
位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
新课讲解
如图,⊙O与⊙O1是等圆,∠AOB=∠A1OB1=60°,请问上述结论还成立吗?为什么
·
O
A
B
A1
·
O1
B1
·
新课讲解
弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
课堂小结
1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
当堂小练
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
D
当堂小练
2.如图,AB为⊙O的弦,∠A=40°,则AB所对的圆心角等于( )
A.40°
B.80°
C.100°
D.120°
C
拓展与延伸
如图,在⊙O中,弦AB>CD,OM⊥AB,ON⊥CD,M,N分别为垂足,那么OM,ON的大小关系是( )
A.OM>ON
B.OM=ON
C.OM
C
1.如图是两个同心圆,其中两条直径互相垂直,大圆的半径是2,则阴影部分的面积之和为 (结果保留π).
2π
课后练习
3.如图,在☉O中,若AC=BC,∠OAB=50°,则∠BOC= .
2.(2023珠海期中改编)如图,AB是☉O的直径,,∠COD=34°.
(1)∠BOC= °,∠DOE= °;
(2)∠AOE= °;
(3)∠AEO= °.
40°
51
78
34
34
4.【例1】(人教9上P89改编)如图,在☉O中,,∠A=36°,则∠C= .
72°
5.【例2】(北师9下P104、人教9上P123)如图,在☉O中,,点D,E分别是☉O的半径OA与OB的中点,求证:CD=CE.
证明:如图,连接CO,
∵OA=OB,且D,E分别是OA,OB的中点,
∴OD=OE,
又,∴∠COD=∠COE,
在△COD和△COE中,,
∴△COD≌△COE(SAS),∴CD=CE.
6.【例3】(北师9下P73、人教9上P85)如图,在☉O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)若∠AOB=∠COD,求证:OE=OF;
(2)若OE=OF,求证:
(1)若∠AOB=∠COD,求证:OE=OF;
证明:(1)∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=AOB,∠FOD=COD,
∵∠AOB=∠COD,∴∠EOB=∠FOD,
在△EOB和△FOD中,,
∴△EOB≌△FOD(AAS),∴OE=OF.
(2)若OE=OF,求证:
(2)∵OE⊥AB,OF⊥CD,
∴∠OEB=∠OFD=90°,
在Rt△BEO和Rt△DFO中,,
∴Rt△BEO≌Rt△DFO(HL),∴BE=DF,
∵OA=OB,OC=OD,∴AB=2BE,CD=2DF,
∴AB=CD,
7.如图,AB是☉O的直径,C,D是☉O上两点,弦BC=CD=DA,则∠BCD= .
120°
8.(北师9下P72、人教9上P90)如图,A,B是☉O上的两点,∠AOB=120°,C是的中点.求证:四边形OACB是菱形.
证明:连接OC,
∵C是的中点,∠AOB=120°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,∴四边形OACB是菱形.
★9. 0.55 (人教9上P85改编)如图,AB,CD是☉O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且,求证:OE=OF.
证明:连接OA,OB,OC,OD.
,
AB=CD.
∵OE⊥AB,OF⊥CD,OA=OB=OC=OD,
∴AE=AB,CF=CD,
∴AE=CF(设为λ),设☉O的半径为μ,
由勾股定理得OE=,OF=,∴OE=OF.
请完成课本本节对应习题
布置作业
感谢大家关注
