2024-2025学年北师大版九年级数学下册 3.3 垂径定理 课件(共29张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册 3.3 垂径定理 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 784.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 10:54:55 | ||
图片预览




文档简介
(共29张PPT)
第三章 圆
3.3 垂径定理
1.垂径定理
2.垂径定理的推论. (重点、难点)
学习目标
新课导入
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
你能找到多少条对称轴?
(2)你是用什么方法解决上述问题的?与同伴进行交
流.
新课讲解
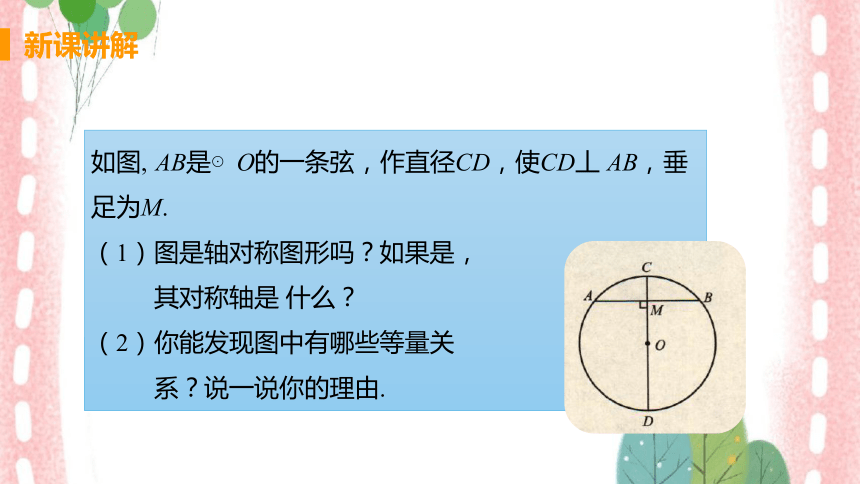
如图, AB是⊙O的一条弦,作直径CD,使CD丄 AB,垂
足为M.
(1)图是轴对称图形吗?如果是,
其对称轴是 什么?
(2)你能发现图中有哪些等量关
系?说一说你的理由.
新课讲解
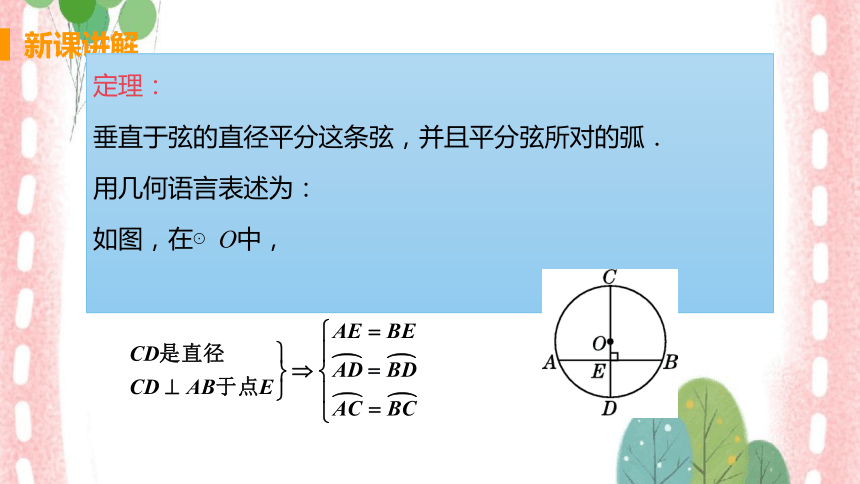
定理:
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
用几何语言表述为:
如图,在⊙O中,
新课讲解
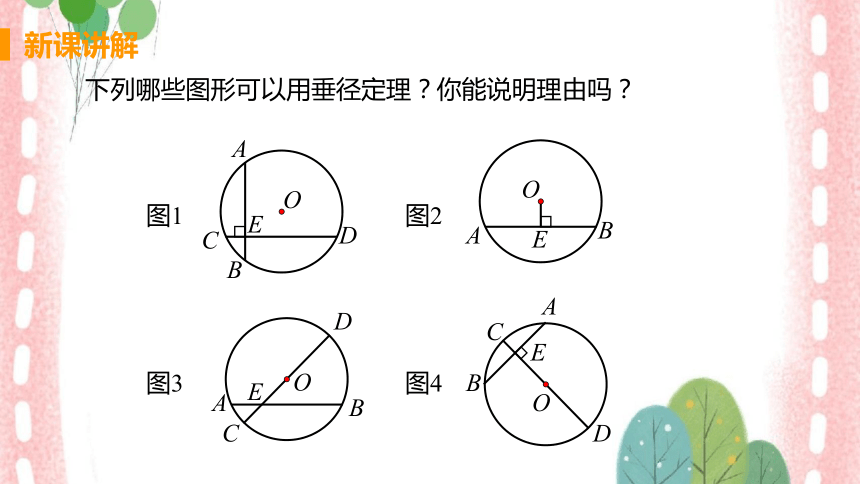
下列哪些图形可以用垂径定理?你能说明理由吗?
D
O
C
A
E
B
D
O
C
A
E
B
图1
图2
图3
图4
O
A
E
B
D
O
C
A
E
B
新课讲解
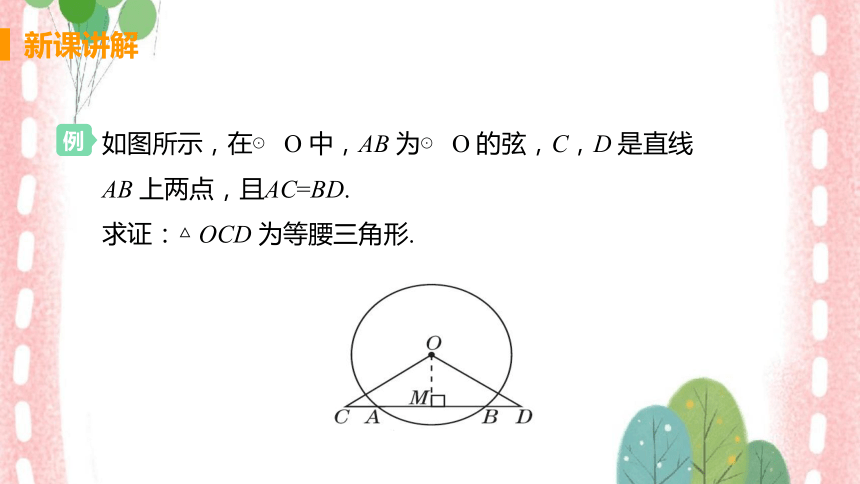
例
如图所示,在⊙ O 中,AB 为⊙ O 的弦,C,D 是直线
AB 上两点,且AC=BD.
求证:△ OCD 为等腰三角形.
新课讲解
分析:
构建垂径定理的基本图形结合线段垂直平分线性质证明.
解:过点O 作OM ⊥ AB,垂足为M,
∵ OM ⊥ AB,∴ AM=BM.
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,∴ OC=OD.
∴△ OCD 为等腰三角形.
新课讲解
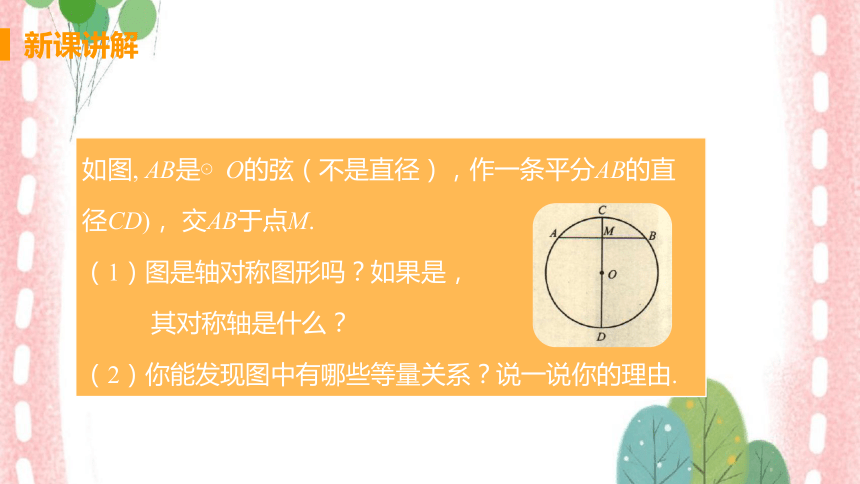
如图, AB是⊙O的弦(不是直径),作一条平分AB的直
径CD), 交AB于点M.
(1)图是轴对称图形吗?如果是,
其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
新课讲解
平分弦(不是直径)的直径垂直于弦,并且平分
弦所对的弧.
新课讲解
推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分
弦所对的弧,即:如图,在⊙O中,
新课讲解
练一练
如图,⊙O的直径CD=10 cm,AB是⊙O的弦,AM
=BM,OM∶OC=3∶5,则AB的长为( )
A.8 cm
cm
C.6 cm
D.2 cm
A
课堂小结
垂径定理:
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
(2)关于垂径定理及其推论可归纳为:一条直线,它具备以下五个性质:
①直线过圆心;
②直线垂直于弦;
③直线平分弦(不是直径);
④直线平分弦所对的优弧;
⑤直线平分弦所对的劣弧.
如果把其中的任意两条作为条件,其余三条作为结论,组成的命题都是真命题.
当堂小练
1.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.3
B.2.5
C.4
D.3.5
C
当堂小练
2.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25 m,BD=1.5 m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2 m
B.2.5 m
C.2.4 m
D.2.1 m
B
拓展与延伸
如图,AB是⊙O的直径,CD是⊙O的一条弦,CD⊥AB于点E,则下列结论:①∠COE=∠DOE;②CE=DE;③BC=BD;④OE=BE.其中,一定正确的有( )
A.1个 B.2个
C.3个 D.4个
C
A.6 B.8
C.10 D.12
1.(1)如图,☉O的半径为10,弦AB的长度是12,ON⊥AB,垂足为N,则ON=( )
B
课后练习
(2)(人教9上P122改编)如图,AB是☉O的直径,弦CD⊥AB于点E,若AB=6,BE=1,则弦CD的长是 .
2
A.6 B.7
C.8 D.10
2.(1)如图,☉O的半径为5,M是AB的中点,且OM=3,则☉O的弦AB等于( )
C
(2)(全国视野)(2023宜昌)如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为 .
4
3.(传统文化)(北师9下P76、人教9上P82)(2023广西)1 400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为37.4 m,拱高(即弧的中点到弦的距离)为7.2 m,求桥拱所在圆的半径(结果精确到0.1 m).
解:设桥拱所在圆的半径为R m,
连接OA,由题意可知AB=37.4 m,CD=7.2 m,
∴OD=OC-CD=(R-7.2)m.∵OD⊥AB,∴AD=AB=18.7 m,
在Rt△OAD中,OA2=AD2+OD2,即R2=18.72+(R-7.2)2,
解得R≈27.9.答:桥拱所在圆的半径约为27.9 m.
4.如图,AB是☉O的弦,C,D是直线AB上的两点,并且AC=BD,求证:OC=OD.
证明:如图,过点O作OE⊥AB于E,则AE=BE.
又∵AC=BD,∴CE=DE,
∴OE是CD的垂直平分线,∴OC=OD.
答案图
小结:圆中常用辅助线——过圆心作弦的垂线.
小结:注意分类讨论思想的应用.
5.☉O的半径为13 cm,弦AB∥CD,AB=10 cm,CD=24 cm,则AB与CD之间的距离是
.
17 cm或7 cm
6.(数学文化)(北师9下P76)(2024珠海一模)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何?”转化为现在的数学语言就是:如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长.
解:如图,连接OA,
设直径CD的长为2x寸,则半径OC=x寸,OE=(x-1)寸.
∵CD为☉O的直径,弦AB⊥CD,AB=10(寸),
∴AE=BE=AB=10=5寸.
又OA=x寸,根据勾股定理,得x2=52+(x-1)2,
解得x=13,∴CD=2x=2×13=26(寸).
7.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上,你认为AC与BD的大小有什么关系?为什么?
解:AC=BD.理由如下:
如图,过点O作OE⊥AB于E,
∴AE=BE,CE=DE,
∴AE-CE=BE-DE,
∴AC=BD.
答案图
★8. 0.50 在半径为1的☉O中,弦AB,AC的长分别为1和,则∠BAC的度数为 .
15°或105°
请完成课本本节对应习题
布置作业
感谢大家欣赏
第三章 圆
3.3 垂径定理
1.垂径定理
2.垂径定理的推论. (重点、难点)
学习目标
新课导入
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
你能找到多少条对称轴?
(2)你是用什么方法解决上述问题的?与同伴进行交
流.
新课讲解
如图, AB是⊙O的一条弦,作直径CD,使CD丄 AB,垂
足为M.
(1)图是轴对称图形吗?如果是,
其对称轴是 什么?
(2)你能发现图中有哪些等量关
系?说一说你的理由.
新课讲解
定理:
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
用几何语言表述为:
如图,在⊙O中,
新课讲解
下列哪些图形可以用垂径定理?你能说明理由吗?
D
O
C
A
E
B
D
O
C
A
E
B
图1
图2
图3
图4
O
A
E
B
D
O
C
A
E
B
新课讲解
例
如图所示,在⊙ O 中,AB 为⊙ O 的弦,C,D 是直线
AB 上两点,且AC=BD.
求证:△ OCD 为等腰三角形.
新课讲解
分析:
构建垂径定理的基本图形结合线段垂直平分线性质证明.
解:过点O 作OM ⊥ AB,垂足为M,
∵ OM ⊥ AB,∴ AM=BM.
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,∴ OC=OD.
∴△ OCD 为等腰三角形.
新课讲解
如图, AB是⊙O的弦(不是直径),作一条平分AB的直
径CD), 交AB于点M.
(1)图是轴对称图形吗?如果是,
其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
新课讲解
平分弦(不是直径)的直径垂直于弦,并且平分
弦所对的弧.
新课讲解
推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分
弦所对的弧,即:如图,在⊙O中,
新课讲解
练一练
如图,⊙O的直径CD=10 cm,AB是⊙O的弦,AM
=BM,OM∶OC=3∶5,则AB的长为( )
A.8 cm
cm
C.6 cm
D.2 cm
A
课堂小结
垂径定理:
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
(2)关于垂径定理及其推论可归纳为:一条直线,它具备以下五个性质:
①直线过圆心;
②直线垂直于弦;
③直线平分弦(不是直径);
④直线平分弦所对的优弧;
⑤直线平分弦所对的劣弧.
如果把其中的任意两条作为条件,其余三条作为结论,组成的命题都是真命题.
当堂小练
1.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.3
B.2.5
C.4
D.3.5
C
当堂小练
2.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25 m,BD=1.5 m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2 m
B.2.5 m
C.2.4 m
D.2.1 m
B
拓展与延伸
如图,AB是⊙O的直径,CD是⊙O的一条弦,CD⊥AB于点E,则下列结论:①∠COE=∠DOE;②CE=DE;③BC=BD;④OE=BE.其中,一定正确的有( )
A.1个 B.2个
C.3个 D.4个
C
A.6 B.8
C.10 D.12
1.(1)如图,☉O的半径为10,弦AB的长度是12,ON⊥AB,垂足为N,则ON=( )
B
课后练习
(2)(人教9上P122改编)如图,AB是☉O的直径,弦CD⊥AB于点E,若AB=6,BE=1,则弦CD的长是 .
2
A.6 B.7
C.8 D.10
2.(1)如图,☉O的半径为5,M是AB的中点,且OM=3,则☉O的弦AB等于( )
C
(2)(全国视野)(2023宜昌)如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为 .
4
3.(传统文化)(北师9下P76、人教9上P82)(2023广西)1 400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为37.4 m,拱高(即弧的中点到弦的距离)为7.2 m,求桥拱所在圆的半径(结果精确到0.1 m).
解:设桥拱所在圆的半径为R m,
连接OA,由题意可知AB=37.4 m,CD=7.2 m,
∴OD=OC-CD=(R-7.2)m.∵OD⊥AB,∴AD=AB=18.7 m,
在Rt△OAD中,OA2=AD2+OD2,即R2=18.72+(R-7.2)2,
解得R≈27.9.答:桥拱所在圆的半径约为27.9 m.
4.如图,AB是☉O的弦,C,D是直线AB上的两点,并且AC=BD,求证:OC=OD.
证明:如图,过点O作OE⊥AB于E,则AE=BE.
又∵AC=BD,∴CE=DE,
∴OE是CD的垂直平分线,∴OC=OD.
答案图
小结:圆中常用辅助线——过圆心作弦的垂线.
小结:注意分类讨论思想的应用.
5.☉O的半径为13 cm,弦AB∥CD,AB=10 cm,CD=24 cm,则AB与CD之间的距离是
.
17 cm或7 cm
6.(数学文化)(北师9下P76)(2024珠海一模)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何?”转化为现在的数学语言就是:如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长.
解:如图,连接OA,
设直径CD的长为2x寸,则半径OC=x寸,OE=(x-1)寸.
∵CD为☉O的直径,弦AB⊥CD,AB=10(寸),
∴AE=BE=AB=10=5寸.
又OA=x寸,根据勾股定理,得x2=52+(x-1)2,
解得x=13,∴CD=2x=2×13=26(寸).
7.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上,你认为AC与BD的大小有什么关系?为什么?
解:AC=BD.理由如下:
如图,过点O作OE⊥AB于E,
∴AE=BE,CE=DE,
∴AE-CE=BE-DE,
∴AC=BD.
答案图
★8. 0.50 在半径为1的☉O中,弦AB,AC的长分别为1和,则∠BAC的度数为 .
15°或105°
请完成课本本节对应习题
布置作业
感谢大家欣赏
