2024-2025学年五年级数学下册期末备考真题分类汇编(浙江专版)选择题(一)【答案+解析】
文档属性
| 名称 | 2024-2025学年五年级数学下册期末备考真题分类汇编(浙江专版)选择题(一)【答案+解析】 |

|
|
| 格式 | docx | ||
| 文件大小 | 573.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 09:58:36 | ||
图片预览




文档简介
2024-2025学年五年级数学下册期末备考真题分类汇编(浙江专版)
选择题(一)
一、单选题
1.(2023五下·金东期末)甲、乙两人跑一段相同的路,甲用0.3小时,乙用小时,他们的速度相比,( )。
A.甲快 B.乙快 C.两人一样快 D.无法比较
2.(2024五下·瑞安期末)观察下图,估一估下面分数,不在 A、B 两点之间的是( )
A. B. C. D.
3.(2024五下·永康期末)将四个长 12cm,宽 8cm,高5cm 的长方体盒子,用彩纸包在一起,最省包装纸的方法是( )(接口处不计)
A. B.
C. D.
4.(2024五下·钱塘期末)用棱长为1cm的小正方体木块拼成长6cm,宽5cm,高4cm的长方体,一共要用( )个这样的小正方体木块。
A.20 B.30 C.24 D.120
5.(2024五下·平阳期末)下图是正方体的展开图,则折叠后,与“爱”相对的字是( )
A.学 B.习 C.数 D.学
6.(2024五下·奉化期末)如果长方体的长、宽、高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A.3 B.9 C.27 D.12
7.(2024五下·海盐期末)聪聪用纸板做一个无盖长方体纸盒,他已经做好了两个相邻的面(如下图),如果继续往下做,最少需要纸板( )平方厘米(接口处忽略不计)。
A.21 B.47 C.52 D.62
8.(2024五下·海盐期末)有两个非零自然数a和b,若a=b+1,则下列说法错误的是( )
A.a和b的和是奇数 B.是最简分数
C.a和b的积是奇数 D.a和b的最小公倍数是ab
9.(2024五下·海盐期末)的分母加45,要使分数的大小不变,分子应( )
A.乘5 B.乘 6 C.加 30 D.加 45
10.(2024五下·乐清期末)甲、乙两条线段各被遮住了一部分(如下图),甲、乙比较( )
A.甲比乙长 B.乙比甲长
C.甲和乙一样长 D.无法比较
11.(2024五下·柯桥期末)小丁按如图所示步骤估测一颗玻璃球的体积:
⑴将 的水倒入一个容积为 的杯子中;
⑵将 5 颗相同的玻璃球放进水中, 结果水未满;
⑶再放入 1 颗相同的玻璃球, 结果水溢出了。
根据以上步骤, 推测这样一颗玻璃球的体积范围最可能是( )
A. 以上, 以下 B. 以上, 以下
C. 以上, 以下 D. 以上, 以下
12.(2024五下·柯桥期末) 下面描述正确的序号是( )。
⑴奇数与偶数相乘, 积是奇数。
⑵有两个自然数 与 , 若 , 且 , 则 与 的最小公倍数是 。
⑶因为一个整数的末位数字是 2 的倍数, 这个整数就是 2 的倍数, 所以一个整数的末位数字是 3 的倍数,这个整数就是 3 的倍数。
⑷从 2024、2023、2022、2021、2020、2019 这六个数中任选两个数求和, 和是偶数的共有 6 种选法。
A.(1)(2)(4) B.(1)(2) C.(2)(4) D.(2)(3)
13.(2024五下·柯桥期末) 分母是 8 的所有最简真分数的和是( )
A.2 B. C.1 D.
14.(2024五下·钱塘期末)统计下面几组信息的数据,适合用复式折线统计图的是( )
A.五(1)班和五(2)班同学的植树棵树情况。
B.沙沙几次数学测试的成绩变化情况。
C.五(3)班同学喜欢喝x、y、z三种品牌牛奶的人数情况。
D.新华商场 2024年1-6月两种不同品牌空调的销售情况。
15.(2024五下·钱塘期末)如下图,甲、乙两条彩带都被遮住了一部分,露出部分的长度相等,则原来两条彩带长度比较的结果是( )
A.甲=乙 B.甲<乙 C.甲>乙 D.无法确定
16.(2023五下·柯桥期末)在 和 之间存在 ( ) 个分数。
A.0 B.1 C.无数 D.10
17.(2024五下·汉川期末)如下图,直线上点A在0和1之间,点A表示的数可能是( )。
A. B. C. D.
18.(2024五下·临平期末)一盒纯牛奶的外包装是长方体形状,包装纸上标注“净含量750mL”,实际外包装长8cm,宽5cm,那么高最有可能是( )cm。
A.15 B.18 C.19 D.25
19.(2024五下·临平期末)5月份的气温变化莫测。乐乐想知道杭州市2024年5月份整月的气温变化趋势,他要收集的数据是杭州市( )。
A.2024年各季度的平均气温
B.2024年5月份每天的平均气温
C.2024年各月的平均气温
D.2024年5月 1 日各时刻的气温
20.(2024五下·临平期末)下面可能与 不相等的分数是( )。
A. B. C. D.
21.(2024五下·临平期末)弟弟要做40道数学口算题,已完成了16道,还需完成全部题目的( )。
A. B. C. D.
22.(2024五下·临平期末)一个正方体的棱长扩大到原来的2 倍,则它的体积扩大到了原来的( )倍。
A.2 B.4 C.6 D.8
23.(2024五下·瑞安期末)下面的情况中,最适合用复式折线统计图表示的是( )
A.瑞安市今年5月份日平均气温变化情况
B.某校五年级各班男生、女生具体人数
C.两家零售店去年12个月销售额变化情况
D.小丽最近4次数学测试成绩变化情况
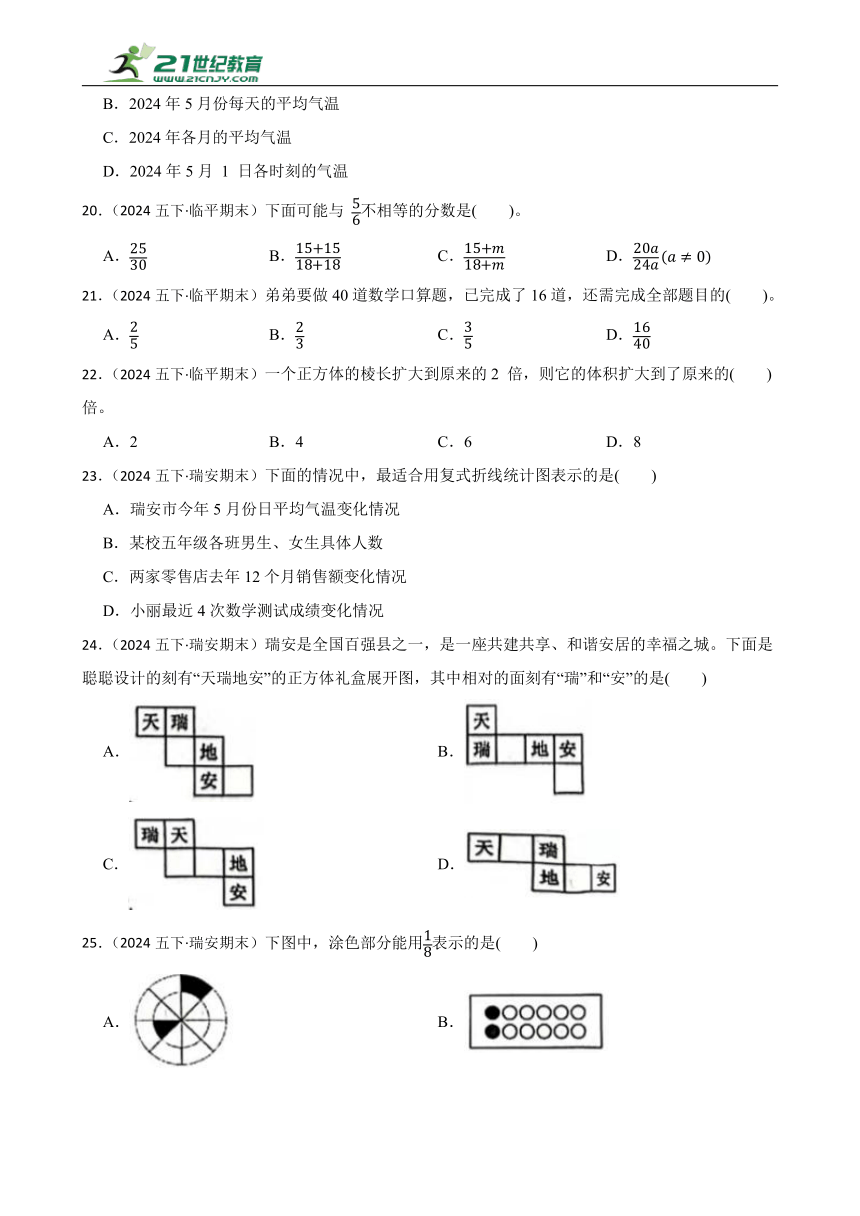
24.(2024五下·瑞安期末)瑞安是全国百强县之一,是一座共建共享、和谐安居的幸福之城。下面是聪聪设计的刻有“天瑞地安”的正方体礼盒展开图,其中相对的面刻有“瑞”和“安”的是( )
A. B.
C. D.
25.(2024五下·瑞安期末)下图中,涂色部分能用表示的是( )
A. B.
C. D.
26.(2024五下·瑞安期末)一个长方体物品长 21厘米,宽15厘米,高0.8厘米。这个物品最有可能是( )
A.手机 B.墨水盒 C.纸巾盒 D.数学书
27.(2024五下·慈溪期末)“神州十八号”飞行乘组将在中国空间站实施首次在轨水生生态研究项目。装有斑马鱼和金鱼藻的生态实验柜正面面积2m2,宽1m,高0.8m,总质量约0.5吨。要计算生态实验柜的体积,正确的算式是( )。
A.2×1 B.2×1×0.5 C.2×0.8 D.2×1×0.8
28.(2024五下·慈溪期末)下列说法中,正确的有( )个。
都是最简分数。
②20个零件中找1个次品(稍重),至少称3次能保证找出次品。
③最小的合数是一个偶数。
④分数可以分为真分数、假分数、带分数。
A.1 B.2 C.3 D.4
29.(2024五下·慈溪期末)如图的长方体礼盒用若干分米的彩带捆绑,并留3分米做手提带,彩带的总长是( )分米。
A.长×4+宽×4+高×4+3 B.长×4+宽×2+高×2+3
C.长×2+宽×4+高×2+3 D.长×2+宽×2+高×4+3
30.(2024五下·慈溪期末)下列图形中,通过折叠不能围成长方体的是( )。
A. B.
C. D.
31.(2024五下·慈溪期末)把一个鸡蛋完全浸没在一个装满水的杯子里,溢出的水大约有( )。
A.500mL B.50mL C.5mL D.5L
32.(2024五下·平阳期末)如图,甲、乙两根彩带都被遮住了一部分,露出部分的长度分别是全长的和,且长度相等。那么比较甲、乙两根彩带的长度,( )
A.甲<乙 B.甲=乙 C.甲>乙 D.无法比较
33.(2024五下·平阳期末)下列分数中,( )是最简分数。
A. B. C. D.
34.(2024五下·乐清期末)某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际想象一下,这个产品最有可能是( )。
A.一部手机 B.一台笔记本电脑
C.一台微波炉 D.一台冰箱
35.(2024五下·永康期末)正方体的棱长扩大到原来的3倍,它的表面积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
36.(2024五下·永康期末)下面能用“”解决的问题是( )
A.奶奶有一块菜地,种生菜,种香菜,两种菜共用了菜地的几分之几?
B.一袋糖果,巧克力味占,水果味占,其他口味占几分之几?
C.食堂7月份用煤吨,正好是6月份的,6月份用煤多少吨?
D.妈妈把半个蛋糕的给笑笑,笑笑吃了几个蛋糕?
37.(2024五下·永康期末)下列分数和小数比大小,正确的是( )
A. B. C. D.
38.(2024五下·永康期末)下面说法中正确的是( )
A.若 a+b=1,那么a和b互为倒数
B.1吨的和2吨的一样重
C.冰箱容积是 250L,它的体积就是 250dm3
D.牙膏盒的体积3分米3
39.(2024五下·永康期末)下列分数中比大的分数是( )
A. B. C. D.
40.(2024五下·上虞期末)下图是课本第 64 页中的最后一题,可以用( )的知识来解决。
A.公倍数 B.公因数 C.偶数
41.(2024五下·上虞期末)如图所示,一个长方体的收纳箱前面的面积是 60dm2,高是 6dm,宽是 5dm,要计算这个收纳箱的体积,正确的算式是( )
A.60×6 B.60×5 C.60×5×6
42.(2024五下·余杭期末)一个长方体游泳池,长25米,宽15米,高2米,在池底上面高1.2米处的地方画一条水位线,水位线长( )米。
A.(25+2)×2 B.(25+15)×2
C.(25+15+2)×2 D.(25+1.2)×2
43.(2024五下·余杭期末)小明在3根长a厘米、6根b厘米、8根c厘米长的小棒中,)平方厘米。选取了12根小棒搭成一个长方体。这个长方体的表面积是( )
A.2ab+2bc+2ac B.2a+4ab C.2b+4bc D.2c2+4bc
44.(2024五下·余杭期末)有一块长方体木料(如右图,单位:厘米)。小刚把它锯成同样大小的两个长方体木块。增加的表面积最多是( )平方厘米。
A.24 B.30 C.40 D.94
45.(2024五下·余杭期末)一个长方体长8cm,宽6cm,高5cm,把它切成棱长为2cm的小正方体,最多可以切( )个。
A.12 B.24 C.30 D.60
46.(2024五下·上城期末)将左图的香皂放入右图纸箱中,这个纸箱的体积是( )。(单位:cm)
A.80cm3 B.5760dm3 C.7200dm3 D.7.2dm3
47.(2024五下·上城期末)下图表示搭长方体模型所用的小棒、长方形的尺寸与数量,下列材料中,正好能搭成长方体模型的是( )
A.
B.
C.
D.
48.(2024五下·上城期末)下图中,长方体容器的底面积是1dm2,两个球浸没时正好水面与容器口平,分别拿出两个球,水面变化如图,那么,小球体积是( )。
A.0.3dm3 B.0.5dm3 C.0.8dm3 D.3dm3
49.(2024五下·钱塘期末)下面几组信息的数据统计,适合用复式折线统计图表示的是( )。
A.五(1)班和五(2)班同学的植树棵树情况
B.沙沙几次数学测试的成绩变化情况
C.五(3)班同学喜欢喝甲、乙、丙三种品牌牛奶的人数情况
D.新华商场2024年1~6月两种不同品牌空调的销量情况
答案解析部分
1.A
解:=1÷3=(小时)
0.3小时<小时,甲快。
故答案为:A。
甲、乙两人跑一段相同的路,用的时间少的,速度较快;先把分数化成小数后再比较大小。
2.D
解:A、B 两点之间的数大约是~之间。
A项:在 A、B 两点之间;
B项:在 A、B 两点之间;
C项:在 A、B 两点之间;
D项:=3÷2=1.5,不在 A、B 两点之间。
故答案为:D。
先确定A、B 两点之间的数大约是~之间。然后据此判断。
3.B
解:12×8的面积最大,最省包装纸的方法,把长×宽的面叠放在一起,是 。
故答案为:B。
最省包装纸的方法要把最大的面叠放在一起。
4.D
解:(6×5×4)÷(1×1×1)
=120÷1
=120(个)。
故答案为:D。
一共要用这样小正方体木块的个数=(长方体的长×宽×高)÷(小正方体木块的棱长×棱长×棱长)。
5.C
解:图中是正方体的展开图,则折叠后,与“爱”相对的字是“数”。
故答案为:C。
折叠后,“我”与“习”相对,“爱”与“数”相对,两个“学”相对。
6.C
解:3×3×3=27。
故答案为:C。
长方体的体积=长×宽×高,长方体的长、宽、高都扩大到原来的3倍,则它的体积扩大到原来的3×3×3=27倍。
7.B
解:5×2×2+3×2×2+5×3
=20+12+15
=32+15
=47(平方厘米)。
故答案为:B。
最少需要纸板的面积=长×高×2+宽×高×2+长×宽。
8.C
解:两个非零自然数a和b,若a=b+1,说面a、b是相邻的自然数,则a、b是互质数;
A项:相邻的自然数一个是奇数,一个是偶数,奇数+偶数=奇数,原题干说法正确
B项:a、b是互质数,则是最简分数,原题干说法正确;
C项:奇数×偶数=偶数,原题干说法错误;
D项:a、b最小公倍数是它们的积ab,原题干说法正确。
故答案为:C。
两个非零自然数a和b,若a=b+1,说面a、b是相邻的自然数,一个是奇数,一个是偶数,则a、b是互质数,据此选择。
9.B
解:(9+45)÷9
=54÷9
=6,分子应乘6。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
10.A
解:甲×=乙×,,所以甲比乙长。
故答案为:A。
因为露出的长度相等,所以得到甲×=乙×,乘积相等,所以只需要比较两个分数的大小即可判断两根线段的长短。
11.B
解:(500-300)÷(5+1)
=200÷6
≈33(立方厘米)
(500-300)÷5
=200÷5
=40(立方厘米)
则这样一颗玻璃球的体积范围最可能是30立方厘米以上,40立方厘米以下。
故答案为:B。
杯子中还剩下的容积=500-300=200毫升,因为将5颗相同的玻璃球放进水中, 结果水未满,但是再放入 1 颗相同的玻璃球,结果水溢出了,说明这样一颗玻璃球的体积范围最小是杯子中还剩下的容积÷6颗,最大是杯子中还剩下的容积÷5颗。
12.C
解:(1)如1×4=4,3×6=18,积是偶数,原题干说法错误;
(2)a、b的最小公倍数是ab,原题干说法正确;
(3)如13、23不是3的倍数,原题干说法错误;
(4)奇数+奇数=偶数,可以选2023+2021、2023+2019、2021+2019;
偶数+偶数=偶数,可以选2024+2022、2024+2020、2022+2020;
3+3=6(种)选法,原题干说法正确。
故答案为:C。
(1)奇数×偶数=偶数;
(2)相邻的自然数是互质数,最小公倍数是它们的积
(3)一个数各个数位上的数的和是3的倍数,这个数就是3的倍数;
(4)奇数+奇数=偶数,偶数+偶数=偶数,据此选一选。
13.A
解:+++
=
=2。
故答案为:A。
分子比分母小的分数是真分数;分子和分母只有公因数1的分数是最简分数,据此写出这几个分数后再相加。
14.D
解:A项:适合复式条形统计图;
B项:适合单式折线统计图;
C项:适合单式条形统计图;
D项:适合复式折线统计图。
故答案为:D。
要统计的数据是两项或者以上时,要用复式统计图,并且条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
15.C
解:甲的=乙的,因为<,所以甲>乙。
故答案为:C。
露出部分的长度相等,也就是甲的=乙的,因为<,所以甲>乙。
16.C
解:在 和 之间存在无数个分数。
故答案为:C。
任何两个不相等的分数之间有无数个分数。
17.C
解:<<<,点A表示的数可能是。
故答案为:C。
点A在0和1之间,并且比大,且靠近的地方,则可能是。
18.C
解:750÷5÷8
=150÷8
≈19(cm)
故答案为:C。
长方体体积=长×宽×高,可以用净含量除以包装的长和宽,采用进一法取整数就是可能的高度。
19.B
解:5月份的气温变化莫测。乐乐想知道杭州市2024年5月份整月的气温变化趋势,他要收集的数据是杭州市2024年5月份每天的平均气温。
故答案为:B。
要想知道5月份整月的气温变化趋势,因此只需要知道5月份每天的平均气温即可。
20.C
解:A:=;
B:=;
C:一定与不相等;
D:=。
故答案为:C。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数值不变。根据分数的基本性质逐项判断即可。
21.C
解:(40-16)÷40
=24÷40
=
故答案为:C。
用要做的道数减去已经完成的道数求出还需完成的道数,用还需完成的道数除以要做的道数即可求出还需完成全部题目的几分之几。
22.D
解:2×2×2=8,一个正方体的棱长扩大到原来的2 倍,则它的体积扩大到了原来的8倍。
故答案为:D。
正方体体积=棱长×棱长×棱长,所以正方体体积扩大的倍数是棱长扩大倍数的立方倍。
23.C
解:A项:适合用单式折线统计图表示;
B项:适合用复式条形统计图表示;
C项:适合用复式折线统计图表示;
D项:适合用单式折线统计图表示。
故答案为:C。
适合用复式条形统计图表示首先得是两项内容,并且清楚地看出数量的增减变化情况。
24.A
解:A项:“瑞”和“安”相对;
B项:“瑞”和“地”相对;
C项:“瑞”不和“安”相对;
D项:“瑞”和“天”相对。
故答案为:A。
正方体相对的面不相邻,据此判断A项中“瑞”和“安”相对。
25.A
解:A项:1÷8=;
B项:1÷6=;
C项:2÷32=;
D项:不是平均分不能用分数表示。
故答案为:A。
分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,分子是几,就表示有几个这样的分数单位。
26.D
解:长21厘米,宽15厘米,高0.8厘米的物品最有可能是数学书。
故答案为:D。
根据实际生活经验以及题干中的具体数据来进行选择。
27.A
解:根据长方体体积公式可知,正确的算式是2×1。
故答案为:A。
长方体体积=底面积×高,正面的面积乘宽即可求出体积。计算体积时与高和总质量无关。
28.B
解:①不是最简分数。原来说法错误;
②20个零件中找1个次品(稍重),至少称3次能保证找出次品。正确;
③最小的合数是一个偶数。正确;
④分数可以分为真分数、假分数。原来说法错误。
故答案为:B。
①分数的分子和分母只有公因数1,这个分数就是最简分数;
②把20个零件分成7、7、6三份,称一次能把次品缩小到6个或7个中;称两次能把次品缩小到2个或3个中;称3次就能找出次品;
③合数是除了1和本身外还有其它因数的数,最小的合数是4;
④带分数严格说属于假分数,是假分数的另外一种表示形式。
29.C
解:根据特征可以确定列式正确的是长×2+宽×4+高×2+3。
故答案为:C。
彩带与长相等的有2段,与宽相等的有4段,与高相等的有2段,再加上手提的3分米长度就是彩带的总长度。
30.D
解:、、都能围成长方体,不能围成长方体。
故答案为:D。
长方体相对的面完全相同,根据长方体的特征判断即可。
31.B
解:把一个鸡蛋完全浸没在一个装满水的杯子里,溢出的水的体积就是鸡蛋的体积,大约有50mL。
故答案为:B。
杯子里面装满水,浸没一个鸡蛋,溢出水的体积就是鸡蛋的体积。一个鸡蛋的体积大约是50立方厘米。
32.C
解:甲长度×=乙长度×,<,所以甲长度大于乙长度。
故答案为:C。
根据分数乘法的意义得到,甲长度×=乙长度×,乘积相等,因此只需要比较两个分数的大小即可判断甲、乙的长短。
33.B
解:A:,分子和分母还有公因数3,不是最简分数;
B:,分子和分母只有公因数1,是最简分数;
C:,分子和分母还有公因数5,不是最简分数;
D:,分子和分母还有公因数13,不是最简分数。
故答案为:B。
最简分数的分子和分母只有公因数1。由此判断即可。
34.C
解:A:一部手机的长度不可能是457mm;
B:一台笔记本电脑的厚度不可能是271mm;
C:这个产品可能是一台微波炉;
D:一台冰箱的高度不可能是271mm。
故答案为:C。
可以先把单位统一成cm,45.7cm×39.5cm×27.1cm,然后根据实际情况判断这个产品即可。
35.C
解:3×3=9。
故答案为:C。
正方体的表面积=棱长×棱长×6,正方体的棱长扩大到原来的3倍,它的表面积扩大到原来的3×3=9倍。
36.D
解:A项:+;
B项:1--;
C项:÷;
D项:×。
故答案为:D。
A项:两种菜共用菜地的分率=生菜占的分率+香菜占的分率;
B项:其他口味占的分率=1-其余各项分别占的分率;
C项:6月份用煤的质量=7月份用煤的质量÷;
D项:笑笑吃的分率=一个蛋糕的一半×笑笑吃的分率。
37.C
解: A项:=3+7÷8=3.875;
B项:=1÷6=,所以<1.67;
C项:=5÷8=0.625<0.635;
D项:=1÷3=>0.333。
故答案为:C。
分数化成小数,用分数的分子除以分母,然后再比较大小。
38.B
解:A项:若 a×b=1,乘积是1的两个数互为倒数,原题干说法错误;
B项:1吨的=2吨的,原题干说法正确;
C项:冰箱容积是 250L,它的体积要大于 250dm3,原题干说法错误;
D项:牙膏盒的体积3立方分米太大,原题干说法错误。
故答案为:B。
A项:互为倒数的两个数相乘等于1;
B项:1吨的是吨,2吨的是吨,所以相等;
C项:冰箱有一定的厚度,所以冰箱的体积大于它的容积;
D项:根据实际生活经验以及题干中的具体数据来进行判断。
39.A
解:A项:13÷2=6.5,7>6.5, >;
B项:14÷2=7, =;
C项:15÷2=7.5,7<7.5, <;
D项:17÷2=8.5,8.5>7, <。
故答案为:A。
当分子大于分母的一半时,这个分数大于。
40.B
12=2×2×3
16=2×2×2×2
44=2×2×11
12、16、44的最大公因数是2×2=4,则每段长是4厘米,所用知识点为公因数。
故答案为:B。
要把右面这些木棒截成同样长的若干段,不能有剩余,每段最长是多少厘米,就是求12、16、44的最大公因数。
41.B
前表面积=长×宽,长方体的体积=长×宽×高。所以长方体的体积=前表面积×宽,即为60×5
故答案为:B。
根据图示确定长方体前面的面积=长×宽,长方体的体积=长×宽×高。再确定正确的算式。
42.B
解:(25+15)×2
=40×2
=80(米)。
故答案为:B。
水位线的长度=(长+宽)×2。
43.D
解:选择4根b和8根c,表面积是:
2×c×c+b×c×4=2c2+4bc。
故答案为:D。
选择4根b和8根c搭成长方体的两个对面是正方形,其余4个面是完全相同的长方形。表面积=长×宽×2+4×长×高。
44.C
解:5×4×2
=20×2
=40(平方厘米)。
故答案为:C。
沿着长5厘米,宽4厘米的面锯开, 增加的表面积最多,增加最多的表面积=长×高×增加面的个数。
45.B
解:8÷2=4(个)
6÷2=3(个)
5÷2=2(个)······1(厘米)
4×3×2
=12×2
=24(个)。
故答案为:B。
最多可以切小正方体的个数=长边最多切的个数×宽边最多切的个数×高边最多切的个数。
46.D
解:4×4×5×(6×5×3)
=16×5×90
=80×90
=7200(立方厘米)
7200立方厘米=7.2立方分米。
故答案为:D。
这个纸箱的体积=香皂的长×宽×高×纸箱最多能放香皂的块数。
47.D
解:A、B项:长方体的4条长、4条宽、4条高都相等,特殊情况下有8条棱长度相等,剩余4条棱长度相等,排除;
C项:不能大成长方体;
D项:能搭成一个长4厘米、宽4厘米,高6厘米的长方体。
故答案为:D。
长方体有12条棱,其中4条长、4条宽、4条高,长度分别相等;长方体有6个面,相对的面完全相同,特殊情况下,有4个面完全相同。
48.D
解:1×(8-5)
=1×3
=3(立方分米)。
故答案为:D。
小球的体积=正方体容器的底面积×(放入大、小球后的总高度-取出大球后的高度) 。
49.D
解:A、用复式条形统计图能更清楚地看出各班植树棵数的多少,不适合用复式折线统计图;
B、只涉及一个人的成绩数据,适合用单式折线统计图;
C、用条形统计图能直观地看出喜欢不同品牌牛奶的人数多少,不适合复式折线统计图;
D、既涉及两种品牌(两组数据),又关注销量随时间的变化趋势,适合用复式折线统计图;
故答案为:D。
复式折线统计图的特点是能同时反映两组或多组数据的变化趋势,通过逐个分析得出只有D涉及两种品牌(两组数据),因此答案为D。
选择题(一)
一、单选题
1.(2023五下·金东期末)甲、乙两人跑一段相同的路,甲用0.3小时,乙用小时,他们的速度相比,( )。
A.甲快 B.乙快 C.两人一样快 D.无法比较
2.(2024五下·瑞安期末)观察下图,估一估下面分数,不在 A、B 两点之间的是( )
A. B. C. D.
3.(2024五下·永康期末)将四个长 12cm,宽 8cm,高5cm 的长方体盒子,用彩纸包在一起,最省包装纸的方法是( )(接口处不计)
A. B.
C. D.
4.(2024五下·钱塘期末)用棱长为1cm的小正方体木块拼成长6cm,宽5cm,高4cm的长方体,一共要用( )个这样的小正方体木块。
A.20 B.30 C.24 D.120
5.(2024五下·平阳期末)下图是正方体的展开图,则折叠后,与“爱”相对的字是( )
A.学 B.习 C.数 D.学
6.(2024五下·奉化期末)如果长方体的长、宽、高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A.3 B.9 C.27 D.12
7.(2024五下·海盐期末)聪聪用纸板做一个无盖长方体纸盒,他已经做好了两个相邻的面(如下图),如果继续往下做,最少需要纸板( )平方厘米(接口处忽略不计)。
A.21 B.47 C.52 D.62
8.(2024五下·海盐期末)有两个非零自然数a和b,若a=b+1,则下列说法错误的是( )
A.a和b的和是奇数 B.是最简分数
C.a和b的积是奇数 D.a和b的最小公倍数是ab
9.(2024五下·海盐期末)的分母加45,要使分数的大小不变,分子应( )
A.乘5 B.乘 6 C.加 30 D.加 45
10.(2024五下·乐清期末)甲、乙两条线段各被遮住了一部分(如下图),甲、乙比较( )
A.甲比乙长 B.乙比甲长
C.甲和乙一样长 D.无法比较
11.(2024五下·柯桥期末)小丁按如图所示步骤估测一颗玻璃球的体积:
⑴将 的水倒入一个容积为 的杯子中;
⑵将 5 颗相同的玻璃球放进水中, 结果水未满;
⑶再放入 1 颗相同的玻璃球, 结果水溢出了。
根据以上步骤, 推测这样一颗玻璃球的体积范围最可能是( )
A. 以上, 以下 B. 以上, 以下
C. 以上, 以下 D. 以上, 以下
12.(2024五下·柯桥期末) 下面描述正确的序号是( )。
⑴奇数与偶数相乘, 积是奇数。
⑵有两个自然数 与 , 若 , 且 , 则 与 的最小公倍数是 。
⑶因为一个整数的末位数字是 2 的倍数, 这个整数就是 2 的倍数, 所以一个整数的末位数字是 3 的倍数,这个整数就是 3 的倍数。
⑷从 2024、2023、2022、2021、2020、2019 这六个数中任选两个数求和, 和是偶数的共有 6 种选法。
A.(1)(2)(4) B.(1)(2) C.(2)(4) D.(2)(3)
13.(2024五下·柯桥期末) 分母是 8 的所有最简真分数的和是( )
A.2 B. C.1 D.
14.(2024五下·钱塘期末)统计下面几组信息的数据,适合用复式折线统计图的是( )
A.五(1)班和五(2)班同学的植树棵树情况。
B.沙沙几次数学测试的成绩变化情况。
C.五(3)班同学喜欢喝x、y、z三种品牌牛奶的人数情况。
D.新华商场 2024年1-6月两种不同品牌空调的销售情况。
15.(2024五下·钱塘期末)如下图,甲、乙两条彩带都被遮住了一部分,露出部分的长度相等,则原来两条彩带长度比较的结果是( )
A.甲=乙 B.甲<乙 C.甲>乙 D.无法确定
16.(2023五下·柯桥期末)在 和 之间存在 ( ) 个分数。
A.0 B.1 C.无数 D.10
17.(2024五下·汉川期末)如下图,直线上点A在0和1之间,点A表示的数可能是( )。
A. B. C. D.
18.(2024五下·临平期末)一盒纯牛奶的外包装是长方体形状,包装纸上标注“净含量750mL”,实际外包装长8cm,宽5cm,那么高最有可能是( )cm。
A.15 B.18 C.19 D.25
19.(2024五下·临平期末)5月份的气温变化莫测。乐乐想知道杭州市2024年5月份整月的气温变化趋势,他要收集的数据是杭州市( )。
A.2024年各季度的平均气温
B.2024年5月份每天的平均气温
C.2024年各月的平均气温
D.2024年5月 1 日各时刻的气温
20.(2024五下·临平期末)下面可能与 不相等的分数是( )。
A. B. C. D.
21.(2024五下·临平期末)弟弟要做40道数学口算题,已完成了16道,还需完成全部题目的( )。
A. B. C. D.
22.(2024五下·临平期末)一个正方体的棱长扩大到原来的2 倍,则它的体积扩大到了原来的( )倍。
A.2 B.4 C.6 D.8
23.(2024五下·瑞安期末)下面的情况中,最适合用复式折线统计图表示的是( )
A.瑞安市今年5月份日平均气温变化情况
B.某校五年级各班男生、女生具体人数
C.两家零售店去年12个月销售额变化情况
D.小丽最近4次数学测试成绩变化情况
24.(2024五下·瑞安期末)瑞安是全国百强县之一,是一座共建共享、和谐安居的幸福之城。下面是聪聪设计的刻有“天瑞地安”的正方体礼盒展开图,其中相对的面刻有“瑞”和“安”的是( )
A. B.
C. D.
25.(2024五下·瑞安期末)下图中,涂色部分能用表示的是( )
A. B.
C. D.
26.(2024五下·瑞安期末)一个长方体物品长 21厘米,宽15厘米,高0.8厘米。这个物品最有可能是( )
A.手机 B.墨水盒 C.纸巾盒 D.数学书
27.(2024五下·慈溪期末)“神州十八号”飞行乘组将在中国空间站实施首次在轨水生生态研究项目。装有斑马鱼和金鱼藻的生态实验柜正面面积2m2,宽1m,高0.8m,总质量约0.5吨。要计算生态实验柜的体积,正确的算式是( )。
A.2×1 B.2×1×0.5 C.2×0.8 D.2×1×0.8
28.(2024五下·慈溪期末)下列说法中,正确的有( )个。
都是最简分数。
②20个零件中找1个次品(稍重),至少称3次能保证找出次品。
③最小的合数是一个偶数。
④分数可以分为真分数、假分数、带分数。
A.1 B.2 C.3 D.4
29.(2024五下·慈溪期末)如图的长方体礼盒用若干分米的彩带捆绑,并留3分米做手提带,彩带的总长是( )分米。
A.长×4+宽×4+高×4+3 B.长×4+宽×2+高×2+3
C.长×2+宽×4+高×2+3 D.长×2+宽×2+高×4+3
30.(2024五下·慈溪期末)下列图形中,通过折叠不能围成长方体的是( )。
A. B.
C. D.
31.(2024五下·慈溪期末)把一个鸡蛋完全浸没在一个装满水的杯子里,溢出的水大约有( )。
A.500mL B.50mL C.5mL D.5L
32.(2024五下·平阳期末)如图,甲、乙两根彩带都被遮住了一部分,露出部分的长度分别是全长的和,且长度相等。那么比较甲、乙两根彩带的长度,( )
A.甲<乙 B.甲=乙 C.甲>乙 D.无法比较
33.(2024五下·平阳期末)下列分数中,( )是最简分数。
A. B. C. D.
34.(2024五下·乐清期末)某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际想象一下,这个产品最有可能是( )。
A.一部手机 B.一台笔记本电脑
C.一台微波炉 D.一台冰箱
35.(2024五下·永康期末)正方体的棱长扩大到原来的3倍,它的表面积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
36.(2024五下·永康期末)下面能用“”解决的问题是( )
A.奶奶有一块菜地,种生菜,种香菜,两种菜共用了菜地的几分之几?
B.一袋糖果,巧克力味占,水果味占,其他口味占几分之几?
C.食堂7月份用煤吨,正好是6月份的,6月份用煤多少吨?
D.妈妈把半个蛋糕的给笑笑,笑笑吃了几个蛋糕?
37.(2024五下·永康期末)下列分数和小数比大小,正确的是( )
A. B. C. D.
38.(2024五下·永康期末)下面说法中正确的是( )
A.若 a+b=1,那么a和b互为倒数
B.1吨的和2吨的一样重
C.冰箱容积是 250L,它的体积就是 250dm3
D.牙膏盒的体积3分米3
39.(2024五下·永康期末)下列分数中比大的分数是( )
A. B. C. D.
40.(2024五下·上虞期末)下图是课本第 64 页中的最后一题,可以用( )的知识来解决。
A.公倍数 B.公因数 C.偶数
41.(2024五下·上虞期末)如图所示,一个长方体的收纳箱前面的面积是 60dm2,高是 6dm,宽是 5dm,要计算这个收纳箱的体积,正确的算式是( )
A.60×6 B.60×5 C.60×5×6
42.(2024五下·余杭期末)一个长方体游泳池,长25米,宽15米,高2米,在池底上面高1.2米处的地方画一条水位线,水位线长( )米。
A.(25+2)×2 B.(25+15)×2
C.(25+15+2)×2 D.(25+1.2)×2
43.(2024五下·余杭期末)小明在3根长a厘米、6根b厘米、8根c厘米长的小棒中,)平方厘米。选取了12根小棒搭成一个长方体。这个长方体的表面积是( )
A.2ab+2bc+2ac B.2a+4ab C.2b+4bc D.2c2+4bc
44.(2024五下·余杭期末)有一块长方体木料(如右图,单位:厘米)。小刚把它锯成同样大小的两个长方体木块。增加的表面积最多是( )平方厘米。
A.24 B.30 C.40 D.94
45.(2024五下·余杭期末)一个长方体长8cm,宽6cm,高5cm,把它切成棱长为2cm的小正方体,最多可以切( )个。
A.12 B.24 C.30 D.60
46.(2024五下·上城期末)将左图的香皂放入右图纸箱中,这个纸箱的体积是( )。(单位:cm)
A.80cm3 B.5760dm3 C.7200dm3 D.7.2dm3
47.(2024五下·上城期末)下图表示搭长方体模型所用的小棒、长方形的尺寸与数量,下列材料中,正好能搭成长方体模型的是( )
A.
B.
C.
D.
48.(2024五下·上城期末)下图中,长方体容器的底面积是1dm2,两个球浸没时正好水面与容器口平,分别拿出两个球,水面变化如图,那么,小球体积是( )。
A.0.3dm3 B.0.5dm3 C.0.8dm3 D.3dm3
49.(2024五下·钱塘期末)下面几组信息的数据统计,适合用复式折线统计图表示的是( )。
A.五(1)班和五(2)班同学的植树棵树情况
B.沙沙几次数学测试的成绩变化情况
C.五(3)班同学喜欢喝甲、乙、丙三种品牌牛奶的人数情况
D.新华商场2024年1~6月两种不同品牌空调的销量情况
答案解析部分
1.A
解:=1÷3=(小时)
0.3小时<小时,甲快。
故答案为:A。
甲、乙两人跑一段相同的路,用的时间少的,速度较快;先把分数化成小数后再比较大小。
2.D
解:A、B 两点之间的数大约是~之间。
A项:在 A、B 两点之间;
B项:在 A、B 两点之间;
C项:在 A、B 两点之间;
D项:=3÷2=1.5,不在 A、B 两点之间。
故答案为:D。
先确定A、B 两点之间的数大约是~之间。然后据此判断。
3.B
解:12×8的面积最大,最省包装纸的方法,把长×宽的面叠放在一起,是 。
故答案为:B。
最省包装纸的方法要把最大的面叠放在一起。
4.D
解:(6×5×4)÷(1×1×1)
=120÷1
=120(个)。
故答案为:D。
一共要用这样小正方体木块的个数=(长方体的长×宽×高)÷(小正方体木块的棱长×棱长×棱长)。
5.C
解:图中是正方体的展开图,则折叠后,与“爱”相对的字是“数”。
故答案为:C。
折叠后,“我”与“习”相对,“爱”与“数”相对,两个“学”相对。
6.C
解:3×3×3=27。
故答案为:C。
长方体的体积=长×宽×高,长方体的长、宽、高都扩大到原来的3倍,则它的体积扩大到原来的3×3×3=27倍。
7.B
解:5×2×2+3×2×2+5×3
=20+12+15
=32+15
=47(平方厘米)。
故答案为:B。
最少需要纸板的面积=长×高×2+宽×高×2+长×宽。
8.C
解:两个非零自然数a和b,若a=b+1,说面a、b是相邻的自然数,则a、b是互质数;
A项:相邻的自然数一个是奇数,一个是偶数,奇数+偶数=奇数,原题干说法正确
B项:a、b是互质数,则是最简分数,原题干说法正确;
C项:奇数×偶数=偶数,原题干说法错误;
D项:a、b最小公倍数是它们的积ab,原题干说法正确。
故答案为:C。
两个非零自然数a和b,若a=b+1,说面a、b是相邻的自然数,一个是奇数,一个是偶数,则a、b是互质数,据此选择。
9.B
解:(9+45)÷9
=54÷9
=6,分子应乘6。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
10.A
解:甲×=乙×,,所以甲比乙长。
故答案为:A。
因为露出的长度相等,所以得到甲×=乙×,乘积相等,所以只需要比较两个分数的大小即可判断两根线段的长短。
11.B
解:(500-300)÷(5+1)
=200÷6
≈33(立方厘米)
(500-300)÷5
=200÷5
=40(立方厘米)
则这样一颗玻璃球的体积范围最可能是30立方厘米以上,40立方厘米以下。
故答案为:B。
杯子中还剩下的容积=500-300=200毫升,因为将5颗相同的玻璃球放进水中, 结果水未满,但是再放入 1 颗相同的玻璃球,结果水溢出了,说明这样一颗玻璃球的体积范围最小是杯子中还剩下的容积÷6颗,最大是杯子中还剩下的容积÷5颗。
12.C
解:(1)如1×4=4,3×6=18,积是偶数,原题干说法错误;
(2)a、b的最小公倍数是ab,原题干说法正确;
(3)如13、23不是3的倍数,原题干说法错误;
(4)奇数+奇数=偶数,可以选2023+2021、2023+2019、2021+2019;
偶数+偶数=偶数,可以选2024+2022、2024+2020、2022+2020;
3+3=6(种)选法,原题干说法正确。
故答案为:C。
(1)奇数×偶数=偶数;
(2)相邻的自然数是互质数,最小公倍数是它们的积
(3)一个数各个数位上的数的和是3的倍数,这个数就是3的倍数;
(4)奇数+奇数=偶数,偶数+偶数=偶数,据此选一选。
13.A
解:+++
=
=2。
故答案为:A。
分子比分母小的分数是真分数;分子和分母只有公因数1的分数是最简分数,据此写出这几个分数后再相加。
14.D
解:A项:适合复式条形统计图;
B项:适合单式折线统计图;
C项:适合单式条形统计图;
D项:适合复式折线统计图。
故答案为:D。
要统计的数据是两项或者以上时,要用复式统计图,并且条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
15.C
解:甲的=乙的,因为<,所以甲>乙。
故答案为:C。
露出部分的长度相等,也就是甲的=乙的,因为<,所以甲>乙。
16.C
解:在 和 之间存在无数个分数。
故答案为:C。
任何两个不相等的分数之间有无数个分数。
17.C
解:<<<,点A表示的数可能是。
故答案为:C。
点A在0和1之间,并且比大,且靠近的地方,则可能是。
18.C
解:750÷5÷8
=150÷8
≈19(cm)
故答案为:C。
长方体体积=长×宽×高,可以用净含量除以包装的长和宽,采用进一法取整数就是可能的高度。
19.B
解:5月份的气温变化莫测。乐乐想知道杭州市2024年5月份整月的气温变化趋势,他要收集的数据是杭州市2024年5月份每天的平均气温。
故答案为:B。
要想知道5月份整月的气温变化趋势,因此只需要知道5月份每天的平均气温即可。
20.C
解:A:=;
B:=;
C:一定与不相等;
D:=。
故答案为:C。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数值不变。根据分数的基本性质逐项判断即可。
21.C
解:(40-16)÷40
=24÷40
=
故答案为:C。
用要做的道数减去已经完成的道数求出还需完成的道数,用还需完成的道数除以要做的道数即可求出还需完成全部题目的几分之几。
22.D
解:2×2×2=8,一个正方体的棱长扩大到原来的2 倍,则它的体积扩大到了原来的8倍。
故答案为:D。
正方体体积=棱长×棱长×棱长,所以正方体体积扩大的倍数是棱长扩大倍数的立方倍。
23.C
解:A项:适合用单式折线统计图表示;
B项:适合用复式条形统计图表示;
C项:适合用复式折线统计图表示;
D项:适合用单式折线统计图表示。
故答案为:C。
适合用复式条形统计图表示首先得是两项内容,并且清楚地看出数量的增减变化情况。
24.A
解:A项:“瑞”和“安”相对;
B项:“瑞”和“地”相对;
C项:“瑞”不和“安”相对;
D项:“瑞”和“天”相对。
故答案为:A。
正方体相对的面不相邻,据此判断A项中“瑞”和“安”相对。
25.A
解:A项:1÷8=;
B项:1÷6=;
C项:2÷32=;
D项:不是平均分不能用分数表示。
故答案为:A。
分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,分子是几,就表示有几个这样的分数单位。
26.D
解:长21厘米,宽15厘米,高0.8厘米的物品最有可能是数学书。
故答案为:D。
根据实际生活经验以及题干中的具体数据来进行选择。
27.A
解:根据长方体体积公式可知,正确的算式是2×1。
故答案为:A。
长方体体积=底面积×高,正面的面积乘宽即可求出体积。计算体积时与高和总质量无关。
28.B
解:①不是最简分数。原来说法错误;
②20个零件中找1个次品(稍重),至少称3次能保证找出次品。正确;
③最小的合数是一个偶数。正确;
④分数可以分为真分数、假分数。原来说法错误。
故答案为:B。
①分数的分子和分母只有公因数1,这个分数就是最简分数;
②把20个零件分成7、7、6三份,称一次能把次品缩小到6个或7个中;称两次能把次品缩小到2个或3个中;称3次就能找出次品;
③合数是除了1和本身外还有其它因数的数,最小的合数是4;
④带分数严格说属于假分数,是假分数的另外一种表示形式。
29.C
解:根据特征可以确定列式正确的是长×2+宽×4+高×2+3。
故答案为:C。
彩带与长相等的有2段,与宽相等的有4段,与高相等的有2段,再加上手提的3分米长度就是彩带的总长度。
30.D
解:、、都能围成长方体,不能围成长方体。
故答案为:D。
长方体相对的面完全相同,根据长方体的特征判断即可。
31.B
解:把一个鸡蛋完全浸没在一个装满水的杯子里,溢出的水的体积就是鸡蛋的体积,大约有50mL。
故答案为:B。
杯子里面装满水,浸没一个鸡蛋,溢出水的体积就是鸡蛋的体积。一个鸡蛋的体积大约是50立方厘米。
32.C
解:甲长度×=乙长度×,<,所以甲长度大于乙长度。
故答案为:C。
根据分数乘法的意义得到,甲长度×=乙长度×,乘积相等,因此只需要比较两个分数的大小即可判断甲、乙的长短。
33.B
解:A:,分子和分母还有公因数3,不是最简分数;
B:,分子和分母只有公因数1,是最简分数;
C:,分子和分母还有公因数5,不是最简分数;
D:,分子和分母还有公因数13,不是最简分数。
故答案为:B。
最简分数的分子和分母只有公因数1。由此判断即可。
34.C
解:A:一部手机的长度不可能是457mm;
B:一台笔记本电脑的厚度不可能是271mm;
C:这个产品可能是一台微波炉;
D:一台冰箱的高度不可能是271mm。
故答案为:C。
可以先把单位统一成cm,45.7cm×39.5cm×27.1cm,然后根据实际情况判断这个产品即可。
35.C
解:3×3=9。
故答案为:C。
正方体的表面积=棱长×棱长×6,正方体的棱长扩大到原来的3倍,它的表面积扩大到原来的3×3=9倍。
36.D
解:A项:+;
B项:1--;
C项:÷;
D项:×。
故答案为:D。
A项:两种菜共用菜地的分率=生菜占的分率+香菜占的分率;
B项:其他口味占的分率=1-其余各项分别占的分率;
C项:6月份用煤的质量=7月份用煤的质量÷;
D项:笑笑吃的分率=一个蛋糕的一半×笑笑吃的分率。
37.C
解: A项:=3+7÷8=3.875;
B项:=1÷6=,所以<1.67;
C项:=5÷8=0.625<0.635;
D项:=1÷3=>0.333。
故答案为:C。
分数化成小数,用分数的分子除以分母,然后再比较大小。
38.B
解:A项:若 a×b=1,乘积是1的两个数互为倒数,原题干说法错误;
B项:1吨的=2吨的,原题干说法正确;
C项:冰箱容积是 250L,它的体积要大于 250dm3,原题干说法错误;
D项:牙膏盒的体积3立方分米太大,原题干说法错误。
故答案为:B。
A项:互为倒数的两个数相乘等于1;
B项:1吨的是吨,2吨的是吨,所以相等;
C项:冰箱有一定的厚度,所以冰箱的体积大于它的容积;
D项:根据实际生活经验以及题干中的具体数据来进行判断。
39.A
解:A项:13÷2=6.5,7>6.5, >;
B项:14÷2=7, =;
C项:15÷2=7.5,7<7.5, <;
D项:17÷2=8.5,8.5>7, <。
故答案为:A。
当分子大于分母的一半时,这个分数大于。
40.B
12=2×2×3
16=2×2×2×2
44=2×2×11
12、16、44的最大公因数是2×2=4,则每段长是4厘米,所用知识点为公因数。
故答案为:B。
要把右面这些木棒截成同样长的若干段,不能有剩余,每段最长是多少厘米,就是求12、16、44的最大公因数。
41.B
前表面积=长×宽,长方体的体积=长×宽×高。所以长方体的体积=前表面积×宽,即为60×5
故答案为:B。
根据图示确定长方体前面的面积=长×宽,长方体的体积=长×宽×高。再确定正确的算式。
42.B
解:(25+15)×2
=40×2
=80(米)。
故答案为:B。
水位线的长度=(长+宽)×2。
43.D
解:选择4根b和8根c,表面积是:
2×c×c+b×c×4=2c2+4bc。
故答案为:D。
选择4根b和8根c搭成长方体的两个对面是正方形,其余4个面是完全相同的长方形。表面积=长×宽×2+4×长×高。
44.C
解:5×4×2
=20×2
=40(平方厘米)。
故答案为:C。
沿着长5厘米,宽4厘米的面锯开, 增加的表面积最多,增加最多的表面积=长×高×增加面的个数。
45.B
解:8÷2=4(个)
6÷2=3(个)
5÷2=2(个)······1(厘米)
4×3×2
=12×2
=24(个)。
故答案为:B。
最多可以切小正方体的个数=长边最多切的个数×宽边最多切的个数×高边最多切的个数。
46.D
解:4×4×5×(6×5×3)
=16×5×90
=80×90
=7200(立方厘米)
7200立方厘米=7.2立方分米。
故答案为:D。
这个纸箱的体积=香皂的长×宽×高×纸箱最多能放香皂的块数。
47.D
解:A、B项:长方体的4条长、4条宽、4条高都相等,特殊情况下有8条棱长度相等,剩余4条棱长度相等,排除;
C项:不能大成长方体;
D项:能搭成一个长4厘米、宽4厘米,高6厘米的长方体。
故答案为:D。
长方体有12条棱,其中4条长、4条宽、4条高,长度分别相等;长方体有6个面,相对的面完全相同,特殊情况下,有4个面完全相同。
48.D
解:1×(8-5)
=1×3
=3(立方分米)。
故答案为:D。
小球的体积=正方体容器的底面积×(放入大、小球后的总高度-取出大球后的高度) 。
49.D
解:A、用复式条形统计图能更清楚地看出各班植树棵数的多少,不适合用复式折线统计图;
B、只涉及一个人的成绩数据,适合用单式折线统计图;
C、用条形统计图能直观地看出喜欢不同品牌牛奶的人数多少,不适合复式折线统计图;
D、既涉及两种品牌(两组数据),又关注销量随时间的变化趋势,适合用复式折线统计图;
故答案为:D。
复式折线统计图的特点是能同时反映两组或多组数据的变化趋势,通过逐个分析得出只有D涉及两种品牌(两组数据),因此答案为D。
同课章节目录
