2025年中考数学课件:专项十 几何探究题 课件(75张PPT)
文档属性
| 名称 | 2025年中考数学课件:专项十 几何探究题 课件(75张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 11:26:07 | ||
图片预览









文档简介
(共75张PPT)
第一部分 专项突破
难点·压轴专项
专项十 几何探究题
几何探究题通常根据基本的几何图形或身边的实物素材(如学具),开展与之
相关的多层次多角度的数学问题探究,借助一定的实物操作与理性思考、分析与探
究,得出一些有价值的猜想与结论,并拓展延伸或应用相关的知识与结论解决问题,
重在经历“问题探究—问题解决”的过程.主要考查类型有:①动点型探究题;②几何
变换操作型探究题;③新定义型探究题;④作图操作型探究题.
类型1 动点型
【解题策略】解决动点问题的关键在于化动为静,抓住其中的等量关系、变量
关系,用运动与变化的观点构建数学模型(函数模型、方程模型或不等式模型)去
分析与解决问题.
例1(1) 问题发现:如图1,点为平面内一动点,且, ,
则的最小值为______, 的最大值为______.
(2) 轻松尝试:如图2,在矩形中,,,为 边的中
点,是边上的动点,将沿所在直线折叠得到,连接 ,则
的最小值为___.
8
(3) 方法运用:在四边形中, ,,,.
① 如图3,当时,求线段 的最大值;
解:如图,以为直角边作等腰直角三角形,则 .
,,, .
.
当取最大值时,最大,即当,,三点共线时,最大,即图中
的长为最大值.
,, .
当时,线段的最大值为 .
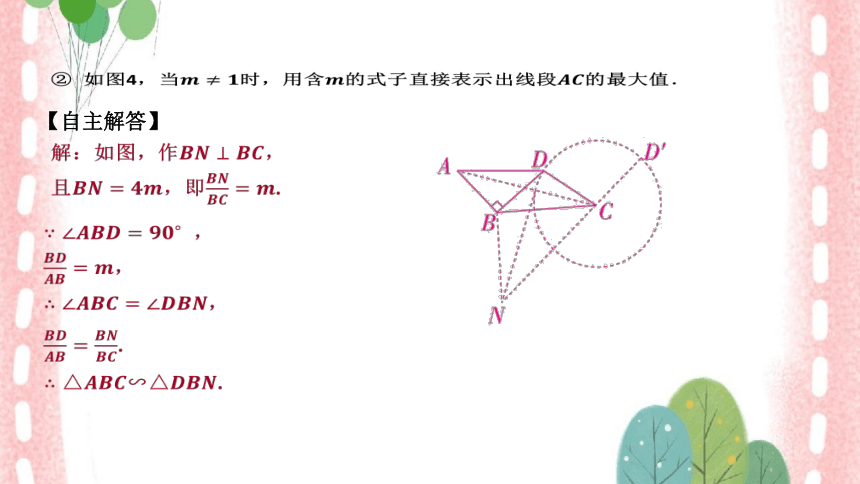
② 如图4,当时,用含的式子直接表示出线段 的最大值.
【自主解答】
解:如图,作 ,
且,即 .
,
,
,
.
.
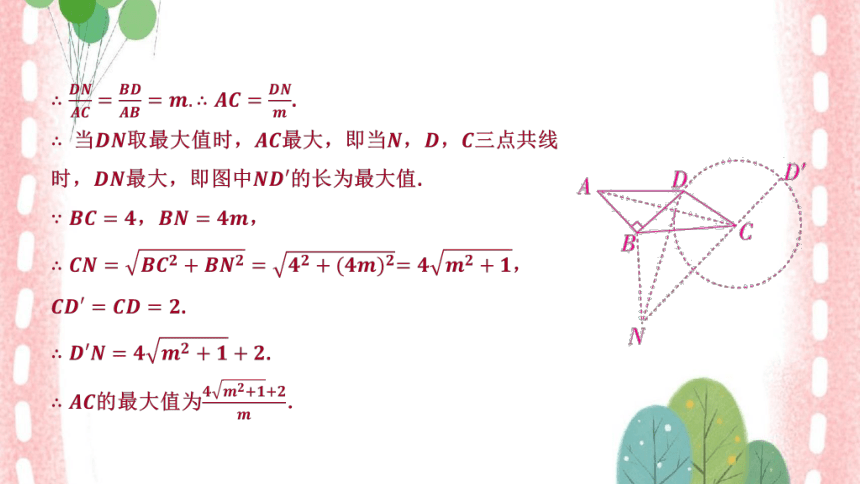
.
当取最大值时,最大,即当,, 三点共线
时,最大,即图中 的长为最大值.
, ,
,
.
.
的最大值为 .
类型2 几何变换操作型
【解题策略】一是分析变换前图形的形状、位置、大小;二是对变换过程作全
面分析,抓住变换要素及变换过程中的不变量和变量;三是借助变换的性质,化动
为静,动静结合,从特殊情形入手与类比;四是进一步分析与探究相关图形性质的
变与不变.
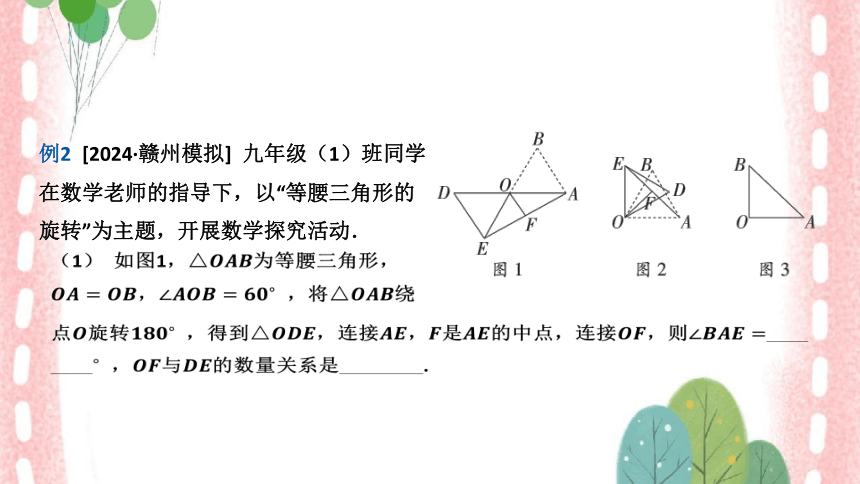
例2 [2024·赣州模拟] 九年级(1)班同学
在数学老师的指导下,以“等腰三角形的
旋转”为主题,开展数学探究活动.
(1) 如图1, 为等腰三角形,
, ,将 绕
点旋转 ,得到,连接,是的中点,连接,则 ____
____ ,与 的数量关系是________.
【操作探究】
【迁移探究】
(2) 如图2,(1)中的其他条件不变,当绕点逆时针旋转时,点 正好落
在的平分线上,得到,求出此时的度数及与 的数量关系.
【拓展应用】
(3) 如图3,在等腰三角形中,, .将 绕
点旋转,得到,连接,是的中点,连接.当 时,
请直接写出 的长.
【自主解答】
(1) 如图1, 为等腰三角形,
, ,将绕点 旋转 ,得到,连接,是
的中点,连接,则____ ,与 的数量关系是___________.
90
【迁移探究】
(2) 如图2,(1)中的其他条件不变,当绕点逆时针旋转时,点 正好落
在的平分线上,得到,求出此时的度数及与 的数量关系.
解:由旋转的性质,可知 .
为等边三角形,平分, 为等边三角形,
, .
.
, , 是等腰直角三角形.
.
是的中点, .
是等腰直角三角形. .
【拓展应用】
(3) 如图3,在等腰三角形中,, .将 绕
点旋转,得到,连接,是的中点,连接.当 时,
请直接写出 的长.
【自主解答】
解:分以下两种情况进行讨论:
①如答图1,当点在 右边时,
, , 为等腰直角三角形.
.
, .由旋转的性质,得
,
为等边三角形.是的中点,, 平分
.
.
②如答图2,当点在 左边时,
同理,可得 ,, .
综上所述,的长为 或2.
类型3 新定义型
【解题策略】首先认真阅读与理解新定义图形的概念、性质,将相关内容转化
为熟悉的或已知的内容,在此基础上,结合所学知识分析与求解相关问题.
例3 [2024·吉安三模] 我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1、
图2、图3中,,是的中线,,垂足为.像 这样的三角
形均为“中垂三角形”.设,, .
【特例探索】
(1)① 如图1,当 ,时,________, ________.
② 如图2,当 ,时,求和 的值.
【归纳证明】
(2) 请你观察(1)中的计算结果,猜想,, 三者之间的关系,用等式表示出
来,并利用图3证明你发现的关系式.
(3) 利用(2)中的结论,解答下列问题:
在边长为3的菱形中,为对角线,的交点,, 分别为线段
,的中点,连接,并延长,交于点,,分别交于点, ,
如图4所示,求 的值.
【自主解答】
(1)① 如图1,当 ,时,_____, _____.
[解析] 在图1中,, .
.
② 如图2,当 ,时,求和 的值.
[答案] 同理可得,,则, .
【归纳证明】
(2) 请你观察(1)中的计算结果,猜想,, 三者之间的关系,用等式表示出
来,并利用图3证明你发现的关系式.
[答案] 关系式为 .
证明:如图3,易得:, ,则
.
(3) 利用(2)中的结论,解答下列问题:
在边长为3的菱形中,为对角线,的交点,, 分别为线段
,的中点,连接,并延长,交于点,,分别交于点, ,
如图4所示,求 的值.
【自主解答】
[答案] 连接,分别为线段,的中点, ,
.
点,分别是, 的中点.
,, .
同理可得, .
, .
同理可得,则 .
类型4 作图操作型
【解题策略】解答此类作图操作型问题,首先要动手实践与作图,在作图中增
强直观感受与体验,其次弄清作图之后的图形变化特征,上升到理性思考与推理,
最后发现相关图形的形状、位置与大小关系的本质特征.
例4 【课本再现】
(1) 在证明“三角形内角和定理”时,小明只撕下三角形纸片的一个角拼成图1即
可证明,其中与 相等的角是________.
【类比迁移】
(2) 如图2,在四边形中,与互余.小明发现四边形 中这
对互余的角可类比(1)中思路进行拼合:先作,再过点 作
于点,连接,发现,, 之间的数量关系是________.
【方法运用】
(3) 如图3,在四边形中,连接, ,点是 两边垂
直平分线的交点,连接, .
① 求证: .
② 连接,如图4,已知,,,求 的长
(用含, 的式子表示).
【自主解答】
(1) 在证明“三角形内角和定理”时,小明只撕下三角形纸片的一个角拼成图1即
可证明,其中与 相等的角是_______.
【类比迁移】
(2) 如图2,在四边形中,与互余.小明发现四边形 中这
对互余的角可类比(1)中思路进行拼合:先作,再过点 作
于点,连接,发现,, 之间的数量关系是________________
__.
【方法运用】
(3) 如图3,在四边形中,连接, ,点是 两边垂
直平分线的交点,连接, .
① 求证: .
解:如图3,连接,作的外接圆 .
点是两边垂直平分线的交点, 点是 的外心.
, .
,, .
.
② 连接,如图4,已知,,,求 的长
(用含, 的式子表示).
【自主解答】
解:如图4,在射线的下方作,过点 作
于点,连接 .
,, .
,., .
. ,
. .
,
, ,
.
.
类型1 新定义型
1.我们定义:有一组邻角相等的凸四边形
叫作“等邻角四边形”.
(1) 【概念理解】
请你根据上述定义举一个等邻角四边形的
例子,例如________是等邻角四边形.
(2) 【问题探究】
如图1,在等邻角四边形中,,, 的垂直平分线恰好交
于边上一点,连接,,试探究与 的数量关系,并说明理由.
. .
. .
(3) 【应用拓展】
如图2,在与中, ,, .将
绕着点顺时针旋转角得到 (如图3),当四边
形 为等邻角四边形时,求出它的面积.
(1) 【概念理解】
请你根据上述定义举一个等邻角四边形的例子,例如__________________________
_______________是等邻角四边形.
直角梯形或矩形或正方形(答案不唯一)
(2) 【问题探究】
如图1,在等邻角四边形中,,, 的垂直平分线恰好交
于边上一点,连接,,试探究与 的数量关系,并说明理由.
解:.理由如下:连接, ,如图1所示.
是的垂直平分线,是的垂直平分线,, .
,, .
, .
(3) 【应用拓展】
如图2,在与中, ,, .将
绕着点顺时针旋转角得到 (如图3),当四边
形 为等邻角四边形时,求出它的面积.
解:分两种情况考虑:①当时,延长,交于点 ,如答图2
所示.
.
由已知易得 .
设,由勾股定理得 ,
解得 .
过点作于点, .
,即,解得 .
,
.
.
②当 时,过点 作
于点 ,如答图3所示.
易得 ,
.
.
综上所述,四边形的面积为 或
.
2.[2024·中山市一模] 我们定义:对角线互
相垂直且相等的四边形叫作“神奇四边形”.
(1) 在我们学过的四边形:①平行四边
形、②矩形、③菱形、④正方形中,是“神
奇四边形”的是________(填序号).
(2) 如图1,在正方形中,为上一点,连接,过点作 于点
,交于点,连接, .
① 求证:四边形 是“神奇四边形”.
② 如图2,点,,,分别是,,, 的中点,试判断四边形
是不是“神奇四边形”.
(3) 如图3,点,分别在正方形的边,上,把正方形沿直线 翻
折,使得的对应边恰好经过点,过点作于点.若 ,正方
形的边长为6,求线段 的长.
(1) 在我们学过的四边形:①平行四边
形、②矩形、③菱形、④正方形中,是“神
奇四边形”的是____(填序号).
④
(2) 如图1,在正方形中,为
上一点,连接,过点作于点 ,
交于点,连接, .
① 求证:四边形 是“神奇四边形”.
证明: 四边形 是正方形,
.
.
, .
.
在和中,
.又, 四边形 是“神奇四边形”.
② 如图2,点,,,分别是,,, 的中点,试判断四边形
是不是“神奇四边形”.
解:四边形 是“神奇四边形”.理由如下:
,为,的中点,为的中位线., .
同理,可得,,,,, ,
, 四边形为平行四边形., .
平行四边形为菱形.,, ,
.
四边形为正方形. 四边形 是“神奇四边形”.
(3) 如图3,点,分别在正方形的边,上,把正方形沿直线 翻
折,使得的对应边恰好经过点,过点作于点.若 ,正方
形的边长为6,求线段 的长.
解:如图3,延长交于点 ,由翻折的性质可知,
,,, .
四边形是正方形,边长为6,, .
, .
.设,则 ,在
中,由勾股定理得:
,.. ,
.
,即线段 的长
为 .
类型2 几何变换操作型
3.[2024·景德镇二模] 【问题情境】在数学
活动课上,同学们用两张矩形纸片进行探
究活动.小组同学准备了两张矩形纸片
和,其中, ,将
它们按如图1所示的方式放置,点, 分别
【观察发现】
(1) 如图2所示,当 时,小组成员发现与 存在的数量关系为______;
位置关系为________.
落在,边上时,点,恰好为边,的中点.然后将矩形纸片 绕
点按顺时针方向旋转,旋转角为 ,连接与 .
. .
. .
【探索猜想】
(2) 如图3所示,当 时,
(1)中发现的结论是否仍然成立?请说明
理由.
【拓展延伸】
(3) 在矩形的旋转过程中,交
于点,交于点,连接, ,
是否为定值?如果是,请直接写
出此定值;如果不是,请你说明理由.
(1) 如图2所示,当 时,小组成员发现与 存在的数量关系为______
__;位置关系为_________.
解:如图2,延长交于点 .
点,恰好为边, 的中点,
, .
四边形和都是矩形, ,
.
, ,
, ,
.故答案为:; .
[答案] ;
【探索猜想】
(2) 如图3所示,当 时,(1)中发现的结论是否仍然成立?请
说明理由.
[答案] 当 时,(1)中发现的结论仍然成立.理
由如下:
如图3,连接, .
四边形和都是矩形, .
,即 .
,, .
, .
与交于点,与交于点,则 ,
.
当 时,与的数量关系是 ;位置关
系是 .
【拓展延伸】
(3) 在矩形的旋转过程中,交于点,交于点,连接, ,
是否为定值?如果是,请直接写出此定值;如果不是,请你说明理由.
[答案] 为定值65.理由如下:
由(2)得,、、、 均为直角三角形.
根据勾股定理得:,, ,
,
,
,
,即 为定值65.
类型3 动点型
4.综合与实践
如图1,在中,, ,点是平面内一点,连接, ,
分别以,为斜边向上画等腰直角三角形和,连接, .
. .
. .
【特例感知】
(1) 当点在边上时,延长交于点, .
① 如图2,当是边的中点时,________,____ ;
② 如图3,当不是边的中点时,________,____ .
【猜想证明】
(2) 当点不在边上时,猜想与 的关系,并结合图1进行证明.
【拓展应用】
(3) 如图4,在中,,, ,以 ,
为边向上分别作两个正方形和,它们的中心分别为, ,连接
,试求线段 的长.
(1) 当点在边上时,延长交于点, .
① 如图2,当是边的中点时,_____,____ ;
② 如图3,当不是边的中点时,_____,____ .
90
90
【猜想证明】
(2) 当点不在边上时,猜想与 的关系,并结合图1进行证明.
解:,.证明:如图1,过点作 ,过点
作于点,连接 .
, , 四边形 是正方形.
, , .
, , ,
.
, .
又 ,, ,
.
,.延长交于点 ,
.
.
【拓展应用】
(3) 如图4,在中,,, ,以 ,
为边向上分别作两个正方形和,它们的中心分别为, ,连接
,试求线段 的长.
解:如图4,连接,,, .
正方形和的中心分别为,,和 都是等腰直
角三角形.
以为斜边构造等腰直角三角形,连接,则 .
作的中点,连接 .
过点作交于点,过点作于点 .
, ,
.
在中,.故线段的长为 .
类型4 作图操作型
5.综合与实践
【问题情境】
数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质.
已知, ,点为上一动点,将以 为对称轴翻折.同
学们经过思考后进行如下探究:
【独立思考】
小明:“当点落在上时, .”
小红:“若点为的中点,给出与的长,就可求出 的长.”
. .
. .
【实践探究】
奋进小组的同学们经过探究后提出问题1,请你回答:
问题1: 在等腰中,, ,由 翻折得到.
(1) 如图1,当点落在上时,求证: .
(2) 如图2,若点为的中点,,,求 的长.
【问题解决】
小明经过探究发现:若将问题1中的等腰三角形换成
将问题进一步拓展.
问题2: 如图3,在等腰中, , ,
.若,求 的长.
问题1: 在等腰中,, ,由 翻折得到.
(1) 如图1,当点落在上时,求证: .
证明:, .
由 翻折得到,
.
, .
(2) 如图2,若点为的中点,,,求 的长.
解:如答图1,连接,交于点 .
由翻折得到,, ,
.
又 点是 的中点,
, .
在中, .
在中, ,
.
【问题解决】
小明经过探究发现:若将问题1中的等腰三角形换成
将问题进一步拓展.
问题2: 如图3,在等腰中, , ,
.若,求 的长.
[答案] 如答图2,连接,过点作于点,过点作于点 .
, ,
,
.
,
.
.
又, 四边形 是矩形.
.
在中,, ,
.
, .
在 中,
,
.
在中, .
第一部分 专项突破
难点·压轴专项
专项十 几何探究题
几何探究题通常根据基本的几何图形或身边的实物素材(如学具),开展与之
相关的多层次多角度的数学问题探究,借助一定的实物操作与理性思考、分析与探
究,得出一些有价值的猜想与结论,并拓展延伸或应用相关的知识与结论解决问题,
重在经历“问题探究—问题解决”的过程.主要考查类型有:①动点型探究题;②几何
变换操作型探究题;③新定义型探究题;④作图操作型探究题.
类型1 动点型
【解题策略】解决动点问题的关键在于化动为静,抓住其中的等量关系、变量
关系,用运动与变化的观点构建数学模型(函数模型、方程模型或不等式模型)去
分析与解决问题.
例1(1) 问题发现:如图1,点为平面内一动点,且, ,
则的最小值为______, 的最大值为______.
(2) 轻松尝试:如图2,在矩形中,,,为 边的中
点,是边上的动点,将沿所在直线折叠得到,连接 ,则
的最小值为___.
8
(3) 方法运用:在四边形中, ,,,.
① 如图3,当时,求线段 的最大值;
解:如图,以为直角边作等腰直角三角形,则 .
,,, .
.
当取最大值时,最大,即当,,三点共线时,最大,即图中
的长为最大值.
,, .
当时,线段的最大值为 .
② 如图4,当时,用含的式子直接表示出线段 的最大值.
【自主解答】
解:如图,作 ,
且,即 .
,
,
,
.
.
.
当取最大值时,最大,即当,, 三点共线
时,最大,即图中 的长为最大值.
, ,
,
.
.
的最大值为 .
类型2 几何变换操作型
【解题策略】一是分析变换前图形的形状、位置、大小;二是对变换过程作全
面分析,抓住变换要素及变换过程中的不变量和变量;三是借助变换的性质,化动
为静,动静结合,从特殊情形入手与类比;四是进一步分析与探究相关图形性质的
变与不变.
例2 [2024·赣州模拟] 九年级(1)班同学
在数学老师的指导下,以“等腰三角形的
旋转”为主题,开展数学探究活动.
(1) 如图1, 为等腰三角形,
, ,将 绕
点旋转 ,得到,连接,是的中点,连接,则 ____
____ ,与 的数量关系是________.
【操作探究】
【迁移探究】
(2) 如图2,(1)中的其他条件不变,当绕点逆时针旋转时,点 正好落
在的平分线上,得到,求出此时的度数及与 的数量关系.
【拓展应用】
(3) 如图3,在等腰三角形中,, .将 绕
点旋转,得到,连接,是的中点,连接.当 时,
请直接写出 的长.
【自主解答】
(1) 如图1, 为等腰三角形,
, ,将绕点 旋转 ,得到,连接,是
的中点,连接,则____ ,与 的数量关系是___________.
90
【迁移探究】
(2) 如图2,(1)中的其他条件不变,当绕点逆时针旋转时,点 正好落
在的平分线上,得到,求出此时的度数及与 的数量关系.
解:由旋转的性质,可知 .
为等边三角形,平分, 为等边三角形,
, .
.
, , 是等腰直角三角形.
.
是的中点, .
是等腰直角三角形. .
【拓展应用】
(3) 如图3,在等腰三角形中,, .将 绕
点旋转,得到,连接,是的中点,连接.当 时,
请直接写出 的长.
【自主解答】
解:分以下两种情况进行讨论:
①如答图1,当点在 右边时,
, , 为等腰直角三角形.
.
, .由旋转的性质,得
,
为等边三角形.是的中点,, 平分
.
.
②如答图2,当点在 左边时,
同理,可得 ,, .
综上所述,的长为 或2.
类型3 新定义型
【解题策略】首先认真阅读与理解新定义图形的概念、性质,将相关内容转化
为熟悉的或已知的内容,在此基础上,结合所学知识分析与求解相关问题.
例3 [2024·吉安三模] 我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1、
图2、图3中,,是的中线,,垂足为.像 这样的三角
形均为“中垂三角形”.设,, .
【特例探索】
(1)① 如图1,当 ,时,________, ________.
② 如图2,当 ,时,求和 的值.
【归纳证明】
(2) 请你观察(1)中的计算结果,猜想,, 三者之间的关系,用等式表示出
来,并利用图3证明你发现的关系式.
(3) 利用(2)中的结论,解答下列问题:
在边长为3的菱形中,为对角线,的交点,, 分别为线段
,的中点,连接,并延长,交于点,,分别交于点, ,
如图4所示,求 的值.
【自主解答】
(1)① 如图1,当 ,时,_____, _____.
[解析] 在图1中,, .
.
② 如图2,当 ,时,求和 的值.
[答案] 同理可得,,则, .
【归纳证明】
(2) 请你观察(1)中的计算结果,猜想,, 三者之间的关系,用等式表示出
来,并利用图3证明你发现的关系式.
[答案] 关系式为 .
证明:如图3,易得:, ,则
.
(3) 利用(2)中的结论,解答下列问题:
在边长为3的菱形中,为对角线,的交点,, 分别为线段
,的中点,连接,并延长,交于点,,分别交于点, ,
如图4所示,求 的值.
【自主解答】
[答案] 连接,分别为线段,的中点, ,
.
点,分别是, 的中点.
,, .
同理可得, .
, .
同理可得,则 .
类型4 作图操作型
【解题策略】解答此类作图操作型问题,首先要动手实践与作图,在作图中增
强直观感受与体验,其次弄清作图之后的图形变化特征,上升到理性思考与推理,
最后发现相关图形的形状、位置与大小关系的本质特征.
例4 【课本再现】
(1) 在证明“三角形内角和定理”时,小明只撕下三角形纸片的一个角拼成图1即
可证明,其中与 相等的角是________.
【类比迁移】
(2) 如图2,在四边形中,与互余.小明发现四边形 中这
对互余的角可类比(1)中思路进行拼合:先作,再过点 作
于点,连接,发现,, 之间的数量关系是________.
【方法运用】
(3) 如图3,在四边形中,连接, ,点是 两边垂
直平分线的交点,连接, .
① 求证: .
② 连接,如图4,已知,,,求 的长
(用含, 的式子表示).
【自主解答】
(1) 在证明“三角形内角和定理”时,小明只撕下三角形纸片的一个角拼成图1即
可证明,其中与 相等的角是_______.
【类比迁移】
(2) 如图2,在四边形中,与互余.小明发现四边形 中这
对互余的角可类比(1)中思路进行拼合:先作,再过点 作
于点,连接,发现,, 之间的数量关系是________________
__.
【方法运用】
(3) 如图3,在四边形中,连接, ,点是 两边垂
直平分线的交点,连接, .
① 求证: .
解:如图3,连接,作的外接圆 .
点是两边垂直平分线的交点, 点是 的外心.
, .
,, .
.
② 连接,如图4,已知,,,求 的长
(用含, 的式子表示).
【自主解答】
解:如图4,在射线的下方作,过点 作
于点,连接 .
,, .
,., .
. ,
. .
,
, ,
.
.
类型1 新定义型
1.我们定义:有一组邻角相等的凸四边形
叫作“等邻角四边形”.
(1) 【概念理解】
请你根据上述定义举一个等邻角四边形的
例子,例如________是等邻角四边形.
(2) 【问题探究】
如图1,在等邻角四边形中,,, 的垂直平分线恰好交
于边上一点,连接,,试探究与 的数量关系,并说明理由.
. .
. .
(3) 【应用拓展】
如图2,在与中, ,, .将
绕着点顺时针旋转角得到 (如图3),当四边
形 为等邻角四边形时,求出它的面积.
(1) 【概念理解】
请你根据上述定义举一个等邻角四边形的例子,例如__________________________
_______________是等邻角四边形.
直角梯形或矩形或正方形(答案不唯一)
(2) 【问题探究】
如图1,在等邻角四边形中,,, 的垂直平分线恰好交
于边上一点,连接,,试探究与 的数量关系,并说明理由.
解:.理由如下:连接, ,如图1所示.
是的垂直平分线,是的垂直平分线,, .
,, .
, .
(3) 【应用拓展】
如图2,在与中, ,, .将
绕着点顺时针旋转角得到 (如图3),当四边
形 为等邻角四边形时,求出它的面积.
解:分两种情况考虑:①当时,延长,交于点 ,如答图2
所示.
.
由已知易得 .
设,由勾股定理得 ,
解得 .
过点作于点, .
,即,解得 .
,
.
.
②当 时,过点 作
于点 ,如答图3所示.
易得 ,
.
.
综上所述,四边形的面积为 或
.
2.[2024·中山市一模] 我们定义:对角线互
相垂直且相等的四边形叫作“神奇四边形”.
(1) 在我们学过的四边形:①平行四边
形、②矩形、③菱形、④正方形中,是“神
奇四边形”的是________(填序号).
(2) 如图1,在正方形中,为上一点,连接,过点作 于点
,交于点,连接, .
① 求证:四边形 是“神奇四边形”.
② 如图2,点,,,分别是,,, 的中点,试判断四边形
是不是“神奇四边形”.
(3) 如图3,点,分别在正方形的边,上,把正方形沿直线 翻
折,使得的对应边恰好经过点,过点作于点.若 ,正方
形的边长为6,求线段 的长.
(1) 在我们学过的四边形:①平行四边
形、②矩形、③菱形、④正方形中,是“神
奇四边形”的是____(填序号).
④
(2) 如图1,在正方形中,为
上一点,连接,过点作于点 ,
交于点,连接, .
① 求证:四边形 是“神奇四边形”.
证明: 四边形 是正方形,
.
.
, .
.
在和中,
.又, 四边形 是“神奇四边形”.
② 如图2,点,,,分别是,,, 的中点,试判断四边形
是不是“神奇四边形”.
解:四边形 是“神奇四边形”.理由如下:
,为,的中点,为的中位线., .
同理,可得,,,,, ,
, 四边形为平行四边形., .
平行四边形为菱形.,, ,
.
四边形为正方形. 四边形 是“神奇四边形”.
(3) 如图3,点,分别在正方形的边,上,把正方形沿直线 翻
折,使得的对应边恰好经过点,过点作于点.若 ,正方
形的边长为6,求线段 的长.
解:如图3,延长交于点 ,由翻折的性质可知,
,,, .
四边形是正方形,边长为6,, .
, .
.设,则 ,在
中,由勾股定理得:
,.. ,
.
,即线段 的长
为 .
类型2 几何变换操作型
3.[2024·景德镇二模] 【问题情境】在数学
活动课上,同学们用两张矩形纸片进行探
究活动.小组同学准备了两张矩形纸片
和,其中, ,将
它们按如图1所示的方式放置,点, 分别
【观察发现】
(1) 如图2所示,当 时,小组成员发现与 存在的数量关系为______;
位置关系为________.
落在,边上时,点,恰好为边,的中点.然后将矩形纸片 绕
点按顺时针方向旋转,旋转角为 ,连接与 .
. .
. .
【探索猜想】
(2) 如图3所示,当 时,
(1)中发现的结论是否仍然成立?请说明
理由.
【拓展延伸】
(3) 在矩形的旋转过程中,交
于点,交于点,连接, ,
是否为定值?如果是,请直接写
出此定值;如果不是,请你说明理由.
(1) 如图2所示,当 时,小组成员发现与 存在的数量关系为______
__;位置关系为_________.
解:如图2,延长交于点 .
点,恰好为边, 的中点,
, .
四边形和都是矩形, ,
.
, ,
, ,
.故答案为:; .
[答案] ;
【探索猜想】
(2) 如图3所示,当 时,(1)中发现的结论是否仍然成立?请
说明理由.
[答案] 当 时,(1)中发现的结论仍然成立.理
由如下:
如图3,连接, .
四边形和都是矩形, .
,即 .
,, .
, .
与交于点,与交于点,则 ,
.
当 时,与的数量关系是 ;位置关
系是 .
【拓展延伸】
(3) 在矩形的旋转过程中,交于点,交于点,连接, ,
是否为定值?如果是,请直接写出此定值;如果不是,请你说明理由.
[答案] 为定值65.理由如下:
由(2)得,、、、 均为直角三角形.
根据勾股定理得:,, ,
,
,
,
,即 为定值65.
类型3 动点型
4.综合与实践
如图1,在中,, ,点是平面内一点,连接, ,
分别以,为斜边向上画等腰直角三角形和,连接, .
. .
. .
【特例感知】
(1) 当点在边上时,延长交于点, .
① 如图2,当是边的中点时,________,____ ;
② 如图3,当不是边的中点时,________,____ .
【猜想证明】
(2) 当点不在边上时,猜想与 的关系,并结合图1进行证明.
【拓展应用】
(3) 如图4,在中,,, ,以 ,
为边向上分别作两个正方形和,它们的中心分别为, ,连接
,试求线段 的长.
(1) 当点在边上时,延长交于点, .
① 如图2,当是边的中点时,_____,____ ;
② 如图3,当不是边的中点时,_____,____ .
90
90
【猜想证明】
(2) 当点不在边上时,猜想与 的关系,并结合图1进行证明.
解:,.证明:如图1,过点作 ,过点
作于点,连接 .
, , 四边形 是正方形.
, , .
, , ,
.
, .
又 ,, ,
.
,.延长交于点 ,
.
.
【拓展应用】
(3) 如图4,在中,,, ,以 ,
为边向上分别作两个正方形和,它们的中心分别为, ,连接
,试求线段 的长.
解:如图4,连接,,, .
正方形和的中心分别为,,和 都是等腰直
角三角形.
以为斜边构造等腰直角三角形,连接,则 .
作的中点,连接 .
过点作交于点,过点作于点 .
, ,
.
在中,.故线段的长为 .
类型4 作图操作型
5.综合与实践
【问题情境】
数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质.
已知, ,点为上一动点,将以 为对称轴翻折.同
学们经过思考后进行如下探究:
【独立思考】
小明:“当点落在上时, .”
小红:“若点为的中点,给出与的长,就可求出 的长.”
. .
. .
【实践探究】
奋进小组的同学们经过探究后提出问题1,请你回答:
问题1: 在等腰中,, ,由 翻折得到.
(1) 如图1,当点落在上时,求证: .
(2) 如图2,若点为的中点,,,求 的长.
【问题解决】
小明经过探究发现:若将问题1中的等腰三角形换成
将问题进一步拓展.
问题2: 如图3,在等腰中, , ,
.若,求 的长.
问题1: 在等腰中,, ,由 翻折得到.
(1) 如图1,当点落在上时,求证: .
证明:, .
由 翻折得到,
.
, .
(2) 如图2,若点为的中点,,,求 的长.
解:如答图1,连接,交于点 .
由翻折得到,, ,
.
又 点是 的中点,
, .
在中, .
在中, ,
.
【问题解决】
小明经过探究发现:若将问题1中的等腰三角形换成
将问题进一步拓展.
问题2: 如图3,在等腰中, , ,
.若,求 的长.
[答案] 如答图2,连接,过点作于点,过点作于点 .
, ,
,
.
,
.
.
又, 四边形 是矩形.
.
在中,, ,
.
, .
在 中,
,
.
在中, .
同课章节目录
