2025年中考数学专项八 课本再现题课件(共33张PPT)
文档属性
| 名称 | 2025年中考数学专项八 课本再现题课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 00:00:00 | ||
图片预览








文档简介
(共33张PPT)
第一部分 专项突破
难点·压轴专项
专项八 课本再现题
类型1 教材定理证明探究
1.【课本再现】
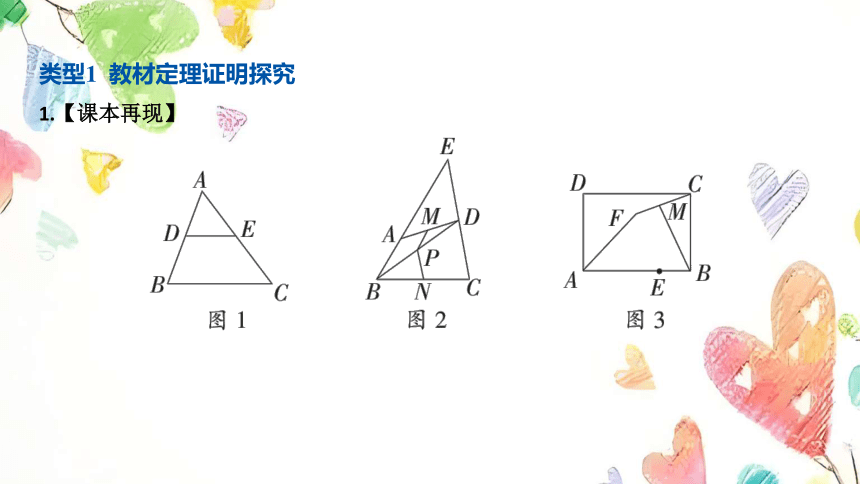
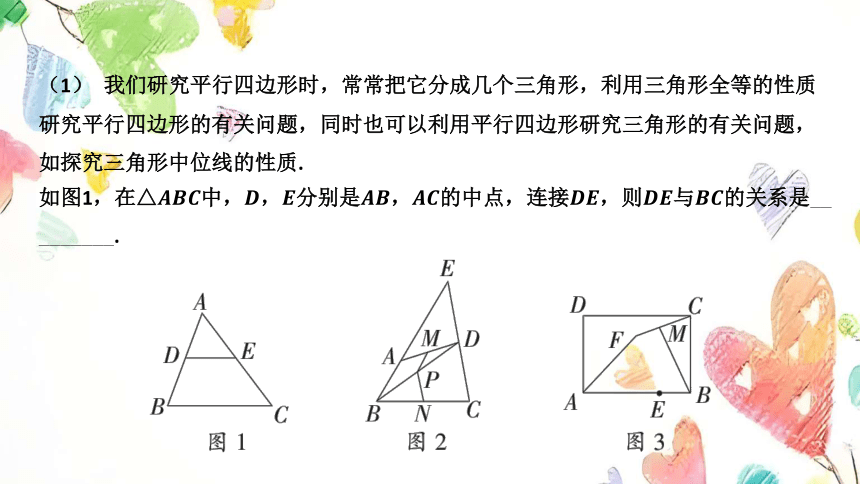
(1) 我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质
研究平行四边形的有关问题,同时也可以利用平行四边形研究三角形的有关问题,
如探究三角形中位线的性质.
如图1,在中,,分别是,的中点,连接,则与 的关系是__
_______.
【定理证明】
(2) 请根据(1)中内容结合图1,写出(1)中结论的证明过程.
【定理应用】
(3) 如图2,在四边形
(4) 如图3,在矩形中,,,点在边上,且 .
将线段绕点旋转一定的角度,得到线段,点是线段
的中点,求旋转过程中线段 长的最大值和最小值.
(1) 我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质
研究平行四边形的有关问题,同时也可以利用平行四边形研究三角形的有关问题,
如探究三角形中位线的性质.
如图1,在中,,分别是,的中点,连接,则与 的关系是
_ ___________________.
且
【定理证明】
(2) 请根据(1)中内容结合图1,写出(1)中结论的证明过程.
解:如答图1,延长至点 ,
使,连接 .
, ,
.
, .
,, .
四边形 为平行四边形.
,, .
【定理应用】
(3) 如图2,在四边形中,点,,分别为,,的中点, ,
的延长线交于点.若 ,则 的度数是______.
(提示:, )
(4) 如图3,在矩形中,,,点在边上,且 .
将线段绕点旋转一定的角度,得到线段,点是线段
的中点,求旋转过程中线段 长的最大值和最小值.
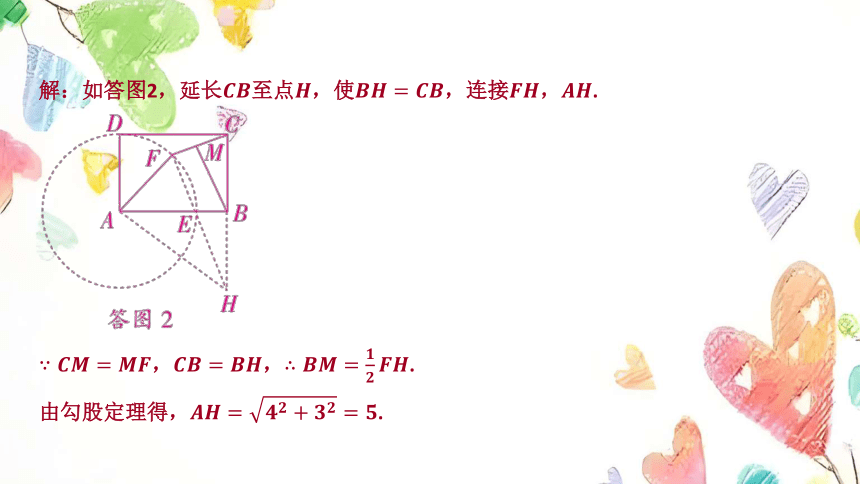
解:如答图2,延长至点,使,连接, .
,, .
由勾股定理得, .
,, .
点在以点为圆心,3为半径的圆上(不与点 重合).
当点在线段上时,最小,最小值为 ;
当点在线段的延长线上时,最大,最大值为 .
故 长的最大值为4,最小值为1.
2.【课本再现】
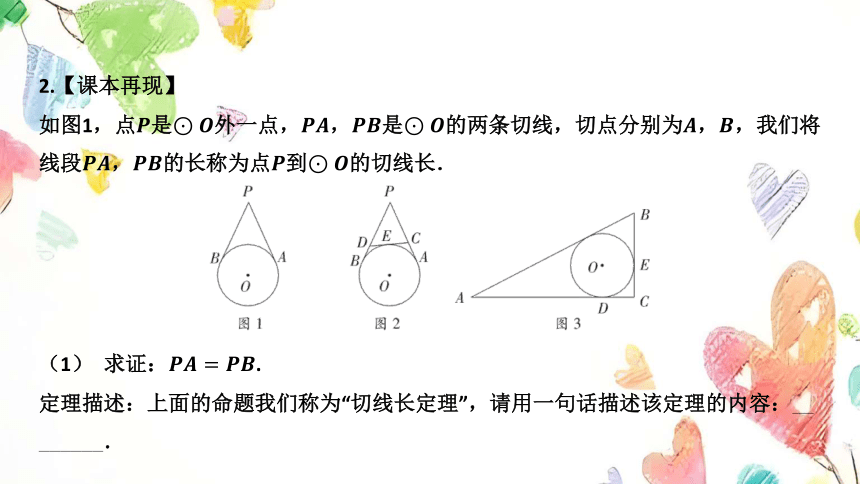
如图1,点是外一点,,是的两条切线,切点分别为, ,我们将
线段,的长称为点到 的切线长.
(1) 求证: .
定理描述:上面的命题我们称为“切线长定理”,请用一句话描述该定理的内容:__
______.
【知识运用】
(2) 如图2,已知,直线是的切线,分别交,于点 ,
,切点为,求 的周长.
【拓展运用】
(3) 如图3,半径为3的与的边,分别相切于点, ,已知
,,,求证:是 的切线.
(1) 求证: .
定理描述:上面的命题我们称为“切线长定理”,请用一句话描述该定理的内容:
_____________________________________.
过圆外一点所画圆的两条切线的长相等.
证明:如图,连接,,,则 .
,是的切线,, .
.
, .
.
【知识运用】
(2) 如图2,已知,直线是的切线,分别交,于点 ,
,切点为,求 的周长.
解: 直线是的切线,切点为,,是 的两条切线,
, .
的周长 .
【拓展运用】
(3) 如图3,半径为3的与的边,分别相切于点, ,已知
,,,求证:是 的切线.
证明:,, ,
.
是直角三角形, .
.
连接,,如图,则 .
连接,,,过点作于点 .
.
解得是 的切线.
类型2 教材方法应用探究
3.[2024·江西二模] 综合与实践
【课本再现】
(1) 如图1,和 都是等边
三角形.
① 与 有什么关系?请用旋转的性
质说明上述关系.
数学小组发现在图1的四边形中,的长度与, 之间存在一定的关系,
可考虑通过旋转构造特殊三角形之间的全等或相似求解.
【特例感知】
② 若 , ,,求 的长.
请你尝试解决以下问题:
【类比应用】
(2) 如图2,在四边形中, , , ,
,,求 的长.
(1) 如图1,和 都是等边三角形.
① 与 有什么关系?请用旋转的性质说明上述关系.
数学小组发现在图1的四边形中,的长度与, 之间存在一定的关系,
可考虑通过旋转构造特殊三角形之间的全等或相似求解.
解:,可看成是绕点旋转得到
【特例感知】
② 若 , ,,求 的长.
解: , , ,
.
.
是等边三角形,, .
.
.
.
请你尝试解决以下问题:
【类比应用】
(2) 如图2,在四边形中, , , ,
,,求 的长.
[答案] , ,
以点为旋转中心,把绕点顺时针旋转 得到
,连接 ,如图.
, ,, .
是等边三角形.
过点作交的延长线于点 ,如图.
, ,
.
, .
.
.
又, 为等腰直角三角形.
, ,
.
在中, ,
.
4.【课本再现】
(1) 如图1,正方形 的对角线相
交于点,点又是正方形 的一
个顶点,而且这两个正方形的边长都为1,
四边形 为两个正方形的重叠部分,
正方形可绕点 转动.则下列结论中正确的是________(填序号即可).
;;③四边形的面积总等于;④连接 ,总
有 .
【类比迁移】
(2) 如图2,矩形的中心 是矩形
的一个顶点,与边 相交
于点,与边相交于点,连接 ,
矩形可绕着点 旋转,猜想
,, 之间的数量关系,并进行证
明.
【拓展应用】
(3) 如图3,在 中,
,, ,
直角的顶点在边 的中点处,它
的两条边,分别与直线, 相交
于点,,可绕着点 旋转,当
时,求线段 的长度.
(1) 如图1,正方形 的对角线相
交于点,点又是正方形 的一
个顶点,而且这两个正方形的边长都为1,
四边形 为两个正方形的重叠部分,
正方形可绕点 转动.则下列结
论中正确的是__________(填序号即可).
; ;③四
边形的面积总等于;④连接 ,
总有 .
①②③④
【类比迁移】
(2) 如图2,矩形的中心 是矩形
的一个顶点,与边 相交
于点,与边相交于点,连接 ,
矩形可绕着点 旋转,猜想
,, 之间的数量关系,并进行证
明.
解:猜想: .证明如下:
如图,连接是矩形 的中心,
点是的中点. .
延长交于点,连接 .
在矩形中, , ,
, .
.
, .
在矩形中, , .
在中,, .
【拓展应用】
(3) 如图3,在中, ,,,直角
的顶点在边的中点处,它的两条边,分别与直线,相交于点, ,
可绕着点旋转,当时,求线段 的长度.
解:设当点在线段上时, ,
.
在中, , .
又由(2)易知 ,
,解得 .
.
②如图,当点在的延长线上时,延长至点,使,连接, .
同理可证 .
.
在中, .
.
解得..故的长度为 或
.
第一部分 专项突破
难点·压轴专项
专项八 课本再现题
类型1 教材定理证明探究
1.【课本再现】
(1) 我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质
研究平行四边形的有关问题,同时也可以利用平行四边形研究三角形的有关问题,
如探究三角形中位线的性质.
如图1,在中,,分别是,的中点,连接,则与 的关系是__
_______.
【定理证明】
(2) 请根据(1)中内容结合图1,写出(1)中结论的证明过程.
【定理应用】
(3) 如图2,在四边形
(4) 如图3,在矩形中,,,点在边上,且 .
将线段绕点旋转一定的角度,得到线段,点是线段
的中点,求旋转过程中线段 长的最大值和最小值.
(1) 我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质
研究平行四边形的有关问题,同时也可以利用平行四边形研究三角形的有关问题,
如探究三角形中位线的性质.
如图1,在中,,分别是,的中点,连接,则与 的关系是
_ ___________________.
且
【定理证明】
(2) 请根据(1)中内容结合图1,写出(1)中结论的证明过程.
解:如答图1,延长至点 ,
使,连接 .
, ,
.
, .
,, .
四边形 为平行四边形.
,, .
【定理应用】
(3) 如图2,在四边形中,点,,分别为,,的中点, ,
的延长线交于点.若 ,则 的度数是______.
(提示:, )
(4) 如图3,在矩形中,,,点在边上,且 .
将线段绕点旋转一定的角度,得到线段,点是线段
的中点,求旋转过程中线段 长的最大值和最小值.
解:如答图2,延长至点,使,连接, .
,, .
由勾股定理得, .
,, .
点在以点为圆心,3为半径的圆上(不与点 重合).
当点在线段上时,最小,最小值为 ;
当点在线段的延长线上时,最大,最大值为 .
故 长的最大值为4,最小值为1.
2.【课本再现】
如图1,点是外一点,,是的两条切线,切点分别为, ,我们将
线段,的长称为点到 的切线长.
(1) 求证: .
定理描述:上面的命题我们称为“切线长定理”,请用一句话描述该定理的内容:__
______.
【知识运用】
(2) 如图2,已知,直线是的切线,分别交,于点 ,
,切点为,求 的周长.
【拓展运用】
(3) 如图3,半径为3的与的边,分别相切于点, ,已知
,,,求证:是 的切线.
(1) 求证: .
定理描述:上面的命题我们称为“切线长定理”,请用一句话描述该定理的内容:
_____________________________________.
过圆外一点所画圆的两条切线的长相等.
证明:如图,连接,,,则 .
,是的切线,, .
.
, .
.
【知识运用】
(2) 如图2,已知,直线是的切线,分别交,于点 ,
,切点为,求 的周长.
解: 直线是的切线,切点为,,是 的两条切线,
, .
的周长 .
【拓展运用】
(3) 如图3,半径为3的与的边,分别相切于点, ,已知
,,,求证:是 的切线.
证明:,, ,
.
是直角三角形, .
.
连接,,如图,则 .
连接,,,过点作于点 .
.
解得是 的切线.
类型2 教材方法应用探究
3.[2024·江西二模] 综合与实践
【课本再现】
(1) 如图1,和 都是等边
三角形.
① 与 有什么关系?请用旋转的性
质说明上述关系.
数学小组发现在图1的四边形中,的长度与, 之间存在一定的关系,
可考虑通过旋转构造特殊三角形之间的全等或相似求解.
【特例感知】
② 若 , ,,求 的长.
请你尝试解决以下问题:
【类比应用】
(2) 如图2,在四边形中, , , ,
,,求 的长.
(1) 如图1,和 都是等边三角形.
① 与 有什么关系?请用旋转的性质说明上述关系.
数学小组发现在图1的四边形中,的长度与, 之间存在一定的关系,
可考虑通过旋转构造特殊三角形之间的全等或相似求解.
解:,可看成是绕点旋转得到
【特例感知】
② 若 , ,,求 的长.
解: , , ,
.
.
是等边三角形,, .
.
.
.
请你尝试解决以下问题:
【类比应用】
(2) 如图2,在四边形中, , , ,
,,求 的长.
[答案] , ,
以点为旋转中心,把绕点顺时针旋转 得到
,连接 ,如图.
, ,, .
是等边三角形.
过点作交的延长线于点 ,如图.
, ,
.
, .
.
.
又, 为等腰直角三角形.
, ,
.
在中, ,
.
4.【课本再现】
(1) 如图1,正方形 的对角线相
交于点,点又是正方形 的一
个顶点,而且这两个正方形的边长都为1,
四边形 为两个正方形的重叠部分,
正方形可绕点 转动.则下列结论中正确的是________(填序号即可).
;;③四边形的面积总等于;④连接 ,总
有 .
【类比迁移】
(2) 如图2,矩形的中心 是矩形
的一个顶点,与边 相交
于点,与边相交于点,连接 ,
矩形可绕着点 旋转,猜想
,, 之间的数量关系,并进行证
明.
【拓展应用】
(3) 如图3,在 中,
,, ,
直角的顶点在边 的中点处,它
的两条边,分别与直线, 相交
于点,,可绕着点 旋转,当
时,求线段 的长度.
(1) 如图1,正方形 的对角线相
交于点,点又是正方形 的一
个顶点,而且这两个正方形的边长都为1,
四边形 为两个正方形的重叠部分,
正方形可绕点 转动.则下列结
论中正确的是__________(填序号即可).
; ;③四
边形的面积总等于;④连接 ,
总有 .
①②③④
【类比迁移】
(2) 如图2,矩形的中心 是矩形
的一个顶点,与边 相交
于点,与边相交于点,连接 ,
矩形可绕着点 旋转,猜想
,, 之间的数量关系,并进行证
明.
解:猜想: .证明如下:
如图,连接是矩形 的中心,
点是的中点. .
延长交于点,连接 .
在矩形中, , ,
, .
.
, .
在矩形中, , .
在中,, .
【拓展应用】
(3) 如图3,在中, ,,,直角
的顶点在边的中点处,它的两条边,分别与直线,相交于点, ,
可绕着点旋转,当时,求线段 的长度.
解:设当点在线段上时, ,
.
在中, , .
又由(2)易知 ,
,解得 .
.
②如图,当点在的延长线上时,延长至点,使,连接, .
同理可证 .
.
在中, .
.
解得..故的长度为 或
.
同课章节目录
