苏科版九年级数学下册第七章 锐角三角函数 章节测试卷(含详解)
文档属性
| 名称 | 苏科版九年级数学下册第七章 锐角三角函数 章节测试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 301.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 12:02:47 | ||
图片预览




文档简介
第七章《锐角三角函数》章节测试卷
一.选择题(共8小题,满分16分,每小题2分)
1.tan45°的值是( )
A. B.1 C. D.
2.如图,传送带和地面所成斜坡的坡度为1:2,它把物体从地面点A处送到离地面2米高的B处,则物体从A到B所经过的路程为( )
A.4 B. C. D.
3.在Rt△ABC中,∠C=90°,,若将△ABC的三边都扩大3倍,则tanA的值为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,如果AC=2BC,那么sinA的值是( )
A. B. C. D.
5.如图所示,△ABC的顶点都是正方形网格的格点,则sinA的值为( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,AB=5,AC=4,下列三角函数表示正确的是( )
A.sinA B.tanA C.cosA D.tanB
7.在△ABC中,tanA=1,cosB,则△ABC的形状( )
A.一定是锐角三角形 B.—定是直角三角形
C.一定是钝角三角形 D.无法确定
8.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB=( )
A. B. C. D.
二.填空题(共10小题,满分20分,每小题2分)
9.cos30°= .
10.在△ABC中,∠C=90°,若BC=5,AB=13,则sinA= .
11.已知α为锐角.若,则α= °.
12.比较大小(用<连接),sin47°,cos53°,tan45° .
13.已知α为锐角,且,则α等于 度.
14.如图,在△ABC中,∠C=90°,∠A=30°,BC=2cm,则AB的长是 cm.
15.已知△ABC中,∠ACB=90°,BC=12,AB=15,则cosB的值为 .
16.如图,某河堤的横断面是梯形ABCD,BC∥AD,已知背水坡CD的坡度i=1:2.4,CD长为13米,则河堤的高BE为 米.
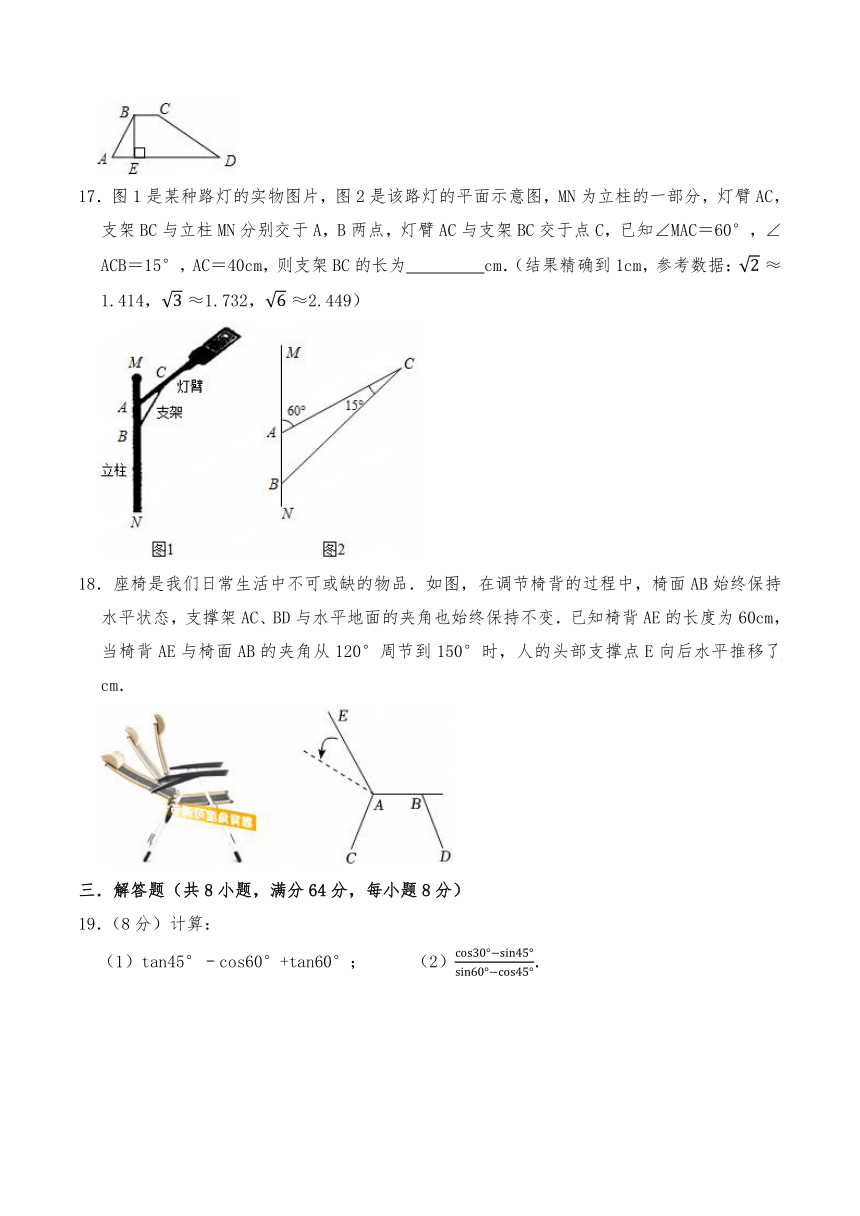
17.图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点C,已知∠MAC=60°,∠ACB=15°,AC=40cm,则支架BC的长为 cm.(结果精确到1cm,参考数据:1.414,1.732,2.449)
18.座椅是我们日常生活中不可或缺的物品.如图,在调节椅背的过程中,椅面AB始终保持水平状态,支撑架AC、BD与水平地面的夹角也始终保持不变.已知椅背AE的长度为60cm,当椅背AE与椅面AB的夹角从120°周节到150°时,人的头部支撑点E向后水平推移了 cm.
三.解答题(共8小题,满分64分,每小题8分)
19.(8分)计算:
(1)tan45°﹣cos60°+tan60°; (2).
20.(8分)如图,在△ABC中,∠C=90°,点D在AC上,∠BDC=45°,BD=10,AB=20.求sinA的值.
21.(8分)如图,已知小张在点A处测得出BC的山顶B的仰角为30°,点A与山脚D处的距离为200米,山坡BD的坡度为1:0.5,求出BC的高度.
22.(8分)如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC,BC=12.
(1)试证明BD=AC;
(2)求AD的长.
23.(8分)如图,某测量队采用无人机技术测量无法直达的A,B两处的直线距离,已知在无人机的镜头O处测得A、B的俯角分别为45°和50°,无人机的飞行高度OC为238米,点A、B、C在同一直线上,求AB的长度(结果保留整数,参考数据:sin50°≈0.77,tan50°≈1.19).
24.(8分)如图,楼梯AB的倾斜角∠ABD为60°,楼梯底部到墙根垂直距离BD为4m,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,求调整后的楼梯AC的长.
25.(8分)如图,AB、CD为两个建筑物,建筑物AB的高度为15m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物两底部之间的水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
26.(8分)图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管CE的长度为0.5米.
(1)真空管上端B到水平线AD的距离.
(2)求安装热水器的铁架水平横管BC的长度(结果精确到0.1米).
(参考数据:sin37°,cos37°,tan37°,sin22°,cos22°,tan22°≈0.4)
参考答案
一.选择题
1.
【分析】直接利用特殊角的三角函数值得出答案.
【解答】解:tan45°=1.
故选:B.
2.
【分析】由已知高度和坡度可求出水平宽度,利用勾股定理求解即可
【解答】解:如图:由已知得:BC=8,
,
∴AC=4,BC=2,
∴AB2,
故选B.
3.
【分析】由于∠A在三角形三边都扩大3倍后没有变化,从而得到∠A的正切值没有变化.
【解答】解:∵△ABC的三边都扩大3倍后∠A没有变化,
∴△ABC的三边都扩大3倍,tanA的值为.
故选:A.
4.
【分析】利用勾股定理得到AB与BC之间的关系,然后根据正弦的定义即可求得答案.
【解答】解:∵在Rt△ABC中,∠C=90°,如果AC=2BC,
∴ABBC,
则sinA,
故选:C.
5.
【分析】连接CE,则CE⊥AB,根据勾股定理求出CA,在Rt△AEC中,根据锐角三角函数定义求出即可.
【解答】解:如图所示:连接CE,则CE⊥AB.
根据图形可知:BC=2,∠BEC=∠AEC=90°,
∴BE=EC,∠EBC=∠ECB=45°,
∵AC,
∴sinA,
故选:A.
6.
【分析】先利用勾股定理求出BC的长,然后根据锐角三角函数的定义对各选项分别进行计算,再利用排除法求解即可.
【解答】解:∵∠ACB=90°,AB=5,AC=4,
∴BC3,
∴sinA,故选项A错误;
tanA,故选项B错误;
cosA,故选项C正确;
tanB,故选项D错误.
故选:C.
7.
【分析】先根据△ABC中,tanA=1,cosB求出∠A及∠B的度数,进而可得出结论.
【解答】解:∵△ABC中,tanA=1,cosB,
∴∠A=45°,∠B=45°,
∴∠C=90°,
∴△ABC是等腰直角三角形.
故选:B.
8.
【分析】先证明△OAB是等边三角形,得∠AOB=60°,即可得出cos∠AOB.
【解答】解:根据题意得:OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴cos∠AOB=cos60°.
故选:B.
二.填空题
9.
【分析】根据特殊角的三角函数值即可求解.
【解答】解:cos30°.
故答案为:.
10.
【分析】根据正弦的定义解答即可.
【解答】解:sinA,
故答案为:.
11.
【分析】根据特殊角的三角函数值计算.
【解答】解:∵sin30°,
∴α=60°.
故答案为:60.
12.
【分析】根据特殊角的三角函数值判断即可.
【解答】解:sin47°<1,cos53°=sin(90°﹣53°)=sin37°<1,tan45°=1,
则cos53°<sin47°<tan45°,
故答案为:cos53°<sin47°<tan45°.
13.
【分析】根据sin60°解答即可.
【解答】解:∵α为锐角,sin(α﹣15°),sin60°,
∴α﹣15°=60°,
∴α=75°.
故答案为:75.
14.
【分析】利用含30度角的直角三角形的性质进行计算,即可解答.
【解答】解:在Rt△ABC中,∠A=30°,∠C=90°,BC=2cm,
∴AB=2BC=4(cm),
故答案为:4.
15.
【分析】根据锐角三角函数的定义即可得到结论.
【解答】解:cosB,
故答案为:.
16.
【分析】在Rt△ABE中,根据tan∠BAE的值,可得到BE、AE的比例关系,进而由勾股定理求得BE、AE的长,由此得解.
【解答】解:作CF⊥AD于F点,
则CF=BE,
∵CD的坡度i=1:2.4=CF:FD,
∴设CF=5x,则FD=12x,
由题意得CF2+FD2=CD2
即:(5x)2+(12x)2=132
∴x=1,
∴BE=CF=5
故答案为5.
17.
【分析】如图2,过C作CD⊥MN于D,则∠CDB=90°,根据三角函数的定义即可得到结论.
【解答】解:如图2,过C作CD⊥MN于D,
则∠CDB=90°,
∵∠CAD=60°,AC=40(cm),
∴CD=AC sin∠CAD=40×sin60°=4020(cm),
∵∠ACB=15°,
∴∠CBD=∠CAD﹣∠ACB=60°﹣15°=45°,
∴BCCD202020×2.449≈49(cm),
故答案为49.
18.
【分析】通过作垂线,构造直角三角形,利用直角三角形的边角关系进行计算即可.
【解答】解:如图,过点E,点E′分别作AB的垂线,分别与BA的延长线相交于点M、点N,
在Rt△AEM 中,AE=60cm,∠EAM=180°﹣120°=60°,
∴AMAE=30(cm),
在Rt△AE′E 中,AE′=60cm,∠E′AN=180°﹣150°=30°,
∴ANAE=30(cm),
∴MN=AN﹣AM=(3030)cm,
即人的头部支撑点E向后水平推移了(3030)cm.
故答案为:(3030).
三.解答题
19.解:(1)tan45°﹣cos60°+tan60°
=1
;
(2)
=1.
20.解:在直角三角形BDC中,∠BDC=45°,BD=10,
∴BC=BD sin∠BDC=1010.
在直角三角形ABC中,∠C=90°,AB=20,
∴sinA.
21.解:设BC=x,则DC=0.5x,
在Rt△ABC中,tan30°,
∴,
∴x162(米),
答:BC的高度为162米.
22.解:(1)∵AD是BC上的高,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,tanB,
在Rt△ACD中,cos∠DAC,
∵tanB=cos∠DAC,
∴,
∴BD=AC;
(2)在Rt△ACD中,sinC,
设AD=12k,则AC=13k,
∴CD5k,
∵BD=AC=13k,BC=BD+CD=12,
∴13k+5k=12,解得k,
∴AD=128.
23.解:由题意可得∠OAC=45°,∠OBC=50°,∠ACO=∠BCO=90°,
在Rt△AOC中,∠OAC=45°,
∴∠AOC=45°,
∴OC=AC=238米,
在Rt△OBC中,∠OBC=50°,
tan50°1.19,
解得BC=200,
∴AB=AC+BC=238+200=438(米).
答:AB的长度为438米.
24.解:在Rt△ABD中,∠ABD=60°,BD=4m,
∴∠BAD=30°,
∴AD4m,
在Rt△ACD中,∠ACD=45°,
∴ACAD=4m.
25.解:(1)根据题意得∠ADB=∠EAD=45°,
在Rt△ABD中,∴∠BAD=∠ADB=45°,
∴BD=AB=15(米)
答:两建筑物两底部之间的水平距离BD的长度为15米;
(2)延长DC交AE于点F,根据题意可知四边形ABDF是正方形,
∴AF=BD=DF=15,
在Rt△AFC中,∵∠FAC=30°,
∴CF=AFtan∠CAF=15tan30°=5,
∵DF=15,
∴CD=15﹣5,
答:建筑物CD的高度为(15﹣5)米.
26.解:(1)过B作BF⊥AD于F.
在Rt△ABF中,sin∠BAF,
则BF=ABsin∠BAF=3sin37°≈31.8(米).
答:真空管上端B到AD的距离约为1.8米;
(2)在Rt△ABF中,cos∠BAF,
则AF=ABcos∠BAF=3×cos37°≈2.4(米),
∵BF⊥AD,CD⊥AD,BC∥FD,
∴四边形BFDC是矩形.
∴BF=CD,BC=FD,
∵EC=0.5米,
∴DE=CD﹣CE=1.3米,
在Rt△EAD中,tan∠EAD,
则AD3.25(米),
∴BC=DF=AD﹣AF=3.25﹣2.4≈0.9(米),
答:安装热水器的铁架水平横管BC的长度约为0.9米.
一.选择题(共8小题,满分16分,每小题2分)
1.tan45°的值是( )
A. B.1 C. D.
2.如图,传送带和地面所成斜坡的坡度为1:2,它把物体从地面点A处送到离地面2米高的B处,则物体从A到B所经过的路程为( )
A.4 B. C. D.
3.在Rt△ABC中,∠C=90°,,若将△ABC的三边都扩大3倍,则tanA的值为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,如果AC=2BC,那么sinA的值是( )
A. B. C. D.
5.如图所示,△ABC的顶点都是正方形网格的格点,则sinA的值为( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,AB=5,AC=4,下列三角函数表示正确的是( )
A.sinA B.tanA C.cosA D.tanB
7.在△ABC中,tanA=1,cosB,则△ABC的形状( )
A.一定是锐角三角形 B.—定是直角三角形
C.一定是钝角三角形 D.无法确定
8.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB=( )
A. B. C. D.
二.填空题(共10小题,满分20分,每小题2分)
9.cos30°= .
10.在△ABC中,∠C=90°,若BC=5,AB=13,则sinA= .
11.已知α为锐角.若,则α= °.
12.比较大小(用<连接),sin47°,cos53°,tan45° .
13.已知α为锐角,且,则α等于 度.
14.如图,在△ABC中,∠C=90°,∠A=30°,BC=2cm,则AB的长是 cm.
15.已知△ABC中,∠ACB=90°,BC=12,AB=15,则cosB的值为 .
16.如图,某河堤的横断面是梯形ABCD,BC∥AD,已知背水坡CD的坡度i=1:2.4,CD长为13米,则河堤的高BE为 米.
17.图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点C,已知∠MAC=60°,∠ACB=15°,AC=40cm,则支架BC的长为 cm.(结果精确到1cm,参考数据:1.414,1.732,2.449)
18.座椅是我们日常生活中不可或缺的物品.如图,在调节椅背的过程中,椅面AB始终保持水平状态,支撑架AC、BD与水平地面的夹角也始终保持不变.已知椅背AE的长度为60cm,当椅背AE与椅面AB的夹角从120°周节到150°时,人的头部支撑点E向后水平推移了 cm.
三.解答题(共8小题,满分64分,每小题8分)
19.(8分)计算:
(1)tan45°﹣cos60°+tan60°; (2).
20.(8分)如图,在△ABC中,∠C=90°,点D在AC上,∠BDC=45°,BD=10,AB=20.求sinA的值.
21.(8分)如图,已知小张在点A处测得出BC的山顶B的仰角为30°,点A与山脚D处的距离为200米,山坡BD的坡度为1:0.5,求出BC的高度.
22.(8分)如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC,BC=12.
(1)试证明BD=AC;
(2)求AD的长.
23.(8分)如图,某测量队采用无人机技术测量无法直达的A,B两处的直线距离,已知在无人机的镜头O处测得A、B的俯角分别为45°和50°,无人机的飞行高度OC为238米,点A、B、C在同一直线上,求AB的长度(结果保留整数,参考数据:sin50°≈0.77,tan50°≈1.19).
24.(8分)如图,楼梯AB的倾斜角∠ABD为60°,楼梯底部到墙根垂直距离BD为4m,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,求调整后的楼梯AC的长.
25.(8分)如图,AB、CD为两个建筑物,建筑物AB的高度为15m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物两底部之间的水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
26.(8分)图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管CE的长度为0.5米.
(1)真空管上端B到水平线AD的距离.
(2)求安装热水器的铁架水平横管BC的长度(结果精确到0.1米).
(参考数据:sin37°,cos37°,tan37°,sin22°,cos22°,tan22°≈0.4)
参考答案
一.选择题
1.
【分析】直接利用特殊角的三角函数值得出答案.
【解答】解:tan45°=1.
故选:B.
2.
【分析】由已知高度和坡度可求出水平宽度,利用勾股定理求解即可
【解答】解:如图:由已知得:BC=8,
,
∴AC=4,BC=2,
∴AB2,
故选B.
3.
【分析】由于∠A在三角形三边都扩大3倍后没有变化,从而得到∠A的正切值没有变化.
【解答】解:∵△ABC的三边都扩大3倍后∠A没有变化,
∴△ABC的三边都扩大3倍,tanA的值为.
故选:A.
4.
【分析】利用勾股定理得到AB与BC之间的关系,然后根据正弦的定义即可求得答案.
【解答】解:∵在Rt△ABC中,∠C=90°,如果AC=2BC,
∴ABBC,
则sinA,
故选:C.
5.
【分析】连接CE,则CE⊥AB,根据勾股定理求出CA,在Rt△AEC中,根据锐角三角函数定义求出即可.
【解答】解:如图所示:连接CE,则CE⊥AB.
根据图形可知:BC=2,∠BEC=∠AEC=90°,
∴BE=EC,∠EBC=∠ECB=45°,
∵AC,
∴sinA,
故选:A.
6.
【分析】先利用勾股定理求出BC的长,然后根据锐角三角函数的定义对各选项分别进行计算,再利用排除法求解即可.
【解答】解:∵∠ACB=90°,AB=5,AC=4,
∴BC3,
∴sinA,故选项A错误;
tanA,故选项B错误;
cosA,故选项C正确;
tanB,故选项D错误.
故选:C.
7.
【分析】先根据△ABC中,tanA=1,cosB求出∠A及∠B的度数,进而可得出结论.
【解答】解:∵△ABC中,tanA=1,cosB,
∴∠A=45°,∠B=45°,
∴∠C=90°,
∴△ABC是等腰直角三角形.
故选:B.
8.
【分析】先证明△OAB是等边三角形,得∠AOB=60°,即可得出cos∠AOB.
【解答】解:根据题意得:OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴cos∠AOB=cos60°.
故选:B.
二.填空题
9.
【分析】根据特殊角的三角函数值即可求解.
【解答】解:cos30°.
故答案为:.
10.
【分析】根据正弦的定义解答即可.
【解答】解:sinA,
故答案为:.
11.
【分析】根据特殊角的三角函数值计算.
【解答】解:∵sin30°,
∴α=60°.
故答案为:60.
12.
【分析】根据特殊角的三角函数值判断即可.
【解答】解:sin47°<1,cos53°=sin(90°﹣53°)=sin37°<1,tan45°=1,
则cos53°<sin47°<tan45°,
故答案为:cos53°<sin47°<tan45°.
13.
【分析】根据sin60°解答即可.
【解答】解:∵α为锐角,sin(α﹣15°),sin60°,
∴α﹣15°=60°,
∴α=75°.
故答案为:75.
14.
【分析】利用含30度角的直角三角形的性质进行计算,即可解答.
【解答】解:在Rt△ABC中,∠A=30°,∠C=90°,BC=2cm,
∴AB=2BC=4(cm),
故答案为:4.
15.
【分析】根据锐角三角函数的定义即可得到结论.
【解答】解:cosB,
故答案为:.
16.
【分析】在Rt△ABE中,根据tan∠BAE的值,可得到BE、AE的比例关系,进而由勾股定理求得BE、AE的长,由此得解.
【解答】解:作CF⊥AD于F点,
则CF=BE,
∵CD的坡度i=1:2.4=CF:FD,
∴设CF=5x,则FD=12x,
由题意得CF2+FD2=CD2
即:(5x)2+(12x)2=132
∴x=1,
∴BE=CF=5
故答案为5.
17.
【分析】如图2,过C作CD⊥MN于D,则∠CDB=90°,根据三角函数的定义即可得到结论.
【解答】解:如图2,过C作CD⊥MN于D,
则∠CDB=90°,
∵∠CAD=60°,AC=40(cm),
∴CD=AC sin∠CAD=40×sin60°=4020(cm),
∵∠ACB=15°,
∴∠CBD=∠CAD﹣∠ACB=60°﹣15°=45°,
∴BCCD202020×2.449≈49(cm),
故答案为49.
18.
【分析】通过作垂线,构造直角三角形,利用直角三角形的边角关系进行计算即可.
【解答】解:如图,过点E,点E′分别作AB的垂线,分别与BA的延长线相交于点M、点N,
在Rt△AEM 中,AE=60cm,∠EAM=180°﹣120°=60°,
∴AMAE=30(cm),
在Rt△AE′E 中,AE′=60cm,∠E′AN=180°﹣150°=30°,
∴ANAE=30(cm),
∴MN=AN﹣AM=(3030)cm,
即人的头部支撑点E向后水平推移了(3030)cm.
故答案为:(3030).
三.解答题
19.解:(1)tan45°﹣cos60°+tan60°
=1
;
(2)
=1.
20.解:在直角三角形BDC中,∠BDC=45°,BD=10,
∴BC=BD sin∠BDC=1010.
在直角三角形ABC中,∠C=90°,AB=20,
∴sinA.
21.解:设BC=x,则DC=0.5x,
在Rt△ABC中,tan30°,
∴,
∴x162(米),
答:BC的高度为162米.
22.解:(1)∵AD是BC上的高,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,tanB,
在Rt△ACD中,cos∠DAC,
∵tanB=cos∠DAC,
∴,
∴BD=AC;
(2)在Rt△ACD中,sinC,
设AD=12k,则AC=13k,
∴CD5k,
∵BD=AC=13k,BC=BD+CD=12,
∴13k+5k=12,解得k,
∴AD=128.
23.解:由题意可得∠OAC=45°,∠OBC=50°,∠ACO=∠BCO=90°,
在Rt△AOC中,∠OAC=45°,
∴∠AOC=45°,
∴OC=AC=238米,
在Rt△OBC中,∠OBC=50°,
tan50°1.19,
解得BC=200,
∴AB=AC+BC=238+200=438(米).
答:AB的长度为438米.
24.解:在Rt△ABD中,∠ABD=60°,BD=4m,
∴∠BAD=30°,
∴AD4m,
在Rt△ACD中,∠ACD=45°,
∴ACAD=4m.
25.解:(1)根据题意得∠ADB=∠EAD=45°,
在Rt△ABD中,∴∠BAD=∠ADB=45°,
∴BD=AB=15(米)
答:两建筑物两底部之间的水平距离BD的长度为15米;
(2)延长DC交AE于点F,根据题意可知四边形ABDF是正方形,
∴AF=BD=DF=15,
在Rt△AFC中,∵∠FAC=30°,
∴CF=AFtan∠CAF=15tan30°=5,
∵DF=15,
∴CD=15﹣5,
答:建筑物CD的高度为(15﹣5)米.
26.解:(1)过B作BF⊥AD于F.
在Rt△ABF中,sin∠BAF,
则BF=ABsin∠BAF=3sin37°≈31.8(米).
答:真空管上端B到AD的距离约为1.8米;
(2)在Rt△ABF中,cos∠BAF,
则AF=ABcos∠BAF=3×cos37°≈2.4(米),
∵BF⊥AD,CD⊥AD,BC∥FD,
∴四边形BFDC是矩形.
∴BF=CD,BC=FD,
∵EC=0.5米,
∴DE=CD﹣CE=1.3米,
在Rt△EAD中,tan∠EAD,
则AD3.25(米),
∴BC=DF=AD﹣AF=3.25﹣2.4≈0.9(米),
答:安装热水器的铁架水平横管BC的长度约为0.9米.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
