广东省清远市2024-2025学年高二下学期期中联合学业质量监测考试数学试题(含详解)
文档属性
| 名称 | 广东省清远市2024-2025学年高二下学期期中联合学业质量监测考试数学试题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1004.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 15:14:27 | ||
图片预览




文档简介
广东省清远市2024 2025学年高二下学期期中联合学业质量监测考试数学试题
一、单选题(本大题共8小题)
1.某物体沿直线运动,位移(单位:)与时间(单位:)的关系为,则该物体在时的瞬时速度是( )
A. B. C. D.
2.从1,2,3,4,5中不放回地抽取2个数,则在第1次抽到偶数的条件下,第2次抽到奇数的概率是( )
A. B. C. D.
3.某学校为了了解学生美育培养的情况,用分层随机抽样方法抽样调查,拟从美术、音乐、舞蹈兴趣小组中共抽取30名学生,已知该校美术、音乐、舞蹈兴趣小组分别有20,30,50名学生,则不同的抽样结果共有( )
A. B.
C. D.
4.在的展开式中,只有第五项的二项式系数最大,则展开式中的系数是( )
A. B. C. D.7
5.已知随机变量的分布是,则等于( )
A. B. C. D.
6.已知函数,则不等式的解集为( )
A. B. C. D.
7.现有四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为( )
A. B. C. D.
8.已知函数,,则下列说法正确的是( )
A.当时,有2个零点
B.当时,存在增区间
C.若只有一个极值点,则或
D.当时,对任意实数t,总存在实数,,使得
二、多选题(本大题共3小题)
9.下列说法正确的是( )
A.若,则
B.从五个人中选三个人站成一排,则不同的排法有60种
C.过三棱柱任意两顶点的直线中,异面直线共有36对
D.用0,1,2,…,9这十个数字,可以组成有重复数字的三位数的个数为252
10.设N为正整数,在平面直角坐标系中,若(,,且)恰好能表示出12个不同的椭圆方程,则N的可能取值为( )
A.6 B.8 C.7 D.5
11.已知编号为1,2,3的三个盒子,其中1号盒子内装有两个1号球,一个2号球和一个3号球;2号盒子内装有两个1号球,一个3号球;3号盒子内装有三个1号球,两个2号球.若第一次先从1号盒子内随机抽取1个球,将取出的球放入与球同编号的盒子中,第二次从该盒子中任取一个球,则下列说法正确的是( )
A.在第一次抽到2号球的条件下,第二次抽到1号球的概率为
B.第二次抽到3号球的概率为
C.如果第二次抽到的是1号球,则它来自2号盒子的概率最大
D.如果将5个不同的小球放入这三个盒子内,每个盒子至少放1个,则不同的放法有300种
三、填空题(本大题共3小题)
12.已知X服从参数为0.3的两点分布,则 ;若,则 .
13.为确保学生身心健康,全面发展,高中课程内容覆盖学科教学、体育、艺术等类别,我校按照教育部的指导,安排上午四节课,下午三节课,现在安排我班一天中语文、英语、物理、政治、体育各一节,数学两节,要求两节数学课都排在上午或下午、且连续,体育课排在下午,则不同的排法有 种.
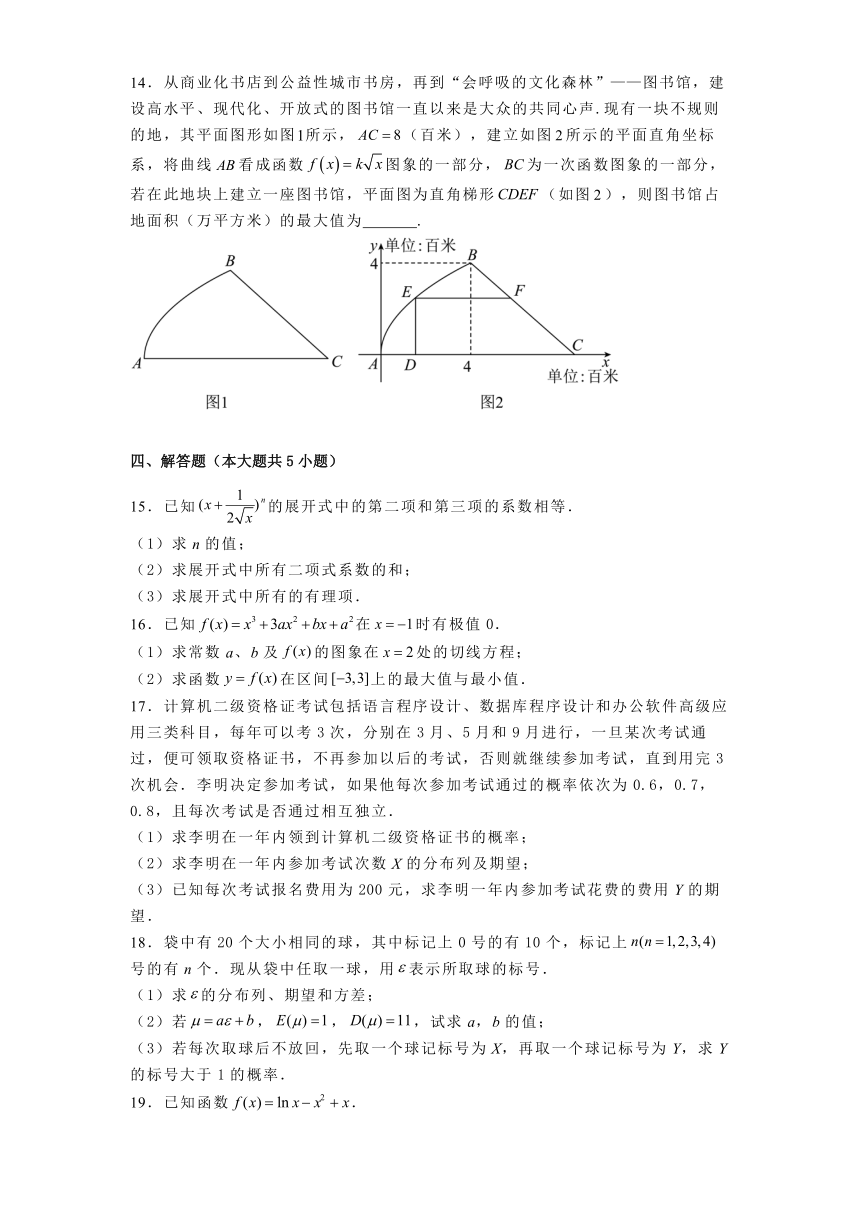
14.从商业化书店到公益性城市书房,再到“会呼吸的文化森林”——图书馆,建设高水平、现代化、开放式的图书馆一直以来是大众的共同心声.现有一块不规则的地,其平面图形如图所示,(百米),建立如图所示的平面直角坐标系,将曲线看成函数图象的一部分,为一次函数图象的一部分,若在此地块上建立一座图书馆,平面图为直角梯形(如图),则图书馆占地面积(万平方米)的最大值为 .
四、解答题(本大题共5小题)
15.已知的展开式中的第二项和第三项的系数相等.
(1)求n的值;
(2)求展开式中所有二项式系数的和;
(3)求展开式中所有的有理项.
16.已知在时有极值0.
(1)求常数a、b及的图象在处的切线方程;
(2)求函数在区间上的最大值与最小值.
17.计算机二级资格证考试包括语言程序设计、数据库程序设计和办公软件高级应用三类科目,每年可以考3次,分别在3月、5月和9月进行,一旦某次考试通过,便可领取资格证书,不再参加以后的考试,否则就继续参加考试,直到用完3次机会.李明决定参加考试,如果他每次参加考试通过的概率依次为0.6,0.7,0.8,且每次考试是否通过相互独立.
(1)求李明在一年内领到计算机二级资格证书的概率;
(2)求李明在一年内参加考试次数X的分布列及期望;
(3)已知每次考试报名费用为200元,求李明一年内参加考试花费的费用Y的期望.
18.袋中有20个大小相同的球,其中标记上0号的有10个,标记上号的有n个.现从袋中任取一球,用表示所取球的标号.
(1)求的分布列、期望和方差;
(2)若,,,试求a,b的值;
(3)若每次取球后不放回,先取一个球记标号为X,再取一个球记标号为Y,求Y的标号大于1的概率.
19.已知函数.
(1)求函数的单调区间;
(2)是否存在x使得成立?若存在,求x的取值范围,若不存在,请说明理由;
(3)若方程有两个不同的实数解,证明:.
参考答案
1.【答案】D
【详解】,
当时,,
即该物体在时的瞬时速度是.
故选D.
2.【答案】D
【详解】设事件为“第i次抽到偶数”,i=1,2,
则事件“在第1次抽到偶数的条件下,第2次抽到奇数”的概率为:
.
故选D.
3.【答案】C
【详解】由题意,美术组要抽取的学生数为,音乐组要抽取的学生数为,舞蹈组要抽取的学生数为,由分步乘法计数原理可知,不同的抽样结果.
故选:C.
4.【答案】C
【详解】在的展开式中,只有第5项的二项式系数最大,
它的展开式共计有9项,,
故二项展开式的通项公式为,
令,求得,可得在的展开式中的系数为,
故选C.
5.【答案】C
【详解】由题意可得,解得,
.
.
故选C.
6.【答案】C
【详解】由函数,所以,则为偶函数,
当时,又因为,且恒成立,
则,所以在时单增,
综上可得等价于,即或,解得
故选:C
7.【答案】C
【详解】根据题意,用四种不同的颜色要对如图形中的五个部分进行着色,每个部分都有4种涂色方法,则有种涂色方法;
若其中任意有公共边的两块着不同颜色,有两种情况:①只用三种颜色涂这5个区域,则有种涂色方法;②用四种颜色涂这5个区域,则有种涂色方法,所以若其中任意有公共边的两块着不同颜色,共有144种涂色方法,故四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为.
故选C
8.【答案】D
【详解】对于A,当时,,令,得,
令,则,所以在R上单调递增,
所以至多有一个零点,即方程至多有一个根,故A错误;
对于B,,
令,得,设,
则,当时,,单调递增,当时,,单调递减,
所以,又当时,,所以恒成立,
即时,是减函数,故B错误;
对于C,当时,由B知,,即,所以,
所以在R上单调递减,无极值,故C错误;
对于D,当时,,,由切线放缩知,
,即在R上单调递减,当时,,当时,,
可得的大致图象如下:
由图可知对任意实数,总存在实数,使得,故D正确.
故选D.
9.【答案】BCD
【详解】对A,由,则或,解得或,故A错误;
对B,从五个人中选三个人站成一排,则不同的排法有种,故B正确;
对C,三棱柱有六个顶,可组成个四面体,而每个四面体有3对异面直线,则共有对,故C正确;
对D,根据分步计数原理可知用0,1,2,…,9这十个数字,可以组成三位数的个数为,其中没有重复数字的三位数的个数为,
所以可以组成有重复数字的三位数的个数为,故D正确.
故选BCD
10.【答案】AC
【详解】若(,,且)恰好能表示出12个不同的椭圆方程,
设有z个不同的值,则,解得,
根据其对称性可知,当或时满足,
故选:AC
11.【答案】AB
【详解】记第一次抽到第i号球的事件分别为,则有,
对于A,在第一次抽到2号球的条件下,则2号球放入2号盒子内,因此第二次抽到1号球的概率为,A正确;
对于B,记第二次在第i号盒内抽到3号球的事件分别为,而两两互斥,和为,
,记第二次抽到3号球的事件为,
,B正确;
对于C,记第二次在第i号盒内抽到1号球的事件分别为,而两两互斥,和为,
,记第二次抽到1号球的事件为,
,
第二次的球取自盒子的编号与第一次取的球的号数相同,
,,
,即第二次抽到的是1号球,则它来自1号盒子的概率最大,C不正确;
对于D,把5个不同的小球分成3组的不同分组方法数是种,
将每一种分组方法分成的小球放在3个盒子中有种不同放法,
由分步乘法计数原理得不同的放法种数是种,D不正确.
故选AB
12.【答案】0.7/ 0.3/
【详解】因为服从参数为0.3的两点分布,
所以, .
当时,,所以.
13.【答案】264
【详解】(1)若两节数学排在下午,有两种情况,1,2节或2,3节,剩下一节对应体育,
第二步,上午4节课全排列即可,有,故共有种,
(2)若两节数学排在上午,有1,2或2,3或3,4,共3种排法,
第二步,排体育,易知有3种排法,
第三步,剩下4节课,全排列,有,故共有,
所以共有种.
14.【答案】/
【详解】由图象可知:图象过点,即,解得:,;
由,得:直线方程为:;
设,则,,
则直角梯形的面积;
令,则,,
当时,;当时,;
在上单调递增,在上单调递增,
,
即图书馆占地面积(万平方米)的最大值为.
15.【答案】(1)5
(2)32
(3)答案见解析
【详解】(1)的展开式的通项为(r=0,1,2,…,n),
∵展开式中的第二项和第三项的系数相等,
∴,即,∴n2-5n=0,解得n=5或n=0(舍);
(2)展开式中所有二项式系数的和为;
(3)二项式展开式的通项为(r=0,1,2,…,5),
当r=0,2,4时,对应项是有理项,
所以展开式中所有的有理项为,,.
16.【答案】(1),切线方程为
(2)最大值为 ,最小值为0.
【详解】(1)因为,又在时有极值0,
则,解得或,
当时,恒成立,则无极值,不合题意;
当时,,
当或时,,即单调递增,
当时,,即单调递减,
所以是的极小值点,合题意.
所以,故,,
所以在处的切线方程为,即.
(2)由(1),,,
所以当时,,当时,,
所以在上单调递减,在上单调递增,
,,,
所以函数在区间上的最大值为112,最小值为0.
17.【答案】(1)
(2)答案见详解
(3)304元
【详解】(1)由题,李明在一年内领到计算机二级资格证书分3种情况,第一次领证,第二次领证,第三次领证,
所以概率为.
(2)的取值分别是,
,,,
所以李明参加考试次数的分布列为:
1 2 3
.
(3)已知每次考试报名费用为200元,考试次数为,则花费的费用,
所以元.
所以李明一年内参加考试花费的费用的期望为元.
18.【答案】(1)分布列见解析,,
(2)或
(3)
【详解】(1)的可能取值为
则,,,
,,
则分布列为:
则,
.
(2)由(1)可知,,,且,
由期望以及方差的性质可得,,
即,解得,
当时,,解得,
当时,,解得,
所以或.
(3)记事件表示的标号大于,
由(1)可知,当时,此时袋中还剩个球,
其中标号大于的有个,所以,
,当时,此时袋中还剩个球,
其中标号大于的有个,所以,
,
当时,此时袋中还剩个球,
其中标号大于的有个,则,
所以
.
19.【答案】(1)单调递增区间是,单调递减区间是
(2)
(3)证明见解析
【详解】(1)首先对函数求导,可得:
,函数的定义域为,
令,即,因为,则,解得,
当时,,所以在上单调递增;
当时,,所以在上单调递减,
综上所得,函数的单调递增区间是,单调递减区间是.
(2)由前面知道,的最大值为,要使能成立,则只能,即,则,有前面讨论,知道函数的单调递增区间是,单调递减区间是.则.
(3)由,得,
若有两个不同的实数解,则,
两式相减得,所以.
不妨设,则,
所以在上单调递增,此时,所以.
所以,即,所以①.
由,得有两个不同的实数解,
令,
当时单调递增,当时单调递减,
由,,所以.
令,则方程有两个不同的实数解.
由前面(1)(2)知,则有.
设,则,
当时,单调递减,当时,单调递增,
此时,即,故,当且仅当时等号成立.
不妨设直线与直线交点的横坐标分别为,
则,
所以②.
综上,.
一、单选题(本大题共8小题)
1.某物体沿直线运动,位移(单位:)与时间(单位:)的关系为,则该物体在时的瞬时速度是( )
A. B. C. D.
2.从1,2,3,4,5中不放回地抽取2个数,则在第1次抽到偶数的条件下,第2次抽到奇数的概率是( )
A. B. C. D.
3.某学校为了了解学生美育培养的情况,用分层随机抽样方法抽样调查,拟从美术、音乐、舞蹈兴趣小组中共抽取30名学生,已知该校美术、音乐、舞蹈兴趣小组分别有20,30,50名学生,则不同的抽样结果共有( )
A. B.
C. D.
4.在的展开式中,只有第五项的二项式系数最大,则展开式中的系数是( )
A. B. C. D.7
5.已知随机变量的分布是,则等于( )
A. B. C. D.
6.已知函数,则不等式的解集为( )
A. B. C. D.
7.现有四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为( )
A. B. C. D.
8.已知函数,,则下列说法正确的是( )
A.当时,有2个零点
B.当时,存在增区间
C.若只有一个极值点,则或
D.当时,对任意实数t,总存在实数,,使得
二、多选题(本大题共3小题)
9.下列说法正确的是( )
A.若,则
B.从五个人中选三个人站成一排,则不同的排法有60种
C.过三棱柱任意两顶点的直线中,异面直线共有36对
D.用0,1,2,…,9这十个数字,可以组成有重复数字的三位数的个数为252
10.设N为正整数,在平面直角坐标系中,若(,,且)恰好能表示出12个不同的椭圆方程,则N的可能取值为( )
A.6 B.8 C.7 D.5
11.已知编号为1,2,3的三个盒子,其中1号盒子内装有两个1号球,一个2号球和一个3号球;2号盒子内装有两个1号球,一个3号球;3号盒子内装有三个1号球,两个2号球.若第一次先从1号盒子内随机抽取1个球,将取出的球放入与球同编号的盒子中,第二次从该盒子中任取一个球,则下列说法正确的是( )
A.在第一次抽到2号球的条件下,第二次抽到1号球的概率为
B.第二次抽到3号球的概率为
C.如果第二次抽到的是1号球,则它来自2号盒子的概率最大
D.如果将5个不同的小球放入这三个盒子内,每个盒子至少放1个,则不同的放法有300种
三、填空题(本大题共3小题)
12.已知X服从参数为0.3的两点分布,则 ;若,则 .
13.为确保学生身心健康,全面发展,高中课程内容覆盖学科教学、体育、艺术等类别,我校按照教育部的指导,安排上午四节课,下午三节课,现在安排我班一天中语文、英语、物理、政治、体育各一节,数学两节,要求两节数学课都排在上午或下午、且连续,体育课排在下午,则不同的排法有 种.
14.从商业化书店到公益性城市书房,再到“会呼吸的文化森林”——图书馆,建设高水平、现代化、开放式的图书馆一直以来是大众的共同心声.现有一块不规则的地,其平面图形如图所示,(百米),建立如图所示的平面直角坐标系,将曲线看成函数图象的一部分,为一次函数图象的一部分,若在此地块上建立一座图书馆,平面图为直角梯形(如图),则图书馆占地面积(万平方米)的最大值为 .
四、解答题(本大题共5小题)
15.已知的展开式中的第二项和第三项的系数相等.
(1)求n的值;
(2)求展开式中所有二项式系数的和;
(3)求展开式中所有的有理项.
16.已知在时有极值0.
(1)求常数a、b及的图象在处的切线方程;
(2)求函数在区间上的最大值与最小值.
17.计算机二级资格证考试包括语言程序设计、数据库程序设计和办公软件高级应用三类科目,每年可以考3次,分别在3月、5月和9月进行,一旦某次考试通过,便可领取资格证书,不再参加以后的考试,否则就继续参加考试,直到用完3次机会.李明决定参加考试,如果他每次参加考试通过的概率依次为0.6,0.7,0.8,且每次考试是否通过相互独立.
(1)求李明在一年内领到计算机二级资格证书的概率;
(2)求李明在一年内参加考试次数X的分布列及期望;
(3)已知每次考试报名费用为200元,求李明一年内参加考试花费的费用Y的期望.
18.袋中有20个大小相同的球,其中标记上0号的有10个,标记上号的有n个.现从袋中任取一球,用表示所取球的标号.
(1)求的分布列、期望和方差;
(2)若,,,试求a,b的值;
(3)若每次取球后不放回,先取一个球记标号为X,再取一个球记标号为Y,求Y的标号大于1的概率.
19.已知函数.
(1)求函数的单调区间;
(2)是否存在x使得成立?若存在,求x的取值范围,若不存在,请说明理由;
(3)若方程有两个不同的实数解,证明:.
参考答案
1.【答案】D
【详解】,
当时,,
即该物体在时的瞬时速度是.
故选D.
2.【答案】D
【详解】设事件为“第i次抽到偶数”,i=1,2,
则事件“在第1次抽到偶数的条件下,第2次抽到奇数”的概率为:
.
故选D.
3.【答案】C
【详解】由题意,美术组要抽取的学生数为,音乐组要抽取的学生数为,舞蹈组要抽取的学生数为,由分步乘法计数原理可知,不同的抽样结果.
故选:C.
4.【答案】C
【详解】在的展开式中,只有第5项的二项式系数最大,
它的展开式共计有9项,,
故二项展开式的通项公式为,
令,求得,可得在的展开式中的系数为,
故选C.
5.【答案】C
【详解】由题意可得,解得,
.
.
故选C.
6.【答案】C
【详解】由函数,所以,则为偶函数,
当时,又因为,且恒成立,
则,所以在时单增,
综上可得等价于,即或,解得
故选:C
7.【答案】C
【详解】根据题意,用四种不同的颜色要对如图形中的五个部分进行着色,每个部分都有4种涂色方法,则有种涂色方法;
若其中任意有公共边的两块着不同颜色,有两种情况:①只用三种颜色涂这5个区域,则有种涂色方法;②用四种颜色涂这5个区域,则有种涂色方法,所以若其中任意有公共边的两块着不同颜色,共有144种涂色方法,故四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为.
故选C
8.【答案】D
【详解】对于A,当时,,令,得,
令,则,所以在R上单调递增,
所以至多有一个零点,即方程至多有一个根,故A错误;
对于B,,
令,得,设,
则,当时,,单调递增,当时,,单调递减,
所以,又当时,,所以恒成立,
即时,是减函数,故B错误;
对于C,当时,由B知,,即,所以,
所以在R上单调递减,无极值,故C错误;
对于D,当时,,,由切线放缩知,
,即在R上单调递减,当时,,当时,,
可得的大致图象如下:
由图可知对任意实数,总存在实数,使得,故D正确.
故选D.
9.【答案】BCD
【详解】对A,由,则或,解得或,故A错误;
对B,从五个人中选三个人站成一排,则不同的排法有种,故B正确;
对C,三棱柱有六个顶,可组成个四面体,而每个四面体有3对异面直线,则共有对,故C正确;
对D,根据分步计数原理可知用0,1,2,…,9这十个数字,可以组成三位数的个数为,其中没有重复数字的三位数的个数为,
所以可以组成有重复数字的三位数的个数为,故D正确.
故选BCD
10.【答案】AC
【详解】若(,,且)恰好能表示出12个不同的椭圆方程,
设有z个不同的值,则,解得,
根据其对称性可知,当或时满足,
故选:AC
11.【答案】AB
【详解】记第一次抽到第i号球的事件分别为,则有,
对于A,在第一次抽到2号球的条件下,则2号球放入2号盒子内,因此第二次抽到1号球的概率为,A正确;
对于B,记第二次在第i号盒内抽到3号球的事件分别为,而两两互斥,和为,
,记第二次抽到3号球的事件为,
,B正确;
对于C,记第二次在第i号盒内抽到1号球的事件分别为,而两两互斥,和为,
,记第二次抽到1号球的事件为,
,
第二次的球取自盒子的编号与第一次取的球的号数相同,
,,
,即第二次抽到的是1号球,则它来自1号盒子的概率最大,C不正确;
对于D,把5个不同的小球分成3组的不同分组方法数是种,
将每一种分组方法分成的小球放在3个盒子中有种不同放法,
由分步乘法计数原理得不同的放法种数是种,D不正确.
故选AB
12.【答案】0.7/ 0.3/
【详解】因为服从参数为0.3的两点分布,
所以, .
当时,,所以.
13.【答案】264
【详解】(1)若两节数学排在下午,有两种情况,1,2节或2,3节,剩下一节对应体育,
第二步,上午4节课全排列即可,有,故共有种,
(2)若两节数学排在上午,有1,2或2,3或3,4,共3种排法,
第二步,排体育,易知有3种排法,
第三步,剩下4节课,全排列,有,故共有,
所以共有种.
14.【答案】/
【详解】由图象可知:图象过点,即,解得:,;
由,得:直线方程为:;
设,则,,
则直角梯形的面积;
令,则,,
当时,;当时,;
在上单调递增,在上单调递增,
,
即图书馆占地面积(万平方米)的最大值为.
15.【答案】(1)5
(2)32
(3)答案见解析
【详解】(1)的展开式的通项为(r=0,1,2,…,n),
∵展开式中的第二项和第三项的系数相等,
∴,即,∴n2-5n=0,解得n=5或n=0(舍);
(2)展开式中所有二项式系数的和为;
(3)二项式展开式的通项为(r=0,1,2,…,5),
当r=0,2,4时,对应项是有理项,
所以展开式中所有的有理项为,,.
16.【答案】(1),切线方程为
(2)最大值为 ,最小值为0.
【详解】(1)因为,又在时有极值0,
则,解得或,
当时,恒成立,则无极值,不合题意;
当时,,
当或时,,即单调递增,
当时,,即单调递减,
所以是的极小值点,合题意.
所以,故,,
所以在处的切线方程为,即.
(2)由(1),,,
所以当时,,当时,,
所以在上单调递减,在上单调递增,
,,,
所以函数在区间上的最大值为112,最小值为0.
17.【答案】(1)
(2)答案见详解
(3)304元
【详解】(1)由题,李明在一年内领到计算机二级资格证书分3种情况,第一次领证,第二次领证,第三次领证,
所以概率为.
(2)的取值分别是,
,,,
所以李明参加考试次数的分布列为:
1 2 3
.
(3)已知每次考试报名费用为200元,考试次数为,则花费的费用,
所以元.
所以李明一年内参加考试花费的费用的期望为元.
18.【答案】(1)分布列见解析,,
(2)或
(3)
【详解】(1)的可能取值为
则,,,
,,
则分布列为:
则,
.
(2)由(1)可知,,,且,
由期望以及方差的性质可得,,
即,解得,
当时,,解得,
当时,,解得,
所以或.
(3)记事件表示的标号大于,
由(1)可知,当时,此时袋中还剩个球,
其中标号大于的有个,所以,
,当时,此时袋中还剩个球,
其中标号大于的有个,所以,
,
当时,此时袋中还剩个球,
其中标号大于的有个,则,
所以
.
19.【答案】(1)单调递增区间是,单调递减区间是
(2)
(3)证明见解析
【详解】(1)首先对函数求导,可得:
,函数的定义域为,
令,即,因为,则,解得,
当时,,所以在上单调递增;
当时,,所以在上单调递减,
综上所得,函数的单调递增区间是,单调递减区间是.
(2)由前面知道,的最大值为,要使能成立,则只能,即,则,有前面讨论,知道函数的单调递增区间是,单调递减区间是.则.
(3)由,得,
若有两个不同的实数解,则,
两式相减得,所以.
不妨设,则,
所以在上单调递增,此时,所以.
所以,即,所以①.
由,得有两个不同的实数解,
令,
当时单调递增,当时单调递减,
由,,所以.
令,则方程有两个不同的实数解.
由前面(1)(2)知,则有.
设,则,
当时,单调递减,当时,单调递增,
此时,即,故,当且仅当时等号成立.
不妨设直线与直线交点的横坐标分别为,
则,
所以②.
综上,.
同课章节目录
