数学:第十二章轴对称复习教案(人教新课标八年级上)
文档属性
| 名称 | 数学:第十二章轴对称复习教案(人教新课标八年级上) |

|
|
| 格式 | doc | ||
| 文件大小 | 595.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-14 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第十二章 《轴对称》复习教案
专题一:轴对称
一、 知识要点:
1.轴对称
(1)轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫轴对称图形.这条直线叫对称轴.
(2)轴对称:把一个图形沿着某一直线折叠,如果它能够与另一个图形重合,就说这两个图形关于这条直线对称,这条直线叫对称轴.
(3)图形轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.关于某条直线对称的两个图形全等.
(4)轴对称图形的性质:轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(5)图形对称轴的作法:要作两个图形的对称轴,只要找到这两个图形的一对对应点,然后连结它们,得到一条线段,再作出这条线段的垂直平分线,这条垂直平分线就是这两个图形的对称轴.
2.线段的垂直平分线
(1)经过线段的中点并且垂直于这条线段的直线,叫做线段的垂直平分线.
(2)线段垂直平分线的性质:线段垂直平分线上的点到线段两个端点的距离相等;到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、题目特点:和本专题有关的题目主要涉及以下几个方面:(1)判别轴对称图形或对称轴的条数;(2)根据轴对称图形的性质作对称轴;(3)用线段垂直平分线的性质解决计算题或进行证明说理.
三、解题切入点:熟练掌握轴对称图形概念、性质以及线段垂直平分线的性质是解决有关问题的关键.
例1 下列图形是轴对称图形的是 ( ).
(A) (B) (C) (D)
分析:要选择哪个图案是轴对称图形,主要根据轴对称图形的特征:沿某条直线折叠,直线两旁的部分能互相重合.观察所给的四个图案,能沿某直线折叠重合的只有最后一个图形.
解:选(D).
例2 如图1,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离相等?
图1 图2
分析:本题是一道与线段垂直平分线性质应用有关的题目.解决问题的关键从实际问题中构建数学模型.如图2,将A、B两个居民区看作两个点,将街道看作直线l,则本题实际上是在直线l上求作一点,这点到点A、B的距离相等.作线段AB的垂直平分线即可解决问题.
解:如图2,(1)连结AB,(2)作线段AB的垂直平分线MN交直线l与点P,则点P就是所求作的奶站的位置.
例3 如图3,△ABC中,∠BAC=120°,若DE、FG分别垂直平分AB、AC,△AEF的周长为10cm,求∠EAF的度数及BC的长.
图3
分析:本题主要考查线段垂直平分线性质的应用.要求BC的长,根据已知可得EA=EB,FA=FC,这样BC的长实际就是AE+EF+AF.要求∠EAF的度数,则只要求到∠BAE+∠CAF的度数即可解决问题.
解:因为∠BAC=120°,所以∠B+∠C=60°,
因为DE垂直平分AB,所以BE=AE,∠B=∠BAE,
因为FG垂直平分AC,所以AF=CF,∠C=∠CAF,
所以AE+EF+AF=BE+EF+CF=BC=10cm,∠EAF=∠BAC-(∠BAE+∠CAF)=120°-(∠B+∠C)=60°.
专项练习1:
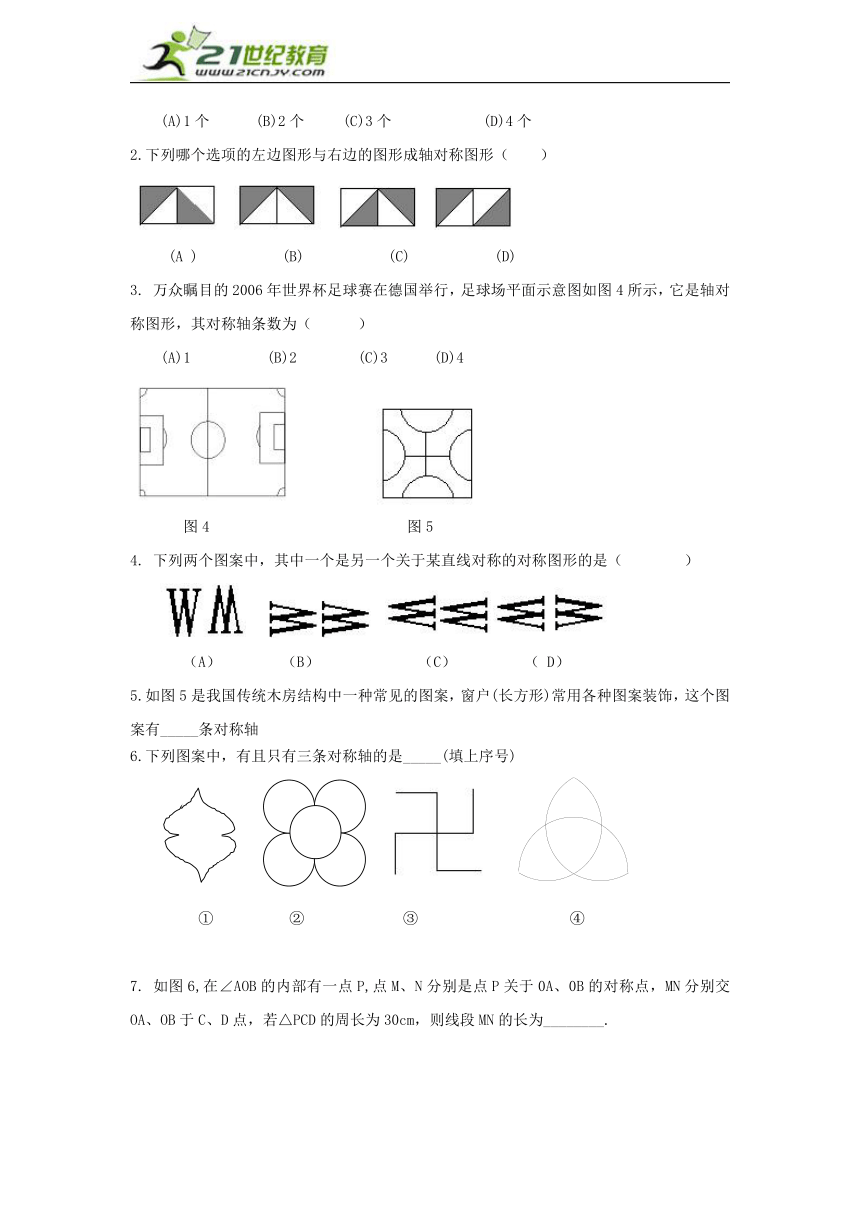
1. 下列图形中,轴对称图形的个数是( )
(A)1个 (B)2个 (C)3个 (D)4个
2.下列哪个选项的左边图形与右边的图形成轴对称图形( )
(A ) (B) (C) (D)
3. 万众瞩目的2006年世界杯足球赛在德国举行,足球场平面示意图如图4所示,它是轴对称图形,其对称轴条数为( )
(A)1 (B)2 (C)3 (D)4
图4 图5
4. 下列两个图案中,其中一个是另一个关于某直线对称的对称图形的是( )
(A) (B) (C) ( D)
5.如图5是我国传统木房结构中一种常见的图案,窗户(长方形)常用各种图案装饰,这个图案有_____条对称轴
6.下列图案中,有且只有三条对称轴的是_____(填上序号)
① ② ③ ④
7. 如图6,在∠AOB的内部有一点P,点M、N分别是点P关于0A、0B的对称点,MN分别交OA、OB于C、D点,若△PCD的周长为30cm,则线段MN的长为________.
图6 图7 图8 图9
8.如图7,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=50°,AB+BC=16cm,则△BCF的周长为_________
9. 如图8,△ABC中,AB=AC,∠A=50°,AB的垂直平分线交AC于D,求∠DBC的度数.
10.如图9,在Rt△ABC中,∠C=90°,DB平分∠ABC交AC于点D,DE的垂直平分斜边AB于E.
(1)请你在图形中找出至少两对相等的线段,并说明它们为什么相等?
(2)如果BC=6,AC=8,则△BDC的周长为多少?
答案:1.B 2.B 3.B 4.D 5.2条; 6.④; 7.30; 8.16cm;
9. 因为AB=AC,AB的垂直平分线交AC于D,所以∠ABC=∠C=65°,∠A=∠ABD=50°,
所以∠DBC=65°-50°=15°.
10. (1)AE=EB(根据DE是AB的垂直平分线),AD=DB(根据线段平分线上的点到线段两个端点的距离相等).DE=DC(根据角平分线上的点到角的两边的距离相等).
(2)因为BD=AD,所以BD+DC+BC=AD+DC+BC=AC+BC=6+8=14.即△BDC的周长为14.
专题二: 轴对称变换
一、 知识要点:
1.轴对称变换:(1)由一个平面图形得到它的轴对称图形叫做轴对称变换.由轴对称变换得到的图形与原图形形状、大小完全相同;新图上的每一点都是原图形上的某一点关于对称轴的对称点;连接任意一对对应点的线段被对称轴垂直平分.
(2)作一个平面图形的对称图形,先作一些点的对应点,再连接这些对应点,就可得到原图形的轴对称图形.对于线段、三角形、四边形等由直线、线段或射线组成的图形,只要作出原图形上的关键点的对应点,然后连接这些对应点,即可得到相应的对称图形.
(3)利用轴对称变换设计图案,主要是借助平移等有关知识.
2.以坐标轴为对称轴作对称图形
(1)点P(x,,y)关于x轴对称的对称点为P1(x,-y),点P(x,y)关于y轴对称点的坐标为P2(-x,y);也就是:若两点关于x轴对称,那么它们的横坐标相同,纵坐标互为相反数;若两点关于y轴对称,那么它们的纵坐标相同,横坐标互为相反数.
(2)作一个图形关于坐标轴对称的图形,一般先作图形上关键点关于坐标轴的对称点,然后连接对称点即可.
二、题型特点:和轴对称变换的主要题型有:(1)作一个平面图形(如三角形,四边形等)关于已知直线的对称图形;(2)求已知点关于坐标轴对称的对称点的坐标;(3)根据轴对称变换设计图案;(4)根据轴对称变换解决实际生活中问题.
三、解题切入点:作一个平面图形的轴对称图形,关键是确定原图形上的关键点,只要作出这些关键点的对称点,然后按原图形的顺序连接即可;求一个点关于坐标轴对称点的坐标,关键是熟练掌握对称点之间的坐标特征;根据轴对称变换解决实际问题,需要从实际问题中构建出数学模型.
例1 如图1,以直线AE为对称轴,画出该图形的另一部分.
分析:要画出图形的另一部分, 首先要找到图形上的关键点A,B,C,D,E,由于点A,D,E在对称轴上,所以它们的对称点与本身重合,这样只要根据对称的性质作出关键点B、C关于直线AE的对称点,然后用线段连结相应的对称点即可得到图形的另一部分.
解:作图过程如下:
(1)分别作出点B、C关于直线AE的对称点F,H,如图2;
(2)连结AF、FD、DH、HE,得到所求的图形,如图3.
图1 图2 图3
例2 用四块如图4①所示的正方形瓷砖拼成一个新的正方形,使拼成的图案是一个轴对称图形.请你在图4②、图4③、图4④中各画一种拼法(要求三种拼法各不相同).
① ② ③ ④
图4
分析:本题是一道与轴对称图形有关的拼图问题,要拼轴对称图案,则需要理解轴对称图形的特征:要某直线折叠后,直线两旁的部分能完全重合.另外还需要掌握平移等有关知识.设计图案问题一般具有开放性,可以根据自己想象设计出美丽的图案.
解:下面给出3种不同答案,供参考.如图5.
图5
例3如图6,(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.
图6 图7
分析:(1)在直角坐标系内作△ABC关于y轴的对称图形,可先确定关键点A、B、C关于y轴的对称点A1、B1、C1的坐标,描出这些点的坐标,然后顺次连结即可.(2)要作△ABC向右平移6个单位的后的△A2B2C2,首先要作出A、B、C三点向右平移6个单位的对应点,然后顺次连接即可;(3)要观察△A1B1C1和△A2B2C2是否关于某直线对称,可连接A1A2,B1B2,C1C2,看它们的垂直平分线是否是同一条直线,如果是,则△A1B1C1和△A2B2C2就关于这条直线对称,否则,不关于某条直线对称.
解: (1)如图7所示,A1(0,4),B1(2,2),C1(1,1);
(2)如图7所示,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1与△A2B2C2关于直线轴对称.
专项练习:
1.在直角坐标系中,点P(-2,-4)关于y轴的对称点的坐标是( ).
(A)(-2,4) (B)(2,-4) (C)(2,4) (D)(-4,-2)
2.点M(1,2)关于x轴对称点的坐标为 ( ).
(A) (-1,2) (B)(-1,-2) (C)(1,-2) (D)(2,-1)
3.点P(3,-2)关于直线x=4对称点的坐标是( ).
(A) (5,-3) (B)(-2,5) (C) (5,-2) (D) (-3,4)
4.已知直线l和l同旁的两点A、B,在直线l上求一点P,使PA+PB最小,那么正确的是( ).
(A)作点A关于直线l的对称点A,连结AB与直线l的交点即为点P
(B)直线AB与直线l的交点为P点
(C)若直线AB//l,则直线l上的任意点即可为点P
(D)过线段AB的中点,向直线a引垂线,垂足即为点P.
5.点M(3a-b,4)与点N(9,2a+b)关于x轴对称,则a=_____,b=_____.
6.点A的坐标是(-2,3),点B与点A关于直线x=1对称,点C与点B关于直线y=-2对称,则点C的坐标为_______.
7.如图8,由5个小正方形组成的图形,请你三种不同的方法,分别添画一个小正方形,使它成为轴对称图形.
图8
8.如图9,作出△ABC关于直线l的对称三角形△A′B′C.′
图9 图10
9. 已知四边形ABCD各顶点为A(1,2), B( 1,4), C(3,5), D (3,3),作四边形ABCD关于直线x=-1的对称图形.
10. 如图10,是一个8×10的正方形格纸,△ABC中A点坐标为(-2 ,1 ).
⑴△ABC和△A′B′C′满足什么几何变换(直接写答案)?
⑵作△A′B′C′关于x轴对称图形△A″B″C″;
⑶求A″、B″、C″三点坐标(直接写答案)
答案:1.B 2.C 3.C 4.A 5.1,-6; 6.(4,-7);
7.如图.
7题 8题
8.如图.
9.如图.
9题 10题
10.(1)△ABC和△A′B′C′满足轴对称变换;(2)如图2所示.(3) A″(2,-1)、B″(1,-2)、
C″(3,-3).
专题三:等腰三角形
一、知识要点:
1. 等腰三角形
(1)有两边相等的三角形叫做等腰三角形.等腰三角形是轴对称图形.
(2)等腰三角形的性质:①等腰三角形的两个底角相等;②等腰三角形的顶角的平分线、底边的中线、底边上的高互相重合.
(3)等腰三角形的判别方法:①直接根据定义;②等角对等边.
2. 等边三角形
(1)三边都相等的三角形叫做等边三角形.是轴对称图形,有三条对称轴.
(2)等边三角形的性质:等边三角形的三个角都是60°.
(3)等边三角形的判别方法:①三个角都相等的三角形是等边三角形;②有一个角是60°的等腰三角形是等边三角形.
二、题目特点:和等腰三角形有关的题目主要有两类:(1)计算题.如求等腰三角形的腰长,周长、角度等;(2)说理题.如证明一个三角形是等腰(或等边)三角形;(3)实际应用题.如根据实际问题构造等腰三角形解决问题.
三、解题切入点:解决和等腰三角形有关的计算问题,要把握等腰三角形的性质,注意分类思想在等腰三角形中的应用.解决证明问题主要依据等腰(或等边)三角形的性质和判定方法,有的问题还需要作恰当的辅助线.
例1 如图1是某房屋顶框架的示意图,其中,AB=AC,AD⊥BC,∠BAC=120°,求∠B、∠C和∠BAD的度数.
分析:由AB=AC,可知△ABC是等腰三角形,等腰三角形的底边上的高,顶角的平分线重合,根据AD⊥BC,可得AD平分∠BAC,进一步可以求到各角的度数.
解:在△ABC中,
因为AB=AC,所以∠B=∠C,
因为∠BAC+∠B+∠C=180°,∠BAC=120°,
所以∠B=∠C=(180°-120°)=30°,
因为AD⊥BC,所以∠BAD=∠BAC=60°. 图1
例2 如图,2一艘轮船在近海处由南向北航行,点C是灯塔,轮船在A处测得在其北偏西38°的方向上,轮船又又A向北航行30海里到B,测得灯塔在其北偏西76°的方向上.
(1) 求∠ACB的度数;
(2) 轮船在B处时,到灯塔C的距离是多少
分析:本题是一道实际问题,解决问题的关键是根据实际问题画出几何图形,通过分析图形中角度之间的关系,借助等腰三角形的知识解决.
解:因为∠NAC=38°,∠NBC=76°,
所以∠NBC=∠ACB+∠NAC,
所以∠ACB=∠NBC-∠NAC=76°-38°=38°.
(2)因为∠ACB=∠NAC=38°, 所以AB=AC, 图2
因为AB=30海里,所以BC=30海里,
即点B到灯塔C的距离是30海里.
例3如图3,已知△ABC为等边三角形,D、E、F分别在边BC、CA、AB,且△DEF也是等边三角形.
除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
分析:本题是一道猜想型探索题.要探索图形中存在哪些相等的线段,可根据等边三角形的性质,通过寻找三角形全等进行探索.
解:(1)图中还有相等的线段是:AE=BF=CD,AF=BD=CE ,
事实上,因为△ABC与△DEF都是等边三角形,
所以∠A=∠B=∠C=60°,∠EDF=∠DEF=∠EFD=60°,DE=EF=FD ,
又因为∠CED+∠AEF=120°,∠CDE+∠CED=120°, 所以∠AEF=∠CDE,
同理,得∠CDE=∠BFD,
所以△AEF≌△BFD≌△CDE(AAS),
所以AE=BF=CD,AF=BD=CE .
专项练习3: 图3
1. △ABC中,AB=AC,它的两边分别是2厘米和4厘米,则它的周长是( )
(A)8厘米 (B)10厘米 (C)8厘米或10厘米 (D)不确定
2.如图4,在△ABC中,已知∠B和∠C的平分线相交于点F,过点F作DF//BC,交AB于点D,交AC于点E,若BD+CE=9,则线段DE的长为( )
(A)9 (B)8 (C)7 (D) 6
图4 图5 图6
3.如图5,△ABC为等边三角形,AD为BD边上的高,E为AC边上的一点,且AE=AD,则
∠EDC=___度.
4. 如图6,在△ABC中,D、E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是_____.
5.分别以等腰三角形的腰与底边向三角形外作正三角形,其周长为24和36,求等腰三角形的周长.
6.如图7,在△ABC中,已知AB=AC,BD、CE是两条角平分线,BD、CE相交于点O,△OBC是等腰三角形吗?为什么?
图7 图8
7.如图8,在Rt△ABC中,∠A=30°,∠C=90°,BC=10,点D是斜边AB的中点,DE⊥AC,交AC于E.求DE的长.
8.如图9,在△ABC中,BP、CP分别是∠ABC和∠ACB的平分线,且PD//AB,PE//AC,求△PED的周长.
9.如图10,已知△ABC中,AB=AC,AF是BC边的中线,D是BA延长线上一点,E在AC上,且AD=AE.求证:DE⊥BC.
图 9 图10 图11
10.如图11,已知AB=AD,∠BAD=60°,∠BCD=120°,延长B到E,使CE=CD,连结DE.求证:BC+DC=AC.
答案:1.B 2.A 3. 15; 4.120°;
5. 由等边三角形的周长为24,36可得等腰三角形的底、腰长可能是8、12.
当腰为12,底边为8时,周长为12+12+8=32,
当腰长为8,底边为12时,周长为8+8+12=28.
所以等腰三角形的周长为32或28.
6. △OBC是等腰三角形.理由:在△ABC中,因为AB=AC,所以∠ABC=∠ACB,
又BD是∠ABC的平分线,所以∠OBC=∠ABC,
又CE是∠ABC的平分线,所以∠OCB=∠ACB,所以∠OCB=∠OBC,
所以OB=OC,即△OBC是等腰三角形.
7. 在Rt△ABC中,因为∠A=30°,BC=10,所以AB=20,因为D为AB中点,所以AD=10,
在Rt△ADE中,因为∠A=30°,AD=10,所以DE=5.
8. 因为BP是∠ABC的平分线,CP是∠ACB的平分线,所以∠ABP=∠CBP,∠ACP=∠BCP,
因为PD//AB,所以∠ABP=∠BPD,所以∠PBC=∠BPD,所以BD=PD,同理PE=EC.
所以△PDE的周长等于PD+PE+DE=BD+DE+EC=BC=5cm.
9.因为AB=AC,BF=CF,所以∠BAF=∠CAF,AF⊥BC,
因为AD=AE,所以∠ADE=∠BAC,
所以∠BAF=∠D,所以DE//AF,所以DE⊥BC.
10.连结BD,因为AB=AD,∠BAD=60°,所以△ABD为等边三角形,
因为CD=CE,∠DCE=60°,所以△CDE为等边三角形,
因为∠ADB=∠CDE=60°,所以∠ADB+∠BDC=∠CDE+∠BDC,即∠ADC=∠BDE,
又AD=BD,CD=ED,所以△ADC≌△BDE,所以AC=BE,
又BE=BC+CE=BC+CD,所以AC=BC+CD.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第十二章 《轴对称》复习教案
专题一:轴对称
一、 知识要点:
1.轴对称
(1)轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫轴对称图形.这条直线叫对称轴.
(2)轴对称:把一个图形沿着某一直线折叠,如果它能够与另一个图形重合,就说这两个图形关于这条直线对称,这条直线叫对称轴.
(3)图形轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.关于某条直线对称的两个图形全等.
(4)轴对称图形的性质:轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(5)图形对称轴的作法:要作两个图形的对称轴,只要找到这两个图形的一对对应点,然后连结它们,得到一条线段,再作出这条线段的垂直平分线,这条垂直平分线就是这两个图形的对称轴.
2.线段的垂直平分线
(1)经过线段的中点并且垂直于这条线段的直线,叫做线段的垂直平分线.
(2)线段垂直平分线的性质:线段垂直平分线上的点到线段两个端点的距离相等;到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、题目特点:和本专题有关的题目主要涉及以下几个方面:(1)判别轴对称图形或对称轴的条数;(2)根据轴对称图形的性质作对称轴;(3)用线段垂直平分线的性质解决计算题或进行证明说理.
三、解题切入点:熟练掌握轴对称图形概念、性质以及线段垂直平分线的性质是解决有关问题的关键.
例1 下列图形是轴对称图形的是 ( ).
(A) (B) (C) (D)
分析:要选择哪个图案是轴对称图形,主要根据轴对称图形的特征:沿某条直线折叠,直线两旁的部分能互相重合.观察所给的四个图案,能沿某直线折叠重合的只有最后一个图形.
解:选(D).
例2 如图1,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离相等?
图1 图2
分析:本题是一道与线段垂直平分线性质应用有关的题目.解决问题的关键从实际问题中构建数学模型.如图2,将A、B两个居民区看作两个点,将街道看作直线l,则本题实际上是在直线l上求作一点,这点到点A、B的距离相等.作线段AB的垂直平分线即可解决问题.
解:如图2,(1)连结AB,(2)作线段AB的垂直平分线MN交直线l与点P,则点P就是所求作的奶站的位置.
例3 如图3,△ABC中,∠BAC=120°,若DE、FG分别垂直平分AB、AC,△AEF的周长为10cm,求∠EAF的度数及BC的长.
图3
分析:本题主要考查线段垂直平分线性质的应用.要求BC的长,根据已知可得EA=EB,FA=FC,这样BC的长实际就是AE+EF+AF.要求∠EAF的度数,则只要求到∠BAE+∠CAF的度数即可解决问题.
解:因为∠BAC=120°,所以∠B+∠C=60°,
因为DE垂直平分AB,所以BE=AE,∠B=∠BAE,
因为FG垂直平分AC,所以AF=CF,∠C=∠CAF,
所以AE+EF+AF=BE+EF+CF=BC=10cm,∠EAF=∠BAC-(∠BAE+∠CAF)=120°-(∠B+∠C)=60°.
专项练习1:
1. 下列图形中,轴对称图形的个数是( )
(A)1个 (B)2个 (C)3个 (D)4个
2.下列哪个选项的左边图形与右边的图形成轴对称图形( )
(A ) (B) (C) (D)
3. 万众瞩目的2006年世界杯足球赛在德国举行,足球场平面示意图如图4所示,它是轴对称图形,其对称轴条数为( )
(A)1 (B)2 (C)3 (D)4
图4 图5
4. 下列两个图案中,其中一个是另一个关于某直线对称的对称图形的是( )
(A) (B) (C) ( D)
5.如图5是我国传统木房结构中一种常见的图案,窗户(长方形)常用各种图案装饰,这个图案有_____条对称轴
6.下列图案中,有且只有三条对称轴的是_____(填上序号)
① ② ③ ④
7. 如图6,在∠AOB的内部有一点P,点M、N分别是点P关于0A、0B的对称点,MN分别交OA、OB于C、D点,若△PCD的周长为30cm,则线段MN的长为________.
图6 图7 图8 图9
8.如图7,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=50°,AB+BC=16cm,则△BCF的周长为_________
9. 如图8,△ABC中,AB=AC,∠A=50°,AB的垂直平分线交AC于D,求∠DBC的度数.
10.如图9,在Rt△ABC中,∠C=90°,DB平分∠ABC交AC于点D,DE的垂直平分斜边AB于E.
(1)请你在图形中找出至少两对相等的线段,并说明它们为什么相等?
(2)如果BC=6,AC=8,则△BDC的周长为多少?
答案:1.B 2.B 3.B 4.D 5.2条; 6.④; 7.30; 8.16cm;
9. 因为AB=AC,AB的垂直平分线交AC于D,所以∠ABC=∠C=65°,∠A=∠ABD=50°,
所以∠DBC=65°-50°=15°.
10. (1)AE=EB(根据DE是AB的垂直平分线),AD=DB(根据线段平分线上的点到线段两个端点的距离相等).DE=DC(根据角平分线上的点到角的两边的距离相等).
(2)因为BD=AD,所以BD+DC+BC=AD+DC+BC=AC+BC=6+8=14.即△BDC的周长为14.
专题二: 轴对称变换
一、 知识要点:
1.轴对称变换:(1)由一个平面图形得到它的轴对称图形叫做轴对称变换.由轴对称变换得到的图形与原图形形状、大小完全相同;新图上的每一点都是原图形上的某一点关于对称轴的对称点;连接任意一对对应点的线段被对称轴垂直平分.
(2)作一个平面图形的对称图形,先作一些点的对应点,再连接这些对应点,就可得到原图形的轴对称图形.对于线段、三角形、四边形等由直线、线段或射线组成的图形,只要作出原图形上的关键点的对应点,然后连接这些对应点,即可得到相应的对称图形.
(3)利用轴对称变换设计图案,主要是借助平移等有关知识.
2.以坐标轴为对称轴作对称图形
(1)点P(x,,y)关于x轴对称的对称点为P1(x,-y),点P(x,y)关于y轴对称点的坐标为P2(-x,y);也就是:若两点关于x轴对称,那么它们的横坐标相同,纵坐标互为相反数;若两点关于y轴对称,那么它们的纵坐标相同,横坐标互为相反数.
(2)作一个图形关于坐标轴对称的图形,一般先作图形上关键点关于坐标轴的对称点,然后连接对称点即可.
二、题型特点:和轴对称变换的主要题型有:(1)作一个平面图形(如三角形,四边形等)关于已知直线的对称图形;(2)求已知点关于坐标轴对称的对称点的坐标;(3)根据轴对称变换设计图案;(4)根据轴对称变换解决实际生活中问题.
三、解题切入点:作一个平面图形的轴对称图形,关键是确定原图形上的关键点,只要作出这些关键点的对称点,然后按原图形的顺序连接即可;求一个点关于坐标轴对称点的坐标,关键是熟练掌握对称点之间的坐标特征;根据轴对称变换解决实际问题,需要从实际问题中构建出数学模型.
例1 如图1,以直线AE为对称轴,画出该图形的另一部分.
分析:要画出图形的另一部分, 首先要找到图形上的关键点A,B,C,D,E,由于点A,D,E在对称轴上,所以它们的对称点与本身重合,这样只要根据对称的性质作出关键点B、C关于直线AE的对称点,然后用线段连结相应的对称点即可得到图形的另一部分.
解:作图过程如下:
(1)分别作出点B、C关于直线AE的对称点F,H,如图2;
(2)连结AF、FD、DH、HE,得到所求的图形,如图3.
图1 图2 图3
例2 用四块如图4①所示的正方形瓷砖拼成一个新的正方形,使拼成的图案是一个轴对称图形.请你在图4②、图4③、图4④中各画一种拼法(要求三种拼法各不相同).
① ② ③ ④
图4
分析:本题是一道与轴对称图形有关的拼图问题,要拼轴对称图案,则需要理解轴对称图形的特征:要某直线折叠后,直线两旁的部分能完全重合.另外还需要掌握平移等有关知识.设计图案问题一般具有开放性,可以根据自己想象设计出美丽的图案.
解:下面给出3种不同答案,供参考.如图5.
图5
例3如图6,(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.
图6 图7
分析:(1)在直角坐标系内作△ABC关于y轴的对称图形,可先确定关键点A、B、C关于y轴的对称点A1、B1、C1的坐标,描出这些点的坐标,然后顺次连结即可.(2)要作△ABC向右平移6个单位的后的△A2B2C2,首先要作出A、B、C三点向右平移6个单位的对应点,然后顺次连接即可;(3)要观察△A1B1C1和△A2B2C2是否关于某直线对称,可连接A1A2,B1B2,C1C2,看它们的垂直平分线是否是同一条直线,如果是,则△A1B1C1和△A2B2C2就关于这条直线对称,否则,不关于某条直线对称.
解: (1)如图7所示,A1(0,4),B1(2,2),C1(1,1);
(2)如图7所示,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1与△A2B2C2关于直线轴对称.
专项练习:
1.在直角坐标系中,点P(-2,-4)关于y轴的对称点的坐标是( ).
(A)(-2,4) (B)(2,-4) (C)(2,4) (D)(-4,-2)
2.点M(1,2)关于x轴对称点的坐标为 ( ).
(A) (-1,2) (B)(-1,-2) (C)(1,-2) (D)(2,-1)
3.点P(3,-2)关于直线x=4对称点的坐标是( ).
(A) (5,-3) (B)(-2,5) (C) (5,-2) (D) (-3,4)
4.已知直线l和l同旁的两点A、B,在直线l上求一点P,使PA+PB最小,那么正确的是( ).
(A)作点A关于直线l的对称点A,连结AB与直线l的交点即为点P
(B)直线AB与直线l的交点为P点
(C)若直线AB//l,则直线l上的任意点即可为点P
(D)过线段AB的中点,向直线a引垂线,垂足即为点P.
5.点M(3a-b,4)与点N(9,2a+b)关于x轴对称,则a=_____,b=_____.
6.点A的坐标是(-2,3),点B与点A关于直线x=1对称,点C与点B关于直线y=-2对称,则点C的坐标为_______.
7.如图8,由5个小正方形组成的图形,请你三种不同的方法,分别添画一个小正方形,使它成为轴对称图形.
图8
8.如图9,作出△ABC关于直线l的对称三角形△A′B′C.′
图9 图10
9. 已知四边形ABCD各顶点为A(1,2), B( 1,4), C(3,5), D (3,3),作四边形ABCD关于直线x=-1的对称图形.
10. 如图10,是一个8×10的正方形格纸,△ABC中A点坐标为(-2 ,1 ).
⑴△ABC和△A′B′C′满足什么几何变换(直接写答案)?
⑵作△A′B′C′关于x轴对称图形△A″B″C″;
⑶求A″、B″、C″三点坐标(直接写答案)
答案:1.B 2.C 3.C 4.A 5.1,-6; 6.(4,-7);
7.如图.
7题 8题
8.如图.
9.如图.
9题 10题
10.(1)△ABC和△A′B′C′满足轴对称变换;(2)如图2所示.(3) A″(2,-1)、B″(1,-2)、
C″(3,-3).
专题三:等腰三角形
一、知识要点:
1. 等腰三角形
(1)有两边相等的三角形叫做等腰三角形.等腰三角形是轴对称图形.
(2)等腰三角形的性质:①等腰三角形的两个底角相等;②等腰三角形的顶角的平分线、底边的中线、底边上的高互相重合.
(3)等腰三角形的判别方法:①直接根据定义;②等角对等边.
2. 等边三角形
(1)三边都相等的三角形叫做等边三角形.是轴对称图形,有三条对称轴.
(2)等边三角形的性质:等边三角形的三个角都是60°.
(3)等边三角形的判别方法:①三个角都相等的三角形是等边三角形;②有一个角是60°的等腰三角形是等边三角形.
二、题目特点:和等腰三角形有关的题目主要有两类:(1)计算题.如求等腰三角形的腰长,周长、角度等;(2)说理题.如证明一个三角形是等腰(或等边)三角形;(3)实际应用题.如根据实际问题构造等腰三角形解决问题.
三、解题切入点:解决和等腰三角形有关的计算问题,要把握等腰三角形的性质,注意分类思想在等腰三角形中的应用.解决证明问题主要依据等腰(或等边)三角形的性质和判定方法,有的问题还需要作恰当的辅助线.
例1 如图1是某房屋顶框架的示意图,其中,AB=AC,AD⊥BC,∠BAC=120°,求∠B、∠C和∠BAD的度数.
分析:由AB=AC,可知△ABC是等腰三角形,等腰三角形的底边上的高,顶角的平分线重合,根据AD⊥BC,可得AD平分∠BAC,进一步可以求到各角的度数.
解:在△ABC中,
因为AB=AC,所以∠B=∠C,
因为∠BAC+∠B+∠C=180°,∠BAC=120°,
所以∠B=∠C=(180°-120°)=30°,
因为AD⊥BC,所以∠BAD=∠BAC=60°. 图1
例2 如图,2一艘轮船在近海处由南向北航行,点C是灯塔,轮船在A处测得在其北偏西38°的方向上,轮船又又A向北航行30海里到B,测得灯塔在其北偏西76°的方向上.
(1) 求∠ACB的度数;
(2) 轮船在B处时,到灯塔C的距离是多少
分析:本题是一道实际问题,解决问题的关键是根据实际问题画出几何图形,通过分析图形中角度之间的关系,借助等腰三角形的知识解决.
解:因为∠NAC=38°,∠NBC=76°,
所以∠NBC=∠ACB+∠NAC,
所以∠ACB=∠NBC-∠NAC=76°-38°=38°.
(2)因为∠ACB=∠NAC=38°, 所以AB=AC, 图2
因为AB=30海里,所以BC=30海里,
即点B到灯塔C的距离是30海里.
例3如图3,已知△ABC为等边三角形,D、E、F分别在边BC、CA、AB,且△DEF也是等边三角形.
除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
分析:本题是一道猜想型探索题.要探索图形中存在哪些相等的线段,可根据等边三角形的性质,通过寻找三角形全等进行探索.
解:(1)图中还有相等的线段是:AE=BF=CD,AF=BD=CE ,
事实上,因为△ABC与△DEF都是等边三角形,
所以∠A=∠B=∠C=60°,∠EDF=∠DEF=∠EFD=60°,DE=EF=FD ,
又因为∠CED+∠AEF=120°,∠CDE+∠CED=120°, 所以∠AEF=∠CDE,
同理,得∠CDE=∠BFD,
所以△AEF≌△BFD≌△CDE(AAS),
所以AE=BF=CD,AF=BD=CE .
专项练习3: 图3
1. △ABC中,AB=AC,它的两边分别是2厘米和4厘米,则它的周长是( )
(A)8厘米 (B)10厘米 (C)8厘米或10厘米 (D)不确定
2.如图4,在△ABC中,已知∠B和∠C的平分线相交于点F,过点F作DF//BC,交AB于点D,交AC于点E,若BD+CE=9,则线段DE的长为( )
(A)9 (B)8 (C)7 (D) 6
图4 图5 图6
3.如图5,△ABC为等边三角形,AD为BD边上的高,E为AC边上的一点,且AE=AD,则
∠EDC=___度.
4. 如图6,在△ABC中,D、E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是_____.
5.分别以等腰三角形的腰与底边向三角形外作正三角形,其周长为24和36,求等腰三角形的周长.
6.如图7,在△ABC中,已知AB=AC,BD、CE是两条角平分线,BD、CE相交于点O,△OBC是等腰三角形吗?为什么?
图7 图8
7.如图8,在Rt△ABC中,∠A=30°,∠C=90°,BC=10,点D是斜边AB的中点,DE⊥AC,交AC于E.求DE的长.
8.如图9,在△ABC中,BP、CP分别是∠ABC和∠ACB的平分线,且PD//AB,PE//AC,求△PED的周长.
9.如图10,已知△ABC中,AB=AC,AF是BC边的中线,D是BA延长线上一点,E在AC上,且AD=AE.求证:DE⊥BC.
图 9 图10 图11
10.如图11,已知AB=AD,∠BAD=60°,∠BCD=120°,延长B到E,使CE=CD,连结DE.求证:BC+DC=AC.
答案:1.B 2.A 3. 15; 4.120°;
5. 由等边三角形的周长为24,36可得等腰三角形的底、腰长可能是8、12.
当腰为12,底边为8时,周长为12+12+8=32,
当腰长为8,底边为12时,周长为8+8+12=28.
所以等腰三角形的周长为32或28.
6. △OBC是等腰三角形.理由:在△ABC中,因为AB=AC,所以∠ABC=∠ACB,
又BD是∠ABC的平分线,所以∠OBC=∠ABC,
又CE是∠ABC的平分线,所以∠OCB=∠ACB,所以∠OCB=∠OBC,
所以OB=OC,即△OBC是等腰三角形.
7. 在Rt△ABC中,因为∠A=30°,BC=10,所以AB=20,因为D为AB中点,所以AD=10,
在Rt△ADE中,因为∠A=30°,AD=10,所以DE=5.
8. 因为BP是∠ABC的平分线,CP是∠ACB的平分线,所以∠ABP=∠CBP,∠ACP=∠BCP,
因为PD//AB,所以∠ABP=∠BPD,所以∠PBC=∠BPD,所以BD=PD,同理PE=EC.
所以△PDE的周长等于PD+PE+DE=BD+DE+EC=BC=5cm.
9.因为AB=AC,BF=CF,所以∠BAF=∠CAF,AF⊥BC,
因为AD=AE,所以∠ADE=∠BAC,
所以∠BAF=∠D,所以DE//AF,所以DE⊥BC.
10.连结BD,因为AB=AD,∠BAD=60°,所以△ABD为等边三角形,
因为CD=CE,∠DCE=60°,所以△CDE为等边三角形,
因为∠ADB=∠CDE=60°,所以∠ADB+∠BDC=∠CDE+∠BDC,即∠ADC=∠BDE,
又AD=BD,CD=ED,所以△ADC≌△BDE,所以AC=BE,
又BE=BC+CE=BC+CD,所以AC=BC+CD.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
