沪科版七下(2024版)第10章 小结与复习 教案
文档属性
| 名称 | 沪科版七下(2024版)第10章 小结与复习 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 596.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 09:31:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
分课时教学设计
《小结与复习》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《相交线、平行线与平移》是对本单元核心知识(相交线形成的角、平行线的判定与性质、平移变换)的系统整合与拓展应用。教材通过知识结构图梳理和帮助学生构建几何知识网络。同时,教材注重数学思想方法的渗透,如类比(判定与性质的互逆关系)、转化(平移中的全等变换)、数形结合(平移与坐标系),并设计综合应用题,强化学生运用知识解决问题的能力。此外,教材通过评价量表引导学生自我反思,关注推理过程的严谨性、几何语言的规范性及数学思维的条理性,体现“教—学—评”一致性。
学习者分析 学生已掌握相交线形成的角(邻补角、对顶角)、平行线的判定与性质、平移的基本概念与性质,但存在以下问题: 知识整合不足:部分学生难以将“三线八角”分类、平行线判定与性质、平移的性质关联起来,形成碎片化记忆。 推理能力薄弱:在综合应用中,学生易混淆判定与性质的条件与结论(如误用“同位角相等”推导平行线而非反之),且推理过程跳步、逻辑不严谨。 空间想象局限:在复杂图形中(如多条直线相交、组合图形平移),学生难以准确识别角关系或对应点,导致解题困难。 规范表述欠缺:几何语言表述不准确(如“角相等”未指明“同位角”)、符号使用不规范(如平移方向描述模糊)。
教学目标 1.复习对顶角与三线八角。 2.复习巩固平行线的判定和方法。 3.复习巩固垂线的相关基本事实和性质。 4.复习巩固平移的概念和性质。
教学重点 1.相交线、平行线、平移核心知识的系统整合。 2.综合运用平行线判定与性质、平移的性质解决实际问题。
教学难点 1.理解判定与性质的互逆关系,避免混淆条件与结论; 2.在复杂图形中准确识别角关系或对应点,规范推理过程。
学习活动设计
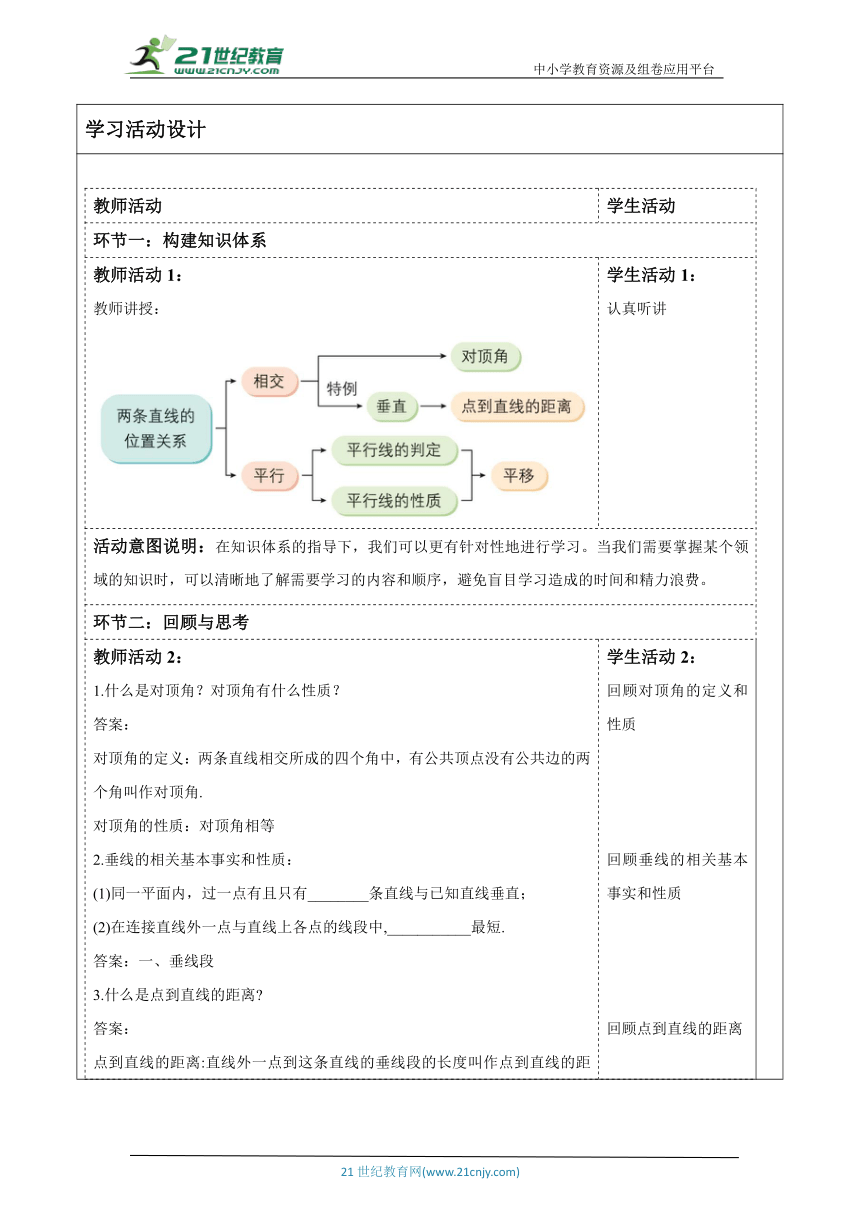
教师活动学生活动环节一:构建知识体系教师活动1: 教师讲授: 学生活动1: 认真听讲活动意图说明:在知识体系的指导下,我们可以更有针对性地进行学习。当我们需要掌握某个领域的知识时,可以清晰地了解需要学习的内容和顺序,避免盲目学习造成的时间和精力浪费。环节二:回顾与思考教师活动2: 1.什么是对顶角?对顶角有什么性质? 答案: 对顶角的定义:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角. 对顶角的性质:对顶角相等 2.垂线的相关基本事实和性质: (1)同一平面内,过一点有且只有________条直线与已知直线垂直; (2)在连接直线外一点与直线上各点的线段中,___________最短. 答案:一、垂线段 3.什么是点到直线的距离 答案: 点到直线的距离:直线外一点到这条直线的垂线段的长度叫作点到直线的距离. 4.平行线的判定方法: (1)两条直线被第三条直线所截,如果_____________,那么这两条直线平.简单地说,_______________________________________; (2)两条直线被第三条直线所截,如果_____________,那么这两条直线平.简单地说,_______________________________________; (3)两条直线被第三条直线所截,如果_____________,那么这两条直线平.简单地说,_______________________________________。 答案: (1)同位角相等、同位角相等,两直线平行 (2)内错角相等、内错角相等,两直线平行 (3)同旁内角互补、同旁内角互补,两直线平行 5.平行线的相关基本事实和性质: (1)经过直线外一点,有且只有_________条直线与这条直线平行; (2)如果两直线平行,那么同位角___________,内错角____________,同旁内角_____________; (3)如果两条直线和第三条直线平行,那么这两条直线____________. 答案:一、相等、相等、互补、平行 6.平移的概念和性质: (1)什么叫作平移 确定平移的要素是什么 (2)一个图形和它经过平移后所得的图形,连接各组对应点的线段________;平移只改变图形的位置,不改变图形的____________. 答案: 在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫作平移. 平移的要素:1. 平移的方向;2. 平移的距离. 互相平行(或在同一条直线上)且相等、形状和大小学生活动2: 回顾对顶角的定义和性质 回顾垂线的相关基本事实和性质 回顾点到直线的距离 回顾平行线的判定方法 认真听讲 回顾平行线的相关基本事实和性质 回顾平移的概念和性质活动意图说明:通过反复回顾和思考,学生可以对所学知识进行更深入的理解,发现其中的内在联系和规律,形成更加稳固的知识体系。环节三:自评与互评教师活动3: 教师讲授: 1.寻找日常生活中的相交线、平行线的例子或图片,并与同学进行交流。 2.比较本章内容与小学已学过的内容,你有哪些新的认识 与同学交流. 3.通过相交线、平行线的学习,你能体会几何图形研究的一般思路和方法吗 学生活动4: 认真思考,合作交流活动意图说明:通过自评,学生可以认识到自己的学习成果与目标的差距,从而激发内在的学习动力。同时互评过程中,学生可以分享自己的学习方法和经验,促进知识的共享和互补。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.在平面内,过一点画已知直线的垂线,可画垂线的条数是( ) A.1 B.2 C.无数 D.不存在 2.如图,下列条件能判断的是( ) A. B. C. D. 3.如图,点在直线上,AB∥CD,,则的度数是( ) A. B. C. D. 选做题: 4.如图,直线相交于点O,把分成两部分,若,且,则的度数是 . 5.下列叙述正确的有 . ()若,则;()的平方根是;()任何数都有立方根;()两个无理数的和有可能是有理数;()过一点有且只有一条直线与已知直线平行;()从直线外一点到这条直线的垂线段叫做这点到这条直线的距离. 6.如图,在长为,宽为的长方形地块上,有纵横交错的几条小路,宽均为,其他部分均种植花草.则种植花草的面积是 . 【综合拓展类作业】 7.如图,在四边形中,是延长线的一点,连接交于点,若. (1)求证:; (2)若,求的度数.
作业设计 【知识技能类作业】 必做题: 1.如图,由下列条件:①;②;③;④;不能判定的条件为( ) A.① B.② C.③ D.④ 2.如图,直线AB,AF被BC所截,与∠2是同位角的是( ) A.∠1 B.∠5 C.∠3 D.∠4 3.如图,将直角△ABC沿边AC的方向平移到△DEF的位置,连结BE,若CD=6,AF=14,则BE的长为( ) A.4 B.6 C.8 D.12 【综合拓展类作业】 4.如图,已知点在直线上,点在线段上,与交于点. (1)求证:; (2)若,求的度数.
教学反思 学生能够运用所学知识解决实际问题,但在推理过程中仍存在以下问题: 逻辑不严谨:部分学生混淆判定与性质的条件与结论,如误用“同位角相等”推导平行线而非反之,需通过对比练习(如“判定与性质互逆推理”)强化理解。 表述不规范:几何语言表述不准确(如“角相等”未指明“同位角”)、符号使用不规范(如平移方向描述模糊),需通过“结构化板书”训练(如规范书写“∵a∥b ∴∠1=∠2”)提升规范性。 空间想象不足:在复杂图形中(如多条直线相交、组合图形平移),学生难以准确识别角关系或对应点,需通过“分步标记法”(如用不同颜色标记对应点)和变式训练强化能力。 针对以上问题,后续教学可增加以下措施: 对比训练:设计“判定与性质互逆推理”专题练习,明确条件与结论的对应关系; 规范训练:通过“结构化板书”和“小组互评”强化几何语言和推理过程的规范性; 变式拓展:增加复杂图形(如多条直线相交、组合图形平移)的练习,提升空间想象能力。
21世纪教育网(www.21cnjy.com)
分课时教学设计
《小结与复习》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《相交线、平行线与平移》是对本单元核心知识(相交线形成的角、平行线的判定与性质、平移变换)的系统整合与拓展应用。教材通过知识结构图梳理和帮助学生构建几何知识网络。同时,教材注重数学思想方法的渗透,如类比(判定与性质的互逆关系)、转化(平移中的全等变换)、数形结合(平移与坐标系),并设计综合应用题,强化学生运用知识解决问题的能力。此外,教材通过评价量表引导学生自我反思,关注推理过程的严谨性、几何语言的规范性及数学思维的条理性,体现“教—学—评”一致性。
学习者分析 学生已掌握相交线形成的角(邻补角、对顶角)、平行线的判定与性质、平移的基本概念与性质,但存在以下问题: 知识整合不足:部分学生难以将“三线八角”分类、平行线判定与性质、平移的性质关联起来,形成碎片化记忆。 推理能力薄弱:在综合应用中,学生易混淆判定与性质的条件与结论(如误用“同位角相等”推导平行线而非反之),且推理过程跳步、逻辑不严谨。 空间想象局限:在复杂图形中(如多条直线相交、组合图形平移),学生难以准确识别角关系或对应点,导致解题困难。 规范表述欠缺:几何语言表述不准确(如“角相等”未指明“同位角”)、符号使用不规范(如平移方向描述模糊)。
教学目标 1.复习对顶角与三线八角。 2.复习巩固平行线的判定和方法。 3.复习巩固垂线的相关基本事实和性质。 4.复习巩固平移的概念和性质。
教学重点 1.相交线、平行线、平移核心知识的系统整合。 2.综合运用平行线判定与性质、平移的性质解决实际问题。
教学难点 1.理解判定与性质的互逆关系,避免混淆条件与结论; 2.在复杂图形中准确识别角关系或对应点,规范推理过程。
学习活动设计
教师活动学生活动环节一:构建知识体系教师活动1: 教师讲授: 学生活动1: 认真听讲活动意图说明:在知识体系的指导下,我们可以更有针对性地进行学习。当我们需要掌握某个领域的知识时,可以清晰地了解需要学习的内容和顺序,避免盲目学习造成的时间和精力浪费。环节二:回顾与思考教师活动2: 1.什么是对顶角?对顶角有什么性质? 答案: 对顶角的定义:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角. 对顶角的性质:对顶角相等 2.垂线的相关基本事实和性质: (1)同一平面内,过一点有且只有________条直线与已知直线垂直; (2)在连接直线外一点与直线上各点的线段中,___________最短. 答案:一、垂线段 3.什么是点到直线的距离 答案: 点到直线的距离:直线外一点到这条直线的垂线段的长度叫作点到直线的距离. 4.平行线的判定方法: (1)两条直线被第三条直线所截,如果_____________,那么这两条直线平.简单地说,_______________________________________; (2)两条直线被第三条直线所截,如果_____________,那么这两条直线平.简单地说,_______________________________________; (3)两条直线被第三条直线所截,如果_____________,那么这两条直线平.简单地说,_______________________________________。 答案: (1)同位角相等、同位角相等,两直线平行 (2)内错角相等、内错角相等,两直线平行 (3)同旁内角互补、同旁内角互补,两直线平行 5.平行线的相关基本事实和性质: (1)经过直线外一点,有且只有_________条直线与这条直线平行; (2)如果两直线平行,那么同位角___________,内错角____________,同旁内角_____________; (3)如果两条直线和第三条直线平行,那么这两条直线____________. 答案:一、相等、相等、互补、平行 6.平移的概念和性质: (1)什么叫作平移 确定平移的要素是什么 (2)一个图形和它经过平移后所得的图形,连接各组对应点的线段________;平移只改变图形的位置,不改变图形的____________. 答案: 在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫作平移. 平移的要素:1. 平移的方向;2. 平移的距离. 互相平行(或在同一条直线上)且相等、形状和大小学生活动2: 回顾对顶角的定义和性质 回顾垂线的相关基本事实和性质 回顾点到直线的距离 回顾平行线的判定方法 认真听讲 回顾平行线的相关基本事实和性质 回顾平移的概念和性质活动意图说明:通过反复回顾和思考,学生可以对所学知识进行更深入的理解,发现其中的内在联系和规律,形成更加稳固的知识体系。环节三:自评与互评教师活动3: 教师讲授: 1.寻找日常生活中的相交线、平行线的例子或图片,并与同学进行交流。 2.比较本章内容与小学已学过的内容,你有哪些新的认识 与同学交流. 3.通过相交线、平行线的学习,你能体会几何图形研究的一般思路和方法吗 学生活动4: 认真思考,合作交流活动意图说明:通过自评,学生可以认识到自己的学习成果与目标的差距,从而激发内在的学习动力。同时互评过程中,学生可以分享自己的学习方法和经验,促进知识的共享和互补。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.在平面内,过一点画已知直线的垂线,可画垂线的条数是( ) A.1 B.2 C.无数 D.不存在 2.如图,下列条件能判断的是( ) A. B. C. D. 3.如图,点在直线上,AB∥CD,,则的度数是( ) A. B. C. D. 选做题: 4.如图,直线相交于点O,把分成两部分,若,且,则的度数是 . 5.下列叙述正确的有 . ()若,则;()的平方根是;()任何数都有立方根;()两个无理数的和有可能是有理数;()过一点有且只有一条直线与已知直线平行;()从直线外一点到这条直线的垂线段叫做这点到这条直线的距离. 6.如图,在长为,宽为的长方形地块上,有纵横交错的几条小路,宽均为,其他部分均种植花草.则种植花草的面积是 . 【综合拓展类作业】 7.如图,在四边形中,是延长线的一点,连接交于点,若. (1)求证:; (2)若,求的度数.
作业设计 【知识技能类作业】 必做题: 1.如图,由下列条件:①;②;③;④;不能判定的条件为( ) A.① B.② C.③ D.④ 2.如图,直线AB,AF被BC所截,与∠2是同位角的是( ) A.∠1 B.∠5 C.∠3 D.∠4 3.如图,将直角△ABC沿边AC的方向平移到△DEF的位置,连结BE,若CD=6,AF=14,则BE的长为( ) A.4 B.6 C.8 D.12 【综合拓展类作业】 4.如图,已知点在直线上,点在线段上,与交于点. (1)求证:; (2)若,求的度数.
教学反思 学生能够运用所学知识解决实际问题,但在推理过程中仍存在以下问题: 逻辑不严谨:部分学生混淆判定与性质的条件与结论,如误用“同位角相等”推导平行线而非反之,需通过对比练习(如“判定与性质互逆推理”)强化理解。 表述不规范:几何语言表述不准确(如“角相等”未指明“同位角”)、符号使用不规范(如平移方向描述模糊),需通过“结构化板书”训练(如规范书写“∵a∥b ∴∠1=∠2”)提升规范性。 空间想象不足:在复杂图形中(如多条直线相交、组合图形平移),学生难以准确识别角关系或对应点,需通过“分步标记法”(如用不同颜色标记对应点)和变式训练强化能力。 针对以上问题,后续教学可增加以下措施: 对比训练:设计“判定与性质互逆推理”专题练习,明确条件与结论的对应关系; 规范训练:通过“结构化板书”和“小组互评”强化几何语言和推理过程的规范性; 变式拓展:增加复杂图形(如多条直线相交、组合图形平移)的练习,提升空间想象能力。
21世纪教育网(www.21cnjy.com)
