苏教版高一下册数学必修第二册11.3 余弦定理、正弦定理的应用 同步练习(含详解)
文档属性
| 名称 | 苏教版高一下册数学必修第二册11.3 余弦定理、正弦定理的应用 同步练习(含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 499.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 06:58:49 | ||
图片预览




文档简介
苏教版高一下册数学必修第二册-11.3 余弦定理、正弦定理的应用 同步练习
[A 基础达标]
1.某观察站C与两灯塔A,B的距离分别为300米和500米,测得灯塔A在观察站C的北偏东30°方向上,灯塔B在观察站C的正西方向上,则两灯塔A,B间的距离为( )
A.500米 B.600米
C.700米 D.800米
2.若某人在点A测得金字塔顶端仰角为30°,此人往金字塔方向走了80 m到达点B,测得金字塔顶端的仰角为45°,则金字塔的高度最接近于(忽略人的身高)( )
A.110 m B.112 m
C.220 m D.224 m
3.有一坡面长为10 m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,要通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长( )
A.5 m B.10 m
C.10 m D.10 m
4.一船向正北方向航行,看见正西方向有相距10 n mile的两个灯塔恰好与它在一条直线上,船继续航行半小时后,看见一灯塔在船的南偏西60°方向,另一灯塔在船的南偏西75°方向,则这艘船的速度是( )
A.5 n mile/h B.5 n mile/h
C.10 n mile/h D.10 n mile/h
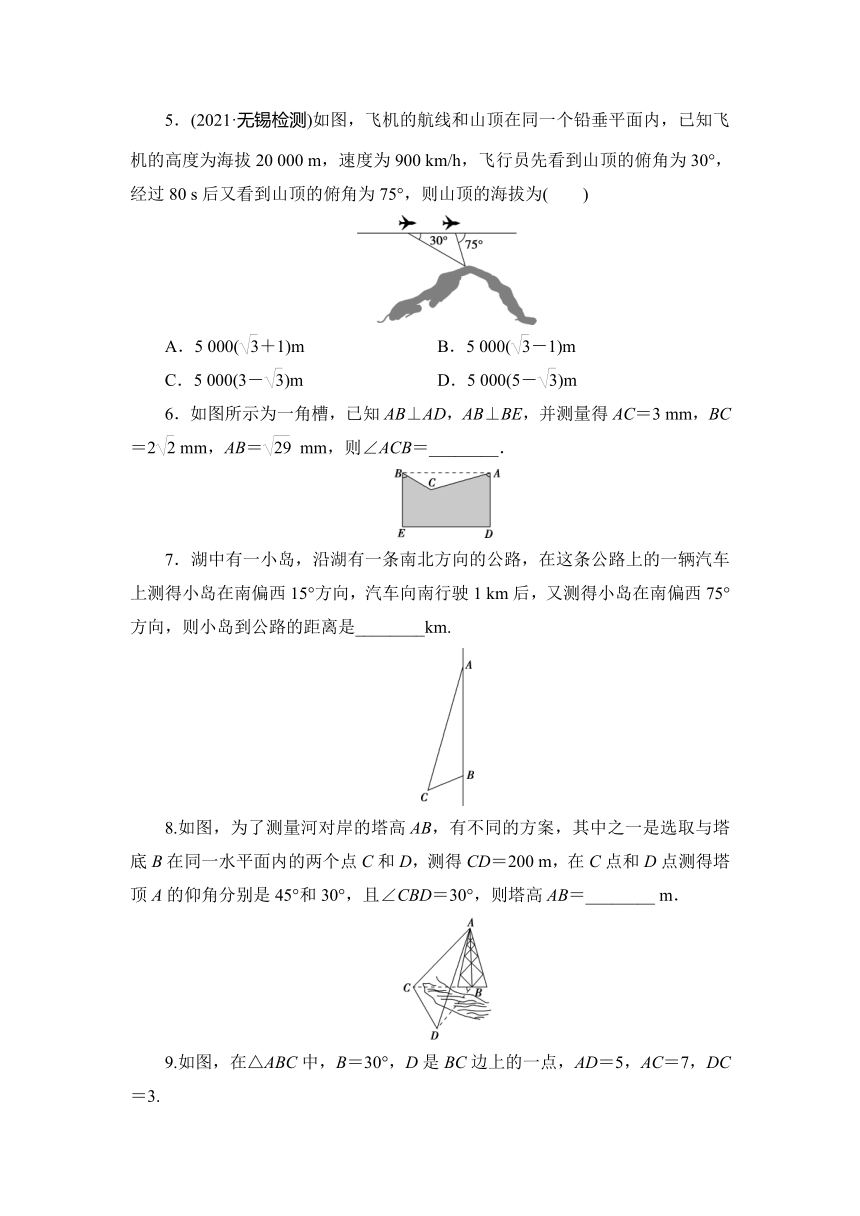
5.(2021·无锡检测)如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20 000 m,速度为900 km/h,飞行员先看到山顶的俯角为30°,经过80 s后又看到山顶的俯角为75°,则山顶的海拔为( )
A.5 000(+1)m B.5 000(-1)m
C.5 000(3-)m D.5 000(5-)m
6.如图所示为一角槽,已知AB⊥AD,AB⊥BE,并测量得AC=3 mm,BC=2 mm,AB= mm,则∠ACB=________.
7.湖中有一小岛,沿湖有一条南北方向的公路,在这条公路上的一辆汽车上测得小岛在南偏西15°方向,汽车向南行驶1 km后,又测得小岛在南偏西75°方向,则小岛到公路的距离是________km.
8.如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个点C和D,测得CD=200 m,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,则塔高AB=________ m.
9.如图,在△ABC中,B=30°,D是BC边上的一点,AD=5,AC=7,DC=3.
(1)求△ADC的面积;
(2)求边AB的长.
10.空中有一气球D,在它正西方向的地面上有一点A,在此处测得气球的仰角为45°,同时在气球的南偏东60°方向的地面上有一点B,在此处测得气球的仰角为30°,两观察点A,B相距266 m,计算气球的高度.
[B 能力提升]
11.如图,A,B两船相距10 n mile,B船在A船南偏西45°方向上,B船向正南方向行驶,A船以B船速度的倍追赶B船,A船若用最短的时间追上B船,A船行驶的角度为( )
A.南偏西30°
B.南偏西15°
C.南偏东30°
D.南偏东15°
12.海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径A,B两点间的距离,现在珊瑚群岛上取两点C,D,测得CD=80,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,则A,B两点间的距离为( )
A.80 B.80
C.160 D.80
13.已知△ABC的三个内角满足2B=A+C,且AB=1,BC=4,则边BC上的中线AD的长为________.
14.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”这道题讲的是有一个三角形沙田,三边分别为13里,14里,15里,假设1里按500米计算,则该沙田的面积为________平方千米.
[C 拓展探究]
15.如图,在海岛A上有一座海拔1 km的山,山顶设有一个观察站P(观察站高度忽略不计),上午11时,测得一轮船在岛北偏东30°方向,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°方向,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
参考答案
[A 基础达标]
1.解析:选C.由题意,在△ABC中,AC=300米,BC=500米,∠ACB=120°.利用余弦定理可得AB2=3002+5002-2×300×500×cos 120°,所以AB=700米.故选C.
2.解析:选A.如图,设CD为金字塔,AB=80 m.设CD=h,则由已知得(80+h)×=h,h=40(+1)≈109.从选项来看110最接近,故选A.
3.解析:选C.如图,∠BDA=75°,∠ACB=30°,∠DBC=45°,BD=10 m.由正弦定理,得=,所以CD===10(m).
4.解析:选D.如图,依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,从而CD=CA=10 n mile,在直角三角形ABC中,由正弦定理可得AB=5 n mile,所以这艘船的速度是10 n mile/h.故选D.
5.解析:选C.如图,过点C作CD⊥AB于点D.
由题意知∠A=30°,∠CBD=75°,则∠ACB=45°,AB=900×80×=20(km).
所以在△ABC中,由正弦定理,得BC=10 km.
因为CD⊥AD,所以CD=BC sin ∠CBD=BC×sin 75°=10sin 75°=5+5(km).
山顶的海拔为[20-(5+5)]km=5 000(3-)m.故选C.
6.
解析:在△ABC中,由余弦定理得
cos ∠ACB==-.
因为∠ACB∈(0,π),所以∠ACB=.
答案:
7.解析:如图,∠CAB=15°,∠CBA=180°-75°=105°,∠ACB=180°-105°-15°=60°,AB=1 km.由正弦定理得=,BC==(km).设C到直线AB的距离为d,则d=BC sin 75°=×=(km).
答案:
8.
解析:在Rt△ABC中,∠ACB=45°.
设AB=h,则BC=h,
在Rt△ABD中,∠ADB=30°,
所以BD=h.
在△BCD中,∠CBD=30°,CD=200 m,
由余弦定理可得
40 000=h2+3h2-2h·h·,
解得h=200(负值舍去),
所以塔高AB=200 m.
答案:200
9.解:(1)在△ADC中,由余弦定理得
cos ∠ADC===-.
因为∠ADC为三角形的内角,所以∠ADC=120°,所以sin ∠ADC=.
所以S△ADC=AD·DC·sin ∠ADC=×5×3×=.
(2)在△ABD中,∠ADB=60°,由正弦定理得=,
所以AB=×=5.
10.解:如图,设CD=x m,
在Rt△ACD中,∠DAC=45°,
所以AC=CD=x m.
在Rt△BCD中,∠CBD=30°,
所以CB==x(m).
在△ABC中,∠ACB=90°+60°=150°,
由余弦定理得AB2=AC2+BC2-2·AC·BC·cos ∠ACB,
所以2662=x2+(x)2-2·x·x·.
解得x=38(负值舍去).所以气球的高度为38 m.
[B 能力提升]
11.解析:选B.设B船的速度为v,A船的速度为v,经过t时,A船在C点追上B船,则BC=tv,AC=tv,∠ABC=135°,如图所示:
在△ABC中,由正弦定理得,=,所以sin ∠BAC==tv·×=.因为0°12.解析:选D.在△ADC中, ∠ADC=∠ADB+∠CDB=135°+15°=150°,
所以∠DAC=180°-∠ACD-∠ADC=15°,所以AD=DC=80,
在△BDC中,∠DCB=∠ACB+∠ACD=120°+15°=135°,
所以∠DBC=180°-∠BCD-∠BDC=30°.
所以=,所以BD==80.
在△BDA中, AB2=AD2+BD2-2AD·BD·cos 135°
=802+(80)2-2×80×80×(-)=802×5,所以AB=80,故选D.
13.解析:由2B=A+C,及A+B+C=π知,B=.
在△ABD中,AB=1,BD==2,
所以AD2=AB2+BD2-2AB·BD cos =3.
因此AD=.
答案:
14.解析:设△ABC 的对应边边长分别为a=13里,b=14里,c=15里,cos C= =,
所以sin C=,所以S=×13×14××250 000=21×106平方米=21平方千米.
答案:21
[C 拓展探究]
15.解:(1)在Rt△PAB中,∠APB=60°,AP=1 km,
所以AB=AP tan 60°=(km).
在Rt△PAC中,∠APC=30°,
所以AC=AP tan 30°=(km).
在△ACB中,∠CAB=30°+60°=90°,
所以BC== =(km).
则船的航行速度为÷=2(km/h).
(2)在△ACD中,∠DAC=90°-60°=30°,
sin ∠DCA=sin (180°-∠ACB)=sin ∠ACB===,
sin ∠CDA=sin (∠ACB-30°)
=sin ∠ACB·cos 30°-cos ∠ACB·sin 30°
=×- =.
由正弦定理得=,
所以AD=
==(km).
故此时船距岛A有 km.
[A 基础达标]
1.某观察站C与两灯塔A,B的距离分别为300米和500米,测得灯塔A在观察站C的北偏东30°方向上,灯塔B在观察站C的正西方向上,则两灯塔A,B间的距离为( )
A.500米 B.600米
C.700米 D.800米
2.若某人在点A测得金字塔顶端仰角为30°,此人往金字塔方向走了80 m到达点B,测得金字塔顶端的仰角为45°,则金字塔的高度最接近于(忽略人的身高)( )
A.110 m B.112 m
C.220 m D.224 m
3.有一坡面长为10 m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,要通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长( )
A.5 m B.10 m
C.10 m D.10 m
4.一船向正北方向航行,看见正西方向有相距10 n mile的两个灯塔恰好与它在一条直线上,船继续航行半小时后,看见一灯塔在船的南偏西60°方向,另一灯塔在船的南偏西75°方向,则这艘船的速度是( )
A.5 n mile/h B.5 n mile/h
C.10 n mile/h D.10 n mile/h
5.(2021·无锡检测)如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20 000 m,速度为900 km/h,飞行员先看到山顶的俯角为30°,经过80 s后又看到山顶的俯角为75°,则山顶的海拔为( )
A.5 000(+1)m B.5 000(-1)m
C.5 000(3-)m D.5 000(5-)m
6.如图所示为一角槽,已知AB⊥AD,AB⊥BE,并测量得AC=3 mm,BC=2 mm,AB= mm,则∠ACB=________.
7.湖中有一小岛,沿湖有一条南北方向的公路,在这条公路上的一辆汽车上测得小岛在南偏西15°方向,汽车向南行驶1 km后,又测得小岛在南偏西75°方向,则小岛到公路的距离是________km.
8.如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个点C和D,测得CD=200 m,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,则塔高AB=________ m.
9.如图,在△ABC中,B=30°,D是BC边上的一点,AD=5,AC=7,DC=3.
(1)求△ADC的面积;
(2)求边AB的长.
10.空中有一气球D,在它正西方向的地面上有一点A,在此处测得气球的仰角为45°,同时在气球的南偏东60°方向的地面上有一点B,在此处测得气球的仰角为30°,两观察点A,B相距266 m,计算气球的高度.
[B 能力提升]
11.如图,A,B两船相距10 n mile,B船在A船南偏西45°方向上,B船向正南方向行驶,A船以B船速度的倍追赶B船,A船若用最短的时间追上B船,A船行驶的角度为( )
A.南偏西30°
B.南偏西15°
C.南偏东30°
D.南偏东15°
12.海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径A,B两点间的距离,现在珊瑚群岛上取两点C,D,测得CD=80,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,则A,B两点间的距离为( )
A.80 B.80
C.160 D.80
13.已知△ABC的三个内角满足2B=A+C,且AB=1,BC=4,则边BC上的中线AD的长为________.
14.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”这道题讲的是有一个三角形沙田,三边分别为13里,14里,15里,假设1里按500米计算,则该沙田的面积为________平方千米.
[C 拓展探究]
15.如图,在海岛A上有一座海拔1 km的山,山顶设有一个观察站P(观察站高度忽略不计),上午11时,测得一轮船在岛北偏东30°方向,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°方向,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
参考答案
[A 基础达标]
1.解析:选C.由题意,在△ABC中,AC=300米,BC=500米,∠ACB=120°.利用余弦定理可得AB2=3002+5002-2×300×500×cos 120°,所以AB=700米.故选C.
2.解析:选A.如图,设CD为金字塔,AB=80 m.设CD=h,则由已知得(80+h)×=h,h=40(+1)≈109.从选项来看110最接近,故选A.
3.解析:选C.如图,∠BDA=75°,∠ACB=30°,∠DBC=45°,BD=10 m.由正弦定理,得=,所以CD===10(m).
4.解析:选D.如图,依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,从而CD=CA=10 n mile,在直角三角形ABC中,由正弦定理可得AB=5 n mile,所以这艘船的速度是10 n mile/h.故选D.
5.解析:选C.如图,过点C作CD⊥AB于点D.
由题意知∠A=30°,∠CBD=75°,则∠ACB=45°,AB=900×80×=20(km).
所以在△ABC中,由正弦定理,得BC=10 km.
因为CD⊥AD,所以CD=BC sin ∠CBD=BC×sin 75°=10sin 75°=5+5(km).
山顶的海拔为[20-(5+5)]km=5 000(3-)m.故选C.
6.
解析:在△ABC中,由余弦定理得
cos ∠ACB==-.
因为∠ACB∈(0,π),所以∠ACB=.
答案:
7.解析:如图,∠CAB=15°,∠CBA=180°-75°=105°,∠ACB=180°-105°-15°=60°,AB=1 km.由正弦定理得=,BC==(km).设C到直线AB的距离为d,则d=BC sin 75°=×=(km).
答案:
8.
解析:在Rt△ABC中,∠ACB=45°.
设AB=h,则BC=h,
在Rt△ABD中,∠ADB=30°,
所以BD=h.
在△BCD中,∠CBD=30°,CD=200 m,
由余弦定理可得
40 000=h2+3h2-2h·h·,
解得h=200(负值舍去),
所以塔高AB=200 m.
答案:200
9.解:(1)在△ADC中,由余弦定理得
cos ∠ADC===-.
因为∠ADC为三角形的内角,所以∠ADC=120°,所以sin ∠ADC=.
所以S△ADC=AD·DC·sin ∠ADC=×5×3×=.
(2)在△ABD中,∠ADB=60°,由正弦定理得=,
所以AB=×=5.
10.解:如图,设CD=x m,
在Rt△ACD中,∠DAC=45°,
所以AC=CD=x m.
在Rt△BCD中,∠CBD=30°,
所以CB==x(m).
在△ABC中,∠ACB=90°+60°=150°,
由余弦定理得AB2=AC2+BC2-2·AC·BC·cos ∠ACB,
所以2662=x2+(x)2-2·x·x·.
解得x=38(负值舍去).所以气球的高度为38 m.
[B 能力提升]
11.解析:选B.设B船的速度为v,A船的速度为v,经过t时,A船在C点追上B船,则BC=tv,AC=tv,∠ABC=135°,如图所示:
在△ABC中,由正弦定理得,=,所以sin ∠BAC==tv·×=.因为0°
所以∠DAC=180°-∠ACD-∠ADC=15°,所以AD=DC=80,
在△BDC中,∠DCB=∠ACB+∠ACD=120°+15°=135°,
所以∠DBC=180°-∠BCD-∠BDC=30°.
所以=,所以BD==80.
在△BDA中, AB2=AD2+BD2-2AD·BD·cos 135°
=802+(80)2-2×80×80×(-)=802×5,所以AB=80,故选D.
13.解析:由2B=A+C,及A+B+C=π知,B=.
在△ABD中,AB=1,BD==2,
所以AD2=AB2+BD2-2AB·BD cos =3.
因此AD=.
答案:
14.解析:设△ABC 的对应边边长分别为a=13里,b=14里,c=15里,cos C= =,
所以sin C=,所以S=×13×14××250 000=21×106平方米=21平方千米.
答案:21
[C 拓展探究]
15.解:(1)在Rt△PAB中,∠APB=60°,AP=1 km,
所以AB=AP tan 60°=(km).
在Rt△PAC中,∠APC=30°,
所以AC=AP tan 30°=(km).
在△ACB中,∠CAB=30°+60°=90°,
所以BC== =(km).
则船的航行速度为÷=2(km/h).
(2)在△ACD中,∠DAC=90°-60°=30°,
sin ∠DCA=sin (180°-∠ACB)=sin ∠ACB===,
sin ∠CDA=sin (∠ACB-30°)
=sin ∠ACB·cos 30°-cos ∠ACB·sin 30°
=×- =.
由正弦定理得=,
所以AD=
==(km).
故此时船距岛A有 km.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
