【小升初培优讲义】关于圆柱的应用题讲义(含解析)-2024-2025学年六年级下册数学人教版
文档属性
| 名称 | 【小升初培优讲义】关于圆柱的应用题讲义(含解析)-2024-2025学年六年级下册数学人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 21:24:03 | ||
图片预览





文档简介
小升初培优讲义 关于圆柱的应用题
(
第一部分
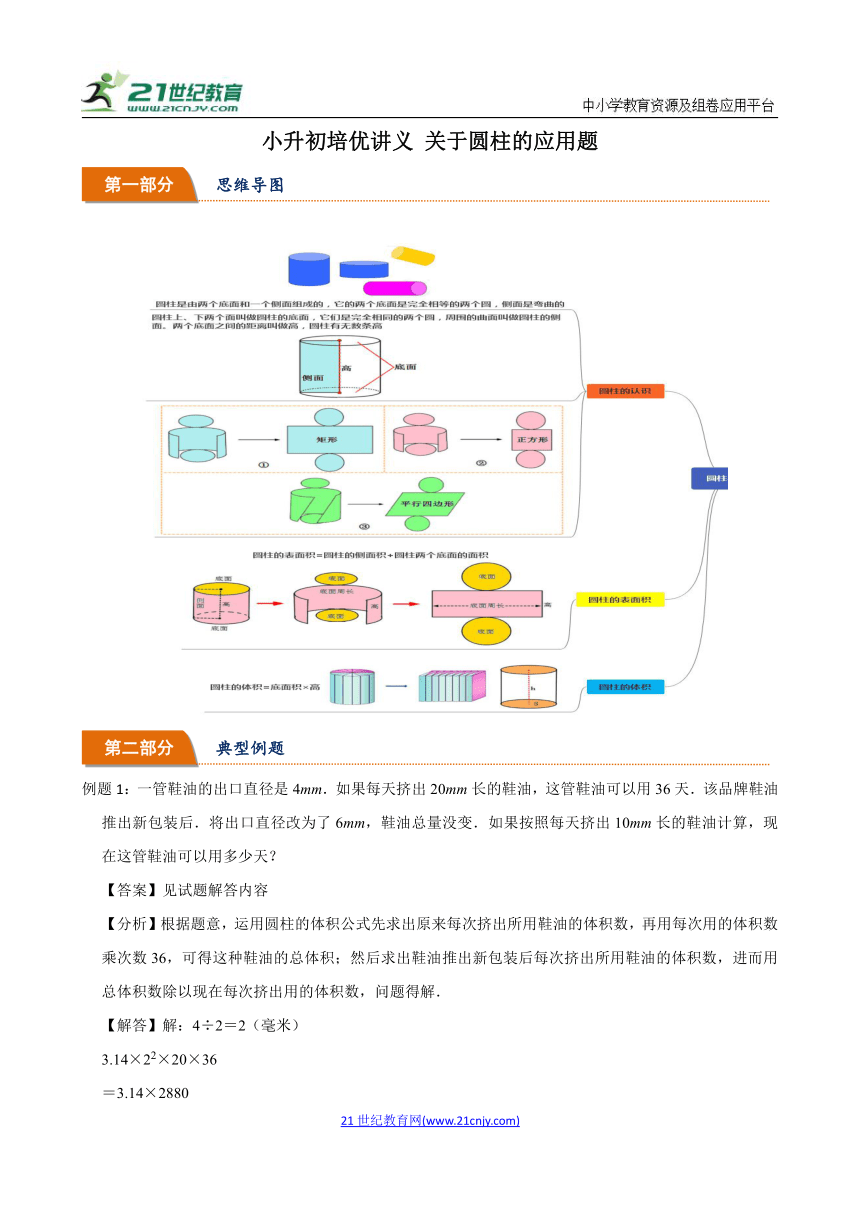
思维导图
)
(
第二部分
典型例题
)
例题1:一管鞋油的出口直径是4mm.如果每天挤出20mm长的鞋油,这管鞋油可以用36天.该品牌鞋油推出新包装后.将出口直径改为了6mm,鞋油总量没变.如果按照每天挤出10mm长的鞋油计算,现在这管鞋油可以用多少天?
【答案】见试题解答内容
【分析】根据题意,运用圆柱的体积公式先求出原来每次挤出所用鞋油的体积数,再用每次用的体积数乘次数36,可得这种鞋油的总体积;然后求出鞋油推出新包装后每次挤出所用鞋油的体积数,进而用总体积数除以现在每次挤出用的体积数,问题得解.
【解答】解:4÷2=2(毫米)
3.14×22×20×36
=3.14×2880
=9043.2(立方毫米)
6÷2=3(毫米)
3.14×32×10=282.6(立方毫米)
9043.2÷282.6=32(天)
答:现在这管鞋油可以用32天.
【点评】解决此题关键是理解鞋油的总体积数不变,运用圆柱的体积公式:V=Sh解决问题.
例题2:某品牌牙膏出口处直径为0.6cm,明明每次刷牙都挤出1cm长的牙膏,这样的一支牙膏他可用48次.该品牌牙膏推出的新包装只是将出口处直径改为0.8cm,牙膏的总容量不变,明明还是按习惯每次挤出1cm长的牙膏,这样一支新包装的牙膏他能用多少次?
【答案】见试题解答内容
【分析】根据题意,利用圆柱的体积公式:V=Sh,先求牙膏的体积,然后根据体积不变,求新包装牙膏可以用多少次.
【解答】解:3.14×(0.6÷2)2×1×48÷[3.14×(0.8÷2)2×1]
=3.14×0.09×1×48÷[3.14×0.16×1]
=27(次)
答:这样一支新包装的牙膏他能用27次.
【点评】本题主要考查圆柱的应用,关键利用圆柱体积公式做题.
例题3:工人师傅正在修建一个圆形的蓄水池,王大爷每步长约60厘米,沿着池边走了一圈刚好是53步,这个蓄水池的直径大约是多少米?(得数保留整数)
【答案】见试题解答内容
【分析】根据题意,可用320乘0.5计算出这个圆的周长,然后再利用圆的周长公式进行解答即可.
【解答】解:60厘米=0.6米
53×0.6÷3.14
=31.8÷3.14
≈10(米)
答:这个蓄水池的直径大约是10米.
【点评】此题考查了圆的周长C=πd的计算应用.
例题4:一块圆柱形铝锭,底面积60cm2,高10cm,要把这块铝锭熔铸成高18cm的圆锥,熔铸后的铝锭底面积是多少?
【答案】见试题解答内容
【分析】根据熔铸后体积不变,进行解答:先根据“圆柱的体积=的面积×高”求出铝锭的体积,即圆锥的体积,继而根据“圆锥的底面积=圆锥的体积×3÷高”解答即可.
【解答】解:60×10×3÷18
=1800÷18
=100(平方厘米)
答:熔铸后的铝锭底面积是100平方厘米.
【点评】解答此题的关键是要明确体积不变,即圆柱形铝块的体积为后来熔铸成的圆锥的体积,然后根据圆锥体积和底面积及高的关系进行解答即可.
例题5:一个圆柱形水池,底面周长是31.4米,水面离池口50米,再注入多少立方米的水可注满水池?
【答案】3925立方米。
【分析】圆的周长公式:C=2πr,把数据代入公式求出圆的半径,然后再根据圆柱的容积(体积)公式:V=πr2h,把数据代入公式解答。
【解答】解:31.4÷3.14÷2=5(米)
3.14×52×50
=3.14×1250
=3925(立方米)
答:再注入3925立方米的水可将池灌满。
【点评】此题主要考查圆柱的容积(体积)公式在实际生活中的应用,关键是熟记公式。
(
第三部分
知识精讲
)
(
知识清单+方法技巧
) 1.圆柱的特征 【知识点归纳】 圆柱就是由两个大小相同的圆和一个侧面组成的.它的底面是完全相同的两个圆,侧面是一个曲面. 2.圆柱的展开图 【知识点归纳】 圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,宽等于圆柱的高. 3.圆柱的侧面积和表面积 【知识点归纳】 圆柱的表面积=侧面积+2个底面积 侧面积=底面周长×高。圆柱的侧面展开是一个长方形,其长就是圆柱底面周长,长方形的宽就是圆柱的高,所以圆柱的侧面积=底面周长×高,圆柱的表面共有一个侧面和上下两个底面,所以表面积=侧面积+2个底面积 4.长方体和正方体的体积 【知识点归纳】 长方体体积公式:V=abh.(a表示底面的长,b表示底面的宽,h表示高) 正方体体积公式:V=a3.(a表示棱长) 5.圆柱的侧面积、表面积和体积 【知识点归纳】 圆柱的侧面积=底面的周长×高,用字母表示: S侧=Ch(C表示底面的周长,h表示圆柱的高),或S侧=2πrh 圆柱的底面积=πr2 圆柱的表面积=侧面积+两个底面积,用字母表示: S表=2πr2+2πrh 圆柱的体积=底面积×高,用字母表示: V=πr2h.
(
第四部分
高频真题
)
1.修建一个圆柱形的蓄水池,底面直径是20米,深2.5米,在池子的内壁和下底面抹上水泥,抹水泥的面积是多少平方米?
2.一种电热水炉的水龙头内直径是1厘米,打开水龙头后水的流速是40厘米/秒。一个容积为1.5升的保温壶,1分钟能装满水吗?
3.一个圆柱形蓄水池深4米,平均每天用水8吨,7天后水池的水减少了20%(每立方米的水重1吨),这个水池的占地面积是多少?
4.如图,是用塑料薄膜覆盖的蔬菜大棚,长16米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
5.王老师要做一个无盖的长方体玻璃鱼缸,要求每个顶点连接的三条棱长分别是5分米、4分米、3分米,请你帮王老师设计一下怎样才节省材料(画图表示并计算一下至少要用玻璃多少平方分米?)
6.有一个花坛,高0.5米,底面是边长2.3米的正方形.四周用砖砌成,厚度是0.3米,中间填满泥土,花坛里大约有多少立方米泥土?
7.一个圆柱形油漆桶,从里面量底面周长是18.84分米,高是6分米,如果每升油漆重1.5千克,这个油漆桶可装油漆多少千克?
8.会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?
9.大厅里有6根圆柱,每根柱子的底面半径是4分米,高5米,如果每平方米需要油漆费5元,漆这6根柱子,一共需用油漆费多少元?
10.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆(如图)
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?(记得要算上两边的半圆哦)
(2)大棚内有空间约有多大?
11.只列综合算式或方程,不计算。
一个装满稻谷的圆柱形粮囤,底面半径是2米,高是0.8米。每立方米稻谷的质量约为700千克,这个粮囤存放的稻谷的质量约为多少千克?(π取3.14)
12.一个圆柱形蓄水池的底面直径是14米,深4米,如果在池壁和底面贴瓷砖,贴瓷砖的面积是少平方米?这个蓄水池能蓄水多少立方米?
13.一种长方体的通风管道,每根长5米,横截面是正方形,边长是60厘米.做20根这样的通风管道要用铁皮多少平方米?
14.一个圆柱形蓄水池底面内直径为2m,深2m。
(1)这个蓄水池的占地面积是几平方米?
(2)在池的内壁与底面抹上水泥,抹水泥部分的面积是多少平方米?
(3)蓄水池的容积是几立方米?
15.做一对无盖的圆柱形铁皮水桶,高12厘米,底面直径20厘米,用铁皮多少平方厘米?
16.一个用塑料薄膜覆盖的蔬菜大棚,长10米,横截面是半径为2米的半圆形,覆盖在这个大棚至少需要塑料薄膜多少平方米?
17.一段圆柱形实心钢材长100cm,横截面半径是5cm.每立方厘米钢重7.8g,这段钢材重多少千克?
18.某市对科技馆一楼大厅的5根圆柱重新修饰,每根柱子高10m,底面周长为18.84dm。现全部涂上油漆,如果按每平方米油漆费为20元计算,需要花多少元?
19.油桶的外表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克.漆一个油桶大约需要多少千克防锈油漆?(得数保留一位小数)
20.把一根2米长的圆柱体钢材从中间截成两段后,表面积增加了0.6平方分米,如果每立方分米钢材重7.8千克,这根钢材重多少千克?
21.一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,每分前轮钟转12周。每分钟前轮滚多远?
22.在喀斯喀特山脉南段的火山口湖中,有一根神奇的木头,垂直水中漂浮了超过120年,这根木头被称为“湖中老人”。据测量,这根“湖中老人”长度大约有9米,直径约60厘米,请你计算一下这根圆木的体积合多少立方米(圆木看为近似圆柱,不考虑其他等情况,得数保留两位小数)
23.祈年殿中央有4根同样大小的圆柱形“龙井柱”,“龙井柱”的高是19.2m,底面直径是1.2m。如果把每根“龙井柱”的表面刷一层油漆,平均每平方米用油漆0.8kg,共需油漆多少千克?(得数保留一位小数)
24.一个圆柱形的蓄水池,底面直径是8米,深5米。如果在水池的底面和内壁抹上水泥,抹水泥的面积是多少平方米?
25.由于近年来干旱少雨,小明家修建一口圆柱形水窖,底面直径是4m,窖深3m.
(1)在它的底面和内壁都抹上水泥,抹水泥部分的面积是多少?
(2)如果按水窖容量的储存水,水窖中的水约有多少立方米?(得数保留整数)
26.某酒店门口的三翼旋转门,门内每扇长方形玻璃门高2.5米,宽2米。
(1)制作这样的3扇玻璃门一共需要多少平方米的玻璃?
(2)这个旋转门内的空间大约有多少立方米?(可以用含有π的式子表示)
27.一节圆柱形铁皮烟囱的底面周长为25.12分米,长为2.5米,做6节这样的烟囱需要多少平方米的铁皮?
28.一根圆柱形水管,内直径是20厘米,水流的速度是4米/秒,这根水管1分钟能流过多少立方米的水?
29.在一只底面半径是10cm,高是20cm的圆柱形容器中,水深8cm,要在容器中放入长和宽都是8cm,高是15cm的一块铁块,把铁块竖放在水中,使底面与容器底面接触,这时水深是多少厘米?
30.一个圆柱形蓄水池,底面周长是25.12米,高5米,沿着这个蓄水池的四周及底部抹水泥,如果每平方米用水泥20千克,一共需要多少千克的水泥?
31.如图,一块蜂窝煤的底面直径是12厘米,高是8厘米.其中有12个相同的孔,每个孔的直径是2厘米.做15块这样的蜂窝煤共需用煤多少立方厘米?(π取3.14)
32.一台压路机的滚筒是圆柱形,滚筒的宽是2m,横截面半径是0.5m,滚筒滚动一周,压过的路面是多少平方米?
33.一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路的面积是多少平方米?
34.王师傅用铁皮做了一个无盖的圆柱形水桶,底面直径是10dm,高是底面直径的。做这个水桶至少需要铁皮多少平方分米?这个水桶最多能装水多少升?
35.小丽买了一个水杯,水杯中间贴了一圈装饰带(见如图),这条装饰带宽4厘米,装饰带展开后面积是多少?这个水杯的体积是多少?(单位:厘米,π值取3.14)
36.如图是小东妈妈的茶杯。
(1)这只茶杯最多能装多少升的水?(茶杯厚度不计)
(2)茶杯中部贴有一圈防烫装饰带,这圈防烫装饰带贴在茶杯上的面积是多少平方厘米?
37.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去洗手,走时忘记关掉水龙头,10分钟浪费多少升水?
38.一节用铁皮卷成的圆柱形烟囱长3米,管口直径是40厘米,做这个烟囱至少需要铁皮多少平方米?
39.一种压路机的前轮是圆柱形,轮宽1.6米,底面半径0.5米,该前轮转动一周可以压路的面积是多少平方米?
40.一个压路机的前轮是圆柱体,它的直径是1.5米,轮宽2米,前轮向前滚动200周,压过的路面是多少平方米?
41.用铁皮制作一担圆柱形水桶(无盖),底面直径为6dm,高是8dm.
(1)做这担水桶需铁皮多少dm2?
(2)这担水桶可盛水多少L?
42.修建一个圆柱形的沼气池,底面直径是2米,深2米。在沼气池的内壁与下底面抹上水泥,抹水泥的面积是多少平方米?
43.把一根长4m的圆柱形钢材沿垂直于高的面截成相等的两段以后,表面积增加了6.28m2,如果每立方米钢材重7800kg.(1)原来这根钢材的表面积是多少?
(2)这根钢材重多少千克?
44.为了抗旱,小平家挖了一个底面半径5m、深2m的圆柱形蓄水池,并且用水泥涂抹水池的内壁与底部,防止漏水.一场暴雨过后,小平沿水池边缘走了一圈,并测得池中水深1.2m.
(1)涂抹水泥的面积是多少平方米?
(2)池中水的体积是多少?
45.一种易燃易爆化工原料铁桶,它的底面直径6分米,高14分米.为了搬运安全,需要在桶上安装两个橡胶护圈(如图).至少需要橡胶带多少分米?
46.春节期间,为了增添节日气氛。体育文化广场增添了1根大花柱,花柱高3.5米,底面半径0.5米,花柱的侧面和上面都插满鲜花,如果每平方米装饰40朵花,这根花柱一共需要多少朵花?
47.在一个数学实验活动中.先往一个长方体的容器中注水,水深4.4厘米(如图);然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有冰柱浸没在水里,如图.
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
48.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆。
(1)这个蔬菜大棚的占地面积是多少平方米?
(2)覆盖住这个大棚的塑料薄膜大约有多少平方米?
(3)大棚内的空间大约有多少立方米?
49.某苗圃基地计划建一个圆柱形无盖蓄水池,从外面量得底面直径3.6米,高2米,底的厚度与壁的厚度都是0.3米。这个蓄水池的容积是多少立方米?(得数保留整数)
50.小虹用布制作一顶帽子.上面是圆柱形,底面直径16cm,高15cm;帽檐部分是一个圆环,外圆直径40cm.制作这顶帽子,至少要用多少平方厘米的布?
51.工厂要生产一节烟囱,烟囱长2.5m,横截面是直径为40cm的圆。做一节烟囱一共需要铁皮多少平方米?(接头处忽略不计)
52.一根圆柱形钢管,内直径是4厘米,外直径是8厘米,长是6米。如果每立方厘米钢材重7.8克,那么这根钢管大约重多少千克?(π值取3.14,结果保留整千克)
53.一个圆柱形的粮囤,从里面量得底面半径是2m,高是2.5m,如果每立方米玉米重约0.8吨,这个粮囤能装多少吨玉米?
54.一个蔬菜大棚(如图),长20米,横截面是一个半径2米的半圆形,表面用单层塑料薄膜覆盖(包括两端横截面).
(1)这个大棚的种植面积是多少平方米?
(2)搭建这个大棚至少要用塑料薄膜多少平方米?
(3)大棚内的空间有多大?
55.如图是一个铁皮做成的易拉罐。(单位:厘米)
(1)这个易拉罐的底面积是多少平方厘米?
(2)做一个这样的易拉罐,至少需要多少平方厘米的铁皮?
参考答案与试题解析
1.修建一个圆柱形的蓄水池,底面直径是20米,深2.5米,在池子的内壁和下底面抹上水泥,抹水泥的面积是多少平方米?
【答案】471平方米。
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,已知在池子的四壁和下底面抹上水泥,把数据代入公式解答。
【解答】解:3.14×20×2.5+3.14×(20÷2)2
=157+3.14×100
=157+314
=471(平方米)
答:抹水泥的面积是471平方米。
【点评】此题主要考查圆柱的表面积公式在实际生活中的应用,关键是熟记公式。
2.一种电热水炉的水龙头内直径是1厘米,打开水龙头后水的流速是40厘米/秒。一个容积为1.5升的保温壶,1分钟能装满水吗?
【答案】能。
【分析】首先根据圆柱的容积(体积)公式:V=Sh,把数据代入公式求出1秒流出水的体积,再根据除法的意义求出1.5升里有多少个1秒流出水的体积即可。
【解答】解:1升=1000立方厘米
1.5升=1500立方厘米
3.14×(1÷2)2×40
=3.14×0.25×40
=31.4(立方厘米)
1500÷31.4≈47.77(秒)
1分钟=60秒
47.77秒<1分钟
答:1分钟能装满水。
【点评】此题主要考查圆柱的容积(体积)公式在实际生活中的应用。
3.一个圆柱形蓄水池深4米,平均每天用水8吨,7天后水池的水减少了20%(每立方米的水重1吨),这个水池的占地面积是多少?
【答案】见试题解答内容
【分析】先根据总用水量=平均每天用水量×天数求出7天的总用水量,再除以1求出水的体积,再根据百分数乘法的意义求出水池减少的水的高度,再根据圆柱体积变形公式S=V÷h可求这个水池的占地面积.
【解答】解:8×7÷1÷(4×20%)
=56÷1÷0.8
=56÷0.8
=70(平方米)
答:这个水池的占地面积是70平方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
4.如图,是用塑料薄膜覆盖的蔬菜大棚,长16米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
【答案】见试题解答内容
【分析】(1)根据题干,这个大棚的种植面积就是这个长15米,宽2米的长方形的面积,根据长方形的面积公式即可解答;
(2)覆盖在这个大棚上的塑料薄膜的面积,即它所在的圆柱的侧面积的一半,加上一个圆柱的底面积;由此利用圆柱的侧面积和底面积公式即可解答.
【解答】解:(1)16×2=32(平方米)
答:这个大棚的种植面积是32平方米.
(2)3.14×2×16÷2+3.14×(2÷2)2
=50.24+3.14
=53.38(平方米)
答:覆盖在这个大棚上的塑料薄膜约有53.38平方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
5.王老师要做一个无盖的长方体玻璃鱼缸,要求每个顶点连接的三条棱长分别是5分米、4分米、3分米,请你帮王老师设计一下怎样才节省材料(画图表示并计算一下至少要用玻璃多少平方分米?)
【答案】见试题解答内容
【分析】求这个鱼缸用的玻璃的面积就是求5个面的面积,缺少上面(最大长为5分米,宽为4分米),根据长方体表面积的计算方法求解.
【解答】解:如图:
5×4+4×3×2+5×3×2
=20+24+30
=74(平方分米);
答:制作这个鱼缸至少用玻璃74平方分米.
【点评】此题考查长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可.
6.有一个花坛,高0.5米,底面是边长2.3米的正方形.四周用砖砌成,厚度是0.3米,中间填满泥土,花坛里大约有多少立方米泥土?
【答案】见试题解答内容
【分析】求花坛里大约有多少立方米的泥土,就是求它的容积,关键是理解四周用砖砌成,厚度是0.3米,也就是花坛里面的边长是(2.3﹣0.3×2)米,再利用长方体的体积(容积)公式解答.
【解答】解:求花坛的容积:
(2.3﹣0.3×2)×(2.3﹣0.3×2)×0.5
=1.7×1.7×0.5
=1.445(立方米);
答:花坛里大约有1.445立方米的泥土.
【点评】此题主要考查长方体体积(容积)的计算,解答关键是理解花坛里的正方形的边长要减去两个0.3米,根据公式解答即可.
7.一个圆柱形油漆桶,从里面量底面周长是18.84分米,高是6分米,如果每升油漆重1.5千克,这个油漆桶可装油漆多少千克?
【答案】254.34千克。
【分析】先根据油桶的底面周长依次求出底面半径和底面积,再根据圆柱体体积=底面积×高求出油桶的容积,最后用汽油的比重乘以容积即可。
【解答】解:1.5×[3.14×(18.84÷2÷3.14)2×6]
=1.5×[3.14×9×6]
=1.5×169.56
=254.34(千克)
答:这个油桶可装汽油254.34千克。
【点评】此题主要考查的是圆柱的体积公式的灵活应用,解答此题的关键是求出底面半径和面积。
8.会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?
【答案】见试题解答内容
【分析】由于是在圆柱形柱子上刷油漆,也就是要刷它的侧面积,所以要求刷这些柱子用油漆多少千克,就要先求10根柱子的侧面积是多少,再乘0.5即可.
【解答】解:3.14×0.6×6×10×0.5,
=3.14×36×0.5,
=56.52(千克);
答:刷这些柱子要用油漆56.52千克.
【点评】解答此题要注意刷油漆的部分是侧面积,不是圆柱的表面积.
9.大厅里有6根圆柱,每根柱子的底面半径是4分米,高5米,如果每平方米需要油漆费5元,漆这6根柱子,一共需用油漆费多少元?
【答案】376.8元。
【分析】给圆柱子涂油漆,只能涂侧面积,知道柱子的底面半径和高,2πrh可得一个柱子的侧面积,乘6求得涂油漆的总面积,总面积乘单位面积需要的钱数,则可得一共需要的钱数。
【解答】解:4分米=0.4米
3.14×0.4×2×5×6
=3.14×(0.4×2×5×6)
=3.14×24
=75.36(平方米)
5×75.36=376.8(元)
答:一共需用油漆费376.8元。
【点评】此题只需求圆柱的侧面积,根据已知运用公式求出,进而求总面积,最后求出需用的钱数,细心计算即可。
10.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆(如图)
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?(记得要算上两边的半圆哦)
(2)大棚内有空间约有多大?
【答案】见试题解答内容
【分析】这个蔬菜大棚的形状是底面是半圆的半个圆柱体.
(1)求搭建这个蔬菜大棚大约要用多少平方米的塑料薄膜,就是求圆柱表面积的一半;
(2)求大棚内的空间大约有多大,就是求圆柱体积的一半.由此根据圆柱的表面积及体积公式,即可列式解答.
【解答】解:(1)[2×2×3.14×20+3.14×22×2]÷2
=[251.2+25.12]÷2
=276.32÷2
=138.16(平方米);
答:搭建这个大棚大约要用138平方米的塑料薄膜.
(2)3.14×22×20÷2
=251.2÷2
=125.6(立方米);
答:大棚内的空间大约是126立方米.
【点评】此题主要利用圆柱的表面积和体积的公式解决问题,关键是理解大棚的形状半个圆柱.
11.只列综合算式或方程,不计算。
一个装满稻谷的圆柱形粮囤,底面半径是2米,高是0.8米。每立方米稻谷的质量约为700千克,这个粮囤存放的稻谷的质量约为多少千克?(π取3.14)
【答案】7033.6千克。
【分析】圆柱的体积公式:V=πr2h,据此代入数据求出圆柱的体积,再用圆柱的体积乘700即可求出这个粮囤可存放的稻谷质量。
【解答】解:3.14×22×0.8
=3.14×4×0.8
=12.56×0.8
=10.048(立方米)
10.048×700=7033.6(千克)
答:这个粮囤存放的稻谷的质量约为7033.6千克。
【点评】本题考查的是圆柱体积计算公式的运用。
12.一个圆柱形蓄水池的底面直径是14米,深4米,如果在池壁和底面贴瓷砖,贴瓷砖的面积是少平方米?这个蓄水池能蓄水多少立方米?
【答案】329.7平方米,615.44立方米。
【分析】贴瓷砖的面积是求圆柱的侧面积与一个底面积的和,运用圆柱的侧面积公式及圆的面积公式列式解答即可。这个蓄水池可装水多少立方米,是求圆柱形水池的容积,即求圆柱的体积,运用圆柱的体积计算公式,代入数据解决问题。
【解答】解:3.14×14×4+3.14×(14÷2)2
=175.84+3.14×49
=175.84+153.86
=329.7(平方米)
3.14×(14÷2)2×4
=3.14×49×4
=615.44(立方米)
答:贴瓷砖的面积是329.7平方米;这个蓄水池可装水615.44立方米。
【点评】此题主要考查圆柱的侧面积以及体积计算公式的运用。
13.一种长方体的通风管道,每根长5米,横截面是正方形,边长是60厘米.做20根这样的通风管道要用铁皮多少平方米?
【答案】见试题解答内容
【分析】由题意可知,通风管是没有底面的,所以只求它的4个侧面的面积,根据长方体的表面积的计算方法,先求出1根通风管需要材料,然后乘20即可.
【解答】解:60厘米=0.6米
0.6×4×5×20
=0.6×20×20
=240(平方米)
答:做20根这样的通风管道要用铁皮240平方米.
【点评】此题属于长方体的表面积的实际应用,解答关键是搞清求的是哪几个面的面积,再根据长方体的表面积的计算方法进行解答.
14.一个圆柱形蓄水池底面内直径为2m,深2m。
(1)这个蓄水池的占地面积是几平方米?
(2)在池的内壁与底面抹上水泥,抹水泥部分的面积是多少平方米?
(3)蓄水池的容积是几立方米?
【答案】(1)3.14平方米;(2)15.7平方米;(3)6.28立方米。
【分析】(1)根据圆面积计算公式等于π乘底面圆半径的平方计算即可;
(2)抹水泥部分的面积是蓄水池的侧面积加上底面积,侧面积=底面周长×高,底面直径和高已知,代入公式即可求解;
(3)利用圆柱的体积V=Sh,即可求出蓄水池的容积。
【解答】解:(1)3.14×(2÷2)2
=3.14×1
=3.14(平方米)
答:这个蓄水池的占地面积是3.14平方米。
(2)3.14×2×2+3.14
=12.56+3.14
=15.7(平方米)
答:抹水泥部分的面积是15.7平方米。
(3)3.14×2
=3.14×2
=6.28(立方米)
答:蓄水池的容积是6.28立方米。
【点评】此题主要考查圆柱的侧面积和体积的计算方法,关键是明白:抹水泥部分的面积是蓄水池的侧面积加上底面积。
15.做一对无盖的圆柱形铁皮水桶,高12厘米,底面直径20厘米,用铁皮多少平方厘米?
【答案】见试题解答内容
【分析】一个水桶需要的铁皮的面积=水桶的侧面积+底面积,利用圆柱的侧面积和圆的面积公式即可得解,得数再乘2即可.
【解答】解:3.14×20×12+3.14×(20÷2)2
=753.6+314
=1067.6(平方厘米)
1067.6×2=2135.2(平方厘米)
答:用铁皮2135.2平方厘米.
【点评】此题主要考查圆柱的侧面积和圆的面积的计算方法,要记住求的是一对水桶需要的铁皮的面积.
16.一个用塑料薄膜覆盖的蔬菜大棚,长10米,横截面是半径为2米的半圆形,覆盖在这个大棚至少需要塑料薄膜多少平方米?
【答案】见试题解答内容
【分析】这个大棚的形状是底面是半圆的半个圆柱体,求搭建这个大棚大约要用多少平方米的塑料薄膜,就是求圆柱表面积的一半;由此根据圆柱的表面积=侧面积+两个底面积,即可列式解答.
【解答】解:[(2×2×3.14)×10+3.14×22×2]÷2
=[125.6+12.56×2]÷2
=[125.6+25.12]÷2
=150.72÷2
=75.36(平方米)
答:覆盖在这个大棚至少需要塑料薄膜75.36平方米.
【点评】此题主要利用圆柱的表面积和体积的公式解决问题,关键是理解大棚的形状半个圆柱.
17.一段圆柱形实心钢材长100cm,横截面半径是5cm.每立方厘米钢重7.8g,这段钢材重多少千克?
【答案】见试题解答内容
【分析】先利用圆柱的体积公式V=πr2h求出它的体积,然后再乘上7.8,求出这段钢材重多少克,再化成千克即可.
【解答】解:3.14×52×100×7.8
=3.14×25×100×7.8
=7850×7.8
=61230(克)
61230克=61.23千克
答:这段钢材重61.23千克.
【点评】此题是考查圆柱的体积计算,利用公式V=πr2h求出体积,然后再进一步解答.注意统一单位.
18.某市对科技馆一楼大厅的5根圆柱重新修饰,每根柱子高10m,底面周长为18.84dm。现全部涂上油漆,如果按每平方米油漆费为20元计算,需要花多少元?
【答案】1884元。
【分析】根据题干可知,每根柱子需要涂漆的只是柱子的侧面,由此利用圆柱的侧面积公式S侧=Ch计算出每个柱子的侧面积,再乘5就是涂漆的总面积,再依条件求出油漆费即可。
【解答】解:18.84dm=1.884m
1.884×10×5×20
=1.884×1000
=1884(元)
答:需要花1884元。
【点评】此题主要考查圆柱表面积的实际应用,解答关键是要弄清涂漆面积,再依条件解决问题即可。
19.油桶的外表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克.漆一个油桶大约需要多少千克防锈油漆?(得数保留一位小数)
【答案】见试题解答内容
【分析】要求漆一个油桶大约需要多少防锈漆,应先求得油桶的表面积,表面积是两个底面与侧面积的和,由圆柱体侧面积和圆的面积计算方法求出,最后乘每平方米所用油漆的质量,得出答案.
【解答】解:油桶的侧面积:
3.14×0.6×1=1.884(平方米)
油桶的两个底面的面积:
3.14×(0.6÷2)2×2
=3.14×0.32×2
=3.14×0.09×2
=0.5652(平方米);
油桶的表面积:
1.884+0.5652=2.4492(平方米)
大约需要防锈漆:
0.2×2.4492≈0.5(千克)
答:漆一个油桶大约需要0.5千克防锈漆.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
20.把一根2米长的圆柱体钢材从中间截成两段后,表面积增加了0.6平方分米,如果每立方分米钢材重7.8千克,这根钢材重多少千克?
【答案】这根钢材重46.8千克。
【分析】0.6平方分米是圆柱形钢材的两个底面的面积,由此根据圆柱的体积公式:V=sh,求出圆柱形钢材的体积,再用体积乘7.8千克就是钢材的质量。
【解答】解:2米=20分米,
(0.6÷2)×20×7.8
=0.3×20×7.8
=6×7.8
=46.8(千克)
答:这根钢材重46.8千克。
【点评】关键是知道0.6平方分米是哪部分的面积,再利用相应的公式解决问题。
21.一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,每分前轮钟转12周。每分钟前轮滚多远?
【答案】30.144米。
【分析】根据圆的周长公式C=πd,把数据代入公式求出前轮滚动一周可前进多少米,然后再乘12即可。
【解答】解:3.14×0.8×12
=2.512×12
=30.144(米)
答:每分钟前轮滚30.144米。
【点评】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式。
22.在喀斯喀特山脉南段的火山口湖中,有一根神奇的木头,垂直水中漂浮了超过120年,这根木头被称为“湖中老人”。据测量,这根“湖中老人”长度大约有9米,直径约60厘米,请你计算一下这根圆木的体积合多少立方米(圆木看为近似圆柱,不考虑其他等情况,得数保留两位小数)
【答案】2.54立方米。
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:60厘米=0.6米
3.14×(0.6÷2)2×9
=3.14×0.09×9
=2.5434(立方米)
≈2.54(立方米)
答:这根圆木的体积合2.54立方米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
23.祈年殿中央有4根同样大小的圆柱形“龙井柱”,“龙井柱”的高是19.2m,底面直径是1.2m。如果把每根“龙井柱”的表面刷一层油漆,平均每平方米用油漆0.8kg,共需油漆多少千克?(得数保留一位小数)
【答案】231.5千克。
【分析】圆柱的侧面积=底面周长×高,求出一根“龙井柱”的侧面积,再用乘法求出4根同样大小的圆柱形“龙井柱”,把每根“龙井柱”的表面刷一层油漆,平均每平方米用油漆0.8kg,共需油漆多少千克。
【解答】解:3.14×1.2×19.2×4×0.8
=3.768×19.2×4×0.8
=72.3456×4×0.8
=289.3824×0.8
≈231.5(千克)
答:共需油漆231.5千克。
【点评】本题解答的关键是计算圆柱体的侧面积。
24.一个圆柱形的蓄水池,底面直径是8米,深5米。如果在水池的底面和内壁抹上水泥,抹水泥的面积是多少平方米?
【答案】175.84平方米。
【分析】求水池的底面和四周抹上水泥的面积,即抹水泥的部分的面积=侧面积+一个底的面积,根据圆柱的表面积公式S=2πr +Ch解答即可。
【解答】解:3.14×(8÷2) +3.14×8×5
=3.14×16+3.14×8×5
=50.24+125.6
=175.84(平方米)
答:抹水泥的面积是175.84平方米。
【点评】本题考查学生对圆柱表面积公式的掌握和运用。
25.由于近年来干旱少雨,小明家修建一口圆柱形水窖,底面直径是4m,窖深3m.
(1)在它的底面和内壁都抹上水泥,抹水泥部分的面积是多少?
(2)如果按水窖容量的储存水,水窖中的水约有多少立方米?(得数保留整数)
【答案】见试题解答内容
【分析】(1)由题意可知:抹水泥部分的面积=圆柱形水窖的侧面积+下底的面积,又因圆柱的侧面积=底面周长×高,圆锥的底面直径已知,于是可以求出其底面周长和底面积,进而可以求出抹水泥部分的面积;
(2)利用圆柱的体积公式v=πr2h即可求出这个圆柱形水窖最多能装多少水,然后乘上即可.
【解答】解:(1)3.14×4×2+3.14×(4÷2)2
=12.56×2+3.14×4
=12.56+12.56
=25.12(平方米)
答:抹水泥部分的面积是25.12平方米.
(2)3.14×(4÷2)2×3
=3.14×4×3
≈30(立方米)
答:水窖中的水约有30立方米.
【点评】此题主要考查圆柱的侧面积和圆的面积及体积的计算方法.
26.某酒店门口的三翼旋转门,门内每扇长方形玻璃门高2.5米,宽2米。
(1)制作这样的3扇玻璃门一共需要多少平方米的玻璃?
(2)这个旋转门内的空间大约有多少立方米?(可以用含有π的式子表示)
【答案】(1)15平方米;
(2)10π立方米。
【分析】(1)根据长方形的面积公式:S=ab,将数据代入,即可得出答案;
(2)旋转门内的空间等同于半径为为2米,高为2.5米的圆柱的体积,根据圆柱的体积公式:V=Sh=πr h,将数据代入即可得出答案。
【解答】解:(1)2.5×2×3
=5×3
=15(平方米)
答:一共需要15平方米的玻璃。
(2)π×2 ×2.5
=π×4×2.5
=10π(立方米)
答:这个旋转门内的空间大约有10π立方米。
【点评】本题考查学生对长方形面积公式和圆柱体积公式的掌握和运用。
27.一节圆柱形铁皮烟囱的底面周长为25.12分米,长为2.5米,做6节这样的烟囱需要多少平方米的铁皮?
【答案】37.68平方米。
【分析】根据圆柱的侧面积公式:S=Ch,求出一节圆柱形铁皮烟囱的面积,再乘6即可求出做6节这样的烟囱需要多少平方米的铁皮。
【解答】解:25.12分米=2.512米
2.512×2.5×6
=6.28×6
=37.68(平方米)
答:做6节这样的烟囱需要37.68平方米的铁皮。
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
28.一根圆柱形水管,内直径是20厘米,水流的速度是4米/秒,这根水管1分钟能流过多少立方米的水?
【答案】7.536立方米。
【分析】水在自来水管内的形状是圆柱形,可利用V=Sh先求出每秒流水的体积,再求1分钟可流水多少立方米即可。
【解答】解:20厘米=0.2米,1分=60秒
3.14×(0.2÷2)2×4×60
=3.14×0.01×240
=7.536(立方米)
答:这根水管1分钟能流过7.536立方米的水。
【点评】此题是利用圆柱的体积公式解决实际问题,要注意统一单位。
29.在一只底面半径是10cm,高是20cm的圆柱形容器中,水深8cm,要在容器中放入长和宽都是8cm,高是15cm的一块铁块,把铁块竖放在水中,使底面与容器底面接触,这时水深是多少厘米?
【答案】见试题解答内容
【分析】放入铁块前后的水的体积不变,根据水深8厘米,可以先求得水的体积,那么放入铁块后,容器的底面积变小了,也就是圆柱的底面积减去长方体的底面积,由此可以求得此时水的深度.
【解答】解:3.14×102×8÷(3.14×102﹣8×8)
=3.14×100×8÷(314﹣64)
=2512÷250
=10.048(厘米),
答:这时水深10.048厘米.
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式,重点是求出把铁块竖放在水中圆柱容器的底面积.
30.一个圆柱形蓄水池,底面周长是25.12米,高5米,沿着这个蓄水池的四周及底部抹水泥,如果每平方米用水泥20千克,一共需要多少千克的水泥?
【答案】3516.8千克
【分析】由于蓄水池是无盖,所以抹水泥的面积数这个圆柱的一个底面加上侧面积,圆柱的侧面积=底面周长×高,再根据圆的面积公式,把数据代入公式求出抹水泥的面积,进而求出每平方米用水泥的质量。
【解答】解:25.12×5+3.14×(25.12÷3.14÷2)2
=125.6+3.14×16
=125.6+50.24
=175.84(平方米)
20×175.84=3516.8(千克)
答:一共需要3516.8千克水泥。
【点评】此题主要考查圆柱的表面积公式、体积公式在实际生活中的应用。
31.如图,一块蜂窝煤的底面直径是12厘米,高是8厘米.其中有12个相同的孔,每个孔的直径是2厘米.做15块这样的蜂窝煤共需用煤多少立方厘米?(π取3.14)
【答案】见试题解答内容
【分析】求一块蜂窝煤的用煤量,就用这块蜂窝煤的总体积减去16个圆柱形小孔的体积;由此根据圆柱的体积公式V=sh=π(d÷2)2h分别求出蜂窝煤的体积和圆孔的体积,再用蜂窝煤的总体积减去16个圆孔的体积即可.
【解答】解:煤球的体积:3.14×(12÷2)2×8
=3.14×36×8
=113.04×8
=904.32(立方厘米);
煤球的12个圆柱形孔的体积是:
3.14×(2÷2)2×8×12
=3.14×8×12
=25.12×12
=301.44(立方厘米);
煤球的体积是:
904.32﹣301.44=602.88(立方厘米)
做15块这样的蜂窝煤需要:
602.88×15=9043.2(立方厘米)
答:做15块蜂窝煤需要用煤9043.2立方厘米.
【点评】本题主要是灵活利用圆柱的体积V=Sh=π(d÷2)2h解决生活中的实际问题.
32.一台压路机的滚筒是圆柱形,滚筒的宽是2m,横截面半径是0.5m,滚筒滚动一周,压过的路面是多少平方米?
【答案】6.28平方米。
【分析】滚筒滚动一周,压过的路面面积就是滚筒的侧面积。利用圆柱的侧面积=圆柱的底面周长×高,即可求得压过的路面面积。据此解答。
【解答】解:3.14×0.5×2×2
=3.14×1×2
=6.28(平方米)
答:压过的路面是6.28平方米。
【点评】本题考查了圆柱侧面积在生活中的应用。掌握圆柱的侧面积计算方法是解答的关键。
33.一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路的面积是多少平方米?
【答案】7.536平方米。
【分析】由题意可知,路机的前轮是圆柱形,轮宽2米,也就是圆柱的高,直径1.2米,求前轮转动一周,压路的面积是多少,计算求圆柱的侧面积,圆柱的侧面积=底面周长×高,由此解答。
【解答】解:3.14×1.2×2
=3.768×2
=7.536(平方米)
答:压路的面积是7.536平方米。
【点评】此题属于圆柱的表面积的实际应用,解答此题主要分清所求物体的形状,求压路面积是求圆柱的侧面积,根据圆柱的侧面积公式解答即可。
34.王师傅用铁皮做了一个无盖的圆柱形水桶,底面直径是10dm,高是底面直径的。做这个水桶至少需要铁皮多少平方分米?这个水桶最多能装水多少升?
【答案】329.7平方分米,628升。
【分析】首先分清制作没有盖的圆柱形铁皮水桶,需要计算几个面的面积:即侧面面积与底面圆的面积,根据圆柱体侧面积和圆的面积计算方法即可求出需要多少平方分米的铁皮;再根据圆柱体积(容积)公式V=sh,列式解答即可求出这个水桶的容积。
【解答】解:高:108(dm)
3.14×(10÷2)2+3.14×10×8
=78.5+251.2
=329.7(平方分米)
3.14×(10÷2)2×8
=3.14×25×8
=3.14×200
=628(立方分米)
628立方分米=628升
答:做这个水桶至少需要铁皮329.7平方分米,这个水桶最多能装水628升。
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
35.小丽买了一个水杯,水杯中间贴了一圈装饰带(见如图),这条装饰带宽4厘米,装饰带展开后面积是多少?这个水杯的体积是多少?(单位:厘米,π值取3.14)
【答案】75.36平方厘米,339.12立方厘米。
【分析】装饰带展开后是一个长方形,长方形的长为圆柱的底面周长,宽为4厘米,再根据长方形的面积公式S=ab进行解答;根据圆柱的体积公式V=πr2h,代入数据进行解答。
【解答】解:3.14×6×4
=18.84×4
=75.36(平方厘米)
3.14×(6÷2)2×12
=3.14×9×12
=28.26×12
=339.12(立方厘米)
答:装饰带展开后面积是75.36平方厘米,这个水杯的体积是339.12立方厘米。
【点评】考查了圆柱的侧面积和体积公式的运用。
36.如图是小东妈妈的茶杯。
(1)这只茶杯最多能装多少升的水?(茶杯厚度不计)
(2)茶杯中部贴有一圈防烫装饰带,这圈防烫装饰带贴在茶杯上的面积是多少平方厘米?
【答案】(1)0.2826。
(2)75.36。
【分析】(1)已知圆柱的底面直径是6厘米,高是10厘米,根据圆柱的体积公式:V=π(d÷2)2h可求出圆柱的容积。
(2)茶杯中部的一圈装饰带是小明怕烫伤妈妈的手特意贴上的,它的面积是一个宽为4厘米,长为直径为6厘米的圆的周长的长方形的面积,根据长方形的面积公式进行计算即可。
【解答】解:(1)3.14×(6÷2)2×10
=3.14×9×10
=282.6(立方厘米)
282.6=0.2826升
答:这只茶杯最多能装0.2826升水。
(2)3.14×6×4
=3.14×24
=75.36(平方厘米)
答:它的面积是75.36平方厘米。
【点评】本题主要考查了学生对圆柱的体积和侧面积计算方法的灵活运用。
37.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去洗手,走时忘记关掉水龙头,10分钟浪费多少升水?
【答案】15.072升。
【分析】把流过的水看成圆柱,它的底面直径是2厘米、高是(8×10×60)厘米,由此根据圆柱的体积公式V=sh=πr2h计算即可。
【解答】解:3.14×(2÷2)2×(8×10×60)
=3.14×1×4800
=15072(cm3)
15072立方厘米=15.072(升)
答:10分钟浪费15.072升水。
【点评】把不规则的形状物体,转化成规则的形状来求解体积是解答本题的关键。
38.一节用铁皮卷成的圆柱形烟囱长3米,管口直径是40厘米,做这个烟囱至少需要铁皮多少平方米?
【答案】3.768平方米。
【分析】根据“圆柱侧面积=底面周长×高”进行计算,烟囱的长就是圆柱的高,管口直径是圆柱的底面直径,根据“圆周长C=πd”可求出底面周长。
【解答】解:40厘米=0.4米
3.14×0.4×3
=1.256×3
=3.768(平方米)
答:做这个烟囱至少需要铁皮3.768平方米。
【点评】此题主要考查圆柱侧面积的计算方法,注意烟囱是无底的圆柱形。
39.一种压路机的前轮是圆柱形,轮宽1.6米,底面半径0.5米,该前轮转动一周可以压路的面积是多少平方米?
【答案】见试题解答内容
【分析】根据题意,这台压路机的前轮是一个圆柱,求该前轮转动一周可以压路的面积就是求圆柱的侧面积,圆柱的侧面积=底面周长×高,据此回答.
【解答】解:根据题意得
3.14×2×0.5×1.6
=3.14×1.6
=5.024(平方米)
答:该前轮转动一周可以压路的面积是5.024平方米.
【点评】本题考查了圆柱的侧面积,解决本题的关键是运用圆柱的侧面积公式.
40.一个压路机的前轮是圆柱体,它的直径是1.5米,轮宽2米,前轮向前滚动200周,压过的路面是多少平方米?
【答案】见试题解答内容
【分析】根据圆柱的侧面积公式:S=ch,把数据代入公式求出前轮滚动一周压路的面积在乘200即可,据此列式解答.
【解答】解:3.14×1.5×2×200
=9.42×200
=1884(平方米),
答:压路的面积是1884平方米.
【点评】此题主要考查圆柱的侧面积搜狗在实际生活中的应用,关键是熟记公式.
41.用铁皮制作一担圆柱形水桶(无盖),底面直径为6dm,高是8dm.
(1)做这担水桶需铁皮多少dm2?
(2)这担水桶可盛水多少L?
【答案】见试题解答内容
【分析】(1)由于水桶无盖,所以需要铁皮的面积是这个圆柱的侧面积加一个底面的面积,根据圆柱的侧面积公式:S=ch,圆的面积公式:S=πr2.求出一个,再求一担.
(2)根据圆柱的容积公式:V=Sh,把数据分别代入公式解答.先求出一只水桶盛水多少,再求一担水的体积.
【解答】解:(1)3.14×6×8+3.14×(6÷2)2
=150.72+3.14×9
=150.72+28.26
=178.98(平方分米)
178.98×2=357.96(平方分米)
答:做一担这样的铁桶至少需要357.96平方分米的铁皮.
(2)3.14×(6÷2)2×8×2
=3.14×9×8×2
=452.16(立方分米)
452.16立方分米=452.16升
答:这担水桶最多能盛水452.16升.
【点评】此题主要考查圆柱的表面积公式、容积公式在实际生活中的应用.
42.修建一个圆柱形的沼气池,底面直径是2米,深2米。在沼气池的内壁与下底面抹上水泥,抹水泥的面积是多少平方米?
【答案】15.7平方米。
【分析】圆柱的侧面积=底面周长×高,用侧面积加上一个底面积即可。
【解答】解:2÷2=1(米)
3.14×2×2+3.14×1×1
=12.56+3.14
=15.7(平方米)
答:抹水泥的面积是15.7平方米。
【点评】熟练掌握圆的周长和面积公式,是解答此题的关键。
43.把一根长4m的圆柱形钢材沿垂直于高的面截成相等的两段以后,表面积增加了6.28m2,如果每立方米钢材重7800kg.(1)原来这根钢材的表面积是多少?
(2)这根钢材重多少千克?
【答案】见试题解答内容
【分析】(1)增加部分的面积是6.28平方米是圆柱形钢材的两个底面的面积,先用6.28除以2,求出一个底面的面积,再根据圆的面积公式求出圆的半径的平方,进而得出圆的半径,然后根据圆的周长公式求出底面周长,再乘高,求出侧面积,然后用侧面积加上两个底面积就是原来这根钢材的表面积是多少;
(2)由此根据圆柱的体积公式,V=Sh,求出圆柱形钢材的体积,再用体积乘7800千克就是钢材的重量.
【解答】解:(1)6.28÷2=3.14(平方米)
3.14÷3.14=1(平方米)
即底面半径的平方是1平方米,所底面半径是1米;
3.14×1×2=6.28(米)
6.28×4+6.28
=25.12+6.28
=31.4(平方米)
答:原来这根钢材的表面积是31.4平方米.
(2)3.14×4×7800
=12.56×7800
=97968(千克)
答:这根钢材重97968千克.
【点评】解决本题关键是明确增加的表面积就是原来圆柱两个底面积的面积,再根据圆的面积公式、周长公式,以及圆柱表面积的计算方法和体积的计算方法求解.
44.为了抗旱,小平家挖了一个底面半径5m、深2m的圆柱形蓄水池,并且用水泥涂抹水池的内壁与底部,防止漏水.一场暴雨过后,小平沿水池边缘走了一圈,并测得池中水深1.2m.
(1)涂抹水泥的面积是多少平方米?
(2)池中水的体积是多少?
【答案】见试题解答内容
【分析】(1)根据题意,涂抹水泥的面积是这个圆柱的侧面积+一个底面积,再根据圆柱侧面积=底面周长×高,进行解答;
(2)根据圆柱的体积公式:V=Sh,代入数据,进行解答.
【解答】解:(1)2×3.14×5×2+3.14×52
=62.8+78.5
=141.3(平方米)
答:涂抹水泥的面积是141.3平方米.
(2)3.14×52×1.2
=78.5×1.2
=94.2(立方米)
答:池中水的体积是94.2立方米.
【点评】此题主要考查圆柱的表面积公式和体积公式的灵活运用.
45.一种易燃易爆化工原料铁桶,它的底面直径6分米,高14分米.为了搬运安全,需要在桶上安装两个橡胶护圈(如图).至少需要橡胶带多少分米?
【答案】见试题解答内容
【分析】根据圆的周长公式:C=πd,把数据代入公式求出圆柱铁桶的底面周长然后乘2即可.据此解答.
【解答】解:3.14×6×2
=18.84×2
=37.68(分米),
答:至少需要橡胶带37.68分米.
【点评】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式.
46.春节期间,为了增添节日气氛。体育文化广场增添了1根大花柱,花柱高3.5米,底面半径0.5米,花柱的侧面和上面都插满鲜花,如果每平方米装饰40朵花,这根花柱一共需要多少朵花?
【答案】471朵花。
【分析】根据圆柱的侧面积公式:S=Ch,圆的面积公式:S=πr2,把数据代入公式求出这个柱子的侧面积和上面的面积,然后用侧面积与上面的面积和乘每平方米插花的数量即可,据此解答。
【解答】解:(3.14×0.5×2×3.5+3.14×0.52)×40
=(3.14×3.5+3.14×0.25)×40
=(10.99+0.785)×40
=11.775×40
=471(朵)
答:这根花柱一共需要471朵花。
【点评】此题主要考查圆柱的侧面积公式、圆的面积公式在实际生活中的应用,关键是熟记公式。
47.在一个数学实验活动中.先往一个长方体的容器中注水,水深4.4厘米(如图);然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有冰柱浸没在水里,如图.
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
【答案】见试题解答内容
【分析】(1)原来水柱只有4.4厘米,因为“水面上升到5.5厘米处”说明了冰柱插入水中水面上升了(5.5﹣4.4)厘米,用底面积乘以上升的水1.1厘米的高度,就是冰柱的体积,再求整个冰柱的体积即可.
(2)根据“冰化成水,体积减少原来的,要求这根冰柱融化后将变成多少毫升的水,是把冰的体积看作单位“1”,则水是原来冰柱的(1),再根据求一个数的几分之几是多少用乘法计算,据此解答即可.
(3)因为冰柱垂直放入长方体的容器中,使水的高度上升了:5.5﹣4.4=1.1(厘米),所以根据整个冰柱化成水后的体积与上升的高度进行计算即可.
【解答】(1)10×10×(5.5﹣4.4)
=100×1.1
=110×3
=330立方厘米(立方厘米)
答:整根冰柱的体积是330立方厘米;
(2)330×(1)
=330
=297(立方厘米)
297立方厘米=297毫升
答:这根冰柱融化后将变成297毫升的水.
(3)4.4+297÷(10×10)
=4.4+297÷100
=4.4+2.97
=7.37(厘米)
答:当冰柱完全融化时,容器内水深一共是7.37厘米.
【点评】解答此题的关键是利用物体排开水的体积等于浸入水的物体的体积,先求出浸入水中的体积,从而问题得解.
48.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆。
(1)这个蔬菜大棚的占地面积是多少平方米?
(2)覆盖住这个大棚的塑料薄膜大约有多少平方米?
(3)大棚内的空间大约有多少立方米?
【答案】(1)80。
(2)138。
(3)125.6。
【分析】(1)根据题干,这个大棚的占地面积就是这个长20米,宽2×2=4米的长方形的面积,根据长方形的面积公式S=a×b即可解答。
(2)覆盖在这个大棚上的塑料薄膜的面积,即它所在的圆柱的侧面积的一半,加上一个圆柱的底面积;由此利用圆柱的侧面积和底面积公式S=πr2即可解答。
(3)大棚所在的圆柱的体积的一半,就是这个大棚的空间,根据圆柱的体积公式V=πr2h解答即可。
【解答】解:(1)20×(2×2)=80(平方米)
答:这个大棚的种植面积是80平方米。
(2)3.14×2×2×20÷2+3.14×22
=125.6+12.56
=138.16
≈138(平方米)
答:覆盖在这个大棚上的塑料薄膜约有138平方米。
(3)3.14×22×20÷2
=251.2÷2
=125.6(立方米)
答:大棚的空间大约是125.6立方米。
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
49.某苗圃基地计划建一个圆柱形无盖蓄水池,从外面量得底面直径3.6米,高2米,底的厚度与壁的厚度都是0.3米。这个蓄水池的容积是多少立方米?(得数保留整数)
【答案】12立方米。
【分析】先求出这个蓄水池的底面内直径和高,再根据圆柱形的容积=底面积×高即可求解。
【解答】解:2﹣0.3=1.7(米)
3.6﹣0.3×2
=3.6﹣0.6
=3(米)
3.14×(3÷2)2×1.7
=3.14×2.25×1.7
≈12(立方米)
答:这个蓄水池的容积是12立方米。
【点评】此题主要考查圆柱的容积公式的计算应用,关键是求出蓄水池的底面内直径和高。
50.小虹用布制作一顶帽子.上面是圆柱形,底面直径16cm,高15cm;帽檐部分是一个圆环,外圆直径40cm.制作这顶帽子,至少要用多少平方厘米的布?
【答案】见试题解答内容
【分析】根据题意,这个帽子是由一个无底的圆柱的表面积+一个圆环的面积,圆柱的底面直径是16cm,高是15cm;圆环的内直径是16cm,外直径是40cm;然后再根据圆柱的表面积公式和圆环的面积公式进行解答.
【解答】解:3.14×16×15+3.14×(16÷2)2+3.14×[(40÷2)2﹣(16÷2)2]
=753.6+200.96+1055.04
=2009.6(平方厘米)
答:至少要用2009.6平方厘米的布.
【点评】此题重点考查圆环的面积和圆柱的表面积计算方法的灵活运用.
51.工厂要生产一节烟囱,烟囱长2.5m,横截面是直径为40cm的圆。做一节烟囱一共需要铁皮多少平方米?(接头处忽略不计)
【答案】3.14平方米。
【分析】烟囱只有侧面没有底面,根据圆柱的侧面积公式S=Ch,把数据代入公式解答即可。注意单位的转化。
【解答】解:40cm=0.4m
3.14×0.4×2.5
=3.14×1
=3.14(m2)
答:做一节烟囱一共需要铁皮3.14平方米。
【点评】本题考查了圆柱侧面积公式S=Ch的灵活运用。
52.一根圆柱形钢管,内直径是4厘米,外直径是8厘米,长是6米。如果每立方厘米钢材重7.8克,那么这根钢管大约重多少千克?(π值取3.14,结果保留整千克)
【答案】176千克。
【分析】这根钢管的底面积是一个环形,这个环形的面积=半径为(8÷2)的外圆的面积﹣半径为(4÷2)的内圆的面积,长6米即高600厘米,根据V=sh算出钢管的体积,再用体积乘钢管每立方厘米的重量就是钢管的总重量,算出答案化成千克即可。
【解答】解:内半径:4÷2=2(厘米)
外半径:8÷2=4(厘米)
6米=600厘米
钢管的底面积:3.14×42﹣3.14×22
=3.14×12
=37.68(平方厘米)
钢管的体积:37.68×600=22608(立方厘米)
钢管的重量:22608×7.8
=176342.4(克)
≈176(千克)
答:这根钢重176千克。
【点评】解答这道题的关键是知道钢管的底面积是一个环形,并且会求环形面积的方法。
53.一个圆柱形的粮囤,从里面量得底面半径是2m,高是2.5m,如果每立方米玉米重约0.8吨,这个粮囤能装多少吨玉米?
【答案】25.12吨。
【分析】根据圆柱体积公式:圆柱的体积=底面积×高,先求出圆柱的体积,再乘0.8即可。
【解答】解:3.14×22×2.5×0.8
=12.56×2
=25.12(吨)
答:这个粮囤能装25.12吨玉米。
【点评】熟练掌握圆柱的体积公式:圆柱体积=底面积×高,是解决此题的关键。
54.一个蔬菜大棚(如图),长20米,横截面是一个半径2米的半圆形,表面用单层塑料薄膜覆盖(包括两端横截面).
(1)这个大棚的种植面积是多少平方米?
(2)搭建这个大棚至少要用塑料薄膜多少平方米?
(3)大棚内的空间有多大?
【答案】见试题解答内容
【分析】(1)根据题干,这个大棚的种植面积就是这个长20米,宽2×2=4米的长方形的面积,根据长方形的面积公式即可解答;
(2)覆盖在这个大棚上的塑料薄膜的面积,即它所在的圆柱的侧面积的一半,加上一个圆柱的底面积;由此利用圆柱的侧面积和底面积公式即可解答;
(3)大棚所在的圆柱的体积的一半,就是这个大棚的空间,根据圆柱的体积公式解答即可.
【解答】解:(1)20×(2×2)=80(平方米),
答:这个大棚的种植面积是80平方米.
(2)3.14×2×2×20÷2+3.14×22,
=125.6+12.56,
=138.16(平方米),
答:覆盖在这个大棚上的塑料薄膜约有138.16平方米.
(3)3.14×22×20÷2,
=251.2÷2,
=125.6(立方米),
答:大棚的空间大约是125.6立方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
55.如图是一个铁皮做成的易拉罐。(单位:厘米)
(1)这个易拉罐的底面积是多少平方厘米?
(2)做一个这样的易拉罐,至少需要多少平方厘米的铁皮?
【答案】12.56平方厘米;175.84平方厘米。
【分析】(1)易拉罐的底面直径是4厘米,可求出半径,根据圆的面积公式:S=πr 可求出易拉罐的底面积;
(2)根据圆柱的表面积=侧面积+底面圆的面积×2=πdh+2πr ,列式解答即可。
【解答】解:(1)3.14×(4÷2)
=3.14×4
=12.56(平方厘米)
答:底面积是12.56平方厘米。
(2)3.14×4×12+12.56×2
=150.72+25.12
=175.84(平方厘米)
答:至少需要175.84平方厘米的铁皮。
【点评】熟练掌握圆柱侧面积和圆面积的求法是解题的关键。
21世纪教育网(www.21cnjy.com)
(
第一部分
思维导图
)
(
第二部分
典型例题
)
例题1:一管鞋油的出口直径是4mm.如果每天挤出20mm长的鞋油,这管鞋油可以用36天.该品牌鞋油推出新包装后.将出口直径改为了6mm,鞋油总量没变.如果按照每天挤出10mm长的鞋油计算,现在这管鞋油可以用多少天?
【答案】见试题解答内容
【分析】根据题意,运用圆柱的体积公式先求出原来每次挤出所用鞋油的体积数,再用每次用的体积数乘次数36,可得这种鞋油的总体积;然后求出鞋油推出新包装后每次挤出所用鞋油的体积数,进而用总体积数除以现在每次挤出用的体积数,问题得解.
【解答】解:4÷2=2(毫米)
3.14×22×20×36
=3.14×2880
=9043.2(立方毫米)
6÷2=3(毫米)
3.14×32×10=282.6(立方毫米)
9043.2÷282.6=32(天)
答:现在这管鞋油可以用32天.
【点评】解决此题关键是理解鞋油的总体积数不变,运用圆柱的体积公式:V=Sh解决问题.
例题2:某品牌牙膏出口处直径为0.6cm,明明每次刷牙都挤出1cm长的牙膏,这样的一支牙膏他可用48次.该品牌牙膏推出的新包装只是将出口处直径改为0.8cm,牙膏的总容量不变,明明还是按习惯每次挤出1cm长的牙膏,这样一支新包装的牙膏他能用多少次?
【答案】见试题解答内容
【分析】根据题意,利用圆柱的体积公式:V=Sh,先求牙膏的体积,然后根据体积不变,求新包装牙膏可以用多少次.
【解答】解:3.14×(0.6÷2)2×1×48÷[3.14×(0.8÷2)2×1]
=3.14×0.09×1×48÷[3.14×0.16×1]
=27(次)
答:这样一支新包装的牙膏他能用27次.
【点评】本题主要考查圆柱的应用,关键利用圆柱体积公式做题.
例题3:工人师傅正在修建一个圆形的蓄水池,王大爷每步长约60厘米,沿着池边走了一圈刚好是53步,这个蓄水池的直径大约是多少米?(得数保留整数)
【答案】见试题解答内容
【分析】根据题意,可用320乘0.5计算出这个圆的周长,然后再利用圆的周长公式进行解答即可.
【解答】解:60厘米=0.6米
53×0.6÷3.14
=31.8÷3.14
≈10(米)
答:这个蓄水池的直径大约是10米.
【点评】此题考查了圆的周长C=πd的计算应用.
例题4:一块圆柱形铝锭,底面积60cm2,高10cm,要把这块铝锭熔铸成高18cm的圆锥,熔铸后的铝锭底面积是多少?
【答案】见试题解答内容
【分析】根据熔铸后体积不变,进行解答:先根据“圆柱的体积=的面积×高”求出铝锭的体积,即圆锥的体积,继而根据“圆锥的底面积=圆锥的体积×3÷高”解答即可.
【解答】解:60×10×3÷18
=1800÷18
=100(平方厘米)
答:熔铸后的铝锭底面积是100平方厘米.
【点评】解答此题的关键是要明确体积不变,即圆柱形铝块的体积为后来熔铸成的圆锥的体积,然后根据圆锥体积和底面积及高的关系进行解答即可.
例题5:一个圆柱形水池,底面周长是31.4米,水面离池口50米,再注入多少立方米的水可注满水池?
【答案】3925立方米。
【分析】圆的周长公式:C=2πr,把数据代入公式求出圆的半径,然后再根据圆柱的容积(体积)公式:V=πr2h,把数据代入公式解答。
【解答】解:31.4÷3.14÷2=5(米)
3.14×52×50
=3.14×1250
=3925(立方米)
答:再注入3925立方米的水可将池灌满。
【点评】此题主要考查圆柱的容积(体积)公式在实际生活中的应用,关键是熟记公式。
(
第三部分
知识精讲
)
(
知识清单+方法技巧
) 1.圆柱的特征 【知识点归纳】 圆柱就是由两个大小相同的圆和一个侧面组成的.它的底面是完全相同的两个圆,侧面是一个曲面. 2.圆柱的展开图 【知识点归纳】 圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,宽等于圆柱的高. 3.圆柱的侧面积和表面积 【知识点归纳】 圆柱的表面积=侧面积+2个底面积 侧面积=底面周长×高。圆柱的侧面展开是一个长方形,其长就是圆柱底面周长,长方形的宽就是圆柱的高,所以圆柱的侧面积=底面周长×高,圆柱的表面共有一个侧面和上下两个底面,所以表面积=侧面积+2个底面积 4.长方体和正方体的体积 【知识点归纳】 长方体体积公式:V=abh.(a表示底面的长,b表示底面的宽,h表示高) 正方体体积公式:V=a3.(a表示棱长) 5.圆柱的侧面积、表面积和体积 【知识点归纳】 圆柱的侧面积=底面的周长×高,用字母表示: S侧=Ch(C表示底面的周长,h表示圆柱的高),或S侧=2πrh 圆柱的底面积=πr2 圆柱的表面积=侧面积+两个底面积,用字母表示: S表=2πr2+2πrh 圆柱的体积=底面积×高,用字母表示: V=πr2h.
(
第四部分
高频真题
)
1.修建一个圆柱形的蓄水池,底面直径是20米,深2.5米,在池子的内壁和下底面抹上水泥,抹水泥的面积是多少平方米?
2.一种电热水炉的水龙头内直径是1厘米,打开水龙头后水的流速是40厘米/秒。一个容积为1.5升的保温壶,1分钟能装满水吗?
3.一个圆柱形蓄水池深4米,平均每天用水8吨,7天后水池的水减少了20%(每立方米的水重1吨),这个水池的占地面积是多少?
4.如图,是用塑料薄膜覆盖的蔬菜大棚,长16米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
5.王老师要做一个无盖的长方体玻璃鱼缸,要求每个顶点连接的三条棱长分别是5分米、4分米、3分米,请你帮王老师设计一下怎样才节省材料(画图表示并计算一下至少要用玻璃多少平方分米?)
6.有一个花坛,高0.5米,底面是边长2.3米的正方形.四周用砖砌成,厚度是0.3米,中间填满泥土,花坛里大约有多少立方米泥土?
7.一个圆柱形油漆桶,从里面量底面周长是18.84分米,高是6分米,如果每升油漆重1.5千克,这个油漆桶可装油漆多少千克?
8.会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?
9.大厅里有6根圆柱,每根柱子的底面半径是4分米,高5米,如果每平方米需要油漆费5元,漆这6根柱子,一共需用油漆费多少元?
10.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆(如图)
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?(记得要算上两边的半圆哦)
(2)大棚内有空间约有多大?
11.只列综合算式或方程,不计算。
一个装满稻谷的圆柱形粮囤,底面半径是2米,高是0.8米。每立方米稻谷的质量约为700千克,这个粮囤存放的稻谷的质量约为多少千克?(π取3.14)
12.一个圆柱形蓄水池的底面直径是14米,深4米,如果在池壁和底面贴瓷砖,贴瓷砖的面积是少平方米?这个蓄水池能蓄水多少立方米?
13.一种长方体的通风管道,每根长5米,横截面是正方形,边长是60厘米.做20根这样的通风管道要用铁皮多少平方米?
14.一个圆柱形蓄水池底面内直径为2m,深2m。
(1)这个蓄水池的占地面积是几平方米?
(2)在池的内壁与底面抹上水泥,抹水泥部分的面积是多少平方米?
(3)蓄水池的容积是几立方米?
15.做一对无盖的圆柱形铁皮水桶,高12厘米,底面直径20厘米,用铁皮多少平方厘米?
16.一个用塑料薄膜覆盖的蔬菜大棚,长10米,横截面是半径为2米的半圆形,覆盖在这个大棚至少需要塑料薄膜多少平方米?
17.一段圆柱形实心钢材长100cm,横截面半径是5cm.每立方厘米钢重7.8g,这段钢材重多少千克?
18.某市对科技馆一楼大厅的5根圆柱重新修饰,每根柱子高10m,底面周长为18.84dm。现全部涂上油漆,如果按每平方米油漆费为20元计算,需要花多少元?
19.油桶的外表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克.漆一个油桶大约需要多少千克防锈油漆?(得数保留一位小数)
20.把一根2米长的圆柱体钢材从中间截成两段后,表面积增加了0.6平方分米,如果每立方分米钢材重7.8千克,这根钢材重多少千克?
21.一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,每分前轮钟转12周。每分钟前轮滚多远?
22.在喀斯喀特山脉南段的火山口湖中,有一根神奇的木头,垂直水中漂浮了超过120年,这根木头被称为“湖中老人”。据测量,这根“湖中老人”长度大约有9米,直径约60厘米,请你计算一下这根圆木的体积合多少立方米(圆木看为近似圆柱,不考虑其他等情况,得数保留两位小数)
23.祈年殿中央有4根同样大小的圆柱形“龙井柱”,“龙井柱”的高是19.2m,底面直径是1.2m。如果把每根“龙井柱”的表面刷一层油漆,平均每平方米用油漆0.8kg,共需油漆多少千克?(得数保留一位小数)
24.一个圆柱形的蓄水池,底面直径是8米,深5米。如果在水池的底面和内壁抹上水泥,抹水泥的面积是多少平方米?
25.由于近年来干旱少雨,小明家修建一口圆柱形水窖,底面直径是4m,窖深3m.
(1)在它的底面和内壁都抹上水泥,抹水泥部分的面积是多少?
(2)如果按水窖容量的储存水,水窖中的水约有多少立方米?(得数保留整数)
26.某酒店门口的三翼旋转门,门内每扇长方形玻璃门高2.5米,宽2米。
(1)制作这样的3扇玻璃门一共需要多少平方米的玻璃?
(2)这个旋转门内的空间大约有多少立方米?(可以用含有π的式子表示)
27.一节圆柱形铁皮烟囱的底面周长为25.12分米,长为2.5米,做6节这样的烟囱需要多少平方米的铁皮?
28.一根圆柱形水管,内直径是20厘米,水流的速度是4米/秒,这根水管1分钟能流过多少立方米的水?
29.在一只底面半径是10cm,高是20cm的圆柱形容器中,水深8cm,要在容器中放入长和宽都是8cm,高是15cm的一块铁块,把铁块竖放在水中,使底面与容器底面接触,这时水深是多少厘米?
30.一个圆柱形蓄水池,底面周长是25.12米,高5米,沿着这个蓄水池的四周及底部抹水泥,如果每平方米用水泥20千克,一共需要多少千克的水泥?
31.如图,一块蜂窝煤的底面直径是12厘米,高是8厘米.其中有12个相同的孔,每个孔的直径是2厘米.做15块这样的蜂窝煤共需用煤多少立方厘米?(π取3.14)
32.一台压路机的滚筒是圆柱形,滚筒的宽是2m,横截面半径是0.5m,滚筒滚动一周,压过的路面是多少平方米?
33.一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路的面积是多少平方米?
34.王师傅用铁皮做了一个无盖的圆柱形水桶,底面直径是10dm,高是底面直径的。做这个水桶至少需要铁皮多少平方分米?这个水桶最多能装水多少升?
35.小丽买了一个水杯,水杯中间贴了一圈装饰带(见如图),这条装饰带宽4厘米,装饰带展开后面积是多少?这个水杯的体积是多少?(单位:厘米,π值取3.14)
36.如图是小东妈妈的茶杯。
(1)这只茶杯最多能装多少升的水?(茶杯厚度不计)
(2)茶杯中部贴有一圈防烫装饰带,这圈防烫装饰带贴在茶杯上的面积是多少平方厘米?
37.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去洗手,走时忘记关掉水龙头,10分钟浪费多少升水?
38.一节用铁皮卷成的圆柱形烟囱长3米,管口直径是40厘米,做这个烟囱至少需要铁皮多少平方米?
39.一种压路机的前轮是圆柱形,轮宽1.6米,底面半径0.5米,该前轮转动一周可以压路的面积是多少平方米?
40.一个压路机的前轮是圆柱体,它的直径是1.5米,轮宽2米,前轮向前滚动200周,压过的路面是多少平方米?
41.用铁皮制作一担圆柱形水桶(无盖),底面直径为6dm,高是8dm.
(1)做这担水桶需铁皮多少dm2?
(2)这担水桶可盛水多少L?
42.修建一个圆柱形的沼气池,底面直径是2米,深2米。在沼气池的内壁与下底面抹上水泥,抹水泥的面积是多少平方米?
43.把一根长4m的圆柱形钢材沿垂直于高的面截成相等的两段以后,表面积增加了6.28m2,如果每立方米钢材重7800kg.(1)原来这根钢材的表面积是多少?
(2)这根钢材重多少千克?
44.为了抗旱,小平家挖了一个底面半径5m、深2m的圆柱形蓄水池,并且用水泥涂抹水池的内壁与底部,防止漏水.一场暴雨过后,小平沿水池边缘走了一圈,并测得池中水深1.2m.
(1)涂抹水泥的面积是多少平方米?
(2)池中水的体积是多少?
45.一种易燃易爆化工原料铁桶,它的底面直径6分米,高14分米.为了搬运安全,需要在桶上安装两个橡胶护圈(如图).至少需要橡胶带多少分米?
46.春节期间,为了增添节日气氛。体育文化广场增添了1根大花柱,花柱高3.5米,底面半径0.5米,花柱的侧面和上面都插满鲜花,如果每平方米装饰40朵花,这根花柱一共需要多少朵花?
47.在一个数学实验活动中.先往一个长方体的容器中注水,水深4.4厘米(如图);然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有冰柱浸没在水里,如图.
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
48.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆。
(1)这个蔬菜大棚的占地面积是多少平方米?
(2)覆盖住这个大棚的塑料薄膜大约有多少平方米?
(3)大棚内的空间大约有多少立方米?
49.某苗圃基地计划建一个圆柱形无盖蓄水池,从外面量得底面直径3.6米,高2米,底的厚度与壁的厚度都是0.3米。这个蓄水池的容积是多少立方米?(得数保留整数)
50.小虹用布制作一顶帽子.上面是圆柱形,底面直径16cm,高15cm;帽檐部分是一个圆环,外圆直径40cm.制作这顶帽子,至少要用多少平方厘米的布?
51.工厂要生产一节烟囱,烟囱长2.5m,横截面是直径为40cm的圆。做一节烟囱一共需要铁皮多少平方米?(接头处忽略不计)
52.一根圆柱形钢管,内直径是4厘米,外直径是8厘米,长是6米。如果每立方厘米钢材重7.8克,那么这根钢管大约重多少千克?(π值取3.14,结果保留整千克)
53.一个圆柱形的粮囤,从里面量得底面半径是2m,高是2.5m,如果每立方米玉米重约0.8吨,这个粮囤能装多少吨玉米?
54.一个蔬菜大棚(如图),长20米,横截面是一个半径2米的半圆形,表面用单层塑料薄膜覆盖(包括两端横截面).
(1)这个大棚的种植面积是多少平方米?
(2)搭建这个大棚至少要用塑料薄膜多少平方米?
(3)大棚内的空间有多大?
55.如图是一个铁皮做成的易拉罐。(单位:厘米)
(1)这个易拉罐的底面积是多少平方厘米?
(2)做一个这样的易拉罐,至少需要多少平方厘米的铁皮?
参考答案与试题解析
1.修建一个圆柱形的蓄水池,底面直径是20米,深2.5米,在池子的内壁和下底面抹上水泥,抹水泥的面积是多少平方米?
【答案】471平方米。
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,已知在池子的四壁和下底面抹上水泥,把数据代入公式解答。
【解答】解:3.14×20×2.5+3.14×(20÷2)2
=157+3.14×100
=157+314
=471(平方米)
答:抹水泥的面积是471平方米。
【点评】此题主要考查圆柱的表面积公式在实际生活中的应用,关键是熟记公式。
2.一种电热水炉的水龙头内直径是1厘米,打开水龙头后水的流速是40厘米/秒。一个容积为1.5升的保温壶,1分钟能装满水吗?
【答案】能。
【分析】首先根据圆柱的容积(体积)公式:V=Sh,把数据代入公式求出1秒流出水的体积,再根据除法的意义求出1.5升里有多少个1秒流出水的体积即可。
【解答】解:1升=1000立方厘米
1.5升=1500立方厘米
3.14×(1÷2)2×40
=3.14×0.25×40
=31.4(立方厘米)
1500÷31.4≈47.77(秒)
1分钟=60秒
47.77秒<1分钟
答:1分钟能装满水。
【点评】此题主要考查圆柱的容积(体积)公式在实际生活中的应用。
3.一个圆柱形蓄水池深4米,平均每天用水8吨,7天后水池的水减少了20%(每立方米的水重1吨),这个水池的占地面积是多少?
【答案】见试题解答内容
【分析】先根据总用水量=平均每天用水量×天数求出7天的总用水量,再除以1求出水的体积,再根据百分数乘法的意义求出水池减少的水的高度,再根据圆柱体积变形公式S=V÷h可求这个水池的占地面积.
【解答】解:8×7÷1÷(4×20%)
=56÷1÷0.8
=56÷0.8
=70(平方米)
答:这个水池的占地面积是70平方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
4.如图,是用塑料薄膜覆盖的蔬菜大棚,长16米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
【答案】见试题解答内容
【分析】(1)根据题干,这个大棚的种植面积就是这个长15米,宽2米的长方形的面积,根据长方形的面积公式即可解答;
(2)覆盖在这个大棚上的塑料薄膜的面积,即它所在的圆柱的侧面积的一半,加上一个圆柱的底面积;由此利用圆柱的侧面积和底面积公式即可解答.
【解答】解:(1)16×2=32(平方米)
答:这个大棚的种植面积是32平方米.
(2)3.14×2×16÷2+3.14×(2÷2)2
=50.24+3.14
=53.38(平方米)
答:覆盖在这个大棚上的塑料薄膜约有53.38平方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
5.王老师要做一个无盖的长方体玻璃鱼缸,要求每个顶点连接的三条棱长分别是5分米、4分米、3分米,请你帮王老师设计一下怎样才节省材料(画图表示并计算一下至少要用玻璃多少平方分米?)
【答案】见试题解答内容
【分析】求这个鱼缸用的玻璃的面积就是求5个面的面积,缺少上面(最大长为5分米,宽为4分米),根据长方体表面积的计算方法求解.
【解答】解:如图:
5×4+4×3×2+5×3×2
=20+24+30
=74(平方分米);
答:制作这个鱼缸至少用玻璃74平方分米.
【点评】此题考查长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可.
6.有一个花坛,高0.5米,底面是边长2.3米的正方形.四周用砖砌成,厚度是0.3米,中间填满泥土,花坛里大约有多少立方米泥土?
【答案】见试题解答内容
【分析】求花坛里大约有多少立方米的泥土,就是求它的容积,关键是理解四周用砖砌成,厚度是0.3米,也就是花坛里面的边长是(2.3﹣0.3×2)米,再利用长方体的体积(容积)公式解答.
【解答】解:求花坛的容积:
(2.3﹣0.3×2)×(2.3﹣0.3×2)×0.5
=1.7×1.7×0.5
=1.445(立方米);
答:花坛里大约有1.445立方米的泥土.
【点评】此题主要考查长方体体积(容积)的计算,解答关键是理解花坛里的正方形的边长要减去两个0.3米,根据公式解答即可.
7.一个圆柱形油漆桶,从里面量底面周长是18.84分米,高是6分米,如果每升油漆重1.5千克,这个油漆桶可装油漆多少千克?
【答案】254.34千克。
【分析】先根据油桶的底面周长依次求出底面半径和底面积,再根据圆柱体体积=底面积×高求出油桶的容积,最后用汽油的比重乘以容积即可。
【解答】解:1.5×[3.14×(18.84÷2÷3.14)2×6]
=1.5×[3.14×9×6]
=1.5×169.56
=254.34(千克)
答:这个油桶可装汽油254.34千克。
【点评】此题主要考查的是圆柱的体积公式的灵活应用,解答此题的关键是求出底面半径和面积。
8.会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?
【答案】见试题解答内容
【分析】由于是在圆柱形柱子上刷油漆,也就是要刷它的侧面积,所以要求刷这些柱子用油漆多少千克,就要先求10根柱子的侧面积是多少,再乘0.5即可.
【解答】解:3.14×0.6×6×10×0.5,
=3.14×36×0.5,
=56.52(千克);
答:刷这些柱子要用油漆56.52千克.
【点评】解答此题要注意刷油漆的部分是侧面积,不是圆柱的表面积.
9.大厅里有6根圆柱,每根柱子的底面半径是4分米,高5米,如果每平方米需要油漆费5元,漆这6根柱子,一共需用油漆费多少元?
【答案】376.8元。
【分析】给圆柱子涂油漆,只能涂侧面积,知道柱子的底面半径和高,2πrh可得一个柱子的侧面积,乘6求得涂油漆的总面积,总面积乘单位面积需要的钱数,则可得一共需要的钱数。
【解答】解:4分米=0.4米
3.14×0.4×2×5×6
=3.14×(0.4×2×5×6)
=3.14×24
=75.36(平方米)
5×75.36=376.8(元)
答:一共需用油漆费376.8元。
【点评】此题只需求圆柱的侧面积,根据已知运用公式求出,进而求总面积,最后求出需用的钱数,细心计算即可。
10.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆(如图)
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?(记得要算上两边的半圆哦)
(2)大棚内有空间约有多大?
【答案】见试题解答内容
【分析】这个蔬菜大棚的形状是底面是半圆的半个圆柱体.
(1)求搭建这个蔬菜大棚大约要用多少平方米的塑料薄膜,就是求圆柱表面积的一半;
(2)求大棚内的空间大约有多大,就是求圆柱体积的一半.由此根据圆柱的表面积及体积公式,即可列式解答.
【解答】解:(1)[2×2×3.14×20+3.14×22×2]÷2
=[251.2+25.12]÷2
=276.32÷2
=138.16(平方米);
答:搭建这个大棚大约要用138平方米的塑料薄膜.
(2)3.14×22×20÷2
=251.2÷2
=125.6(立方米);
答:大棚内的空间大约是126立方米.
【点评】此题主要利用圆柱的表面积和体积的公式解决问题,关键是理解大棚的形状半个圆柱.
11.只列综合算式或方程,不计算。
一个装满稻谷的圆柱形粮囤,底面半径是2米,高是0.8米。每立方米稻谷的质量约为700千克,这个粮囤存放的稻谷的质量约为多少千克?(π取3.14)
【答案】7033.6千克。
【分析】圆柱的体积公式:V=πr2h,据此代入数据求出圆柱的体积,再用圆柱的体积乘700即可求出这个粮囤可存放的稻谷质量。
【解答】解:3.14×22×0.8
=3.14×4×0.8
=12.56×0.8
=10.048(立方米)
10.048×700=7033.6(千克)
答:这个粮囤存放的稻谷的质量约为7033.6千克。
【点评】本题考查的是圆柱体积计算公式的运用。
12.一个圆柱形蓄水池的底面直径是14米,深4米,如果在池壁和底面贴瓷砖,贴瓷砖的面积是少平方米?这个蓄水池能蓄水多少立方米?
【答案】329.7平方米,615.44立方米。
【分析】贴瓷砖的面积是求圆柱的侧面积与一个底面积的和,运用圆柱的侧面积公式及圆的面积公式列式解答即可。这个蓄水池可装水多少立方米,是求圆柱形水池的容积,即求圆柱的体积,运用圆柱的体积计算公式,代入数据解决问题。
【解答】解:3.14×14×4+3.14×(14÷2)2
=175.84+3.14×49
=175.84+153.86
=329.7(平方米)
3.14×(14÷2)2×4
=3.14×49×4
=615.44(立方米)
答:贴瓷砖的面积是329.7平方米;这个蓄水池可装水615.44立方米。
【点评】此题主要考查圆柱的侧面积以及体积计算公式的运用。
13.一种长方体的通风管道,每根长5米,横截面是正方形,边长是60厘米.做20根这样的通风管道要用铁皮多少平方米?
【答案】见试题解答内容
【分析】由题意可知,通风管是没有底面的,所以只求它的4个侧面的面积,根据长方体的表面积的计算方法,先求出1根通风管需要材料,然后乘20即可.
【解答】解:60厘米=0.6米
0.6×4×5×20
=0.6×20×20
=240(平方米)
答:做20根这样的通风管道要用铁皮240平方米.
【点评】此题属于长方体的表面积的实际应用,解答关键是搞清求的是哪几个面的面积,再根据长方体的表面积的计算方法进行解答.
14.一个圆柱形蓄水池底面内直径为2m,深2m。
(1)这个蓄水池的占地面积是几平方米?
(2)在池的内壁与底面抹上水泥,抹水泥部分的面积是多少平方米?
(3)蓄水池的容积是几立方米?
【答案】(1)3.14平方米;(2)15.7平方米;(3)6.28立方米。
【分析】(1)根据圆面积计算公式等于π乘底面圆半径的平方计算即可;
(2)抹水泥部分的面积是蓄水池的侧面积加上底面积,侧面积=底面周长×高,底面直径和高已知,代入公式即可求解;
(3)利用圆柱的体积V=Sh,即可求出蓄水池的容积。
【解答】解:(1)3.14×(2÷2)2
=3.14×1
=3.14(平方米)
答:这个蓄水池的占地面积是3.14平方米。
(2)3.14×2×2+3.14
=12.56+3.14
=15.7(平方米)
答:抹水泥部分的面积是15.7平方米。
(3)3.14×2
=3.14×2
=6.28(立方米)
答:蓄水池的容积是6.28立方米。
【点评】此题主要考查圆柱的侧面积和体积的计算方法,关键是明白:抹水泥部分的面积是蓄水池的侧面积加上底面积。
15.做一对无盖的圆柱形铁皮水桶,高12厘米,底面直径20厘米,用铁皮多少平方厘米?
【答案】见试题解答内容
【分析】一个水桶需要的铁皮的面积=水桶的侧面积+底面积,利用圆柱的侧面积和圆的面积公式即可得解,得数再乘2即可.
【解答】解:3.14×20×12+3.14×(20÷2)2
=753.6+314
=1067.6(平方厘米)
1067.6×2=2135.2(平方厘米)
答:用铁皮2135.2平方厘米.
【点评】此题主要考查圆柱的侧面积和圆的面积的计算方法,要记住求的是一对水桶需要的铁皮的面积.
16.一个用塑料薄膜覆盖的蔬菜大棚,长10米,横截面是半径为2米的半圆形,覆盖在这个大棚至少需要塑料薄膜多少平方米?
【答案】见试题解答内容
【分析】这个大棚的形状是底面是半圆的半个圆柱体,求搭建这个大棚大约要用多少平方米的塑料薄膜,就是求圆柱表面积的一半;由此根据圆柱的表面积=侧面积+两个底面积,即可列式解答.
【解答】解:[(2×2×3.14)×10+3.14×22×2]÷2
=[125.6+12.56×2]÷2
=[125.6+25.12]÷2
=150.72÷2
=75.36(平方米)
答:覆盖在这个大棚至少需要塑料薄膜75.36平方米.
【点评】此题主要利用圆柱的表面积和体积的公式解决问题,关键是理解大棚的形状半个圆柱.
17.一段圆柱形实心钢材长100cm,横截面半径是5cm.每立方厘米钢重7.8g,这段钢材重多少千克?
【答案】见试题解答内容
【分析】先利用圆柱的体积公式V=πr2h求出它的体积,然后再乘上7.8,求出这段钢材重多少克,再化成千克即可.
【解答】解:3.14×52×100×7.8
=3.14×25×100×7.8
=7850×7.8
=61230(克)
61230克=61.23千克
答:这段钢材重61.23千克.
【点评】此题是考查圆柱的体积计算,利用公式V=πr2h求出体积,然后再进一步解答.注意统一单位.
18.某市对科技馆一楼大厅的5根圆柱重新修饰,每根柱子高10m,底面周长为18.84dm。现全部涂上油漆,如果按每平方米油漆费为20元计算,需要花多少元?
【答案】1884元。
【分析】根据题干可知,每根柱子需要涂漆的只是柱子的侧面,由此利用圆柱的侧面积公式S侧=Ch计算出每个柱子的侧面积,再乘5就是涂漆的总面积,再依条件求出油漆费即可。
【解答】解:18.84dm=1.884m
1.884×10×5×20
=1.884×1000
=1884(元)
答:需要花1884元。
【点评】此题主要考查圆柱表面积的实际应用,解答关键是要弄清涂漆面积,再依条件解决问题即可。
19.油桶的外表面要刷上防锈油漆,每平方米需用防锈油漆0.2千克.漆一个油桶大约需要多少千克防锈油漆?(得数保留一位小数)
【答案】见试题解答内容
【分析】要求漆一个油桶大约需要多少防锈漆,应先求得油桶的表面积,表面积是两个底面与侧面积的和,由圆柱体侧面积和圆的面积计算方法求出,最后乘每平方米所用油漆的质量,得出答案.
【解答】解:油桶的侧面积:
3.14×0.6×1=1.884(平方米)
油桶的两个底面的面积:
3.14×(0.6÷2)2×2
=3.14×0.32×2
=3.14×0.09×2
=0.5652(平方米);
油桶的表面积:
1.884+0.5652=2.4492(平方米)
大约需要防锈漆:
0.2×2.4492≈0.5(千克)
答:漆一个油桶大约需要0.5千克防锈漆.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
20.把一根2米长的圆柱体钢材从中间截成两段后,表面积增加了0.6平方分米,如果每立方分米钢材重7.8千克,这根钢材重多少千克?
【答案】这根钢材重46.8千克。
【分析】0.6平方分米是圆柱形钢材的两个底面的面积,由此根据圆柱的体积公式:V=sh,求出圆柱形钢材的体积,再用体积乘7.8千克就是钢材的质量。
【解答】解:2米=20分米,
(0.6÷2)×20×7.8
=0.3×20×7.8
=6×7.8
=46.8(千克)
答:这根钢材重46.8千克。
【点评】关键是知道0.6平方分米是哪部分的面积,再利用相应的公式解决问题。
21.一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,每分前轮钟转12周。每分钟前轮滚多远?
【答案】30.144米。
【分析】根据圆的周长公式C=πd,把数据代入公式求出前轮滚动一周可前进多少米,然后再乘12即可。
【解答】解:3.14×0.8×12
=2.512×12
=30.144(米)
答:每分钟前轮滚30.144米。
【点评】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式。
22.在喀斯喀特山脉南段的火山口湖中,有一根神奇的木头,垂直水中漂浮了超过120年,这根木头被称为“湖中老人”。据测量,这根“湖中老人”长度大约有9米,直径约60厘米,请你计算一下这根圆木的体积合多少立方米(圆木看为近似圆柱,不考虑其他等情况,得数保留两位小数)
【答案】2.54立方米。
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:60厘米=0.6米
3.14×(0.6÷2)2×9
=3.14×0.09×9
=2.5434(立方米)
≈2.54(立方米)
答:这根圆木的体积合2.54立方米。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
23.祈年殿中央有4根同样大小的圆柱形“龙井柱”,“龙井柱”的高是19.2m,底面直径是1.2m。如果把每根“龙井柱”的表面刷一层油漆,平均每平方米用油漆0.8kg,共需油漆多少千克?(得数保留一位小数)
【答案】231.5千克。
【分析】圆柱的侧面积=底面周长×高,求出一根“龙井柱”的侧面积,再用乘法求出4根同样大小的圆柱形“龙井柱”,把每根“龙井柱”的表面刷一层油漆,平均每平方米用油漆0.8kg,共需油漆多少千克。
【解答】解:3.14×1.2×19.2×4×0.8
=3.768×19.2×4×0.8
=72.3456×4×0.8
=289.3824×0.8
≈231.5(千克)
答:共需油漆231.5千克。
【点评】本题解答的关键是计算圆柱体的侧面积。
24.一个圆柱形的蓄水池,底面直径是8米,深5米。如果在水池的底面和内壁抹上水泥,抹水泥的面积是多少平方米?
【答案】175.84平方米。
【分析】求水池的底面和四周抹上水泥的面积,即抹水泥的部分的面积=侧面积+一个底的面积,根据圆柱的表面积公式S=2πr +Ch解答即可。
【解答】解:3.14×(8÷2) +3.14×8×5
=3.14×16+3.14×8×5
=50.24+125.6
=175.84(平方米)
答:抹水泥的面积是175.84平方米。
【点评】本题考查学生对圆柱表面积公式的掌握和运用。
25.由于近年来干旱少雨,小明家修建一口圆柱形水窖,底面直径是4m,窖深3m.
(1)在它的底面和内壁都抹上水泥,抹水泥部分的面积是多少?
(2)如果按水窖容量的储存水,水窖中的水约有多少立方米?(得数保留整数)
【答案】见试题解答内容
【分析】(1)由题意可知:抹水泥部分的面积=圆柱形水窖的侧面积+下底的面积,又因圆柱的侧面积=底面周长×高,圆锥的底面直径已知,于是可以求出其底面周长和底面积,进而可以求出抹水泥部分的面积;
(2)利用圆柱的体积公式v=πr2h即可求出这个圆柱形水窖最多能装多少水,然后乘上即可.
【解答】解:(1)3.14×4×2+3.14×(4÷2)2
=12.56×2+3.14×4
=12.56+12.56
=25.12(平方米)
答:抹水泥部分的面积是25.12平方米.
(2)3.14×(4÷2)2×3
=3.14×4×3
≈30(立方米)
答:水窖中的水约有30立方米.
【点评】此题主要考查圆柱的侧面积和圆的面积及体积的计算方法.
26.某酒店门口的三翼旋转门,门内每扇长方形玻璃门高2.5米,宽2米。
(1)制作这样的3扇玻璃门一共需要多少平方米的玻璃?
(2)这个旋转门内的空间大约有多少立方米?(可以用含有π的式子表示)
【答案】(1)15平方米;
(2)10π立方米。
【分析】(1)根据长方形的面积公式:S=ab,将数据代入,即可得出答案;
(2)旋转门内的空间等同于半径为为2米,高为2.5米的圆柱的体积,根据圆柱的体积公式:V=Sh=πr h,将数据代入即可得出答案。
【解答】解:(1)2.5×2×3
=5×3
=15(平方米)
答:一共需要15平方米的玻璃。
(2)π×2 ×2.5
=π×4×2.5
=10π(立方米)
答:这个旋转门内的空间大约有10π立方米。
【点评】本题考查学生对长方形面积公式和圆柱体积公式的掌握和运用。
27.一节圆柱形铁皮烟囱的底面周长为25.12分米,长为2.5米,做6节这样的烟囱需要多少平方米的铁皮?
【答案】37.68平方米。
【分析】根据圆柱的侧面积公式:S=Ch,求出一节圆柱形铁皮烟囱的面积,再乘6即可求出做6节这样的烟囱需要多少平方米的铁皮。
【解答】解:25.12分米=2.512米
2.512×2.5×6
=6.28×6
=37.68(平方米)
答:做6节这样的烟囱需要37.68平方米的铁皮。
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
28.一根圆柱形水管,内直径是20厘米,水流的速度是4米/秒,这根水管1分钟能流过多少立方米的水?
【答案】7.536立方米。
【分析】水在自来水管内的形状是圆柱形,可利用V=Sh先求出每秒流水的体积,再求1分钟可流水多少立方米即可。
【解答】解:20厘米=0.2米,1分=60秒
3.14×(0.2÷2)2×4×60
=3.14×0.01×240
=7.536(立方米)
答:这根水管1分钟能流过7.536立方米的水。
【点评】此题是利用圆柱的体积公式解决实际问题,要注意统一单位。
29.在一只底面半径是10cm,高是20cm的圆柱形容器中,水深8cm,要在容器中放入长和宽都是8cm,高是15cm的一块铁块,把铁块竖放在水中,使底面与容器底面接触,这时水深是多少厘米?
【答案】见试题解答内容
【分析】放入铁块前后的水的体积不变,根据水深8厘米,可以先求得水的体积,那么放入铁块后,容器的底面积变小了,也就是圆柱的底面积减去长方体的底面积,由此可以求得此时水的深度.
【解答】解:3.14×102×8÷(3.14×102﹣8×8)
=3.14×100×8÷(314﹣64)
=2512÷250
=10.048(厘米),
答:这时水深10.048厘米.
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式,重点是求出把铁块竖放在水中圆柱容器的底面积.
30.一个圆柱形蓄水池,底面周长是25.12米,高5米,沿着这个蓄水池的四周及底部抹水泥,如果每平方米用水泥20千克,一共需要多少千克的水泥?
【答案】3516.8千克
【分析】由于蓄水池是无盖,所以抹水泥的面积数这个圆柱的一个底面加上侧面积,圆柱的侧面积=底面周长×高,再根据圆的面积公式,把数据代入公式求出抹水泥的面积,进而求出每平方米用水泥的质量。
【解答】解:25.12×5+3.14×(25.12÷3.14÷2)2
=125.6+3.14×16
=125.6+50.24
=175.84(平方米)
20×175.84=3516.8(千克)
答:一共需要3516.8千克水泥。
【点评】此题主要考查圆柱的表面积公式、体积公式在实际生活中的应用。
31.如图,一块蜂窝煤的底面直径是12厘米,高是8厘米.其中有12个相同的孔,每个孔的直径是2厘米.做15块这样的蜂窝煤共需用煤多少立方厘米?(π取3.14)
【答案】见试题解答内容
【分析】求一块蜂窝煤的用煤量,就用这块蜂窝煤的总体积减去16个圆柱形小孔的体积;由此根据圆柱的体积公式V=sh=π(d÷2)2h分别求出蜂窝煤的体积和圆孔的体积,再用蜂窝煤的总体积减去16个圆孔的体积即可.
【解答】解:煤球的体积:3.14×(12÷2)2×8
=3.14×36×8
=113.04×8
=904.32(立方厘米);
煤球的12个圆柱形孔的体积是:
3.14×(2÷2)2×8×12
=3.14×8×12
=25.12×12
=301.44(立方厘米);
煤球的体积是:
904.32﹣301.44=602.88(立方厘米)
做15块这样的蜂窝煤需要:
602.88×15=9043.2(立方厘米)
答:做15块蜂窝煤需要用煤9043.2立方厘米.
【点评】本题主要是灵活利用圆柱的体积V=Sh=π(d÷2)2h解决生活中的实际问题.
32.一台压路机的滚筒是圆柱形,滚筒的宽是2m,横截面半径是0.5m,滚筒滚动一周,压过的路面是多少平方米?
【答案】6.28平方米。
【分析】滚筒滚动一周,压过的路面面积就是滚筒的侧面积。利用圆柱的侧面积=圆柱的底面周长×高,即可求得压过的路面面积。据此解答。
【解答】解:3.14×0.5×2×2
=3.14×1×2
=6.28(平方米)
答:压过的路面是6.28平方米。
【点评】本题考查了圆柱侧面积在生活中的应用。掌握圆柱的侧面积计算方法是解答的关键。
33.一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路的面积是多少平方米?
【答案】7.536平方米。
【分析】由题意可知,路机的前轮是圆柱形,轮宽2米,也就是圆柱的高,直径1.2米,求前轮转动一周,压路的面积是多少,计算求圆柱的侧面积,圆柱的侧面积=底面周长×高,由此解答。
【解答】解:3.14×1.2×2
=3.768×2
=7.536(平方米)
答:压路的面积是7.536平方米。
【点评】此题属于圆柱的表面积的实际应用,解答此题主要分清所求物体的形状,求压路面积是求圆柱的侧面积,根据圆柱的侧面积公式解答即可。
34.王师傅用铁皮做了一个无盖的圆柱形水桶,底面直径是10dm,高是底面直径的。做这个水桶至少需要铁皮多少平方分米?这个水桶最多能装水多少升?
【答案】329.7平方分米,628升。
【分析】首先分清制作没有盖的圆柱形铁皮水桶,需要计算几个面的面积:即侧面面积与底面圆的面积,根据圆柱体侧面积和圆的面积计算方法即可求出需要多少平方分米的铁皮;再根据圆柱体积(容积)公式V=sh,列式解答即可求出这个水桶的容积。
【解答】解:高:108(dm)
3.14×(10÷2)2+3.14×10×8
=78.5+251.2
=329.7(平方分米)
3.14×(10÷2)2×8
=3.14×25×8
=3.14×200
=628(立方分米)
628立方分米=628升
答:做这个水桶至少需要铁皮329.7平方分米,这个水桶最多能装水628升。
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
35.小丽买了一个水杯,水杯中间贴了一圈装饰带(见如图),这条装饰带宽4厘米,装饰带展开后面积是多少?这个水杯的体积是多少?(单位:厘米,π值取3.14)
【答案】75.36平方厘米,339.12立方厘米。
【分析】装饰带展开后是一个长方形,长方形的长为圆柱的底面周长,宽为4厘米,再根据长方形的面积公式S=ab进行解答;根据圆柱的体积公式V=πr2h,代入数据进行解答。
【解答】解:3.14×6×4
=18.84×4
=75.36(平方厘米)
3.14×(6÷2)2×12
=3.14×9×12
=28.26×12
=339.12(立方厘米)
答:装饰带展开后面积是75.36平方厘米,这个水杯的体积是339.12立方厘米。
【点评】考查了圆柱的侧面积和体积公式的运用。
36.如图是小东妈妈的茶杯。
(1)这只茶杯最多能装多少升的水?(茶杯厚度不计)
(2)茶杯中部贴有一圈防烫装饰带,这圈防烫装饰带贴在茶杯上的面积是多少平方厘米?
【答案】(1)0.2826。
(2)75.36。
【分析】(1)已知圆柱的底面直径是6厘米,高是10厘米,根据圆柱的体积公式:V=π(d÷2)2h可求出圆柱的容积。
(2)茶杯中部的一圈装饰带是小明怕烫伤妈妈的手特意贴上的,它的面积是一个宽为4厘米,长为直径为6厘米的圆的周长的长方形的面积,根据长方形的面积公式进行计算即可。
【解答】解:(1)3.14×(6÷2)2×10
=3.14×9×10
=282.6(立方厘米)
282.6=0.2826升
答:这只茶杯最多能装0.2826升水。
(2)3.14×6×4
=3.14×24
=75.36(平方厘米)
答:它的面积是75.36平方厘米。
【点评】本题主要考查了学生对圆柱的体积和侧面积计算方法的灵活运用。
37.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去洗手,走时忘记关掉水龙头,10分钟浪费多少升水?
【答案】15.072升。
【分析】把流过的水看成圆柱,它的底面直径是2厘米、高是(8×10×60)厘米,由此根据圆柱的体积公式V=sh=πr2h计算即可。
【解答】解:3.14×(2÷2)2×(8×10×60)
=3.14×1×4800
=15072(cm3)
15072立方厘米=15.072(升)
答:10分钟浪费15.072升水。
【点评】把不规则的形状物体,转化成规则的形状来求解体积是解答本题的关键。
38.一节用铁皮卷成的圆柱形烟囱长3米,管口直径是40厘米,做这个烟囱至少需要铁皮多少平方米?
【答案】3.768平方米。
【分析】根据“圆柱侧面积=底面周长×高”进行计算,烟囱的长就是圆柱的高,管口直径是圆柱的底面直径,根据“圆周长C=πd”可求出底面周长。
【解答】解:40厘米=0.4米
3.14×0.4×3
=1.256×3
=3.768(平方米)
答:做这个烟囱至少需要铁皮3.768平方米。
【点评】此题主要考查圆柱侧面积的计算方法,注意烟囱是无底的圆柱形。
39.一种压路机的前轮是圆柱形,轮宽1.6米,底面半径0.5米,该前轮转动一周可以压路的面积是多少平方米?
【答案】见试题解答内容
【分析】根据题意,这台压路机的前轮是一个圆柱,求该前轮转动一周可以压路的面积就是求圆柱的侧面积,圆柱的侧面积=底面周长×高,据此回答.
【解答】解:根据题意得
3.14×2×0.5×1.6
=3.14×1.6
=5.024(平方米)
答:该前轮转动一周可以压路的面积是5.024平方米.
【点评】本题考查了圆柱的侧面积,解决本题的关键是运用圆柱的侧面积公式.
40.一个压路机的前轮是圆柱体,它的直径是1.5米,轮宽2米,前轮向前滚动200周,压过的路面是多少平方米?
【答案】见试题解答内容
【分析】根据圆柱的侧面积公式:S=ch,把数据代入公式求出前轮滚动一周压路的面积在乘200即可,据此列式解答.
【解答】解:3.14×1.5×2×200
=9.42×200
=1884(平方米),
答:压路的面积是1884平方米.
【点评】此题主要考查圆柱的侧面积搜狗在实际生活中的应用,关键是熟记公式.
41.用铁皮制作一担圆柱形水桶(无盖),底面直径为6dm,高是8dm.
(1)做这担水桶需铁皮多少dm2?
(2)这担水桶可盛水多少L?
【答案】见试题解答内容
【分析】(1)由于水桶无盖,所以需要铁皮的面积是这个圆柱的侧面积加一个底面的面积,根据圆柱的侧面积公式:S=ch,圆的面积公式:S=πr2.求出一个,再求一担.
(2)根据圆柱的容积公式:V=Sh,把数据分别代入公式解答.先求出一只水桶盛水多少,再求一担水的体积.
【解答】解:(1)3.14×6×8+3.14×(6÷2)2
=150.72+3.14×9
=150.72+28.26
=178.98(平方分米)
178.98×2=357.96(平方分米)
答:做一担这样的铁桶至少需要357.96平方分米的铁皮.
(2)3.14×(6÷2)2×8×2
=3.14×9×8×2
=452.16(立方分米)
452.16立方分米=452.16升
答:这担水桶最多能盛水452.16升.
【点评】此题主要考查圆柱的表面积公式、容积公式在实际生活中的应用.
42.修建一个圆柱形的沼气池,底面直径是2米,深2米。在沼气池的内壁与下底面抹上水泥,抹水泥的面积是多少平方米?
【答案】15.7平方米。
【分析】圆柱的侧面积=底面周长×高,用侧面积加上一个底面积即可。
【解答】解:2÷2=1(米)
3.14×2×2+3.14×1×1
=12.56+3.14
=15.7(平方米)
答:抹水泥的面积是15.7平方米。
【点评】熟练掌握圆的周长和面积公式,是解答此题的关键。
43.把一根长4m的圆柱形钢材沿垂直于高的面截成相等的两段以后,表面积增加了6.28m2,如果每立方米钢材重7800kg.(1)原来这根钢材的表面积是多少?
(2)这根钢材重多少千克?
【答案】见试题解答内容
【分析】(1)增加部分的面积是6.28平方米是圆柱形钢材的两个底面的面积,先用6.28除以2,求出一个底面的面积,再根据圆的面积公式求出圆的半径的平方,进而得出圆的半径,然后根据圆的周长公式求出底面周长,再乘高,求出侧面积,然后用侧面积加上两个底面积就是原来这根钢材的表面积是多少;
(2)由此根据圆柱的体积公式,V=Sh,求出圆柱形钢材的体积,再用体积乘7800千克就是钢材的重量.
【解答】解:(1)6.28÷2=3.14(平方米)
3.14÷3.14=1(平方米)
即底面半径的平方是1平方米,所底面半径是1米;
3.14×1×2=6.28(米)
6.28×4+6.28
=25.12+6.28
=31.4(平方米)
答:原来这根钢材的表面积是31.4平方米.
(2)3.14×4×7800
=12.56×7800
=97968(千克)
答:这根钢材重97968千克.
【点评】解决本题关键是明确增加的表面积就是原来圆柱两个底面积的面积,再根据圆的面积公式、周长公式,以及圆柱表面积的计算方法和体积的计算方法求解.
44.为了抗旱,小平家挖了一个底面半径5m、深2m的圆柱形蓄水池,并且用水泥涂抹水池的内壁与底部,防止漏水.一场暴雨过后,小平沿水池边缘走了一圈,并测得池中水深1.2m.
(1)涂抹水泥的面积是多少平方米?
(2)池中水的体积是多少?
【答案】见试题解答内容
【分析】(1)根据题意,涂抹水泥的面积是这个圆柱的侧面积+一个底面积,再根据圆柱侧面积=底面周长×高,进行解答;
(2)根据圆柱的体积公式:V=Sh,代入数据,进行解答.
【解答】解:(1)2×3.14×5×2+3.14×52
=62.8+78.5
=141.3(平方米)
答:涂抹水泥的面积是141.3平方米.
(2)3.14×52×1.2
=78.5×1.2
=94.2(立方米)
答:池中水的体积是94.2立方米.
【点评】此题主要考查圆柱的表面积公式和体积公式的灵活运用.
45.一种易燃易爆化工原料铁桶,它的底面直径6分米,高14分米.为了搬运安全,需要在桶上安装两个橡胶护圈(如图).至少需要橡胶带多少分米?
【答案】见试题解答内容
【分析】根据圆的周长公式:C=πd,把数据代入公式求出圆柱铁桶的底面周长然后乘2即可.据此解答.
【解答】解:3.14×6×2
=18.84×2
=37.68(分米),
答:至少需要橡胶带37.68分米.
【点评】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式.
46.春节期间,为了增添节日气氛。体育文化广场增添了1根大花柱,花柱高3.5米,底面半径0.5米,花柱的侧面和上面都插满鲜花,如果每平方米装饰40朵花,这根花柱一共需要多少朵花?
【答案】471朵花。
【分析】根据圆柱的侧面积公式:S=Ch,圆的面积公式:S=πr2,把数据代入公式求出这个柱子的侧面积和上面的面积,然后用侧面积与上面的面积和乘每平方米插花的数量即可,据此解答。
【解答】解:(3.14×0.5×2×3.5+3.14×0.52)×40
=(3.14×3.5+3.14×0.25)×40
=(10.99+0.785)×40
=11.775×40
=471(朵)
答:这根花柱一共需要471朵花。
【点评】此题主要考查圆柱的侧面积公式、圆的面积公式在实际生活中的应用,关键是熟记公式。
47.在一个数学实验活动中.先往一个长方体的容器中注水,水深4.4厘米(如图);然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有冰柱浸没在水里,如图.
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
【答案】见试题解答内容
【分析】(1)原来水柱只有4.4厘米,因为“水面上升到5.5厘米处”说明了冰柱插入水中水面上升了(5.5﹣4.4)厘米,用底面积乘以上升的水1.1厘米的高度,就是冰柱的体积,再求整个冰柱的体积即可.
(2)根据“冰化成水,体积减少原来的,要求这根冰柱融化后将变成多少毫升的水,是把冰的体积看作单位“1”,则水是原来冰柱的(1),再根据求一个数的几分之几是多少用乘法计算,据此解答即可.
(3)因为冰柱垂直放入长方体的容器中,使水的高度上升了:5.5﹣4.4=1.1(厘米),所以根据整个冰柱化成水后的体积与上升的高度进行计算即可.
【解答】(1)10×10×(5.5﹣4.4)
=100×1.1
=110×3
=330立方厘米(立方厘米)
答:整根冰柱的体积是330立方厘米;
(2)330×(1)
=330
=297(立方厘米)
297立方厘米=297毫升
答:这根冰柱融化后将变成297毫升的水.
(3)4.4+297÷(10×10)
=4.4+297÷100
=4.4+2.97
=7.37(厘米)
答:当冰柱完全融化时,容器内水深一共是7.37厘米.
【点评】解答此题的关键是利用物体排开水的体积等于浸入水的物体的体积,先求出浸入水中的体积,从而问题得解.
48.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆。
(1)这个蔬菜大棚的占地面积是多少平方米?
(2)覆盖住这个大棚的塑料薄膜大约有多少平方米?
(3)大棚内的空间大约有多少立方米?
【答案】(1)80。
(2)138。
(3)125.6。
【分析】(1)根据题干,这个大棚的占地面积就是这个长20米,宽2×2=4米的长方形的面积,根据长方形的面积公式S=a×b即可解答。
(2)覆盖在这个大棚上的塑料薄膜的面积,即它所在的圆柱的侧面积的一半,加上一个圆柱的底面积;由此利用圆柱的侧面积和底面积公式S=πr2即可解答。
(3)大棚所在的圆柱的体积的一半,就是这个大棚的空间,根据圆柱的体积公式V=πr2h解答即可。
【解答】解:(1)20×(2×2)=80(平方米)
答:这个大棚的种植面积是80平方米。
(2)3.14×2×2×20÷2+3.14×22
=125.6+12.56
=138.16
≈138(平方米)
答:覆盖在这个大棚上的塑料薄膜约有138平方米。
(3)3.14×22×20÷2
=251.2÷2
=125.6(立方米)
答:大棚的空间大约是125.6立方米。
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
49.某苗圃基地计划建一个圆柱形无盖蓄水池,从外面量得底面直径3.6米,高2米,底的厚度与壁的厚度都是0.3米。这个蓄水池的容积是多少立方米?(得数保留整数)
【答案】12立方米。
【分析】先求出这个蓄水池的底面内直径和高,再根据圆柱形的容积=底面积×高即可求解。
【解答】解:2﹣0.3=1.7(米)
3.6﹣0.3×2
=3.6﹣0.6
=3(米)
3.14×(3÷2)2×1.7
=3.14×2.25×1.7
≈12(立方米)
答:这个蓄水池的容积是12立方米。
【点评】此题主要考查圆柱的容积公式的计算应用,关键是求出蓄水池的底面内直径和高。
50.小虹用布制作一顶帽子.上面是圆柱形,底面直径16cm,高15cm;帽檐部分是一个圆环,外圆直径40cm.制作这顶帽子,至少要用多少平方厘米的布?
【答案】见试题解答内容
【分析】根据题意,这个帽子是由一个无底的圆柱的表面积+一个圆环的面积,圆柱的底面直径是16cm,高是15cm;圆环的内直径是16cm,外直径是40cm;然后再根据圆柱的表面积公式和圆环的面积公式进行解答.
【解答】解:3.14×16×15+3.14×(16÷2)2+3.14×[(40÷2)2﹣(16÷2)2]
=753.6+200.96+1055.04
=2009.6(平方厘米)
答:至少要用2009.6平方厘米的布.
【点评】此题重点考查圆环的面积和圆柱的表面积计算方法的灵活运用.
51.工厂要生产一节烟囱,烟囱长2.5m,横截面是直径为40cm的圆。做一节烟囱一共需要铁皮多少平方米?(接头处忽略不计)
【答案】3.14平方米。
【分析】烟囱只有侧面没有底面,根据圆柱的侧面积公式S=Ch,把数据代入公式解答即可。注意单位的转化。
【解答】解:40cm=0.4m
3.14×0.4×2.5
=3.14×1
=3.14(m2)
答:做一节烟囱一共需要铁皮3.14平方米。
【点评】本题考查了圆柱侧面积公式S=Ch的灵活运用。
52.一根圆柱形钢管,内直径是4厘米,外直径是8厘米,长是6米。如果每立方厘米钢材重7.8克,那么这根钢管大约重多少千克?(π值取3.14,结果保留整千克)
【答案】176千克。
【分析】这根钢管的底面积是一个环形,这个环形的面积=半径为(8÷2)的外圆的面积﹣半径为(4÷2)的内圆的面积,长6米即高600厘米,根据V=sh算出钢管的体积,再用体积乘钢管每立方厘米的重量就是钢管的总重量,算出答案化成千克即可。
【解答】解:内半径:4÷2=2(厘米)
外半径:8÷2=4(厘米)
6米=600厘米
钢管的底面积:3.14×42﹣3.14×22
=3.14×12
=37.68(平方厘米)
钢管的体积:37.68×600=22608(立方厘米)
钢管的重量:22608×7.8
=176342.4(克)
≈176(千克)
答:这根钢重176千克。
【点评】解答这道题的关键是知道钢管的底面积是一个环形,并且会求环形面积的方法。
53.一个圆柱形的粮囤,从里面量得底面半径是2m,高是2.5m,如果每立方米玉米重约0.8吨,这个粮囤能装多少吨玉米?
【答案】25.12吨。
【分析】根据圆柱体积公式:圆柱的体积=底面积×高,先求出圆柱的体积,再乘0.8即可。
【解答】解:3.14×22×2.5×0.8
=12.56×2
=25.12(吨)
答:这个粮囤能装25.12吨玉米。
【点评】熟练掌握圆柱的体积公式:圆柱体积=底面积×高,是解决此题的关键。
54.一个蔬菜大棚(如图),长20米,横截面是一个半径2米的半圆形,表面用单层塑料薄膜覆盖(包括两端横截面).
(1)这个大棚的种植面积是多少平方米?
(2)搭建这个大棚至少要用塑料薄膜多少平方米?
(3)大棚内的空间有多大?
【答案】见试题解答内容
【分析】(1)根据题干,这个大棚的种植面积就是这个长20米,宽2×2=4米的长方形的面积,根据长方形的面积公式即可解答;
(2)覆盖在这个大棚上的塑料薄膜的面积,即它所在的圆柱的侧面积的一半,加上一个圆柱的底面积;由此利用圆柱的侧面积和底面积公式即可解答;
(3)大棚所在的圆柱的体积的一半,就是这个大棚的空间,根据圆柱的体积公式解答即可.
【解答】解:(1)20×(2×2)=80(平方米),
答:这个大棚的种植面积是80平方米.
(2)3.14×2×2×20÷2+3.14×22,
=125.6+12.56,
=138.16(平方米),
答:覆盖在这个大棚上的塑料薄膜约有138.16平方米.
(3)3.14×22×20÷2,
=251.2÷2,
=125.6(立方米),
答:大棚的空间大约是125.6立方米.
【点评】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决.
55.如图是一个铁皮做成的易拉罐。(单位:厘米)
(1)这个易拉罐的底面积是多少平方厘米?
(2)做一个这样的易拉罐,至少需要多少平方厘米的铁皮?
【答案】12.56平方厘米;175.84平方厘米。
【分析】(1)易拉罐的底面直径是4厘米,可求出半径,根据圆的面积公式:S=πr 可求出易拉罐的底面积;
(2)根据圆柱的表面积=侧面积+底面圆的面积×2=πdh+2πr ,列式解答即可。
【解答】解:(1)3.14×(4÷2)
=3.14×4
=12.56(平方厘米)
答:底面积是12.56平方厘米。
(2)3.14×4×12+12.56×2
=150.72+25.12
=175.84(平方厘米)
答:至少需要175.84平方厘米的铁皮。
【点评】熟练掌握圆柱侧面积和圆面积的求法是解题的关键。
21世纪教育网(www.21cnjy.com)
