5.2.3 简单复合函数的导数 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修2
文档属性
| 名称 | 5.2.3 简单复合函数的导数 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修2 |  | |
| 格式 | docx | ||
| 文件大小 | 122.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 21:02:53 | ||
图片预览


文档简介
5.2.3 简单复合函数的导数
1. 理解复合函数的概念.
2. 理解复合函数的求导法则,并能求简单的复合函数的导数.
3. 能运用复合函数求导及导数运算法则解决综合问题.
活动一 理解复合函数的概念
1. 定义:一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
2. 指出以下函数可以看作是由哪两个基本初等函数复合而成的:
(1) y=ln (x2+1);
(2) y=e3x+1;
(3) y=sin (2x+3).
思考
如何将复合函数拆分?
3. 若f(x)=,g(x)=1+sin 2x,则f(g(x))= ,g(f(x))= .
活动二 掌握复合函数的求导公式
例1 求下列函数的导数(从不同的角度思考):
(1) y=(3x-1)2;
(2) y=sin 2x.
复合函数求导公式:
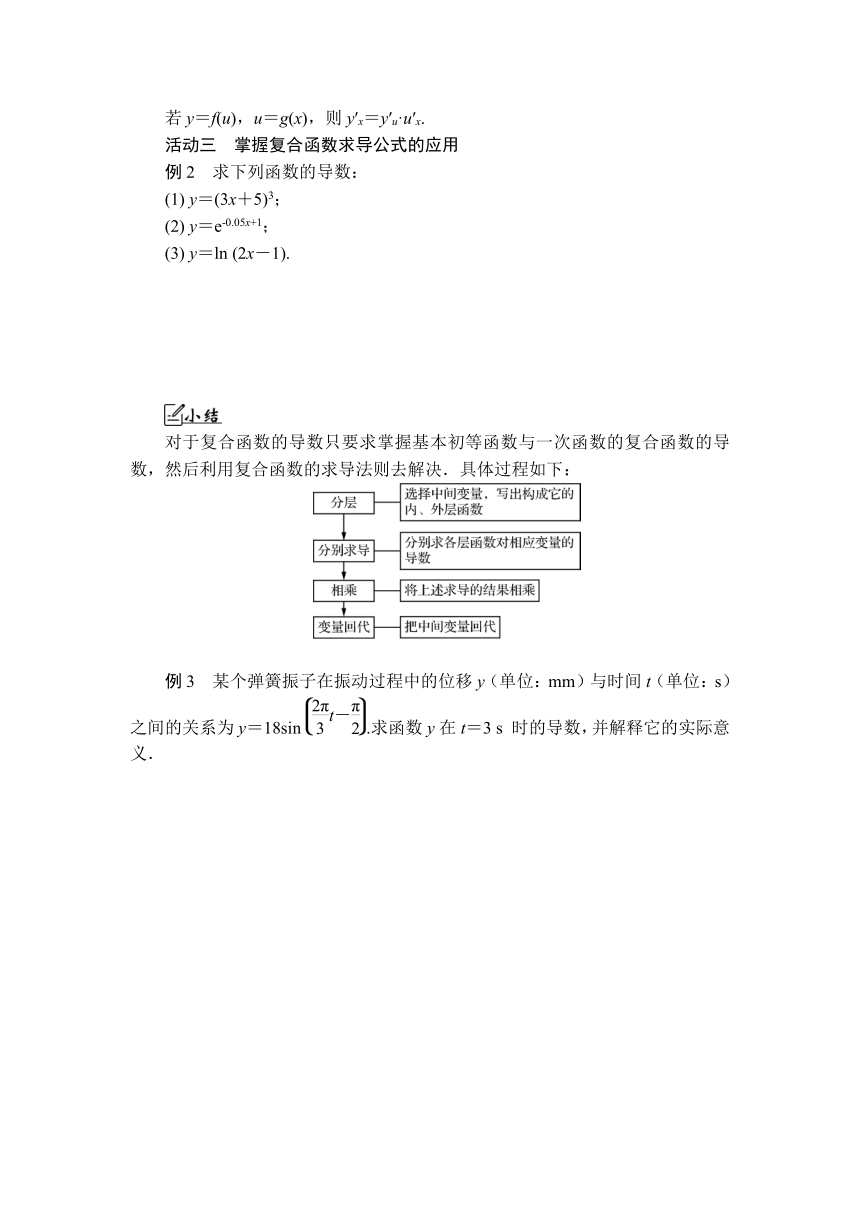
若y=f(u),u=g(x),则y′x=y′u·u′x.
活动三 掌握复合函数求导公式的应用
例2 求下列函数的导数:
(1) y=(3x+5)3;
(2) y=e-0.05x+1;
(3) y=ln (2x-1).
对于复合函数的导数只要求掌握基本初等函数与一次函数的复合函数的导数,然后利用复合函数的求导法则去解决.具体过程如下:
例3 某个弹簧振子在振动过程中的位移y(单位:mm)与时间t(单位:s)之间的关系为y=18sin .求函数y在t=3 s 时的导数,并解释它的实际意义.
1. (2024临沂月考)已知y=cos 2x,则y′等于( )
A. sin 2x B. 2sin 2x C. -4cos 2x D. -2sin 2x
2. 随着科学技术的发展,放射性同位素技术已经被广泛应用于医学、航天等众多领域,并取得了显著经济效益.假设某放射性同位素的衰变过程中,其含量N(单位:贝克)与时间t(单位:天)满足函数关系N(t)=N0,其中N0为初始时该放射性同位素的含量.已知t=15时,该放射性同位素的瞬时变化率为-,则该放射性同位素含量为4.5贝克时衰变所需时间为( )
A. 20天 B. 30天 C. 45天 D. 60天
3. (多选)下列函数中,求导正确的是( )
A. 若f(x)=,则f′(x)=
B. 若f(x)=e2x,则f′(x)=e2x
C. 若f(x)=,则f′(x)=
D. 若f(x)=cos ,则f′(x)=-sin
4. (2024南充月考)若函数f(x)=sin 2x的导函数为f′(x),则f′= .
5.(2024石家庄月考)求曲线y=ex-1+2sin (x-1)在点(1,1)处的切线方程.
5.2.3 简单复合函数的导数
【活动方案】
2. (1) y=ln (x2+1)可由y=ln u,u=x2+1复合而成.
(2) y=e3x+1可由y=eu,u=3x+1复合而成.
(3) y=sin (2x+3)可由y=sin u,u=2x+3复合而成.
思考:从左向右,从外向内拆分.
3. 1+sin 2
例1 (1) 方法一:y′x=[(3x-1)2]′=(9x2-6x+1)′=18x-6=6(3x-1).
方法二:将y=(3x-1)2看成由y=u2和u=3x-1复合而成,则y′u=2u,u′x=3,则y′x=y′u·u′x=2(3x-1)×3=6(3x-1).
(2) 方法一:y′x=(sin 2x)′=(2sin x cos x)′=2cos2x-2sin2x=2cos2x.
方法二:将y=sin 2x看成由y=sin u和u=2x复合而成,则y′u=cos u,u′x=2,则y′x=y′u·u′x=cos 2x·2=2cos 2x.
例2 (1) 函数y=(3x+5)3可以看作函数y=u3和u=3x+5的复合函数.根据复合函数的求导法则,有y′x=y′u· u′x=(u3)′·(3x+5)′=3u2×3=9(3x+5)2.
(2) 函数y=e-0.05x+1可以看作函数y=eu和u=-0.05x+1的复合函数.根据复合函数的求导法则,有y′x=y′u· u′x=(eu)′·(-0.05x+1)′=-0.05eu=-0.05e-0.05x+1.
(3) 函数y=ln (2x-1)可以看作函数y=ln u和u=2x-1的复合函数.根据复合函数的求导法则,有y′x=y′u· u′x=(ln u)′·(2x-1)′=2×=.
例3 函数y=18sin 可以看作函数y=18sin u和u=t-的复合函数,根据复合函数的求导法则,有y′t=y′u· u′t=(18sin u)′·(t-)′=18cos u×=12πcos (t-).
当t=3时,y′t=12πcos =0.
它表示当t=3s时,弹簧振子振动的瞬时速度为0mm/s.
【检测反馈】
1. D 因为y=cos 2x,所以y′=(2x)′(-sin 2x)=-2sin 2x.
2. D 由N(t)=N02-,得N′(t)=-·N0·ln 2.因为当t=15时,该放射性同位素的瞬时变化率为-,即N′(15)=-N0=-,解得N0=18,则N(t)=18·,当该放射性同位素含量为4.5贝克时,即N(t)=4.5,所以18·=4.5,即=,所以-=-2,解得t=60.
3. AC 对于A,f′(x)==,故A正确;对于B,f′(x)=e2x·2=2e2x,故B错误;对于C,f′(x)=′=·(2x-1·2=(2x-1=,故C正确;对于D,f′(x)=·2=-2sin ,故D错误.故选AC.
4. 1 由题意,得f′(x)=2cos 2x,则f′=2cos =1.
5. 令y=f(x)=ex-1+2sin (x-1),
则f′(x)=ex-1+2cos (x-1),
可得f(1)=e0+2sin 0=1,f′(1)=e0+2cos 0=3,
故切线方程为y-1=3(x-1),
化简,得3x-y-2=0.
1. 理解复合函数的概念.
2. 理解复合函数的求导法则,并能求简单的复合函数的导数.
3. 能运用复合函数求导及导数运算法则解决综合问题.
活动一 理解复合函数的概念
1. 定义:一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
2. 指出以下函数可以看作是由哪两个基本初等函数复合而成的:
(1) y=ln (x2+1);
(2) y=e3x+1;
(3) y=sin (2x+3).
思考
如何将复合函数拆分?
3. 若f(x)=,g(x)=1+sin 2x,则f(g(x))= ,g(f(x))= .
活动二 掌握复合函数的求导公式
例1 求下列函数的导数(从不同的角度思考):
(1) y=(3x-1)2;
(2) y=sin 2x.
复合函数求导公式:
若y=f(u),u=g(x),则y′x=y′u·u′x.
活动三 掌握复合函数求导公式的应用
例2 求下列函数的导数:
(1) y=(3x+5)3;
(2) y=e-0.05x+1;
(3) y=ln (2x-1).
对于复合函数的导数只要求掌握基本初等函数与一次函数的复合函数的导数,然后利用复合函数的求导法则去解决.具体过程如下:
例3 某个弹簧振子在振动过程中的位移y(单位:mm)与时间t(单位:s)之间的关系为y=18sin .求函数y在t=3 s 时的导数,并解释它的实际意义.
1. (2024临沂月考)已知y=cos 2x,则y′等于( )
A. sin 2x B. 2sin 2x C. -4cos 2x D. -2sin 2x
2. 随着科学技术的发展,放射性同位素技术已经被广泛应用于医学、航天等众多领域,并取得了显著经济效益.假设某放射性同位素的衰变过程中,其含量N(单位:贝克)与时间t(单位:天)满足函数关系N(t)=N0,其中N0为初始时该放射性同位素的含量.已知t=15时,该放射性同位素的瞬时变化率为-,则该放射性同位素含量为4.5贝克时衰变所需时间为( )
A. 20天 B. 30天 C. 45天 D. 60天
3. (多选)下列函数中,求导正确的是( )
A. 若f(x)=,则f′(x)=
B. 若f(x)=e2x,则f′(x)=e2x
C. 若f(x)=,则f′(x)=
D. 若f(x)=cos ,则f′(x)=-sin
4. (2024南充月考)若函数f(x)=sin 2x的导函数为f′(x),则f′= .
5.(2024石家庄月考)求曲线y=ex-1+2sin (x-1)在点(1,1)处的切线方程.
5.2.3 简单复合函数的导数
【活动方案】
2. (1) y=ln (x2+1)可由y=ln u,u=x2+1复合而成.
(2) y=e3x+1可由y=eu,u=3x+1复合而成.
(3) y=sin (2x+3)可由y=sin u,u=2x+3复合而成.
思考:从左向右,从外向内拆分.
3. 1+sin 2
例1 (1) 方法一:y′x=[(3x-1)2]′=(9x2-6x+1)′=18x-6=6(3x-1).
方法二:将y=(3x-1)2看成由y=u2和u=3x-1复合而成,则y′u=2u,u′x=3,则y′x=y′u·u′x=2(3x-1)×3=6(3x-1).
(2) 方法一:y′x=(sin 2x)′=(2sin x cos x)′=2cos2x-2sin2x=2cos2x.
方法二:将y=sin 2x看成由y=sin u和u=2x复合而成,则y′u=cos u,u′x=2,则y′x=y′u·u′x=cos 2x·2=2cos 2x.
例2 (1) 函数y=(3x+5)3可以看作函数y=u3和u=3x+5的复合函数.根据复合函数的求导法则,有y′x=y′u· u′x=(u3)′·(3x+5)′=3u2×3=9(3x+5)2.
(2) 函数y=e-0.05x+1可以看作函数y=eu和u=-0.05x+1的复合函数.根据复合函数的求导法则,有y′x=y′u· u′x=(eu)′·(-0.05x+1)′=-0.05eu=-0.05e-0.05x+1.
(3) 函数y=ln (2x-1)可以看作函数y=ln u和u=2x-1的复合函数.根据复合函数的求导法则,有y′x=y′u· u′x=(ln u)′·(2x-1)′=2×=.
例3 函数y=18sin 可以看作函数y=18sin u和u=t-的复合函数,根据复合函数的求导法则,有y′t=y′u· u′t=(18sin u)′·(t-)′=18cos u×=12πcos (t-).
当t=3时,y′t=12πcos =0.
它表示当t=3s时,弹簧振子振动的瞬时速度为0mm/s.
【检测反馈】
1. D 因为y=cos 2x,所以y′=(2x)′(-sin 2x)=-2sin 2x.
2. D 由N(t)=N02-,得N′(t)=-·N0·ln 2.因为当t=15时,该放射性同位素的瞬时变化率为-,即N′(15)=-N0=-,解得N0=18,则N(t)=18·,当该放射性同位素含量为4.5贝克时,即N(t)=4.5,所以18·=4.5,即=,所以-=-2,解得t=60.
3. AC 对于A,f′(x)==,故A正确;对于B,f′(x)=e2x·2=2e2x,故B错误;对于C,f′(x)=′=·(2x-1·2=(2x-1=,故C正确;对于D,f′(x)=·2=-2sin ,故D错误.故选AC.
4. 1 由题意,得f′(x)=2cos 2x,则f′=2cos =1.
5. 令y=f(x)=ex-1+2sin (x-1),
则f′(x)=ex-1+2cos (x-1),
可得f(1)=e0+2sin 0=1,f′(1)=e0+2cos 0=3,
故切线方程为y-1=3(x-1),
化简,得3x-y-2=0.
