第四章 数列 同步学案(含答案)2024~2025学年高二数学人教A版(2019)选择性必修2
文档属性
| 名称 | 第四章 数列 同步学案(含答案)2024~2025学年高二数学人教A版(2019)选择性必修2 | 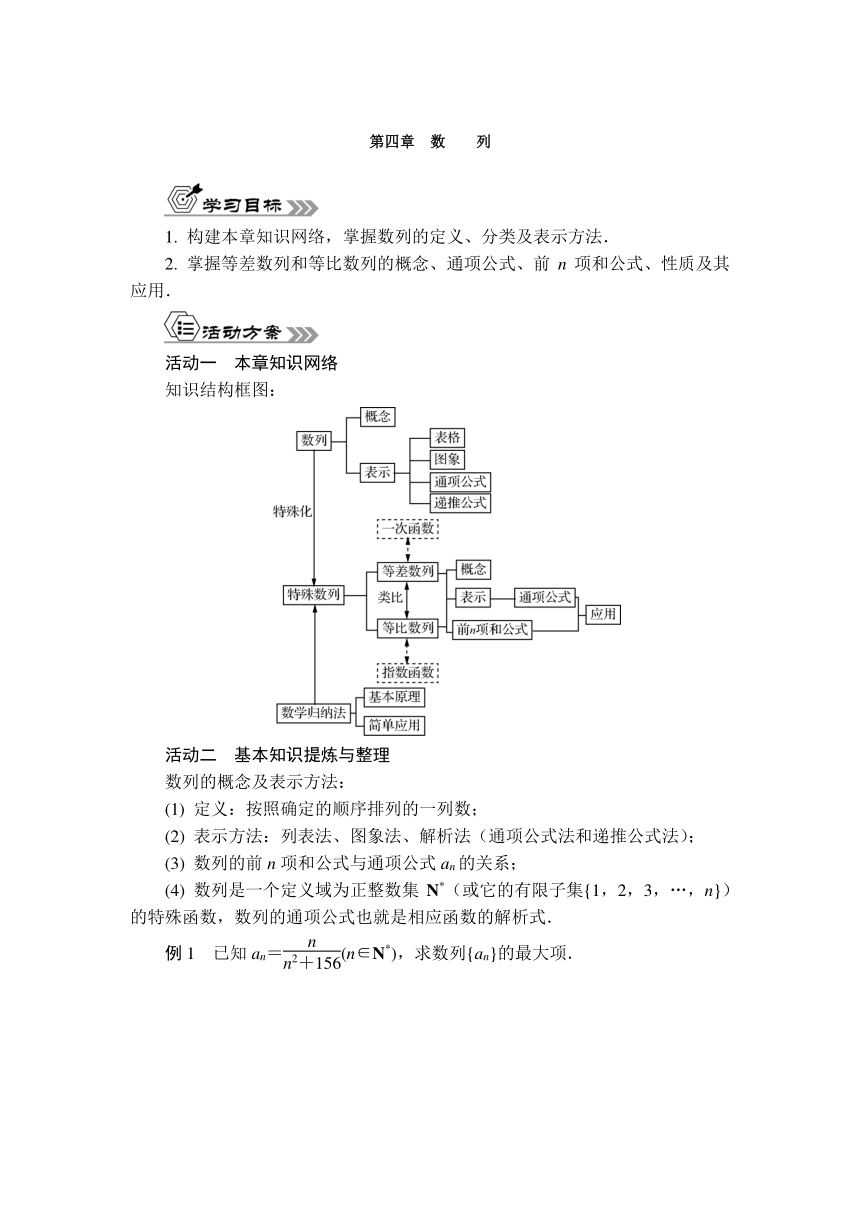 | |
| 格式 | docx | ||
| 文件大小 | 214.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 21:08:15 | ||
图片预览





文档简介
第四章 数 列
1. 构建本章知识网络,掌握数列的定义、分类及表示方法.
2. 掌握等差数列和等比数列的概念、通项公式、前n项和公式、性质及其应用.
活动一 本章知识网络
知识结构框图:
活动二 基本知识提炼与整理
数列的概念及表示方法:
(1) 定义:按照确定的顺序排列的一列数;
(2) 表示方法:列表法、图象法、解析法(通项公式法和递推公式法);
(3) 数列的前n项和公式与通项公式an的关系;
(4) 数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的特殊函数,数列的通项公式也就是相应函数的解析式.
例1 已知an=(n∈N*),求数列{an}的最大项.
例2 (2024荆州期末)已知数列{an}满足a1=48,an+1=若ak=13,则k的值为( )
A. 8 B. 9 C. 10 D. 11
例3 (2024河南期末)已知数列{an}是递增数列,an=m(2n-1)-n2,n∈N*,则实数m的取值范围为( )
A. (2,+∞) B. (1,2) C. D. (2,3)
活动三 掌握等差数列与等比数列的综合应用
例4 已知正项等比数列{an}满足a4=2a3+3a2,Sn为其前n项和,且S4=40.
(1) 求an;
(2) 若等差数列{bn}满足:b1=a1,b4=a1+a3.
①证明:当n=1时,是数列{bn}中的项,并指出是第几项;
②求出所有的n,使得是数列{bn}中的项.
例5 (2024青岛期末)如图所示的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中,后人称为“三角垛”,“三角垛”的最上层有1个球,第二层有3个球,第三层有6个球,…,设各层的球数构成一个数列{an}.
(1) 写出an与an+1的递推关系,并求数列{an}的通项公式;
(2) 记等比数列{bn}的前n项和为Sn,且bn+1=2Sn+2,在bn与bn+1之间插入n个数,若这n+2个数恰能组成一个公差为dn的等差数列,求数列{an·dn}的前n项和Tn.
例6 (2024上海闵行区月考)若有穷数列a1,a2,…,an(n是正整数),满足a1=an,a2=an-1,…,an=a1,即ai=an-i+1(i是正整数,且1≤i≤n),就称该数列为“对称数列”.例如,数列1,3,5,5,3,1就是“对称数列”.
(1) 已知数列{bn}是项数为7的对称数列,且b1,b2,b3,b4成等差数列,b1=2,b4=11,试写出{bn}的每一项;
(2) 对于确定的正整数m>1,写出所有项数不超过2m的“对称数列”,使得1,2,22,…,2m-1依次是该数列中连续的项;当m=10时,求其中一个“对称数列”前19项的和S19.
例7 在数列{an}中,已知a1=1,a2=a,an+1=k(an+an+2)对任意n∈N*都成立,数列{an}的前n项和为Sn.
(1) 若{an}是等差数列,求k的值;
(2) 若a=1,k=-,求Sn;
(3) 是否存在实数k,使数列{an}是公比不为1的等比数列,且任意相邻三项am,am+1,am+2按某顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由.
1. (2024岳阳开学考试)在数列{an}中,若a1=1,an+1=,则a12的值为( )
A. -2 B. - C. 1 D. 4
2. (2024福州期末)已知数列{an}的首项为1,且(n+2)an+1=2nan对任意正整数n恒成立,则数列的前n项和Sn为( )
A. B. C. D.
3. (多选)(2024泰州期末)若数列{an}的前n项和Sn=n2,数列{bn}的通项公式为bn=3n-1,则下列说法中正确的是( )
A. an=2n-1
B. 数列{bn}的前n项和Tn=
C. 若cn=,则数列{cn}的前n项和Cn<
D. 若dn=,数列{dn}的前n项和为Dn,则不存在正整数m,使得Dm=
4. 已知在数列{an}中,a1=1,an+1=,则数列{an}的通项公式为 .
5. 在数列{an}中,a1=2,an+1-2an=(-2)n+2.
(1) 计算a2,a3,猜想数列{an}的通项公式并加以证明;
(2) 设Sn为数列{an}的前n项和,求证:数列{Sn}中任意连续三项按适当顺序排列后,可以组成等差数列.
第四章 数 列
【活动方案】
例1 因为an=,
所以an+1=,
所以an+1-an=.
当1≤n≤11时,an+1>an,数列{an}递增;
当n=12时,a13=a12=;
当n≥13时,an+1所以数列{an}的最大项是第12项或第13项.
例2 C 由题意,得a2=a1=24,a3=a2=12,a4=a3=6,a5=a4=3,a6=a5+2=5,a7=a6+2=7,a8=a7+2=9,a9=a8+2=11,a10=a9+2=13,所以当ak=13时,k=10.
例3 C 因为数列{an}为递增数列,所以 n∈N*,an+1-an=m(2n+1-1)-(n+1)2-[m(2n-1)-n2]=m·2n-2n-1>0,整理得m>.令bn=,则bn+1-bn=-=<0,n∈N*,所以数列{bn}递减,故b1=是数列{bn}的最大项,可得实数m的取值范围为.
例4 (1) 设正项等比数列{an}的公比为q(q>0).
由a4=2a3+3a2,得a2q2=2a2q+3a2,则q2-2q-3=0,
解得q=3或q=-1(舍去).
由S4===40,
解得a1=1,
所以an=3n-1.
(2) 因为b1=a1=1,b4=a1+a3=1+9=10,
所以公差d==3,
所以bn=b1+(n-1)d=3n-2.
①当n=1时,==28,
令3n-2=28,得n=10,
即当n=1时,是数列{bn}中的第10项.
②设是{bn}中的第m项,
则=bm,
即=3m-2,
则m===n+.
由1≤3-<3,m,n∈N*,可得当且仅当3-=1时,m=n+成立,
即仅有n=1时,是数列{bn}中的项.
例5 (1) 由题图可得an+1-an=n+1,又a1=1,
所以an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=n+(n-1)+…+2+1=.
(2) 由bn+1=2Sn+2,
得bn=2Sn-1+2(n≥2),
两式相减得bn+1-bn=2Sn-2Sn-1=2bn,
则bn+1=3bn(n≥2).
因为数列{bn}为等比数列,
所以其公比为q=3.
当n=1时,b2=2S1+2=2b1+2=3b1,
解得b1=2,
可得bn=2·3n-1,则bn+1=2×3n.
因为bn+1=bn+(n+2-1)dn,
所以dn==,
所以an·dn=2n·3n-1,
可得Tn=2(1×30+2×31+3×32+…+n·3n-1),
则3Tn=2(1×31+2×32+3×33+…+n·3n),
两式相减,得-2Tn=2(1+31+32+33+…+3n-1-n·3n)=-2n·3n=-1+(-2n+1)·3n,
故Tn=+·3n.
例6 (1) 设数列b1,b2,b3,b4的公差为d,
则b4=b1+3d=2+3d=11,解得d=3,
所以数列{bn}的每一项依次为2,5,8,11,8,5,2.
(2) 若1,2,22,…,2m-1依次是该数列中连续的项,且是对称数列,
则至少有1+2(m-1)=2m-1(项),
从而所有项数不超过2m的“对称数列”有:
1,2,22,…,2m-2,2m-1,2m-1,2m-2,…,22,2,1;
2m-1,2m-2,…,22,2,1,1,2,22,…,2m-2,2m-1;
1,2,22,…,2m-2,2m-1,2m-2,…,22,2,1;
2m-1,2m-2,…,22,2,1,2,22,…,2m-2,2m-1,
共有4个这样的数列(2个2m项的,2个2m-1项的).
当m=10时,求数列1,2,22,…,2m-2,2m-1,2m-2,…,22,2,1的前19项,
则S19=1+2+22+…+28+29+28+…+22+2+1
=+=210-1+29-1=1 534.
例7 (1) 由题意,得an+1-an=an+2-an+1,
即2an+1=an+an+2,即an+1=(an+an+2),
故k=.
(2) 由k=-,得an+1=-(an+an+2),
即2an+1=-an-an+2,an+2+an+1=-(an+1+an),
故an+3+an+2=-(an+2+an+1)=an+1+an.
当n是偶数时,Sn=a1+a2+a3+a4+…+an-1+an=(a1+a2)=n;
当n是奇数时,a2+a3=-(a1+a2)=-2,
Sn=a1+a2+a3+a4+…+an-1+an
=a1+(a2+a3)+(a4+a5)+…+(an-1+an),
=1+×(-2)=2-n.
综上,Sn=
(3) 若{an}是等比数列,则公比q==a,
由题意,得a≠1,故am=am-1,am+1=am,am+2=am+1.
①若am+1为等差中项,则2am+1=am+am+2,
即2am=am-1+am+1,即2a=1+a2,
解得a=1(舍去);
②若am为等差中项,则2am=am+1+am+2,
即2am-1=am+am+1,即2=a+a2.
因为a≠1,所以a=-2,
所以k====-;
③若am+2为等差中项,则2am+2=am+am+1,
即2am+1=am+am-1,即2a2=a+1.
因为a≠1,所以a=-,所以k==-.
综上,存在实数k满足题意,k=-.
【检测反馈】
1. A 在数列{an}中,由a1=1,an+1=,得a2=4,a3=-2,a4=1,所以数列{an}是周期为3的周期数列,所以a12=a3=-2.
2. C 由题意易知an≠0,因为(n+2)an+1=2nan,所以=,可得=,所以an=an-1=·an-2=··an-3=…=····…··a1.因为a1=1,所以an=,则==-,所以Sn=1-+-+-+…+-=1-=.
3. ACD 对于A,当n≥2时,an=n2-(n-1)2=2n-1.又n=1时,a1=S1=1,符合an=2n-1,所以an=2n-1,故A正确;对于B,Tn==,故B错误;对于C,cn===,所以Cn=c1+c2+c3+…+cn=(1-+-+…+-)=<,故C正确;对于D,因为dn===-,所以Dn=d1+d2+d3+…+dn=-+-+…+-=3-.令3-=,可得=.令bn=,则bn+1-bn=-=<0,所以数列{bn}为递减数列.又b3=,b4=,所以=无正整数解,故D正确.故选ACD.
4. an= 因为an+1=,所以=2+,所以数列是首项为1,公差为2的等差数列,所以=2n-1,所以an=.
5. (1) a2=-4,a3=8,猜想an=-(-2)n.
由an+1-2an=(-2)n+2,
得an+1+(-2)n+1=2[an+(-2)n].
又a1+(-2)1=0,故an+(-2)n=0.
因此数列{an}的通项公式为an=-(-2)n.
(2) 由(1)可得=-2,
所以{an}是以2为首项,-2为公比的等比数列.
因为(Sn-Sn+1)-(Sn+2-Sn)=-2an+1-an+2=0,所以Sn-Sn+1=Sn+2-Sn.
从而Sn+1,Sn,Sn+2或Sn+2,Sn,Sn+1成等差数列,
于是数列{Sn}中任意连续三项Sn,Sn+1,Sn+2,排列为Sn+1,Sn,Sn+2或排列为Sn+2,Sn,Sn+1后,可以组成等差数列.
1. 构建本章知识网络,掌握数列的定义、分类及表示方法.
2. 掌握等差数列和等比数列的概念、通项公式、前n项和公式、性质及其应用.
活动一 本章知识网络
知识结构框图:
活动二 基本知识提炼与整理
数列的概念及表示方法:
(1) 定义:按照确定的顺序排列的一列数;
(2) 表示方法:列表法、图象法、解析法(通项公式法和递推公式法);
(3) 数列的前n项和公式与通项公式an的关系;
(4) 数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的特殊函数,数列的通项公式也就是相应函数的解析式.
例1 已知an=(n∈N*),求数列{an}的最大项.
例2 (2024荆州期末)已知数列{an}满足a1=48,an+1=若ak=13,则k的值为( )
A. 8 B. 9 C. 10 D. 11
例3 (2024河南期末)已知数列{an}是递增数列,an=m(2n-1)-n2,n∈N*,则实数m的取值范围为( )
A. (2,+∞) B. (1,2) C. D. (2,3)
活动三 掌握等差数列与等比数列的综合应用
例4 已知正项等比数列{an}满足a4=2a3+3a2,Sn为其前n项和,且S4=40.
(1) 求an;
(2) 若等差数列{bn}满足:b1=a1,b4=a1+a3.
①证明:当n=1时,是数列{bn}中的项,并指出是第几项;
②求出所有的n,使得是数列{bn}中的项.
例5 (2024青岛期末)如图所示的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中,后人称为“三角垛”,“三角垛”的最上层有1个球,第二层有3个球,第三层有6个球,…,设各层的球数构成一个数列{an}.
(1) 写出an与an+1的递推关系,并求数列{an}的通项公式;
(2) 记等比数列{bn}的前n项和为Sn,且bn+1=2Sn+2,在bn与bn+1之间插入n个数,若这n+2个数恰能组成一个公差为dn的等差数列,求数列{an·dn}的前n项和Tn.
例6 (2024上海闵行区月考)若有穷数列a1,a2,…,an(n是正整数),满足a1=an,a2=an-1,…,an=a1,即ai=an-i+1(i是正整数,且1≤i≤n),就称该数列为“对称数列”.例如,数列1,3,5,5,3,1就是“对称数列”.
(1) 已知数列{bn}是项数为7的对称数列,且b1,b2,b3,b4成等差数列,b1=2,b4=11,试写出{bn}的每一项;
(2) 对于确定的正整数m>1,写出所有项数不超过2m的“对称数列”,使得1,2,22,…,2m-1依次是该数列中连续的项;当m=10时,求其中一个“对称数列”前19项的和S19.
例7 在数列{an}中,已知a1=1,a2=a,an+1=k(an+an+2)对任意n∈N*都成立,数列{an}的前n项和为Sn.
(1) 若{an}是等差数列,求k的值;
(2) 若a=1,k=-,求Sn;
(3) 是否存在实数k,使数列{an}是公比不为1的等比数列,且任意相邻三项am,am+1,am+2按某顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由.
1. (2024岳阳开学考试)在数列{an}中,若a1=1,an+1=,则a12的值为( )
A. -2 B. - C. 1 D. 4
2. (2024福州期末)已知数列{an}的首项为1,且(n+2)an+1=2nan对任意正整数n恒成立,则数列的前n项和Sn为( )
A. B. C. D.
3. (多选)(2024泰州期末)若数列{an}的前n项和Sn=n2,数列{bn}的通项公式为bn=3n-1,则下列说法中正确的是( )
A. an=2n-1
B. 数列{bn}的前n项和Tn=
C. 若cn=,则数列{cn}的前n项和Cn<
D. 若dn=,数列{dn}的前n项和为Dn,则不存在正整数m,使得Dm=
4. 已知在数列{an}中,a1=1,an+1=,则数列{an}的通项公式为 .
5. 在数列{an}中,a1=2,an+1-2an=(-2)n+2.
(1) 计算a2,a3,猜想数列{an}的通项公式并加以证明;
(2) 设Sn为数列{an}的前n项和,求证:数列{Sn}中任意连续三项按适当顺序排列后,可以组成等差数列.
第四章 数 列
【活动方案】
例1 因为an=,
所以an+1=,
所以an+1-an=.
当1≤n≤11时,an+1>an,数列{an}递增;
当n=12时,a13=a12=;
当n≥13时,an+1
例2 C 由题意,得a2=a1=24,a3=a2=12,a4=a3=6,a5=a4=3,a6=a5+2=5,a7=a6+2=7,a8=a7+2=9,a9=a8+2=11,a10=a9+2=13,所以当ak=13时,k=10.
例3 C 因为数列{an}为递增数列,所以 n∈N*,an+1-an=m(2n+1-1)-(n+1)2-[m(2n-1)-n2]=m·2n-2n-1>0,整理得m>.令bn=,则bn+1-bn=-=<0,n∈N*,所以数列{bn}递减,故b1=是数列{bn}的最大项,可得实数m的取值范围为.
例4 (1) 设正项等比数列{an}的公比为q(q>0).
由a4=2a3+3a2,得a2q2=2a2q+3a2,则q2-2q-3=0,
解得q=3或q=-1(舍去).
由S4===40,
解得a1=1,
所以an=3n-1.
(2) 因为b1=a1=1,b4=a1+a3=1+9=10,
所以公差d==3,
所以bn=b1+(n-1)d=3n-2.
①当n=1时,==28,
令3n-2=28,得n=10,
即当n=1时,是数列{bn}中的第10项.
②设是{bn}中的第m项,
则=bm,
即=3m-2,
则m===n+.
由1≤3-<3,m,n∈N*,可得当且仅当3-=1时,m=n+成立,
即仅有n=1时,是数列{bn}中的项.
例5 (1) 由题图可得an+1-an=n+1,又a1=1,
所以an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=n+(n-1)+…+2+1=.
(2) 由bn+1=2Sn+2,
得bn=2Sn-1+2(n≥2),
两式相减得bn+1-bn=2Sn-2Sn-1=2bn,
则bn+1=3bn(n≥2).
因为数列{bn}为等比数列,
所以其公比为q=3.
当n=1时,b2=2S1+2=2b1+2=3b1,
解得b1=2,
可得bn=2·3n-1,则bn+1=2×3n.
因为bn+1=bn+(n+2-1)dn,
所以dn==,
所以an·dn=2n·3n-1,
可得Tn=2(1×30+2×31+3×32+…+n·3n-1),
则3Tn=2(1×31+2×32+3×33+…+n·3n),
两式相减,得-2Tn=2(1+31+32+33+…+3n-1-n·3n)=-2n·3n=-1+(-2n+1)·3n,
故Tn=+·3n.
例6 (1) 设数列b1,b2,b3,b4的公差为d,
则b4=b1+3d=2+3d=11,解得d=3,
所以数列{bn}的每一项依次为2,5,8,11,8,5,2.
(2) 若1,2,22,…,2m-1依次是该数列中连续的项,且是对称数列,
则至少有1+2(m-1)=2m-1(项),
从而所有项数不超过2m的“对称数列”有:
1,2,22,…,2m-2,2m-1,2m-1,2m-2,…,22,2,1;
2m-1,2m-2,…,22,2,1,1,2,22,…,2m-2,2m-1;
1,2,22,…,2m-2,2m-1,2m-2,…,22,2,1;
2m-1,2m-2,…,22,2,1,2,22,…,2m-2,2m-1,
共有4个这样的数列(2个2m项的,2个2m-1项的).
当m=10时,求数列1,2,22,…,2m-2,2m-1,2m-2,…,22,2,1的前19项,
则S19=1+2+22+…+28+29+28+…+22+2+1
=+=210-1+29-1=1 534.
例7 (1) 由题意,得an+1-an=an+2-an+1,
即2an+1=an+an+2,即an+1=(an+an+2),
故k=.
(2) 由k=-,得an+1=-(an+an+2),
即2an+1=-an-an+2,an+2+an+1=-(an+1+an),
故an+3+an+2=-(an+2+an+1)=an+1+an.
当n是偶数时,Sn=a1+a2+a3+a4+…+an-1+an=(a1+a2)=n;
当n是奇数时,a2+a3=-(a1+a2)=-2,
Sn=a1+a2+a3+a4+…+an-1+an
=a1+(a2+a3)+(a4+a5)+…+(an-1+an),
=1+×(-2)=2-n.
综上,Sn=
(3) 若{an}是等比数列,则公比q==a,
由题意,得a≠1,故am=am-1,am+1=am,am+2=am+1.
①若am+1为等差中项,则2am+1=am+am+2,
即2am=am-1+am+1,即2a=1+a2,
解得a=1(舍去);
②若am为等差中项,则2am=am+1+am+2,
即2am-1=am+am+1,即2=a+a2.
因为a≠1,所以a=-2,
所以k====-;
③若am+2为等差中项,则2am+2=am+am+1,
即2am+1=am+am-1,即2a2=a+1.
因为a≠1,所以a=-,所以k==-.
综上,存在实数k满足题意,k=-.
【检测反馈】
1. A 在数列{an}中,由a1=1,an+1=,得a2=4,a3=-2,a4=1,所以数列{an}是周期为3的周期数列,所以a12=a3=-2.
2. C 由题意易知an≠0,因为(n+2)an+1=2nan,所以=,可得=,所以an=an-1=·an-2=··an-3=…=····…··a1.因为a1=1,所以an=,则==-,所以Sn=1-+-+-+…+-=1-=.
3. ACD 对于A,当n≥2时,an=n2-(n-1)2=2n-1.又n=1时,a1=S1=1,符合an=2n-1,所以an=2n-1,故A正确;对于B,Tn==,故B错误;对于C,cn===,所以Cn=c1+c2+c3+…+cn=(1-+-+…+-)=<,故C正确;对于D,因为dn===-,所以Dn=d1+d2+d3+…+dn=-+-+…+-=3-.令3-=,可得=.令bn=,则bn+1-bn=-=<0,所以数列{bn}为递减数列.又b3=,b4=,所以=无正整数解,故D正确.故选ACD.
4. an= 因为an+1=,所以=2+,所以数列是首项为1,公差为2的等差数列,所以=2n-1,所以an=.
5. (1) a2=-4,a3=8,猜想an=-(-2)n.
由an+1-2an=(-2)n+2,
得an+1+(-2)n+1=2[an+(-2)n].
又a1+(-2)1=0,故an+(-2)n=0.
因此数列{an}的通项公式为an=-(-2)n.
(2) 由(1)可得=-2,
所以{an}是以2为首项,-2为公比的等比数列.
因为(Sn-Sn+1)-(Sn+2-Sn)=-2an+1-an+2=0,所以Sn-Sn+1=Sn+2-Sn.
从而Sn+1,Sn,Sn+2或Sn+2,Sn,Sn+1成等差数列,
于是数列{Sn}中任意连续三项Sn,Sn+1,Sn+2,排列为Sn+1,Sn,Sn+2或排列为Sn+2,Sn,Sn+1后,可以组成等差数列.
