第五章 一元函数的导数及其应用 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修2
文档属性
| 名称 | 第五章 一元函数的导数及其应用 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修2 | 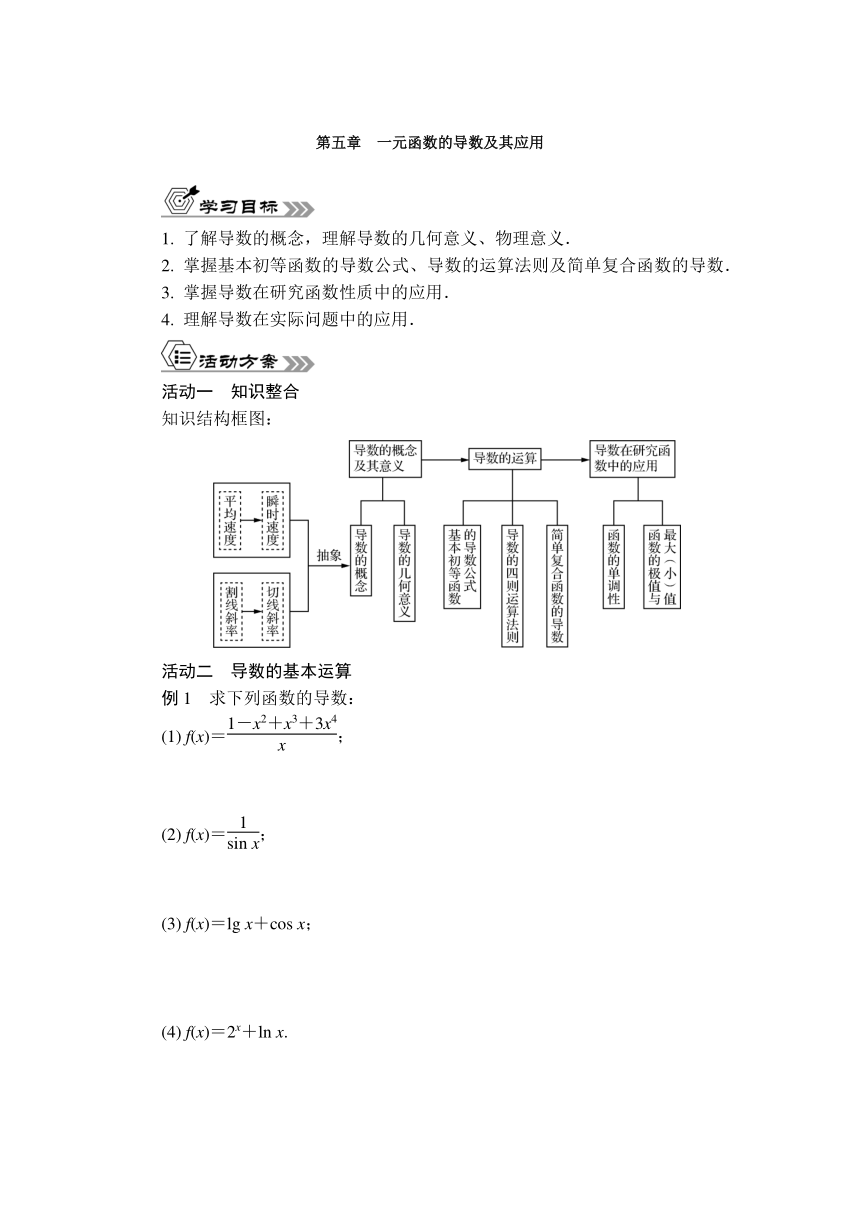 | |
| 格式 | docx | ||
| 文件大小 | 175.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 21:08:25 | ||
图片预览





文档简介
第五章 一元函数的导数及其应用
1. 了解导数的概念,理解导数的几何意义、物理意义.
2. 掌握基本初等函数的导数公式、导数的运算法则及简单复合函数的导数.
3. 掌握导数在研究函数性质中的应用.
4. 理解导数在实际问题中的应用.
活动一 知识整合
知识结构框图:
活动二 导数的基本运算
例1 求下列函数的导数:
(1) f(x)=;
(2) f(x)=;
(3) f(x)=lg x+cos x;
(4) f(x)=2x+ln x.
(5) f(x)=sin 3x cos x;
(6) f(x)=ln (2x+1)+32x.
活动三 理解导数的几何意义
例2 设曲线C:y=x3-3x和直线x=a(a>0)的交点为P,曲线C在点P处的切线与 x轴 交于点Q(-a,0),求实数a的值.
活动四 掌握利用导数解决函数的单调性的方法
例3 (2024遂宁月考)已知函数f(x)=x2+ax-ln x.
(1) 若函数y=f(x)在区间[1,3]上单调递增,求实数a的取值范围;
(2) 当a=1时,讨论函数f(x)在区间(0,t](t>0)上的单调性.
例4 (2024张家口月考)已知函数f(x)=xex,g(x)=x+ln x+m.
(1) 求函数f(x)的极值;
(2) 若g(x)≤f(x)恒成立,求实数m的取值范围.
活动五 掌握利用导数解决函数的极值与最值问题的方法
例5 设函数f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1) 求a,b,c的值;
(2) 求函数f(x)的单调增区间,并求函数f(x)在区间[-1,3]上的最大值和最小值.
例6 (2024枣庄阶段练习)已知函数f(x)=ax2+(2-a)x-ln x.
(1) 讨论f(x)的单调性;
(2) 若f(x)有两个零点,求实数a的取值范围.
活动六 导数在实际问题中的应用
例7 某物流公司购买了一块长AM=30m,宽AN=20m的矩形地AMPN,规划建设占地如图中矩形ABCD的仓库,其余地方为道路和停车场,要求顶点C在地块的对角线MN上,点B,D分别在边AM,AN上.假设AB的长度为xm.
(1) 要使仓库占地ABCD的面积不小于144m2, AB的长度应在什么范围内?
(2) 若规划建设仓库的高度是与AB长度相同的长方体形建筑,当AB的长度为多少时?仓库的容量最大.(墙体楼板所占空间忽略不计)
活动七 导数的综合应用
例8 设函数f(x)=-x(x-a)2(x∈R,a∈R).
(1) 当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2) 当a≠0时,求函数f(x)的极大值和极小值;
(3) 当a>3时,证明存在k∈[-1,0],使得不等式f(k-cos x)≥f(k2-cos2x)对任意的x∈R恒成立.
1.(2024温州期末)已知函数f(x)满足f(x)=f′sin x-cos x,则f′的值为( )
A. B. C. - D. -
2. 函数f(x)=x2-ln x的单调减区间是( )
A. (0,) B. [,+∞)
C. (-∞,-),(0,) D. [-,0),(0,)
3. (多选)(2024淮南开学考试)已知函数f(x)=,则下列命题中正确的是( )
A. 曲线y=f(x)在点(1,0)处的切线方程是x-ey-1=0
B. 函数f(x)有极大值,且极大值点x0∈(1,2)
C. f(2)D. 函数f(x)有两个零点
4. (2024武汉月考)若函数f(x)=x3+x2-2在区间(a-4,a)上存在最小值,则实数a的取值范围是 .
5. 已知函数f(x)=.
(1) 求函数f(x)的单调增区间;
(2) 求函数f(x)在区间[1,3]上的最大值和最小值.
第五章 一元函数的导数及其应用
【活动方案】
例1 (1) f′(x)=9x2+2x--1 (2) f′(x)=-
(3)f′(x)=-sin x (4) f′(x)=2x ln 2+
(5) f′(x)=3cos 3x cos x-sin 3x sin x (6) f′(x)=+9x ln 9
例2 由题意,得点P(a,a3-3a).
因为y′=3x2-3,
所以在点P处的切线的斜率为3a2-3,
所以切线方程为y-(a3-3a)=(3a2-3)(x-a).
令y=0,得x=.
由题意,得=-a,解得a=±.
又a>0,所以a=.
例3 (1) 因为f(x)=x2+ax-ln x,
所以f′(x)=2x+a-.
由题意,得f′(x)≥0在区间[1,3]上恒成立,
所以a≥-2x在区间[1,3]上恒成立.
令g(x)=-2x,x∈[1,3],则g′(x)=--2<0,
所以g(x)在区间[1,3]上单调递减,
所以g(x)≤g(1)=-1,可得a≥-1,
即实数a的取值范围为[-1,+∞).
(2) 当a=1时,f(x)=x2+x-ln x,
则f′(x)=2x+1-=,
当0时,f′(x)>0,
即f(x)在区间上单调递减,在区间上单调递增,
所以当0当t>时,f(x)在区间上单调递减,在区间上单调递增.
例4 (1) 由题意,得f′(x)=(x+1)ex.
令f′(x)=0,得x=-1.
f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,+∞)
f′(x) - 0 +
f(x) 单调递减 极小值- 单调递增
所以函数f(x)的极小值为-,无极大值.
(2) 不等式g(x)≤f(x)恒成立,
即x+ln x+m≤xex恒成立,
即m≤xex-x-ln x,x>0恒成立,
所以m≤(xex-x-ln x)min,x>0.
设h(x)=xex-x-ln x,x>0,
则h′(x)=(x+1)ex-1-=(x+1),其中x+1>0.
设m(x)=ex-,
则m′(x)=ex+>0,
所以m(x)在区间(0,+∞)单调递增.
因为m<0,m(1)>0,
所以存在x0∈,使得m(x0)=0,
即h′(x0)=0,即ex0=.
当x∈(0,x0)时,h′(x)<0,h(x)单调递减;
当x∈(x0,+∞)时,h′(x)>0,h(x)单调递增,
所以当x=x0时,函数h(x)取得最小值h(x0)=x0ex0-x0-ln x0.
由ex0=,可得x0=-ln x0,
所以h(x0)=x0ex0-x0-ln x0=1-x0+x0=1,
所以m≤1,即实数m的取值范围是(-∞,1].
例5 (1) 因为函数f(x)是奇函数,
所以f(-x)=-f(x),
即-ax3-bx+c=-ax3-bx-c,
所以c=0.
因为f′(x)=3ax2+b,且f′(x)的最小值为-12,所以b=-12.
因为函数f(x)的图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,
所以f′(1)=3a-12=-6,则a=2,
综上,a=2,b=-12,c=0.
(2) 由(1),得f(x)=2x3-12x,
所以f′(x)=6x2-12.
令f′(x)>0,得x<-或x>,
所以函数f(x)的单调增区间是(-∞,-)和(,+∞).
因为f()=-8,f(3)=18,f(-1)=10,
所以函数f(x)在区间[-1,3]上的最大值为18,最小值为-8.
例6 (1) 由题意,得f(x)的定义域为(0,+∞),
且f′(x)=2ax+(2-a)-=.
当a≥0时,ax+1>0.
由f′(x)>0,得x>;
由f′(x)<0,得0所以f(x)在区间上单调递减,在区间上单调递增.
当a<0时,由f′(x)=2ax+(2-a)-==0,
解得x1=,x2=-.
当a<-2时,x1=>x2=-.
令f′(x)>0,得-令f′(x)<0,得x<-或x>,
所以f(x)在区间和上单调递减,在区间上单调递增;
当a=-2时,=-,可得f′(x)≤0,所以f(x)在区间(0,+∞)单调递减;
当-2令f′(x)>0,得令f′(x)<0,得0-,
所以f(x)在区间和上单调递减,在区间上单调递增.
综上,当a≥0时,f(x)在区间上单调递减,在区间上单调递增;当-2(2) 由(1)可知,当a≥0时,f(x)在区间上单调递减,在区间上单调递增.
当x→0时,y→+∞;当x→+∞时,y→+∞.
若f(x)有两个零点,则f<0,即f=+1-+ln 2<0,
解得a>4(1+ln 2);
当a=-2时,f(x)在区间(0,+∞)上单调递减,不可能有两个零点;
当a<0且a≠-2时,在x1=和x2=-处取得极值,
f=+1-+ln 2=1+ln 2->0,
f=-+1-ln ,
令-=t>0,下证h(t)=t+1-ln t>0,
h′(t)=1-=,
当01时,h′(t)>0,
所以函数h(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
可得h(t)>h(1)=2>0,
所以f=-+1-ln >0,
所以当a<0且a≠-2时,f(x)不可能有两个零点.
综上,实数a的取值范围为(4(1+ln 2),+∞).
例7 (1) 由题意,得=,则AD=20-x,所以S矩形ABCD=x.
因为仓库占地面积不小于144m2,
所以x≥144,解得12≤x≤18.
综上,要使仓库占地面积不小于144m2,AB的长度应在[12,18]范围内.
(2) 由题意,得V=x2(0则V′=40x-2x2.由V′=0,得x=0或x=20.
当x∈(0,20)时,V′>0;
当x∈(20,30)时,V′<0,
所以当x=20时,V取最大值,
故当AB的长度为20m时,仓库的容量最大.
例8 (1) 当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,则f(2)=-2,且f′(x)=-3x2+4x-1,所以f′(2)=-5,
所以切线方程为y+2=-5(x-2),即5x+y-8=0.
(2) 由f′(x)=-3x2+4ax-a2=-(3x-a)(x-a)=0,得x=a或x=.
若a>0,则f′(x),f(x)的变化情况如下表:
x (-∞,) a (a,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 - 单调递增 0 单调递减
所以当x=时,f(x)有极小值f=-;当x=a时,f(x)有极大值f(a)=0.
若a<0,则f′(x),f(x)的变化情况如下表:
x (-∞,a) a (,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 0 单调递增 - 单调递减
所以当x=a时,f(x)有极小值f(a)=0;
当x=时,f(x)有极大值f=-.
(3) 由a>3,得>1.
当k∈[-1,0]时,k-cos x≤1,k2-cos2x≤1,
由(2),得函数f(x)在区间(-∞,1]上单调递减,
要使f(k-cosx)≥f(k2-cos2x)在R上恒成立,
只要k-cosx≤k2-cos2x在R上恒成立,
即cos2x-cosx≤k2-k在R上恒成立.
设g(x)=cos2x-cosx=-,
则g(x)max=g(-1)=2,
所以k2-k≥2,解得k≥2或k≤-1,
所以在区间[-1,0]上存在k=-1,使得f(k-cos x)≥f(k2-cos2x)对任意的x∈R恒成立.
【检测反馈】
1.A 由题意,得f′(x)=f′cos x+sin x,则f′=f′cos +sin =f′+,解得f′=.
2. A f′(x)=2x-=,令f′(x)<0,得0<x<,故函数f(x)的单调减区间为(0,).
3. AB 对于A,f′(x)==,则f′(1)=,所以曲线y=f(x)在点(1,0)处的切线方程是y-0=(x-1),即x-ey-1=0,故A正确;对于B,设h(x)=1-x ln x,则h′(x)=-ln x-1,当00,h(x)单调递增,当x>时,h′(x)<0,h(x)单调递减,所以h(x)max=h=1+>0,令x=et→0,则t=ln x→-∞,所以h(x)=1-x ln x=1-→1,而h(1)=1>0,h(2)=1-2ln 2<0,由零点存在定理可知h(x)=1-x ln x的零点x0∈(1,2),即函数f(x)有极大值,且极大值点x0∈(1,2),故B正确;对于C,由以上可知f(x)在区间(x0,+∞)上单调递减,且x0∈(1,2),所以f(2)>f(3),故C错误;对于D,由f(x)==0,得x=1,所以f(x)只有唯一的零点x=1,故D错误.故选AB.
4. [1,4) 由f(x)=x3+x2-2,得f′(x)=x2+2x=x(x+2),所以当x<-2或x>0时,f′(x)>0;当-25. (1) 由题意,得f′(x)=.
令f′(x)>0,得x<2;
令f′(x)<0,得x>2,
故函数f(x)在区间(-∞,2)上单调递增,在区间(2,+∞)上单调递减.
即函数f(x)的单调增区间为(-∞,2).
(2) 由(1),得函数f(x)在区间[1,2)上单调递增,在区间(2,3]上单调递减,
故函数f(x)在x=2处取得极大值,f(2)=.
又因为f(1)=0,f(3)=,
所以函数f(x)在区间[1,3]上的最小值为0,最大值为.
1. 了解导数的概念,理解导数的几何意义、物理意义.
2. 掌握基本初等函数的导数公式、导数的运算法则及简单复合函数的导数.
3. 掌握导数在研究函数性质中的应用.
4. 理解导数在实际问题中的应用.
活动一 知识整合
知识结构框图:
活动二 导数的基本运算
例1 求下列函数的导数:
(1) f(x)=;
(2) f(x)=;
(3) f(x)=lg x+cos x;
(4) f(x)=2x+ln x.
(5) f(x)=sin 3x cos x;
(6) f(x)=ln (2x+1)+32x.
活动三 理解导数的几何意义
例2 设曲线C:y=x3-3x和直线x=a(a>0)的交点为P,曲线C在点P处的切线与 x轴 交于点Q(-a,0),求实数a的值.
活动四 掌握利用导数解决函数的单调性的方法
例3 (2024遂宁月考)已知函数f(x)=x2+ax-ln x.
(1) 若函数y=f(x)在区间[1,3]上单调递增,求实数a的取值范围;
(2) 当a=1时,讨论函数f(x)在区间(0,t](t>0)上的单调性.
例4 (2024张家口月考)已知函数f(x)=xex,g(x)=x+ln x+m.
(1) 求函数f(x)的极值;
(2) 若g(x)≤f(x)恒成立,求实数m的取值范围.
活动五 掌握利用导数解决函数的极值与最值问题的方法
例5 设函数f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1) 求a,b,c的值;
(2) 求函数f(x)的单调增区间,并求函数f(x)在区间[-1,3]上的最大值和最小值.
例6 (2024枣庄阶段练习)已知函数f(x)=ax2+(2-a)x-ln x.
(1) 讨论f(x)的单调性;
(2) 若f(x)有两个零点,求实数a的取值范围.
活动六 导数在实际问题中的应用
例7 某物流公司购买了一块长AM=30m,宽AN=20m的矩形地AMPN,规划建设占地如图中矩形ABCD的仓库,其余地方为道路和停车场,要求顶点C在地块的对角线MN上,点B,D分别在边AM,AN上.假设AB的长度为xm.
(1) 要使仓库占地ABCD的面积不小于144m2, AB的长度应在什么范围内?
(2) 若规划建设仓库的高度是与AB长度相同的长方体形建筑,当AB的长度为多少时?仓库的容量最大.(墙体楼板所占空间忽略不计)
活动七 导数的综合应用
例8 设函数f(x)=-x(x-a)2(x∈R,a∈R).
(1) 当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2) 当a≠0时,求函数f(x)的极大值和极小值;
(3) 当a>3时,证明存在k∈[-1,0],使得不等式f(k-cos x)≥f(k2-cos2x)对任意的x∈R恒成立.
1.(2024温州期末)已知函数f(x)满足f(x)=f′sin x-cos x,则f′的值为( )
A. B. C. - D. -
2. 函数f(x)=x2-ln x的单调减区间是( )
A. (0,) B. [,+∞)
C. (-∞,-),(0,) D. [-,0),(0,)
3. (多选)(2024淮南开学考试)已知函数f(x)=,则下列命题中正确的是( )
A. 曲线y=f(x)在点(1,0)处的切线方程是x-ey-1=0
B. 函数f(x)有极大值,且极大值点x0∈(1,2)
C. f(2)
4. (2024武汉月考)若函数f(x)=x3+x2-2在区间(a-4,a)上存在最小值,则实数a的取值范围是 .
5. 已知函数f(x)=.
(1) 求函数f(x)的单调增区间;
(2) 求函数f(x)在区间[1,3]上的最大值和最小值.
第五章 一元函数的导数及其应用
【活动方案】
例1 (1) f′(x)=9x2+2x--1 (2) f′(x)=-
(3)f′(x)=-sin x (4) f′(x)=2x ln 2+
(5) f′(x)=3cos 3x cos x-sin 3x sin x (6) f′(x)=+9x ln 9
例2 由题意,得点P(a,a3-3a).
因为y′=3x2-3,
所以在点P处的切线的斜率为3a2-3,
所以切线方程为y-(a3-3a)=(3a2-3)(x-a).
令y=0,得x=.
由题意,得=-a,解得a=±.
又a>0,所以a=.
例3 (1) 因为f(x)=x2+ax-ln x,
所以f′(x)=2x+a-.
由题意,得f′(x)≥0在区间[1,3]上恒成立,
所以a≥-2x在区间[1,3]上恒成立.
令g(x)=-2x,x∈[1,3],则g′(x)=--2<0,
所以g(x)在区间[1,3]上单调递减,
所以g(x)≤g(1)=-1,可得a≥-1,
即实数a的取值范围为[-1,+∞).
(2) 当a=1时,f(x)=x2+x-ln x,
则f′(x)=2x+1-=,
当0
即f(x)在区间上单调递减,在区间上单调递增,
所以当0
例4 (1) 由题意,得f′(x)=(x+1)ex.
令f′(x)=0,得x=-1.
f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,+∞)
f′(x) - 0 +
f(x) 单调递减 极小值- 单调递增
所以函数f(x)的极小值为-,无极大值.
(2) 不等式g(x)≤f(x)恒成立,
即x+ln x+m≤xex恒成立,
即m≤xex-x-ln x,x>0恒成立,
所以m≤(xex-x-ln x)min,x>0.
设h(x)=xex-x-ln x,x>0,
则h′(x)=(x+1)ex-1-=(x+1),其中x+1>0.
设m(x)=ex-,
则m′(x)=ex+>0,
所以m(x)在区间(0,+∞)单调递增.
因为m<0,m(1)>0,
所以存在x0∈,使得m(x0)=0,
即h′(x0)=0,即ex0=.
当x∈(0,x0)时,h′(x)<0,h(x)单调递减;
当x∈(x0,+∞)时,h′(x)>0,h(x)单调递增,
所以当x=x0时,函数h(x)取得最小值h(x0)=x0ex0-x0-ln x0.
由ex0=,可得x0=-ln x0,
所以h(x0)=x0ex0-x0-ln x0=1-x0+x0=1,
所以m≤1,即实数m的取值范围是(-∞,1].
例5 (1) 因为函数f(x)是奇函数,
所以f(-x)=-f(x),
即-ax3-bx+c=-ax3-bx-c,
所以c=0.
因为f′(x)=3ax2+b,且f′(x)的最小值为-12,所以b=-12.
因为函数f(x)的图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,
所以f′(1)=3a-12=-6,则a=2,
综上,a=2,b=-12,c=0.
(2) 由(1),得f(x)=2x3-12x,
所以f′(x)=6x2-12.
令f′(x)>0,得x<-或x>,
所以函数f(x)的单调增区间是(-∞,-)和(,+∞).
因为f()=-8,f(3)=18,f(-1)=10,
所以函数f(x)在区间[-1,3]上的最大值为18,最小值为-8.
例6 (1) 由题意,得f(x)的定义域为(0,+∞),
且f′(x)=2ax+(2-a)-=.
当a≥0时,ax+1>0.
由f′(x)>0,得x>;
由f′(x)<0,得0
当a<0时,由f′(x)=2ax+(2-a)-==0,
解得x1=,x2=-.
当a<-2时,x1=>x2=-.
令f′(x)>0,得-
所以f(x)在区间和上单调递减,在区间上单调递增;
当a=-2时,=-,可得f′(x)≤0,所以f(x)在区间(0,+∞)单调递减;
当-2
所以f(x)在区间和上单调递减,在区间上单调递增.
综上,当a≥0时,f(x)在区间上单调递减,在区间上单调递增;当-2
当x→0时,y→+∞;当x→+∞时,y→+∞.
若f(x)有两个零点,则f<0,即f=+1-+ln 2<0,
解得a>4(1+ln 2);
当a=-2时,f(x)在区间(0,+∞)上单调递减,不可能有两个零点;
当a<0且a≠-2时,在x1=和x2=-处取得极值,
f=+1-+ln 2=1+ln 2->0,
f=-+1-ln ,
令-=t>0,下证h(t)=t+1-ln t>0,
h′(t)=1-=,
当0
所以函数h(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
可得h(t)>h(1)=2>0,
所以f=-+1-ln >0,
所以当a<0且a≠-2时,f(x)不可能有两个零点.
综上,实数a的取值范围为(4(1+ln 2),+∞).
例7 (1) 由题意,得=,则AD=20-x,所以S矩形ABCD=x.
因为仓库占地面积不小于144m2,
所以x≥144,解得12≤x≤18.
综上,要使仓库占地面积不小于144m2,AB的长度应在[12,18]范围内.
(2) 由题意,得V=x2(0
当x∈(0,20)时,V′>0;
当x∈(20,30)时,V′<0,
所以当x=20时,V取最大值,
故当AB的长度为20m时,仓库的容量最大.
例8 (1) 当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,则f(2)=-2,且f′(x)=-3x2+4x-1,所以f′(2)=-5,
所以切线方程为y+2=-5(x-2),即5x+y-8=0.
(2) 由f′(x)=-3x2+4ax-a2=-(3x-a)(x-a)=0,得x=a或x=.
若a>0,则f′(x),f(x)的变化情况如下表:
x (-∞,) a (a,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 - 单调递增 0 单调递减
所以当x=时,f(x)有极小值f=-;当x=a时,f(x)有极大值f(a)=0.
若a<0,则f′(x),f(x)的变化情况如下表:
x (-∞,a) a (,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 0 单调递增 - 单调递减
所以当x=a时,f(x)有极小值f(a)=0;
当x=时,f(x)有极大值f=-.
(3) 由a>3,得>1.
当k∈[-1,0]时,k-cos x≤1,k2-cos2x≤1,
由(2),得函数f(x)在区间(-∞,1]上单调递减,
要使f(k-cosx)≥f(k2-cos2x)在R上恒成立,
只要k-cosx≤k2-cos2x在R上恒成立,
即cos2x-cosx≤k2-k在R上恒成立.
设g(x)=cos2x-cosx=-,
则g(x)max=g(-1)=2,
所以k2-k≥2,解得k≥2或k≤-1,
所以在区间[-1,0]上存在k=-1,使得f(k-cos x)≥f(k2-cos2x)对任意的x∈R恒成立.
【检测反馈】
1.A 由题意,得f′(x)=f′cos x+sin x,则f′=f′cos +sin =f′+,解得f′=.
2. A f′(x)=2x-=,令f′(x)<0,得0<x<,故函数f(x)的单调减区间为(0,).
3. AB 对于A,f′(x)==,则f′(1)=,所以曲线y=f(x)在点(1,0)处的切线方程是y-0=(x-1),即x-ey-1=0,故A正确;对于B,设h(x)=1-x ln x,则h′(x)=-ln x-1,当0
4. [1,4) 由f(x)=x3+x2-2,得f′(x)=x2+2x=x(x+2),所以当x<-2或x>0时,f′(x)>0;当-2
令f′(x)>0,得x<2;
令f′(x)<0,得x>2,
故函数f(x)在区间(-∞,2)上单调递增,在区间(2,+∞)上单调递减.
即函数f(x)的单调增区间为(-∞,2).
(2) 由(1),得函数f(x)在区间[1,2)上单调递增,在区间(2,3]上单调递减,
故函数f(x)在x=2处取得极大值,f(2)=.
又因为f(1)=0,f(3)=,
所以函数f(x)在区间[1,3]上的最小值为0,最大值为.
