6.3.2 空间线面关系的判定 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 6.3.2 空间线面关系的判定 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 418.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 21:07:01 | ||
图片预览




文档简介
6.3.2 空间线面关系的判定(1)
1. 能用向量语言描述线线、线面、面面的平行关系.
2. 能用向量方法判定、证明空间线面的平行关系.
活动一 用空间向量处理平行关系
1. 知识回顾
(1) 直线的方向向量与平面的法向量:
(2) 空间直线与直线、直线与平面、平面与平面的位置关系的判定和性质:
2. 设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为μ,v,则
平行
l与m a∥b
l与α a⊥μ
α与β μ∥v
活动二 用空间向量证明线线平行
例1 在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2,P,Q,R,S分别是AA1,D1C1,AB,CC1的中点.求证:PQ∥RS.
要证明两直线平行,可先求出两直线的方向向量,然后证明两直线的方向向量共线,从而证明两直线平行.
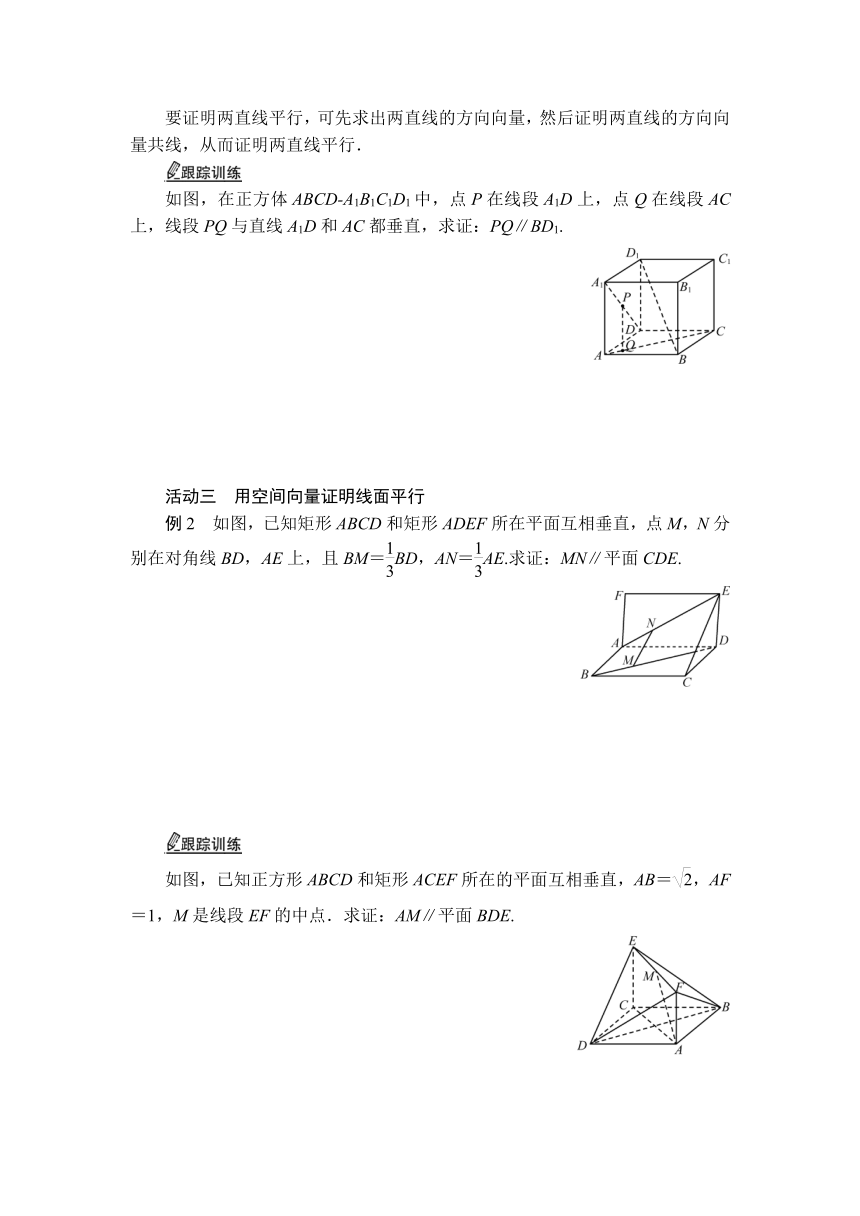
如图,在正方体ABCD-A1B1C1D1中,点P在线段A1D上,点Q在线段AC上,线段PQ与直线A1D和AC都垂直,求证:PQ∥BD1.
活动三 用空间向量证明线面平行
例2 如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且BM=BD,AN=AE.求证:MN∥平面CDE.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1,M是线段EF的中点.求证:AM∥平面BDE.
利用空间向量证明线面平行的方法:
(1) 利用共面向量法:证明直线的方向向量p与平面内的两个不共线向量a,b是共面向量,即满足p=xa+yb(x,y∈R),则p,a,b共面,从而可证直线与平面平行;
(2) 利用共线向量法:证明直线的方向向量p与该平面内的某一向量共线,再结合线面平行的判定定理即可证明线面平行;
(3) 利用法向量法:求出直线的方向向量与平面的法向量,证明方向向量与法向量垂直,从而证明直线与平面平行.
活动四 利用空间向量证明面面平行
例3 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO
如图,在长方体ABCD-A1B1C1D1中,DA=2,DC=3,DD1=4,M,N,E,F分别为棱A1D1,A1B1,D1C1,B1C1的中点.求证:平面AMN∥平面EFBD.
利用空间向量证明面面平行的方法:
(1) 转化为线面平行、线线平行,然后借助向量共线进行证明;
(2) 通过证明两个平面的法向量平行证明.
1. 已知平面α的一个法向量是(2,-1,1),α∥β,则下列向量可作为平面β的一个法向量的是( )
A. (4,2,-2) B. (2,0,4) C. (2,-1,-5) D. (4,-2,2)
2. (2024扬州月考)已知u=(3,a+b,a-b)(a,b∈R)是直线l的一个方向向量,n=(1,1,3)是平面α的一个法向量.若l∥α,则2b-4a的值为( )
A. 3 B. 4 C. 5 D. 6
3. (多选)(2023荆州阶段练习)已知空间中两条不同的直线l,m,两个不同的平面α,β,则下列说法中错误的是( )
A. 若直线l的一个方向向量为a=(1,-1,2),直线m的一个方向向量为b=(2,-2,4),则l∥m
B. 若直线l的方向向量为a=(0,1,-1),平面α的法向量为n=(1,-1,-1),则l∥α
C. 若平面α,β的法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β
D. 若平面α经过三个点A(1,0,-1), B(0,-1,0),C(-1,2,0),向量n=(1,u,t)是平面α的一个法向量,则u+t=1
4. 已知空间四点A(-2,3,1),B(2,-5,3),C(10,0,10),D(8,4,a),如果四边形ABCD为梯形,那么实数a的值为________.
5. (2024江苏月考)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.求证:BM∥平面ADEF.
6.3.2 空间线面关系的判定(2)
1. 能用向量法判断一些简单的线线、线面、面面垂直关系.
2. 能用向量方法证明空间线面位置关系的一些定理.
3. 掌握用向量方法判定、证明有关空间线面垂直关系的方法步骤.
活动一 探究用空间向量证明空间线面关系的方法
设空间两条直线l1,l2的方向向量分别为e1,e2,两个平面α1,α2的法向量分别为n1,n2,则有如下结论:
平行 垂直
l1与l2
l1与α1
α1与α2
活动二 用空间向量证明一些常见定理
例1 证明:在平面内的一条直线,如果它和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直.(三垂线定理)
写出三垂线定理的逆定理,并用向量的方法加以证明.
例2 证明:如果一条直线和平面内的两条相交直线垂直,那么这条直线垂直于这个平面.(直线与平面垂直的判定定理)
用向量方法证明:经过一个平面的垂线的平面垂直于该平面.
活动三 利用向量方法判断空间线面垂直关系
例3 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=,M是CC1的中点.求证:A1B⊥AM.
例4 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.求证:AB1⊥平面A1BD.
变式 在例4中增加条件E,F分别是BC,BB1的中点,求证:EF⊥平面ADE.
例5 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.求证:平面ADE⊥平面ABE.
1. (教材改编)已知平面α的一个法向量n1=(3,0,λ),平面β的一个法向量n2=(2,1,6),若α⊥β,则λ的值为( )
A. B. 4 C. -1 D. 1
2. (教材改编)已知直线l的方向向量a=(1,2,3),平面α的一个法向量n=(k-1,k,k+1),若l⊥α,则k的值为( )
A. - B. 1 C. 2 D. 3
3. (多选)(2024安阳期中)在空间直角坐标系中,设a,b分别是异面直线l1,l2的两个方向向量,u,v分别是平面α,β的两个法向量,若a=(1,1,2),b=(4,4,2),u=(-1,0,2),v=(2,2,1),则下列说法中正确的是( )
A. l1⊥α B. l2⊥β C. α∥β D. α⊥β
4. (2024广东月考)如图,已知PA⊥平面ABCD,四边形ABCD为正方形,E为CD的中点,F是AD上的一点,当BF⊥PE时,=________.
5. 如图,△ABC是一个正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD.求证:平面DEA⊥平面ECA.
6.3.2 空间线面关系的判定(1)
【活动方案】
1. (1) 直线l上的向量e(e≠0)以及与e共线的非零向量叫作直线l的方向向量.
如果表示非零向量n的有向线段所在直线垂直于平面α,那么称向量n垂直于平面α,记作n⊥α.此时,我们将向量n叫作平面α的法向量.
(2) 略
例1 方法一:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系D-xyz,
则P(3,0,1),Q(0,2,2),R(3,2,0),S(0,4,1),
所以=(-3,2,1),=(-3,2,1),
所以=,所以∥.
又PQ,RS无公共点,所以PQ∥RS.
方法二:因为=+=-+,=+=+-,
所以=,所以∥.
又PQ,RS无公共点,所以RS∥PQ.
跟踪训练 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,设正方体的棱长为1,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),D1(0,0,1),
所以=(1,0,1),=(-1,1,0).
设=(a,b,c),则即
取=(1,1,-1).
易知=(-1,-1,1),所以=-,
所以∥.
又PQ,BD1无公共点,所以PQ∥BD1.
例2 因为矩形ABCD和矩形ADEF所在平面互相垂直,所以AB,AD,AF互相垂直.
不妨设AB,AD,AF的长分别为3a,3b,3c,以{,,}为正交基底,建立空间直角坐标系 Axyz,
则B(3a,0,0),D(0,3b,0),F(0,0,3c),E(0,3b,3c),
所以=(-3a,3b,0),=(0,-3b,-3c).
因为==(-a,b,0),==(0,-b,-c),
所以=++=(0,-b,-c)+(3a,0,0)+(-a,b,0)=(2a,0,-c).
又平面CDE的一个法向量是=(0,3b,0),
由·=(2a,0,-c)·(0,3b,0)=0,
得⊥.
因为MN不在平面CDE内,
所以MN∥平面CDE.
跟踪训练 由题意,得CD,CB,CE两两垂直,以CD,CB,CE所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系C-xyz.
设AC∩BD=N,连接NE,
则N(,,0),E(0,0,1),
所以=(-,-,1).
又A(,,0),M(,,1),
所以=(-,-,1),
所以=,且A NE,所以NE∥AM.
又因为NE 平面BDE,AM 平面BDE,
所以AM∥平面BDE.
例3 以DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz,在CC1上任取一点Q,连接BQ,D1Q.
设正方体的棱长为1,CQ的长为m,
则O(,,0),P(0,0,),A(1,0,0),B(1,1,0),D1(0,0,1),Q(0,1,m).
方法一:因为=(-,-,),=(-1,-1,1)=2,所以∥,
所以OP∥BD1.
因为=(-1,0,),=(-1,0,m),
当m=时,=,即AP∥BQ,此时有平面PAO∥平面D1BQ,
故当Q为CC1的中点时,平面D1BQ∥平面PAO.
方法二:=(,-,0),=(-,-,).
设平面PAO的法向量为n1=(x,y,z),
则n1⊥,n1⊥,
所以
取x=1,则n1=(1,1,2).
又因为=(-1,-1,1),=(0,-1,1-m).
设平面D1BQ的法向量为n2=(a,b,c),
则n2⊥,n2⊥,
所以
取c=1,则n2=(m,1-m,1).
要使平面D1BQ∥平面PAO,需满足n1∥n2,
所以==,解得m=,
所以Q(0,1,).
故当Q为CC1的中点时,平面D1BQ∥平面PAO.
跟踪训练 以DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz,
则A(2,0,0),B(2,3,0),M(1,0,4),N(2,,4),E(0,,4),F(1,3,4),
所以=(1,,0),=(1,,0),=(-1,0,4),=(-1,0,4),
所以=,=,
所以MN∥EF,AM∥BF,
所以易得MN∥平面EFBD,AM∥平面EFBD.
又MN∩AM=M,所以平面AMN∥平面EFBD.
【检测反馈】
1. D 因为α∥β,所以平面α的法向量和平面β的法向量平行.设平面β的法向量为(x,y,z),则(2,-1,1)=λ(x,y,z),λ≠0,对比四个选项可知,只有D符合要求.
2. A 因为l∥α,所以u⊥n,则u·n=0,所以3×1+(a+b)×1+(a-b)×3=0,整理,得2b-4a=3.
3. BCD 对于A,因为b=2a,所以a∥b,所以l∥m,故A正确;对于B,a·n=0×1+1×(-1)+(-1)×(-1)=0,则a⊥n,所以l∥α或l α,故B错误;对于C,若n1=λn2(λ≠0),则(0,1,3)=λ(1,0,2),得此方程组无解,所以α∥β不成立,故C错误;对于D,=(-1,-1,1),=(-1,3,0),因为n=(1,u,t)是平面α的一个法向量,所以解得所以u+t=,故D错误.故选BCD.
4. 9 由题意知=(4,-8,2),=(8,5,7),=(2,-4,10-a),=(10,1,a-1).显然与不平行.又四边形ABCD为梯形,所以∥,解得a=9.
5. 因为平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,四边形ADEF是正方形,
所以AD⊥ED.又ED 平面ADEF,
所以ED⊥平面ABCD,所以,,两两垂直.
以D为坐标原点,,,分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,
则D(0,0,0),A(2,0,0),B(2,2,0),C(0,4,0),E(0,0,2),F(2,0,2).
又M为CE的中点,所以M(0,2,1),
则=(-2,0,1),=(-2,0,0),=(0,0,2),
所以=+,故,,共面.
又BM 平面ADEF,所以BM∥平面ADEF.
6.3.2 空间线面关系的判定(2)
【活动方案】
平行 垂直
l1与l2 e1∥e2 e1⊥e2
l1与α1 e1⊥n1 e1∥n1
α1与α2 n1∥n2 n1⊥n2
例1 已知:如图,OB是平面α的斜线,O为斜足,AB⊥α,A为垂足,CD α,且CD⊥OA.
求证:CD⊥OB.
证明:因为CD⊥OA,
所以·=0.
因为AB⊥α,CD α,
所以AB⊥CD,所以·=0.
又=+,
所以·=·(+)=·+·=0,
所以CD⊥OB.
跟踪训练 三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在这个平面内的射影垂直.
已知:如图,OB是平面α的斜线,O为斜足,AB⊥α,A为垂足,CD α,且OB⊥CD.求证:CD⊥OA.
证明:因为OB⊥CD,
所以·=0.
因为AB⊥α,CD α,
所以BA⊥CD,所以·=0.
又=+,
所以·=·(+)=·+·=0,
故CD⊥OA.
例2 已知:如图,m α,n α,m∩n=B,l⊥m,l⊥n.
求证:l⊥α.
证明:如图,在平面α内任意作一条直线g,在直线l,m,n,g上分别取非零向量l,m,n,g.
因为直线m与n相交,
所以向量m与n不共线.
由共面向量定理可知,存在唯一的有序实数组(x,y),使得g=x m+y n,
所以l·g=l·(x m+y n)=x l·m+y l·n.
因为l⊥m,l⊥n,
所以l·m=0,l·n=0,
所以l·g=0,即l⊥g.
因为l垂直于α内任意一条直线,
所以l⊥α.
跟踪训练 已知:平面α,β,AB⊥α,且AB β.
求证:α⊥β.
证明:设平面α的法向量为n1(n1有无数个),平面β的法向量为n2.
因为⊥α,n1⊥α,
所以n1∥.
设=λn1,λ为非零实数.
因为AB 平面β,
所以n2⊥,
所以n2·=0,即n2·λn1=0.
因为λ≠0,
所以n2·n1=0,
所以平面α⊥平面β.
例3 以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.
因为BC=1,∠ACB=90°,∠BAC=30°,
所以AC=,
所以A(,0,0),A1(,0,),B(0,1,0),
M(0,0,),
所以=(-,1,-),=(-,0,),
所以·=0,
所以A1B⊥AM.
例4 取BC的中点O,连接AO.
因为△ABC为正三角形,所以AO⊥BC.
因为在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,且平面ABC∩平面BCC1B1=BC,AO 平面ABC,
所以AO⊥平面BCC1B1.
取B1C1的中点O1,连接OO1,以O为坐标原点,OB,OO1,OA所在直线分别为x轴,y轴,z轴,建立空间直角坐标系O-xyz,
则B(1,0,0),D(-1,1,0),A1(0,2,),A(0,0,),B1(1,2,0),
所以=(1,2,-),=(-1,2,),=(-2,1,0).
因为·=1×(-1)+2×2+(-)×=0,·=1×(-2)+2×1+(-)×0=0,
所以⊥,⊥,
即AB1⊥BA1,AB1⊥BD.
又因为BA1∩BD=B,BA1 平面A1BD,BD 平面A1BD,
所以AB1⊥平面A1BD.
变式 建系同例4,点E与点O重合.
由E(0,0,0),A(0,0,),D(-1,1,0),F(1,1,0),
得=(1,1,0),=(0,0,),=(-1,1,0),
所以·=0,·=0,
所以⊥,⊥,
即EF⊥EA,EF⊥ED.
又EA∩ED=E,EA 平面ADE,ED 平面ADE,
所以EF⊥平面ADE.
例5 取BE的中点O,连接OC.
因为AB⊥平面BCE,所以以O为坐标原点建立如图所示的空间直角坐标系Oxyz,
则C(1,0,0),B(0,,0),E(0,-,0),D(1,0,1),A(0,,2),
所以=(0,-2,-2),=(-1,,1).
设平面ADE的法向量为n=(a,b,c),
则即
令b=1,则a=0,c=-,
所以n=(0,1,-).
又AB⊥平面BCE,OC 平面BCE,
所以AB⊥OC.
因为BE⊥OC,AB∩BE=B,AB 平面ABE,BE 平面ABE,
所以OC⊥平面ABE,
所以平面ABE的一个法向量为m=(1,0,0).
因为n·m=(0,1,-)·(1,0,0)=0,
所以n⊥m,所以平面ADE⊥平面ABE.
【检测反馈】
1. C 因为α⊥β,所以n1⊥n2,可得6+6λ=0,解得λ=-1.
2. C 因为l⊥α,所以a∥n,则==,解得k=2.
3. BD 对于A,因为a=(1,1,2),u=(-1,0,2),所以a与u既不平行也不垂直,所以直线l1与平面α不垂直,故A错误;对于B,因为b=(4,4,2),v=(2,2,1),所以b=2v,所以l2⊥β,故B正确;对于C,因为u=(-1,0,2),v=(2,2,1),所以u与v不平行,所以平面α与平面β不平行,故C错误;对于D,因为u·v=-1×2+0×2+2×1=0,所以u⊥v,即平面α与平面β垂直,故D正确.故选BD.
4. 1 以AB,AD,AP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.设正方形ABCD的边长为1,PA=a,则B(1,0,0),E(,1,0),P(0,0,a).设F(0,y,0),则=(-1,y,0),=(,1,-a).因为BF⊥PE,所以·=-+y=0,解得y=,即F(0,,0)是AD的中点,故=1.
5. 建立如图所示的空间直角坐标系C-xyz,不妨设CA=2,则CE=2,BD=1,C(0,0,0),A(,1,0),B(0,2,0),E(0,0,2),D(0,2,1),
所以=(,1,-2),=(0,0,2),=(0,2,-1).
设平面ECA与平面DEA的法向量分别是n1=(x1,y1,z1),n2=(x2,y2,z2),
则即解得
即解得
不妨取n1=(1,-,0),n2=(,1,2).
因为n1·n2=0,所以n1⊥n2,
所以平面DEA⊥平面ECA.
1. 能用向量语言描述线线、线面、面面的平行关系.
2. 能用向量方法判定、证明空间线面的平行关系.
活动一 用空间向量处理平行关系
1. 知识回顾
(1) 直线的方向向量与平面的法向量:
(2) 空间直线与直线、直线与平面、平面与平面的位置关系的判定和性质:
2. 设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为μ,v,则
平行
l与m a∥b
l与α a⊥μ
α与β μ∥v
活动二 用空间向量证明线线平行
例1 在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2,P,Q,R,S分别是AA1,D1C1,AB,CC1的中点.求证:PQ∥RS.
要证明两直线平行,可先求出两直线的方向向量,然后证明两直线的方向向量共线,从而证明两直线平行.
如图,在正方体ABCD-A1B1C1D1中,点P在线段A1D上,点Q在线段AC上,线段PQ与直线A1D和AC都垂直,求证:PQ∥BD1.
活动三 用空间向量证明线面平行
例2 如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且BM=BD,AN=AE.求证:MN∥平面CDE.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1,M是线段EF的中点.求证:AM∥平面BDE.
利用空间向量证明线面平行的方法:
(1) 利用共面向量法:证明直线的方向向量p与平面内的两个不共线向量a,b是共面向量,即满足p=xa+yb(x,y∈R),则p,a,b共面,从而可证直线与平面平行;
(2) 利用共线向量法:证明直线的方向向量p与该平面内的某一向量共线,再结合线面平行的判定定理即可证明线面平行;
(3) 利用法向量法:求出直线的方向向量与平面的法向量,证明方向向量与法向量垂直,从而证明直线与平面平行.
活动四 利用空间向量证明面面平行
例3 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO
如图,在长方体ABCD-A1B1C1D1中,DA=2,DC=3,DD1=4,M,N,E,F分别为棱A1D1,A1B1,D1C1,B1C1的中点.求证:平面AMN∥平面EFBD.
利用空间向量证明面面平行的方法:
(1) 转化为线面平行、线线平行,然后借助向量共线进行证明;
(2) 通过证明两个平面的法向量平行证明.
1. 已知平面α的一个法向量是(2,-1,1),α∥β,则下列向量可作为平面β的一个法向量的是( )
A. (4,2,-2) B. (2,0,4) C. (2,-1,-5) D. (4,-2,2)
2. (2024扬州月考)已知u=(3,a+b,a-b)(a,b∈R)是直线l的一个方向向量,n=(1,1,3)是平面α的一个法向量.若l∥α,则2b-4a的值为( )
A. 3 B. 4 C. 5 D. 6
3. (多选)(2023荆州阶段练习)已知空间中两条不同的直线l,m,两个不同的平面α,β,则下列说法中错误的是( )
A. 若直线l的一个方向向量为a=(1,-1,2),直线m的一个方向向量为b=(2,-2,4),则l∥m
B. 若直线l的方向向量为a=(0,1,-1),平面α的法向量为n=(1,-1,-1),则l∥α
C. 若平面α,β的法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β
D. 若平面α经过三个点A(1,0,-1), B(0,-1,0),C(-1,2,0),向量n=(1,u,t)是平面α的一个法向量,则u+t=1
4. 已知空间四点A(-2,3,1),B(2,-5,3),C(10,0,10),D(8,4,a),如果四边形ABCD为梯形,那么实数a的值为________.
5. (2024江苏月考)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.求证:BM∥平面ADEF.
6.3.2 空间线面关系的判定(2)
1. 能用向量法判断一些简单的线线、线面、面面垂直关系.
2. 能用向量方法证明空间线面位置关系的一些定理.
3. 掌握用向量方法判定、证明有关空间线面垂直关系的方法步骤.
活动一 探究用空间向量证明空间线面关系的方法
设空间两条直线l1,l2的方向向量分别为e1,e2,两个平面α1,α2的法向量分别为n1,n2,则有如下结论:
平行 垂直
l1与l2
l1与α1
α1与α2
活动二 用空间向量证明一些常见定理
例1 证明:在平面内的一条直线,如果它和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直.(三垂线定理)
写出三垂线定理的逆定理,并用向量的方法加以证明.
例2 证明:如果一条直线和平面内的两条相交直线垂直,那么这条直线垂直于这个平面.(直线与平面垂直的判定定理)
用向量方法证明:经过一个平面的垂线的平面垂直于该平面.
活动三 利用向量方法判断空间线面垂直关系
例3 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=,M是CC1的中点.求证:A1B⊥AM.
例4 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.求证:AB1⊥平面A1BD.
变式 在例4中增加条件E,F分别是BC,BB1的中点,求证:EF⊥平面ADE.
例5 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.求证:平面ADE⊥平面ABE.
1. (教材改编)已知平面α的一个法向量n1=(3,0,λ),平面β的一个法向量n2=(2,1,6),若α⊥β,则λ的值为( )
A. B. 4 C. -1 D. 1
2. (教材改编)已知直线l的方向向量a=(1,2,3),平面α的一个法向量n=(k-1,k,k+1),若l⊥α,则k的值为( )
A. - B. 1 C. 2 D. 3
3. (多选)(2024安阳期中)在空间直角坐标系中,设a,b分别是异面直线l1,l2的两个方向向量,u,v分别是平面α,β的两个法向量,若a=(1,1,2),b=(4,4,2),u=(-1,0,2),v=(2,2,1),则下列说法中正确的是( )
A. l1⊥α B. l2⊥β C. α∥β D. α⊥β
4. (2024广东月考)如图,已知PA⊥平面ABCD,四边形ABCD为正方形,E为CD的中点,F是AD上的一点,当BF⊥PE时,=________.
5. 如图,△ABC是一个正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD.求证:平面DEA⊥平面ECA.
6.3.2 空间线面关系的判定(1)
【活动方案】
1. (1) 直线l上的向量e(e≠0)以及与e共线的非零向量叫作直线l的方向向量.
如果表示非零向量n的有向线段所在直线垂直于平面α,那么称向量n垂直于平面α,记作n⊥α.此时,我们将向量n叫作平面α的法向量.
(2) 略
例1 方法一:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系D-xyz,
则P(3,0,1),Q(0,2,2),R(3,2,0),S(0,4,1),
所以=(-3,2,1),=(-3,2,1),
所以=,所以∥.
又PQ,RS无公共点,所以PQ∥RS.
方法二:因为=+=-+,=+=+-,
所以=,所以∥.
又PQ,RS无公共点,所以RS∥PQ.
跟踪训练 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,设正方体的棱长为1,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),D1(0,0,1),
所以=(1,0,1),=(-1,1,0).
设=(a,b,c),则即
取=(1,1,-1).
易知=(-1,-1,1),所以=-,
所以∥.
又PQ,BD1无公共点,所以PQ∥BD1.
例2 因为矩形ABCD和矩形ADEF所在平面互相垂直,所以AB,AD,AF互相垂直.
不妨设AB,AD,AF的长分别为3a,3b,3c,以{,,}为正交基底,建立空间直角坐标系 Axyz,
则B(3a,0,0),D(0,3b,0),F(0,0,3c),E(0,3b,3c),
所以=(-3a,3b,0),=(0,-3b,-3c).
因为==(-a,b,0),==(0,-b,-c),
所以=++=(0,-b,-c)+(3a,0,0)+(-a,b,0)=(2a,0,-c).
又平面CDE的一个法向量是=(0,3b,0),
由·=(2a,0,-c)·(0,3b,0)=0,
得⊥.
因为MN不在平面CDE内,
所以MN∥平面CDE.
跟踪训练 由题意,得CD,CB,CE两两垂直,以CD,CB,CE所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系C-xyz.
设AC∩BD=N,连接NE,
则N(,,0),E(0,0,1),
所以=(-,-,1).
又A(,,0),M(,,1),
所以=(-,-,1),
所以=,且A NE,所以NE∥AM.
又因为NE 平面BDE,AM 平面BDE,
所以AM∥平面BDE.
例3 以DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz,在CC1上任取一点Q,连接BQ,D1Q.
设正方体的棱长为1,CQ的长为m,
则O(,,0),P(0,0,),A(1,0,0),B(1,1,0),D1(0,0,1),Q(0,1,m).
方法一:因为=(-,-,),=(-1,-1,1)=2,所以∥,
所以OP∥BD1.
因为=(-1,0,),=(-1,0,m),
当m=时,=,即AP∥BQ,此时有平面PAO∥平面D1BQ,
故当Q为CC1的中点时,平面D1BQ∥平面PAO.
方法二:=(,-,0),=(-,-,).
设平面PAO的法向量为n1=(x,y,z),
则n1⊥,n1⊥,
所以
取x=1,则n1=(1,1,2).
又因为=(-1,-1,1),=(0,-1,1-m).
设平面D1BQ的法向量为n2=(a,b,c),
则n2⊥,n2⊥,
所以
取c=1,则n2=(m,1-m,1).
要使平面D1BQ∥平面PAO,需满足n1∥n2,
所以==,解得m=,
所以Q(0,1,).
故当Q为CC1的中点时,平面D1BQ∥平面PAO.
跟踪训练 以DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D-xyz,
则A(2,0,0),B(2,3,0),M(1,0,4),N(2,,4),E(0,,4),F(1,3,4),
所以=(1,,0),=(1,,0),=(-1,0,4),=(-1,0,4),
所以=,=,
所以MN∥EF,AM∥BF,
所以易得MN∥平面EFBD,AM∥平面EFBD.
又MN∩AM=M,所以平面AMN∥平面EFBD.
【检测反馈】
1. D 因为α∥β,所以平面α的法向量和平面β的法向量平行.设平面β的法向量为(x,y,z),则(2,-1,1)=λ(x,y,z),λ≠0,对比四个选项可知,只有D符合要求.
2. A 因为l∥α,所以u⊥n,则u·n=0,所以3×1+(a+b)×1+(a-b)×3=0,整理,得2b-4a=3.
3. BCD 对于A,因为b=2a,所以a∥b,所以l∥m,故A正确;对于B,a·n=0×1+1×(-1)+(-1)×(-1)=0,则a⊥n,所以l∥α或l α,故B错误;对于C,若n1=λn2(λ≠0),则(0,1,3)=λ(1,0,2),得此方程组无解,所以α∥β不成立,故C错误;对于D,=(-1,-1,1),=(-1,3,0),因为n=(1,u,t)是平面α的一个法向量,所以解得所以u+t=,故D错误.故选BCD.
4. 9 由题意知=(4,-8,2),=(8,5,7),=(2,-4,10-a),=(10,1,a-1).显然与不平行.又四边形ABCD为梯形,所以∥,解得a=9.
5. 因为平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,四边形ADEF是正方形,
所以AD⊥ED.又ED 平面ADEF,
所以ED⊥平面ABCD,所以,,两两垂直.
以D为坐标原点,,,分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,
则D(0,0,0),A(2,0,0),B(2,2,0),C(0,4,0),E(0,0,2),F(2,0,2).
又M为CE的中点,所以M(0,2,1),
则=(-2,0,1),=(-2,0,0),=(0,0,2),
所以=+,故,,共面.
又BM 平面ADEF,所以BM∥平面ADEF.
6.3.2 空间线面关系的判定(2)
【活动方案】
平行 垂直
l1与l2 e1∥e2 e1⊥e2
l1与α1 e1⊥n1 e1∥n1
α1与α2 n1∥n2 n1⊥n2
例1 已知:如图,OB是平面α的斜线,O为斜足,AB⊥α,A为垂足,CD α,且CD⊥OA.
求证:CD⊥OB.
证明:因为CD⊥OA,
所以·=0.
因为AB⊥α,CD α,
所以AB⊥CD,所以·=0.
又=+,
所以·=·(+)=·+·=0,
所以CD⊥OB.
跟踪训练 三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在这个平面内的射影垂直.
已知:如图,OB是平面α的斜线,O为斜足,AB⊥α,A为垂足,CD α,且OB⊥CD.求证:CD⊥OA.
证明:因为OB⊥CD,
所以·=0.
因为AB⊥α,CD α,
所以BA⊥CD,所以·=0.
又=+,
所以·=·(+)=·+·=0,
故CD⊥OA.
例2 已知:如图,m α,n α,m∩n=B,l⊥m,l⊥n.
求证:l⊥α.
证明:如图,在平面α内任意作一条直线g,在直线l,m,n,g上分别取非零向量l,m,n,g.
因为直线m与n相交,
所以向量m与n不共线.
由共面向量定理可知,存在唯一的有序实数组(x,y),使得g=x m+y n,
所以l·g=l·(x m+y n)=x l·m+y l·n.
因为l⊥m,l⊥n,
所以l·m=0,l·n=0,
所以l·g=0,即l⊥g.
因为l垂直于α内任意一条直线,
所以l⊥α.
跟踪训练 已知:平面α,β,AB⊥α,且AB β.
求证:α⊥β.
证明:设平面α的法向量为n1(n1有无数个),平面β的法向量为n2.
因为⊥α,n1⊥α,
所以n1∥.
设=λn1,λ为非零实数.
因为AB 平面β,
所以n2⊥,
所以n2·=0,即n2·λn1=0.
因为λ≠0,
所以n2·n1=0,
所以平面α⊥平面β.
例3 以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.
因为BC=1,∠ACB=90°,∠BAC=30°,
所以AC=,
所以A(,0,0),A1(,0,),B(0,1,0),
M(0,0,),
所以=(-,1,-),=(-,0,),
所以·=0,
所以A1B⊥AM.
例4 取BC的中点O,连接AO.
因为△ABC为正三角形,所以AO⊥BC.
因为在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,且平面ABC∩平面BCC1B1=BC,AO 平面ABC,
所以AO⊥平面BCC1B1.
取B1C1的中点O1,连接OO1,以O为坐标原点,OB,OO1,OA所在直线分别为x轴,y轴,z轴,建立空间直角坐标系O-xyz,
则B(1,0,0),D(-1,1,0),A1(0,2,),A(0,0,),B1(1,2,0),
所以=(1,2,-),=(-1,2,),=(-2,1,0).
因为·=1×(-1)+2×2+(-)×=0,·=1×(-2)+2×1+(-)×0=0,
所以⊥,⊥,
即AB1⊥BA1,AB1⊥BD.
又因为BA1∩BD=B,BA1 平面A1BD,BD 平面A1BD,
所以AB1⊥平面A1BD.
变式 建系同例4,点E与点O重合.
由E(0,0,0),A(0,0,),D(-1,1,0),F(1,1,0),
得=(1,1,0),=(0,0,),=(-1,1,0),
所以·=0,·=0,
所以⊥,⊥,
即EF⊥EA,EF⊥ED.
又EA∩ED=E,EA 平面ADE,ED 平面ADE,
所以EF⊥平面ADE.
例5 取BE的中点O,连接OC.
因为AB⊥平面BCE,所以以O为坐标原点建立如图所示的空间直角坐标系Oxyz,
则C(1,0,0),B(0,,0),E(0,-,0),D(1,0,1),A(0,,2),
所以=(0,-2,-2),=(-1,,1).
设平面ADE的法向量为n=(a,b,c),
则即
令b=1,则a=0,c=-,
所以n=(0,1,-).
又AB⊥平面BCE,OC 平面BCE,
所以AB⊥OC.
因为BE⊥OC,AB∩BE=B,AB 平面ABE,BE 平面ABE,
所以OC⊥平面ABE,
所以平面ABE的一个法向量为m=(1,0,0).
因为n·m=(0,1,-)·(1,0,0)=0,
所以n⊥m,所以平面ADE⊥平面ABE.
【检测反馈】
1. C 因为α⊥β,所以n1⊥n2,可得6+6λ=0,解得λ=-1.
2. C 因为l⊥α,所以a∥n,则==,解得k=2.
3. BD 对于A,因为a=(1,1,2),u=(-1,0,2),所以a与u既不平行也不垂直,所以直线l1与平面α不垂直,故A错误;对于B,因为b=(4,4,2),v=(2,2,1),所以b=2v,所以l2⊥β,故B正确;对于C,因为u=(-1,0,2),v=(2,2,1),所以u与v不平行,所以平面α与平面β不平行,故C错误;对于D,因为u·v=-1×2+0×2+2×1=0,所以u⊥v,即平面α与平面β垂直,故D正确.故选BD.
4. 1 以AB,AD,AP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.设正方形ABCD的边长为1,PA=a,则B(1,0,0),E(,1,0),P(0,0,a).设F(0,y,0),则=(-1,y,0),=(,1,-a).因为BF⊥PE,所以·=-+y=0,解得y=,即F(0,,0)是AD的中点,故=1.
5. 建立如图所示的空间直角坐标系C-xyz,不妨设CA=2,则CE=2,BD=1,C(0,0,0),A(,1,0),B(0,2,0),E(0,0,2),D(0,2,1),
所以=(,1,-2),=(0,0,2),=(0,2,-1).
设平面ECA与平面DEA的法向量分别是n1=(x1,y1,z1),n2=(x2,y2,z2),
则即解得
即解得
不妨取n1=(1,-,0),n2=(,1,2).
因为n1·n2=0,所以n1⊥n2,
所以平面DEA⊥平面ECA.
