2024-2025学年上海实验学校高二下学期数学周测试题(含答案)
文档属性
| 名称 | 2024-2025学年上海实验学校高二下学期数学周测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 770.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 00:00:00 | ||
图片预览




文档简介
上实验2024-2025学年第二学期高二年级数学测验六
2025.4
一、填空题
1.某医院对某学校高三年级的600名学生进行身体健康调查,采用男女分层抽样法抽取一个容量为50的样本,已知女生比男生少抽了10人,则该年级的女生人数是________.
2.某校高一年级抽样的30名女生的身高(cm)数据从小到大排序如下:
148 149 154 154 155 155 155 157 157 158
158 159 160 161 161 162 162 162 162 163
163 163 164 164 165 165 170 171 172 172
经计算,原来这组数据的第80百分位数为164.5.现将其去掉最后一个数据172,则剩余数据的第80百分位数________.(选填“变大”“变小”或“不变”).
3.某兴趣小组研究光照时长和向日葵种子发芽数量(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉后,相关系数________(选填“变大”“变小”或“不变”).
4.以下是一些城市的海拔高度与该城市的大气压的对照表.我们已知大气压与海拔高度是近似线性的关系。
城市 海拔高度 大气压
北京 31.2 99.86
哈尔滨 171.7 98.51
上海 4.5 100.53
昆明 1891.4 80.80
拉萨 3658.0 65.23
则我们可以利用一元线性回归分析(其中海拔高度为解释变量,大气压为反应变量),估计珠穆朗玛峰顶(海拔8848.9米)的大气压为________(近似到小数点后两位).
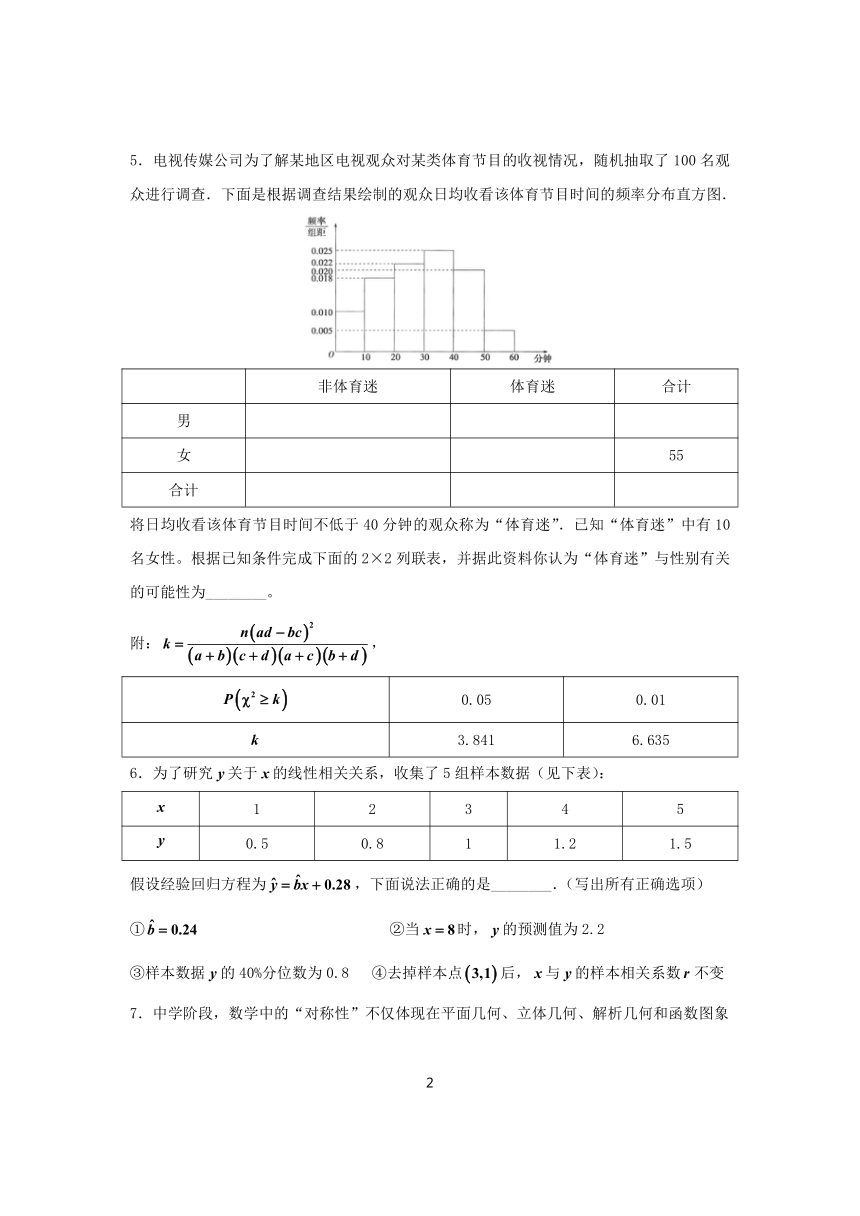
5.电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.
非体育迷 体育迷 合计
男
女 55
合计
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.已知“体育迷”中有10名女性。根据已知条件完成下面的2×2列联表,并据此资料你认为“体育迷”与性别有关的可能性为________。
附:,
0.05 0.01
3.841 6.635
6.为了研究关于的线性相关关系,收集了5组样本数据(见下表):
1 2 3 4 5
0.5 0.8 1 1.2 1.5
假设经验回归方程为,下面说法正确的是________.(写出所有正确选项)
① ②当时,的预测值为2.2
③样本数据的40%分位数为0.8 ④去掉样本点后,与的样本相关系数不变
7.中学阶段,数学中的“对称性”不仅体现在平面几何、立体几何、解析几何和函数图象
中,还体现在概率问题中.例如,甲乙两人进行比赛,若甲每场比赛获胜概率均为,且每场比赛结果相互独立,则由对称性可知,在5场比赛后,甲获胜次数不低于3场的概率为.现甲乙两人分别进行独立重复试验,每人抛掷一枚质地均匀的硬币.若甲抛掷次,乙抛掷次,,则抛掷结果中甲正面朝上次数大于乙正面朝上次数的概率________.
8.已知数列,的通项公式分别为,,,,从数列中任取一项,则该项也是数列中的项的概率为________.(结果用分数表示)
9.项数为的数列满足,当且仅当时,(其中,2, ,规定:,),称为“好数列”,在项数为6且的所有中,随机选取一个数列,该数列是“好数列”的概率
是________.
10.6根长度相同的绳子平行放置在桌面上,分别将左、右两边的6个绳头各自随机均分成3组,然后将每组内的两个绳头打结,则这6根绳子恰能围成一个大圈的概率为________.
11.在平面直角坐标系中,曲线,曲线.经过上一点作一条倾斜角为的直线,与交于两个不同的点、,则的取值范围为________.
12.双曲线具有如下光学性质:如图,,是双曲线的左、右焦点,从右焦点发出的光线交双曲线右支于点,经过双曲线反射后,反射光线的反向延长线过左焦点.若双曲线的方程为,下列结论正确的是________.
①若,则;
②当过时,光由所经过的路程为10;
③射线所在直线的斜率为,则;
④若,直线与相切,则.
二、选择题
13.给出如下列联表
患心脏病 患其它病 合计
高血压 20 10 30
不高血压 30 50 80
合计 50 60 110
,
参照公式,得到的正确结论是( )
A.有99%以上的把握认为“高血压与患心脏病无关”
B.有99%以上的把握认为“高血压与患心脏病有关”
C.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病无关”
D.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病有关”
14.数据3.2,3.4,3.8,4.2,4.3,4.5,,6.6的第65百分位数是4.5,则实数的取值范围是( )
A. B. C. D.
15.一组样本数据,, ,的平均数为,标准差为.另一组样本数据,, ,的平均数为,标准差为.两组数据合成一组新数据,, ,,, ,,新数据的平均数为,标准差为,则( )
A. B. C. D.与的大小与有关
16.信息熵是信息论中的一个重要概念.设随机变量所有可能的取值为1,2,…,,且,,定义的信息熵.
命题1:若,则随着的增大而增大;
命题2:若,随机变量所有可能的取值为1,2,…,,且,则.则以下结论正确的是( )
A.命题1正确,命题2错误 B.命题1错误,命题2正确
C.两个命题都错误 D.两个命题都正确
三、解答题
17.某中学的小乔同学参加上海市举办的禁毒知识测试大赛,本次大赛由十道选择题组成,得分规则为:作对一题得1分,做错一题扣去1分,不做得0分,总得分7分才算及格。小乔的目标是及格,在这次考试中,他确定他做的前六题全对,记6分,而他做余下的四道题中,每道题作对的概率均为.考试中,小乔思量:从余下的四道题中再做一题并且及格的概率;从余下的四道题中恰做两道并且及格的概率,他发现,只做一道反而更容易及格.
(1)设小乔从余下的四道题中恰做三题并且及格的概率为,从余下的四道题中全做并且及格的概率为,求及;
(2)计算:小乔从余下的四道题中,恰做几道时及格的概率最大?
18.组合数有许多丰富有趣的性质,例如,二项式系数的和有下述性质:.小明同学想进一步探究组合数平方和的性质,请帮他完成下面的探究.
(1)计算:,,并与,比较,你有什么发现?写出一般性结论并证明;
(2)证明:
(3)利用上述(1)(2)两小问的结论,证明:.
19.某工厂生产某款电池,在满电状态下能够持续放电时间不低于10小时的为合格品,工程师选择某台生产电池的机器进行参数调试,在调试前后,分别在其产品中随机抽取样本数据进行统计,制作了如下的列联表:
产品 合格 不合格 合计
调试前 45 15 60
调试后 35 5 40
合计 80 20 100
(1)根据表中数据,依据显著性水平的独立性检验,能否认为参数调试与产品质量有关联;
(2)现从调试前的样本中按合格和不合格,用分层随机抽样法抽取8件产品重新做参数调试,再从这8件产品中随机抽取3件做对比分析,记抽取的3件中合格的件数为,求的分布和期望;
(3)用样本分布的频率估计总体分布的概率,若现在随机抽取调试后的产品1000件,记其中合格的件数为,求使事件“”的概率最大时的取值.
参考公式及数据:,其中.
0.05 0.025 0.01 0.005 0.001
3.841 5.024 6.635 7.879 10.828
20.已知椭圆过点,且的左焦点为,直线与交于,两点.
(1)求椭圆的方程;
(2)若,且点的坐标为,求直线的斜率;
(3)若,其中为坐标原点,求面积的最大值.
四、附加题
21.已知半圆,圆,作图与半圆,圆轴均相切,点,且
(1)求的周长
(2)证明:为等比数列
(3)证明:对任意正整数
参考答案
一、填空题
1.; 2.变小; 3.变大; 4.; 5.不到95%; 6.①②④; 7.; 8.; 9.; 10.; 11. 12.①③
11.在平面直角坐标系中,曲线,曲线.经过上一点作一条倾斜角为的直线,与交于两个不同的点、,则的取值范围为________.
【答案】
【解析】设,则直线的方程为,代入曲线的方程,
得,化简可得:,(1),
由于与交于两个不同的点,故关于的方程(1)的判别式,计算得
因此有,(2),
设的横坐标分别为,由(1)知,
因此,结合的倾斜角为可知,
由(2)可知,,故,
从而得,故答案为:.
12.双曲线具有如下光学性质:如图,,是双曲线的左、右焦点,从右焦点发出的光线交双曲线右支于点,经过双曲线反射后,反射光线的反向延长线过左焦点.若双曲线的方程为,下列结论正确的是________.
①若,则;
②当过时,光由所经过的路程为10;
③射线所在直线的斜率为,则;
④若,直线与相切,则.
【答案】①③
【解析】对于①:若,则,因为在双曲线右支上,
所以,由勾股定理得:,
二者联立解得:,故①正确;
对于②:光由所经过的路程为:
,故②错误;
对于③:双曲线的方程为,设左,右顶点分别为,如图所示:
当与同向共线时,的方向为,此时,最小,
因为在双曲线右支上,所以所在直线的斜率为,即,故③正确;
对于④:设直线的方程为,
,消去可得:,其中,即,解得代入,有,解得,
由在双曲线右支上,即,解得舍去,
所以,所以,故④错误;
故答案为:①③.
二、选择题
13.B 14.A 15.A 16.A
15.一组样本数据,, ,的平均数为,标准差为.另一组样本数据,, ,的平均数为,标准差为.两组数据合成一组新数据,, ,,, ,,新数据的平均数为,标准差为,则( )
A. B. C. D.与的大小与有关
【答案】A
【解析】对于数据,可得,
对于数据,可得,
对于数据,可得:
平均数
标准差
故选:.
16.信息熵是信息论中的一个重要概念.设随机变量所有可能的取值为1,2,…,,且,,定义的信息熵.
命题1:若,则随着的增大而增大;
命题2:若,随机变量所有可能的取值为1,2,…,,且,则.则以下结论正确的是( )
A.命题1正确,命题2错误 B.命题1错误,命题2正确
C.两个命题都错误 D.两个命题都正确
【答案】A
【解析】若,则
由对数函数的单调性可知,随着的增大而增大,故命题1正确;
D.依题意知,,
又
,
故命题2错误.故选:.
三.解答题
17.(1) (2)时,恰做一道及格概率最大;时,恰做一道或三道并且及格的概率最大;时,恰做三道及格概率最大.
18.(1)
规律:,证明略 (2)证明略 (3)证明略
19.(1)无关 (2)分布列如下, (3)
20.(1) (2)或 (3)最大面积是4
四、附加题
21.已知半圆,圆,作图与半圆,圆轴均相切,点,且
(1)求的周长
(2)证明:为等比数列
(3)证明:对任意正整数
【答案】(1)2 (2)证明见解析 (3)证明见解
【解析】(1)圆与轴均相切,且圆的圆心坐标为
圆的半径分别为,又圆分别与半圆内切,圆相外切,
则的周长为
(2)证明:依题意,有,
则
消去可得,整理得:
由题意可知,,即,
是首项为1,公比为的等比数列;
(3)证明:由(2)得,,则
令,则当时,,
要证,需证
即证
当
(当且仅当时等号成立)
即对任意正整数.
2025.4
一、填空题
1.某医院对某学校高三年级的600名学生进行身体健康调查,采用男女分层抽样法抽取一个容量为50的样本,已知女生比男生少抽了10人,则该年级的女生人数是________.
2.某校高一年级抽样的30名女生的身高(cm)数据从小到大排序如下:
148 149 154 154 155 155 155 157 157 158
158 159 160 161 161 162 162 162 162 163
163 163 164 164 165 165 170 171 172 172
经计算,原来这组数据的第80百分位数为164.5.现将其去掉最后一个数据172,则剩余数据的第80百分位数________.(选填“变大”“变小”或“不变”).
3.某兴趣小组研究光照时长和向日葵种子发芽数量(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉后,相关系数________(选填“变大”“变小”或“不变”).
4.以下是一些城市的海拔高度与该城市的大气压的对照表.我们已知大气压与海拔高度是近似线性的关系。
城市 海拔高度 大气压
北京 31.2 99.86
哈尔滨 171.7 98.51
上海 4.5 100.53
昆明 1891.4 80.80
拉萨 3658.0 65.23
则我们可以利用一元线性回归分析(其中海拔高度为解释变量,大气压为反应变量),估计珠穆朗玛峰顶(海拔8848.9米)的大气压为________(近似到小数点后两位).
5.电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.
非体育迷 体育迷 合计
男
女 55
合计
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.已知“体育迷”中有10名女性。根据已知条件完成下面的2×2列联表,并据此资料你认为“体育迷”与性别有关的可能性为________。
附:,
0.05 0.01
3.841 6.635
6.为了研究关于的线性相关关系,收集了5组样本数据(见下表):
1 2 3 4 5
0.5 0.8 1 1.2 1.5
假设经验回归方程为,下面说法正确的是________.(写出所有正确选项)
① ②当时,的预测值为2.2
③样本数据的40%分位数为0.8 ④去掉样本点后,与的样本相关系数不变
7.中学阶段,数学中的“对称性”不仅体现在平面几何、立体几何、解析几何和函数图象
中,还体现在概率问题中.例如,甲乙两人进行比赛,若甲每场比赛获胜概率均为,且每场比赛结果相互独立,则由对称性可知,在5场比赛后,甲获胜次数不低于3场的概率为.现甲乙两人分别进行独立重复试验,每人抛掷一枚质地均匀的硬币.若甲抛掷次,乙抛掷次,,则抛掷结果中甲正面朝上次数大于乙正面朝上次数的概率________.
8.已知数列,的通项公式分别为,,,,从数列中任取一项,则该项也是数列中的项的概率为________.(结果用分数表示)
9.项数为的数列满足,当且仅当时,(其中,2, ,规定:,),称为“好数列”,在项数为6且的所有中,随机选取一个数列,该数列是“好数列”的概率
是________.
10.6根长度相同的绳子平行放置在桌面上,分别将左、右两边的6个绳头各自随机均分成3组,然后将每组内的两个绳头打结,则这6根绳子恰能围成一个大圈的概率为________.
11.在平面直角坐标系中,曲线,曲线.经过上一点作一条倾斜角为的直线,与交于两个不同的点、,则的取值范围为________.
12.双曲线具有如下光学性质:如图,,是双曲线的左、右焦点,从右焦点发出的光线交双曲线右支于点,经过双曲线反射后,反射光线的反向延长线过左焦点.若双曲线的方程为,下列结论正确的是________.
①若,则;
②当过时,光由所经过的路程为10;
③射线所在直线的斜率为,则;
④若,直线与相切,则.
二、选择题
13.给出如下列联表
患心脏病 患其它病 合计
高血压 20 10 30
不高血压 30 50 80
合计 50 60 110
,
参照公式,得到的正确结论是( )
A.有99%以上的把握认为“高血压与患心脏病无关”
B.有99%以上的把握认为“高血压与患心脏病有关”
C.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病无关”
D.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病有关”
14.数据3.2,3.4,3.8,4.2,4.3,4.5,,6.6的第65百分位数是4.5,则实数的取值范围是( )
A. B. C. D.
15.一组样本数据,, ,的平均数为,标准差为.另一组样本数据,, ,的平均数为,标准差为.两组数据合成一组新数据,, ,,, ,,新数据的平均数为,标准差为,则( )
A. B. C. D.与的大小与有关
16.信息熵是信息论中的一个重要概念.设随机变量所有可能的取值为1,2,…,,且,,定义的信息熵.
命题1:若,则随着的增大而增大;
命题2:若,随机变量所有可能的取值为1,2,…,,且,则.则以下结论正确的是( )
A.命题1正确,命题2错误 B.命题1错误,命题2正确
C.两个命题都错误 D.两个命题都正确
三、解答题
17.某中学的小乔同学参加上海市举办的禁毒知识测试大赛,本次大赛由十道选择题组成,得分规则为:作对一题得1分,做错一题扣去1分,不做得0分,总得分7分才算及格。小乔的目标是及格,在这次考试中,他确定他做的前六题全对,记6分,而他做余下的四道题中,每道题作对的概率均为.考试中,小乔思量:从余下的四道题中再做一题并且及格的概率;从余下的四道题中恰做两道并且及格的概率,他发现,只做一道反而更容易及格.
(1)设小乔从余下的四道题中恰做三题并且及格的概率为,从余下的四道题中全做并且及格的概率为,求及;
(2)计算:小乔从余下的四道题中,恰做几道时及格的概率最大?
18.组合数有许多丰富有趣的性质,例如,二项式系数的和有下述性质:.小明同学想进一步探究组合数平方和的性质,请帮他完成下面的探究.
(1)计算:,,并与,比较,你有什么发现?写出一般性结论并证明;
(2)证明:
(3)利用上述(1)(2)两小问的结论,证明:.
19.某工厂生产某款电池,在满电状态下能够持续放电时间不低于10小时的为合格品,工程师选择某台生产电池的机器进行参数调试,在调试前后,分别在其产品中随机抽取样本数据进行统计,制作了如下的列联表:
产品 合格 不合格 合计
调试前 45 15 60
调试后 35 5 40
合计 80 20 100
(1)根据表中数据,依据显著性水平的独立性检验,能否认为参数调试与产品质量有关联;
(2)现从调试前的样本中按合格和不合格,用分层随机抽样法抽取8件产品重新做参数调试,再从这8件产品中随机抽取3件做对比分析,记抽取的3件中合格的件数为,求的分布和期望;
(3)用样本分布的频率估计总体分布的概率,若现在随机抽取调试后的产品1000件,记其中合格的件数为,求使事件“”的概率最大时的取值.
参考公式及数据:,其中.
0.05 0.025 0.01 0.005 0.001
3.841 5.024 6.635 7.879 10.828
20.已知椭圆过点,且的左焦点为,直线与交于,两点.
(1)求椭圆的方程;
(2)若,且点的坐标为,求直线的斜率;
(3)若,其中为坐标原点,求面积的最大值.
四、附加题
21.已知半圆,圆,作图与半圆,圆轴均相切,点,且
(1)求的周长
(2)证明:为等比数列
(3)证明:对任意正整数
参考答案
一、填空题
1.; 2.变小; 3.变大; 4.; 5.不到95%; 6.①②④; 7.; 8.; 9.; 10.; 11. 12.①③
11.在平面直角坐标系中,曲线,曲线.经过上一点作一条倾斜角为的直线,与交于两个不同的点、,则的取值范围为________.
【答案】
【解析】设,则直线的方程为,代入曲线的方程,
得,化简可得:,(1),
由于与交于两个不同的点,故关于的方程(1)的判别式,计算得
因此有,(2),
设的横坐标分别为,由(1)知,
因此,结合的倾斜角为可知,
由(2)可知,,故,
从而得,故答案为:.
12.双曲线具有如下光学性质:如图,,是双曲线的左、右焦点,从右焦点发出的光线交双曲线右支于点,经过双曲线反射后,反射光线的反向延长线过左焦点.若双曲线的方程为,下列结论正确的是________.
①若,则;
②当过时,光由所经过的路程为10;
③射线所在直线的斜率为,则;
④若,直线与相切,则.
【答案】①③
【解析】对于①:若,则,因为在双曲线右支上,
所以,由勾股定理得:,
二者联立解得:,故①正确;
对于②:光由所经过的路程为:
,故②错误;
对于③:双曲线的方程为,设左,右顶点分别为,如图所示:
当与同向共线时,的方向为,此时,最小,
因为在双曲线右支上,所以所在直线的斜率为,即,故③正确;
对于④:设直线的方程为,
,消去可得:,其中,即,解得代入,有,解得,
由在双曲线右支上,即,解得舍去,
所以,所以,故④错误;
故答案为:①③.
二、选择题
13.B 14.A 15.A 16.A
15.一组样本数据,, ,的平均数为,标准差为.另一组样本数据,, ,的平均数为,标准差为.两组数据合成一组新数据,, ,,, ,,新数据的平均数为,标准差为,则( )
A. B. C. D.与的大小与有关
【答案】A
【解析】对于数据,可得,
对于数据,可得,
对于数据,可得:
平均数
标准差
故选:.
16.信息熵是信息论中的一个重要概念.设随机变量所有可能的取值为1,2,…,,且,,定义的信息熵.
命题1:若,则随着的增大而增大;
命题2:若,随机变量所有可能的取值为1,2,…,,且,则.则以下结论正确的是( )
A.命题1正确,命题2错误 B.命题1错误,命题2正确
C.两个命题都错误 D.两个命题都正确
【答案】A
【解析】若,则
由对数函数的单调性可知,随着的增大而增大,故命题1正确;
D.依题意知,,
又
,
故命题2错误.故选:.
三.解答题
17.(1) (2)时,恰做一道及格概率最大;时,恰做一道或三道并且及格的概率最大;时,恰做三道及格概率最大.
18.(1)
规律:,证明略 (2)证明略 (3)证明略
19.(1)无关 (2)分布列如下, (3)
20.(1) (2)或 (3)最大面积是4
四、附加题
21.已知半圆,圆,作图与半圆,圆轴均相切,点,且
(1)求的周长
(2)证明:为等比数列
(3)证明:对任意正整数
【答案】(1)2 (2)证明见解析 (3)证明见解
【解析】(1)圆与轴均相切,且圆的圆心坐标为
圆的半径分别为,又圆分别与半圆内切,圆相外切,
则的周长为
(2)证明:依题意,有,
则
消去可得,整理得:
由题意可知,,即,
是首项为1,公比为的等比数列;
(3)证明:由(2)得,,则
令,则当时,,
要证,需证
即证
当
(当且仅当时等号成立)
即对任意正整数.
同课章节目录
