期末冲刺练习卷(二)(含解析)-2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 期末冲刺练习卷(二)(含解析)-2024-2025学年数学七年级下册苏科版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 981.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 18:58:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末冲刺练习卷(二)-2024-2025学年数学七年级下册苏科版(2024)
一、填空题
1.若是关于的二元一次方程,则 .
2.中国华为公司研发的麒麟芯片是全球第一款采用工艺制造的最先进手机处理器.已知,则数据“”用科学记数法表示为 .
3.如图,在上网课时把平板放在三角形支架上用到的数学道理是 .
4.已知三角形两边的长分别为1、5,第三边长为整数,则第三边的长为 .
5.命题“如果互为相反数,那么”的逆命题为 .
6.一个多边形的内角和是它的外角和的2倍,则这个多边形是 边形.
7.若方程组的解x、y的和为7,则 .
8.关于x的不等式组恰有三个整数解,则的取值范围是 .
9.若关于x,y的方程组的解是,则方程组的解是 .
10.世纪欧拉引进了求和符号“”(其中,且和表示正整数),对这个符号我们进行如下定义:表示从开始取数一直取到,全部加起来,即.例如:当时,.若,则 .
11.计算: .
12.已知三角形的三边长分别为2,x,3,且x为奇数,则 .
13.近来中国芯片技术获得重大突破,芯片已经量产,已知 ,将数据用科学记数法表示为 .
14.一个多边形的每一个外角都等于,则这个多边形的内角和为 .
15.一把直尺和一块直角三角尺(含角)如图所示摆放,直尺的一边与三角尺的两直角边分别交于点D、点E,直尺的另一边过A点且与三角尺的直角边交于点F,若,则度数为 .
16.已知不等式组无解,则的取值范围为 .
17.如图,在ABC中,AD是中线,点E是AB中点,且,若AEF的面积是2,则CDF的面积为 .
18.一机器人以0.3m/s的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止所需时间为 s.
二、解答题
19.计算:
(1);
(2).
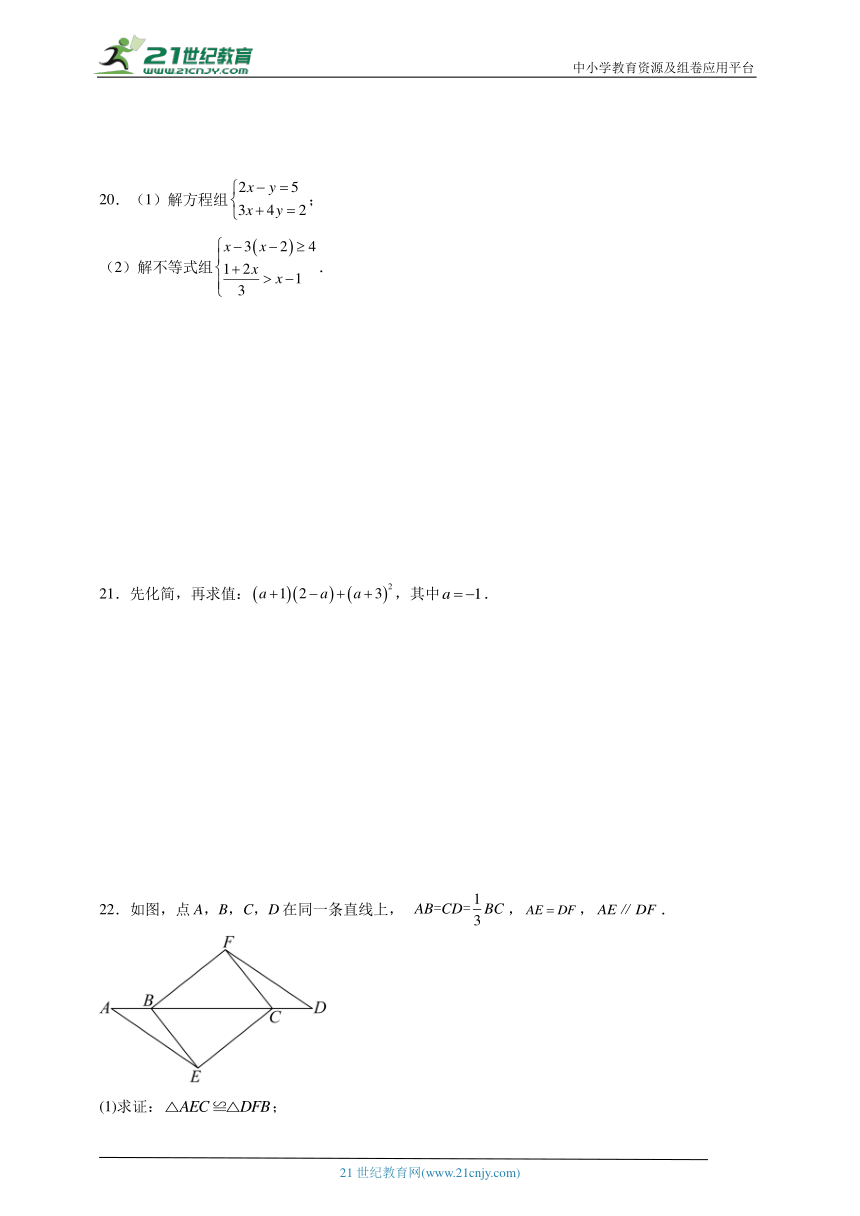
20.(1)解方程组;
(2)解不等式组.
21.先化简,再求值:,其中.
22.如图,点A,B,C,D在同一条直线上, ,,.
(1)求证:;
(2)若,求四边形的面积.
23.如图,在边长为1的小正方形组成的网格中,将平移得到,连接,.
(1)根据题意,补全图形;
(2)图中和的数量关系是 ;
(3)在上画出一点P,使得.
24.对于任意实数m,n,定义一种新运算:,其中,等式右边是通常的加减运算.如:.若关于x的不等式组恰有3个整数解,求t的取值范围.
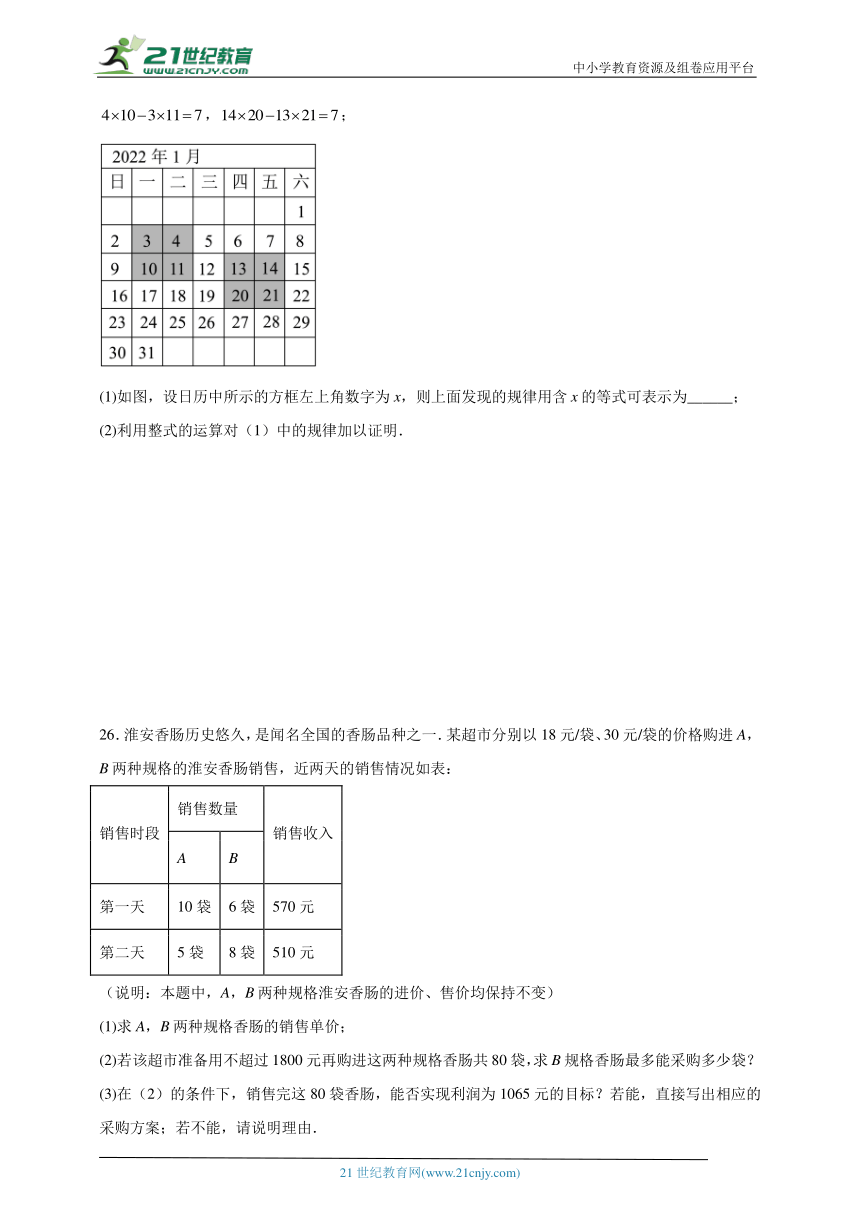
25.在日历上,我们可以发现其中某些数满足一定的规律,如图是2022年1月份的日历,我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减.例如:,;
(1)如图,设日历中所示的方框左上角数字为x,则上面发现的规律用含x的等式可表示为______;
(2)利用整式的运算对(1)中的规律加以证明.
26.淮安香肠历史悠久,是闻名全国的香肠品种之一.某超市分别以18元/袋、30元/袋的价格购进A,B两种规格的淮安香肠销售,近两天的销售情况如表:
销售时段 销售数量 销售收入
A B
第一天 10袋 6袋 570元
第二天 5袋 8袋 510元
(说明:本题中,A,B两种规格淮安香肠的进价、售价均保持不变)
(1)求A,B两种规格香肠的销售单价;
(2)若该超市准备用不超过1800元再购进这两种规格香肠共80袋,求B规格香肠最多能采购多少袋?
(3)在(2)的条件下,销售完这80袋香肠,能否实现利润为1065元的目标?若能,直接写出相应的采购方案;若不能,请说明理由.
27.有些代数问题,我们可以采用构造几何图形的方法研究,借助直观、形象的几何模型,加深认识和理解,从中感悟“数形结合”的思想方法,感悟代数和几何内在的一致性.如图1是由两个边长分别为m,n的小正方形和两个全等的小长方形拼成的大正方形,则根据大正方形的面积可以验证公式:.
(1)图2是由四个全等的直角三角形(边长分别为a,b,c,且)和一个小正方形拼成的大正方形,利用图1验证公式的方法求出a、b、c满足的等量关系式;
(2)如图2,在(1)的条件下,若,,求阴影部分的面积;
(3)如图3,以(2)中的a,b,c为边长作三个正方形,并将以a,b为边长的两个小正方形放置于以c为边长的大正方形内,若阴影部分的面积为1,求四边形的面积.
28.已知在中,,为锐角,是边上的高,在射线上取一点,使,在平面内取一点F,使,且点E,F在直线的异侧,连接交于点.
(1)如图1,当时,补全图形,并证明.;
(2)在图1中用等式表示线段,,的数量关系,并证明;
(3)设当的大小变化时,若,直接写出线段长的取值范围.
《期末冲刺练习卷(二)-2024-2025学年数学七年级下册苏科版(2024)》参考答案
1.
【分析】根据二元一次方程的定义可得到关于a的方程和不等式,进而求解即可.
【详解】∵是关于的二元一次方程,
∴ ,解得 ,
故答案为:-2.
【点睛】本题主要考查二元一次方程的定义,掌握二元一次方程的定义是解题的关键.
2.
【分析】本题主要考查了科学记数法,科学记数法的表现形式为的形式,其中,为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值大于等于时,是正数,当原数绝对值小于时,是负数;由此进行求解即可得到答案.
【详解】解:,
故答案为:.
3.三角形具有稳定性
【分析】根据三角形具有稳定性进行求解即可.
【详解】解:在上网课时把平板放在三角形支架上用到的数学道理是三角形具有稳定性,
故答案为:三角形具有稳定性.
【点睛】本题主要考查了三角形的稳定性,熟知三角形具有稳定性是解题的关键.
4.5
【详解】分析:根据三角形的三边关系“任意两边之和>第三边,任意两边之差<第三边”,求得第三边的取值范围,再进一步根据第三边是整数求解.
详解:根据三角形的三边关系,得
第三边>4,而<6.
又第三条边长为整数,
则第三边是5.
点睛:此题主要是考查了三角形的三边关系,同时注意整数这一条件.
5.如果,那么互为相反数
【分析】把原命题的条件作为逆命题的结论,把原命题的结论作为逆命题的条件,即可.
【详解】“如果互为相反数,那么”的逆命题为:“如果,那么互为相反数”.
故答案是:如果,那么互为相反数.
【点睛】本题主要考查逆命题的定义,掌握逆命题与原命题的关系,是解题的关键.
6.六
【分析】本题考查了多边形内角和与外角和,熟练掌握多边形内角和公式是解题的关键.设这个多边形的边数为,根据多边形外角和等于360度和多边形内角和公式列方程解之即可.
【详解】解:设这个多边形为边形
根据题意可知,这个边形的内角和为
则
解得:
故答案为:六.
7.6
【分析】本题考查根据二元一次方程组的解的情况求参数,两个方程相加后,结合方程组的解的情况,得到关于的方程,进行求解即可.
【详解】解:
,得:,
∴,
由题意,得:,
∴,
∴;
故答案为:6.
8.
【分析】本题考查了一元一次不等式组的整数解,不等式组整理后,表示出不等式组的解集,由不等式组有个整数解,确定出的范围即可,根据整数解的个数得出关于的解题的关键.
【详解】解:,
解不等式得:,
解不等式得:,
∵不等式组恰有三个整数解,
∴,
故答案为:.
9.
【分析】本题主要考查二元一次方程组的解法,关键是熟练掌握二元一次方程组的解法即代入消元法和加减消元法,本题要注意整体思想的运用.
根据题意得到,进而求解即可.
【详解】∵关于x,y的方程组的解是,
∴方程组中
∴.
故答案为:.
10.
【分析】本题考查了多项式乘多项式求和,恒等式的问题,根据,把代入,然后通过法则进行计算对比即可求解,掌握多项式乘以多项式的运算法则是解题的关键.
【详解】解:∵,且中二次项系数为,
∴,
∴
,
∴,
∴,
∴,,
故答案为:.
11.
【分析】逆用积的乘方公式计算即可.
【详解】,
故答案为:.
【点睛】本题考查利用积的乘方进行计算,解题的关键是逆用积的乘方公式.
12.3
【分析】本题考查三角形的三边关系,根据三角形的三边关系求出的范围,进而确定的值即可.
【详解】解:∵三角形三边长分别为2,3,x,x为奇数,
∴,即:,则.
故答案为:3.
13.
【分析】本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是:负整数指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
【详解】
故答案为:
14.1260
【分析】本题主要考查了多变形的内角与外角.首先根据外角和与一个外角的度数可得多边形的边数,再根据多边形的内角和公式进行计算即可.
【详解】解:一个多边形的每一个外角都等于,
这个多边形的边数为:,
这个多边形的内角和为:,
故答案为:.
15./48度
【分析】本题主要考查了平行线的性质,直角三角形的性质.根据题意可得,从而得到,即可求解.
【详解】解:根据题意得:,
∴,
∵,
∴,
∴.
故答案为:
16.
【分析】求出不等式组中每个不等式的解集,根据已知即可得出关于a的不等式,即可得出答案.
【详解】解:不等式组无解,
,
解得:,
故答案为:.
【点睛】本题考查了一元一次不等式组的应用,解此题的关键是能得出关于a的不等式,题目比较好,难度适中.
17.8
【分析】根据三角形面积公式,利用AD=3AF得到S△ADE=6,再利用点E是AB中点得到S△BDE=6,接着利用AD是中线得到S△ACD=12,然后利用从而得到S△CDF的值.
【详解】解:∵DF=2AF,
∴AD=3AF,
∴S△ADE=3S△AEF=3×2=6,
∵点E是AB中点,
∴S△ADE=S△BDE=6,
∴S△ABD=12,
∵AD是中线,
∴S△ABD=S△ACD=12,
∵DF=2AF,
∴,
∴S△CDF=12×=8.
故答案为:8.
【点睛】本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S=×底×高;三角形的中线将三角形分成面积相等的两部分.
18.160
【分析】该机器人所经过的路径是一个正多边形,利用360°除以45°,即可求得正多边形的边数,即可求得周长,利用周长除以速度即可求得所需时间.
【详解】解:360÷45=8,
则所走的路程是:6×8=48m,
则所用时间是:48÷0.3=160s,
故答案为:160.
【点睛】题目主要考查多边形的外角和及有理数的乘除法的应用,熟练掌握运用多边形外角的定理是解题关键.
19.(1)0
(2)
【分析】本题主要考查了实数混合运算,幂的混合运算,解题的关键是熟练掌握运算法则,准确计算.
(1)根据负整数指数幂、零指数幂运算法则,进行计算即可;
(2)根据同底数幂乘法,幂的乘方和积的乘方运算法则,进行计算即可.
【详解】(1)解:
;
(2)解:
.
20.(1);(2)
【分析】本题主要考查了解二元一次方程组,解不等式组,熟练掌握解二元一次方程组和不等式组的方法,是解题的关键.
(1)用加减消元法解二元一次方程组即可;
(2)先求出两个不等式的解集,再求出不等式组的解集即可.
【详解】解:(1),
得:,
解得:,
把代入①得:,
解得:,
∴不等式组的解集为;
(2),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
21.,4
【分析】本题主要考查了整式化简求值,先根据整式混合运算法则进行化简,然后再代入数据进行求值即可.
【详解】解:
,
把代入得:原式.
22.(1)见解析
(2)9
【分析】(1)由,得,进一步证得,根据边角边求证;
(2)以为底作为高,则,,由,求得;求证,得,所以.
【详解】(1)证明:∵,
∴,
∵,
∴,
在和中,
∴;
(2)解:在中,以为底作为高,
∴,,
∵,
∴,
∵,
∴,
∵,
∴,,
在和中,
,
∴,
∴,
∴.
【点睛】本题考查平行的性质,全等三角形的判定和性质,三角形面积计算;能够灵活运用全等三角形性质是解题的关键.
23.(1)见解析
(2)互补
(3)见解析
【分析】本题考查图形的平移,平行线的性质,平移作图.熟练掌握平移的性质,是解题的关键.
(1)根据的位置,确定平移规则,画出,再连接,即可;
(2)根据平移的性质,作答即可;
(3)根据格点特点,过点作,交于点P,则点P即为所求.
【详解】(1)解:如图,,,即为所求;
(2)解:根据平移可知:,
∴,
即和互补.
(3)解:如图,根据网格特点,过点作,交于点P,则点P即为所求.
∵,
∴,
根据平移可知:,
∴.
24.
【分析】此题主要考查了一元一次不等式组的整数解,新定义运算,熟练掌握不等式的解法及运算法则是解本题的关键.根据新定义得出关于x的不等式组,根据解集中恰有3个整数解,确定出t的范围即可.
【详解】解:由题意得:.即,
∴,
∵该不等式组恰有3个整数解,即整数解,8,9,
∴,
解得.
故t的取值范围是.
25.(1)
(2)证明见解析
【分析】(1)根据题意用含x的式子表示其余三个数,表达规律即可;
(2)根据整式乘法公式,把化简,即可证明.
【详解】(1)解:设日历中所示的方框左上角数字为x,
则其余三个数从小到大依次是:,
∴规律用含x的式子可表示为;
故答案为:;
(2)证明:
【点睛】本题考查整式的混合运算和列代数式,解题的关键是掌握多项式乘以多项式的运算法则.
26.(1)A规格香肠的销售单价是30元/袋,B规格香肠的销售单价是45元/袋
(2)B规格香肠最多能采购30袋
(3)不能实现利润为1065元的目标,理由见解析
【分析】本题主要考查了二元一次方程组和一元一次不等式的应用,一元一次方程的应用,解题的关键是根据等量关系列出方程,根据不等关系列出不等式.
(1)设A规格香肠的销售单价是x元/袋,B规格香肠的销售单价是y元/袋,根据表格中的数据列出方程组,解方程组即可;
(2)设采购B规格香肠m袋,则采购A规格香肠袋,根据两种规格香肠总价格不超过1800元,列出不等式,解不等式即可;
(3)根据利润为1065元,列出方程,求出m的值,然后再与(2)中m的范围进行比较即可得出答案.
【详解】(1)解:设A规格香肠的销售单价是x元/袋,B规格香肠的销售单价是y元/袋,
根据题意得:,
解得:.
答:A规格香肠的销售单价是30元/袋,B规格香肠的销售单价是45元/袋;
(2)解:设采购B规格香肠m袋,则采购A规格香肠袋,
根据题意得:,
解得:,
∴m的最大值为30,
答:B规格香肠最多能采购30袋;
(3)解:在(2)的条件下,销售完这80袋香肠,不能实现利润为1065元的目标,理由如下:
根据题意得:,
解得:,
又∵,
∴不符合题意,舍去,
∴在(2)的条件下,销售完这80袋香肠,不实现利润为1065元的目标.
27.(1)
(2)
(3)
【分析】本题考查完全平方公式的应用:
(1)大正方形的面积用两种方法表示出来,即可得出答案;
(2)根据完全平方公式变形得出,再求出面积即可;
(3)四边形的面积为,再求解即可.
【详解】(1)解:大正方形的面积为:,
大正方形是由中间的小正方形和4个全等的三角形组成,面积为:,
所以;
(2)解: ∵,,
∴,
∴,
∴,
∴阴影部分的面积为:;
(3)解: ∵,
∴四边形的面积为.
28.(1)见解析
(2),证明见解析;
(3)或
【分析】(1)根据,,由同角的余角相等即可得出结论;
(2)连接,易证,继而可证明,由此可知为的中点,由已知可得,进而得出三条线段的关系;
(3)分M在D点左侧和右侧两种情况讨论,根据求出取值范围,再根据线段和差关系利用不等式性质变形求解即可.
【详解】(1)解:如图,
证明:∵,
∴,
又∵,
∴
∴.
(2)结论:.
证明:连接,
∵,,
∴,
∴,
在和中,
∵,
∴
∴,,
又∵,
∴,
又在和中,
∵,
∴
∴,即:,
∵,
∴,
∴.
(3)当时,M在点D右侧,如图:
当时,,即,
又∵,
∴,
∴
∵,即
当时,若,则.
可知时,M在点D左侧,如图:
当时,,即,
又∵,
∴,
∴
∵,
∴当时,若,则,
综上所述:线段长的取值范围为:或.
【点睛】本题主要考查了全等三角形的综合和不等式性质的应用,解(2)题关键是证明三角形全等得出点M是的中点.解(3)题关键是利用线段和差关系和不等式性质变形得出结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末冲刺练习卷(二)-2024-2025学年数学七年级下册苏科版(2024)
一、填空题
1.若是关于的二元一次方程,则 .
2.中国华为公司研发的麒麟芯片是全球第一款采用工艺制造的最先进手机处理器.已知,则数据“”用科学记数法表示为 .
3.如图,在上网课时把平板放在三角形支架上用到的数学道理是 .
4.已知三角形两边的长分别为1、5,第三边长为整数,则第三边的长为 .
5.命题“如果互为相反数,那么”的逆命题为 .
6.一个多边形的内角和是它的外角和的2倍,则这个多边形是 边形.
7.若方程组的解x、y的和为7,则 .
8.关于x的不等式组恰有三个整数解,则的取值范围是 .
9.若关于x,y的方程组的解是,则方程组的解是 .
10.世纪欧拉引进了求和符号“”(其中,且和表示正整数),对这个符号我们进行如下定义:表示从开始取数一直取到,全部加起来,即.例如:当时,.若,则 .
11.计算: .
12.已知三角形的三边长分别为2,x,3,且x为奇数,则 .
13.近来中国芯片技术获得重大突破,芯片已经量产,已知 ,将数据用科学记数法表示为 .
14.一个多边形的每一个外角都等于,则这个多边形的内角和为 .
15.一把直尺和一块直角三角尺(含角)如图所示摆放,直尺的一边与三角尺的两直角边分别交于点D、点E,直尺的另一边过A点且与三角尺的直角边交于点F,若,则度数为 .
16.已知不等式组无解,则的取值范围为 .
17.如图,在ABC中,AD是中线,点E是AB中点,且,若AEF的面积是2,则CDF的面积为 .
18.一机器人以0.3m/s的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止所需时间为 s.
二、解答题
19.计算:
(1);
(2).
20.(1)解方程组;
(2)解不等式组.
21.先化简,再求值:,其中.
22.如图,点A,B,C,D在同一条直线上, ,,.
(1)求证:;
(2)若,求四边形的面积.
23.如图,在边长为1的小正方形组成的网格中,将平移得到,连接,.
(1)根据题意,补全图形;
(2)图中和的数量关系是 ;
(3)在上画出一点P,使得.
24.对于任意实数m,n,定义一种新运算:,其中,等式右边是通常的加减运算.如:.若关于x的不等式组恰有3个整数解,求t的取值范围.
25.在日历上,我们可以发现其中某些数满足一定的规律,如图是2022年1月份的日历,我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减.例如:,;
(1)如图,设日历中所示的方框左上角数字为x,则上面发现的规律用含x的等式可表示为______;
(2)利用整式的运算对(1)中的规律加以证明.
26.淮安香肠历史悠久,是闻名全国的香肠品种之一.某超市分别以18元/袋、30元/袋的价格购进A,B两种规格的淮安香肠销售,近两天的销售情况如表:
销售时段 销售数量 销售收入
A B
第一天 10袋 6袋 570元
第二天 5袋 8袋 510元
(说明:本题中,A,B两种规格淮安香肠的进价、售价均保持不变)
(1)求A,B两种规格香肠的销售单价;
(2)若该超市准备用不超过1800元再购进这两种规格香肠共80袋,求B规格香肠最多能采购多少袋?
(3)在(2)的条件下,销售完这80袋香肠,能否实现利润为1065元的目标?若能,直接写出相应的采购方案;若不能,请说明理由.
27.有些代数问题,我们可以采用构造几何图形的方法研究,借助直观、形象的几何模型,加深认识和理解,从中感悟“数形结合”的思想方法,感悟代数和几何内在的一致性.如图1是由两个边长分别为m,n的小正方形和两个全等的小长方形拼成的大正方形,则根据大正方形的面积可以验证公式:.
(1)图2是由四个全等的直角三角形(边长分别为a,b,c,且)和一个小正方形拼成的大正方形,利用图1验证公式的方法求出a、b、c满足的等量关系式;
(2)如图2,在(1)的条件下,若,,求阴影部分的面积;
(3)如图3,以(2)中的a,b,c为边长作三个正方形,并将以a,b为边长的两个小正方形放置于以c为边长的大正方形内,若阴影部分的面积为1,求四边形的面积.
28.已知在中,,为锐角,是边上的高,在射线上取一点,使,在平面内取一点F,使,且点E,F在直线的异侧,连接交于点.
(1)如图1,当时,补全图形,并证明.;
(2)在图1中用等式表示线段,,的数量关系,并证明;
(3)设当的大小变化时,若,直接写出线段长的取值范围.
《期末冲刺练习卷(二)-2024-2025学年数学七年级下册苏科版(2024)》参考答案
1.
【分析】根据二元一次方程的定义可得到关于a的方程和不等式,进而求解即可.
【详解】∵是关于的二元一次方程,
∴ ,解得 ,
故答案为:-2.
【点睛】本题主要考查二元一次方程的定义,掌握二元一次方程的定义是解题的关键.
2.
【分析】本题主要考查了科学记数法,科学记数法的表现形式为的形式,其中,为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值大于等于时,是正数,当原数绝对值小于时,是负数;由此进行求解即可得到答案.
【详解】解:,
故答案为:.
3.三角形具有稳定性
【分析】根据三角形具有稳定性进行求解即可.
【详解】解:在上网课时把平板放在三角形支架上用到的数学道理是三角形具有稳定性,
故答案为:三角形具有稳定性.
【点睛】本题主要考查了三角形的稳定性,熟知三角形具有稳定性是解题的关键.
4.5
【详解】分析:根据三角形的三边关系“任意两边之和>第三边,任意两边之差<第三边”,求得第三边的取值范围,再进一步根据第三边是整数求解.
详解:根据三角形的三边关系,得
第三边>4,而<6.
又第三条边长为整数,
则第三边是5.
点睛:此题主要是考查了三角形的三边关系,同时注意整数这一条件.
5.如果,那么互为相反数
【分析】把原命题的条件作为逆命题的结论,把原命题的结论作为逆命题的条件,即可.
【详解】“如果互为相反数,那么”的逆命题为:“如果,那么互为相反数”.
故答案是:如果,那么互为相反数.
【点睛】本题主要考查逆命题的定义,掌握逆命题与原命题的关系,是解题的关键.
6.六
【分析】本题考查了多边形内角和与外角和,熟练掌握多边形内角和公式是解题的关键.设这个多边形的边数为,根据多边形外角和等于360度和多边形内角和公式列方程解之即可.
【详解】解:设这个多边形为边形
根据题意可知,这个边形的内角和为
则
解得:
故答案为:六.
7.6
【分析】本题考查根据二元一次方程组的解的情况求参数,两个方程相加后,结合方程组的解的情况,得到关于的方程,进行求解即可.
【详解】解:
,得:,
∴,
由题意,得:,
∴,
∴;
故答案为:6.
8.
【分析】本题考查了一元一次不等式组的整数解,不等式组整理后,表示出不等式组的解集,由不等式组有个整数解,确定出的范围即可,根据整数解的个数得出关于的解题的关键.
【详解】解:,
解不等式得:,
解不等式得:,
∵不等式组恰有三个整数解,
∴,
故答案为:.
9.
【分析】本题主要考查二元一次方程组的解法,关键是熟练掌握二元一次方程组的解法即代入消元法和加减消元法,本题要注意整体思想的运用.
根据题意得到,进而求解即可.
【详解】∵关于x,y的方程组的解是,
∴方程组中
∴.
故答案为:.
10.
【分析】本题考查了多项式乘多项式求和,恒等式的问题,根据,把代入,然后通过法则进行计算对比即可求解,掌握多项式乘以多项式的运算法则是解题的关键.
【详解】解:∵,且中二次项系数为,
∴,
∴
,
∴,
∴,
∴,,
故答案为:.
11.
【分析】逆用积的乘方公式计算即可.
【详解】,
故答案为:.
【点睛】本题考查利用积的乘方进行计算,解题的关键是逆用积的乘方公式.
12.3
【分析】本题考查三角形的三边关系,根据三角形的三边关系求出的范围,进而确定的值即可.
【详解】解:∵三角形三边长分别为2,3,x,x为奇数,
∴,即:,则.
故答案为:3.
13.
【分析】本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是:负整数指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
【详解】
故答案为:
14.1260
【分析】本题主要考查了多变形的内角与外角.首先根据外角和与一个外角的度数可得多边形的边数,再根据多边形的内角和公式进行计算即可.
【详解】解:一个多边形的每一个外角都等于,
这个多边形的边数为:,
这个多边形的内角和为:,
故答案为:.
15./48度
【分析】本题主要考查了平行线的性质,直角三角形的性质.根据题意可得,从而得到,即可求解.
【详解】解:根据题意得:,
∴,
∵,
∴,
∴.
故答案为:
16.
【分析】求出不等式组中每个不等式的解集,根据已知即可得出关于a的不等式,即可得出答案.
【详解】解:不等式组无解,
,
解得:,
故答案为:.
【点睛】本题考查了一元一次不等式组的应用,解此题的关键是能得出关于a的不等式,题目比较好,难度适中.
17.8
【分析】根据三角形面积公式,利用AD=3AF得到S△ADE=6,再利用点E是AB中点得到S△BDE=6,接着利用AD是中线得到S△ACD=12,然后利用从而得到S△CDF的值.
【详解】解:∵DF=2AF,
∴AD=3AF,
∴S△ADE=3S△AEF=3×2=6,
∵点E是AB中点,
∴S△ADE=S△BDE=6,
∴S△ABD=12,
∵AD是中线,
∴S△ABD=S△ACD=12,
∵DF=2AF,
∴,
∴S△CDF=12×=8.
故答案为:8.
【点睛】本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S=×底×高;三角形的中线将三角形分成面积相等的两部分.
18.160
【分析】该机器人所经过的路径是一个正多边形,利用360°除以45°,即可求得正多边形的边数,即可求得周长,利用周长除以速度即可求得所需时间.
【详解】解:360÷45=8,
则所走的路程是:6×8=48m,
则所用时间是:48÷0.3=160s,
故答案为:160.
【点睛】题目主要考查多边形的外角和及有理数的乘除法的应用,熟练掌握运用多边形外角的定理是解题关键.
19.(1)0
(2)
【分析】本题主要考查了实数混合运算,幂的混合运算,解题的关键是熟练掌握运算法则,准确计算.
(1)根据负整数指数幂、零指数幂运算法则,进行计算即可;
(2)根据同底数幂乘法,幂的乘方和积的乘方运算法则,进行计算即可.
【详解】(1)解:
;
(2)解:
.
20.(1);(2)
【分析】本题主要考查了解二元一次方程组,解不等式组,熟练掌握解二元一次方程组和不等式组的方法,是解题的关键.
(1)用加减消元法解二元一次方程组即可;
(2)先求出两个不等式的解集,再求出不等式组的解集即可.
【详解】解:(1),
得:,
解得:,
把代入①得:,
解得:,
∴不等式组的解集为;
(2),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
21.,4
【分析】本题主要考查了整式化简求值,先根据整式混合运算法则进行化简,然后再代入数据进行求值即可.
【详解】解:
,
把代入得:原式.
22.(1)见解析
(2)9
【分析】(1)由,得,进一步证得,根据边角边求证;
(2)以为底作为高,则,,由,求得;求证,得,所以.
【详解】(1)证明:∵,
∴,
∵,
∴,
在和中,
∴;
(2)解:在中,以为底作为高,
∴,,
∵,
∴,
∵,
∴,
∵,
∴,,
在和中,
,
∴,
∴,
∴.
【点睛】本题考查平行的性质,全等三角形的判定和性质,三角形面积计算;能够灵活运用全等三角形性质是解题的关键.
23.(1)见解析
(2)互补
(3)见解析
【分析】本题考查图形的平移,平行线的性质,平移作图.熟练掌握平移的性质,是解题的关键.
(1)根据的位置,确定平移规则,画出,再连接,即可;
(2)根据平移的性质,作答即可;
(3)根据格点特点,过点作,交于点P,则点P即为所求.
【详解】(1)解:如图,,,即为所求;
(2)解:根据平移可知:,
∴,
即和互补.
(3)解:如图,根据网格特点,过点作,交于点P,则点P即为所求.
∵,
∴,
根据平移可知:,
∴.
24.
【分析】此题主要考查了一元一次不等式组的整数解,新定义运算,熟练掌握不等式的解法及运算法则是解本题的关键.根据新定义得出关于x的不等式组,根据解集中恰有3个整数解,确定出t的范围即可.
【详解】解:由题意得:.即,
∴,
∵该不等式组恰有3个整数解,即整数解,8,9,
∴,
解得.
故t的取值范围是.
25.(1)
(2)证明见解析
【分析】(1)根据题意用含x的式子表示其余三个数,表达规律即可;
(2)根据整式乘法公式,把化简,即可证明.
【详解】(1)解:设日历中所示的方框左上角数字为x,
则其余三个数从小到大依次是:,
∴规律用含x的式子可表示为;
故答案为:;
(2)证明:
【点睛】本题考查整式的混合运算和列代数式,解题的关键是掌握多项式乘以多项式的运算法则.
26.(1)A规格香肠的销售单价是30元/袋,B规格香肠的销售单价是45元/袋
(2)B规格香肠最多能采购30袋
(3)不能实现利润为1065元的目标,理由见解析
【分析】本题主要考查了二元一次方程组和一元一次不等式的应用,一元一次方程的应用,解题的关键是根据等量关系列出方程,根据不等关系列出不等式.
(1)设A规格香肠的销售单价是x元/袋,B规格香肠的销售单价是y元/袋,根据表格中的数据列出方程组,解方程组即可;
(2)设采购B规格香肠m袋,则采购A规格香肠袋,根据两种规格香肠总价格不超过1800元,列出不等式,解不等式即可;
(3)根据利润为1065元,列出方程,求出m的值,然后再与(2)中m的范围进行比较即可得出答案.
【详解】(1)解:设A规格香肠的销售单价是x元/袋,B规格香肠的销售单价是y元/袋,
根据题意得:,
解得:.
答:A规格香肠的销售单价是30元/袋,B规格香肠的销售单价是45元/袋;
(2)解:设采购B规格香肠m袋,则采购A规格香肠袋,
根据题意得:,
解得:,
∴m的最大值为30,
答:B规格香肠最多能采购30袋;
(3)解:在(2)的条件下,销售完这80袋香肠,不能实现利润为1065元的目标,理由如下:
根据题意得:,
解得:,
又∵,
∴不符合题意,舍去,
∴在(2)的条件下,销售完这80袋香肠,不实现利润为1065元的目标.
27.(1)
(2)
(3)
【分析】本题考查完全平方公式的应用:
(1)大正方形的面积用两种方法表示出来,即可得出答案;
(2)根据完全平方公式变形得出,再求出面积即可;
(3)四边形的面积为,再求解即可.
【详解】(1)解:大正方形的面积为:,
大正方形是由中间的小正方形和4个全等的三角形组成,面积为:,
所以;
(2)解: ∵,,
∴,
∴,
∴,
∴阴影部分的面积为:;
(3)解: ∵,
∴四边形的面积为.
28.(1)见解析
(2),证明见解析;
(3)或
【分析】(1)根据,,由同角的余角相等即可得出结论;
(2)连接,易证,继而可证明,由此可知为的中点,由已知可得,进而得出三条线段的关系;
(3)分M在D点左侧和右侧两种情况讨论,根据求出取值范围,再根据线段和差关系利用不等式性质变形求解即可.
【详解】(1)解:如图,
证明:∵,
∴,
又∵,
∴
∴.
(2)结论:.
证明:连接,
∵,,
∴,
∴,
在和中,
∵,
∴
∴,,
又∵,
∴,
又在和中,
∵,
∴
∴,即:,
∵,
∴,
∴.
(3)当时,M在点D右侧,如图:
当时,,即,
又∵,
∴,
∴
∵,即
当时,若,则.
可知时,M在点D左侧,如图:
当时,,即,
又∵,
∴,
∴
∵,
∴当时,若,则,
综上所述:线段长的取值范围为:或.
【点睛】本题主要考查了全等三角形的综合和不等式性质的应用,解(2)题关键是证明三角形全等得出点M是的中点.解(3)题关键是利用线段和差关系和不等式性质变形得出结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
