期末冲刺练习卷(一)-2024-2025学年数学八年级下册人教版(含解析)
文档属性
| 名称 | 期末冲刺练习卷(一)-2024-2025学年数学八年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 957.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 19:16:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末冲刺练习卷(一)-2024-2025学年数学八年级下册人教版
一、单选题
1.下列各数中,能使有意义的是( )
A.6 B.0 C.3 D.
2.下列各组数据中,不是勾股数的是( )
A.3,4,5 B.5,7,9 C.8,15,17 D.7,24,25
3.下列命题是假命题的是( )
A.平行四边形的对边相等 B.四条边都相等的四边形是菱形
C.矩形的两条对角线互相垂直 D.正方形的对角线垂直平分且相等
4.下列等式成立的是( )
A. B. C. D.
5.菲尔兹奖是数学领域的一项国际大奖,被视为数学界的诺贝尔奖,其规定获奖数学家年龄不得超过40岁.截至目前,菲尔兹奖得主中最年轻的8位数学家获奖时年龄分别为:29,27,31,31,31,29,29,31,则该组由年龄组成的数据的众数和中位数是( )
A.29,31 B.29,29 C.31,30 D.31,31
6.如图,在平坦的地面上,为测量位于水塘旁的两点A,B间的距离,先确定一点O,分别取的中点C,D,量得m,则A,B之间的距离是( )
A.20m B.40m C.60m D.80m
7.已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
8.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 实践能力 成长记录
甲 90 83 95
乙 88 90 95
丙 90 88 90
A.甲 B.乙、丙 C.甲、乙 D.甲、丙
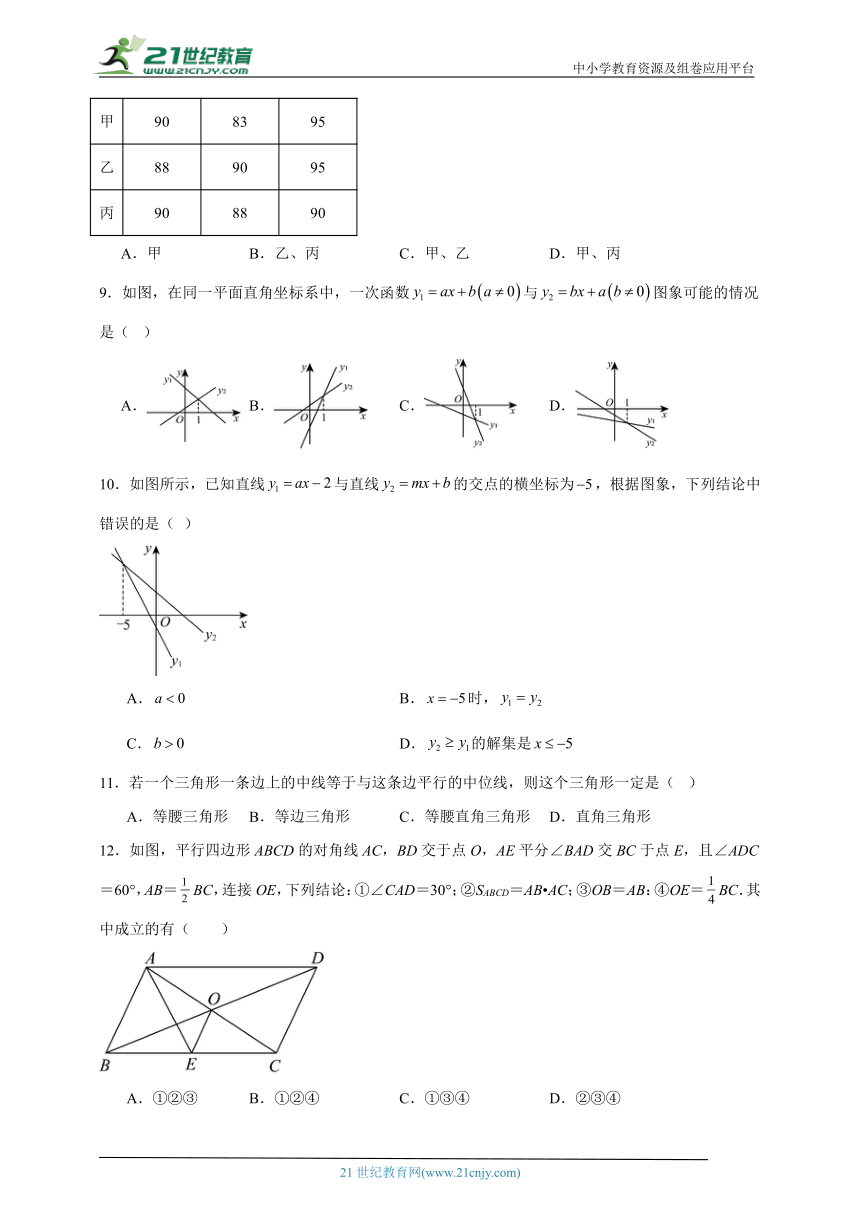
9.如图,在同一平面直角坐标系中,一次函数与图象可能的情况是( )
A. B. C. D.
10.如图所示,已知直线与直线的交点的横坐标为,根据图象,下列结论中错误的是( )
A. B.时,
C. D.的解集是
11.若一个三角形一条边上的中线等于与这条边平行的中位线,则这个三角形一定是( )
A.等腰三角形 B.等边三角形 C.等腰直角三角形 D.直角三角形
12.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE,下列结论:①∠CAD=30°;②SABCD=AB AC;③OB=AB:④OE=BC.其中成立的有( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
13.计算: .
14.为了弘扬古诗词文化,某校举办了主题为“赏中华诗词,寻文化基因,品文学之美”的古诗词知识竞赛,进入决赛的10名学生成绩统计如下表,这名学生决赛成绩的中位数应是 分.
决赛成绩/分
人数/名
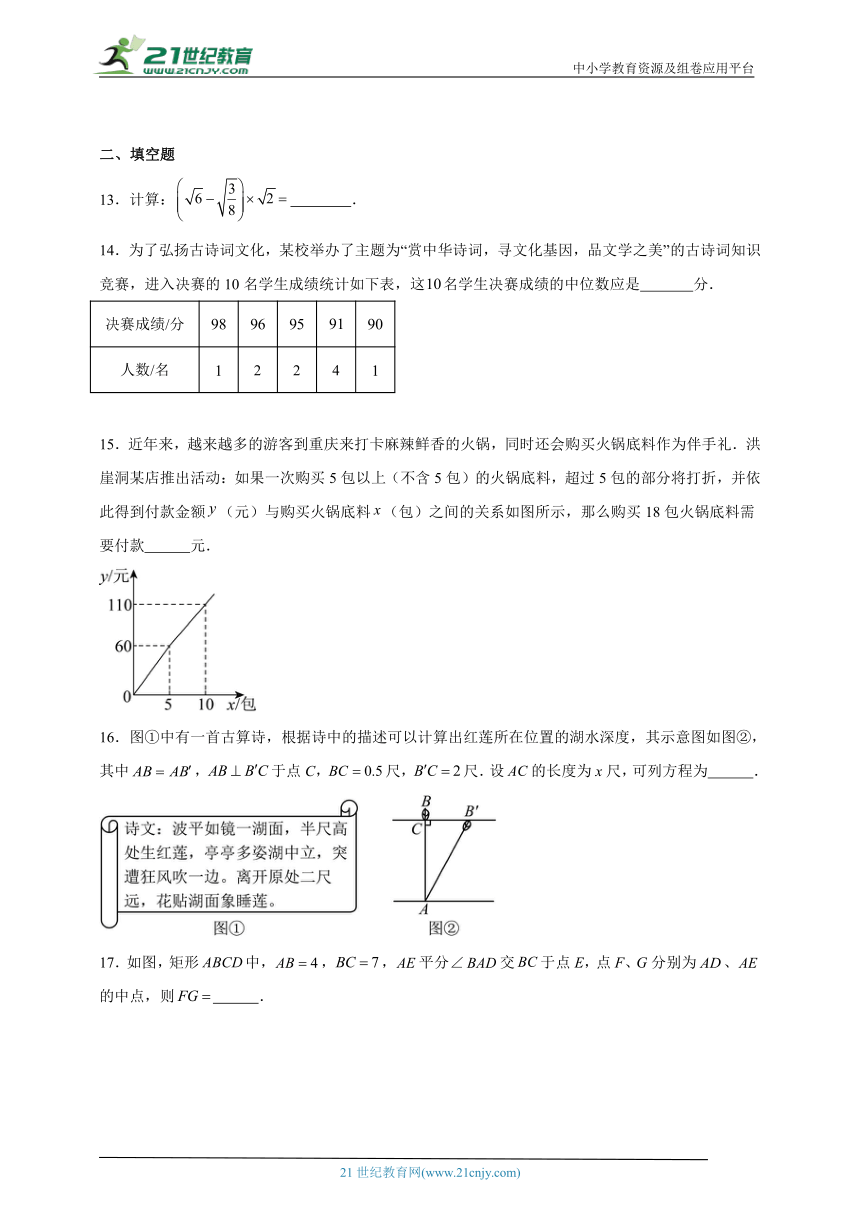
15.近年来,越来越多的游客到重庆来打卡麻辣鲜香的火锅,同时还会购买火锅底料作为伴手礼.洪崖洞某店推出活动:如果一次购买5包以上(不含5包)的火锅底料,超过5包的部分将打折,并依此得到付款金额(元)与购买火锅底料(包)之间的关系如图所示,那么购买18包火锅底料需要付款 元.
16.图①中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图②,其中,于点C,尺,尺.设的长度为x尺,可列方程为 .
17.如图,矩形中,,,平分∠交于点E,点F、G分别为、的中点,则 .
18.如图,是一个有盖的盒子,长宽高如图中标注,若在盒中放一根细棒,则细棒的最大长度是 .
19.如图,在边长为8的菱形中,为边的中点,连接交对角线于点.若,则这个菱形的面积为 .
三、解答题
20.计算:.
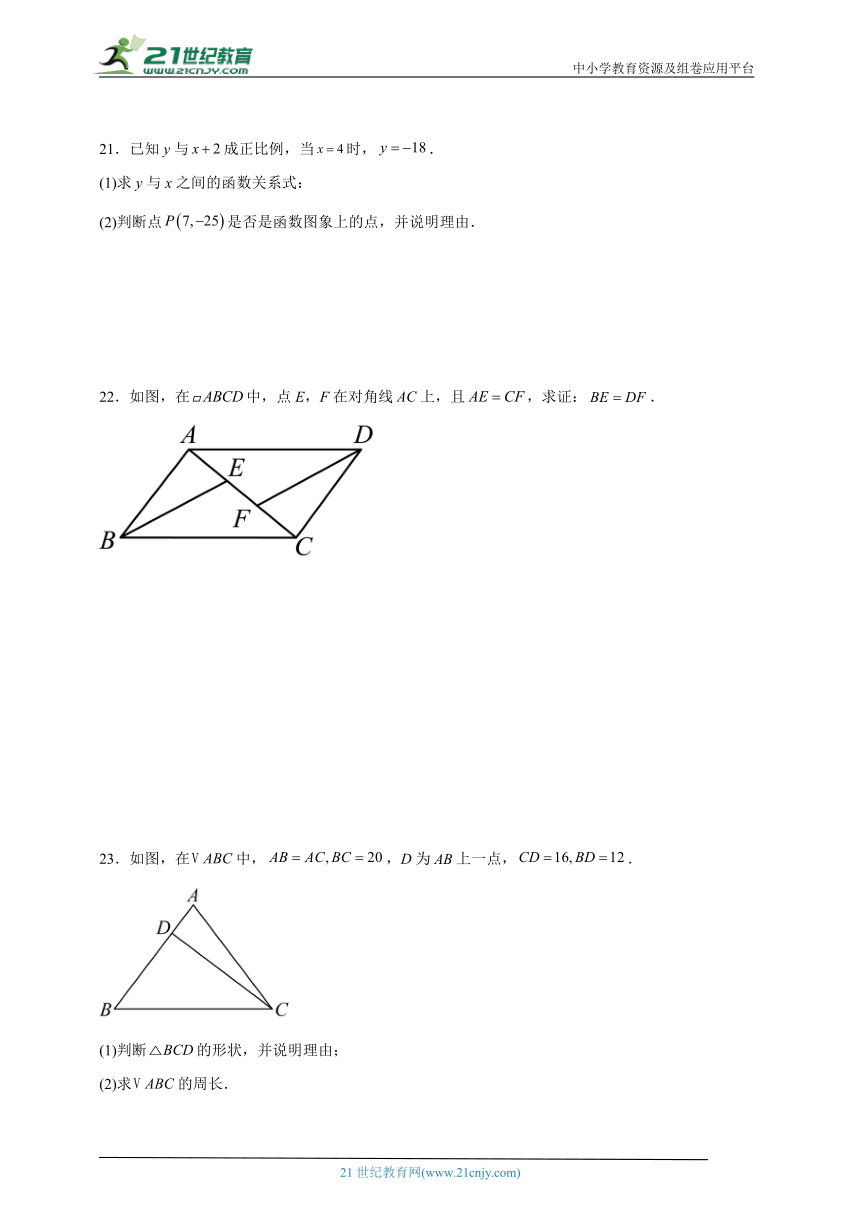
21.已知y与成正比例,当时,.
(1)求y与x之间的函数关系式:
(2)判断点是否是函数图象上的点,并说明理由.
22.如图,在中,点E,F在对角线上,且,求证:.
23.如图,在中,,D为上一点,.
(1)判断的形状,并说明理由;
(2)求的周长.
24.甲、乙两家水果批发店销售同一种香梨,甲店每千克香梨的价格为5元,乙店为了吸引顾客制定如下方案:当一次性购买不超过10千克时,每千克价格为6元,超过10千克时,超过部分每千克价格为3元.设小王在同一家店一次性购买香梨x千克().
(1)若在甲店购买需花费元,在乙店购买需花费元,分别求关于x的函数解析式;
(2)请结合x的范围,计算并说明在哪家店购买更省钱.
25.教育部印发的《义务教育课程方案和课程标准(2022年版)》优化了课程设置,将劳动课程从综合实践活动课程中独立出来.某校为了解本校学生一周的课外劳动情况,随机抽取部分学生,调查了他们一周的课外劳动时间,将数据进行整理并制成如图所示的统计图.
请根据图中提供的信息,解答下列问题.
(1)本次调查数据的中位数是________,众数是________.
(2)该校本次调查的学生一周的平均课外劳动时间是多少?
(3)若该校共有2000名学生,请估计该校学生一周的课外劳动时间不少于的人数.
26.如图,在中,F是的中点,E是线段的延长线上一动点,连接,过点C作,与线段的延长线交于点D,连接.
(1)求证:四边形是平行四边形.
(2)若,则在点E的运动过程中,
①当为何值时,四边形是矩形;
②当为何值时,四边形是菱形.
27.如图,在平面直角坐标系中,一次函数的图象交x轴于点,交y轴于点B,直线与y轴交于点D,与直线交于点,点M是线段上的一个动点(点M不与点C重合),过点M作x轴的垂线,交直线于点N.设点M的横坐标为m.
(1)求a的值和直线的函数表达式.
(2)以线段,为邻边作,直线与x轴交于点E.
①当时,设线段的长度为l,求l与m之间的关系式;
②连接,,当的面积为3时,请求出m的值.
《期末冲刺练习卷(一)-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C D C C D D
题号 11 12
答案 D B
1.A
【分析】本题考查了二次根式有意义的条件,根据题意可得,解不等式即可求解.
【详解】解:∵有意义
∴,
∴,只有A选项正确,
故选:A.
2.B
【分析】判断是否为勾股数,首先这三个数都要是正整数,同时还需验证两较小数的平方和是否等于最大数的平方.
【详解】、,能构成直角三角形,都是正整数,故选项错误;
、,不能构成直角三角形,故选项正确;
、,能构成直角三角形,都是正整数,故选项错误;
、,能构成直角三角形,都是正整数,故选项错误.
故选:.
【点睛】此题主要考查了勾股数的定义,熟记勾股数的定义是解题的关键.
3.C
【分析】.
【详解】解:A、平行四边形的对边相等,是真命题,选项说法正确,不符合题意;
B、四条边都相等的四边形是菱形,是真命题,选项说法正确,不符合题意;
C、矩形的对角线不垂直,是假命题,选项说法错误,符合题意;
D、正方形的对角线垂直平分且相等,是真命题,选项说法正确,不符合题意;
故选:C.
4.D
【分析】根据二次根式的运算法则即可逐一判断.
【详解】解:A、3和不能合并,故A错误;
B、,故B错误;
C、,故C错误;
D、,正确;
故选:D.
【点睛】本题考查了二次根式的运算,解题的关键是掌握基本的运算法则.
5.C
【分析】由数据可知,31出现4次,次数最多,所以众数为31;将数据按从小到大的顺序排列,可求出中位数.
【详解】解:由数据可知,31出现4次,次数最多,所以众数为31;
将数据从小到大排列为:27,29,29,29,31,31,31,31
所以中位数为:;
故答案为:C.
【点睛】本题考查众数和中位数,属于基础题,解题的关键在于理解众数和中位数的定义,并将数据按大小顺序排列.
6.D
【分析】根据三角形的中位线定理进行求解即可.
【详解】解:∵C,D为的中点,
∴是的中位线,
∴;
故选D.
【点睛】本题考查三角形的中位线定理.熟练掌握三角形的中位线定理,是解题的关键.
7.C
【分析】本题可根据两个非负数相加和为0,则这两个非负数的值均为0解出x、y的值,然后运用勾股定理求出斜边的长.斜边长的平方即为正方形的面积.
【详解】依题意得:,
∴,
斜边长,
所以正方形的面积.
故选C.
考点:本题综合考查了勾股定理与非负数的性质
点评:解这类题的关键是利用直角三角形,用勾股定理来寻求未知系数的等量关系.
8.C
【分析】利用平均数的定义分别进行计算成绩,然后判断谁优秀.
【详解】由题意知,甲的总评成绩=90×50%+83×20%+95×30%=90.1,
乙的总评成绩=88×50%+90×20%+95×30%=90.5,
丙的总评成绩=90×50%+88×20%+90×30%=89.6,
∴甲乙的学期总评成绩是优秀.
故选:C.
【点睛】本题考查了加权平均数的计算方法.
9.D
【分析】对于每个选项,先确定一个解析式所对应的图象,根据一次函数图象与系数的关系确定、的符号,然后根据此符号看另一个函数图象的位置是否正确.
本题考查了一次函数图象:一次函数、为常数,是一条直线,当,图象经过第一、三象限,随的增大而增大;当,图象经过第二、四象限,随的增大而减小;图象与轴的交点坐标为.
【详解】解:根据题意,得,解得,故交点坐标为;
A、对于,,;对于,则,,a的符号不一致,
∴A选项不正确,不符合题意;
B、对于,,;对于,则,,b的符号不一致,
∴B选项错误,不符合题意;
C、对于,,;对于,则,,a的符号不一致,
∴C选项错误,不符合题意;
D、对于,,;对于,则,,
∴D选项正确,符合题意.
故选:D.
10.D
【分析】本题主要考查了一次函数与一元一次不等式、一次函数与一元一次方程的应用,依据题意,根据所给函数图象的分布及两直线的交点的横坐标为-5进而逐个判断可以得解.
【详解】解:由题意,∵直线的图象经过第二、三、四象限,
∴,故A正确,不合题意.
∵直线与直线的交点的横坐标为,
∴方程的解是,故B正确,不合题意.
∵直线的图象与y轴交于正半轴,
∴,故C正确,不合题意.
结合图象可得,当时,直线上的点都不在直线的下方,
∴不等式的解集为,即不等式的解集是,故D错误,符合题意.
故选:D.
11.D
【分析】本题考查三角形的中位线定理,等腰三角形的判定和性质,根据题意,画出图形,证明三角形为直角三角形即可得.
【详解】解:如图,为的中位线,为的中线,且,
∴
∴,,
∵,
即,
∴,即.
∴是直角三角形.
故选D.
12.B
【分析】由 ABCD中,∠ADC=60°,易得△ABE是等边三角形,又由AB=BC,,证得①∠CAD=30°;继而证得AC⊥AB,得②S ABCD=AB AC;可得OE是三角形的中位线,证得④OE=BC.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
,
∵BD>BC,
∴AB≠OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
,故④正确.
故选B.
【点睛】此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△ABE是等边三角形,OE是△ABC的中位线是关键.
13./
【分析】本题考查了二次根式的混合运算,二次根式的性质化简,掌握相关运算法则是解题关键.先根据乘法分配律展开,再计算乘法,然后化为最简二次根式计算即可.
【详解】解:
,
故答案为:.
14.
【分析】本题考查中位数的知识,解题的关键是先对这位学生的成绩从小到大的顺序排序,根据中位数的定义,即可.
【详解】先对这位学生的成绩进行排序,
∴,,,,,,,,,,
∴处于中间位置的两位数是平均数为:,
∴中位数为.
故答案为:.
15.
【分析】本题考查了一次函数的应用,待定系数法求得时的解析式,进而将代入,即可求解.
【详解】解:设时,与的函数关系式为,
将代入得,
解得:
∴
当时,
故答案为:.
16.
【分析】本题考查了勾股定理的实际应用,正确理解题意,运用勾股定理建立方程是解题的关键.
设的长度为x尺,则,在中,由勾股定理即可建立方程.
【详解】解:设的长度为x尺,则,
∵,
由勾股定理得:,
∴,
故答案为:.
17.
【分析】连接.由矩形的性质可间接证明,结合角平分线的定义得出,即得出,从而可求出,再由勾股定理可求出,最后根据三角形中位线定理求解即可.
【详解】解:如图,连接.
∵四边形为矩形,
∴,,,,
∴.
∵平分交于点E,
∴,
∴,
∴,
∴,
∴.
∵点F、G分别为、的中点,
∴.
故答案为:.
【点睛】本题考查矩形的性质,平行线的性质,角平分线的定义,等腰三角形的判定和性质,勾股定理,三角形中位线定理.正确连接辅助线是解题关键.
18.17
【分析】在,根据勾股定理求得,中,根据勾股定理即可得到结论.
【详解】解:依题意,在中,,
在中,,
故答案为:17.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
19.
【分析】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形面积,连接交于O,如图,根据菱形的性质得到,,再利用得到,证明得,则,所以,接着利用勾股定理计算出,从而得到,然后根据菱形的面积公式计算它的面积.
【详解】解:连接交于O,如图,
∵四边形为菱形,
∴,,
∵E为边的中点,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,
∴,
∴菱形的面积.
故答案为:.
20.2
【分析】本题考查二次根式的混合运算,先进行除法运算,化简二次根式,再进行合并即可.
【详解】解:原式
.
21.(1)
(2)不是,理由见解析
【分析】(1)利用正比例函数的定义设,然后把已知对应的值代入求出k,从而得到y与x之间的函数关系式;
(2)通过一次函数图象上的坐标特征进行判断.
【详解】(1)解:设,
把,代入得,解得,
∴,
即y与x之间的函数关系式为;
(2)点不是函数图象上的点.
理由如下:
当时,,
∴点不是函数图象上的点.
【点睛】本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.
22.见解析
【分析】本题考查平行四边形的性质,全等三角形的判定和性质,根据平行四边形的性质,证明,即可得出结论.
【详解】证明:∵,
∴,
∴.
在和中,
,
∴.
∴.
23.(1)直角三角形,理由见解析
(2)
【分析】本题考查了等腰三角形的定义,勾股定理及其逆定理,熟练掌握知识点是解题的关键.
(1)勾股定理逆定理直接证明即可;
(2)设,则,在中,由勾股定理得,解得,则,即可求解周长.
【详解】(1)解:是直角三角形.理由如下:
∵,
∴,
即
∴是直角三角形,;
(2)解:设,则,
由(1),得,
∴,
在中,由勾股定理,得,即,
解得.
∴.
∴的周长为.
24.(1)
(2)当时,在乙店购买更省钱;当时,在两家店购买一样省钱;当时,在甲店购买更省钱
【分析】本题考查一次函数的实际应用,正确的求出函数解析式,是解题的关键:
(1)根据两家批发店的方案列出函数关系式即可;
(2)分和两种情况进行讨论求解即可.
【详解】(1)解:由题意,得关于x的函数解析式为.
当时,;
当时,.
∴关于x的函数解析式为;
(2)①当时,,此时在甲店购买更省钱.
②当时,令,解得.
令,解得.
令,解得.
综上所述,当时,在乙店购买更省钱;当时,在两家店购买一样省钱;当时,在甲店购买更省钱.
25.(1)3;3
(2)
(3)1400人
【分析】本题考查求中位数,众数,平均数,利用样本估计总体:
(1)根据中位数和众数的计算方法,进行求解即可;
(2)利用加权平均数的计算公式进行计算即可;
(3)利用样本估计总体的思想,进行求解即可.
【详解】(1)解:由图可知:调查总人数为:(人);
第20个和第21个数据均为3,故中位数为3;
3出现的次数最多,故众数为3;
故答案为:3,3;
(2);
答:该校本次调查的学生一周的平均课外劳动时间是;
(3)(人);
答:估计该校学生一周的课外劳动时间不少于的人数为人.
26.(1)见解析
(2)①2;②4
【分析】本题考查平行四边形的判定,矩形的性质和菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,掌握相关判定方法和性质是解题的关键:
(1)证明,得到,即可得证;
(2)①根据四边形是矩形,推出,根据含30度角的直角三角形即可得出结果;②根据菱形的性质,推出是等边三角形,即可得出结果.
【详解】(1)证明:∵,
∴.
∵F是的中点,
∴.
在和中,
,
∴.
∴.
又,即,
∴四边形是平行四边形.
(2)解:①当四边形是矩形时,.
∵,
∴.
∴.
∴;
②当四边形是菱形时,.
∵,
∴.
∴是等边三角形.
∴.
27.(1),
(2)①;②或
【分析】(1)根据直线的解析式求出点C的坐标,用待定系数法求出直线的解析式即可;
(2)①用含m的代数式表示出的长,再根据得出结论即可;
②根据面积得出l的值,然后根据①的关系式的出m的值.
【详解】(1)点在直线上,
,
一次函数的图象过点和点,
,
解得,
直线的解析式为;
(2)①点在直线上,且的横坐标为,
的纵坐标为:,
点在直线上,且点的横坐标为,
点的纵坐标为:,
,
点,线段的长度为,
,
,
,
即;
②的面积为,
,
即,
解得,
由①知,,
,
解得,
即的值为或.
【点睛】本题考查一次函数和几何综合,平行四边形的性质,熟练掌握一次函数的图象和性质,待定系数法求解析式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末冲刺练习卷(一)-2024-2025学年数学八年级下册人教版
一、单选题
1.下列各数中,能使有意义的是( )
A.6 B.0 C.3 D.
2.下列各组数据中,不是勾股数的是( )
A.3,4,5 B.5,7,9 C.8,15,17 D.7,24,25
3.下列命题是假命题的是( )
A.平行四边形的对边相等 B.四条边都相等的四边形是菱形
C.矩形的两条对角线互相垂直 D.正方形的对角线垂直平分且相等
4.下列等式成立的是( )
A. B. C. D.
5.菲尔兹奖是数学领域的一项国际大奖,被视为数学界的诺贝尔奖,其规定获奖数学家年龄不得超过40岁.截至目前,菲尔兹奖得主中最年轻的8位数学家获奖时年龄分别为:29,27,31,31,31,29,29,31,则该组由年龄组成的数据的众数和中位数是( )
A.29,31 B.29,29 C.31,30 D.31,31
6.如图,在平坦的地面上,为测量位于水塘旁的两点A,B间的距离,先确定一点O,分别取的中点C,D,量得m,则A,B之间的距离是( )
A.20m B.40m C.60m D.80m
7.已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
8.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 实践能力 成长记录
甲 90 83 95
乙 88 90 95
丙 90 88 90
A.甲 B.乙、丙 C.甲、乙 D.甲、丙
9.如图,在同一平面直角坐标系中,一次函数与图象可能的情况是( )
A. B. C. D.
10.如图所示,已知直线与直线的交点的横坐标为,根据图象,下列结论中错误的是( )
A. B.时,
C. D.的解集是
11.若一个三角形一条边上的中线等于与这条边平行的中位线,则这个三角形一定是( )
A.等腰三角形 B.等边三角形 C.等腰直角三角形 D.直角三角形
12.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE,下列结论:①∠CAD=30°;②SABCD=AB AC;③OB=AB:④OE=BC.其中成立的有( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
13.计算: .
14.为了弘扬古诗词文化,某校举办了主题为“赏中华诗词,寻文化基因,品文学之美”的古诗词知识竞赛,进入决赛的10名学生成绩统计如下表,这名学生决赛成绩的中位数应是 分.
决赛成绩/分
人数/名
15.近年来,越来越多的游客到重庆来打卡麻辣鲜香的火锅,同时还会购买火锅底料作为伴手礼.洪崖洞某店推出活动:如果一次购买5包以上(不含5包)的火锅底料,超过5包的部分将打折,并依此得到付款金额(元)与购买火锅底料(包)之间的关系如图所示,那么购买18包火锅底料需要付款 元.
16.图①中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图②,其中,于点C,尺,尺.设的长度为x尺,可列方程为 .
17.如图,矩形中,,,平分∠交于点E,点F、G分别为、的中点,则 .
18.如图,是一个有盖的盒子,长宽高如图中标注,若在盒中放一根细棒,则细棒的最大长度是 .
19.如图,在边长为8的菱形中,为边的中点,连接交对角线于点.若,则这个菱形的面积为 .
三、解答题
20.计算:.
21.已知y与成正比例,当时,.
(1)求y与x之间的函数关系式:
(2)判断点是否是函数图象上的点,并说明理由.
22.如图,在中,点E,F在对角线上,且,求证:.
23.如图,在中,,D为上一点,.
(1)判断的形状,并说明理由;
(2)求的周长.
24.甲、乙两家水果批发店销售同一种香梨,甲店每千克香梨的价格为5元,乙店为了吸引顾客制定如下方案:当一次性购买不超过10千克时,每千克价格为6元,超过10千克时,超过部分每千克价格为3元.设小王在同一家店一次性购买香梨x千克().
(1)若在甲店购买需花费元,在乙店购买需花费元,分别求关于x的函数解析式;
(2)请结合x的范围,计算并说明在哪家店购买更省钱.
25.教育部印发的《义务教育课程方案和课程标准(2022年版)》优化了课程设置,将劳动课程从综合实践活动课程中独立出来.某校为了解本校学生一周的课外劳动情况,随机抽取部分学生,调查了他们一周的课外劳动时间,将数据进行整理并制成如图所示的统计图.
请根据图中提供的信息,解答下列问题.
(1)本次调查数据的中位数是________,众数是________.
(2)该校本次调查的学生一周的平均课外劳动时间是多少?
(3)若该校共有2000名学生,请估计该校学生一周的课外劳动时间不少于的人数.
26.如图,在中,F是的中点,E是线段的延长线上一动点,连接,过点C作,与线段的延长线交于点D,连接.
(1)求证:四边形是平行四边形.
(2)若,则在点E的运动过程中,
①当为何值时,四边形是矩形;
②当为何值时,四边形是菱形.
27.如图,在平面直角坐标系中,一次函数的图象交x轴于点,交y轴于点B,直线与y轴交于点D,与直线交于点,点M是线段上的一个动点(点M不与点C重合),过点M作x轴的垂线,交直线于点N.设点M的横坐标为m.
(1)求a的值和直线的函数表达式.
(2)以线段,为邻边作,直线与x轴交于点E.
①当时,设线段的长度为l,求l与m之间的关系式;
②连接,,当的面积为3时,请求出m的值.
《期末冲刺练习卷(一)-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C D C C D D
题号 11 12
答案 D B
1.A
【分析】本题考查了二次根式有意义的条件,根据题意可得,解不等式即可求解.
【详解】解:∵有意义
∴,
∴,只有A选项正确,
故选:A.
2.B
【分析】判断是否为勾股数,首先这三个数都要是正整数,同时还需验证两较小数的平方和是否等于最大数的平方.
【详解】、,能构成直角三角形,都是正整数,故选项错误;
、,不能构成直角三角形,故选项正确;
、,能构成直角三角形,都是正整数,故选项错误;
、,能构成直角三角形,都是正整数,故选项错误.
故选:.
【点睛】此题主要考查了勾股数的定义,熟记勾股数的定义是解题的关键.
3.C
【分析】.
【详解】解:A、平行四边形的对边相等,是真命题,选项说法正确,不符合题意;
B、四条边都相等的四边形是菱形,是真命题,选项说法正确,不符合题意;
C、矩形的对角线不垂直,是假命题,选项说法错误,符合题意;
D、正方形的对角线垂直平分且相等,是真命题,选项说法正确,不符合题意;
故选:C.
4.D
【分析】根据二次根式的运算法则即可逐一判断.
【详解】解:A、3和不能合并,故A错误;
B、,故B错误;
C、,故C错误;
D、,正确;
故选:D.
【点睛】本题考查了二次根式的运算,解题的关键是掌握基本的运算法则.
5.C
【分析】由数据可知,31出现4次,次数最多,所以众数为31;将数据按从小到大的顺序排列,可求出中位数.
【详解】解:由数据可知,31出现4次,次数最多,所以众数为31;
将数据从小到大排列为:27,29,29,29,31,31,31,31
所以中位数为:;
故答案为:C.
【点睛】本题考查众数和中位数,属于基础题,解题的关键在于理解众数和中位数的定义,并将数据按大小顺序排列.
6.D
【分析】根据三角形的中位线定理进行求解即可.
【详解】解:∵C,D为的中点,
∴是的中位线,
∴;
故选D.
【点睛】本题考查三角形的中位线定理.熟练掌握三角形的中位线定理,是解题的关键.
7.C
【分析】本题可根据两个非负数相加和为0,则这两个非负数的值均为0解出x、y的值,然后运用勾股定理求出斜边的长.斜边长的平方即为正方形的面积.
【详解】依题意得:,
∴,
斜边长,
所以正方形的面积.
故选C.
考点:本题综合考查了勾股定理与非负数的性质
点评:解这类题的关键是利用直角三角形,用勾股定理来寻求未知系数的等量关系.
8.C
【分析】利用平均数的定义分别进行计算成绩,然后判断谁优秀.
【详解】由题意知,甲的总评成绩=90×50%+83×20%+95×30%=90.1,
乙的总评成绩=88×50%+90×20%+95×30%=90.5,
丙的总评成绩=90×50%+88×20%+90×30%=89.6,
∴甲乙的学期总评成绩是优秀.
故选:C.
【点睛】本题考查了加权平均数的计算方法.
9.D
【分析】对于每个选项,先确定一个解析式所对应的图象,根据一次函数图象与系数的关系确定、的符号,然后根据此符号看另一个函数图象的位置是否正确.
本题考查了一次函数图象:一次函数、为常数,是一条直线,当,图象经过第一、三象限,随的增大而增大;当,图象经过第二、四象限,随的增大而减小;图象与轴的交点坐标为.
【详解】解:根据题意,得,解得,故交点坐标为;
A、对于,,;对于,则,,a的符号不一致,
∴A选项不正确,不符合题意;
B、对于,,;对于,则,,b的符号不一致,
∴B选项错误,不符合题意;
C、对于,,;对于,则,,a的符号不一致,
∴C选项错误,不符合题意;
D、对于,,;对于,则,,
∴D选项正确,符合题意.
故选:D.
10.D
【分析】本题主要考查了一次函数与一元一次不等式、一次函数与一元一次方程的应用,依据题意,根据所给函数图象的分布及两直线的交点的横坐标为-5进而逐个判断可以得解.
【详解】解:由题意,∵直线的图象经过第二、三、四象限,
∴,故A正确,不合题意.
∵直线与直线的交点的横坐标为,
∴方程的解是,故B正确,不合题意.
∵直线的图象与y轴交于正半轴,
∴,故C正确,不合题意.
结合图象可得,当时,直线上的点都不在直线的下方,
∴不等式的解集为,即不等式的解集是,故D错误,符合题意.
故选:D.
11.D
【分析】本题考查三角形的中位线定理,等腰三角形的判定和性质,根据题意,画出图形,证明三角形为直角三角形即可得.
【详解】解:如图,为的中位线,为的中线,且,
∴
∴,,
∵,
即,
∴,即.
∴是直角三角形.
故选D.
12.B
【分析】由 ABCD中,∠ADC=60°,易得△ABE是等边三角形,又由AB=BC,,证得①∠CAD=30°;继而证得AC⊥AB,得②S ABCD=AB AC;可得OE是三角形的中位线,证得④OE=BC.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
,
∵BD>BC,
∴AB≠OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
,故④正确.
故选B.
【点睛】此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△ABE是等边三角形,OE是△ABC的中位线是关键.
13./
【分析】本题考查了二次根式的混合运算,二次根式的性质化简,掌握相关运算法则是解题关键.先根据乘法分配律展开,再计算乘法,然后化为最简二次根式计算即可.
【详解】解:
,
故答案为:.
14.
【分析】本题考查中位数的知识,解题的关键是先对这位学生的成绩从小到大的顺序排序,根据中位数的定义,即可.
【详解】先对这位学生的成绩进行排序,
∴,,,,,,,,,,
∴处于中间位置的两位数是平均数为:,
∴中位数为.
故答案为:.
15.
【分析】本题考查了一次函数的应用,待定系数法求得时的解析式,进而将代入,即可求解.
【详解】解:设时,与的函数关系式为,
将代入得,
解得:
∴
当时,
故答案为:.
16.
【分析】本题考查了勾股定理的实际应用,正确理解题意,运用勾股定理建立方程是解题的关键.
设的长度为x尺,则,在中,由勾股定理即可建立方程.
【详解】解:设的长度为x尺,则,
∵,
由勾股定理得:,
∴,
故答案为:.
17.
【分析】连接.由矩形的性质可间接证明,结合角平分线的定义得出,即得出,从而可求出,再由勾股定理可求出,最后根据三角形中位线定理求解即可.
【详解】解:如图,连接.
∵四边形为矩形,
∴,,,,
∴.
∵平分交于点E,
∴,
∴,
∴,
∴,
∴.
∵点F、G分别为、的中点,
∴.
故答案为:.
【点睛】本题考查矩形的性质,平行线的性质,角平分线的定义,等腰三角形的判定和性质,勾股定理,三角形中位线定理.正确连接辅助线是解题关键.
18.17
【分析】在,根据勾股定理求得,中,根据勾股定理即可得到结论.
【详解】解:依题意,在中,,
在中,,
故答案为:17.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
19.
【分析】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形面积,连接交于O,如图,根据菱形的性质得到,,再利用得到,证明得,则,所以,接着利用勾股定理计算出,从而得到,然后根据菱形的面积公式计算它的面积.
【详解】解:连接交于O,如图,
∵四边形为菱形,
∴,,
∵E为边的中点,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,
∴,
∴菱形的面积.
故答案为:.
20.2
【分析】本题考查二次根式的混合运算,先进行除法运算,化简二次根式,再进行合并即可.
【详解】解:原式
.
21.(1)
(2)不是,理由见解析
【分析】(1)利用正比例函数的定义设,然后把已知对应的值代入求出k,从而得到y与x之间的函数关系式;
(2)通过一次函数图象上的坐标特征进行判断.
【详解】(1)解:设,
把,代入得,解得,
∴,
即y与x之间的函数关系式为;
(2)点不是函数图象上的点.
理由如下:
当时,,
∴点不是函数图象上的点.
【点睛】本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.
22.见解析
【分析】本题考查平行四边形的性质,全等三角形的判定和性质,根据平行四边形的性质,证明,即可得出结论.
【详解】证明:∵,
∴,
∴.
在和中,
,
∴.
∴.
23.(1)直角三角形,理由见解析
(2)
【分析】本题考查了等腰三角形的定义,勾股定理及其逆定理,熟练掌握知识点是解题的关键.
(1)勾股定理逆定理直接证明即可;
(2)设,则,在中,由勾股定理得,解得,则,即可求解周长.
【详解】(1)解:是直角三角形.理由如下:
∵,
∴,
即
∴是直角三角形,;
(2)解:设,则,
由(1),得,
∴,
在中,由勾股定理,得,即,
解得.
∴.
∴的周长为.
24.(1)
(2)当时,在乙店购买更省钱;当时,在两家店购买一样省钱;当时,在甲店购买更省钱
【分析】本题考查一次函数的实际应用,正确的求出函数解析式,是解题的关键:
(1)根据两家批发店的方案列出函数关系式即可;
(2)分和两种情况进行讨论求解即可.
【详解】(1)解:由题意,得关于x的函数解析式为.
当时,;
当时,.
∴关于x的函数解析式为;
(2)①当时,,此时在甲店购买更省钱.
②当时,令,解得.
令,解得.
令,解得.
综上所述,当时,在乙店购买更省钱;当时,在两家店购买一样省钱;当时,在甲店购买更省钱.
25.(1)3;3
(2)
(3)1400人
【分析】本题考查求中位数,众数,平均数,利用样本估计总体:
(1)根据中位数和众数的计算方法,进行求解即可;
(2)利用加权平均数的计算公式进行计算即可;
(3)利用样本估计总体的思想,进行求解即可.
【详解】(1)解:由图可知:调查总人数为:(人);
第20个和第21个数据均为3,故中位数为3;
3出现的次数最多,故众数为3;
故答案为:3,3;
(2);
答:该校本次调查的学生一周的平均课外劳动时间是;
(3)(人);
答:估计该校学生一周的课外劳动时间不少于的人数为人.
26.(1)见解析
(2)①2;②4
【分析】本题考查平行四边形的判定,矩形的性质和菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,掌握相关判定方法和性质是解题的关键:
(1)证明,得到,即可得证;
(2)①根据四边形是矩形,推出,根据含30度角的直角三角形即可得出结果;②根据菱形的性质,推出是等边三角形,即可得出结果.
【详解】(1)证明:∵,
∴.
∵F是的中点,
∴.
在和中,
,
∴.
∴.
又,即,
∴四边形是平行四边形.
(2)解:①当四边形是矩形时,.
∵,
∴.
∴.
∴;
②当四边形是菱形时,.
∵,
∴.
∴是等边三角形.
∴.
27.(1),
(2)①;②或
【分析】(1)根据直线的解析式求出点C的坐标,用待定系数法求出直线的解析式即可;
(2)①用含m的代数式表示出的长,再根据得出结论即可;
②根据面积得出l的值,然后根据①的关系式的出m的值.
【详解】(1)点在直线上,
,
一次函数的图象过点和点,
,
解得,
直线的解析式为;
(2)①点在直线上,且的横坐标为,
的纵坐标为:,
点在直线上,且点的横坐标为,
点的纵坐标为:,
,
点,线段的长度为,
,
,
,
即;
②的面积为,
,
即,
解得,
由①知,,
,
解得,
即的值为或.
【点睛】本题考查一次函数和几何综合,平行四边形的性质,熟练掌握一次函数的图象和性质,待定系数法求解析式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
