第七单元用方程解决问题(知识梳理+拔高训练)一-2024-2025学年五年级数学下学期培优检测卷(北师大版)
文档属性
| 名称 | 第七单元用方程解决问题(知识梳理+拔高训练)一-2024-2025学年五年级数学下学期培优检测卷(北师大版) |

|
|
| 格式 | docx | ||
| 文件大小 | 335.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 15:29:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第七单元用方程解决问题(知识梳理+拔高训练)一
知识梳理
知识点01:解形如“ax±x=b”类型的方程
根据乘法分配律和等式的性质来解,具体步骤如下:
ax±x=b
解:(a±1)x=b
x=b÷(a±1)
知识点02:解如“ax±x=b”类型的方程
根据乘法分配律和等式的性质来解,具体步骤如下:
ax±bx=c
解:(a±b)x=c
x=c÷(a±b)
知识点03:解决相遇问题
可以根据“速度和×相遇时间=路程和”这个等量关系来列方程。
速度和×相遇时间=路程和;路程和÷相遇时间=速度和;路程和÷速度和=相遇时间。
知识点04:方程法解题
就是把题中的末知量用x表示,使未知量x与已知量处于同等地位,直接参加运算。根据题意先找出等量关系,列出含有末知数的等式,再求得未知量的值的一种解题方法。
拔高训练
一、填空题(共20分)
1.(2分)
一辆货车和一辆轿车分别从两地同时出发,相向而行,行驶了x时后相遇。
方程:86x+72x=316
补充的条件是:
2.(2分)甲、乙两车分别从A、B两地同时出发,相向而行,甲车每小时行60km,乙车每小时行80km,经过小时两车相遇,A、B两地相距( )km。
3.(2分)聪聪和妈妈一起随旅游团游览王家大院,经导游介绍,聪聪了解到:王家大院高家崖建筑群的房屋有342间,比大小院落数量的9倍还多27,根据这些信息,聪聪提出了一个数学问题,并用方程“9x+27=342”来解决。请你推断一下,他提出的问题是( ),这个方程的解是( )。
4.(2分)芳芳做乘法计算题时,把其中一个因数32当作23来算,结果得到的积比正确的积少了432,那么,另一个因数是( ),正确的积应该是( )。
5.(2分)某车间有60名工人,生产一种螺栓和螺帽,平均每人每小时生产螺栓15个或螺帽10个,应分配( )人生产螺栓,( )人生产螺帽,才能使生产的螺栓和螺帽刚好配套。(每个螺栓配两个螺帽)
6.(2分)登山自动扶梯以均匀速度由下往上行驶,两位性急的孩子要从扶梯向上走,已知男孩子每分钟走20级台阶,女孩子每分钟走16级,结果男孩子用了6分钟到达山顶,女孩子用了7分钟到达山顶。则该扶梯共有( )级。
7.(2分)工厂接到加工300个零件的订单,先由张师傅独自加工3小时,每时加工12个,后又安排王师傅也参与加工,王师傅每时加工10个,完成这批零件订单共用了( )时。
8.(2分)公交车从甲站到乙站每间隔5分钟一趟,全程走15分钟,某人骑自行车从乙站往甲站行走,开始时恰好遇见一辆公交车,行走过程中又遇见10辆,到甲站时又一辆公交车刚要出发,这人走了( )分钟。
9.(2分)百达电影院在1时内售出甲、乙两种电影票一共30张,甲电影票35元一张,乙电影票25元一张,共收入950元。其中售出甲电影票( )张,乙电影票( )张。
10.(2分)如图所示,用火柴棒按下图的方式摆等腰梯形:摆1个等腰梯形需要4×1+1=5(根)火柴棒,摆2个等腰梯形需要4×2+1=9(根)火柴棒,摆3个等腰梯形需要4×3+1=13(根)火柴棒……
(1)像这样摆下去,摆m个等腰梯形一共需要( )根火柴棒。
(2)有101根火柴棒,可以摆( )个这样的等腰梯形。
二、判断题(共10分)
11.(2分)A、B两地之间相距1800千米,甲、乙两辆卡车从两地同时相对开出,甲车每小时行50千米,乙车每小时行40千米,经过几小时两车相遇?
列式是:1800÷50=36(小时)
1800÷40=45(小时)
45+36=81(小时) ( )
12.(2分)计算图中两条彩带一共长多少米,列出的方程是6.9=x+2.7。
13.(2分)m的5倍比它的2倍多10,列式为5m-2m=10。( )
14.(2分)3x+0.7=3.4的解是x=0.9。( )
15.(2分)比一个数的3倍还多12的数是50,那么这个数是162。( )
三、选择题(共10分)
16.(2分)一套桌椅的售价为196元,一张桌子的售价比一把椅子的售价的3倍少8元,一张桌子、一把椅子的售价分别是多少元?设一把椅子的售价为元,列式正确的是( )。
A. B. C. D.
17.(2分)下面不能用方程“”来表示的是( )。
A. B.
C. D.
18.(2分)两地相距360千米,甲乙两辆货车从两地相对开出,经过3小时后相遇,已知甲货车每时行驶55千米,乙货车每时行驶千米,不正确的方程为( )。
A. B.
C. D.
19.(2分)为创建全国文明城市,学校开展“我是文明使者,争当最美少年”实践活动。四、五年级学生共有240人报名参加文明交通志愿者行动,其中五年级报名人数是四年级的2倍,五年级有( )人报名参加文明交通志愿者行动。
A.80 B.200 C.100 D.160
20.(2分)六一节当天,奇思和淘气这对好朋友相约同时从家里出发,在途中交换一份亲手为对方创作的六一节礼物。已知他们两家相1100米,淘气的步行速度约为60米/分。10分钟后他们相遇了。下列说法正确的是( )。
A.相遇的地点离淘气家近一些
B.奇思的速度比淘气快
C.相遇时淘气走的路程更长。
D.交换礼物后,如果保持速度不变,淘气先到家。
四、计算题(共12分)
21.(6分)看图列方程并解答。
22.(6分)看图列式或列方程计算。
五、解答题(共48分)
23.(6分)六一儿童节这天,中一班的王老师买来了一袋糖果准备分给小朋友们。如果每名小朋友分4个,那么还剩10个;如果每名小朋友分5个,那么就差5个。有多少名小朋友?
24.(6分)原来甲桶水比乙桶水多24千克,甲桶水用去8千克、乙桶水用去2千克后,甲桶水的质量是乙桶水的1.5倍,原来两桶水各重多少千克?
25.(6分)学校买来篮球和足球若干个,篮球个数是足球的4倍,已知足球比篮球少12个,篮球和足球各有多少个?(列方程解答)
26.(6分)五(1)班进行男女生夹弹珠比赛。女生比男生多夹了60个,女生夹弹珠的个数是男生的3倍。男女生各夹了多少个弹珠?(先写出等量关系,再用方程解答。)
(1)等量关系:
(2)解答:
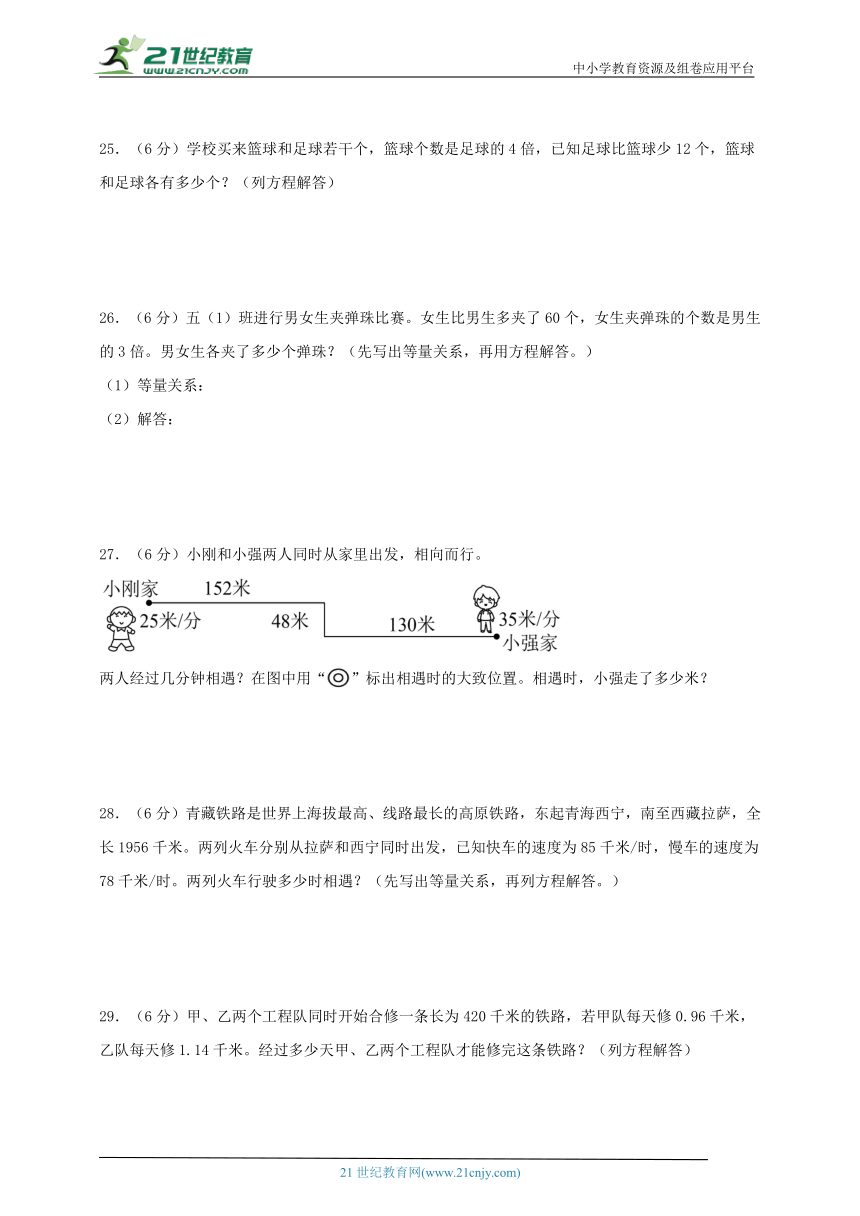
27.(6分)小刚和小强两人同时从家里出发,相向而行。
两人经过几分钟相遇?在图中用“”标出相遇时的大致位置。相遇时,小强走了多少米?
28.(6分)青藏铁路是世界上海拔最高、线路最长的高原铁路,东起青海西宁,南至西藏拉萨,全长1956千米。两列火车分别从拉萨和西宁同时出发,已知快车的速度为85千米/时,慢车的速度为78千米/时。两列火车行驶多少时相遇?(先写出等量关系,再列方程解答。)
29.(6分)甲、乙两个工程队同时开始合修一条长为420千米的铁路,若甲队每天修0.96千米,乙队每天修1.14千米。经过多少天甲、乙两个工程队才能修完这条铁路?(列方程解答)
30.(6分)端午节假期,小青乘火车回家,到车站后,爸爸骑车接她。爸爸以80米/分的速度去火车站,小青以20米/分的速度从火车站同时出发,已知小青家与火车站的距离为1200米。
(1)估计他们在何处相遇,在图中标出来。
(2)他们几分钟后相遇?(用方程解答)相遇点离家多少米?
参考答案
1.两地相距316千米
2.140x
【分析】根据行程问题的关系量:路程=速度×时间,甲的路程=60×x,乙的路程=80×x,然后把甲、乙的路程加起来就是A、B两地的距离,据此解答。
【解答】甲的路程是:60×x=60xkm
乙的路程是:80×x=80xkm
甲、乙的路程和,即A、B两地相距:60x+80x=140xkm
故答案为:140x
【点评】此题考查的是相遇问题,注意要用字母表示数。
3.高家崖建筑群的大小院落有多少间 x=35
【分析】已知高家崖建筑群的房屋比大小院落数量的9倍还多27,设大小院落数量有x间,可得高家崖建筑群的房屋有9x+27间,即可得到题目中的方程;解上步所得方程,方程的解是大小院落数量,据此不难推断提出的问题。
【解答】解:设大小院落数量有x间,则高家崖建筑群的房屋有9x+27间。
9x+27=342
9x+27-27=342-27
9x=342-27
9x=315
x=35
他提出的问题是“高家崖建筑群的大小院落有多少间”,这个方程的解是x=35。
【点评】本题是一道有关利用方程求解的题目,关键在于找出等量关系。
4. 48 1536
【分析】设另一个因数是x,那么正确的积就是32x,错误的积是23x,两个积之间的差是432,列方程:32x-23x=432,解方程,求出另一个因数,进而求出正确的积。
【解答】解:设另一个因数是x。
32x-23x=432
9x=432
x=432÷9
x=48
32×48=1536
芳芳做乘法计算题时,把其中一个因数32当作23来算,结果得到的积比正确的积少了432,那么,另一个因数是48,正确的积应该是1536。
【点评】本题考查方程的实际应用,根据两次运算的差,设出未知数,找出相关的量,求出另一个因数,进而解答。
5.15 45
【分析】每个螺栓配两个螺帽, 要使生产的螺栓和螺帽刚好配套,则螺帽的数量是螺栓的2倍。螺栓的数量=15×生产螺栓的人数,螺帽的数量=10×生产螺帽的人数。设应分配x人生产螺栓,(60-x)人生产螺帽,根据数量关系式:螺帽的数量=2×螺栓的数量,列出方程求出方程的解。
【解答】设:应分配x人生产螺栓,(60-x)人生产螺帽。
螺帽:60-15=45(人)
则应分配15人生产螺栓,45人生产螺帽,才能使生产的螺栓和螺帽刚好配套。
6.168
【分析】根据题意可知,自动扶梯的可见级数是固定的,人上升的速度应为:人速度+扶梯速度,男孩和女孩走的扶梯的级数相等,设:扶梯的速度为x级/分,男孩走的级数为:6×(20+x),女孩走的级数为:7×(16+x),男孩和女孩走的级数相等,列方程:6×(20+x)=7×(16+x),解方程,求出扶梯每分钟的级数,进而求出扶梯共有多少级。
【解答】解:设扶梯速度为x级/分钟
6×(20+x)=7×(16+x)
120+6x=112+7x
7x-6x=120-112
x=8
6×(20+8)
=6×28
=168(级)
【点评】本题的关键是人走,扶梯也走,人上升的速度是人的速度和扶梯的速度的和,列方程,解方程。
7.15
【分析】可以设王师傅加工了x小时,由于张师傅独自加工3小时,则张师傅加工了:(x+3)小时,张师傅加工的数量+王师傅加工的数量=300,由此即可列出方程,再根据等式的性质解方程即可,最后求出x的值再加3小时就是完成这批订单用的时间。
【解答】解:设王师傅加工了x小时,则张师傅加工了:(x+3)小时。
10x+12×(x+3)=300
10x+12x+36=300
22x=300-36
22x=264
x=264÷22
x=12
12+3=15(小时)
【点评】本题主要考查列方程解应用题,找准等量关系是解题的关键。
8.40
【分析】公交车全程走15分钟,每间隔5分钟发一趟车,他出发时,正好一辆公交车到站。由此可知,15÷5=3,路上有3-1=2(辆)公交车,且甲站有1辆公交车要发车。根据题意,只要求出从他出发开始,一共发了多少辆车即可求出他骑行了多少时间。他全程一共遇见了10辆,减去他出发时已经在路上的2辆,即一共发车了8辆。
【解答】据分析:他出发时路上有:(15÷5)-1
=3-1
=2(辆)
他从出发到甲站,要经过:
5×(10-2)
=5×8
=40(分钟)
【点评】此题属于多次相遇问题,考查学生分析问题的能力,可以画线段图来便于理解。
9. 20 10
【分析】根据题意可设甲电影票售出未知数x张,则乙电影票售出张,已知甲、乙电影票得单价,根据总价=单价×数量,可列出方程解出答案。
【解答】设甲电影票售出未知数x张,则乙电影票售出张,可列出方程:
即甲电影票售出20张,乙电影票售出(张)。
10.(1)4m+1/1+4m
(2)25
【分析】(1)摆1个等腰梯形需要4×1+1=5根火柴棒,摆2个等腰梯形需要4×2+1=9根火柴棒,摆3个等腰梯形需要4×3+1=13根火柴棒,……,摆m个等腰梯形需要4×m+1=(4m+1)根火柴棒,据此解答。
(2)求有101根火柴棒,可以摆多少个这样的等腰梯形,即4m+1=101,据此求出m的值即可解答。
【解答】(1)摆1个等腰梯形需要4×1+1=5根火柴棒,
摆2个等腰梯形需要4×2+1=9根火柴棒,
摆3个等腰梯形需要4×3+1=13根火柴棒,
摆m个等腰梯形需要4×m+1=(4m+1)根火柴棒。
(2)4m+1=101
解:4m+1-1=101-1
4m=100
4m÷4=100÷4
m=25
可以摆25个这样的等腰梯形。
11.错误
【解答】1800÷(50+40)=20(小时)
故答案为错误.
12.×
【分析】设第一条彩带长x米,则第二条长x+2.7米,又知第二条长6.9米,所以可得方程6.9=x+2.7,解方程得到的x为第一条彩带长,再与第二条长度相加才得两条彩带一共长多少米。
【解答】解:设第一条彩带长x米,
x+2.7=6.9
x+2.7﹣2.7=6.9﹣2.7
x=4.2
4.2+6.9=11.1(米)
故答案为:×。
【点晴】本题考查了列方程解应用题,注意求得的x不是两条彩带一共的长度。
13.√
【解答】根据题中的数量关系,可列方程为:5m-2m=10。
故答案为:√
14.√
【分析】根据题意,把x=0.9代入方程3x+0.7=3.4,能使方程左右两边相等的,就是方程的解,否则不是。
【解答】把x=0.9代入方程3x+0.7=3.4
左边为:
3×0.9+0.7
=2.7+0.7
=3.4
右边=3.4
左边=右边,所以,x=0.9是方程3x+0.7=3.4的解。
故答案为:√
【点评】可以根据方程的解的检验方法,把方程的解代入原方程,能使方程左右两边相等的,就是方程的解。
15.×
【解答】设这个数是x,依据题意3x加12等于50可列方程:3x+12=50,依据等式的性质,方程两边同时减12,再同时除以3求解。
【解答】解:设这个数是x
3x+12=50
3x+12-12=50-12
3x=38
3x÷3=38÷3
x=
这个数是。
所以这个数是,原题干计算错误;
故答案为:×
【点评】列出方程并依据等式的性质解方程是本题考查知识点。
16.D
【分析】一张桌子的售价比一把椅子的售价的3倍少8元,一把椅子的售价为元,则一张桌子的售价为元,一套桌椅的售价为196元,一张桌子的售价加上一把椅子的售价等于一套桌椅的售价,由此可列式。
【解答】由分析可知,一张桌子的售价+一张椅子的售价=一套桌椅的售价,设一把椅子的售价为元,则列方程为:
故答案为:D
17.D
【分析】把x看作单位“1”,x的就是x,方程表示x与x的和是60。据此选择即可。
【解答】A.把x看作单位“1”平均分成3份,这样的1份占单位“1”的,即,观察线段图可知:x与x的和是60,可以列出方程。
B.把x看作单位“1”平均分成3份,这样的1份占单位“1”的,即,观察线段图可知:x与x的和是60,可以列出方程。
C.把阴影部分(x平方米)看作单位“1”平均分成3份,这样的1份占阴影部分的,这样的1份的面积是x平方米,阴影部分的面积和x平方米的和是60,可以列出方程。
D.把阴影部分(x平方米)看作单位“1”平均分成2份,这样的1份占阴影部分的,这样的1份的面积是x平方米,阴影部分的面积和x平方米的和是60,可以列出方程。
故答案为:D
【点评】解决此题关键是明确单位“1”及等量关系式。
18.B
【分析】由题意可知,本题的等量关系式:①客车所行的路程+货车所行的路程=两地之间的距离;②速度之和×相遇时间=两地路程;③货车所行的路程=两地之间的距离-客车所行的路程;由此分别列方程解答即可。
【解答】A.符合等量关系式①,此方程正确;
B.等量关系错误,此方程不正确;
C.符合等量关系式②,此方程正确;
D.符合等量关系式③,此方程正确;
故答案为:B
【点评】本题主要考查列方程解决实际问题的能力,关键是要分析题意、找准等量关系式。
19.D
【分析】将四年级报名的人数设为x人,那么五年级有2x人报名。根据“四年级报名人数+五年级报名人数=240人”这一等量关系,列方程解方程即可。
【解答】解:设四年级有x人报名。
x+2x=240
3x=240
x=240÷3
x=80
80×2=160(人)
所以,五年级有160人报名参加文明交通志愿者行动。
故答案为:D
【点评】本题考查了简易方程的应用,根据题意找出数量关系是解题的关键。
20.C
【分析】先根据:速度=路程÷时间,求出两人的速度和,再求出奇思的速度;然后再逐项进行分析判断,即可解答。
【解答】1100÷10=110(米/分);110-60=50(米/分)。
A.60>50,相遇的地点更靠近奇思家,原题干说法错误;
B.60>50,奇思的速度比淘气慢,原题干说法错误;
C.60>50,相遇时,淘气的路程更长,原题干说法正确;
D.10分钟后,他们相遇,交换礼物后,如果保持速度不变,两人同时到家,原题干说法错误。
故答案为:C
【点评】利用速度、时间和路程三者的关系,求出两人的速度,进而解答问题。
21.见详解
【分析】由图知:男生有x人,女生人数是男生的3倍,则女生有3x人,男生女生共48人,据此列出方程,解此方程可得男生女生各自的人数。
【解答】
解:
女生有:(人)
男生有12人,女生有36人。
22.52分
【分析】
由线段图以及相遇问题的公式,可得出等量关系:速度和×相遇时间=相遇路程,据此列出方程,并求解。
【解答】(5+3)=416
解:8=416
8÷8=416÷8
=52
经过52分后相遇。
23.15名
【分析】设有x名小朋友。如果每名小朋友分4个,还剩10个,则x名小朋友一共分了4x个,加上剩下的10个,可得这袋糖果一共有(4x+10)个;如果每名小朋友分5个,一共分了5x个,再减去差的5个,可知这袋糖果一共有(5x-5)个。糖果的总个数不变,据此列出方程:4x+10=5x-5,根据等式的性质解出方程即可。
【解答】解:设有x名小朋友。
4x+10=5x-5
10=5x-5-4x
10=x-5
10+5=x
x=15
答:有15名小朋友。
24.甲桶水:62千克;乙桶水:38千克
【分析】设甲桶水重x千克,甲桶水比乙用水多24千克,则乙桶水为(x-24)千克,甲桶水用去8千克,还剩(x-8)千克,乙桶水用去2千克,乙桶水还剩(x-24-2)千克,甲桶水的质量是乙桶水的1.5倍,即甲桶水用去8千克后剩下的水的质量=乙水桶用去2千克后×1.5,列方程:x-8=(x-24-2)×1.5,解方程,即可解答。
【解答】解:设甲水桶重x千克,则乙水桶重x-24千克。
x-8=(x-24-2)×1.5
x-8=1.5x-24×1.5-2×1.5
1.5x-x=24×1.5+2×1.5-8
0.5x=36+3-8
0.5x=39-8
0.5x=31
x=31÷0.5
x=62
乙桶水重:62-24=38(千克)
答:甲桶水重62千克,乙桶水重38千克。
【点评】本题考查方程的实际应用,利用甲桶水的质量与乙桶水质量之间的关系,设出未知数,找出相关的量,列方程,解方程。
25.篮球有16个,足球有4个
【分析】设足球有x个,则篮球有4x个,根据等量关系:篮球个数-足球的个数=12个,列方程解答即可。
【解答】解:设足球有x个,则篮球有4x个。
4x-x=12
3x=12
3x÷3=12÷3
x=4
4+12=16(个)
答:篮球有16个,足球有4个。
【点评】本题主要考查了列方程解应用题,关键是根据等量关系:篮球个数-足球的个数=12个,列方程。
26.(1)等量关系:男生夹的个数的3倍-男生夹的个数=60
(2)30个;90个
【分析】设男生夹了x个,根据:女生比男生多夹了60个,女生夹弹珠的个数是男生的3倍,男生夹的个数的3倍-男生夹的个数=60,据此列出方程,求出x的值是多少,然后用x乘3即可计算出女生夹了多少。
【解答】等量关系:男生夹的个数的3倍-男生夹的个数=60
解:设男生夹了x个。
3x-x=60
2x=60
2x÷2=60÷2
x=30
30×3=90(个)
答:男生夹了30个,女生夹了90个。
【点评】此题主要考查了一元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
27.5.5分钟;192.5米;图见详解
【分析】设两人经过x分钟相遇,小刚行驶的路程=小刚行驶的速度×相遇的时间=25x,小强行驶的路程=小强行驶的速度×相遇的时间=35x。则根据数量关系式小刚行驶的路程+小强行驶的路程=总路程列出方程。总路程是三段的路程和为330千米,求出方程的解。再用小强的速度×相遇的时间得出小强走的千米数。
【解答】
解:设两人经过x分钟相遇。
35x+25x=152+48+130
60x=330
60x÷60=330÷60
x=5.5
35×5.5=192.5(米)
答:两人经过5.5分钟相遇,相遇时,小强走了192.5米。
28.12时
【分析】
根据题意,先设两列火车行驶x时相遇,结合相遇公式:速度和×相遇时间=路程可知,用快车的速度加上慢车的速度之和,再乘上x就等于全长。据此列式为:(85+78)x=1956,求出x即可。
【解答】
根据题意可知,等量关系式为:(快车速度+慢车速度)×相遇时间=全长。
解:设两列火车行驶x时相遇。
(85+78)x=1956
163x=1956
163x÷163=1956÷163
x=12
答:两列火车行驶12时相遇。
29.200天
【分析】设经过x天甲、乙两个工程队才能修完这条铁路,甲队每天修0.96千米,x天修0.96x千米;乙队每天修1.14千米,x天修1.14x千米,甲队修的长度+乙队修的长度=这条铁路的长度,列方程:0.96x+1.14x=420,解方程,即可解答。
【解答】解:设经过x天甲、乙两个工程队才能修完这条铁路。
0.96x+1.14x=420
2.1x=420
x=420÷2.1
x=200
答:经过200天甲、乙两个工程队才能修完这条铁路。
【点评】本题考查相遇问题,关键甲、乙两队修铁路的长度与总长度之间的关系,设出未知数,找出相关的量,列方程,解方程。
30.(1)见详解
(2)960米
【分析】(1)由于爸爸的速度快,小青的速度比较慢,而且爸爸比小青的速度快得多,所以在过中点,离火车站近点的地方相遇,标注合理即可。
(2)可以设他们x分钟相遇,小青每分钟走的路程×相遇时间+爸爸每分钟走的路程×时间=1200,据此即可列方程,再根据等式的性质解方程即可,再用爸爸每分钟走的路程×时间即可求出相遇点离家多少米。。
【解答】(1)如下图所示:
(2)解:设他们x分钟后相遇。
80x+20x=1200
100x=1200
100x÷100=1200÷100
x=12
12×80=960(米)
答:相遇点离家960米。
【点评】本题主要考查列方程解一个未知数的题目以及相遇问题的公式,熟练掌握它的公式并灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七单元用方程解决问题(知识梳理+拔高训练)一
知识梳理
知识点01:解形如“ax±x=b”类型的方程
根据乘法分配律和等式的性质来解,具体步骤如下:
ax±x=b
解:(a±1)x=b
x=b÷(a±1)
知识点02:解如“ax±x=b”类型的方程
根据乘法分配律和等式的性质来解,具体步骤如下:
ax±bx=c
解:(a±b)x=c
x=c÷(a±b)
知识点03:解决相遇问题
可以根据“速度和×相遇时间=路程和”这个等量关系来列方程。
速度和×相遇时间=路程和;路程和÷相遇时间=速度和;路程和÷速度和=相遇时间。
知识点04:方程法解题
就是把题中的末知量用x表示,使未知量x与已知量处于同等地位,直接参加运算。根据题意先找出等量关系,列出含有末知数的等式,再求得未知量的值的一种解题方法。
拔高训练
一、填空题(共20分)
1.(2分)
一辆货车和一辆轿车分别从两地同时出发,相向而行,行驶了x时后相遇。
方程:86x+72x=316
补充的条件是:
2.(2分)甲、乙两车分别从A、B两地同时出发,相向而行,甲车每小时行60km,乙车每小时行80km,经过小时两车相遇,A、B两地相距( )km。
3.(2分)聪聪和妈妈一起随旅游团游览王家大院,经导游介绍,聪聪了解到:王家大院高家崖建筑群的房屋有342间,比大小院落数量的9倍还多27,根据这些信息,聪聪提出了一个数学问题,并用方程“9x+27=342”来解决。请你推断一下,他提出的问题是( ),这个方程的解是( )。
4.(2分)芳芳做乘法计算题时,把其中一个因数32当作23来算,结果得到的积比正确的积少了432,那么,另一个因数是( ),正确的积应该是( )。
5.(2分)某车间有60名工人,生产一种螺栓和螺帽,平均每人每小时生产螺栓15个或螺帽10个,应分配( )人生产螺栓,( )人生产螺帽,才能使生产的螺栓和螺帽刚好配套。(每个螺栓配两个螺帽)
6.(2分)登山自动扶梯以均匀速度由下往上行驶,两位性急的孩子要从扶梯向上走,已知男孩子每分钟走20级台阶,女孩子每分钟走16级,结果男孩子用了6分钟到达山顶,女孩子用了7分钟到达山顶。则该扶梯共有( )级。
7.(2分)工厂接到加工300个零件的订单,先由张师傅独自加工3小时,每时加工12个,后又安排王师傅也参与加工,王师傅每时加工10个,完成这批零件订单共用了( )时。
8.(2分)公交车从甲站到乙站每间隔5分钟一趟,全程走15分钟,某人骑自行车从乙站往甲站行走,开始时恰好遇见一辆公交车,行走过程中又遇见10辆,到甲站时又一辆公交车刚要出发,这人走了( )分钟。
9.(2分)百达电影院在1时内售出甲、乙两种电影票一共30张,甲电影票35元一张,乙电影票25元一张,共收入950元。其中售出甲电影票( )张,乙电影票( )张。
10.(2分)如图所示,用火柴棒按下图的方式摆等腰梯形:摆1个等腰梯形需要4×1+1=5(根)火柴棒,摆2个等腰梯形需要4×2+1=9(根)火柴棒,摆3个等腰梯形需要4×3+1=13(根)火柴棒……
(1)像这样摆下去,摆m个等腰梯形一共需要( )根火柴棒。
(2)有101根火柴棒,可以摆( )个这样的等腰梯形。
二、判断题(共10分)
11.(2分)A、B两地之间相距1800千米,甲、乙两辆卡车从两地同时相对开出,甲车每小时行50千米,乙车每小时行40千米,经过几小时两车相遇?
列式是:1800÷50=36(小时)
1800÷40=45(小时)
45+36=81(小时) ( )
12.(2分)计算图中两条彩带一共长多少米,列出的方程是6.9=x+2.7。
13.(2分)m的5倍比它的2倍多10,列式为5m-2m=10。( )
14.(2分)3x+0.7=3.4的解是x=0.9。( )
15.(2分)比一个数的3倍还多12的数是50,那么这个数是162。( )
三、选择题(共10分)
16.(2分)一套桌椅的售价为196元,一张桌子的售价比一把椅子的售价的3倍少8元,一张桌子、一把椅子的售价分别是多少元?设一把椅子的售价为元,列式正确的是( )。
A. B. C. D.
17.(2分)下面不能用方程“”来表示的是( )。
A. B.
C. D.
18.(2分)两地相距360千米,甲乙两辆货车从两地相对开出,经过3小时后相遇,已知甲货车每时行驶55千米,乙货车每时行驶千米,不正确的方程为( )。
A. B.
C. D.
19.(2分)为创建全国文明城市,学校开展“我是文明使者,争当最美少年”实践活动。四、五年级学生共有240人报名参加文明交通志愿者行动,其中五年级报名人数是四年级的2倍,五年级有( )人报名参加文明交通志愿者行动。
A.80 B.200 C.100 D.160
20.(2分)六一节当天,奇思和淘气这对好朋友相约同时从家里出发,在途中交换一份亲手为对方创作的六一节礼物。已知他们两家相1100米,淘气的步行速度约为60米/分。10分钟后他们相遇了。下列说法正确的是( )。
A.相遇的地点离淘气家近一些
B.奇思的速度比淘气快
C.相遇时淘气走的路程更长。
D.交换礼物后,如果保持速度不变,淘气先到家。
四、计算题(共12分)
21.(6分)看图列方程并解答。
22.(6分)看图列式或列方程计算。
五、解答题(共48分)
23.(6分)六一儿童节这天,中一班的王老师买来了一袋糖果准备分给小朋友们。如果每名小朋友分4个,那么还剩10个;如果每名小朋友分5个,那么就差5个。有多少名小朋友?
24.(6分)原来甲桶水比乙桶水多24千克,甲桶水用去8千克、乙桶水用去2千克后,甲桶水的质量是乙桶水的1.5倍,原来两桶水各重多少千克?
25.(6分)学校买来篮球和足球若干个,篮球个数是足球的4倍,已知足球比篮球少12个,篮球和足球各有多少个?(列方程解答)
26.(6分)五(1)班进行男女生夹弹珠比赛。女生比男生多夹了60个,女生夹弹珠的个数是男生的3倍。男女生各夹了多少个弹珠?(先写出等量关系,再用方程解答。)
(1)等量关系:
(2)解答:
27.(6分)小刚和小强两人同时从家里出发,相向而行。
两人经过几分钟相遇?在图中用“”标出相遇时的大致位置。相遇时,小强走了多少米?
28.(6分)青藏铁路是世界上海拔最高、线路最长的高原铁路,东起青海西宁,南至西藏拉萨,全长1956千米。两列火车分别从拉萨和西宁同时出发,已知快车的速度为85千米/时,慢车的速度为78千米/时。两列火车行驶多少时相遇?(先写出等量关系,再列方程解答。)
29.(6分)甲、乙两个工程队同时开始合修一条长为420千米的铁路,若甲队每天修0.96千米,乙队每天修1.14千米。经过多少天甲、乙两个工程队才能修完这条铁路?(列方程解答)
30.(6分)端午节假期,小青乘火车回家,到车站后,爸爸骑车接她。爸爸以80米/分的速度去火车站,小青以20米/分的速度从火车站同时出发,已知小青家与火车站的距离为1200米。
(1)估计他们在何处相遇,在图中标出来。
(2)他们几分钟后相遇?(用方程解答)相遇点离家多少米?
参考答案
1.两地相距316千米
2.140x
【分析】根据行程问题的关系量:路程=速度×时间,甲的路程=60×x,乙的路程=80×x,然后把甲、乙的路程加起来就是A、B两地的距离,据此解答。
【解答】甲的路程是:60×x=60xkm
乙的路程是:80×x=80xkm
甲、乙的路程和,即A、B两地相距:60x+80x=140xkm
故答案为:140x
【点评】此题考查的是相遇问题,注意要用字母表示数。
3.高家崖建筑群的大小院落有多少间 x=35
【分析】已知高家崖建筑群的房屋比大小院落数量的9倍还多27,设大小院落数量有x间,可得高家崖建筑群的房屋有9x+27间,即可得到题目中的方程;解上步所得方程,方程的解是大小院落数量,据此不难推断提出的问题。
【解答】解:设大小院落数量有x间,则高家崖建筑群的房屋有9x+27间。
9x+27=342
9x+27-27=342-27
9x=342-27
9x=315
x=35
他提出的问题是“高家崖建筑群的大小院落有多少间”,这个方程的解是x=35。
【点评】本题是一道有关利用方程求解的题目,关键在于找出等量关系。
4. 48 1536
【分析】设另一个因数是x,那么正确的积就是32x,错误的积是23x,两个积之间的差是432,列方程:32x-23x=432,解方程,求出另一个因数,进而求出正确的积。
【解答】解:设另一个因数是x。
32x-23x=432
9x=432
x=432÷9
x=48
32×48=1536
芳芳做乘法计算题时,把其中一个因数32当作23来算,结果得到的积比正确的积少了432,那么,另一个因数是48,正确的积应该是1536。
【点评】本题考查方程的实际应用,根据两次运算的差,设出未知数,找出相关的量,求出另一个因数,进而解答。
5.15 45
【分析】每个螺栓配两个螺帽, 要使生产的螺栓和螺帽刚好配套,则螺帽的数量是螺栓的2倍。螺栓的数量=15×生产螺栓的人数,螺帽的数量=10×生产螺帽的人数。设应分配x人生产螺栓,(60-x)人生产螺帽,根据数量关系式:螺帽的数量=2×螺栓的数量,列出方程求出方程的解。
【解答】设:应分配x人生产螺栓,(60-x)人生产螺帽。
螺帽:60-15=45(人)
则应分配15人生产螺栓,45人生产螺帽,才能使生产的螺栓和螺帽刚好配套。
6.168
【分析】根据题意可知,自动扶梯的可见级数是固定的,人上升的速度应为:人速度+扶梯速度,男孩和女孩走的扶梯的级数相等,设:扶梯的速度为x级/分,男孩走的级数为:6×(20+x),女孩走的级数为:7×(16+x),男孩和女孩走的级数相等,列方程:6×(20+x)=7×(16+x),解方程,求出扶梯每分钟的级数,进而求出扶梯共有多少级。
【解答】解:设扶梯速度为x级/分钟
6×(20+x)=7×(16+x)
120+6x=112+7x
7x-6x=120-112
x=8
6×(20+8)
=6×28
=168(级)
【点评】本题的关键是人走,扶梯也走,人上升的速度是人的速度和扶梯的速度的和,列方程,解方程。
7.15
【分析】可以设王师傅加工了x小时,由于张师傅独自加工3小时,则张师傅加工了:(x+3)小时,张师傅加工的数量+王师傅加工的数量=300,由此即可列出方程,再根据等式的性质解方程即可,最后求出x的值再加3小时就是完成这批订单用的时间。
【解答】解:设王师傅加工了x小时,则张师傅加工了:(x+3)小时。
10x+12×(x+3)=300
10x+12x+36=300
22x=300-36
22x=264
x=264÷22
x=12
12+3=15(小时)
【点评】本题主要考查列方程解应用题,找准等量关系是解题的关键。
8.40
【分析】公交车全程走15分钟,每间隔5分钟发一趟车,他出发时,正好一辆公交车到站。由此可知,15÷5=3,路上有3-1=2(辆)公交车,且甲站有1辆公交车要发车。根据题意,只要求出从他出发开始,一共发了多少辆车即可求出他骑行了多少时间。他全程一共遇见了10辆,减去他出发时已经在路上的2辆,即一共发车了8辆。
【解答】据分析:他出发时路上有:(15÷5)-1
=3-1
=2(辆)
他从出发到甲站,要经过:
5×(10-2)
=5×8
=40(分钟)
【点评】此题属于多次相遇问题,考查学生分析问题的能力,可以画线段图来便于理解。
9. 20 10
【分析】根据题意可设甲电影票售出未知数x张,则乙电影票售出张,已知甲、乙电影票得单价,根据总价=单价×数量,可列出方程解出答案。
【解答】设甲电影票售出未知数x张,则乙电影票售出张,可列出方程:
即甲电影票售出20张,乙电影票售出(张)。
10.(1)4m+1/1+4m
(2)25
【分析】(1)摆1个等腰梯形需要4×1+1=5根火柴棒,摆2个等腰梯形需要4×2+1=9根火柴棒,摆3个等腰梯形需要4×3+1=13根火柴棒,……,摆m个等腰梯形需要4×m+1=(4m+1)根火柴棒,据此解答。
(2)求有101根火柴棒,可以摆多少个这样的等腰梯形,即4m+1=101,据此求出m的值即可解答。
【解答】(1)摆1个等腰梯形需要4×1+1=5根火柴棒,
摆2个等腰梯形需要4×2+1=9根火柴棒,
摆3个等腰梯形需要4×3+1=13根火柴棒,
摆m个等腰梯形需要4×m+1=(4m+1)根火柴棒。
(2)4m+1=101
解:4m+1-1=101-1
4m=100
4m÷4=100÷4
m=25
可以摆25个这样的等腰梯形。
11.错误
【解答】1800÷(50+40)=20(小时)
故答案为错误.
12.×
【分析】设第一条彩带长x米,则第二条长x+2.7米,又知第二条长6.9米,所以可得方程6.9=x+2.7,解方程得到的x为第一条彩带长,再与第二条长度相加才得两条彩带一共长多少米。
【解答】解:设第一条彩带长x米,
x+2.7=6.9
x+2.7﹣2.7=6.9﹣2.7
x=4.2
4.2+6.9=11.1(米)
故答案为:×。
【点晴】本题考查了列方程解应用题,注意求得的x不是两条彩带一共的长度。
13.√
【解答】根据题中的数量关系,可列方程为:5m-2m=10。
故答案为:√
14.√
【分析】根据题意,把x=0.9代入方程3x+0.7=3.4,能使方程左右两边相等的,就是方程的解,否则不是。
【解答】把x=0.9代入方程3x+0.7=3.4
左边为:
3×0.9+0.7
=2.7+0.7
=3.4
右边=3.4
左边=右边,所以,x=0.9是方程3x+0.7=3.4的解。
故答案为:√
【点评】可以根据方程的解的检验方法,把方程的解代入原方程,能使方程左右两边相等的,就是方程的解。
15.×
【解答】设这个数是x,依据题意3x加12等于50可列方程:3x+12=50,依据等式的性质,方程两边同时减12,再同时除以3求解。
【解答】解:设这个数是x
3x+12=50
3x+12-12=50-12
3x=38
3x÷3=38÷3
x=
这个数是。
所以这个数是,原题干计算错误;
故答案为:×
【点评】列出方程并依据等式的性质解方程是本题考查知识点。
16.D
【分析】一张桌子的售价比一把椅子的售价的3倍少8元,一把椅子的售价为元,则一张桌子的售价为元,一套桌椅的售价为196元,一张桌子的售价加上一把椅子的售价等于一套桌椅的售价,由此可列式。
【解答】由分析可知,一张桌子的售价+一张椅子的售价=一套桌椅的售价,设一把椅子的售价为元,则列方程为:
故答案为:D
17.D
【分析】把x看作单位“1”,x的就是x,方程表示x与x的和是60。据此选择即可。
【解答】A.把x看作单位“1”平均分成3份,这样的1份占单位“1”的,即,观察线段图可知:x与x的和是60,可以列出方程。
B.把x看作单位“1”平均分成3份,这样的1份占单位“1”的,即,观察线段图可知:x与x的和是60,可以列出方程。
C.把阴影部分(x平方米)看作单位“1”平均分成3份,这样的1份占阴影部分的,这样的1份的面积是x平方米,阴影部分的面积和x平方米的和是60,可以列出方程。
D.把阴影部分(x平方米)看作单位“1”平均分成2份,这样的1份占阴影部分的,这样的1份的面积是x平方米,阴影部分的面积和x平方米的和是60,可以列出方程。
故答案为:D
【点评】解决此题关键是明确单位“1”及等量关系式。
18.B
【分析】由题意可知,本题的等量关系式:①客车所行的路程+货车所行的路程=两地之间的距离;②速度之和×相遇时间=两地路程;③货车所行的路程=两地之间的距离-客车所行的路程;由此分别列方程解答即可。
【解答】A.符合等量关系式①,此方程正确;
B.等量关系错误,此方程不正确;
C.符合等量关系式②,此方程正确;
D.符合等量关系式③,此方程正确;
故答案为:B
【点评】本题主要考查列方程解决实际问题的能力,关键是要分析题意、找准等量关系式。
19.D
【分析】将四年级报名的人数设为x人,那么五年级有2x人报名。根据“四年级报名人数+五年级报名人数=240人”这一等量关系,列方程解方程即可。
【解答】解:设四年级有x人报名。
x+2x=240
3x=240
x=240÷3
x=80
80×2=160(人)
所以,五年级有160人报名参加文明交通志愿者行动。
故答案为:D
【点评】本题考查了简易方程的应用,根据题意找出数量关系是解题的关键。
20.C
【分析】先根据:速度=路程÷时间,求出两人的速度和,再求出奇思的速度;然后再逐项进行分析判断,即可解答。
【解答】1100÷10=110(米/分);110-60=50(米/分)。
A.60>50,相遇的地点更靠近奇思家,原题干说法错误;
B.60>50,奇思的速度比淘气慢,原题干说法错误;
C.60>50,相遇时,淘气的路程更长,原题干说法正确;
D.10分钟后,他们相遇,交换礼物后,如果保持速度不变,两人同时到家,原题干说法错误。
故答案为:C
【点评】利用速度、时间和路程三者的关系,求出两人的速度,进而解答问题。
21.见详解
【分析】由图知:男生有x人,女生人数是男生的3倍,则女生有3x人,男生女生共48人,据此列出方程,解此方程可得男生女生各自的人数。
【解答】
解:
女生有:(人)
男生有12人,女生有36人。
22.52分
【分析】
由线段图以及相遇问题的公式,可得出等量关系:速度和×相遇时间=相遇路程,据此列出方程,并求解。
【解答】(5+3)=416
解:8=416
8÷8=416÷8
=52
经过52分后相遇。
23.15名
【分析】设有x名小朋友。如果每名小朋友分4个,还剩10个,则x名小朋友一共分了4x个,加上剩下的10个,可得这袋糖果一共有(4x+10)个;如果每名小朋友分5个,一共分了5x个,再减去差的5个,可知这袋糖果一共有(5x-5)个。糖果的总个数不变,据此列出方程:4x+10=5x-5,根据等式的性质解出方程即可。
【解答】解:设有x名小朋友。
4x+10=5x-5
10=5x-5-4x
10=x-5
10+5=x
x=15
答:有15名小朋友。
24.甲桶水:62千克;乙桶水:38千克
【分析】设甲桶水重x千克,甲桶水比乙用水多24千克,则乙桶水为(x-24)千克,甲桶水用去8千克,还剩(x-8)千克,乙桶水用去2千克,乙桶水还剩(x-24-2)千克,甲桶水的质量是乙桶水的1.5倍,即甲桶水用去8千克后剩下的水的质量=乙水桶用去2千克后×1.5,列方程:x-8=(x-24-2)×1.5,解方程,即可解答。
【解答】解:设甲水桶重x千克,则乙水桶重x-24千克。
x-8=(x-24-2)×1.5
x-8=1.5x-24×1.5-2×1.5
1.5x-x=24×1.5+2×1.5-8
0.5x=36+3-8
0.5x=39-8
0.5x=31
x=31÷0.5
x=62
乙桶水重:62-24=38(千克)
答:甲桶水重62千克,乙桶水重38千克。
【点评】本题考查方程的实际应用,利用甲桶水的质量与乙桶水质量之间的关系,设出未知数,找出相关的量,列方程,解方程。
25.篮球有16个,足球有4个
【分析】设足球有x个,则篮球有4x个,根据等量关系:篮球个数-足球的个数=12个,列方程解答即可。
【解答】解:设足球有x个,则篮球有4x个。
4x-x=12
3x=12
3x÷3=12÷3
x=4
4+12=16(个)
答:篮球有16个,足球有4个。
【点评】本题主要考查了列方程解应用题,关键是根据等量关系:篮球个数-足球的个数=12个,列方程。
26.(1)等量关系:男生夹的个数的3倍-男生夹的个数=60
(2)30个;90个
【分析】设男生夹了x个,根据:女生比男生多夹了60个,女生夹弹珠的个数是男生的3倍,男生夹的个数的3倍-男生夹的个数=60,据此列出方程,求出x的值是多少,然后用x乘3即可计算出女生夹了多少。
【解答】等量关系:男生夹的个数的3倍-男生夹的个数=60
解:设男生夹了x个。
3x-x=60
2x=60
2x÷2=60÷2
x=30
30×3=90(个)
答:男生夹了30个,女生夹了90个。
【点评】此题主要考查了一元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
27.5.5分钟;192.5米;图见详解
【分析】设两人经过x分钟相遇,小刚行驶的路程=小刚行驶的速度×相遇的时间=25x,小强行驶的路程=小强行驶的速度×相遇的时间=35x。则根据数量关系式小刚行驶的路程+小强行驶的路程=总路程列出方程。总路程是三段的路程和为330千米,求出方程的解。再用小强的速度×相遇的时间得出小强走的千米数。
【解答】
解:设两人经过x分钟相遇。
35x+25x=152+48+130
60x=330
60x÷60=330÷60
x=5.5
35×5.5=192.5(米)
答:两人经过5.5分钟相遇,相遇时,小强走了192.5米。
28.12时
【分析】
根据题意,先设两列火车行驶x时相遇,结合相遇公式:速度和×相遇时间=路程可知,用快车的速度加上慢车的速度之和,再乘上x就等于全长。据此列式为:(85+78)x=1956,求出x即可。
【解答】
根据题意可知,等量关系式为:(快车速度+慢车速度)×相遇时间=全长。
解:设两列火车行驶x时相遇。
(85+78)x=1956
163x=1956
163x÷163=1956÷163
x=12
答:两列火车行驶12时相遇。
29.200天
【分析】设经过x天甲、乙两个工程队才能修完这条铁路,甲队每天修0.96千米,x天修0.96x千米;乙队每天修1.14千米,x天修1.14x千米,甲队修的长度+乙队修的长度=这条铁路的长度,列方程:0.96x+1.14x=420,解方程,即可解答。
【解答】解:设经过x天甲、乙两个工程队才能修完这条铁路。
0.96x+1.14x=420
2.1x=420
x=420÷2.1
x=200
答:经过200天甲、乙两个工程队才能修完这条铁路。
【点评】本题考查相遇问题,关键甲、乙两队修铁路的长度与总长度之间的关系,设出未知数,找出相关的量,列方程,解方程。
30.(1)见详解
(2)960米
【分析】(1)由于爸爸的速度快,小青的速度比较慢,而且爸爸比小青的速度快得多,所以在过中点,离火车站近点的地方相遇,标注合理即可。
(2)可以设他们x分钟相遇,小青每分钟走的路程×相遇时间+爸爸每分钟走的路程×时间=1200,据此即可列方程,再根据等式的性质解方程即可,再用爸爸每分钟走的路程×时间即可求出相遇点离家多少米。。
【解答】(1)如下图所示:
(2)解:设他们x分钟后相遇。
80x+20x=1200
100x=1200
100x÷100=1200÷100
x=12
12×80=960(米)
答:相遇点离家960米。
【点评】本题主要考查列方程解一个未知数的题目以及相遇问题的公式,熟练掌握它的公式并灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
