综合实践题常见考点 押题练 2025年中考数学三轮复习备考
文档属性
| 名称 | 综合实践题常见考点 押题练 2025年中考数学三轮复习备考 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 17:30:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
综合实践题常见考点 押题练
2025年中考数学三轮复习备考
1.《黑神话:悟空》游戏中选取的27处山西极具代表性的古建筑,由南至北横跨9个地市,不仅展示了山西深厚的文化底蕴,也为当地文旅产业带来新的发展机遇.飞虹塔是山西省非常有名的一座塔楼,某实践小组欲测量飞虹塔的高度,测量过程见下表.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
测量步骤 步骤1:把长为2米的标杆垂直立于地面点处,塔尖点和标杆顶端确定的直线交水平于点,测得米; 步骤2:将标杆沿着的方向平移到点处,塔尖点和标杆顶端确定的直线交直线于点,测得米,米;(以上数据均为近似值)
(1)嘉嘉发现当米时,轻松的计算出飞虹塔的高度,请你按嘉嘉的发现条件,计算飞虹塔的高度.
(2)依据嘉嘉方法的启发,请你根据表格信息,求飞虹塔的大致高度.
2.综合与实践
【知识背景】
大豆,通称黄豆,属一年生草本,是我国重要粮食作物之一,已有五千年栽培历史,古称“菽”.某校综合实践小组以探究“大豆种植密度优化方案”为主题开展试验研究,探究大豆产量与种植密度的关系.
【研究步骤】
①在劳动实践基地中选定6块单位面积(1平方米)的地块作为试验田,并选定适宜的大豆品种;
②在不同试验田中种植株数不同的大豆,严格控制影响大豆生长的其他变量,在大豆成熟期,对每株大豆的产量进行统计;
③数据分析,形成结论.
【实验数据】
实验田编号 1 2 3 4 5 6
单位面积试验田种植株数x 30 40 50 60 70 80
单株的平均产量y/粒 51 46 41 36 31 26
【数学建模】
请根据以上材料,完成下列任务:
(1)根据表中信息推理,单位面积试验田中大豆单株的平均产量y(粒)是种植株数x的______函数(填“一次”“二次”或“反比例”),y与x的函数关系式为_______.
(2)若要使单位面积试验田中大豆的总产量(单位:粒)最多,请通过计算说明单位面积试验田中大豆植株种植的方案.
(3)单位面积试验田中大豆的总产量能否达到2160粒?请说明理由.
3.综合与实践
【主题】“潮汐车道”设计
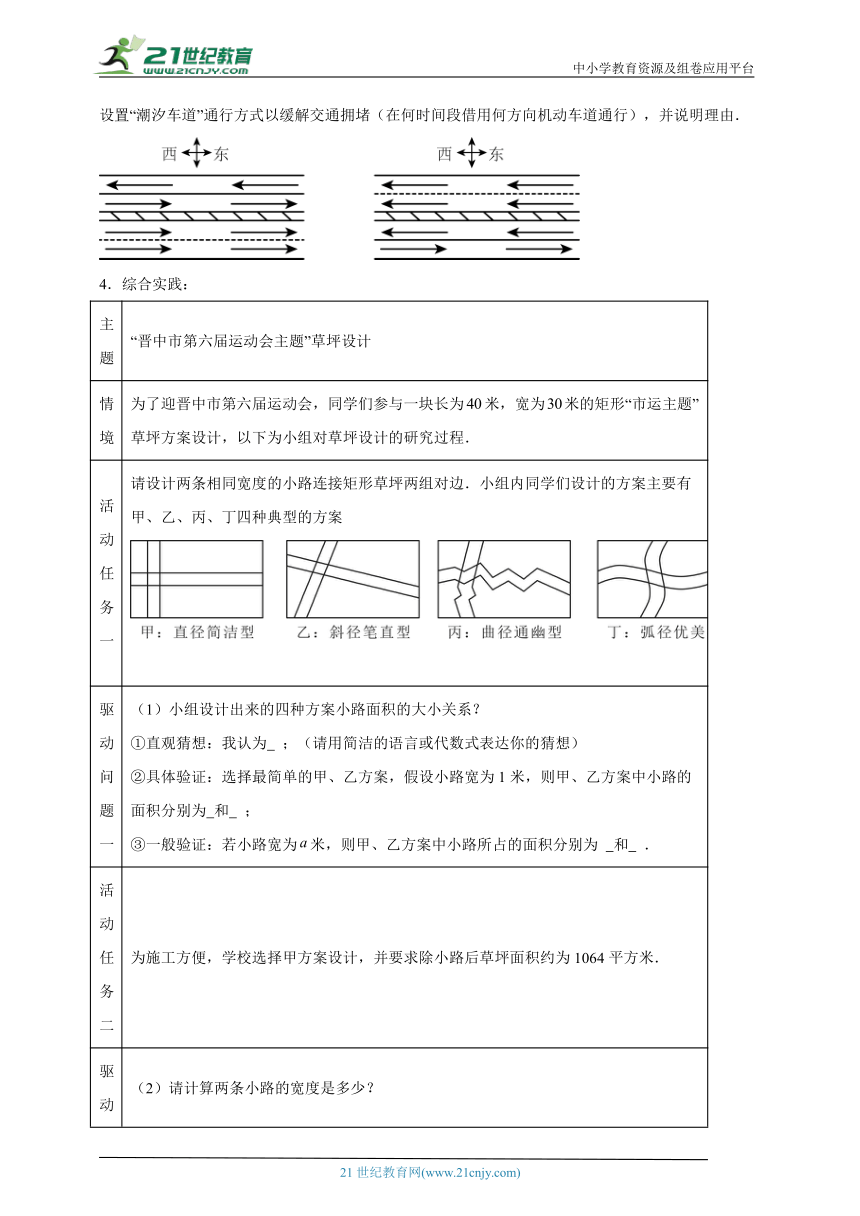
【背景素材】某跨海大桥东西走向,双向四条车道,在上下班高峰期经常拥堵,交警部门统计了不同时段双向车流量(辆/分钟),发现时间和汽车流量的变化规律符合一次函数的特征,计划通过“潮汐车道(如图所示,大流量方向的汽车可在该路段借用相邻的对向一条机动车道通行)”动态调整车道方向以缓解拥堵.
【原始数据】
时间 8时 11时 14时 17时 20时
自东向西车流量(辆/分钟) 200 320 440 560 680
自西向东车流量(辆/分钟) 500 440 380 320 260
【实践操作】
步骤1:建立车流量模型:根据原始数据,分别表示与、与之间的函数关系;
步骤2:交通流量分析:计算8时至20时每小时的车辆总流量,定义大流量方向车流量为;
步骤3:潮汐车道方案设计:根据分析结果,划分需要启用“潮汐车道”的具体时段方式.
【实践探索】
(1)求出与、与之间的函数关系;
(2)经查阅资料得:当时需要启用“潮汐车道”以改善交通情况.该路段从8时至20时,如何设置“潮汐车道”通行方式以缓解交通拥堵(在何时间段借用何方向机动车道通行),并说明理由.
4.综合实践:
主题 “晋中市第六届运动会主题”草坪设计
情境 为了迎晋中市第六届运动会,同学们参与一块长为米,宽为米的矩形“市运主题”草坪方案设计,以下为小组对草坪设计的研究过程.
活动任务一 请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
驱动问题一 (1)小组设计出来的四种方案小路面积的大小关系? ①直观猜想:我认为 ;(请用简洁的语言或代数式表达你的猜想) ②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 和 ; ③一般验证:若小路宽为米,则甲、乙方案中小路所占的面积分别为 和 .
活动任务二 为施工方便,学校选择甲方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二 (2)请计算两条小路的宽度是多少?
活动任务三 为了在草坪上布置市运会会徽标志,将在草坪上的市运宣传主题墙前(墙长15米),用篱笆(篱笆长30米)围(三边)成面积为100平方米的矩形ABCD,如图.
驱动问题三 (3)为了使篱笆恰好用完同时围住三面,小组的同学对下列问题展开探究,设矩形宽AB=x,长BC=y. ①请列出y关于x的函数关系. ②求宽AB的值
5.【综合与实践】某兴趣小组利用物理学中杠杆原理制作简易跷跷板,小组先设计方案,然后动手制作,再结合实际进行调试.请完成下列方案设计中的任务.
【知识背景】如图,在木板的左端有一个固定质量为千克的靠背,质量为m千克的小孩紧贴靠背而坐,选定木板中点偏右的位置作为跷跷板的支点,支点与靠背的距离为l米,选定支点右侧a米处为零刻度线.质量为M千克的大人坐在零刻度线的右侧,大人可以通过调整自己的位置使跷跷板保持平衡.
设大人与零刻度线的距离为y米,根据杠杆原理可得:.
【方案设计】目标:设计有标注刻度的简易跷跷板,使得两边分别坐上人后跷跷板平衡.设定,,零刻度线与末刻度线的距离定为1米.
任务一:确定l和a的值.
(1)当跷跷板左边不坐上小孩,且大人在零刻度线时,跷跷板平衡,则l与a的关系式:________;
(2)当跷跷板左边坐上质量为20千克的小孩,大人从零刻度线移至末刻度线时,跷跷板平衡,则l与a的关系式:________;
(3)根据(1)和(2)的结论可得l与a的值:________,________;
任务二:确定刻度线的位置.
(4)根据任务一,求y关于m的函数表达式;
(5)从零刻度线开始,小孩这端的质量每增加5千克,大人坐在木板上移动一个刻度能使跷跷板保持平衡,求相邻刻度线间的距离.
6.【综合与实践】杆秤是一种生活中常见的称重工具,它的设计巧妙地运用了物理原理,使得测量物体质量变得简单而准确.杆秤的物理原理,包括杠杆原理、力的平衡以及刻度与读数等方面的内容.某兴趣小组想利用物理学中杠杆原理制作简易杆秤.小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务.
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得:.其中秤盘质量克,重物质量克,秤砣质量克,秤纽与秤盘的水平距离为厘米,秤纽与零刻线的水平距离为厘米,秤砣与零刻线的水平距离为厘米.
【方案设计】目标:设计简易杆秤.设定,,最大可称重物质量为克,零刻线与末刻线的距离定为厘米.
任务一:确定和的值.
当秤盘不放重物,秤砣在零刻线时,杆秤平衡;
当秤盘放入质量为克的重物,秤砣从零刻线移至末刻线时,杆秤平衡;
(1)求和的值.
任务二:确定刻线的位置.
(2)根据任务一,求关于的函数解析式.
7.请阅读下面关于运用跨学科类比进行的一次研究活动的材料:
[背景]
小梧跟同学提到他家附近在规划开一个超市,有同学问道:“你家附近不是已经有一个A超市了吗?再开一个能吸引顾客吗?”这个问题引起了大家对超市的吸引力展开研究的兴趣.
[过程]
为了简化问题,同学们首先以“在楼层数相同、同样商品的品质和价格相同、售货服务的品质也大致相同的情况下,影响超市吸引力的主要因素”为主题对该市居民展开随机调查.结果显示:超市的占地面积、住处与超市的距离这两个因素的影响程度显著大于其他因素.
大家根据调查进行了总结:
①可以把“平均每周到超市购物次数p”作为超市吸引力指标;
②占地面积越大吸引力越大;
③距离越大吸引力越小.
在此次调查所收集到的居民平均每周到各超市购物次数的基础上,同学们进一步调查了相应超市的占地面积s(单位:)及其与居民住处的距离r(单位:m),并对p,s,r之间的关系进行研究.
一开始,同学们猜想p可能是的正比例函数,但经过检验,发现与实际数据相差较大.这时,小梧提出:“我联想到牛顿万有引力定律,这个定律揭示了两个物体之间的引力大小与各个物体的质量成正比,而与它们之间距离的平方成反比,可以表示为(G是引力常数),我们是不是可以作个类比,试一下看p与的关系如何?”.按他的建议,同学们利用调查所得的数据在平面直角坐标系中绘制了p与对应关系的散点图,如图所示.
根据阅读材料思考:
(1)观察图中散点的分布规律,请用一种函数来合理估计p与的对应关系,直接写出它的一般形式;
(2)为了清晰表示位置,同学们选A超市为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表长,则小悟家的坐标为超市的占地面积为,规划中的B超市在A超市的正东方向.根据(1)中的对应关系,解决下列问题:
①若B超市与A超市距离,且对小梧家的吸引力与A超市相同,求B超市占地面积的范围;
②小梧家在东西向的百花巷,百花巷横向排列着较为密集的居民楼.现规划B超市开在距A超市处,且占地面积最大为,要想与A超市竞争百花巷的居民,该规划是否合适?请说明理由.
8.综合与实践
问题情境:
学校有一块矩形空地,空地中有一条小路可近似地看成抛物线的一部分,该抛物线的顶点在矩形空地的边上.为了将此矩形空地加以利用,设置课外活动区和劳动实践区,其余部分为绿化区域,现面向全体同学征集设计方案.
方案设计:
小慧同学设计了如下方案:
第一步,如图1,在矩形中,,以边所在直线为轴,边所在直线为轴建立平面直角坐标系,其中抛物线与轴交于点,与轴交于点,抛物线的顶点在矩形的边上.根据测得的数据得到小路所在抛物线的函数表达式为.
第二步:如图2,连接,将其作为小路,在线段上取一点,过点作轴与抛物线交于点,连接,将设置为课外活动区.
第三步:如图2,在线段上取一点,过点分别作轴于点,轴于点,将四边形设置为劳动实践区.
问题解决:
(1)请直接写出直线的函数表达式.
(2)①当是以为底边的等腰三角形时,求所设置的课外活动区底边的长;②求所设置的劳动实践区(四边形)的最大面积.
(3)在满足(2)的条件下,请直接写出此矩形空地中绿化区域的面积.(小路的面积忽略不计)
9.小南同学在跨学科项目式学习活动中得知,心率(单位:次/分钟)与运动类型、性别、运动时间等因素有关.为了解跑步时的心率变化情况,他在班级展开实践活动.
跑步之前,测量了班级40名同学的心率,并绘制出如图所示的频数分布直方图,并通过查阅资料得知,跑步时心率与速度之间大致符合一次函数关系.在实验过程中,通过同学们佩戴的电子手环测得不同跑步速度(单位:)所对应的心率,当速度为时,通过计算得到这40名同学心率的平均值为162次/分钟.小南查看数据时发现,从起跑至最大速度时,自己的心率随着时间(单位:秒)的变化呈现均匀增大的规律,部分数据如表所示.
(单位:秒) 0 5 10 15 20
(单位:次/分钟) 80 90 100 110 120
(1)根据上表数据,请求出小南起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间的函数关系式;(不要求写出自变量的取值范围)
(2)已知小南在起跑45秒后速度达到最大,
①请估计小南跑步的最大速度;
②达到最大速度之后,小南坚持以此最大速度跑了一段时间,又经过1分钟将速度降至最大速度的四分之一时停下运动.休息15分钟后,小南的心率匀速降低至跑步前的状态.若此次实践活动中,小南的心率在100次/分钟以上的时间不低于15分钟,则他以最大速度跑步的时间至少是多少分钟?
10.学校组织九年级学生进行跨学科主题学习活动,利用函数的相关知识研究某种化学试剂的挥发情况.在两种不同的场景A和场景B下做对比实验,设实验过程中,该试剂挥发时间为x分钟时,在场景A,B中的剩余质量分别为,(单位:克).
下面是某研究小组的探究过程,请补充完整:
记录,与x的几组对应值如下:
x(分钟) 0 5 10 15 20 …
(克) 25 23.5 20 14.5 7 …
(克) 25 20 15 10 5 …
(1)在同一平面直角坐标系中,描出上表中各组数值所对应的点,,并画出函数,的图象;
(2)进一步探究发现,场景A的图象是抛物线的一部分,与x之间近似满足二次函数:.场景B的图象是直线的一部分,与x之间近似满足一次函数().则 , , ;
(3)查阅文献可知,该化学试剂的质量不低于4克时,才能发挥作用,在上述实验中,记该化学试剂在场景A,B中发挥作用的时间分别为,,则 (填“”,“”或“”).
11.综合与实践
【背景】小明家有一块半径为的圆形花园,现拟定在花园内部修建一个矩形菜地.
【方案】如图所示,以该圆形花园的圆心为原点,建立平面直角坐标系,以花园内一个定点木桩为矩形菜地的一个顶点,有两个动顶点落在花园的圆周上,还有一个动顶点D落在花园内部.已知花园圆周上有一个定点水泵(图中未标出).
【设想】
(1)针对该方案,小彬同学认为该动顶点D的轨迹是一个不完整的圆,请你证明这一个设想;
【讨论】
(2)小明希望矩形菜地的动顶点D离水泵之间的距离越小越好,求的最小值以及此时矩形菜地的面积;
【探究】
(3)①小余同学认为连接线段得到,记其面积为,记矩形菜地的面积为,则存在实数使得成立,求实数的值;
②子莹同学猜想若知道矩形菜地一边的长度为,便可知道矩形菜地的面积,请直接写出与满足的函数关系式(不考虑点在轴上的情况).
12.[概率中的方案设计]小红和小明在操场上做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如图),然后蒙上眼睛,并在一定距离外向圈内掷小石子,掷中阴影部分时小红胜,否则小明胜,未掷入圈内(半径为3m的圆内)或掷在边界上重掷.
(1)你认为游戏公平吗 为什么
(2)游戏结束,小明边走边想:能否用频率估计概率的方法,来估算不规则图形的面积呢 请你设计一个方案,解决这一问题(要求画出图形,说明设计步骤、原理,并给出计算公式)
参考答案
1.(1)飞虹塔的高度是42米;
(2)飞虹塔的大致高度为
【分析】本题主要考查相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键;
(1)由题意易得,然后可根据相似三角形的性质进行求解;
(2)设,则有,,由题意易得,然后根据相似三角形的性质可得,进而问题可求解.
【详解】(1)解:∵,
∴,
∴,
∵,
∴;
答:飞虹塔的高度是42米;
(2)解:设,则有,,
∵,
∴,
∴,
∵,
∴,即,
∵,
∴,即,
解得:,
经检验:是原方程的解,
∴;
答:飞虹塔的大致高度为.
2.(1)一次,
(2)单位面积试验田中种植66株大豆可使单位面积试验田中大豆的总产量最多
(3)单位面积试验田中大豆的总产量能达到2160粒.理由见解析
【分析】本题考查了用待定系数法求一次函数的表达式,二次函数的最值,二次函数的实际应用,熟练掌握一次函数和二次函数的图象与性质是解题的关键.
(1)由表格可知y随x的增大而减小,且x每增加10,y减小5,因此y是x的一次函数,设y与x的关系式为,在表格中取两组值代入,求出k、b的值,即可解题;
(2)设单位面积试验田中大豆的总产量为W粒,根据建立W与x的函数关系式,再结合二次函数最值情况求解,即可解题;
(3)根据建立等式求解,并结合对解进行判断,即可解题.
【详解】(1)解:由表格可知y随x的增大而减小,且x每增加10,y减小5,因此y是x的一次函数,
设y与x的函数关系式为,
由表格数据可得,
解得,
y与x的函数关系式为,
故答案为:一次,.
(2)解:设单位面积试验田中大豆的总产量为W粒.
由题意得.
,,
∴当时,W的值最大,
∴单位面积试验田中种植66株大豆可使单位面积试验田中大豆的总产量最多.
(3)解:单位面积试验田中大豆的总产量能达到2160粒.理由如下:
令,得,
解得或,满足,
∴单位面积试验田中大豆的总产量能达到2160粒.
3.(1);
(2)8时到9时,可变车道的方向设置为自西向东;18时到20时,可变车道的方向设置为自东向西
【分析】本题考查一次函数的实际应用,正确的求出函数解析式,是解题的关键:
(1)根据表格,易得示与、与之间均为一次函数关系,设出关系式,待定系数法求出函数解析式即可;
(2)求出,分别求出,时的范围,进而设置“潮汐车道”通行方式即可.
【详解】(1)解:设(、为常数,且),
将,和,代入得:
,解得:,
∴;
设(、为常数,且),
将,和,代入得:
,解得:,
∴;
(2),
当时,即:,解得:,
当时,即:,解得:,
∴8时到9时,可变车道的方向设置为自西向东;
18时到20时,可变车道的方向设置为自动向西.
4.(1)①直观猜想:我认为:四种方案小路面积的大小相等;②,;③,;(2)小路的宽为;(3)①②10米
【分析】(1)通过平移知识求解;
(2)根据草坪的面积列方程求解;
(3)①根据题意列出关系式,
②根据题意得出一元二次方程,解方程求解.
【详解】解:(1)①直观猜想:我认为:四种方案小路面积的大小相等,
故答案为:四种方案小路面积的大小相等;
②甲:;
乙:,
故答案为:,;
③甲:,
乙:,
故答案为:,;
(2)设小路的宽为,则,
解得:或(不合题意,舍去),
答:小路的宽为;
(3)①方法1:,
,
方法2:,
;
②由题意得:
解之得:
当
本题考查了平移的应用,一元二次方程的实际应用,根与系数的关系,掌握平移的作用是解题的关键.
5.(1)5a;(2);(3),;(4):(5)相邻刻度线间的距离为0.25m
【分析】本题主要考查了一次函数的应用,一元一次方程;解题时要熟练掌握并能灵活运用是关键.
(1)依据题意,根据杠杆原理,可得,代入数据可以得解;
(2)依据题意得,,进而计算可以得解;
(3)依据题意,由(1)与(2)可得,,求出后再求得,可以得解;
(4)依据题意,由(3)可知,,,故,计算即可得解;
(5)依据题意,由(4)可知,,故当时,;当市,,进而可以判断得解.
【详解】解:(1)由题意,根据杠杆原理,
.
.
.
故答案为:.
(2)由题意得,.
.
故答案为:.
(3)由题意,由(1)与(2)可得,,
.
.
故答案为:;.
(4)由(3)可知,,,
.
.
(5)由(4)可知,,
当时,;当时,.
相邻刻度线间的距离为.
6.(1);(2)
【分析】本题考查了一次函数的应用;
(1)依据题意,又当秤盘不放重物,秤砣在零刻线时,杆秤平衡;当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,可得,且,进而计算可以得解;
(2)依据题意,由(1)可知:,,则,进而可以得解.
【详解】解:(1)由题意得:,,
当,时,,
;
当,时,,
;
联立①②可得,
解得.
(2)由(1)可知:,,
∴,
∴.
∴关于的函数解析式为.
7.(1)
(2)①B超市占地面积s的范围为;②该规划不合适,理由见解析
【分析】(1)观察图中散点的分布规律可知程正比例函数,即可解答;
(2)①设超市的坐标为,占地面积为.记超市的吸引力为超市的吸引力为.可得.再根据.解得.根据函数性质即可确定范围;
②设为1个单位长度,因为超市开在距超市处,所以超市的坐标为,任取百花巷上一点,设,记超市的面积为超市的面积为,
设,根据,得出设根据二次函数性质得出有最小值.设.根据二次函数性质得出当恒成立,再根据,即可求解;
【详解】(1)解:观察图中散点的分布规律可知程正比例函数,故.
(2)①解:设超市的坐标为,占地面积为.
记超市的吸引力为超市的吸引力为.
因为超市为原点,小梧家的坐标为,
根据勾股定理,小梧家到超市的距离为,到超市的距离为.
因为超市对居民的吸引力,
所以.
因为两家超市对小梧家的吸引力相同,所以.
所以.
所以.
因为,抛物线开口向上,对称轴,
所以在上,随的增大而增大.
所以当时,取得最小值800,当时,取得最大值2000.
所以超市占地面积的范围为.
②解:设为1个单位长度,因为超市开在距超市处,
所以超市的坐标为,
任取百花巷上一点,设,
根据勾股定理,点到超市的距离为,到超市的距离为.
记超市的面积为超市的面积为,
设,
因为超市的占地面积为超市占地面积最大为,
所以.
因为,
所以
设
则该二次函数中,
因为,所以有最小值.
设.
因为,抛物线开口向上,对称轴为,
所以在上随的增大而减小.
因为当时,,
所以当时,.
因为,所以.
即当恒成立,
因为,
所以,即对于任意的值,都有.
所以在规划的条件下,百花巷上不存在超市对居民吸引力大于超市的位置,故该规划不合适.
该题主要考查了二次函数的综合应用,勾股定理等知识点,解题的关键是理解题意.
8.(1)
(2)①;②劳动实践区(四边形)的最大面积为;
(3)矩形空地中绿化区域的面积为
【分析】(1)根据题意得到,由二次函数图象的性质得到,运用待定系数法即可求解;
(2)①设,则,且,运用两点之间距离公式得到,,根据等腰三角形的定义得到,由此列式求解得到,可得,,由此即可求解;
②根据题意得到,四边形是矩形,设,则,所以,根据二次函数最大值的计算方法即可求解;
(3)根据题意可得抛物线的顶点坐标为,得到,求出,再算出,,由即可求解.
【详解】(1)解:∵以边所在直线为轴,,
∴,
已知小路所在抛物线的函数表达式为,
当时,,
∴,
设直线的函数表达式,
∴,
解得,,
∴直线的函数表达式;
(2)解:①直线的函数表达式,点在线段上,且轴,
∴设,则,且,
∴,
,
∵是以为底边的等腰三角形,
∴,
∴,
整理得,,则
解得,,(舍去),
当时,,,
∴,,,
∴;
②线段上取一点,过点分别作轴于点,轴于点,
∴,
∴四边形是矩形,
设,
∴,
∴,
∵,
∴当时,即,有最大值,最大值为,
∴所设置的劳动实践区(四边形)的最大面积为;
(3)解:抛物线的顶点在矩形的边上,
∴抛物线的顶点坐标的横坐标为,纵坐标为,
∴,
∴,
又∵矩形中,,
∴,
由(2)可得,是以为底边的等腰三角形,,,,
如图所示,过点作于点,
∴,
在中,,
∴,
∵,
∴,
∴,
∴
,
∴矩形空地中绿化区域的面积为.(小路的面积忽略不计)
本题主要考查二次函数图象与几何图形的综合运用,掌握二次二次函数图形的性质,最值的计算,待定系数法求一次函数解析式,矩形的判定和性质,等腰三角形的定义,勾股定理等知识,数形结合分析是解题的关键.
9.(1)
(2)①小南跑步的最大速度为8.8千米/小时②他以最大速度跑步的时间至少是
【分析】本题考查的是一次函数的应用及加权平均数的计算,
(1)用待定系数法直接计算求出即可;
(2)①用待定系数法求出,再将代入计算得出结论;②先求从起跑到速度达到最大这段时间内,心率保持在100次/分钟以上的时长为:,得出停下时,,再用待定系数法求出休息时段心率p与休息时间t的一次函数关系式,进而得出,设最大速度跑步的时间为,列不等式计算解决即可.
【详解】(1)解:由表格知,起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间为一次函数关系,
设小南起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间的函数关系式为,
把,分别代入,
,
解得:,
则小南起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间的函数关系式为,
(2)①由题意得:,
设,
把,分别代入,
,
解得:,
,
当时,,
当时,,
解得:,
答:小南跑步的最大速度为8.8千米/小时;
②当时,,
,
又,
从起跑到速度达到最大这段时间内,小南的心率保持在100次/分钟以上的时长为:
,
当,
将代入得,
即停下时,,
由休息15分钟后,小南的心率匀速降低至跑步前的状态可知,休息时段心率p与休息时间t是一次函数关系,设休息时段,
把代入,
,
解得:,
,
当时,,
,
由于休息时心率匀速降低,
因此在休息这段时间小南的心率保持在100次/分钟以上的时长为,
设最大速度跑步的时间为,
则的时段:,
,
则他以最大速度跑步的时间至少是.
10.(1)见详解
(2),,
(3)
【分析】本题主要考查了一次函数、二次函数的应用,读懂题意是解答本题的关键.
(1)依据题意,根据表格数据描点,连线即可作图得解;
(2)根据函数图象确定点的坐标,利用待定系数法解答即可;
(3)依据题意,分别求出当时的值,即可得出答案.
【详解】(1)解:(1)由题意,作图如下.
(2)解:由题意,场景的图象是抛物线的一部分,与之间近似满足函数关系.
又点,在函数图象上,
.
解得:.
场景函数关系式为.
对于场景的图象是直线的一部分,与之间近似满足函数关系.
又,在函数图象上,
.
解得:.
场景函数关系式为.
∴,,.
(3)解:由题意,当时,
场景中,,
解得:(舍),
即:,
场景中,,
解得:,
.
11.(1)见解析(2)最小值为,此时菜地面积为(3)①;②当点位于轴下方时 ;当点位于轴上方时
【分析】(1)如图所示,过点作交于点,则由垂径定理可知 ,证明,推出,即可得到点的轨迹是以为圆心,半径为2的圆,且该圆不经过点,进而证明结论;
(2)由(1)可知,当三点共线时有最小值为,如图所示,记与交于点,求出,过点作,则有,求出, 过点作,垂足为,连接,证明为正三角形,求出,,即可解答;
(3)①连接,记交轴于点,作于点,证明为中位线 ,根据,即可求解;②分点位于轴下方和上方两种情况讨论,利用三角形中位线的性质求出,再利用勾股定理求出,即可解答.
【详解】(1)证明:如图所示,过点作交于点,则由垂径定理可知 ,
∵四边形是矩形
∴
∵
∴
在与中
∴
∴
∴点的轨迹是以为圆心,半径为2的圆,且该圆不经过点,即小彬设想成立 ;
(2)由(1)可知,当三点共线时有最小值为,
如图所示,记与交于点
∵,为上的点
∴为的直径 ,,
过点作,则有
∴
∴
∴
由同弧所对的圆心角是圆周角的2倍可知
∴
过点作,垂足为,连接
∵
∴为正三角形
∴为边上的中线,且平分
∴,
∴
∴
∴
∴菜地面积;
(3)①如图所示,连接,记交轴于点,作于点,
∵
∴为中点
∵为中点
∴为中位线
∴
∵
∴
∴;
②第一种情况,当点位于轴下方时,如图:
∴,
;
第二种情况,当点位于轴上方时,如图:
同理得:.
本题考查了圆周角定理,垂径定理,勾股定理,矩形的性质,函数解析式,解直角三角形,坐标与图形,熟练掌握以上知识是解题的关键.
12.(1)不公平,理由见解析;(2)
【分析】(1)首先分别计算小红和小明获胜的概率,相比较,获胜概率不同,所以可判定不公平;
(2)首先设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为),然后往图形中掷点,掷在正方形外或边界上不作记录,其次当所掷次数充分大时,记录并统计结果,设掷入正方形内次,其中次掷入不规则图形内,最后用频率估计概率,大概可得出结果.
【详解】(1)不公平.理由如下:
(掷中阴影部分),即小红获胜的概率为,则小明获胜的概率为,,
游戏不公平
(2)能利用频率估计概率的方法估算不规则图形的面积设计方案:①设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为),如图所示;
②往图形中掷点(如蒙上眼睛往图形中随意掷小石子,掷在正方形外或边界上不作记录);
③当所掷次数充分大时,记录并统计结果,设掷入正方形内次,其中次掷入不规则图形内;
④设不规则图形的面积为,用频率估计概率,即掷入不规则图形内的频率(掷入不规则图形内),而(掷入不规则图形内),故,即.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
综合实践题常见考点 押题练
2025年中考数学三轮复习备考
1.《黑神话:悟空》游戏中选取的27处山西极具代表性的古建筑,由南至北横跨9个地市,不仅展示了山西深厚的文化底蕴,也为当地文旅产业带来新的发展机遇.飞虹塔是山西省非常有名的一座塔楼,某实践小组欲测量飞虹塔的高度,测量过程见下表.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
测量步骤 步骤1:把长为2米的标杆垂直立于地面点处,塔尖点和标杆顶端确定的直线交水平于点,测得米; 步骤2:将标杆沿着的方向平移到点处,塔尖点和标杆顶端确定的直线交直线于点,测得米,米;(以上数据均为近似值)
(1)嘉嘉发现当米时,轻松的计算出飞虹塔的高度,请你按嘉嘉的发现条件,计算飞虹塔的高度.
(2)依据嘉嘉方法的启发,请你根据表格信息,求飞虹塔的大致高度.
2.综合与实践
【知识背景】
大豆,通称黄豆,属一年生草本,是我国重要粮食作物之一,已有五千年栽培历史,古称“菽”.某校综合实践小组以探究“大豆种植密度优化方案”为主题开展试验研究,探究大豆产量与种植密度的关系.
【研究步骤】
①在劳动实践基地中选定6块单位面积(1平方米)的地块作为试验田,并选定适宜的大豆品种;
②在不同试验田中种植株数不同的大豆,严格控制影响大豆生长的其他变量,在大豆成熟期,对每株大豆的产量进行统计;
③数据分析,形成结论.
【实验数据】
实验田编号 1 2 3 4 5 6
单位面积试验田种植株数x 30 40 50 60 70 80
单株的平均产量y/粒 51 46 41 36 31 26
【数学建模】
请根据以上材料,完成下列任务:
(1)根据表中信息推理,单位面积试验田中大豆单株的平均产量y(粒)是种植株数x的______函数(填“一次”“二次”或“反比例”),y与x的函数关系式为_______.
(2)若要使单位面积试验田中大豆的总产量(单位:粒)最多,请通过计算说明单位面积试验田中大豆植株种植的方案.
(3)单位面积试验田中大豆的总产量能否达到2160粒?请说明理由.
3.综合与实践
【主题】“潮汐车道”设计
【背景素材】某跨海大桥东西走向,双向四条车道,在上下班高峰期经常拥堵,交警部门统计了不同时段双向车流量(辆/分钟),发现时间和汽车流量的变化规律符合一次函数的特征,计划通过“潮汐车道(如图所示,大流量方向的汽车可在该路段借用相邻的对向一条机动车道通行)”动态调整车道方向以缓解拥堵.
【原始数据】
时间 8时 11时 14时 17时 20时
自东向西车流量(辆/分钟) 200 320 440 560 680
自西向东车流量(辆/分钟) 500 440 380 320 260
【实践操作】
步骤1:建立车流量模型:根据原始数据,分别表示与、与之间的函数关系;
步骤2:交通流量分析:计算8时至20时每小时的车辆总流量,定义大流量方向车流量为;
步骤3:潮汐车道方案设计:根据分析结果,划分需要启用“潮汐车道”的具体时段方式.
【实践探索】
(1)求出与、与之间的函数关系;
(2)经查阅资料得:当时需要启用“潮汐车道”以改善交通情况.该路段从8时至20时,如何设置“潮汐车道”通行方式以缓解交通拥堵(在何时间段借用何方向机动车道通行),并说明理由.
4.综合实践:
主题 “晋中市第六届运动会主题”草坪设计
情境 为了迎晋中市第六届运动会,同学们参与一块长为米,宽为米的矩形“市运主题”草坪方案设计,以下为小组对草坪设计的研究过程.
活动任务一 请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
驱动问题一 (1)小组设计出来的四种方案小路面积的大小关系? ①直观猜想:我认为 ;(请用简洁的语言或代数式表达你的猜想) ②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 和 ; ③一般验证:若小路宽为米,则甲、乙方案中小路所占的面积分别为 和 .
活动任务二 为施工方便,学校选择甲方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二 (2)请计算两条小路的宽度是多少?
活动任务三 为了在草坪上布置市运会会徽标志,将在草坪上的市运宣传主题墙前(墙长15米),用篱笆(篱笆长30米)围(三边)成面积为100平方米的矩形ABCD,如图.
驱动问题三 (3)为了使篱笆恰好用完同时围住三面,小组的同学对下列问题展开探究,设矩形宽AB=x,长BC=y. ①请列出y关于x的函数关系. ②求宽AB的值
5.【综合与实践】某兴趣小组利用物理学中杠杆原理制作简易跷跷板,小组先设计方案,然后动手制作,再结合实际进行调试.请完成下列方案设计中的任务.
【知识背景】如图,在木板的左端有一个固定质量为千克的靠背,质量为m千克的小孩紧贴靠背而坐,选定木板中点偏右的位置作为跷跷板的支点,支点与靠背的距离为l米,选定支点右侧a米处为零刻度线.质量为M千克的大人坐在零刻度线的右侧,大人可以通过调整自己的位置使跷跷板保持平衡.
设大人与零刻度线的距离为y米,根据杠杆原理可得:.
【方案设计】目标:设计有标注刻度的简易跷跷板,使得两边分别坐上人后跷跷板平衡.设定,,零刻度线与末刻度线的距离定为1米.
任务一:确定l和a的值.
(1)当跷跷板左边不坐上小孩,且大人在零刻度线时,跷跷板平衡,则l与a的关系式:________;
(2)当跷跷板左边坐上质量为20千克的小孩,大人从零刻度线移至末刻度线时,跷跷板平衡,则l与a的关系式:________;
(3)根据(1)和(2)的结论可得l与a的值:________,________;
任务二:确定刻度线的位置.
(4)根据任务一,求y关于m的函数表达式;
(5)从零刻度线开始,小孩这端的质量每增加5千克,大人坐在木板上移动一个刻度能使跷跷板保持平衡,求相邻刻度线间的距离.
6.【综合与实践】杆秤是一种生活中常见的称重工具,它的设计巧妙地运用了物理原理,使得测量物体质量变得简单而准确.杆秤的物理原理,包括杠杆原理、力的平衡以及刻度与读数等方面的内容.某兴趣小组想利用物理学中杠杆原理制作简易杆秤.小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务.
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得:.其中秤盘质量克,重物质量克,秤砣质量克,秤纽与秤盘的水平距离为厘米,秤纽与零刻线的水平距离为厘米,秤砣与零刻线的水平距离为厘米.
【方案设计】目标:设计简易杆秤.设定,,最大可称重物质量为克,零刻线与末刻线的距离定为厘米.
任务一:确定和的值.
当秤盘不放重物,秤砣在零刻线时,杆秤平衡;
当秤盘放入质量为克的重物,秤砣从零刻线移至末刻线时,杆秤平衡;
(1)求和的值.
任务二:确定刻线的位置.
(2)根据任务一,求关于的函数解析式.
7.请阅读下面关于运用跨学科类比进行的一次研究活动的材料:
[背景]
小梧跟同学提到他家附近在规划开一个超市,有同学问道:“你家附近不是已经有一个A超市了吗?再开一个能吸引顾客吗?”这个问题引起了大家对超市的吸引力展开研究的兴趣.
[过程]
为了简化问题,同学们首先以“在楼层数相同、同样商品的品质和价格相同、售货服务的品质也大致相同的情况下,影响超市吸引力的主要因素”为主题对该市居民展开随机调查.结果显示:超市的占地面积、住处与超市的距离这两个因素的影响程度显著大于其他因素.
大家根据调查进行了总结:
①可以把“平均每周到超市购物次数p”作为超市吸引力指标;
②占地面积越大吸引力越大;
③距离越大吸引力越小.
在此次调查所收集到的居民平均每周到各超市购物次数的基础上,同学们进一步调查了相应超市的占地面积s(单位:)及其与居民住处的距离r(单位:m),并对p,s,r之间的关系进行研究.
一开始,同学们猜想p可能是的正比例函数,但经过检验,发现与实际数据相差较大.这时,小梧提出:“我联想到牛顿万有引力定律,这个定律揭示了两个物体之间的引力大小与各个物体的质量成正比,而与它们之间距离的平方成反比,可以表示为(G是引力常数),我们是不是可以作个类比,试一下看p与的关系如何?”.按他的建议,同学们利用调查所得的数据在平面直角坐标系中绘制了p与对应关系的散点图,如图所示.
根据阅读材料思考:
(1)观察图中散点的分布规律,请用一种函数来合理估计p与的对应关系,直接写出它的一般形式;
(2)为了清晰表示位置,同学们选A超市为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表长,则小悟家的坐标为超市的占地面积为,规划中的B超市在A超市的正东方向.根据(1)中的对应关系,解决下列问题:
①若B超市与A超市距离,且对小梧家的吸引力与A超市相同,求B超市占地面积的范围;
②小梧家在东西向的百花巷,百花巷横向排列着较为密集的居民楼.现规划B超市开在距A超市处,且占地面积最大为,要想与A超市竞争百花巷的居民,该规划是否合适?请说明理由.
8.综合与实践
问题情境:
学校有一块矩形空地,空地中有一条小路可近似地看成抛物线的一部分,该抛物线的顶点在矩形空地的边上.为了将此矩形空地加以利用,设置课外活动区和劳动实践区,其余部分为绿化区域,现面向全体同学征集设计方案.
方案设计:
小慧同学设计了如下方案:
第一步,如图1,在矩形中,,以边所在直线为轴,边所在直线为轴建立平面直角坐标系,其中抛物线与轴交于点,与轴交于点,抛物线的顶点在矩形的边上.根据测得的数据得到小路所在抛物线的函数表达式为.
第二步:如图2,连接,将其作为小路,在线段上取一点,过点作轴与抛物线交于点,连接,将设置为课外活动区.
第三步:如图2,在线段上取一点,过点分别作轴于点,轴于点,将四边形设置为劳动实践区.
问题解决:
(1)请直接写出直线的函数表达式.
(2)①当是以为底边的等腰三角形时,求所设置的课外活动区底边的长;②求所设置的劳动实践区(四边形)的最大面积.
(3)在满足(2)的条件下,请直接写出此矩形空地中绿化区域的面积.(小路的面积忽略不计)
9.小南同学在跨学科项目式学习活动中得知,心率(单位:次/分钟)与运动类型、性别、运动时间等因素有关.为了解跑步时的心率变化情况,他在班级展开实践活动.
跑步之前,测量了班级40名同学的心率,并绘制出如图所示的频数分布直方图,并通过查阅资料得知,跑步时心率与速度之间大致符合一次函数关系.在实验过程中,通过同学们佩戴的电子手环测得不同跑步速度(单位:)所对应的心率,当速度为时,通过计算得到这40名同学心率的平均值为162次/分钟.小南查看数据时发现,从起跑至最大速度时,自己的心率随着时间(单位:秒)的变化呈现均匀增大的规律,部分数据如表所示.
(单位:秒) 0 5 10 15 20
(单位:次/分钟) 80 90 100 110 120
(1)根据上表数据,请求出小南起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间的函数关系式;(不要求写出自变量的取值范围)
(2)已知小南在起跑45秒后速度达到最大,
①请估计小南跑步的最大速度;
②达到最大速度之后,小南坚持以此最大速度跑了一段时间,又经过1分钟将速度降至最大速度的四分之一时停下运动.休息15分钟后,小南的心率匀速降低至跑步前的状态.若此次实践活动中,小南的心率在100次/分钟以上的时间不低于15分钟,则他以最大速度跑步的时间至少是多少分钟?
10.学校组织九年级学生进行跨学科主题学习活动,利用函数的相关知识研究某种化学试剂的挥发情况.在两种不同的场景A和场景B下做对比实验,设实验过程中,该试剂挥发时间为x分钟时,在场景A,B中的剩余质量分别为,(单位:克).
下面是某研究小组的探究过程,请补充完整:
记录,与x的几组对应值如下:
x(分钟) 0 5 10 15 20 …
(克) 25 23.5 20 14.5 7 …
(克) 25 20 15 10 5 …
(1)在同一平面直角坐标系中,描出上表中各组数值所对应的点,,并画出函数,的图象;
(2)进一步探究发现,场景A的图象是抛物线的一部分,与x之间近似满足二次函数:.场景B的图象是直线的一部分,与x之间近似满足一次函数().则 , , ;
(3)查阅文献可知,该化学试剂的质量不低于4克时,才能发挥作用,在上述实验中,记该化学试剂在场景A,B中发挥作用的时间分别为,,则 (填“”,“”或“”).
11.综合与实践
【背景】小明家有一块半径为的圆形花园,现拟定在花园内部修建一个矩形菜地.
【方案】如图所示,以该圆形花园的圆心为原点,建立平面直角坐标系,以花园内一个定点木桩为矩形菜地的一个顶点,有两个动顶点落在花园的圆周上,还有一个动顶点D落在花园内部.已知花园圆周上有一个定点水泵(图中未标出).
【设想】
(1)针对该方案,小彬同学认为该动顶点D的轨迹是一个不完整的圆,请你证明这一个设想;
【讨论】
(2)小明希望矩形菜地的动顶点D离水泵之间的距离越小越好,求的最小值以及此时矩形菜地的面积;
【探究】
(3)①小余同学认为连接线段得到,记其面积为,记矩形菜地的面积为,则存在实数使得成立,求实数的值;
②子莹同学猜想若知道矩形菜地一边的长度为,便可知道矩形菜地的面积,请直接写出与满足的函数关系式(不考虑点在轴上的情况).
12.[概率中的方案设计]小红和小明在操场上做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如图),然后蒙上眼睛,并在一定距离外向圈内掷小石子,掷中阴影部分时小红胜,否则小明胜,未掷入圈内(半径为3m的圆内)或掷在边界上重掷.
(1)你认为游戏公平吗 为什么
(2)游戏结束,小明边走边想:能否用频率估计概率的方法,来估算不规则图形的面积呢 请你设计一个方案,解决这一问题(要求画出图形,说明设计步骤、原理,并给出计算公式)
参考答案
1.(1)飞虹塔的高度是42米;
(2)飞虹塔的大致高度为
【分析】本题主要考查相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键;
(1)由题意易得,然后可根据相似三角形的性质进行求解;
(2)设,则有,,由题意易得,然后根据相似三角形的性质可得,进而问题可求解.
【详解】(1)解:∵,
∴,
∴,
∵,
∴;
答:飞虹塔的高度是42米;
(2)解:设,则有,,
∵,
∴,
∴,
∵,
∴,即,
∵,
∴,即,
解得:,
经检验:是原方程的解,
∴;
答:飞虹塔的大致高度为.
2.(1)一次,
(2)单位面积试验田中种植66株大豆可使单位面积试验田中大豆的总产量最多
(3)单位面积试验田中大豆的总产量能达到2160粒.理由见解析
【分析】本题考查了用待定系数法求一次函数的表达式,二次函数的最值,二次函数的实际应用,熟练掌握一次函数和二次函数的图象与性质是解题的关键.
(1)由表格可知y随x的增大而减小,且x每增加10,y减小5,因此y是x的一次函数,设y与x的关系式为,在表格中取两组值代入,求出k、b的值,即可解题;
(2)设单位面积试验田中大豆的总产量为W粒,根据建立W与x的函数关系式,再结合二次函数最值情况求解,即可解题;
(3)根据建立等式求解,并结合对解进行判断,即可解题.
【详解】(1)解:由表格可知y随x的增大而减小,且x每增加10,y减小5,因此y是x的一次函数,
设y与x的函数关系式为,
由表格数据可得,
解得,
y与x的函数关系式为,
故答案为:一次,.
(2)解:设单位面积试验田中大豆的总产量为W粒.
由题意得.
,,
∴当时,W的值最大,
∴单位面积试验田中种植66株大豆可使单位面积试验田中大豆的总产量最多.
(3)解:单位面积试验田中大豆的总产量能达到2160粒.理由如下:
令,得,
解得或,满足,
∴单位面积试验田中大豆的总产量能达到2160粒.
3.(1);
(2)8时到9时,可变车道的方向设置为自西向东;18时到20时,可变车道的方向设置为自东向西
【分析】本题考查一次函数的实际应用,正确的求出函数解析式,是解题的关键:
(1)根据表格,易得示与、与之间均为一次函数关系,设出关系式,待定系数法求出函数解析式即可;
(2)求出,分别求出,时的范围,进而设置“潮汐车道”通行方式即可.
【详解】(1)解:设(、为常数,且),
将,和,代入得:
,解得:,
∴;
设(、为常数,且),
将,和,代入得:
,解得:,
∴;
(2),
当时,即:,解得:,
当时,即:,解得:,
∴8时到9时,可变车道的方向设置为自西向东;
18时到20时,可变车道的方向设置为自动向西.
4.(1)①直观猜想:我认为:四种方案小路面积的大小相等;②,;③,;(2)小路的宽为;(3)①②10米
【分析】(1)通过平移知识求解;
(2)根据草坪的面积列方程求解;
(3)①根据题意列出关系式,
②根据题意得出一元二次方程,解方程求解.
【详解】解:(1)①直观猜想:我认为:四种方案小路面积的大小相等,
故答案为:四种方案小路面积的大小相等;
②甲:;
乙:,
故答案为:,;
③甲:,
乙:,
故答案为:,;
(2)设小路的宽为,则,
解得:或(不合题意,舍去),
答:小路的宽为;
(3)①方法1:,
,
方法2:,
;
②由题意得:
解之得:
当
本题考查了平移的应用,一元二次方程的实际应用,根与系数的关系,掌握平移的作用是解题的关键.
5.(1)5a;(2);(3),;(4):(5)相邻刻度线间的距离为0.25m
【分析】本题主要考查了一次函数的应用,一元一次方程;解题时要熟练掌握并能灵活运用是关键.
(1)依据题意,根据杠杆原理,可得,代入数据可以得解;
(2)依据题意得,,进而计算可以得解;
(3)依据题意,由(1)与(2)可得,,求出后再求得,可以得解;
(4)依据题意,由(3)可知,,,故,计算即可得解;
(5)依据题意,由(4)可知,,故当时,;当市,,进而可以判断得解.
【详解】解:(1)由题意,根据杠杆原理,
.
.
.
故答案为:.
(2)由题意得,.
.
故答案为:.
(3)由题意,由(1)与(2)可得,,
.
.
故答案为:;.
(4)由(3)可知,,,
.
.
(5)由(4)可知,,
当时,;当时,.
相邻刻度线间的距离为.
6.(1);(2)
【分析】本题考查了一次函数的应用;
(1)依据题意,又当秤盘不放重物,秤砣在零刻线时,杆秤平衡;当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,可得,且,进而计算可以得解;
(2)依据题意,由(1)可知:,,则,进而可以得解.
【详解】解:(1)由题意得:,,
当,时,,
;
当,时,,
;
联立①②可得,
解得.
(2)由(1)可知:,,
∴,
∴.
∴关于的函数解析式为.
7.(1)
(2)①B超市占地面积s的范围为;②该规划不合适,理由见解析
【分析】(1)观察图中散点的分布规律可知程正比例函数,即可解答;
(2)①设超市的坐标为,占地面积为.记超市的吸引力为超市的吸引力为.可得.再根据.解得.根据函数性质即可确定范围;
②设为1个单位长度,因为超市开在距超市处,所以超市的坐标为,任取百花巷上一点,设,记超市的面积为超市的面积为,
设,根据,得出设根据二次函数性质得出有最小值.设.根据二次函数性质得出当恒成立,再根据,即可求解;
【详解】(1)解:观察图中散点的分布规律可知程正比例函数,故.
(2)①解:设超市的坐标为,占地面积为.
记超市的吸引力为超市的吸引力为.
因为超市为原点,小梧家的坐标为,
根据勾股定理,小梧家到超市的距离为,到超市的距离为.
因为超市对居民的吸引力,
所以.
因为两家超市对小梧家的吸引力相同,所以.
所以.
所以.
因为,抛物线开口向上,对称轴,
所以在上,随的增大而增大.
所以当时,取得最小值800,当时,取得最大值2000.
所以超市占地面积的范围为.
②解:设为1个单位长度,因为超市开在距超市处,
所以超市的坐标为,
任取百花巷上一点,设,
根据勾股定理,点到超市的距离为,到超市的距离为.
记超市的面积为超市的面积为,
设,
因为超市的占地面积为超市占地面积最大为,
所以.
因为,
所以
设
则该二次函数中,
因为,所以有最小值.
设.
因为,抛物线开口向上,对称轴为,
所以在上随的增大而减小.
因为当时,,
所以当时,.
因为,所以.
即当恒成立,
因为,
所以,即对于任意的值,都有.
所以在规划的条件下,百花巷上不存在超市对居民吸引力大于超市的位置,故该规划不合适.
该题主要考查了二次函数的综合应用,勾股定理等知识点,解题的关键是理解题意.
8.(1)
(2)①;②劳动实践区(四边形)的最大面积为;
(3)矩形空地中绿化区域的面积为
【分析】(1)根据题意得到,由二次函数图象的性质得到,运用待定系数法即可求解;
(2)①设,则,且,运用两点之间距离公式得到,,根据等腰三角形的定义得到,由此列式求解得到,可得,,由此即可求解;
②根据题意得到,四边形是矩形,设,则,所以,根据二次函数最大值的计算方法即可求解;
(3)根据题意可得抛物线的顶点坐标为,得到,求出,再算出,,由即可求解.
【详解】(1)解:∵以边所在直线为轴,,
∴,
已知小路所在抛物线的函数表达式为,
当时,,
∴,
设直线的函数表达式,
∴,
解得,,
∴直线的函数表达式;
(2)解:①直线的函数表达式,点在线段上,且轴,
∴设,则,且,
∴,
,
∵是以为底边的等腰三角形,
∴,
∴,
整理得,,则
解得,,(舍去),
当时,,,
∴,,,
∴;
②线段上取一点,过点分别作轴于点,轴于点,
∴,
∴四边形是矩形,
设,
∴,
∴,
∵,
∴当时,即,有最大值,最大值为,
∴所设置的劳动实践区(四边形)的最大面积为;
(3)解:抛物线的顶点在矩形的边上,
∴抛物线的顶点坐标的横坐标为,纵坐标为,
∴,
∴,
又∵矩形中,,
∴,
由(2)可得,是以为底边的等腰三角形,,,,
如图所示,过点作于点,
∴,
在中,,
∴,
∵,
∴,
∴,
∴
,
∴矩形空地中绿化区域的面积为.(小路的面积忽略不计)
本题主要考查二次函数图象与几何图形的综合运用,掌握二次二次函数图形的性质,最值的计算,待定系数法求一次函数解析式,矩形的判定和性质,等腰三角形的定义,勾股定理等知识,数形结合分析是解题的关键.
9.(1)
(2)①小南跑步的最大速度为8.8千米/小时②他以最大速度跑步的时间至少是
【分析】本题考查的是一次函数的应用及加权平均数的计算,
(1)用待定系数法直接计算求出即可;
(2)①用待定系数法求出,再将代入计算得出结论;②先求从起跑到速度达到最大这段时间内,心率保持在100次/分钟以上的时长为:,得出停下时,,再用待定系数法求出休息时段心率p与休息时间t的一次函数关系式,进而得出,设最大速度跑步的时间为,列不等式计算解决即可.
【详解】(1)解:由表格知,起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间为一次函数关系,
设小南起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间的函数关系式为,
把,分别代入,
,
解得:,
则小南起跑至最大速度时心率(单位:次/每分钟)与跑步时间(单位:秒)之间的函数关系式为,
(2)①由题意得:,
设,
把,分别代入,
,
解得:,
,
当时,,
当时,,
解得:,
答:小南跑步的最大速度为8.8千米/小时;
②当时,,
,
又,
从起跑到速度达到最大这段时间内,小南的心率保持在100次/分钟以上的时长为:
,
当,
将代入得,
即停下时,,
由休息15分钟后,小南的心率匀速降低至跑步前的状态可知,休息时段心率p与休息时间t是一次函数关系,设休息时段,
把代入,
,
解得:,
,
当时,,
,
由于休息时心率匀速降低,
因此在休息这段时间小南的心率保持在100次/分钟以上的时长为,
设最大速度跑步的时间为,
则的时段:,
,
则他以最大速度跑步的时间至少是.
10.(1)见详解
(2),,
(3)
【分析】本题主要考查了一次函数、二次函数的应用,读懂题意是解答本题的关键.
(1)依据题意,根据表格数据描点,连线即可作图得解;
(2)根据函数图象确定点的坐标,利用待定系数法解答即可;
(3)依据题意,分别求出当时的值,即可得出答案.
【详解】(1)解:(1)由题意,作图如下.
(2)解:由题意,场景的图象是抛物线的一部分,与之间近似满足函数关系.
又点,在函数图象上,
.
解得:.
场景函数关系式为.
对于场景的图象是直线的一部分,与之间近似满足函数关系.
又,在函数图象上,
.
解得:.
场景函数关系式为.
∴,,.
(3)解:由题意,当时,
场景中,,
解得:(舍),
即:,
场景中,,
解得:,
.
11.(1)见解析(2)最小值为,此时菜地面积为(3)①;②当点位于轴下方时 ;当点位于轴上方时
【分析】(1)如图所示,过点作交于点,则由垂径定理可知 ,证明,推出,即可得到点的轨迹是以为圆心,半径为2的圆,且该圆不经过点,进而证明结论;
(2)由(1)可知,当三点共线时有最小值为,如图所示,记与交于点,求出,过点作,则有,求出, 过点作,垂足为,连接,证明为正三角形,求出,,即可解答;
(3)①连接,记交轴于点,作于点,证明为中位线 ,根据,即可求解;②分点位于轴下方和上方两种情况讨论,利用三角形中位线的性质求出,再利用勾股定理求出,即可解答.
【详解】(1)证明:如图所示,过点作交于点,则由垂径定理可知 ,
∵四边形是矩形
∴
∵
∴
在与中
∴
∴
∴点的轨迹是以为圆心,半径为2的圆,且该圆不经过点,即小彬设想成立 ;
(2)由(1)可知,当三点共线时有最小值为,
如图所示,记与交于点
∵,为上的点
∴为的直径 ,,
过点作,则有
∴
∴
∴
由同弧所对的圆心角是圆周角的2倍可知
∴
过点作,垂足为,连接
∵
∴为正三角形
∴为边上的中线,且平分
∴,
∴
∴
∴
∴菜地面积;
(3)①如图所示,连接,记交轴于点,作于点,
∵
∴为中点
∵为中点
∴为中位线
∴
∵
∴
∴;
②第一种情况,当点位于轴下方时,如图:
∴,
;
第二种情况,当点位于轴上方时,如图:
同理得:.
本题考查了圆周角定理,垂径定理,勾股定理,矩形的性质,函数解析式,解直角三角形,坐标与图形,熟练掌握以上知识是解题的关键.
12.(1)不公平,理由见解析;(2)
【分析】(1)首先分别计算小红和小明获胜的概率,相比较,获胜概率不同,所以可判定不公平;
(2)首先设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为),然后往图形中掷点,掷在正方形外或边界上不作记录,其次当所掷次数充分大时,记录并统计结果,设掷入正方形内次,其中次掷入不规则图形内,最后用频率估计概率,大概可得出结果.
【详解】(1)不公平.理由如下:
(掷中阴影部分),即小红获胜的概率为,则小明获胜的概率为,,
游戏不公平
(2)能利用频率估计概率的方法估算不规则图形的面积设计方案:①设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为),如图所示;
②往图形中掷点(如蒙上眼睛往图形中随意掷小石子,掷在正方形外或边界上不作记录);
③当所掷次数充分大时,记录并统计结果,设掷入正方形内次,其中次掷入不规则图形内;
④设不规则图形的面积为,用频率估计概率,即掷入不规则图形内的频率(掷入不规则图形内),而(掷入不规则图形内),故,即.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
