数学:第二章相似图形复习课件(鲁教版八年级上)
文档属性
| 名称 | 数学:第二章相似图形复习课件(鲁教版八年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 406.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-14 20:05:00 | ||
图片预览







文档简介
课件25张PPT。回顾与思考第二章 相似图形一、比例的性质?比例的基本性质─比例的合比性质─比例的等比性质──如果 ,那么称 线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.相似多边形的对应角相等,
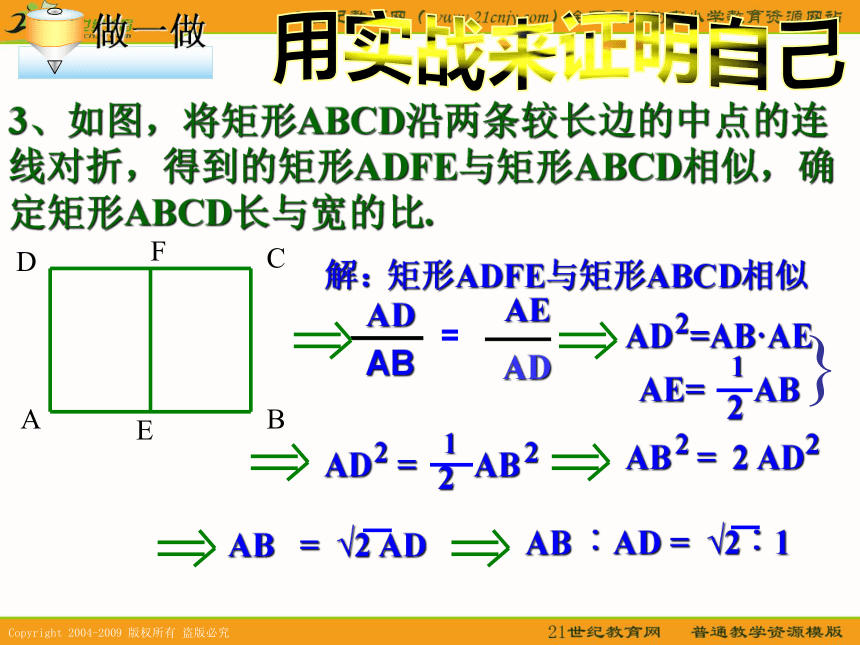
对应边成比例.二、黄金分割与相似多边形三、相似三角形的定义?判定?性质?1、定义:三角对应角相等、三边对应成比例的两个三角形叫相似三角形2、判定:两角相等的两个三角形相似三边对应成比例的两个三角形相似 两边对应成比例且夹角相等的两个三角形相似3、性质: 相似三角形对应高的比,对应角平分线的比和对应中线的比都等于相似比相似三角形对应角相等,对应边成比例相似三角形周长的比等于相似比相似三角形面积的比等于相似比的平方相似多边形的周长比等于相似比相似多边形面积的比等于相似比的平方3、性质: 如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.这个点叫做位似中心.这时的相似比又称为位似比. 位似图形上任意一对对应点到位似中心的距离之比等于位似比.四、位似图形用实战来证明自己1、将一个等腰直角三角形放大,使放大后的边是原三角形对应边的3倍,并分别确定放大前后对应斜边的比值、对应直角边的比值.解:放大前后对应斜边的比值是1︰3、对应直角边的比值是1︰3.复习题 A组题用实战来证明自己2、四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长.用实战来证明自己3、如图,将矩形ABCD沿两条较长边的中点的连线对折,得到的矩形ADFE与矩形ABCD相似,确定矩形ABCD长与宽的比.解:矩形ADFE与矩形ABCD相似{用实战来证明自己4、如图,BC//DE//FG,图中有几对相似三角形?你是怎样判断的?解:△ABC∽△ADE△ABC∽△AFG△ADE∽△AFG有三对,它们是: 根据BC//DE//FG,可得同位角相等,
由此得到两个三角形相似.用实战来证明自己5、如图,已知△ADF∽△ABC,AD=6cm,DB=3cm,BC=9.9cm,∠A=70°,∠B=50°.
(1)求∠ADE的大小;(2)求∠AED的的小;
(3)求DE的长.解:(1) △ADF∽△ABC∠ADE=∠B=50°(2) ∠A=70°
∠ADE=50°{∠AED=60°(3) △ADF∽△ABCDE=6.6 cm70°50°639.9???用实战来证明自己6、如图,小明欲测量红塔
的高,他站在该塔的影子
上前后移动,直到他本身
影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18m,已知小明的身高
是1.6m,他的影子长是2m.(1)图中△ABC与△ADE
是否相似?为什么?(2)求红塔的高.解:(1)相似因为∠A是公共角,∠BCA和∠DEA是直角(2)由△ABC∽△ADE得,DE=16 m?18m2m1.6m用实战来证明自己7、如果两个相似多边形面积的比为4︰9,那么这两个相似多边形对应边的比是多少?用实战来证明自己8、如图,在△ABC中,已知DE//BC,AD=3BD,=48,求解:DE//BC∠ADE=∠B∠AED=∠C{{△ADE∽△ABCAD=3BD{{3份1份用实战来证明自己9、如图,AB、CD交于点O,且AC//BD.
则OA·OD=OC·OB吗?为什么?解:OA·OD=OC·OB,理由如下:AC//BD{∠A=∠B∠C=∠D{△AOC∽△BODOA·OD=OC·OBA10、(1)在平面直角坐标系中描出点A(4,2),B(2,4),C(0,4),D(0,2),E(2,0),顺次连接点A、B、C、D、E、A,得到一个五边形ABCDE.用实战来证明自己(2)将点A、B、C、D、E的横坐标和纵坐标都除以2,得到五个新的点,顺次连接这五个 点,得到一个新的五边形,这两个五边形相似吗?如果将点A、B、C、D、E的横坐标和纵坐标都除以 3 呢?解:●●●●●BCDE●●●●●ABCDE 所以、 除以 2 后得到的
新五边形与原五边形相似 同样, 除以 3 后
得到的新五边形与
原五边形相似 用实战来证明自己B组题1、如图,在长8cm、宽6cm的矩形中,截去一个矩形(图中阴影部分所示),使留下的矩形与原矩形相似,那么留下的矩形面积为多少?解:由题意得x 48 = 6 8 ((2用实战来证明自己2、如图,能保证使△ACD与△ABC相似的条件是( )(1)AC︰CD = AB︰BC(2)CD︰AD = BC︰AC解:已知∠A是两个三角形的公共角,要使△ACD与△ABC相似,就要使△ACD中∠A的两边与△ABC中的∠A的两
边对应成比例——即ADACACAB=∴应该选:CC用实战来证明自己3、如图,王华在晚上由路灯A走向路灯B,当他走到点
P时,发现身后他影子的顶部刚好接触到路灯A的底部,
当他向前再行12m到达点Q时,发现身前他影子的顶部
刚好接触到路灯B的底部.已知王华的身高是1.6m,两
个路灯的高度都是9.6m,且AP=QB= x m.
(1)求两个路灯之间的距离;
(2)当王华走到路灯B时,他在路灯A下的影长是多少?解:xx121.69.6(1)由题得:x2x+12 =1.69.6解得:x = 3 m∴两个路灯之间的距离是18 m用实战来证明自己(2)当王华走到路灯B时,他在路灯A下的影长是多少?解:1.69.618x设他的影子长为 x m,则由题得:x18+x=1.69.6解得 x = 3.6 m∴他的影子长为 3.6 m.?AB用实战来证明自己4、如图,为了测量一条河的宽度,测量人员在对岸岸
边P点处观察到一根柱子,再在他们所在的这一侧岸上
选择点A和B,使得B、A、P在一条直线上,且与河岸
垂直.随后确定点C、D,使BC⊥BP,AD⊥BP,由观
测可以确定CP与AD的交点D.他们测得AB=45m,BC
=90m,AD=60m,从而确定河宽PA=90m.
你认为他们的结论对吗?还有其他的测量方法吗?ABCDP45m90m60m解:结论正确!理由如下:由△PAD∽△PBC得PAPB=ADBC PAPA+45=6090PA=90改变点C的位置,仍可以得到相应的结论.?用实战来证明自己C组题1、如图,BC与EF在一条直线上,AC//DF.将图(2)
中的三角形截去一块,使它变为与图(1)相似的图形.G方法1:作EG//AB,
交DF于点G,沿EG
将△DEG截去即可.PQ方法2:在EF上任取一点P过点P作PQ//AB,交DF于点Q,沿PQ将图(2)截开,得△PQF∽△ABC.用实战来证明自己2、教学楼旁边有一颗树,学习了相似三角形后,数学兴趣小组的
同学们想利用树影测量树高.课外活动时在阳光下他们测得一根
长为1m的竹竿的影长是0.9m,但当他们马上测量树高时,发现树
的影子不全落在地面上,有一部分落在教学楼的墙壁上(如图),
经过一番争论,小组同学认为继续测量也可以求出树高.他们测
得落在地面的影长2.7m,落在墙壁上的影长1.2m,请你和他们一
起算一下,树高为多少?DBACEHFG解:首先在图上标上字母,过点C作CE⊥AB,垂足为E根据题意,可得:△AEC∽△FGH2.7m2.7m1.2m1.2m1m0.9AEFG=CEHGAE1=2.70.9AE= 3 m∴树高AB = 3 + 1.2 = 4.2 m数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸…………结束寄语通过今天的学习,你有什么收获?数学使人聪明
对应边成比例.二、黄金分割与相似多边形三、相似三角形的定义?判定?性质?1、定义:三角对应角相等、三边对应成比例的两个三角形叫相似三角形2、判定:两角相等的两个三角形相似三边对应成比例的两个三角形相似 两边对应成比例且夹角相等的两个三角形相似3、性质: 相似三角形对应高的比,对应角平分线的比和对应中线的比都等于相似比相似三角形对应角相等,对应边成比例相似三角形周长的比等于相似比相似三角形面积的比等于相似比的平方相似多边形的周长比等于相似比相似多边形面积的比等于相似比的平方3、性质: 如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.这个点叫做位似中心.这时的相似比又称为位似比. 位似图形上任意一对对应点到位似中心的距离之比等于位似比.四、位似图形用实战来证明自己1、将一个等腰直角三角形放大,使放大后的边是原三角形对应边的3倍,并分别确定放大前后对应斜边的比值、对应直角边的比值.解:放大前后对应斜边的比值是1︰3、对应直角边的比值是1︰3.复习题 A组题用实战来证明自己2、四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长.用实战来证明自己3、如图,将矩形ABCD沿两条较长边的中点的连线对折,得到的矩形ADFE与矩形ABCD相似,确定矩形ABCD长与宽的比.解:矩形ADFE与矩形ABCD相似{用实战来证明自己4、如图,BC//DE//FG,图中有几对相似三角形?你是怎样判断的?解:△ABC∽△ADE△ABC∽△AFG△ADE∽△AFG有三对,它们是: 根据BC//DE//FG,可得同位角相等,
由此得到两个三角形相似.用实战来证明自己5、如图,已知△ADF∽△ABC,AD=6cm,DB=3cm,BC=9.9cm,∠A=70°,∠B=50°.
(1)求∠ADE的大小;(2)求∠AED的的小;
(3)求DE的长.解:(1) △ADF∽△ABC∠ADE=∠B=50°(2) ∠A=70°
∠ADE=50°{∠AED=60°(3) △ADF∽△ABCDE=6.6 cm70°50°639.9???用实战来证明自己6、如图,小明欲测量红塔
的高,他站在该塔的影子
上前后移动,直到他本身
影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18m,已知小明的身高
是1.6m,他的影子长是2m.(1)图中△ABC与△ADE
是否相似?为什么?(2)求红塔的高.解:(1)相似因为∠A是公共角,∠BCA和∠DEA是直角(2)由△ABC∽△ADE得,DE=16 m?18m2m1.6m用实战来证明自己7、如果两个相似多边形面积的比为4︰9,那么这两个相似多边形对应边的比是多少?用实战来证明自己8、如图,在△ABC中,已知DE//BC,AD=3BD,=48,求解:DE//BC∠ADE=∠B∠AED=∠C{{△ADE∽△ABCAD=3BD{{3份1份用实战来证明自己9、如图,AB、CD交于点O,且AC//BD.
则OA·OD=OC·OB吗?为什么?解:OA·OD=OC·OB,理由如下:AC//BD{∠A=∠B∠C=∠D{△AOC∽△BODOA·OD=OC·OBA10、(1)在平面直角坐标系中描出点A(4,2),B(2,4),C(0,4),D(0,2),E(2,0),顺次连接点A、B、C、D、E、A,得到一个五边形ABCDE.用实战来证明自己(2)将点A、B、C、D、E的横坐标和纵坐标都除以2,得到五个新的点,顺次连接这五个 点,得到一个新的五边形,这两个五边形相似吗?如果将点A、B、C、D、E的横坐标和纵坐标都除以 3 呢?解:●●●●●BCDE●●●●●ABCDE 所以、 除以 2 后得到的
新五边形与原五边形相似 同样, 除以 3 后
得到的新五边形与
原五边形相似 用实战来证明自己B组题1、如图,在长8cm、宽6cm的矩形中,截去一个矩形(图中阴影部分所示),使留下的矩形与原矩形相似,那么留下的矩形面积为多少?解:由题意得x 48 = 6 8 ((2用实战来证明自己2、如图,能保证使△ACD与△ABC相似的条件是( )(1)AC︰CD = AB︰BC(2)CD︰AD = BC︰AC解:已知∠A是两个三角形的公共角,要使△ACD与△ABC相似,就要使△ACD中∠A的两边与△ABC中的∠A的两
边对应成比例——即ADACACAB=∴应该选:CC用实战来证明自己3、如图,王华在晚上由路灯A走向路灯B,当他走到点
P时,发现身后他影子的顶部刚好接触到路灯A的底部,
当他向前再行12m到达点Q时,发现身前他影子的顶部
刚好接触到路灯B的底部.已知王华的身高是1.6m,两
个路灯的高度都是9.6m,且AP=QB= x m.
(1)求两个路灯之间的距离;
(2)当王华走到路灯B时,他在路灯A下的影长是多少?解:xx121.69.6(1)由题得:x2x+12 =1.69.6解得:x = 3 m∴两个路灯之间的距离是18 m用实战来证明自己(2)当王华走到路灯B时,他在路灯A下的影长是多少?解:1.69.618x设他的影子长为 x m,则由题得:x18+x=1.69.6解得 x = 3.6 m∴他的影子长为 3.6 m.?AB用实战来证明自己4、如图,为了测量一条河的宽度,测量人员在对岸岸
边P点处观察到一根柱子,再在他们所在的这一侧岸上
选择点A和B,使得B、A、P在一条直线上,且与河岸
垂直.随后确定点C、D,使BC⊥BP,AD⊥BP,由观
测可以确定CP与AD的交点D.他们测得AB=45m,BC
=90m,AD=60m,从而确定河宽PA=90m.
你认为他们的结论对吗?还有其他的测量方法吗?ABCDP45m90m60m解:结论正确!理由如下:由△PAD∽△PBC得PAPB=ADBC PAPA+45=6090PA=90改变点C的位置,仍可以得到相应的结论.?用实战来证明自己C组题1、如图,BC与EF在一条直线上,AC//DF.将图(2)
中的三角形截去一块,使它变为与图(1)相似的图形.G方法1:作EG//AB,
交DF于点G,沿EG
将△DEG截去即可.PQ方法2:在EF上任取一点P过点P作PQ//AB,交DF于点Q,沿PQ将图(2)截开,得△PQF∽△ABC.用实战来证明自己2、教学楼旁边有一颗树,学习了相似三角形后,数学兴趣小组的
同学们想利用树影测量树高.课外活动时在阳光下他们测得一根
长为1m的竹竿的影长是0.9m,但当他们马上测量树高时,发现树
的影子不全落在地面上,有一部分落在教学楼的墙壁上(如图),
经过一番争论,小组同学认为继续测量也可以求出树高.他们测
得落在地面的影长2.7m,落在墙壁上的影长1.2m,请你和他们一
起算一下,树高为多少?DBACEHFG解:首先在图上标上字母,过点C作CE⊥AB,垂足为E根据题意,可得:△AEC∽△FGH2.7m2.7m1.2m1.2m1m0.9AEFG=CEHGAE1=2.70.9AE= 3 m∴树高AB = 3 + 1.2 = 4.2 m数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸…………结束寄语通过今天的学习,你有什么收获?数学使人聪明
