甘肃省定西市渭源县新寨中学2024-2025学年第二学期第二次阶段考试七年级数学试卷(含答案)
文档属性
| 名称 | 甘肃省定西市渭源县新寨中学2024-2025学年第二学期第二次阶段考试七年级数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 874.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 20:56:59 | ||
图片预览



文档简介
2024-2025甘肃省定西市渭源县新寨中学第二次阶段考试
七年级 数学
考生注意:本试卷满分为120分,考试时间为100分钟.
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.要了解某初中全校1200名学生的课外阅读情况,若采用抽样调查的方法进行调查,则下面具有代表性的调查方式是( )
A.调查100名女生
B.调查100名男生
C.调查九年级100名学生
D.调查七、八、九年级各100名学生
2.如果把点A(﹣1,4)向右平移2个单位长度,再向上平移3个单位长度,则平移后的坐标是( )
A.(1,7) B.(﹣1,7) C.(1,﹣7) D.(﹣1,﹣7)
3.实数a,b在数轴上的对应点的位置如图所示,则下列结论正确的是( )
A.a<﹣2 B.|b|>1 C.ab>0 D.a+b<0
4.下列各数为无理数的是( )
A.0.618 B. C. D.3.14
5.如图,E为△ABC边CA延长线上一点,过点E作ED∥BC.若∠BAC=70°,∠CED=50°,则∠B=( )
A.50° B.60° C.70° D.80°
6.下列说法中,一定正确的是( )
A.如果a>b,那么ac>bc B.如果ac<bc,那么a<b
C.如果a>b,那么ac2>bc2 D.如果ac2>bc2,那么a>b
7.如图,直线l1∥l2,分别与直线l交于点A,B,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=40°,则∠2的度数是( )
A.100° B.110° C.115° D.120°
8.关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A.a≤2 B.1<a≤2 C.a≥1 D.1≤a<2
9.第一道鸡兔同笼问题收录于《孙子算经》:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?意思是现在笼子里既有鸡又有兔,有35个头,94只脚,设有鸡、兔各为x,y只,那么下列选项中,方程组列正确的是( )
A. B.
C. D.
10.如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:
①∠D=40°;
②2∠D+∠EHC=90°;
③FD平分∠HFB;
④FH平分∠GFD.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共6小题,每小题3分,共18分.
11.用“*”表示一种新运算:对于任意正实数a,b,都有,例如图,那么5*144= .
12.化简绝对值: .
13.如图,△ABC在平面直角坐标系中,其中点A(0,3),B(﹣4,﹣1),C(4,0),将△ABC的顶点A平移至点P(4,2)的位置后,那么点C的对应点的坐标是 .
14.不等式组的解集为x>a,请你写出一个符合条件的a的值: .
15.某校为满足学生午餐的多样性,将学生午餐分成了A、B、C三类供学生自主选择.在前期的调研中,从全校1500人中随机抽取了100人进行问卷调查,并将问卷的结果整理后绘制成如图.根据该数据,估计全校约有 人会选择C类午餐.
16.已知1.2584,2.711,则 , .
三.解答题(共10小题,共72分)
17.(6分)(1)计算;(2)若(2x﹣1)3=﹣8,求x的值.
18.(5分)已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)若点M到x轴的距离为3,求点M的坐标?
(2)若点N的坐标为(5,﹣1),且MN∥x轴,求点M的坐标?
19.(6分)解方程组
(1) (2).
(5分)求不等式组的整数解.
21.(5分)在平面直角坐标系中,A,B,C三点的坐标分别为(﹣5,4),(﹣3,0),(0,2).
(1)在图中画出三角形ABC,并求其面积;
(2)已知三角形A'B'C'是由△ABC经过平移得到的,若P(a,b)为三角形ABC内的一点,则点P在三角形A'B'C'内的对应点P'的坐标是 .
22.(8分)某中学七年级(1)班去体育用品商店买一些篮球和排球,供班上同学进行体育锻炼时使用,共买了2个篮球和6个排球,花570元,并且每个排球比篮球便宜25元.
(1)求篮球和排球的单价各是多少;
(2)商店里搞活动,有两种套餐,①套餐打折:五个篮球和五个排球为一套餐,套餐打八折;②满减活动:满999减100,满1999减200;两种活动不重复参与,学校打算购买14个篮球,12个排球,请问如何安排更划算?
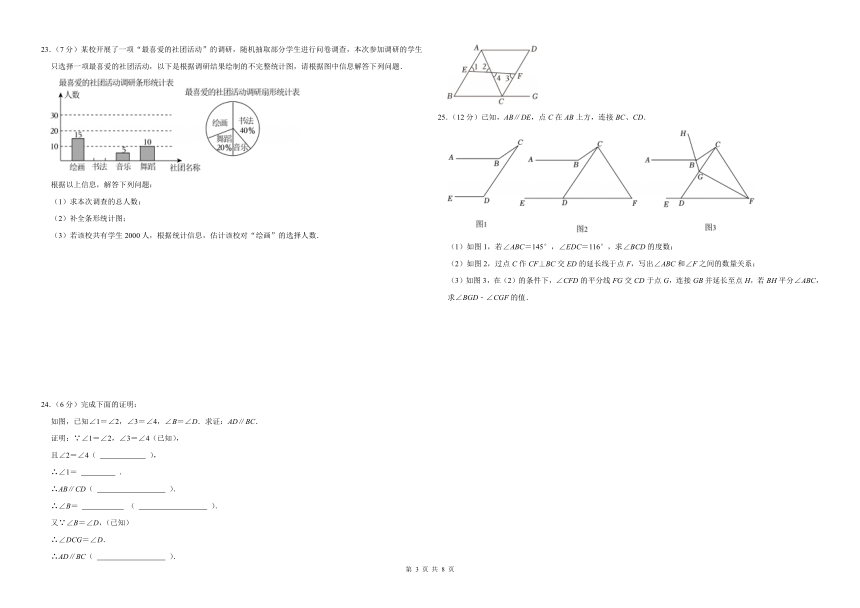
23.(7分)某校开展了一项“最喜爱的社团活动”的调研,随机抽取部分学生进行问卷调查,本次参加调研的学生只选择一项最喜爱的社团活动,以下是根据调研结果绘制的不完整统计图,请根据图中信息解答下列问题.
根据以上信息,解答下列问题:
(1)求本次调查的总人数;
(2)补全条形统计图;
(3)若该校共有学生2000人,根据统计信息,估计该校对“绘画”的选择人数.
24.(6分)完成下面的证明:
如图,已知∠1=∠2,∠3=∠4,∠B=∠D.求证:AD∥BC.
证明:∵∠1=∠2,∠3=∠4(已知),
且∠2=∠4( ),
∴∠1= .
∴AB∥CD( ).
∴∠B= ( ).
又∵∠B=∠D,(已知)
∴∠DCG=∠D.
∴AD∥BC( ).
25.(12分)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,若∠ABC=145°,∠EDC=116°,求∠BCD的度数;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,写出∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线FG交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
26.(12分)综合与实践
【探索发现】
(1)已知:如图,∠BAP=40°,∠APC=75°,∠PCD=35°,求证:AB∥CD.
【深入思考】
(2)某条河流的两岸各安置了一盏旋转探照灯.如图所示,PQ∥MN,灯A的光线从AM开始顺时针旋转至AN便立即回转,灯B的光线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒3度,灯B转动的速度是每秒2度.如果灯B的光线先转动10秒,灯A的光线才开始转动,那么在灯B的光线到达BQ之前,灯A转动几秒时,两灯的光束互相平行?
【拓展延伸】
(3)如图,在(2)的条件下,“如果灯B的光线先转动10秒”改为“两灯同时转动”,在灯A的光线到达AN之前,若两灯射出的光束交于点C,过C作∠ACD=135°,CD交PQ于点D,∠MAB=135°,则在转动过程中,请求出∠BAC与∠BCD的数量关系.
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C B D B B D A
二.填空题(共6小题)
11.17
12.
.(8,﹣1)
. 1(答案不唯一)
.630
.12.584 , ﹣0.2711
三.解答题(共10小题)
17.解:(1)原式=5﹣3﹣6=﹣4;
(2)(2x﹣1)3=﹣8,
开立方得:2x﹣1=﹣2,
解得:x.
18.解:(1)∵点M(m﹣1,2m+3),点M到x轴的距离为3,
∴|2m+3|=3,
解得,m=0或m=﹣3,
当m=0时,点M的坐标为(﹣1,3),
当m=﹣3时,点M的坐标为(﹣4,﹣3);
(2)∵点M(m﹣1,2m+3),点N(5,﹣1)且MN∥x轴,
∴2m+3=﹣1,
解得,m=﹣2,
故点M的坐标为(﹣3,﹣1).
19.解方程组
(1)(2).
解:(1),
①+②得:3x=3,即x=1,
把x=1代入①得:y=3,
则方程组的解为;
(2)方程组整理得:,
①×4﹣②×3得:7x=42,即x=6,
把x=6代入①得:y=4,
则方程组的解为.
20.求不等式组的整数解.
解:解不等式①,得:x≤1,
解不等式②,得:x>﹣2,
∴原不等式组的解集为:﹣2<x≤1,
∴原不等式组的整数解为:﹣1,0,1.
21.解:(1)如图所示:△ABC即为所求,
△ABC的面积为:4×52×52×42×3=8;
(2)由(1)可知,三角形A'B'C'可以由三角形ABC向右平移4个单位,然后向下平移3个单位得到,
∴P(a,b)为三角形ABC内的一点,则点P在三角形A'B'C'内的对应点P'的坐标是(a+4,b﹣3).
故答案为:(a+4,b﹣3).
22.解:(1)设篮球单价为每个x元,排球单价为每个y元,
由题意可得,
解方程组得,
答:篮球每个90元,排球每个65元;
(2)若按照①套餐打折购买费用为:2(5×90+5×65)×0.8+4×90+2×65=1730(元),
若参加②满减活动购买费用为:14×90+12×65=2040(元),
又2040>1999,
所以2040﹣200=1840(元).
而1840>1730,所以选择套餐①所花费用比选择套餐②所花费用低.
答:选用套餐①购买更划算.
23.某校开展了一项“最喜爱的社团活动”的调研,随机抽取部分学生进行问卷调查,本次参加调研的学生只选择一项最喜爱的社团活动,以下是根据调研结果绘制的不完整统计图,请根据图中信息解答下列问题.
根据以上信息,解答下列问题:
(1)求本次调查的总人数;
(2)补全条形统计图;
(3)若该校共有学生2000人,根据统计信息,估计该校对“绘画”的选择人数.
解:(1)10÷20%=50(人),
答:本次调查的总人数为50人;
(2)书法人数为:50×40%=20(人),
补全条形统计图如下:
(3)2000600(人),
答:估计该校对“绘画”的选择人数为600人.
24.完成下面的证明:
如图,已知∠1=∠2,∠3=∠4,∠B=∠D.求证:AD∥BC.
证明:∵∠1=∠2,∠3=∠4(已知),
且∠2=∠4( 对顶角相等 ),
∴∠1= ∠3 .
∴AB∥CD( 内错角相等,两直线平行 ).
∴∠B= ∠DCG ( 两直线平行,同位角相等 ).
又∵∠B=∠D,(已知)
∴∠DCG=∠D.
∴AD∥BC( 内错角相等,两直线平行 ).
25.已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,若∠ABC=145°,∠EDC=116°,求∠BCD的度数;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,写出∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线FG交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
解:(1)过点C作CM∥AB,
∴∠BCM=∠ABC=145°,
∵AB∥DE,
∴CM∥DE
∴∠DCM=∠EDC=116°,
∵∠BCM=∠BCD+∠DCM,
∴∠BCD=∠BCM﹣∠DCM=29°;
(2)∠ABC﹣∠F=90°,理由:
过点C作CN∥AB,如图,
∴∠ABC=∠BCN,
∵AB∥DE,
∴CN∥EF,
∴∠F=∠FCN,
∵∠BCN=∠BCF+∠FCN,
∴∠ABC=∠BCF+∠F,
∵CF⊥BC,
∴∠BCF=90°,
∴∠ABC=90°+∠F,
即∠ABC﹣∠F=90°;
(3)延长HG交EF于点Q,过点G作GP∥EF,如图3,
∴∠BGD=∠CGQ,
∵AB∥DE,
∴∠ABH=∠EQG,
∵GP∥EF,
∴∠EQG=∠PGQ,∠EFG=∠PGF,
∴∠PGQ=∠ABH,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF=∠FGQ,
∵∠FGQ=∠PGQ﹣∠PGF,
∴∠FGQ=∠ABH﹣∠EFG,
∵,,
∴,
∵∠ABC﹣∠CFD=90°,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF,
即∠BGD﹣∠CGF=45°.
26.1)证明:过P作PQ∥AB,
∴∠QPA=∠BAP=40°,
∵∠APC=75°,
∴∠CPQ=∠APC﹣∠APQ=35°,
∵∠DCP=35°,
∴∠CPQ=∠DCP,
∴PQ∥CD,
又∵PQ∥AB,
∴AB∥CD;
(2)解:灯A的光线从AM开始顺时针旋转至AN所用时间为180÷3=60秒,灯B的光线从BP开始顺时针旋转至BQ所用时间为180÷2=90秒,
设灯A转动t秒时,两灯的光束互相平行,
当0<t≤60时,设AM′与PQ交于M′,如图,
∵PQ∥MN,
∴∠PM′A=∠MAM′=(3t)°,
∵AM′∥BP′,
∴∠MAM′=∠PBP′=2(t+10)°,
∴3t=2(t+10),
解得t=20;
当60<t≤90﹣10,即60<t≤80时,设AM′与PQ交于M′,如图,
∵PQ∥MN,
∴∠PM′A=∠MAM′=180×2﹣3t=(360﹣3t)°,
∵AM′∥BP′,PQ∥MN,
∴四边形AM′BP′是平行四边形,
∴∠MAM′=∠PBP′=2(t+10)°,
∴360﹣3t=2(t+10),
解得t=68;
综上,当灯A转动20或68秒时,两灯的光束互相平行;
(3)解:∵灯A转动的速度是每秒3度,灯B转动的速度是每秒2度,
∴∠PBC=(2t)°,∠MAC=(3t)°,
∵PQ∥MN,
∴∠PBA=∠MAB=135°(两直线平行,内错角相等),
∴∠BAC=∠MAC﹣∠MAB=(3t﹣135)°,∠ABC=∠PBA﹣∠PBC=(135﹣2t)°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣(3t﹣135)°﹣(135﹣2t)°=(180﹣t)°,
∵∠ACD=135°,
∴∠BCD=∠ACD﹣∠ACB=(t﹣45)°,
又∵∠BAC=(3t﹣135)°=3(t﹣45)°,
∴∠BAC=3∠BCD.
七年级 数学
考生注意:本试卷满分为120分,考试时间为100分钟.
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.要了解某初中全校1200名学生的课外阅读情况,若采用抽样调查的方法进行调查,则下面具有代表性的调查方式是( )
A.调查100名女生
B.调查100名男生
C.调查九年级100名学生
D.调查七、八、九年级各100名学生
2.如果把点A(﹣1,4)向右平移2个单位长度,再向上平移3个单位长度,则平移后的坐标是( )
A.(1,7) B.(﹣1,7) C.(1,﹣7) D.(﹣1,﹣7)
3.实数a,b在数轴上的对应点的位置如图所示,则下列结论正确的是( )
A.a<﹣2 B.|b|>1 C.ab>0 D.a+b<0
4.下列各数为无理数的是( )
A.0.618 B. C. D.3.14
5.如图,E为△ABC边CA延长线上一点,过点E作ED∥BC.若∠BAC=70°,∠CED=50°,则∠B=( )
A.50° B.60° C.70° D.80°
6.下列说法中,一定正确的是( )
A.如果a>b,那么ac>bc B.如果ac<bc,那么a<b
C.如果a>b,那么ac2>bc2 D.如果ac2>bc2,那么a>b
7.如图,直线l1∥l2,分别与直线l交于点A,B,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=40°,则∠2的度数是( )
A.100° B.110° C.115° D.120°
8.关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A.a≤2 B.1<a≤2 C.a≥1 D.1≤a<2
9.第一道鸡兔同笼问题收录于《孙子算经》:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?意思是现在笼子里既有鸡又有兔,有35个头,94只脚,设有鸡、兔各为x,y只,那么下列选项中,方程组列正确的是( )
A. B.
C. D.
10.如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:
①∠D=40°;
②2∠D+∠EHC=90°;
③FD平分∠HFB;
④FH平分∠GFD.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共6小题,每小题3分,共18分.
11.用“*”表示一种新运算:对于任意正实数a,b,都有,例如图,那么5*144= .
12.化简绝对值: .
13.如图,△ABC在平面直角坐标系中,其中点A(0,3),B(﹣4,﹣1),C(4,0),将△ABC的顶点A平移至点P(4,2)的位置后,那么点C的对应点的坐标是 .
14.不等式组的解集为x>a,请你写出一个符合条件的a的值: .
15.某校为满足学生午餐的多样性,将学生午餐分成了A、B、C三类供学生自主选择.在前期的调研中,从全校1500人中随机抽取了100人进行问卷调查,并将问卷的结果整理后绘制成如图.根据该数据,估计全校约有 人会选择C类午餐.
16.已知1.2584,2.711,则 , .
三.解答题(共10小题,共72分)
17.(6分)(1)计算;(2)若(2x﹣1)3=﹣8,求x的值.
18.(5分)已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)若点M到x轴的距离为3,求点M的坐标?
(2)若点N的坐标为(5,﹣1),且MN∥x轴,求点M的坐标?
19.(6分)解方程组
(1) (2).
(5分)求不等式组的整数解.
21.(5分)在平面直角坐标系中,A,B,C三点的坐标分别为(﹣5,4),(﹣3,0),(0,2).
(1)在图中画出三角形ABC,并求其面积;
(2)已知三角形A'B'C'是由△ABC经过平移得到的,若P(a,b)为三角形ABC内的一点,则点P在三角形A'B'C'内的对应点P'的坐标是 .
22.(8分)某中学七年级(1)班去体育用品商店买一些篮球和排球,供班上同学进行体育锻炼时使用,共买了2个篮球和6个排球,花570元,并且每个排球比篮球便宜25元.
(1)求篮球和排球的单价各是多少;
(2)商店里搞活动,有两种套餐,①套餐打折:五个篮球和五个排球为一套餐,套餐打八折;②满减活动:满999减100,满1999减200;两种活动不重复参与,学校打算购买14个篮球,12个排球,请问如何安排更划算?
23.(7分)某校开展了一项“最喜爱的社团活动”的调研,随机抽取部分学生进行问卷调查,本次参加调研的学生只选择一项最喜爱的社团活动,以下是根据调研结果绘制的不完整统计图,请根据图中信息解答下列问题.
根据以上信息,解答下列问题:
(1)求本次调查的总人数;
(2)补全条形统计图;
(3)若该校共有学生2000人,根据统计信息,估计该校对“绘画”的选择人数.
24.(6分)完成下面的证明:
如图,已知∠1=∠2,∠3=∠4,∠B=∠D.求证:AD∥BC.
证明:∵∠1=∠2,∠3=∠4(已知),
且∠2=∠4( ),
∴∠1= .
∴AB∥CD( ).
∴∠B= ( ).
又∵∠B=∠D,(已知)
∴∠DCG=∠D.
∴AD∥BC( ).
25.(12分)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,若∠ABC=145°,∠EDC=116°,求∠BCD的度数;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,写出∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线FG交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
26.(12分)综合与实践
【探索发现】
(1)已知:如图,∠BAP=40°,∠APC=75°,∠PCD=35°,求证:AB∥CD.
【深入思考】
(2)某条河流的两岸各安置了一盏旋转探照灯.如图所示,PQ∥MN,灯A的光线从AM开始顺时针旋转至AN便立即回转,灯B的光线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒3度,灯B转动的速度是每秒2度.如果灯B的光线先转动10秒,灯A的光线才开始转动,那么在灯B的光线到达BQ之前,灯A转动几秒时,两灯的光束互相平行?
【拓展延伸】
(3)如图,在(2)的条件下,“如果灯B的光线先转动10秒”改为“两灯同时转动”,在灯A的光线到达AN之前,若两灯射出的光束交于点C,过C作∠ACD=135°,CD交PQ于点D,∠MAB=135°,则在转动过程中,请求出∠BAC与∠BCD的数量关系.
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C B D B B D A
二.填空题(共6小题)
11.17
12.
.(8,﹣1)
. 1(答案不唯一)
.630
.12.584 , ﹣0.2711
三.解答题(共10小题)
17.解:(1)原式=5﹣3﹣6=﹣4;
(2)(2x﹣1)3=﹣8,
开立方得:2x﹣1=﹣2,
解得:x.
18.解:(1)∵点M(m﹣1,2m+3),点M到x轴的距离为3,
∴|2m+3|=3,
解得,m=0或m=﹣3,
当m=0时,点M的坐标为(﹣1,3),
当m=﹣3时,点M的坐标为(﹣4,﹣3);
(2)∵点M(m﹣1,2m+3),点N(5,﹣1)且MN∥x轴,
∴2m+3=﹣1,
解得,m=﹣2,
故点M的坐标为(﹣3,﹣1).
19.解方程组
(1)(2).
解:(1),
①+②得:3x=3,即x=1,
把x=1代入①得:y=3,
则方程组的解为;
(2)方程组整理得:,
①×4﹣②×3得:7x=42,即x=6,
把x=6代入①得:y=4,
则方程组的解为.
20.求不等式组的整数解.
解:解不等式①,得:x≤1,
解不等式②,得:x>﹣2,
∴原不等式组的解集为:﹣2<x≤1,
∴原不等式组的整数解为:﹣1,0,1.
21.解:(1)如图所示:△ABC即为所求,
△ABC的面积为:4×52×52×42×3=8;
(2)由(1)可知,三角形A'B'C'可以由三角形ABC向右平移4个单位,然后向下平移3个单位得到,
∴P(a,b)为三角形ABC内的一点,则点P在三角形A'B'C'内的对应点P'的坐标是(a+4,b﹣3).
故答案为:(a+4,b﹣3).
22.解:(1)设篮球单价为每个x元,排球单价为每个y元,
由题意可得,
解方程组得,
答:篮球每个90元,排球每个65元;
(2)若按照①套餐打折购买费用为:2(5×90+5×65)×0.8+4×90+2×65=1730(元),
若参加②满减活动购买费用为:14×90+12×65=2040(元),
又2040>1999,
所以2040﹣200=1840(元).
而1840>1730,所以选择套餐①所花费用比选择套餐②所花费用低.
答:选用套餐①购买更划算.
23.某校开展了一项“最喜爱的社团活动”的调研,随机抽取部分学生进行问卷调查,本次参加调研的学生只选择一项最喜爱的社团活动,以下是根据调研结果绘制的不完整统计图,请根据图中信息解答下列问题.
根据以上信息,解答下列问题:
(1)求本次调查的总人数;
(2)补全条形统计图;
(3)若该校共有学生2000人,根据统计信息,估计该校对“绘画”的选择人数.
解:(1)10÷20%=50(人),
答:本次调查的总人数为50人;
(2)书法人数为:50×40%=20(人),
补全条形统计图如下:
(3)2000600(人),
答:估计该校对“绘画”的选择人数为600人.
24.完成下面的证明:
如图,已知∠1=∠2,∠3=∠4,∠B=∠D.求证:AD∥BC.
证明:∵∠1=∠2,∠3=∠4(已知),
且∠2=∠4( 对顶角相等 ),
∴∠1= ∠3 .
∴AB∥CD( 内错角相等,两直线平行 ).
∴∠B= ∠DCG ( 两直线平行,同位角相等 ).
又∵∠B=∠D,(已知)
∴∠DCG=∠D.
∴AD∥BC( 内错角相等,两直线平行 ).
25.已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,若∠ABC=145°,∠EDC=116°,求∠BCD的度数;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,写出∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线FG交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
解:(1)过点C作CM∥AB,
∴∠BCM=∠ABC=145°,
∵AB∥DE,
∴CM∥DE
∴∠DCM=∠EDC=116°,
∵∠BCM=∠BCD+∠DCM,
∴∠BCD=∠BCM﹣∠DCM=29°;
(2)∠ABC﹣∠F=90°,理由:
过点C作CN∥AB,如图,
∴∠ABC=∠BCN,
∵AB∥DE,
∴CN∥EF,
∴∠F=∠FCN,
∵∠BCN=∠BCF+∠FCN,
∴∠ABC=∠BCF+∠F,
∵CF⊥BC,
∴∠BCF=90°,
∴∠ABC=90°+∠F,
即∠ABC﹣∠F=90°;
(3)延长HG交EF于点Q,过点G作GP∥EF,如图3,
∴∠BGD=∠CGQ,
∵AB∥DE,
∴∠ABH=∠EQG,
∵GP∥EF,
∴∠EQG=∠PGQ,∠EFG=∠PGF,
∴∠PGQ=∠ABH,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF=∠FGQ,
∵∠FGQ=∠PGQ﹣∠PGF,
∴∠FGQ=∠ABH﹣∠EFG,
∵,,
∴,
∵∠ABC﹣∠CFD=90°,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF,
即∠BGD﹣∠CGF=45°.
26.1)证明:过P作PQ∥AB,
∴∠QPA=∠BAP=40°,
∵∠APC=75°,
∴∠CPQ=∠APC﹣∠APQ=35°,
∵∠DCP=35°,
∴∠CPQ=∠DCP,
∴PQ∥CD,
又∵PQ∥AB,
∴AB∥CD;
(2)解:灯A的光线从AM开始顺时针旋转至AN所用时间为180÷3=60秒,灯B的光线从BP开始顺时针旋转至BQ所用时间为180÷2=90秒,
设灯A转动t秒时,两灯的光束互相平行,
当0<t≤60时,设AM′与PQ交于M′,如图,
∵PQ∥MN,
∴∠PM′A=∠MAM′=(3t)°,
∵AM′∥BP′,
∴∠MAM′=∠PBP′=2(t+10)°,
∴3t=2(t+10),
解得t=20;
当60<t≤90﹣10,即60<t≤80时,设AM′与PQ交于M′,如图,
∵PQ∥MN,
∴∠PM′A=∠MAM′=180×2﹣3t=(360﹣3t)°,
∵AM′∥BP′,PQ∥MN,
∴四边形AM′BP′是平行四边形,
∴∠MAM′=∠PBP′=2(t+10)°,
∴360﹣3t=2(t+10),
解得t=68;
综上,当灯A转动20或68秒时,两灯的光束互相平行;
(3)解:∵灯A转动的速度是每秒3度,灯B转动的速度是每秒2度,
∴∠PBC=(2t)°,∠MAC=(3t)°,
∵PQ∥MN,
∴∠PBA=∠MAB=135°(两直线平行,内错角相等),
∴∠BAC=∠MAC﹣∠MAB=(3t﹣135)°,∠ABC=∠PBA﹣∠PBC=(135﹣2t)°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣(3t﹣135)°﹣(135﹣2t)°=(180﹣t)°,
∵∠ACD=135°,
∴∠BCD=∠ACD﹣∠ACB=(t﹣45)°,
又∵∠BAC=(3t﹣135)°=3(t﹣45)°,
∴∠BAC=3∠BCD.
同课章节目录
