【小升初典型奥数】追及问题(含解析)-2024-2025学年六年级下册数学人教版
文档属性
| 名称 | 【小升初典型奥数】追及问题(含解析)-2024-2025学年六年级下册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 00:00:00 | ||
图片预览




文档简介
小升初典型奥数 追及问题
1.甲、乙两车同时从A地向B地开出,甲每小时行38千米,乙每小时行34千米,开出1小时后,甲车因有紧急任务返回A地;到达A地后又立即向B地开出追乙车,当甲车追上乙车时,两车正好都到达B地,求A、B两地的路程.
2.张老师从学校步行去公园,每分钟走60米,走了8分钟后,李老师从学校骑自行车去追张老师,结果在距学校720米的地方追上张老师。李老师骑自行车的速度是多少米/分?
3.李勇、张强两人周末到笔架山锻炼身体,两人同时从山脚开始爬山,到达山顶就立即下山,他们两人下山的速度都是各自上山速度的1.5倍,李勇到达山顶时,张强距山顶还有400米,然后李勇下山,张强爬完400米到山顶也开始下山,李勇回到山脚时,张强刚好返回到半山腰,求从山顶到山脚的距离。
4.和平小学的师生步行去春游.队伍走出10.5千米时,王东骑自行车去追,经过1.5时追上.已知王东骑自行车的速度是师生步行速度的3.5倍.王东和师生每时各行多少千米?
5.一只豹子正在快速追赶前面距离150米的奔跑中的羚羊,已知羚羊每秒跑23米,豹子每秒跑31米。再过20秒,豹子能追上羚羊吗?
6.(行程问题)甲、乙、丙同时从山脚开始爬山,到达山顶后立即下山,不断往返运动。已知山坡长360米,甲、乙、丙的速度比为6:5:4,并且甲、乙、丙的下山速度都是各自上山速度的1.5倍。经过一段时间后,甲到达山顶时,看见乙正在下山,此时乙距离山脚不到180米(乙不在山脚)。求此时丙离山顶的距离。
7.小丁丁和小巧先后沿同一条马路从学校出发去电影院观看电影。小巧先行40米后小丁丁再出发,小巧平均每分钟走72米,小丁丁出发10分钟在途中追上小巧。小丁丁平均每分钟走多少米?
8.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行,甲的速度是每分钟280米,乙的速度是每分钟240米。经过多长时间甲第一次追上乙?
9.一辆货车从甲地开往乙,如果按原速度行驶,将不能准时到达乙地,如果把车速提高,可以比原定时间早1小时到达,如果以原速度行驶120千米后,再将速度提高,则可提前40分钟到达,那么甲、乙两地间的距离是多少千米?
10.一辆卡车从A城驶向B城每小时行60km,开出1.5小时后,一辆轿车从A城驶向B城,每小时行75km,几小时后轿车能追上卡车?
11.甲、乙两人练习跑步,若甲让乙先跑10米,则甲跑5秒可追上乙;若乙比甲先跑2秒,则甲跑4秒能追上乙。问:两人每秒各跑多少米?
12.乙的速度是甲速度的,两人分别由A、B两地同时出发,如果相向而行1小时可以相遇;如果同向而行甲需要多少小时才能追上乙?
13.甲上午6时从A地步行出发,于下午5时到达B地;乙上午10时从A地骑自行车出发,于下午3时到达B地,问:乙在什么时间追上甲?
14.甲乙两人骑自行车,甲的速度是13.5千米/小时,乙的速度是11.8千米/小时,两人从同一地点出发,乙先出发2.5小时后,甲开始追,甲多久能追上乙?
15.开始时竹子高30cm,钟状菌高6cm。如果竹子和钟状菌都在生长旺盛期,竹子每时约增高4厘米,钟状菌每时约增高12厘米。几时后钟状菌的高度能赶上竹子?
16.A、B两地相距120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。
(1)两车分别从A、B两地同时同向而行(甲在乙后),经过多长时间甲车追上乙车?
(2)两车同时从A、B两地相向而行,经过多长时间两车相距10千米?
17.星期六,冬冬从家里出发去少年宫参加以“与光同盟童心同行”为主题活动的志愿者活动。刚走3分钟,爸爸发现冬冬忘带红领巾,于是立即去追。冬冬速度是60米/分,爸爸速度是80米/分,爸爸追上冬冬需要走多少分钟?
18.一位自行车运动员以24千米/时的速度从甲地到乙地,2小时后一辆摩托车以56千米/时的速度也从甲地到乙地,在甲地到乙地中点处追上了自行车运动员。问:甲、乙两地相距多远?
19.猎狗发现前方150米处有一只兔子正在逃跑,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒。在兔子前方520米处是一片灌木丛,猎狗能抓到兔子吗?
20.小红每分钟走70米,爸爸每分钟走100米,他们同时从同一地点背向走3分钟,然后爸爸掉头去追小红。从爸爸开始追小红到追上小红需要多长时间?
21.甲、乙两辆客车在高速公路上,从同一地点出发,同向而行。甲车以每小时80千米的速度行驶了1小时后,乙车出发,以每小时100千米的速度追赶甲车。乙车行多少千米才能追上甲车?
22.甲、乙两车同时由A地到B地,甲车每小时行45千米,乙车每小时行30千米,乙车先出发2小时后甲车才出发,两车同时到达B地.求A,B两地的距离.
23.小李骑自行车从甲地到乙地,出发40分钟后,小王骑电动车从甲地出发,两人同时到达乙地,已知小李骑自行车的速度是15千米/时,小王骑电动车的速度是小李骑自行车的速度的3倍求甲,乙两地的距离.
24.猎狗前面26步远有一只野兔,猎狗追之。兔跑8步的时间狗跑5步,兔跑9步的距离等于狗跑4步的距离。问:兔跑多少步后被猎狗抓获?此时猎狗跑了多少步?
25.小明上学10分钟后,爸爸发现他的数学书没带,就以小明步行6倍的速度骑车去追,追上把书给小明后立即返回,当爸爸回到家时,小明刚好也走到学校,小明从家走到学校一共要多少分钟?
26.早上小明以每分钟50米的速度向学校走去,6分钟后爸爸发现他的语文书没带,于是就以每分钟70米的速度去追小明,几分钟后爸爸才能追上小明?
27.一只兔子在一只猎狗前面80米处,它们同时发现了对方,兔子逃跑,每秒跑6米;猎狗追击,每秒跑8米,正常情况下,经过多长时间猎狗就能追上兔子?
28.有甲、乙两列火车,甲长93m,每秒行驶21m,乙长126m,每秒行驶18m,两车同向而行,开始时甲的车头与乙的车尾相平,过多长时间后甲的车尾与乙的车头相平?
29.快、慢两车分别从甲、乙两地出发,同向而行,慢车在前,快车在后,已知快车比慢车提前出发1小时,快车的速度是96千米/时,慢车的速度是80千米/时.快车出发5小时后追上慢车,甲、乙两地间的距离是多少千米?
30.AB两地相距1800米。甲乙两人同时从AB两地出发,若相向而行12分钟相遇;若同向而行90分钟甲追上乙,把乙需要的资料给他后,用去时1.2倍的速度返回。甲返回到A点时,乙距A点多少米?
31.小俊走路去上学,他的速度为60米/分钟。妈妈在收拾东西的时候,发现小俊没有带数学书,此时小俊已经出发了7分钟。于是妈妈立刻骑自行车从家出发去追小俊,妈妈骑自行车的速度为200米/分钟。问妈妈从家出发算起到追上小俊,一共用了多久?
32.小红和小明沿着400米的环形跑道跑步,小红每秒跑4米,小明每秒跑6米。两人站在起跑线上同向而行,如果小红先跑了10秒钟后,小明才开始跑,小明追上小红需要多少秒?
33.已知一艘船顺水行48千米需4小时,逆水行48千米需6小时。现在轮船从上游A港到下游B港(水速同前面),已知两港间的水路长为72千米,开船时一旅客从宽口扔到水里一块木板,问:船到B港时,木板离B港还有多远?
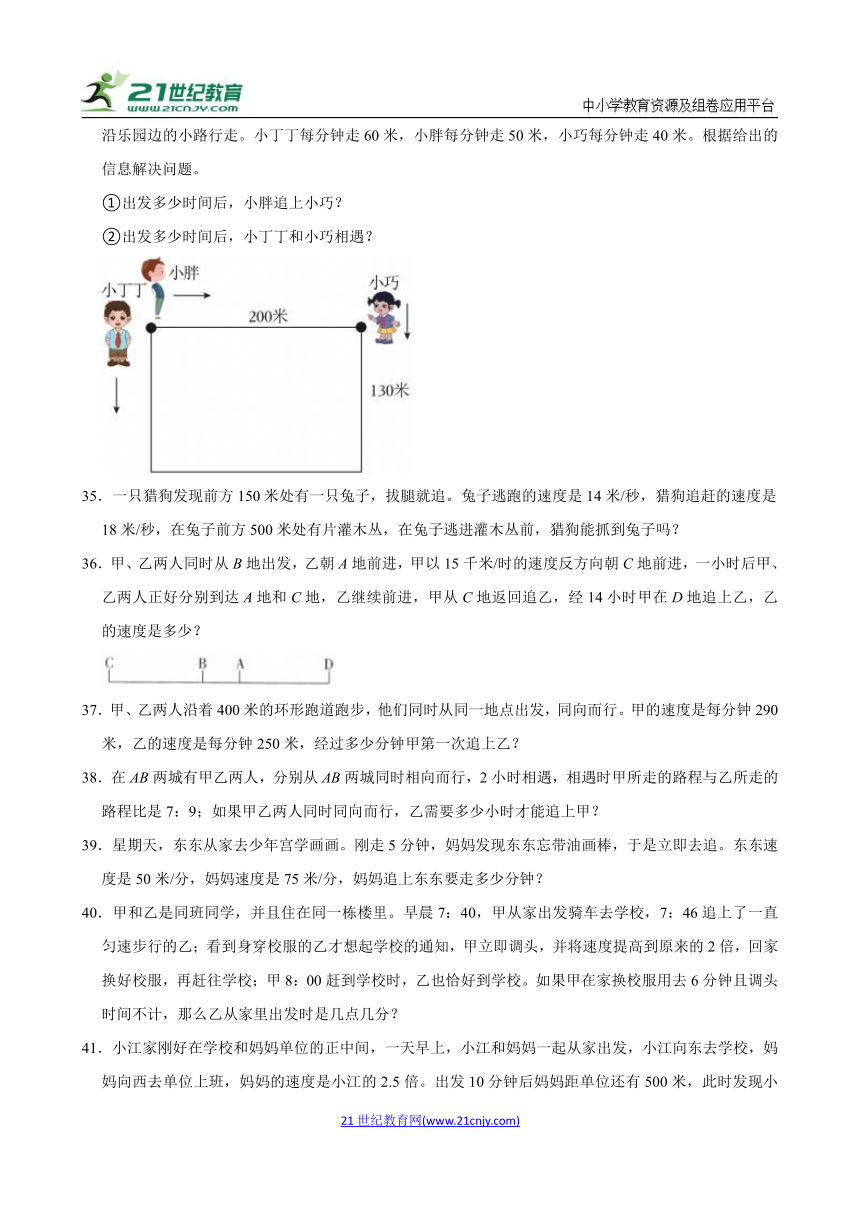
34.如图是一个长方形儿童乐园,长200米。宽130米。小丁丁、小胖、小巧按各自现在的方向同时出发,沿乐园边的小路行走。小丁丁每分钟走60米,小胖每分钟走50米,小巧每分钟走40米。根据给出的信息解决问题。
①出发多少时间后,小胖追上小巧?
②出发多少时间后,小丁丁和小巧相遇?
35.一只猎狗发现前方150米处有一只兔子,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒,在兔子前方500米处有片灌木丛,在兔子逃进灌木丛前,猎狗能抓到兔子吗?
36.甲、乙两人同时从B地出发,乙朝A地前进,甲以15千米/时的速度反方向朝C地前进,一小时后甲、乙两人正好分别到达A地和C地,乙继续前进,甲从C地返回追乙,经14小时甲在D地追上乙,乙的速度是多少?
37.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是每分钟290米,乙的速度是每分钟250米,经过多少分钟甲第一次追上乙?
38.在AB两城有甲乙两人,分别从AB两城同时相向而行,2小时相遇,相遇时甲所走的路程与乙所走的路程比是7:9;如果甲乙两人同时同向而行,乙需要多少小时才能追上甲?
39.星期天,东东从家去少年宫学画画。刚走5分钟,妈妈发现东东忘带油画棒,于是立即去追。东东速度是50米/分,妈妈速度是75米/分,妈妈追上东东要走多少分钟?
40.甲和乙是同班同学,并且住在同一栋楼里。早晨7:40,甲从家出发骑车去学校,7:46追上了一直匀速步行的乙;看到身穿校服的乙才想起学校的通知,甲立即调头,并将速度提高到原来的2倍,回家换好校服,再赶往学校;甲8:00赶到学校时,乙也恰好到学校。如果甲在家换校服用去6分钟且调头时间不计,那么乙从家里出发时是几点几分?
41.小江家刚好在学校和妈妈单位的正中间,一天早上,小江和妈妈一起从家出发,小江向东去学校,妈妈向西去单位上班,妈妈的速度是小江的2.5倍。出发10分钟后妈妈距单位还有500米,此时发现小江的眼镜在包里,妈妈立即掉头加速20%去追小江,在离学校250米处追上小江后,又以原速度返回单位上班,当小江到学校时,妈妈离单位还有多远?
42.甲、乙两人沿着600米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是240米/分。经过多少分钟甲第三次追上乙?
43.甲、乙两人从同一地点出发,同向而行,甲先行2小时后,乙才出发,甲每小时行60千米,乙每小时行80千米,当乙追上甲时,行了多少千米?
44.小明、小红同时从A城沿相反方向出发,两人速度相同。上午9:00,小红迎面与一列长1200米的火车相遇,错开时间为30秒;上午9:30,火车追上小明,并在40秒后超过小明,那么火车每秒行多少米,小明和小红出发时间是几点?
45.在同样的时间里,兔子能跑3步,狗能跑2步,兔子一步跑1米,狗一步跑1.5米,如果狗和兔子在100米的直跑道上赛跑,赛程为一个往返,狗和兔子调头的时间相等,那么谁将获胜?
46.一条环形跑道长600米,甲练习骑自行车,平均每分钟行550米,乙练习长跑平均每分钟跑250米.两人同时从同一地点同向出发,经过多少分钟甲从后面追上乙?
47.在高速公路上一辆3m长的小汽车以110km/h的速度超过一辆17m长以100km/h的速度行驶的卡车。求小汽车从追及到超越卡车的整个超车过程用了多少秒?
48.两辆汽车从同一起点出发,沿同一路线同向而行,第一辆汽车每小时行驶80千米,出发1小时后第二辆汽车出发。第二辆汽车每小时行驶120千米,几小时能追上第一辆汽车?
49.弟弟和哥哥跑步,如果弟弟先跑20米,哥哥跑10秒可以追上,如果弟弟先跑4秒,那么哥哥8秒可以追上.求弟弟和哥哥的速度.
50.A、B两城相距650km,有甲、乙两车都从A城开往B城。已知甲车的速度为72千米/时,甲、乙两车的速度比是3:4,甲车比乙车早出发一小时,乙车能在2小时内追上甲车吗?假如不能,需要多少小时才能追上呢?
51.甲、乙两人沿着300米的环形跑道跑步,他们同时从一地出发、同向而行,甲每分钟跑260米,乙每分钟跑220米,乙刚出发就发现鞋带松了,他系鞋带用了0.5分钟。甲从出发到第一次追上乙经过多少分钟?
52.A、B两地相距210千米,甲、乙两车分别从A、B两地同时开出,同向而行。甲车每小时行105千米,乙车每小时行80千米,多少小时后甲车能追上乙车?
53.A、B两地相距250千米,甲、乙两车同时从A、B两地相向而行,1小时后相遇。甲车每小时行驶的路程是乙车的1.5倍,如果甲、乙两车同时分别从A、B两地同向行驶(乙在前,甲在后),经过多少小时甲车能追上乙车?
54.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是230米/分。经过多少分钟甲第一次追上乙?
55.小明8:00从A地骑车出发,11:00到达B地,小华开车从A地出发,速度是小明的3倍;追上小明后,速度增加为小明的4倍。如果小华9:30到达B地,那么小华是在什么时候出发的?
56.一天早晨,莉莉从家出发前往学校,每分钟走60米,莉莉走了10分钟后,爸爸发现她没有带数学书,便立刻骑自行车从家出发去追莉莉,在离家900米处追上了她。爸爸骑自行车每分钟行多少米?
57.甲、乙两人同时从A地出发去B地,5分钟后,甲返回A地去取东西,没有停留,继续步行去B地,如果从两人同时出发开始计时,那么35分钟后两人同时到达,已知甲每分钟所走路程比乙每分钟所走路程的2倍少30米,求A、B两地的距离为多少米?
58.一列客车每分钟行2000m,一列货车每分钟行1500m,货车比客车的车身长135m。两车在平行的轨道上同向行驶,当客车从后面超过货车时,两车交叉的时间是45秒。这列货车和这列客车的车身各长多少米?
59.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是290米/分,乙的速度是250米/分。经过多少分钟甲第二次追上乙?(提示:可以画图思考)
60.“大三峡 大巴山”2023重庆万州环湖马拉松比赛于12月10日举行。本次比赛吸引了八个国家近万名运动员参赛,比赛项目包括全程马拉松(42.195千米)、半程马拉松(21.0975千米)和迷你马拉松(约4.5千米)。规划参赛总人数1万人,其中半程马拉松3000人,迷你马拉松人数是全程马拉松人数的2.5倍。王叔叔和张叔叔都报名参加了全程马拉松项目,8:30他们从起点同时出发,已知张叔叔的平均速度为200米/分,经过30分钟后,王叔叔落后张叔叔600米。这时,王叔叔奋起直追,将平均速度提高到250米/分,终于追上了张叔叔,取得了较好的比赛成绩。
(1)张叔叔跑完全程大约要用多少分钟?(得数保留整数)
(2)规划参加全程马拉松和迷你马拉松各多少人?
(3)前30分钟,王叔叔的平均速度是每分钟多少米?
(4)王叔叔用了多少分钟追上了张叔叔?
追及问题
参考答案与试题解析
1.甲、乙两车同时从A地向B地开出,甲每小时行38千米,乙每小时行34千米,开出1小时后,甲车因有紧急任务返回A地;到达A地后又立即向B地开出追乙车,当甲车追上乙车时,两车正好都到达B地,求A、B两地的路程.
【答案】见试题解答内容
【分析】根据题意可知:开出1小时后,甲返回A地,然后继续追乙;乙一直处于行驶状态,所以相当于乙比甲先行1×2=2(小时),而甲追及乙的过程,路程差就是乙2小时行的路程,利用追及问题个数:追及时间=路程差除以速度差.然后这段时间甲所行的路程,就是A、B两地的路程.
【解答】解:(1×2×34)÷(38﹣34)×38
=68÷4×38
=17×38
=646(千米)
答:A、B两地的路程是646千米.
【点评】本题主要考查追及问题,关键利用路程、速度和时间的关系做题.
2.张老师从学校步行去公园,每分钟走60米,走了8分钟后,李老师从学校骑自行车去追张老师,结果在距学校720米的地方追上张老师。李老师骑自行车的速度是多少米/分?
【答案】180米/分。
【分析】根据题意可知,两位老师都走了720米,张老师每分钟走60米,720除以60等于张老师行走的时间,由于张老师走了8分钟后李老师才去追,所以李老师比张老师少用了8分钟,张老师行走的时间减8等于李老师骑行的时间,再用骑行路程720米除以李老师骑行的时间即等于李老师骑行的速度,据此即可解答。
【解答】解:720÷(720÷60﹣8)
=720÷(12﹣8)
=720÷4
=180(米/分)
答:李老师骑自行车的速度是180米/分。
【点评】此题抓住追及问题中速度不同,所以行驶的时间不同,但是行驶的路程相同。
3.李勇、张强两人周末到笔架山锻炼身体,两人同时从山脚开始爬山,到达山顶就立即下山,他们两人下山的速度都是各自上山速度的1.5倍,李勇到达山顶时,张强距山顶还有400米,然后李勇下山,张强爬完400米到山顶也开始下山,李勇回到山脚时,张强刚好返回到半山腰,求从山顶到山脚的距离。
【答案】2000米。
【分析】通过分析两人在不同阶段的路程关系,利用速度变化与路程的联系来求解从山顶到山脚的距离。
【解答】解:设从山顶到山脚的距离是s米,李勇上山速度为v1,张强上山速度为v2。
李勇到达山顶时,张强距山顶还有400米,此时两人爬山时间相同,根据时间=路程÷速度可得:
即v2
李勇下山速度是1.5v1,张强下山速度是1.5v2。李勇从山顶回到山脚的路程是s,所用时间是:
张强从距离山顶400米,然后到山顶,再从山顶走到半山腰,所用时间是:
因为两人这一阶段时间也相同,所以:
把v2代入可得:
等式两边同时乘1.5v1可得:s
等式两边同时乘2(s﹣400)可得:2s(s﹣400)=1200s+s2
因为s>0
所以2(s﹣400)=1200+s
即2s﹣800=1200+s
所以s=2000
即从山顶到山脚的距离是2000米。
答:从山顶到山脚的距离是2000米。
【点评】本题考查了复杂行程问题的应用,解题关键是找出题干中的等量关系。
4.和平小学的师生步行去春游.队伍走出10.5千米时,王东骑自行车去追,经过1.5时追上.已知王东骑自行车的速度是师生步行速度的3.5倍.王东和师生每时各行多少千米?
【答案】见试题解答内容
【分析】本题为追及问题公式:根据速度差、距离差和追及时间三者之间的关系,利用公式:速度差=距离差÷追及时间根据路程差和追及时间,先求出速度差,然后根据速度的倍数关系,求出一份速度,及师生的速度.
【解答】解:10.5÷1.5=7(千米/小时).
师生:7÷(3.5﹣1)=2.8(千米/小时).
王东:2.8×3.5=9.8(千米/小时)
答:王东每小时行9.8千米,师生每小时行2.8千米.
【点评】本题关键是利用追击问题公式,求速度差.
5.一只豹子正在快速追赶前面距离150米的奔跑中的羚羊,已知羚羊每秒跑23米,豹子每秒跑31米。再过20秒,豹子能追上羚羊吗?
【答案】能。
【分析】根据“路程=速度差×追及时间”,求出豹子20秒钟的追及路程后和150米比较大小,大于等于150,能追上,反之追不上。
【解答】解:(31﹣23)×20
=8×20
=160(米)
160米>150米,即能追上。
答:豹子能追上羚羊。
【点评】本题考查了追及问题的应用。
6.(行程问题)甲、乙、丙同时从山脚开始爬山,到达山顶后立即下山,不断往返运动。已知山坡长360米,甲、乙、丙的速度比为6:5:4,并且甲、乙、丙的下山速度都是各自上山速度的1.5倍。经过一段时间后,甲到达山顶时,看见乙正在下山,此时乙距离山脚不到180米(乙不在山脚)。求此时丙离山顶的距离。
【答案】40米。
【分析】先用假设法表示出甲、乙、丙的上山速度和下山速度,在进行分类讨论,选出符合题意得情况进行解答。
【解答】解:设甲、乙、丙上坡速度分别为6x、5x、4x,则下坡速度分别为9x、7.5x、6x。
根据题意可知,甲达到山顶停下时,它们所用的时间相等。
假设甲两上一下,则乙应该是两上一下不合题意。
假设甲三上两下,则乙应该是两下两上,第三次正在上,不合题意。
假设甲四上三下,所用时间应该为:
43
此时乙可能三上二下,第三下中,则下时的时间为:
33
此时离山顶距离为:
7.5x=360(米)和题意不符
假设甲五上四下,所用时间为:
54
此时乙应该是四上三下,第四下中,则四下时间为:
43
此时距离山顶距离:
7.5x=210(米)符合题意,也就是说甲经历了五上四下,乙经历了四上,第四下中。
此时丙应该是三上三下,第四上中,第四上的时间为:
33
此时丙距离山顶的距离为:
4x=40(米)
答:此时丙距离山顶的距离为40米。
【点评】甲达到山顶停下时,它们所用的时间相等时是关键。
7.小丁丁和小巧先后沿同一条马路从学校出发去电影院观看电影。小巧先行40米后小丁丁再出发,小巧平均每分钟走72米,小丁丁出发10分钟在途中追上小巧。小丁丁平均每分钟走多少米?
【答案】76米。
【分析】有题意可知,小丁丁10分钟走的路程=小巧先走的40米+小巧10分钟走的路程。据此列式计算出小丁丁10分钟走的路程,然后再除以10即可解答。
【解答】解:小丁丁10分钟走:
40+72×10
=40+720
=760(米)
760÷10=76(米/分)
答:小丁丁平均每分钟走76米。
【点评】解答本题的关键是先求出小丁丁10分钟走的路程。
8.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行,甲的速度是每分钟280米,乙的速度是每分钟240米。经过多长时间甲第一次追上乙?
【答案】10分钟。
【分析】当甲第一次追上乙时,甲比乙多行了一圈跑道的长度,所以甲第一次追上乙需要的时间=环形跑道的长度÷(甲的速度﹣乙的速度),据此列式解答即可。
【解答】解:400÷(280﹣240)
=400÷40
=10(分钟)
答:经过10分钟甲第一次追上乙。
【点评】解答本题的关键是理解“当甲第一次追上乙时,甲比乙多行了一圈跑道的长度”,再根据“追及时间=路程差÷速度差”,列式计算。
9.一辆货车从甲地开往乙,如果按原速度行驶,将不能准时到达乙地,如果把车速提高,可以比原定时间早1小时到达,如果以原速度行驶120千米后,再将速度提高,则可提前40分钟到达,那么甲、乙两地间的距离是多少千米?
【答案】270千米。
【分析】把原来车速看成单位“1”,则车速提高后为1×(1),原来的速度相当于它的;提高为1×(1),此时速度相当于最后速度的;那么,后来用的时间为(1)(小时);则原来的速度为120÷(6)=45(千米/时)。则甲、乙两地间的距离是(45×6)千米,据此计算即可。
【解答】解:40(小时)
把原来车速看成单位“1”,则车速提高后为的速度为:1×(1)
即原来速度相当于现在的:1
所以原来的时间为:1÷(1)=6(小时)
同理可知后来的速度相当于最后速度的1÷(1)
后来用的时间为(1)(小时)
原来的速度即为120÷(6)=45(千米/时)
45×6=270(千米)
答:甲、乙两地间的距离是270千米。
【点评】解决此题的关键是求出原来的时间与速度,应认真分析,一步步推算,再求出时间与速度后,运用关系式“速度×时间=路程”解决问题。
10.一辆卡车从A城驶向B城每小时行60km,开出1.5小时后,一辆轿车从A城驶向B城,每小时行75km,几小时后轿车能追上卡车?
【答案】见试题解答内容
【分析】根据追及问题,追及时间=追及的距离÷速度差,先求出这辆卡车1.5小时小时多少千米,再求出轿车与卡车的速度差,进而求出轿车追上卡车的时间.
【解答】解:60×1.5÷(75﹣60)
=90÷15
=6(小时)
答:6小时后轿车能追上卡车.
【点评】此题属于追及问题,利用基本数量关系:追及时间=追及的距离÷速度差,解决问题.
11.甲、乙两人练习跑步,若甲让乙先跑10米,则甲跑5秒可追上乙;若乙比甲先跑2秒,则甲跑4秒能追上乙。问:两人每秒各跑多少米?
【答案】见试题解答内容
【分析】根据题意,由如果甲让乙先跑10米,那么,甲跑5秒就可以追上乙,根据“路程÷时间”=速度,可以求出追及速度(即甲、乙的速度差);即10÷5=2(米/秒),如果让乙先跑2秒,那么甲跑4秒可追上乙,用追及速度乘4就可以求出甲追了多少米,从而求出乙的速度,进而再求出甲的速度。
【解答】解:甲、乙的速度差:10÷5=2(米/秒)
乙先跑2秒,甲需要追4秒,也就是追了2×4=8(米)
则乙速度为:8÷2=4(米/秒)
甲速度为:4+2=6(米/秒)
答:甲每秒跑6米,乙每秒跑4米。
【点评】本题主要考查的是行程问题,属于同一地点不同时出发的追及问题的应用题。此题解答的关键是先求出追及速度,再根据路程、速度、时间三者之间的关系列式解答即可。
12.乙的速度是甲速度的,两人分别由A、B两地同时出发,如果相向而行1小时可以相遇;如果同向而行甲需要多少小时才能追上乙?
【答案】甲需要5小时才能追上乙。
【分析】乙的速度是甲速度的,那么乙的速度:甲的速度=2:3.设乙的速度为每小时行2千米,则甲的速度为每小时行3千米,求出A、B两地之间的距离,甲要追上乙,就要比乙多行A、B之间的距离这段路程,用这个路程除以两人的速度差就是它们行走的时间。
【解答】解:设乙的速度为每小时行2千米,甲的速度为每小时行3千米,
两地相距:(2+3)×1
=5×1
=5(千米)
甲追上乙需:
5÷(3﹣2)
=5÷12
=5(小时)
答:甲需要5小时才能追上乙。
【点评】本题考查了相遇问题的数量关系以及追及问题的数量关系,速度和×相遇时间=总路程,路程差÷速度差=追及时间。
13.甲上午6时从A地步行出发,于下午5时到达B地;乙上午10时从A地骑自行车出发,于下午3时到达B地,问:乙在什么时间追上甲?
【答案】下午1时20分。
【分析】把AB两地之间的距离看作单位“1”,上午6时到下午5时经过了17﹣6=11小时,则速度是;乙上午10时到下午3时经过了15﹣10=5小时,则速度是,速度差是(),追及距离是(10﹣6);然后用追及距离除以速度差求出追及时间,再进一步解答即可。
【解答】解:17﹣6=11(小时)
15﹣10=5(小时)
(10﹣6)÷()
=3(小时)
3小时=3小时20分钟
上午10时+3小时20分钟=下午1时20分
答:乙在下午1时20分追上甲。
【点评】本题考查了追及问题与工程问题的综合应用,关键是求出追及距离和速度差。
14.甲乙两人骑自行车,甲的速度是13.5千米/小时,乙的速度是11.8千米/小时,两人从同一地点出发,乙先出发2.5小时后,甲开始追,甲多久能追上乙?
【答案】小时。
【分析】依据题意可设甲x小时追上乙,利用甲的走的路=乙先走的路+乙后走的路,列方程计算即可。
【解答】解:设甲x小时追上乙,由题意得:
13.5x=2.5×11.8+11.8x
1.7x=29.5
x
答:甲小时能追上乙。
【点评】本题考查的是追及问题的应用。
15.开始时竹子高30cm,钟状菌高6cm。如果竹子和钟状菌都在生长旺盛期,竹子每时约增高4厘米,钟状菌每时约增高12厘米。几时后钟状菌的高度能赶上竹子?
【答案】3时。
【分析】根据题意,开始时竹子比钟状菌高30﹣6=24(厘米);每时钟状菌比竹子多长高12﹣4=8(厘米),然后再用24除以8即可。
【解答】解:(30﹣6)÷(12﹣4)
=24÷8
=3(时)
答:3时后钟状菌的高度可赶上竹子。
【点评】解答此题的关键是确定每时钟状菌比竹子多长多少和现在竹子比钟状菌高的厘米数。
16.A、B两地相距120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。
(1)两车分别从A、B两地同时同向而行(甲在乙后),经过多长时间甲车追上乙车?
(2)两车同时从A、B两地相向而行,经过多长时间两车相距10千米?
【答案】(1)12小时,(2)1.1小时,1.3小时。
【分析】(1)相距路程÷速度差=追及时间,据此解答。
(2)两车所行路程÷速度和=所用时间,据此解答。
【解答】解:(1)120÷(55﹣45)
=120÷10
=12(小时)
答:经过12小时甲车追上乙车。
(2)第一种情况,甲、乙两车在未相遇时相距10千米,
(120﹣10)÷(55+45)
=110÷100
=1.1(小时)
第二种情况:甲、乙两车相遇后又相距10千米,
(120+10)÷(55+45)
=130÷100
=1.3(小时)
答:两车同时从A、B两地相向而行,经过1.1小时或1.3小时两车相距10千米。
【点评】明确追及问题及相遇问题数量间的关系是解决本题的关键。
17.星期六,冬冬从家里出发去少年宫参加以“与光同盟童心同行”为主题活动的志愿者活动。刚走3分钟,爸爸发现冬冬忘带红领巾,于是立即去追。冬冬速度是60米/分,爸爸速度是80米/分,爸爸追上冬冬需要走多少分钟?
【答案】9分钟。
【分析】依据题意可知,爸爸追上冬冬要比冬冬多走(60×3)米,追上的时间=多走的路程÷两人的速度差,由此列式计算。
【解答】解:60×3÷(80﹣60)
=60×3÷20
=9(分)
答:爸爸追上冬冬需要走9分钟。
【点评】本题考查的是追及问题的应用。
18.一位自行车运动员以24千米/时的速度从甲地到乙地,2小时后一辆摩托车以56千米/时的速度也从甲地到乙地,在甲地到乙地中点处追上了自行车运动员。问:甲、乙两地相距多远?
【答案】168千米。
【分析】根据题意,两车路程差为24×2=48(千米),两车速度差每小时为56﹣24=32(千米),根据两车速度差×追及时间=两车路程差,求出追及时间,进而求出甲乙两地的路程,解决问题。
【解答】解:24×2÷(56﹣24)
=48÷32
=1.5(小时)
56×1.5×2
=84×2
=168(千米)
答:甲、乙两地相距168千米。
【点评】根据关系式:路程差÷速度差=追及时间,求出摩托车追上自行车的时间,是解答此题的关键。
19.猎狗发现前方150米处有一只兔子正在逃跑,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒。在兔子前方520米处是一片灌木丛,猎狗能抓到兔子吗?
【答案】不能。
【分析】猎狗追上兔子需要的时间=猎狗与兔子之间相隔的距离÷猎狗与兔子的速度差,再用兔子的速度乘时间,得出这段时间兔子能跑多少米,最后比较即可解答此题。
【解答】解:18﹣14=4(米/秒)
150÷4=37.5(秒)
14×37.5=525(米)
525>520,即猎狗不能抓到兔子。
答:猎狗不能抓到兔子。
【点评】本题主要考查追及问题。
20.小红每分钟走70米,爸爸每分钟走100米,他们同时从同一地点背向走3分钟,然后爸爸掉头去追小红。从爸爸开始追小红到追上小红需要多长时间?
【答案】17分钟。
【分析】根据路程=速度×时间,先求出小红和爸爸各自从同一地点背向走3分钟的路程,再把两人3分钟各自走的路程相加,求出爸爸追小红前两人相差的路程,也就是爸爸要追小红的路程,再根据追及时间=路程差÷速度差,代入数据计算,即可求出从爸爸开始追小红到追上小红需要的时间,据此解答。
【解答】解:(70+100)×3÷(100﹣70)
=170×3÷30
=510÷30
=17(分钟)
答:从爸爸开始追小红到追上小红需要17分钟。
【点评】本题考查了行程中的追及问题,熟练掌握路程、速度、时间三者之间的关系是解题的关键。
21.甲、乙两辆客车在高速公路上,从同一地点出发,同向而行。甲车以每小时80千米的速度行驶了1小时后,乙车出发,以每小时100千米的速度追赶甲车。乙车行多少千米才能追上甲车?
【答案】400千米。
【分析】用要追的距离除以速度差,求出追上用的时间,再用这个时间乘乙的速度即可。
【解答】解:80÷(100﹣80)×100
=80÷20×100
=4×100
=400(千米)
答:乙车行400千米才能追上。
【点评】本题考查的是追及问题。解答关键是要追的距离除以速度差,求出追上用的时间。
22.甲、乙两车同时由A地到B地,甲车每小时行45千米,乙车每小时行30千米,乙车先出发2小时后甲车才出发,两车同时到达B地.求A,B两地的距离.
【答案】见试题解答内容
【分析】乙每小时行30千米 乙车先出发2小时 那就是多行60千米,两车同时到达B地,那么就是说在甲追上乙的那刻二者都到终点,甲每小时可以追到15千米,60千米只要4小时就可以追完;根据速度×时间=路程,那么总路程就是45×4=180千米,由此解答.
【解答】解:45×[30×2÷(45﹣30)]
=45×[60÷15]
=45×4
=180(千米)
答:AB两地相距180千米.
【点评】此题属于追及问题,根据追击的路程÷速度差=追击的时间,再根据路程、速度、时间三者之间的关系列式解答即可.
23.小李骑自行车从甲地到乙地,出发40分钟后,小王骑电动车从甲地出发,两人同时到达乙地,已知小李骑自行车的速度是15千米/时,小王骑电动车的速度是小李骑自行车的速度的3倍求甲,乙两地的距离.
【答案】见试题解答内容
【分析】可设小李骑自行车从甲地到乙地的时间为t小时,则小王骑电动车从甲地到乙地的时间为(t)小时,根据等量关系:从甲地到乙地的路程是一定的,路程方程求解即可.
【解答】解:设小李骑自行车从甲地到乙地的时间为t小时,则小王骑电动车从甲地到乙地的时间为(t)小时,依题意有
15×3(t)﹣15t=0
45(t)﹣15t=0
45t﹣30﹣15t=0
30t﹣30=0
30t=30
t=1
15t=15×1=15(千米)
答:甲,乙两地的距离是15千米.
【点评】考查了追及问题,解题的关键是在互相关联、互相对应的距离差、速度差、追及时间三者之中,找出两者,然后运用公式求出第三者来达到解题目的.
24.猎狗前面26步远有一只野兔,猎狗追之。兔跑8步的时间狗跑5步,兔跑9步的距离等于狗跑4步的距离。问:兔跑多少步后被猎狗抓获?此时猎狗跑了多少步?
【答案】144步,90步。
【分析】依据题意可知,先计算出兔跑(8×9)步的时间狗跑多少步,兔跑(8×9)步的距离等于狗跑多少步的距离,由此计算狗比兔多跑多少步,然后计算兔追上狗跑26步跑多少步,再计算狗跑多少步。
【解答】解:8和9的最小公倍数是:8×9=72
兔跑72步的时间狗跑:5×9=45(步),兔跑72步的距离狗跑:4×8=32(步)
45﹣32=13(步)
72×(26÷13)
=72×2
=144(步)
5×(144÷8)
=5×18
=90(步)
答:兔跑144步后被猎狗抓获,此时猎狗跑了90步。
【点评】本题考查的是追及问题的应用。
25.小明上学10分钟后,爸爸发现他的数学书没带,就以小明步行6倍的速度骑车去追,追上把书给小明后立即返回,当爸爸回到家时,小明刚好也走到学校,小明从家走到学校一共要多少分钟?
【答案】14分钟。
【分析】若以小明爸爸返回时开始算起,小明距离学校为1份,则爸爸回家走了6份,小明家到学校共7份。小明走10分钟共走了5份,每份用时10÷5=2(分钟),所以小明从家到学校用时应该是2×7=14(分钟)。
【解答】解:若以小明爸爸返回时开始算起,小明距离学校为1份,则爸爸回家走了6份,小明家到学校共7份。
10÷5=2(分钟)
2×7=14(分钟)
答:小明从家到学校一共要14分钟。
【点评】要求小明从家走到学校一共要多少分钟,只需要求出小明10分钟走的路程是总路程的几份。
26.早上小明以每分钟50米的速度向学校走去,6分钟后爸爸发现他的语文书没带,于是就以每分钟70米的速度去追小明,几分钟后爸爸才能追上小明?
【答案】15分钟。
【分析】先用50乘6,求出小明6分钟行走的路程;再根据“追及距离÷速度差=追及时间”,用小明6分钟行走的路程除以(70﹣50),即可求出几分钟后爸爸才能追上小明。
【解答】解:50×6÷(70﹣50)
=300÷20
=15(分钟)
答:15分钟后爸爸才能追上小明。
【点评】解答本题需熟练掌握追及距离、速度差与追及时间之间的关系。
27.一只兔子在一只猎狗前面80米处,它们同时发现了对方,兔子逃跑,每秒跑6米;猎狗追击,每秒跑8米,正常情况下,经过多长时间猎狗就能追上兔子?
【答案】40秒。
【分析】根据追及时间=距离差÷速度差,代入数值进行计算即可。
【解答】解:80÷(8+6)
=80÷2
=40(秒)
答:经过40秒猎狗就能追上兔子。
【点评】本题考查追及问题的计算及应用。理解题意,找出数量关系,列式计算即可。
28.有甲、乙两列火车,甲长93m,每秒行驶21m,乙长126m,每秒行驶18m,两车同向而行,开始时甲的车头与乙的车尾相平,过多长时间后甲的车尾与乙的车头相平?
【答案】73秒。
【分析】开始时甲的车头与乙的车尾相平,后来甲的车尾与乙的车头相平,即追及路程为甲、乙车长之和。根据“追及时间=追及路程÷速度差”即可解答。
【解答】解:(93+126)÷(21﹣18)
=219÷3
=73(秒)
答:过73秒后甲的车尾与乙的车头相平。
【点评】本题考查了追及问题的应用,熟练掌握路程、速度、时间三者之间的关系是解题的关键。
29.快、慢两车分别从甲、乙两地出发,同向而行,慢车在前,快车在后,已知快车比慢车提前出发1小时,快车的速度是96千米/时,慢车的速度是80千米/时.快车出发5小时后追上慢车,甲、乙两地间的距离是多少千米?
【答案】见试题解答内容
【分析】根据追及问题公式:距离差=速度差×追及时间 其中速度差=快速﹣慢速,题中快车比慢车提前出发1小时,快车的速度是96千米/时,所以甲、乙两地的距离是快车1小时所行的路程加上慢车起步出发后到快车追上慢车时的距离差.
【解答】解:(96﹣80)×(5﹣1)+96×1
=16×4+96
=64+96
=160(千米)
答:甲、乙两地间的距离是160千米.
【点评】此题既需要根据关系式而且还要更加深刻的理解题意.
30.AB两地相距1800米。甲乙两人同时从AB两地出发,若相向而行12分钟相遇;若同向而行90分钟甲追上乙,把乙需要的资料给他后,用去时1.2倍的速度返回。甲返回到A点时,乙距A点多少米?
【答案】12525米。
【分析】用AB两地相距的距离1800米除以相遇时间就是甲、乙的速度和,用1800米除以90分钟就是甲、乙的速度差,进一步求出甲、乙的速度,再用甲的速度乘90分钟求出甲追上乙时距A地的距离,再根据路程÷速度=时间,求出甲返回A地所用的时间,则可求出乙一共行走的时间,再乘乙的速度即可。
【解答】解:1800÷12=150(米/分钟)
1800÷90=20(米/分钟)
(150+20)÷2
=170÷2
=85(米/分钟)
(150﹣20)÷2
=130÷2
=65(米/分钟)
90×85=7650(米)
7650÷(85×1.2)
=7650÷102
=75(分钟)
65×(90+75)+1800
=65×165+1800
=10725+1800
=12525(米)
答:甲返回到A点时,乙距A点12525米。
【点评】明确路程÷相遇时间=速度和,追及路程÷追及时间=追及速度,以及路程、速度、时间三者的关系是解题的关键。
31.小俊走路去上学,他的速度为60米/分钟。妈妈在收拾东西的时候,发现小俊没有带数学书,此时小俊已经出发了7分钟。于是妈妈立刻骑自行车从家出发去追小俊,妈妈骑自行车的速度为200米/分钟。问妈妈从家出发算起到追上小俊,一共用了多久?
【答案】3分钟。
【分析】由题意可知,妈妈和小俊的路程差为60×7=420(米),即追及路程为420米,根据追及问题中“追及路程÷速度差=追及时间”,代入数据计算即可。
【解答】解:60×7=420(米)
420÷(200﹣60)
=420÷140
=3(分钟)
答:问妈妈从家出发算起到追上小俊,一共用了3分钟。
【点评】此题属于简单的追及应用题,此类题的解答方法是根据“追及路程÷速度差=追及时间”。
32.小红和小明沿着400米的环形跑道跑步,小红每秒跑4米,小明每秒跑6米。两人站在起跑线上同向而行,如果小红先跑了10秒钟后,小明才开始跑,小明追上小红需要多少秒?
【答案】需要20秒。
【分析】小红先跑10秒钟,则两人之间的距离就是4×10=40米,先求出两人的速度差,再用两人之间的距离除以两人的速度差即可解答。
【解答】解:4×10÷(6﹣4)
=40÷2
=20(秒)
答:小明追上小红需要20秒。
【点评】此题运用了关系式:路程差÷速度差=追及时间。
33.已知一艘船顺水行48千米需4小时,逆水行48千米需6小时。现在轮船从上游A港到下游B港(水速同前面),已知两港间的水路长为72千米,开船时一旅客从宽口扔到水里一块木板,问:船到B港时,木板离B港还有多远?
【答案】60千米。
【分析】先算出顺水行的速度和逆水行的速度,然后根据水速=(顺水行速度﹣逆水行速度)÷2来算出水速;根据顺水行时间=路程÷顺水行速度,可以算出船从A港到B港所用的时间;因为木板在水里的速度就是水速,所以用水速乘船从A港到B港所用的时间,可以算出船到B港时,木板行驶的路程;在用总路程减去木板行驶的路程就可以得到木板离B港还有多远。
【解答】解:顺水行速度为:48÷4=12(千米)
逆水行速度为:48÷6=8(千米)
水的速度为:(12﹣8)÷2=2(千米)
从A到B所用时间为:72÷12=6(小时)
6小时木板的路程为:6×2=12(千米)
72﹣12=60(千米)
答:船到B港时,木板离B港还有60千米。
【点评】此题考查的是流水行船问题,需要学生理清题意,并能灵活的运用路程=速度×时间,水速=(顺水行速度﹣逆水行速度)÷2来解题。
34.如图是一个长方形儿童乐园,长200米。宽130米。小丁丁、小胖、小巧按各自现在的方向同时出发,沿乐园边的小路行走。小丁丁每分钟走60米,小胖每分钟走50米,小巧每分钟走40米。根据给出的信息解决问题。
①出发多少时间后,小胖追上小巧?
②出发多少时间后,小丁丁和小巧相遇?
【答案】①20分钟;②4.6分钟。
【分析】①根据图示可知,小胖和小巧的路程差是200米,即追及路程是200米,根据“追及时间=路程差÷速度差”即可求解;
②根据“相遇时间=路程÷速度和”即可求解。
【解答】解:①200÷(50﹣40)
=200÷10
=20(分钟)
答:出发20分钟后,小胖追上小巧。
②(200+130×2)÷(60+40)
=460÷100
=4.6(分钟)
答:出发4.6分钟后,小丁丁和小巧相遇。
【点评】本题考查了行程问题的应用,熟练掌握路程、速度和时间三者的关系是解题的关键。
35.一只猎狗发现前方150米处有一只兔子,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒,在兔子前方500米处有片灌木丛,在兔子逃进灌木丛前,猎狗能抓到兔子吗?
【答案】不能。
【分析】先根据追及距离÷速度差=追及时间求出猎狗追上兔子需要的时间,再用兔子的速度乘这个时间,看是否大于500米。
【解答】解:150÷(18﹣14)
=150÷4
=37.5(秒)
14×37.5=525(米)
525米>500米
答:在兔子逃进灌木丛前,猎狗不能抓到兔子。
【点评】本题考查了追及问题,需熟练掌握追及距离、速度差和追及时间之间的关系。
36.甲、乙两人同时从B地出发,乙朝A地前进,甲以15千米/时的速度反方向朝C地前进,一小时后甲、乙两人正好分别到达A地和C地,乙继续前进,甲从C地返回追乙,经14小时甲在D地追上乙,乙的速度是多少?
【答案】13。
【分析】本题可列方程求解,设乙每小时行x千米,乙行AB的路程用了1小时,所以AB的路程为x千米,则追及路程为(x+15)千米,速度差为(15﹣x)千米/时,因为经14小时甲在D地追上乙,所以CD的路程为(15﹣x)×14,根据追及路程等于CD间的路程列方程解答即可。
【解答】解:设乙每小时走x千米,则甲、乙速度差为(15﹣x)千米。
x+15=(15﹣x)×14
x+15=210﹣14x
15x=195
x=13
答:乙的速度是13千米/时。
【点评】本题考查的是追及问题,可列方程解答,关键是找到等量关系。
37.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是每分钟290米,乙的速度是每分钟250米,经过多少分钟甲第一次追上乙?
【答案】10分钟。
【分析】当甲第一次追上乙时,甲比乙多行了一圈跑道的长度,再根据“追及时间=路程差÷速度差”,列式计算即可解答。
【解答】解:400÷(290﹣250)
=400÷40
=10(分钟)
答:经过10分钟甲第一次追上乙。
【点评】本题解题关键是理解“当甲第一次追上乙时,甲比乙多行了一圈跑道的长度”,再根据追及时间=路程差÷速度差,列式计算。
38.在AB两城有甲乙两人,分别从AB两城同时相向而行,2小时相遇,相遇时甲所走的路程与乙所走的路程比是7:9;如果甲乙两人同时同向而行,乙需要多少小时才能追上甲?
【答案】见试题解答内容
【分析】两人1小时可以走全程的,根据速度比是7:9,可以求出乙每小时可以比甲多走全程的的.
【解答】解:
116(小时)
答:乙需要16小时才能追上甲.
【点评】此题的关键求出两人的速度差占AB两城距离的几分之几.
39.星期天,东东从家去少年宫学画画。刚走5分钟,妈妈发现东东忘带油画棒,于是立即去追。东东速度是50米/分,妈妈速度是75米/分,妈妈追上东东要走多少分钟?
【答案】10分钟。
【分析】根据“路程=速度×时间”求出追击路程,根据“追及时间=追及路程÷速度差”即可求解。
【解答】解:50×5÷(75﹣50)
=250÷25
=10(分钟)
答:妈妈追上东东要走10分钟。
【点评】本题考查了简单的追及问题。
40.甲和乙是同班同学,并且住在同一栋楼里。早晨7:40,甲从家出发骑车去学校,7:46追上了一直匀速步行的乙;看到身穿校服的乙才想起学校的通知,甲立即调头,并将速度提高到原来的2倍,回家换好校服,再赶往学校;甲8:00赶到学校时,乙也恰好到学校。如果甲在家换校服用去6分钟且调头时间不计,那么乙从家里出发时是几点几分?
【答案】7点25分。
【分析】依据题意可知,从甲看见穿校服的乙开始,乙到校用时(8时﹣7时46分),甲用时(8时﹣7时46分﹣6分),已知甲的速度是原来的2倍,所以相同距离,时间减半。刚开始甲追上乙用时(7时46分﹣7时40分),由此计算甲折返到相遇地点还有多少分,就是乙到学校的距离,根据比例关系计算乙从家到相遇点用时,由此计算乙从家里出发时间。
【解答】解:8时﹣7时46分=14分
14﹣6=8(分)
7时46分﹣7时40分=6分
8﹣6=2(分)
14÷2×3=21(分)
7时46分﹣21分=7时25分
答:乙从家里出发时是7点25分。
【点评】本题考查的是追及问题的应用。
41.小江家刚好在学校和妈妈单位的正中间,一天早上,小江和妈妈一起从家出发,小江向东去学校,妈妈向西去单位上班,妈妈的速度是小江的2.5倍。出发10分钟后妈妈距单位还有500米,此时发现小江的眼镜在包里,妈妈立即掉头加速20%去追小江,在离学校250米处追上小江后,又以原速度返回单位上班,当小江到学校时,妈妈离单位还有多远?
【答案】5125米。
【分析】依据题意可设小江速度为x米/分钟,则妈妈速度是2.5x米/分,出发10分钟,妈妈走了(2.5x×10)米,妈妈单位到家的距离为(2.5x×10+500)米,妈妈立即掉头加速20%后速度为[2.5x×(1+20%)]米/分,小江和妈妈一起从家出发,两者之间的距离为[(x+2.5x)×10]米,追及时间=两者之间的距离÷两者速度差,由此计算小江走的时间以及路程,然后计算单位和学校之间的距离,再计算妈妈追上小江走的距离,小江走剩下的250米的时间妈妈走的距离,然后计算当小江到学校时,妈妈离单位还有多远。
【解答】解:设小江速度为x米/分钟,则妈妈速度是2.5x米/分,出发10分钟,妈妈走了:2.5x×10=25x(米),妈妈单位到家的距离为:(25x+500)米,
妈妈立即掉头加速20%后速度为:2.5x×(1+20%)=3x(米/分)
小江和妈妈一起从家出发,两者之间的距离为:[(x+2.5x)×10=35x(米),追及时间:35x÷(3x﹣x)=17.5(分钟),小江所走时间:17.5+10=27.5(分钟),所走路程:(17.5+10)x=27.5x(米)
因为小江家刚好在学校和妈妈单位的正中间,则27.5x+250=25x+500,解得x=100,
单位和学校之间的距离:(25×100+500)×2
=3000×2
=6000(米)
妈妈追上小江时,距离学校250米,妈妈此时距离单位:6000﹣250=5750(米)
剩下的路程小江要走:250÷100=2.5(分钟),此时妈妈走了:2.5×100×2.5=625(米),距离单位还有:5750﹣625=5125(米)
答:当小江到学校时,妈妈离单位还有5125米。
【点评】本题考查的是追及问题的应用。
42.甲、乙两人沿着600米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是240米/分。经过多少分钟甲第三次追上乙?
【答案】60分钟。
【分析】由题意可得,他们同时从同一地点出发,同向而行。甲要追上乙,刚开始相当于乙和甲相距600米,追上一次追了600米,追了3次追了(600×3=1800)米。每分钟追(270﹣240=30)米。时间即可求。
【解答】解:600×3÷(270﹣240)
=1800÷30
=60(分钟)
答:经过60分钟甲第三次追上乙。
【点评】明确追及问题数量间的关系是解决本题的关键。
43.甲、乙两人从同一地点出发,同向而行,甲先行2小时后,乙才出发,甲每小时行60千米,乙每小时行80千米,当乙追上甲时,行了多少千米?
【答案】见试题解答内容
【分析】由“甲每小时行60千米,甲先行2小时”可知甲2小时行了60×2=120(千米),即追及路程;两人的速度差为80﹣60=20(千米/小时),那么乙追上甲的时间为120÷20=6(小时),再乘乙的速度即可解决问题.
【解答】解:60×2÷(80﹣60)
=120÷20
=6(小时)
6×80=480(千米)
答:当乙追上甲时,行了480千米.
【点评】此题在解答时,运用了关系式:追及路程÷速度差=追及时间.
44.小明、小红同时从A城沿相反方向出发,两人速度相同。上午9:00,小红迎面与一列长1200米的火车相遇,错开时间为30秒;上午9:30,火车追上小明,并在40秒后超过小明,那么火车每秒行多少米,小明和小红出发时间是几点?
【答案】7:30。
【分析】小红与火车相遇时,相当于小红跟火车的车尾做相遇运动,所以小红与火车的速度和为1200÷30=40(米/秒),火车追上并超过小明时,相当于火车的车尾追上小明,所以速度差为1200÷40=30(米/秒),所以火车速度为(40+30)÷2=35(米/秒),小红和小明的速度为5米/秒,所以九点时,小红跟小明之间的距离为(35﹣5)×60×30=54000(米),小红和小明已经走了54000÷(5+5)÷60=90(分钟),他们应该是7:30出发的。
【解答】解:小红与火车的速度和:1200÷30=40(米/秒)
小明与火车的速度差:1200÷40=30(米/秒)
火车速度为:(40+30)÷2
=70÷2
=35(米/秒)
小红和小明的速度为40﹣35=5(米秒)9:00时,小红跟小明之间的距离:
(35﹣5)×60×30
=1800×30
=54000(米)
54000÷(5+5)÷60
=54000÷10÷60
=5400÷60
=90(分钟)
90分钟=1时30分
9时﹣1时30分=7时30分
答:小明和小红出发时间是7:30。
【点评】此题较为复杂,考查了火车与人的相遇、追及问题,灵活运用行程公式进行求解。
45.在同样的时间里,兔子能跑3步,狗能跑2步,兔子一步跑1米,狗一步跑1.5米,如果狗和兔子在100米的直跑道上赛跑,赛程为一个往返,狗和兔子调头的时间相等,那么谁将获胜?
【答案】见试题解答内容
【分析】先算他们跑完全程需要几步,兔子跑一个往返需要:100×2÷1=200(步);狗跑一个往返需要:100×2÷1.5≈133.3=134(步);由题意,狗跑2步等于兔子跑3步;所以狗跑的步数相当于兔子的134÷2×3=201(步).兔子领先狗1步.所以兔子一定获胜.
【解答】解:兔子跑一个往返需要:
100×2÷1=200(步);
狗跑一个往返需要:
100×2÷1.5≈133.3=134(步);
狗跑的步数相当于兔子跑了:
134÷2×3=201(步);
因此兔子领先:
201﹣200=1(步).
答:兔子将获胜.
【点评】此题解答的关键是求出狗和兔子跑一个来回需要的步数,用步数少的获胜.
46.一条环形跑道长600米,甲练习骑自行车,平均每分钟行550米,乙练习长跑平均每分钟跑250米.两人同时从同一地点同向出发,经过多少分钟甲从后面追上乙?
【答案】见试题解答内容
【分析】这是一道封闭线路上的追及问题.甲和乙同时同地起跑,方向一致.因此,当甲第一次追上乙时,比乙多跑了一圈,也就是甲与乙的路程差是600米.根据“路程差÷速度差=追及时间”即可求出甲追上乙所需的时间.
【解答】解:600÷(550﹣250)
=600÷300
=2(分钟);
答:经过2分钟甲从后面追上乙.
【点评】此类题根据“追及(拉开)路程÷(速度差)=追及(拉开)时间”,代入数值计算即可.
47.在高速公路上一辆3m长的小汽车以110km/h的速度超过一辆17m长以100km/h的速度行驶的卡车。求小汽车从追及到超越卡车的整个超车过程用了多少秒?
【答案】7.2秒。
【分析】小汽车要完全超过卡车追及距离为汽车的长度+卡车的长度,即3+17=20(米),两车的速度差为110﹣100=10(千米/时),10千米/小时米/秒米/秒,则小汽车从追及到超越卡车的整个超车过程用了207.2(秒)。
【解答】解:3+17=20(米)
110﹣100=10(千米/时)
10千米/时米/秒米/秒
20
=20
=7.2(秒)
答:小汽车从追及到超越卡车的整个超车过程用了7.2秒。
【点评】此题属于追及问题,又是从车头相遇到车尾相离,那么追及路程为:快车路程﹣慢车路程=两车车长之和。
48.两辆汽车从同一起点出发,沿同一路线同向而行,第一辆汽车每小时行驶80千米,出发1小时后第二辆汽车出发。第二辆汽车每小时行驶120千米,几小时能追上第一辆汽车?
【答案】2小时。
【分析】由题意可知,两辆汽车的路程差为80千米,也就是追及路程为80千米,根据“追及路程÷速度差=追及时间”。代入数据即可解答。
【解答】解:80÷(120﹣80)
=80÷40
=2(小时)
答:2小时能追上第一辆汽车。
【点评】此题属于简单的追及应用题,此类题的解答方法是根据“追及路程÷速度差=追及时间”,代入数值,计算即可。
49.弟弟和哥哥跑步,如果弟弟先跑20米,哥哥跑10秒可以追上,如果弟弟先跑4秒,那么哥哥8秒可以追上.求弟弟和哥哥的速度.
【答案】见试题解答内容
【分析】根据如果弟弟先跑4秒,那么哥哥8秒可以追上,可知同样的路程,弟弟和哥哥所用时间的比是(4+8):8=3:2,所以弟弟先跑20米,哥哥跑10秒可以追上,此时弟弟所用时间是10÷2×3=15秒,也就是弟弟先跑20米,用时5秒,据此求出弟弟的速度,再求出弟弟15秒走的路程,除以哥哥所用时间,即可求出哥哥的速度,据此即可解答.
【解答】解:弟弟和哥哥所用时间的比是(4+8):8=3:2,
10÷2×3=15(秒)
20÷(15﹣10)
=20÷5
=4(米)
4×15÷10
=60÷10
=6(米)
答:弟弟每秒跑4米,哥哥每秒跑6米.
【点评】解答本题的关键是求出相同路程哥哥与弟弟所用的时间比是一定的.
50.A、B两城相距650km,有甲、乙两车都从A城开往B城。已知甲车的速度为72千米/时,甲、乙两车的速度比是3:4,甲车比乙车早出发一小时,乙车能在2小时内追上甲车吗?假如不能,需要多少小时才能追上呢?
【答案】不能,3。
【分析】根据甲乙两车的速度比可得乙车的速度,再用相距路程除以速度差可得追及时间,再作判断。
【解答】解:设乙车的速度为x千米/时,则
72:x=3:4
3x=72×4
x=96
72÷(96﹣72)
=72÷24
=3(小时)
答:乙车不能在2小时内追上甲车,需要3小时才能追上。
【点评】明确追及问题数量间的关系是解决本题的关键。
51.甲、乙两人沿着300米的环形跑道跑步,他们同时从一地出发、同向而行,甲每分钟跑260米,乙每分钟跑220米,乙刚出发就发现鞋带松了,他系鞋带用了0.5分钟。甲从出发到第一次追上乙经过多少分钟?
【答案】4.75分钟。
【分析】第一次追上乙时甲比乙多跑一圈300米,但是乙系鞋带用了0.5分钟,因此追及路程为300﹣260×0.5=170(米),追及速度为:260﹣220=40米/分钟,根据追击时间=追及路程÷追及速度,列式解答即可。
【解答】解:(300﹣260×0.5)÷(260﹣220)+0.5
=170÷40+0.5
=4.75(分钟)
答:甲从出发到第一次追上乙经过4.75分钟。
【点评】此题属于较复杂的追及问题,关键是明确甲从出发到第一次追上乙时,甲比乙多走的路程为:300﹣220×0.5=190(米)。
52.A、B两地相距210千米,甲、乙两车分别从A、B两地同时开出,同向而行。甲车每小时行105千米,乙车每小时行80千米,多少小时后甲车能追上乙车?
【答案】8.4小时。
【分析】根据“追及时间=路程差÷速度差”代入数据求解即可。
【解答】解:210÷(105﹣80)
=210÷25
=8.4(小时)
答:8.4小时后甲车能追上乙车。
【点评】本题考查了追及问题的应用,熟练掌握路程、速度和时间三者之间的关系是解题的关键。
53.A、B两地相距250千米,甲、乙两车同时从A、B两地相向而行,1小时后相遇。甲车每小时行驶的路程是乙车的1.5倍,如果甲、乙两车同时分别从A、B两地同向行驶(乙在前,甲在后),经过多少小时甲车能追上乙车?
【答案】5小时。
【分析】用A、B两地的距离除以相遇时间,得出甲、乙两车的速度和,甲车每小时行驶的路程是乙车的1.5倍,则甲、乙两车的速度和是乙车的(1+1.5)倍,用除法计算,即可得乙车每小时行驶的路程,进而得出甲车每小时行驶的路程,再用A、B两地的距离除以甲、乙两车的速度差,即可得解。
【解答】解:250÷1÷(1+1.5)
=250÷2.5
=100(千米/时)
100×1.5=150(千米/时)
250÷(150﹣100)
=250÷50
=5(小时)
答:经过5小时甲车能追上乙车。
【点评】本题主要考查了相遇及追及问题,关键是求出甲、乙车每小时行驶的路程。
54.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是230米/分。经过多少分钟甲第一次追上乙?
【答案】10分钟。
【分析】甲的速度比乙的速度快,甲第一次追上乙时,甲比乙多跑了一圈,即追及路程是400米,根据“追及时间=追及路程÷速度差”即可求解。
【解答】解:400÷(270﹣230)
=400÷40
=10(分钟)
答:经过10分钟甲第一次追上乙。
【点评】本题考查了行程中的追及问题。
55.小明8:00从A地骑车出发,11:00到达B地,小华开车从A地出发,速度是小明的3倍;追上小明后,速度增加为小明的4倍。如果小华9:30到达B地,那么小华是在什么时候出发的?
【答案】8:40。
【分析】小明从A地到B地用时(11时﹣8时),假设全程是180,利用速度=路程÷时间,计算小明速度,小华的速度,设小华比小明晚2t分钟出发,计算小华追及时间,开车的时间,利用追上小明之间的路程+加速后行驶的路程=全程列方程计算即可。
【解答】解:11时﹣8时=3时,3时=180分钟,9时30分﹣8时=1时30分,1时30分即90分。
假设全程是180,小明速度:180÷180=1,小华速度:3×1=3,4×1=4。
设小华比小明晚2t分钟出发,则小华追及时间为:1×2t÷(3﹣1)=t(分),开车时间:90﹣2t﹣t=90﹣3t(分)
3t+4×(90﹣3t)=180
9t=180
t=20
20×2=40(分)
8时+40分=8时40分,即8:40
答:小华是在8:40出发的。
【点评】本题考查的是追及问题的应用。
56.一天早晨,莉莉从家出发前往学校,每分钟走60米,莉莉走了10分钟后,爸爸发现她没有带数学书,便立刻骑自行车从家出发去追莉莉,在离家900米处追上了她。爸爸骑自行车每分钟行多少米?
【答案】180米。
【分析】爸爸在距离家900米的地方遇到可可,由此可得追及的路程为900米,莉莉10分钟走了10×60=600(米),爸爸出发到追上莉莉的时间,就是莉莉从600米到900米所用的时间,即(900﹣600)÷60=5(分钟),再根据追及路程÷追及时间=速度差,由此解答即可。
【解答】解:10×60=600(米)
900÷[(900﹣600)÷60]
=900÷[300÷60]
=900÷5
=180(米)
答:爸爸骑自行车每分钟行180米。
【点评】此题考查追及问题。根据追及路程÷追及时间=速度差解答。
57.甲、乙两人同时从A地出发去B地,5分钟后,甲返回A地去取东西,没有停留,继续步行去B地,如果从两人同时出发开始计时,那么35分钟后两人同时到达,已知甲每分钟所走路程比乙每分钟所走路程的2倍少30米,求A、B两地的距离为多少米?
【答案】1750米。
【分析】设乙每分钟行驶的路程为x米,表示出甲每分钟行驶的路程,根据题意列出方程,求出方程的解即可得到乙的速度,再用乙的速度乘35即可求出A、B两地的距离。
【解答】解:设乙每分钟行驶的路程为x米,则甲每分钟行驶的路程为(2x﹣30)米。
35x+5×2×(2x﹣30)=35(2x﹣30)
35x+10(2x﹣30)=70x﹣1050
35x+20x﹣300=70x﹣1050
70x﹣35x﹣20x=1050﹣300
15x=750
x=50
35×50=1750(米)
答:A、B两地的距离为1750米。
【点评】此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解。
58.一列客车每分钟行2000m,一列货车每分钟行1500m,货车比客车的车身长135m。两车在平行的轨道上同向行驶,当客车从后面超过货车时,两车交叉的时间是45秒。这列货车和这列客车的车身各长多少米?
【答案】255米;120米。
【分析】根据题意,客车从车头接近货车车尾到两车分离所行的路程长度相当于两车总长度,根据两车交叉的时间是45秒可以得出两车车身长度和,再根据“货车比客车的车身长135m”利用“和差关系”即可分别求出两车车身分别有多长,依此解答即可。
【解答】解:45秒分
(2000﹣1500)375(米)
货车:(375+135)÷2=255(米)
客车:255﹣135=120(米)
答:货车车身长255米;客车车身长120米。
【点评】本题属于比较简单的追及应用题,此类题的解答方法是根据“(速度差)×追及(拉开)时间=追及(拉开)路程”,代入数值,结合“和差问题”的方法计算即可。
59.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是290米/分,乙的速度是250米/分。经过多少分钟甲第二次追上乙?(提示:可以画图思考)
【答案】20分钟。
【分析】当甲第二次追上乙时,甲比乙多行了两圈跑道的长度,再根据追及时间=路程差÷速度差,列式计算。
【解答】解:400×2÷(290﹣250)
=800÷40
=20(分钟)
答:经过20分钟甲第二次追上乙。
【点评】本题解题关键是理解“当甲第二次追上乙时,甲比乙多行了两圈跑道的长度”,再根据追及时间=路程差÷速度差,列式计算。
60.“大三峡 大巴山”2023重庆万州环湖马拉松比赛于12月10日举行。本次比赛吸引了八个国家近万名运动员参赛,比赛项目包括全程马拉松(42.195千米)、半程马拉松(21.0975千米)和迷你马拉松(约4.5千米)。规划参赛总人数1万人,其中半程马拉松3000人,迷你马拉松人数是全程马拉松人数的2.5倍。王叔叔和张叔叔都报名参加了全程马拉松项目,8:30他们从起点同时出发,已知张叔叔的平均速度为200米/分,经过30分钟后,王叔叔落后张叔叔600米。这时,王叔叔奋起直追,将平均速度提高到250米/分,终于追上了张叔叔,取得了较好的比赛成绩。
(1)张叔叔跑完全程大约要用多少分钟?(得数保留整数)
(2)规划参加全程马拉松和迷你马拉松各多少人?
(3)前30分钟,王叔叔的平均速度是每分钟多少米?
(4)王叔叔用了多少分钟追上了张叔叔?
【答案】(1)211分钟;(2)全程马拉松人数2000人,迷你马拉松人数5000人;(3)180米;(4)12分钟。
【分析】(1)根据题意可知,张叔叔参加的是全程马拉松项目,路程42.195千米,根据“时间=路程÷速度”即可解答张叔叔跑完全程大约要用的时间;
(2)规划参赛总人数1万人,其中半程马拉松3000人,则全程马拉松和迷你马拉松人数之和为(10000﹣3000)人,把全程马拉松人数看作1份,则迷你马拉松人数是2.5份,用全程马拉松和迷你马拉松人数之和除以份数之和即为1份量,即全程马拉松人数,再用1份量乘2.5即是迷你马拉松人数,据此计算;
(3)根据“路程=时间×速度”求出前30分钟张叔叔跑的路程,根据30分钟后王叔叔落后张叔叔600米,即可求出王叔叔前30分钟跑的路程,再根据“速度=路程÷时间”即可求出王叔叔前30分钟的平均速度是多少;
(4)根据“时间=路程差÷速度差”代入数据即可计算。
【解答】解:(1)42.195×1000=42195(米)
42195÷200≈211(分钟)
答:张叔叔跑完全程大约要用211分钟。
(2)(10000﹣3000)÷(1+2.5)
=7000÷3.5
=2000(人)
2000×2.5=5000(人)
答:规划参加全程马拉松人数2000人,迷你马拉松人数5000人。
(3)(30×200﹣600)÷30
=5400÷30
=180(米/分)
答:前30分钟,王叔叔的平均速度是每分钟180米。
(4)600÷(250﹣200)
=600÷50
=12(分钟)
答:王叔叔用了12分钟追上了张叔叔。
【点评】本题考查了行程问题的应用,熟练掌握路程、时间、速度三者之间的关系是解题的关键。
21世纪教育网(www.21cnjy.com)
1.甲、乙两车同时从A地向B地开出,甲每小时行38千米,乙每小时行34千米,开出1小时后,甲车因有紧急任务返回A地;到达A地后又立即向B地开出追乙车,当甲车追上乙车时,两车正好都到达B地,求A、B两地的路程.
2.张老师从学校步行去公园,每分钟走60米,走了8分钟后,李老师从学校骑自行车去追张老师,结果在距学校720米的地方追上张老师。李老师骑自行车的速度是多少米/分?
3.李勇、张强两人周末到笔架山锻炼身体,两人同时从山脚开始爬山,到达山顶就立即下山,他们两人下山的速度都是各自上山速度的1.5倍,李勇到达山顶时,张强距山顶还有400米,然后李勇下山,张强爬完400米到山顶也开始下山,李勇回到山脚时,张强刚好返回到半山腰,求从山顶到山脚的距离。
4.和平小学的师生步行去春游.队伍走出10.5千米时,王东骑自行车去追,经过1.5时追上.已知王东骑自行车的速度是师生步行速度的3.5倍.王东和师生每时各行多少千米?
5.一只豹子正在快速追赶前面距离150米的奔跑中的羚羊,已知羚羊每秒跑23米,豹子每秒跑31米。再过20秒,豹子能追上羚羊吗?
6.(行程问题)甲、乙、丙同时从山脚开始爬山,到达山顶后立即下山,不断往返运动。已知山坡长360米,甲、乙、丙的速度比为6:5:4,并且甲、乙、丙的下山速度都是各自上山速度的1.5倍。经过一段时间后,甲到达山顶时,看见乙正在下山,此时乙距离山脚不到180米(乙不在山脚)。求此时丙离山顶的距离。
7.小丁丁和小巧先后沿同一条马路从学校出发去电影院观看电影。小巧先行40米后小丁丁再出发,小巧平均每分钟走72米,小丁丁出发10分钟在途中追上小巧。小丁丁平均每分钟走多少米?
8.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行,甲的速度是每分钟280米,乙的速度是每分钟240米。经过多长时间甲第一次追上乙?
9.一辆货车从甲地开往乙,如果按原速度行驶,将不能准时到达乙地,如果把车速提高,可以比原定时间早1小时到达,如果以原速度行驶120千米后,再将速度提高,则可提前40分钟到达,那么甲、乙两地间的距离是多少千米?
10.一辆卡车从A城驶向B城每小时行60km,开出1.5小时后,一辆轿车从A城驶向B城,每小时行75km,几小时后轿车能追上卡车?
11.甲、乙两人练习跑步,若甲让乙先跑10米,则甲跑5秒可追上乙;若乙比甲先跑2秒,则甲跑4秒能追上乙。问:两人每秒各跑多少米?
12.乙的速度是甲速度的,两人分别由A、B两地同时出发,如果相向而行1小时可以相遇;如果同向而行甲需要多少小时才能追上乙?
13.甲上午6时从A地步行出发,于下午5时到达B地;乙上午10时从A地骑自行车出发,于下午3时到达B地,问:乙在什么时间追上甲?
14.甲乙两人骑自行车,甲的速度是13.5千米/小时,乙的速度是11.8千米/小时,两人从同一地点出发,乙先出发2.5小时后,甲开始追,甲多久能追上乙?
15.开始时竹子高30cm,钟状菌高6cm。如果竹子和钟状菌都在生长旺盛期,竹子每时约增高4厘米,钟状菌每时约增高12厘米。几时后钟状菌的高度能赶上竹子?
16.A、B两地相距120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。
(1)两车分别从A、B两地同时同向而行(甲在乙后),经过多长时间甲车追上乙车?
(2)两车同时从A、B两地相向而行,经过多长时间两车相距10千米?
17.星期六,冬冬从家里出发去少年宫参加以“与光同盟童心同行”为主题活动的志愿者活动。刚走3分钟,爸爸发现冬冬忘带红领巾,于是立即去追。冬冬速度是60米/分,爸爸速度是80米/分,爸爸追上冬冬需要走多少分钟?
18.一位自行车运动员以24千米/时的速度从甲地到乙地,2小时后一辆摩托车以56千米/时的速度也从甲地到乙地,在甲地到乙地中点处追上了自行车运动员。问:甲、乙两地相距多远?
19.猎狗发现前方150米处有一只兔子正在逃跑,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒。在兔子前方520米处是一片灌木丛,猎狗能抓到兔子吗?
20.小红每分钟走70米,爸爸每分钟走100米,他们同时从同一地点背向走3分钟,然后爸爸掉头去追小红。从爸爸开始追小红到追上小红需要多长时间?
21.甲、乙两辆客车在高速公路上,从同一地点出发,同向而行。甲车以每小时80千米的速度行驶了1小时后,乙车出发,以每小时100千米的速度追赶甲车。乙车行多少千米才能追上甲车?
22.甲、乙两车同时由A地到B地,甲车每小时行45千米,乙车每小时行30千米,乙车先出发2小时后甲车才出发,两车同时到达B地.求A,B两地的距离.
23.小李骑自行车从甲地到乙地,出发40分钟后,小王骑电动车从甲地出发,两人同时到达乙地,已知小李骑自行车的速度是15千米/时,小王骑电动车的速度是小李骑自行车的速度的3倍求甲,乙两地的距离.
24.猎狗前面26步远有一只野兔,猎狗追之。兔跑8步的时间狗跑5步,兔跑9步的距离等于狗跑4步的距离。问:兔跑多少步后被猎狗抓获?此时猎狗跑了多少步?
25.小明上学10分钟后,爸爸发现他的数学书没带,就以小明步行6倍的速度骑车去追,追上把书给小明后立即返回,当爸爸回到家时,小明刚好也走到学校,小明从家走到学校一共要多少分钟?
26.早上小明以每分钟50米的速度向学校走去,6分钟后爸爸发现他的语文书没带,于是就以每分钟70米的速度去追小明,几分钟后爸爸才能追上小明?
27.一只兔子在一只猎狗前面80米处,它们同时发现了对方,兔子逃跑,每秒跑6米;猎狗追击,每秒跑8米,正常情况下,经过多长时间猎狗就能追上兔子?
28.有甲、乙两列火车,甲长93m,每秒行驶21m,乙长126m,每秒行驶18m,两车同向而行,开始时甲的车头与乙的车尾相平,过多长时间后甲的车尾与乙的车头相平?
29.快、慢两车分别从甲、乙两地出发,同向而行,慢车在前,快车在后,已知快车比慢车提前出发1小时,快车的速度是96千米/时,慢车的速度是80千米/时.快车出发5小时后追上慢车,甲、乙两地间的距离是多少千米?
30.AB两地相距1800米。甲乙两人同时从AB两地出发,若相向而行12分钟相遇;若同向而行90分钟甲追上乙,把乙需要的资料给他后,用去时1.2倍的速度返回。甲返回到A点时,乙距A点多少米?
31.小俊走路去上学,他的速度为60米/分钟。妈妈在收拾东西的时候,发现小俊没有带数学书,此时小俊已经出发了7分钟。于是妈妈立刻骑自行车从家出发去追小俊,妈妈骑自行车的速度为200米/分钟。问妈妈从家出发算起到追上小俊,一共用了多久?
32.小红和小明沿着400米的环形跑道跑步,小红每秒跑4米,小明每秒跑6米。两人站在起跑线上同向而行,如果小红先跑了10秒钟后,小明才开始跑,小明追上小红需要多少秒?
33.已知一艘船顺水行48千米需4小时,逆水行48千米需6小时。现在轮船从上游A港到下游B港(水速同前面),已知两港间的水路长为72千米,开船时一旅客从宽口扔到水里一块木板,问:船到B港时,木板离B港还有多远?
34.如图是一个长方形儿童乐园,长200米。宽130米。小丁丁、小胖、小巧按各自现在的方向同时出发,沿乐园边的小路行走。小丁丁每分钟走60米,小胖每分钟走50米,小巧每分钟走40米。根据给出的信息解决问题。
①出发多少时间后,小胖追上小巧?
②出发多少时间后,小丁丁和小巧相遇?
35.一只猎狗发现前方150米处有一只兔子,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒,在兔子前方500米处有片灌木丛,在兔子逃进灌木丛前,猎狗能抓到兔子吗?
36.甲、乙两人同时从B地出发,乙朝A地前进,甲以15千米/时的速度反方向朝C地前进,一小时后甲、乙两人正好分别到达A地和C地,乙继续前进,甲从C地返回追乙,经14小时甲在D地追上乙,乙的速度是多少?
37.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是每分钟290米,乙的速度是每分钟250米,经过多少分钟甲第一次追上乙?
38.在AB两城有甲乙两人,分别从AB两城同时相向而行,2小时相遇,相遇时甲所走的路程与乙所走的路程比是7:9;如果甲乙两人同时同向而行,乙需要多少小时才能追上甲?
39.星期天,东东从家去少年宫学画画。刚走5分钟,妈妈发现东东忘带油画棒,于是立即去追。东东速度是50米/分,妈妈速度是75米/分,妈妈追上东东要走多少分钟?
40.甲和乙是同班同学,并且住在同一栋楼里。早晨7:40,甲从家出发骑车去学校,7:46追上了一直匀速步行的乙;看到身穿校服的乙才想起学校的通知,甲立即调头,并将速度提高到原来的2倍,回家换好校服,再赶往学校;甲8:00赶到学校时,乙也恰好到学校。如果甲在家换校服用去6分钟且调头时间不计,那么乙从家里出发时是几点几分?
41.小江家刚好在学校和妈妈单位的正中间,一天早上,小江和妈妈一起从家出发,小江向东去学校,妈妈向西去单位上班,妈妈的速度是小江的2.5倍。出发10分钟后妈妈距单位还有500米,此时发现小江的眼镜在包里,妈妈立即掉头加速20%去追小江,在离学校250米处追上小江后,又以原速度返回单位上班,当小江到学校时,妈妈离单位还有多远?
42.甲、乙两人沿着600米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是240米/分。经过多少分钟甲第三次追上乙?
43.甲、乙两人从同一地点出发,同向而行,甲先行2小时后,乙才出发,甲每小时行60千米,乙每小时行80千米,当乙追上甲时,行了多少千米?
44.小明、小红同时从A城沿相反方向出发,两人速度相同。上午9:00,小红迎面与一列长1200米的火车相遇,错开时间为30秒;上午9:30,火车追上小明,并在40秒后超过小明,那么火车每秒行多少米,小明和小红出发时间是几点?
45.在同样的时间里,兔子能跑3步,狗能跑2步,兔子一步跑1米,狗一步跑1.5米,如果狗和兔子在100米的直跑道上赛跑,赛程为一个往返,狗和兔子调头的时间相等,那么谁将获胜?
46.一条环形跑道长600米,甲练习骑自行车,平均每分钟行550米,乙练习长跑平均每分钟跑250米.两人同时从同一地点同向出发,经过多少分钟甲从后面追上乙?
47.在高速公路上一辆3m长的小汽车以110km/h的速度超过一辆17m长以100km/h的速度行驶的卡车。求小汽车从追及到超越卡车的整个超车过程用了多少秒?
48.两辆汽车从同一起点出发,沿同一路线同向而行,第一辆汽车每小时行驶80千米,出发1小时后第二辆汽车出发。第二辆汽车每小时行驶120千米,几小时能追上第一辆汽车?
49.弟弟和哥哥跑步,如果弟弟先跑20米,哥哥跑10秒可以追上,如果弟弟先跑4秒,那么哥哥8秒可以追上.求弟弟和哥哥的速度.
50.A、B两城相距650km,有甲、乙两车都从A城开往B城。已知甲车的速度为72千米/时,甲、乙两车的速度比是3:4,甲车比乙车早出发一小时,乙车能在2小时内追上甲车吗?假如不能,需要多少小时才能追上呢?
51.甲、乙两人沿着300米的环形跑道跑步,他们同时从一地出发、同向而行,甲每分钟跑260米,乙每分钟跑220米,乙刚出发就发现鞋带松了,他系鞋带用了0.5分钟。甲从出发到第一次追上乙经过多少分钟?
52.A、B两地相距210千米,甲、乙两车分别从A、B两地同时开出,同向而行。甲车每小时行105千米,乙车每小时行80千米,多少小时后甲车能追上乙车?
53.A、B两地相距250千米,甲、乙两车同时从A、B两地相向而行,1小时后相遇。甲车每小时行驶的路程是乙车的1.5倍,如果甲、乙两车同时分别从A、B两地同向行驶(乙在前,甲在后),经过多少小时甲车能追上乙车?
54.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是230米/分。经过多少分钟甲第一次追上乙?
55.小明8:00从A地骑车出发,11:00到达B地,小华开车从A地出发,速度是小明的3倍;追上小明后,速度增加为小明的4倍。如果小华9:30到达B地,那么小华是在什么时候出发的?
56.一天早晨,莉莉从家出发前往学校,每分钟走60米,莉莉走了10分钟后,爸爸发现她没有带数学书,便立刻骑自行车从家出发去追莉莉,在离家900米处追上了她。爸爸骑自行车每分钟行多少米?
57.甲、乙两人同时从A地出发去B地,5分钟后,甲返回A地去取东西,没有停留,继续步行去B地,如果从两人同时出发开始计时,那么35分钟后两人同时到达,已知甲每分钟所走路程比乙每分钟所走路程的2倍少30米,求A、B两地的距离为多少米?
58.一列客车每分钟行2000m,一列货车每分钟行1500m,货车比客车的车身长135m。两车在平行的轨道上同向行驶,当客车从后面超过货车时,两车交叉的时间是45秒。这列货车和这列客车的车身各长多少米?
59.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是290米/分,乙的速度是250米/分。经过多少分钟甲第二次追上乙?(提示:可以画图思考)
60.“大三峡 大巴山”2023重庆万州环湖马拉松比赛于12月10日举行。本次比赛吸引了八个国家近万名运动员参赛,比赛项目包括全程马拉松(42.195千米)、半程马拉松(21.0975千米)和迷你马拉松(约4.5千米)。规划参赛总人数1万人,其中半程马拉松3000人,迷你马拉松人数是全程马拉松人数的2.5倍。王叔叔和张叔叔都报名参加了全程马拉松项目,8:30他们从起点同时出发,已知张叔叔的平均速度为200米/分,经过30分钟后,王叔叔落后张叔叔600米。这时,王叔叔奋起直追,将平均速度提高到250米/分,终于追上了张叔叔,取得了较好的比赛成绩。
(1)张叔叔跑完全程大约要用多少分钟?(得数保留整数)
(2)规划参加全程马拉松和迷你马拉松各多少人?
(3)前30分钟,王叔叔的平均速度是每分钟多少米?
(4)王叔叔用了多少分钟追上了张叔叔?
追及问题
参考答案与试题解析
1.甲、乙两车同时从A地向B地开出,甲每小时行38千米,乙每小时行34千米,开出1小时后,甲车因有紧急任务返回A地;到达A地后又立即向B地开出追乙车,当甲车追上乙车时,两车正好都到达B地,求A、B两地的路程.
【答案】见试题解答内容
【分析】根据题意可知:开出1小时后,甲返回A地,然后继续追乙;乙一直处于行驶状态,所以相当于乙比甲先行1×2=2(小时),而甲追及乙的过程,路程差就是乙2小时行的路程,利用追及问题个数:追及时间=路程差除以速度差.然后这段时间甲所行的路程,就是A、B两地的路程.
【解答】解:(1×2×34)÷(38﹣34)×38
=68÷4×38
=17×38
=646(千米)
答:A、B两地的路程是646千米.
【点评】本题主要考查追及问题,关键利用路程、速度和时间的关系做题.
2.张老师从学校步行去公园,每分钟走60米,走了8分钟后,李老师从学校骑自行车去追张老师,结果在距学校720米的地方追上张老师。李老师骑自行车的速度是多少米/分?
【答案】180米/分。
【分析】根据题意可知,两位老师都走了720米,张老师每分钟走60米,720除以60等于张老师行走的时间,由于张老师走了8分钟后李老师才去追,所以李老师比张老师少用了8分钟,张老师行走的时间减8等于李老师骑行的时间,再用骑行路程720米除以李老师骑行的时间即等于李老师骑行的速度,据此即可解答。
【解答】解:720÷(720÷60﹣8)
=720÷(12﹣8)
=720÷4
=180(米/分)
答:李老师骑自行车的速度是180米/分。
【点评】此题抓住追及问题中速度不同,所以行驶的时间不同,但是行驶的路程相同。
3.李勇、张强两人周末到笔架山锻炼身体,两人同时从山脚开始爬山,到达山顶就立即下山,他们两人下山的速度都是各自上山速度的1.5倍,李勇到达山顶时,张强距山顶还有400米,然后李勇下山,张强爬完400米到山顶也开始下山,李勇回到山脚时,张强刚好返回到半山腰,求从山顶到山脚的距离。
【答案】2000米。
【分析】通过分析两人在不同阶段的路程关系,利用速度变化与路程的联系来求解从山顶到山脚的距离。
【解答】解:设从山顶到山脚的距离是s米,李勇上山速度为v1,张强上山速度为v2。
李勇到达山顶时,张强距山顶还有400米,此时两人爬山时间相同,根据时间=路程÷速度可得:
即v2
李勇下山速度是1.5v1,张强下山速度是1.5v2。李勇从山顶回到山脚的路程是s,所用时间是:
张强从距离山顶400米,然后到山顶,再从山顶走到半山腰,所用时间是:
因为两人这一阶段时间也相同,所以:
把v2代入可得:
等式两边同时乘1.5v1可得:s
等式两边同时乘2(s﹣400)可得:2s(s﹣400)=1200s+s2
因为s>0
所以2(s﹣400)=1200+s
即2s﹣800=1200+s
所以s=2000
即从山顶到山脚的距离是2000米。
答:从山顶到山脚的距离是2000米。
【点评】本题考查了复杂行程问题的应用,解题关键是找出题干中的等量关系。
4.和平小学的师生步行去春游.队伍走出10.5千米时,王东骑自行车去追,经过1.5时追上.已知王东骑自行车的速度是师生步行速度的3.5倍.王东和师生每时各行多少千米?
【答案】见试题解答内容
【分析】本题为追及问题公式:根据速度差、距离差和追及时间三者之间的关系,利用公式:速度差=距离差÷追及时间根据路程差和追及时间,先求出速度差,然后根据速度的倍数关系,求出一份速度,及师生的速度.
【解答】解:10.5÷1.5=7(千米/小时).
师生:7÷(3.5﹣1)=2.8(千米/小时).
王东:2.8×3.5=9.8(千米/小时)
答:王东每小时行9.8千米,师生每小时行2.8千米.
【点评】本题关键是利用追击问题公式,求速度差.
5.一只豹子正在快速追赶前面距离150米的奔跑中的羚羊,已知羚羊每秒跑23米,豹子每秒跑31米。再过20秒,豹子能追上羚羊吗?
【答案】能。
【分析】根据“路程=速度差×追及时间”,求出豹子20秒钟的追及路程后和150米比较大小,大于等于150,能追上,反之追不上。
【解答】解:(31﹣23)×20
=8×20
=160(米)
160米>150米,即能追上。
答:豹子能追上羚羊。
【点评】本题考查了追及问题的应用。
6.(行程问题)甲、乙、丙同时从山脚开始爬山,到达山顶后立即下山,不断往返运动。已知山坡长360米,甲、乙、丙的速度比为6:5:4,并且甲、乙、丙的下山速度都是各自上山速度的1.5倍。经过一段时间后,甲到达山顶时,看见乙正在下山,此时乙距离山脚不到180米(乙不在山脚)。求此时丙离山顶的距离。
【答案】40米。
【分析】先用假设法表示出甲、乙、丙的上山速度和下山速度,在进行分类讨论,选出符合题意得情况进行解答。
【解答】解:设甲、乙、丙上坡速度分别为6x、5x、4x,则下坡速度分别为9x、7.5x、6x。
根据题意可知,甲达到山顶停下时,它们所用的时间相等。
假设甲两上一下,则乙应该是两上一下不合题意。
假设甲三上两下,则乙应该是两下两上,第三次正在上,不合题意。
假设甲四上三下,所用时间应该为:
43
此时乙可能三上二下,第三下中,则下时的时间为:
33
此时离山顶距离为:
7.5x=360(米)和题意不符
假设甲五上四下,所用时间为:
54
此时乙应该是四上三下,第四下中,则四下时间为:
43
此时距离山顶距离:
7.5x=210(米)符合题意,也就是说甲经历了五上四下,乙经历了四上,第四下中。
此时丙应该是三上三下,第四上中,第四上的时间为:
33
此时丙距离山顶的距离为:
4x=40(米)
答:此时丙距离山顶的距离为40米。
【点评】甲达到山顶停下时,它们所用的时间相等时是关键。
7.小丁丁和小巧先后沿同一条马路从学校出发去电影院观看电影。小巧先行40米后小丁丁再出发,小巧平均每分钟走72米,小丁丁出发10分钟在途中追上小巧。小丁丁平均每分钟走多少米?
【答案】76米。
【分析】有题意可知,小丁丁10分钟走的路程=小巧先走的40米+小巧10分钟走的路程。据此列式计算出小丁丁10分钟走的路程,然后再除以10即可解答。
【解答】解:小丁丁10分钟走:
40+72×10
=40+720
=760(米)
760÷10=76(米/分)
答:小丁丁平均每分钟走76米。
【点评】解答本题的关键是先求出小丁丁10分钟走的路程。
8.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行,甲的速度是每分钟280米,乙的速度是每分钟240米。经过多长时间甲第一次追上乙?
【答案】10分钟。
【分析】当甲第一次追上乙时,甲比乙多行了一圈跑道的长度,所以甲第一次追上乙需要的时间=环形跑道的长度÷(甲的速度﹣乙的速度),据此列式解答即可。
【解答】解:400÷(280﹣240)
=400÷40
=10(分钟)
答:经过10分钟甲第一次追上乙。
【点评】解答本题的关键是理解“当甲第一次追上乙时,甲比乙多行了一圈跑道的长度”,再根据“追及时间=路程差÷速度差”,列式计算。
9.一辆货车从甲地开往乙,如果按原速度行驶,将不能准时到达乙地,如果把车速提高,可以比原定时间早1小时到达,如果以原速度行驶120千米后,再将速度提高,则可提前40分钟到达,那么甲、乙两地间的距离是多少千米?
【答案】270千米。
【分析】把原来车速看成单位“1”,则车速提高后为1×(1),原来的速度相当于它的;提高为1×(1),此时速度相当于最后速度的;那么,后来用的时间为(1)(小时);则原来的速度为120÷(6)=45(千米/时)。则甲、乙两地间的距离是(45×6)千米,据此计算即可。
【解答】解:40(小时)
把原来车速看成单位“1”,则车速提高后为的速度为:1×(1)
即原来速度相当于现在的:1
所以原来的时间为:1÷(1)=6(小时)
同理可知后来的速度相当于最后速度的1÷(1)
后来用的时间为(1)(小时)
原来的速度即为120÷(6)=45(千米/时)
45×6=270(千米)
答:甲、乙两地间的距离是270千米。
【点评】解决此题的关键是求出原来的时间与速度,应认真分析,一步步推算,再求出时间与速度后,运用关系式“速度×时间=路程”解决问题。
10.一辆卡车从A城驶向B城每小时行60km,开出1.5小时后,一辆轿车从A城驶向B城,每小时行75km,几小时后轿车能追上卡车?
【答案】见试题解答内容
【分析】根据追及问题,追及时间=追及的距离÷速度差,先求出这辆卡车1.5小时小时多少千米,再求出轿车与卡车的速度差,进而求出轿车追上卡车的时间.
【解答】解:60×1.5÷(75﹣60)
=90÷15
=6(小时)
答:6小时后轿车能追上卡车.
【点评】此题属于追及问题,利用基本数量关系:追及时间=追及的距离÷速度差,解决问题.
11.甲、乙两人练习跑步,若甲让乙先跑10米,则甲跑5秒可追上乙;若乙比甲先跑2秒,则甲跑4秒能追上乙。问:两人每秒各跑多少米?
【答案】见试题解答内容
【分析】根据题意,由如果甲让乙先跑10米,那么,甲跑5秒就可以追上乙,根据“路程÷时间”=速度,可以求出追及速度(即甲、乙的速度差);即10÷5=2(米/秒),如果让乙先跑2秒,那么甲跑4秒可追上乙,用追及速度乘4就可以求出甲追了多少米,从而求出乙的速度,进而再求出甲的速度。
【解答】解:甲、乙的速度差:10÷5=2(米/秒)
乙先跑2秒,甲需要追4秒,也就是追了2×4=8(米)
则乙速度为:8÷2=4(米/秒)
甲速度为:4+2=6(米/秒)
答:甲每秒跑6米,乙每秒跑4米。
【点评】本题主要考查的是行程问题,属于同一地点不同时出发的追及问题的应用题。此题解答的关键是先求出追及速度,再根据路程、速度、时间三者之间的关系列式解答即可。
12.乙的速度是甲速度的,两人分别由A、B两地同时出发,如果相向而行1小时可以相遇;如果同向而行甲需要多少小时才能追上乙?
【答案】甲需要5小时才能追上乙。
【分析】乙的速度是甲速度的,那么乙的速度:甲的速度=2:3.设乙的速度为每小时行2千米,则甲的速度为每小时行3千米,求出A、B两地之间的距离,甲要追上乙,就要比乙多行A、B之间的距离这段路程,用这个路程除以两人的速度差就是它们行走的时间。
【解答】解:设乙的速度为每小时行2千米,甲的速度为每小时行3千米,
两地相距:(2+3)×1
=5×1
=5(千米)
甲追上乙需:
5÷(3﹣2)
=5÷12
=5(小时)
答:甲需要5小时才能追上乙。
【点评】本题考查了相遇问题的数量关系以及追及问题的数量关系,速度和×相遇时间=总路程,路程差÷速度差=追及时间。
13.甲上午6时从A地步行出发,于下午5时到达B地;乙上午10时从A地骑自行车出发,于下午3时到达B地,问:乙在什么时间追上甲?
【答案】下午1时20分。
【分析】把AB两地之间的距离看作单位“1”,上午6时到下午5时经过了17﹣6=11小时,则速度是;乙上午10时到下午3时经过了15﹣10=5小时,则速度是,速度差是(),追及距离是(10﹣6);然后用追及距离除以速度差求出追及时间,再进一步解答即可。
【解答】解:17﹣6=11(小时)
15﹣10=5(小时)
(10﹣6)÷()
=3(小时)
3小时=3小时20分钟
上午10时+3小时20分钟=下午1时20分
答:乙在下午1时20分追上甲。
【点评】本题考查了追及问题与工程问题的综合应用,关键是求出追及距离和速度差。
14.甲乙两人骑自行车,甲的速度是13.5千米/小时,乙的速度是11.8千米/小时,两人从同一地点出发,乙先出发2.5小时后,甲开始追,甲多久能追上乙?
【答案】小时。
【分析】依据题意可设甲x小时追上乙,利用甲的走的路=乙先走的路+乙后走的路,列方程计算即可。
【解答】解:设甲x小时追上乙,由题意得:
13.5x=2.5×11.8+11.8x
1.7x=29.5
x
答:甲小时能追上乙。
【点评】本题考查的是追及问题的应用。
15.开始时竹子高30cm,钟状菌高6cm。如果竹子和钟状菌都在生长旺盛期,竹子每时约增高4厘米,钟状菌每时约增高12厘米。几时后钟状菌的高度能赶上竹子?
【答案】3时。
【分析】根据题意,开始时竹子比钟状菌高30﹣6=24(厘米);每时钟状菌比竹子多长高12﹣4=8(厘米),然后再用24除以8即可。
【解答】解:(30﹣6)÷(12﹣4)
=24÷8
=3(时)
答:3时后钟状菌的高度可赶上竹子。
【点评】解答此题的关键是确定每时钟状菌比竹子多长多少和现在竹子比钟状菌高的厘米数。
16.A、B两地相距120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。
(1)两车分别从A、B两地同时同向而行(甲在乙后),经过多长时间甲车追上乙车?
(2)两车同时从A、B两地相向而行,经过多长时间两车相距10千米?
【答案】(1)12小时,(2)1.1小时,1.3小时。
【分析】(1)相距路程÷速度差=追及时间,据此解答。
(2)两车所行路程÷速度和=所用时间,据此解答。
【解答】解:(1)120÷(55﹣45)
=120÷10
=12(小时)
答:经过12小时甲车追上乙车。
(2)第一种情况,甲、乙两车在未相遇时相距10千米,
(120﹣10)÷(55+45)
=110÷100
=1.1(小时)
第二种情况:甲、乙两车相遇后又相距10千米,
(120+10)÷(55+45)
=130÷100
=1.3(小时)
答:两车同时从A、B两地相向而行,经过1.1小时或1.3小时两车相距10千米。
【点评】明确追及问题及相遇问题数量间的关系是解决本题的关键。
17.星期六,冬冬从家里出发去少年宫参加以“与光同盟童心同行”为主题活动的志愿者活动。刚走3分钟,爸爸发现冬冬忘带红领巾,于是立即去追。冬冬速度是60米/分,爸爸速度是80米/分,爸爸追上冬冬需要走多少分钟?
【答案】9分钟。
【分析】依据题意可知,爸爸追上冬冬要比冬冬多走(60×3)米,追上的时间=多走的路程÷两人的速度差,由此列式计算。
【解答】解:60×3÷(80﹣60)
=60×3÷20
=9(分)
答:爸爸追上冬冬需要走9分钟。
【点评】本题考查的是追及问题的应用。
18.一位自行车运动员以24千米/时的速度从甲地到乙地,2小时后一辆摩托车以56千米/时的速度也从甲地到乙地,在甲地到乙地中点处追上了自行车运动员。问:甲、乙两地相距多远?
【答案】168千米。
【分析】根据题意,两车路程差为24×2=48(千米),两车速度差每小时为56﹣24=32(千米),根据两车速度差×追及时间=两车路程差,求出追及时间,进而求出甲乙两地的路程,解决问题。
【解答】解:24×2÷(56﹣24)
=48÷32
=1.5(小时)
56×1.5×2
=84×2
=168(千米)
答:甲、乙两地相距168千米。
【点评】根据关系式:路程差÷速度差=追及时间,求出摩托车追上自行车的时间,是解答此题的关键。
19.猎狗发现前方150米处有一只兔子正在逃跑,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒。在兔子前方520米处是一片灌木丛,猎狗能抓到兔子吗?
【答案】不能。
【分析】猎狗追上兔子需要的时间=猎狗与兔子之间相隔的距离÷猎狗与兔子的速度差,再用兔子的速度乘时间,得出这段时间兔子能跑多少米,最后比较即可解答此题。
【解答】解:18﹣14=4(米/秒)
150÷4=37.5(秒)
14×37.5=525(米)
525>520,即猎狗不能抓到兔子。
答:猎狗不能抓到兔子。
【点评】本题主要考查追及问题。
20.小红每分钟走70米,爸爸每分钟走100米,他们同时从同一地点背向走3分钟,然后爸爸掉头去追小红。从爸爸开始追小红到追上小红需要多长时间?
【答案】17分钟。
【分析】根据路程=速度×时间,先求出小红和爸爸各自从同一地点背向走3分钟的路程,再把两人3分钟各自走的路程相加,求出爸爸追小红前两人相差的路程,也就是爸爸要追小红的路程,再根据追及时间=路程差÷速度差,代入数据计算,即可求出从爸爸开始追小红到追上小红需要的时间,据此解答。
【解答】解:(70+100)×3÷(100﹣70)
=170×3÷30
=510÷30
=17(分钟)
答:从爸爸开始追小红到追上小红需要17分钟。
【点评】本题考查了行程中的追及问题,熟练掌握路程、速度、时间三者之间的关系是解题的关键。
21.甲、乙两辆客车在高速公路上,从同一地点出发,同向而行。甲车以每小时80千米的速度行驶了1小时后,乙车出发,以每小时100千米的速度追赶甲车。乙车行多少千米才能追上甲车?
【答案】400千米。
【分析】用要追的距离除以速度差,求出追上用的时间,再用这个时间乘乙的速度即可。
【解答】解:80÷(100﹣80)×100
=80÷20×100
=4×100
=400(千米)
答:乙车行400千米才能追上。
【点评】本题考查的是追及问题。解答关键是要追的距离除以速度差,求出追上用的时间。
22.甲、乙两车同时由A地到B地,甲车每小时行45千米,乙车每小时行30千米,乙车先出发2小时后甲车才出发,两车同时到达B地.求A,B两地的距离.
【答案】见试题解答内容
【分析】乙每小时行30千米 乙车先出发2小时 那就是多行60千米,两车同时到达B地,那么就是说在甲追上乙的那刻二者都到终点,甲每小时可以追到15千米,60千米只要4小时就可以追完;根据速度×时间=路程,那么总路程就是45×4=180千米,由此解答.
【解答】解:45×[30×2÷(45﹣30)]
=45×[60÷15]
=45×4
=180(千米)
答:AB两地相距180千米.
【点评】此题属于追及问题,根据追击的路程÷速度差=追击的时间,再根据路程、速度、时间三者之间的关系列式解答即可.
23.小李骑自行车从甲地到乙地,出发40分钟后,小王骑电动车从甲地出发,两人同时到达乙地,已知小李骑自行车的速度是15千米/时,小王骑电动车的速度是小李骑自行车的速度的3倍求甲,乙两地的距离.
【答案】见试题解答内容
【分析】可设小李骑自行车从甲地到乙地的时间为t小时,则小王骑电动车从甲地到乙地的时间为(t)小时,根据等量关系:从甲地到乙地的路程是一定的,路程方程求解即可.
【解答】解:设小李骑自行车从甲地到乙地的时间为t小时,则小王骑电动车从甲地到乙地的时间为(t)小时,依题意有
15×3(t)﹣15t=0
45(t)﹣15t=0
45t﹣30﹣15t=0
30t﹣30=0
30t=30
t=1
15t=15×1=15(千米)
答:甲,乙两地的距离是15千米.
【点评】考查了追及问题,解题的关键是在互相关联、互相对应的距离差、速度差、追及时间三者之中,找出两者,然后运用公式求出第三者来达到解题目的.
24.猎狗前面26步远有一只野兔,猎狗追之。兔跑8步的时间狗跑5步,兔跑9步的距离等于狗跑4步的距离。问:兔跑多少步后被猎狗抓获?此时猎狗跑了多少步?
【答案】144步,90步。
【分析】依据题意可知,先计算出兔跑(8×9)步的时间狗跑多少步,兔跑(8×9)步的距离等于狗跑多少步的距离,由此计算狗比兔多跑多少步,然后计算兔追上狗跑26步跑多少步,再计算狗跑多少步。
【解答】解:8和9的最小公倍数是:8×9=72
兔跑72步的时间狗跑:5×9=45(步),兔跑72步的距离狗跑:4×8=32(步)
45﹣32=13(步)
72×(26÷13)
=72×2
=144(步)
5×(144÷8)
=5×18
=90(步)
答:兔跑144步后被猎狗抓获,此时猎狗跑了90步。
【点评】本题考查的是追及问题的应用。
25.小明上学10分钟后,爸爸发现他的数学书没带,就以小明步行6倍的速度骑车去追,追上把书给小明后立即返回,当爸爸回到家时,小明刚好也走到学校,小明从家走到学校一共要多少分钟?
【答案】14分钟。
【分析】若以小明爸爸返回时开始算起,小明距离学校为1份,则爸爸回家走了6份,小明家到学校共7份。小明走10分钟共走了5份,每份用时10÷5=2(分钟),所以小明从家到学校用时应该是2×7=14(分钟)。
【解答】解:若以小明爸爸返回时开始算起,小明距离学校为1份,则爸爸回家走了6份,小明家到学校共7份。
10÷5=2(分钟)
2×7=14(分钟)
答:小明从家到学校一共要14分钟。
【点评】要求小明从家走到学校一共要多少分钟,只需要求出小明10分钟走的路程是总路程的几份。
26.早上小明以每分钟50米的速度向学校走去,6分钟后爸爸发现他的语文书没带,于是就以每分钟70米的速度去追小明,几分钟后爸爸才能追上小明?
【答案】15分钟。
【分析】先用50乘6,求出小明6分钟行走的路程;再根据“追及距离÷速度差=追及时间”,用小明6分钟行走的路程除以(70﹣50),即可求出几分钟后爸爸才能追上小明。
【解答】解:50×6÷(70﹣50)
=300÷20
=15(分钟)
答:15分钟后爸爸才能追上小明。
【点评】解答本题需熟练掌握追及距离、速度差与追及时间之间的关系。
27.一只兔子在一只猎狗前面80米处,它们同时发现了对方,兔子逃跑,每秒跑6米;猎狗追击,每秒跑8米,正常情况下,经过多长时间猎狗就能追上兔子?
【答案】40秒。
【分析】根据追及时间=距离差÷速度差,代入数值进行计算即可。
【解答】解:80÷(8+6)
=80÷2
=40(秒)
答:经过40秒猎狗就能追上兔子。
【点评】本题考查追及问题的计算及应用。理解题意,找出数量关系,列式计算即可。
28.有甲、乙两列火车,甲长93m,每秒行驶21m,乙长126m,每秒行驶18m,两车同向而行,开始时甲的车头与乙的车尾相平,过多长时间后甲的车尾与乙的车头相平?
【答案】73秒。
【分析】开始时甲的车头与乙的车尾相平,后来甲的车尾与乙的车头相平,即追及路程为甲、乙车长之和。根据“追及时间=追及路程÷速度差”即可解答。
【解答】解:(93+126)÷(21﹣18)
=219÷3
=73(秒)
答:过73秒后甲的车尾与乙的车头相平。
【点评】本题考查了追及问题的应用,熟练掌握路程、速度、时间三者之间的关系是解题的关键。
29.快、慢两车分别从甲、乙两地出发,同向而行,慢车在前,快车在后,已知快车比慢车提前出发1小时,快车的速度是96千米/时,慢车的速度是80千米/时.快车出发5小时后追上慢车,甲、乙两地间的距离是多少千米?
【答案】见试题解答内容
【分析】根据追及问题公式:距离差=速度差×追及时间 其中速度差=快速﹣慢速,题中快车比慢车提前出发1小时,快车的速度是96千米/时,所以甲、乙两地的距离是快车1小时所行的路程加上慢车起步出发后到快车追上慢车时的距离差.
【解答】解:(96﹣80)×(5﹣1)+96×1
=16×4+96
=64+96
=160(千米)
答:甲、乙两地间的距离是160千米.
【点评】此题既需要根据关系式而且还要更加深刻的理解题意.
30.AB两地相距1800米。甲乙两人同时从AB两地出发,若相向而行12分钟相遇;若同向而行90分钟甲追上乙,把乙需要的资料给他后,用去时1.2倍的速度返回。甲返回到A点时,乙距A点多少米?
【答案】12525米。
【分析】用AB两地相距的距离1800米除以相遇时间就是甲、乙的速度和,用1800米除以90分钟就是甲、乙的速度差,进一步求出甲、乙的速度,再用甲的速度乘90分钟求出甲追上乙时距A地的距离,再根据路程÷速度=时间,求出甲返回A地所用的时间,则可求出乙一共行走的时间,再乘乙的速度即可。
【解答】解:1800÷12=150(米/分钟)
1800÷90=20(米/分钟)
(150+20)÷2
=170÷2
=85(米/分钟)
(150﹣20)÷2
=130÷2
=65(米/分钟)
90×85=7650(米)
7650÷(85×1.2)
=7650÷102
=75(分钟)
65×(90+75)+1800
=65×165+1800
=10725+1800
=12525(米)
答:甲返回到A点时,乙距A点12525米。
【点评】明确路程÷相遇时间=速度和,追及路程÷追及时间=追及速度,以及路程、速度、时间三者的关系是解题的关键。
31.小俊走路去上学,他的速度为60米/分钟。妈妈在收拾东西的时候,发现小俊没有带数学书,此时小俊已经出发了7分钟。于是妈妈立刻骑自行车从家出发去追小俊,妈妈骑自行车的速度为200米/分钟。问妈妈从家出发算起到追上小俊,一共用了多久?
【答案】3分钟。
【分析】由题意可知,妈妈和小俊的路程差为60×7=420(米),即追及路程为420米,根据追及问题中“追及路程÷速度差=追及时间”,代入数据计算即可。
【解答】解:60×7=420(米)
420÷(200﹣60)
=420÷140
=3(分钟)
答:问妈妈从家出发算起到追上小俊,一共用了3分钟。
【点评】此题属于简单的追及应用题,此类题的解答方法是根据“追及路程÷速度差=追及时间”。
32.小红和小明沿着400米的环形跑道跑步,小红每秒跑4米,小明每秒跑6米。两人站在起跑线上同向而行,如果小红先跑了10秒钟后,小明才开始跑,小明追上小红需要多少秒?
【答案】需要20秒。
【分析】小红先跑10秒钟,则两人之间的距离就是4×10=40米,先求出两人的速度差,再用两人之间的距离除以两人的速度差即可解答。
【解答】解:4×10÷(6﹣4)
=40÷2
=20(秒)
答:小明追上小红需要20秒。
【点评】此题运用了关系式:路程差÷速度差=追及时间。
33.已知一艘船顺水行48千米需4小时,逆水行48千米需6小时。现在轮船从上游A港到下游B港(水速同前面),已知两港间的水路长为72千米,开船时一旅客从宽口扔到水里一块木板,问:船到B港时,木板离B港还有多远?
【答案】60千米。
【分析】先算出顺水行的速度和逆水行的速度,然后根据水速=(顺水行速度﹣逆水行速度)÷2来算出水速;根据顺水行时间=路程÷顺水行速度,可以算出船从A港到B港所用的时间;因为木板在水里的速度就是水速,所以用水速乘船从A港到B港所用的时间,可以算出船到B港时,木板行驶的路程;在用总路程减去木板行驶的路程就可以得到木板离B港还有多远。
【解答】解:顺水行速度为:48÷4=12(千米)
逆水行速度为:48÷6=8(千米)
水的速度为:(12﹣8)÷2=2(千米)
从A到B所用时间为:72÷12=6(小时)
6小时木板的路程为:6×2=12(千米)
72﹣12=60(千米)
答:船到B港时,木板离B港还有60千米。
【点评】此题考查的是流水行船问题,需要学生理清题意,并能灵活的运用路程=速度×时间,水速=(顺水行速度﹣逆水行速度)÷2来解题。
34.如图是一个长方形儿童乐园,长200米。宽130米。小丁丁、小胖、小巧按各自现在的方向同时出发,沿乐园边的小路行走。小丁丁每分钟走60米,小胖每分钟走50米,小巧每分钟走40米。根据给出的信息解决问题。
①出发多少时间后,小胖追上小巧?
②出发多少时间后,小丁丁和小巧相遇?
【答案】①20分钟;②4.6分钟。
【分析】①根据图示可知,小胖和小巧的路程差是200米,即追及路程是200米,根据“追及时间=路程差÷速度差”即可求解;
②根据“相遇时间=路程÷速度和”即可求解。
【解答】解:①200÷(50﹣40)
=200÷10
=20(分钟)
答:出发20分钟后,小胖追上小巧。
②(200+130×2)÷(60+40)
=460÷100
=4.6(分钟)
答:出发4.6分钟后,小丁丁和小巧相遇。
【点评】本题考查了行程问题的应用,熟练掌握路程、速度和时间三者的关系是解题的关键。
35.一只猎狗发现前方150米处有一只兔子,拔腿就追。兔子逃跑的速度是14米/秒,猎狗追赶的速度是18米/秒,在兔子前方500米处有片灌木丛,在兔子逃进灌木丛前,猎狗能抓到兔子吗?
【答案】不能。
【分析】先根据追及距离÷速度差=追及时间求出猎狗追上兔子需要的时间,再用兔子的速度乘这个时间,看是否大于500米。
【解答】解:150÷(18﹣14)
=150÷4
=37.5(秒)
14×37.5=525(米)
525米>500米
答:在兔子逃进灌木丛前,猎狗不能抓到兔子。
【点评】本题考查了追及问题,需熟练掌握追及距离、速度差和追及时间之间的关系。
36.甲、乙两人同时从B地出发,乙朝A地前进,甲以15千米/时的速度反方向朝C地前进,一小时后甲、乙两人正好分别到达A地和C地,乙继续前进,甲从C地返回追乙,经14小时甲在D地追上乙,乙的速度是多少?
【答案】13。
【分析】本题可列方程求解,设乙每小时行x千米,乙行AB的路程用了1小时,所以AB的路程为x千米,则追及路程为(x+15)千米,速度差为(15﹣x)千米/时,因为经14小时甲在D地追上乙,所以CD的路程为(15﹣x)×14,根据追及路程等于CD间的路程列方程解答即可。
【解答】解:设乙每小时走x千米,则甲、乙速度差为(15﹣x)千米。
x+15=(15﹣x)×14
x+15=210﹣14x
15x=195
x=13
答:乙的速度是13千米/时。
【点评】本题考查的是追及问题,可列方程解答,关键是找到等量关系。
37.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是每分钟290米,乙的速度是每分钟250米,经过多少分钟甲第一次追上乙?
【答案】10分钟。
【分析】当甲第一次追上乙时,甲比乙多行了一圈跑道的长度,再根据“追及时间=路程差÷速度差”,列式计算即可解答。
【解答】解:400÷(290﹣250)
=400÷40
=10(分钟)
答:经过10分钟甲第一次追上乙。
【点评】本题解题关键是理解“当甲第一次追上乙时,甲比乙多行了一圈跑道的长度”,再根据追及时间=路程差÷速度差,列式计算。
38.在AB两城有甲乙两人,分别从AB两城同时相向而行,2小时相遇,相遇时甲所走的路程与乙所走的路程比是7:9;如果甲乙两人同时同向而行,乙需要多少小时才能追上甲?
【答案】见试题解答内容
【分析】两人1小时可以走全程的,根据速度比是7:9,可以求出乙每小时可以比甲多走全程的的.
【解答】解:
116(小时)
答:乙需要16小时才能追上甲.
【点评】此题的关键求出两人的速度差占AB两城距离的几分之几.
39.星期天,东东从家去少年宫学画画。刚走5分钟,妈妈发现东东忘带油画棒,于是立即去追。东东速度是50米/分,妈妈速度是75米/分,妈妈追上东东要走多少分钟?
【答案】10分钟。
【分析】根据“路程=速度×时间”求出追击路程,根据“追及时间=追及路程÷速度差”即可求解。
【解答】解:50×5÷(75﹣50)
=250÷25
=10(分钟)
答:妈妈追上东东要走10分钟。
【点评】本题考查了简单的追及问题。
40.甲和乙是同班同学,并且住在同一栋楼里。早晨7:40,甲从家出发骑车去学校,7:46追上了一直匀速步行的乙;看到身穿校服的乙才想起学校的通知,甲立即调头,并将速度提高到原来的2倍,回家换好校服,再赶往学校;甲8:00赶到学校时,乙也恰好到学校。如果甲在家换校服用去6分钟且调头时间不计,那么乙从家里出发时是几点几分?
【答案】7点25分。
【分析】依据题意可知,从甲看见穿校服的乙开始,乙到校用时(8时﹣7时46分),甲用时(8时﹣7时46分﹣6分),已知甲的速度是原来的2倍,所以相同距离,时间减半。刚开始甲追上乙用时(7时46分﹣7时40分),由此计算甲折返到相遇地点还有多少分,就是乙到学校的距离,根据比例关系计算乙从家到相遇点用时,由此计算乙从家里出发时间。
【解答】解:8时﹣7时46分=14分
14﹣6=8(分)
7时46分﹣7时40分=6分
8﹣6=2(分)
14÷2×3=21(分)
7时46分﹣21分=7时25分
答:乙从家里出发时是7点25分。
【点评】本题考查的是追及问题的应用。
41.小江家刚好在学校和妈妈单位的正中间,一天早上,小江和妈妈一起从家出发,小江向东去学校,妈妈向西去单位上班,妈妈的速度是小江的2.5倍。出发10分钟后妈妈距单位还有500米,此时发现小江的眼镜在包里,妈妈立即掉头加速20%去追小江,在离学校250米处追上小江后,又以原速度返回单位上班,当小江到学校时,妈妈离单位还有多远?
【答案】5125米。
【分析】依据题意可设小江速度为x米/分钟,则妈妈速度是2.5x米/分,出发10分钟,妈妈走了(2.5x×10)米,妈妈单位到家的距离为(2.5x×10+500)米,妈妈立即掉头加速20%后速度为[2.5x×(1+20%)]米/分,小江和妈妈一起从家出发,两者之间的距离为[(x+2.5x)×10]米,追及时间=两者之间的距离÷两者速度差,由此计算小江走的时间以及路程,然后计算单位和学校之间的距离,再计算妈妈追上小江走的距离,小江走剩下的250米的时间妈妈走的距离,然后计算当小江到学校时,妈妈离单位还有多远。
【解答】解:设小江速度为x米/分钟,则妈妈速度是2.5x米/分,出发10分钟,妈妈走了:2.5x×10=25x(米),妈妈单位到家的距离为:(25x+500)米,
妈妈立即掉头加速20%后速度为:2.5x×(1+20%)=3x(米/分)
小江和妈妈一起从家出发,两者之间的距离为:[(x+2.5x)×10=35x(米),追及时间:35x÷(3x﹣x)=17.5(分钟),小江所走时间:17.5+10=27.5(分钟),所走路程:(17.5+10)x=27.5x(米)
因为小江家刚好在学校和妈妈单位的正中间,则27.5x+250=25x+500,解得x=100,
单位和学校之间的距离:(25×100+500)×2
=3000×2
=6000(米)
妈妈追上小江时,距离学校250米,妈妈此时距离单位:6000﹣250=5750(米)
剩下的路程小江要走:250÷100=2.5(分钟),此时妈妈走了:2.5×100×2.5=625(米),距离单位还有:5750﹣625=5125(米)
答:当小江到学校时,妈妈离单位还有5125米。
【点评】本题考查的是追及问题的应用。
42.甲、乙两人沿着600米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是240米/分。经过多少分钟甲第三次追上乙?
【答案】60分钟。
【分析】由题意可得,他们同时从同一地点出发,同向而行。甲要追上乙,刚开始相当于乙和甲相距600米,追上一次追了600米,追了3次追了(600×3=1800)米。每分钟追(270﹣240=30)米。时间即可求。
【解答】解:600×3÷(270﹣240)
=1800÷30
=60(分钟)
答:经过60分钟甲第三次追上乙。
【点评】明确追及问题数量间的关系是解决本题的关键。
43.甲、乙两人从同一地点出发,同向而行,甲先行2小时后,乙才出发,甲每小时行60千米,乙每小时行80千米,当乙追上甲时,行了多少千米?
【答案】见试题解答内容
【分析】由“甲每小时行60千米,甲先行2小时”可知甲2小时行了60×2=120(千米),即追及路程;两人的速度差为80﹣60=20(千米/小时),那么乙追上甲的时间为120÷20=6(小时),再乘乙的速度即可解决问题.
【解答】解:60×2÷(80﹣60)
=120÷20
=6(小时)
6×80=480(千米)
答:当乙追上甲时,行了480千米.
【点评】此题在解答时,运用了关系式:追及路程÷速度差=追及时间.
44.小明、小红同时从A城沿相反方向出发,两人速度相同。上午9:00,小红迎面与一列长1200米的火车相遇,错开时间为30秒;上午9:30,火车追上小明,并在40秒后超过小明,那么火车每秒行多少米,小明和小红出发时间是几点?
【答案】7:30。
【分析】小红与火车相遇时,相当于小红跟火车的车尾做相遇运动,所以小红与火车的速度和为1200÷30=40(米/秒),火车追上并超过小明时,相当于火车的车尾追上小明,所以速度差为1200÷40=30(米/秒),所以火车速度为(40+30)÷2=35(米/秒),小红和小明的速度为5米/秒,所以九点时,小红跟小明之间的距离为(35﹣5)×60×30=54000(米),小红和小明已经走了54000÷(5+5)÷60=90(分钟),他们应该是7:30出发的。
【解答】解:小红与火车的速度和:1200÷30=40(米/秒)
小明与火车的速度差:1200÷40=30(米/秒)
火车速度为:(40+30)÷2
=70÷2
=35(米/秒)
小红和小明的速度为40﹣35=5(米秒)9:00时,小红跟小明之间的距离:
(35﹣5)×60×30
=1800×30
=54000(米)
54000÷(5+5)÷60
=54000÷10÷60
=5400÷60
=90(分钟)
90分钟=1时30分
9时﹣1时30分=7时30分
答:小明和小红出发时间是7:30。
【点评】此题较为复杂,考查了火车与人的相遇、追及问题,灵活运用行程公式进行求解。
45.在同样的时间里,兔子能跑3步,狗能跑2步,兔子一步跑1米,狗一步跑1.5米,如果狗和兔子在100米的直跑道上赛跑,赛程为一个往返,狗和兔子调头的时间相等,那么谁将获胜?
【答案】见试题解答内容
【分析】先算他们跑完全程需要几步,兔子跑一个往返需要:100×2÷1=200(步);狗跑一个往返需要:100×2÷1.5≈133.3=134(步);由题意,狗跑2步等于兔子跑3步;所以狗跑的步数相当于兔子的134÷2×3=201(步).兔子领先狗1步.所以兔子一定获胜.
【解答】解:兔子跑一个往返需要:
100×2÷1=200(步);
狗跑一个往返需要:
100×2÷1.5≈133.3=134(步);
狗跑的步数相当于兔子跑了:
134÷2×3=201(步);
因此兔子领先:
201﹣200=1(步).
答:兔子将获胜.
【点评】此题解答的关键是求出狗和兔子跑一个来回需要的步数,用步数少的获胜.
46.一条环形跑道长600米,甲练习骑自行车,平均每分钟行550米,乙练习长跑平均每分钟跑250米.两人同时从同一地点同向出发,经过多少分钟甲从后面追上乙?
【答案】见试题解答内容
【分析】这是一道封闭线路上的追及问题.甲和乙同时同地起跑,方向一致.因此,当甲第一次追上乙时,比乙多跑了一圈,也就是甲与乙的路程差是600米.根据“路程差÷速度差=追及时间”即可求出甲追上乙所需的时间.
【解答】解:600÷(550﹣250)
=600÷300
=2(分钟);
答:经过2分钟甲从后面追上乙.
【点评】此类题根据“追及(拉开)路程÷(速度差)=追及(拉开)时间”,代入数值计算即可.
47.在高速公路上一辆3m长的小汽车以110km/h的速度超过一辆17m长以100km/h的速度行驶的卡车。求小汽车从追及到超越卡车的整个超车过程用了多少秒?
【答案】7.2秒。
【分析】小汽车要完全超过卡车追及距离为汽车的长度+卡车的长度,即3+17=20(米),两车的速度差为110﹣100=10(千米/时),10千米/小时米/秒米/秒,则小汽车从追及到超越卡车的整个超车过程用了207.2(秒)。
【解答】解:3+17=20(米)
110﹣100=10(千米/时)
10千米/时米/秒米/秒
20
=20
=7.2(秒)
答:小汽车从追及到超越卡车的整个超车过程用了7.2秒。
【点评】此题属于追及问题,又是从车头相遇到车尾相离,那么追及路程为:快车路程﹣慢车路程=两车车长之和。
48.两辆汽车从同一起点出发,沿同一路线同向而行,第一辆汽车每小时行驶80千米,出发1小时后第二辆汽车出发。第二辆汽车每小时行驶120千米,几小时能追上第一辆汽车?
【答案】2小时。
【分析】由题意可知,两辆汽车的路程差为80千米,也就是追及路程为80千米,根据“追及路程÷速度差=追及时间”。代入数据即可解答。
【解答】解:80÷(120﹣80)
=80÷40
=2(小时)
答:2小时能追上第一辆汽车。
【点评】此题属于简单的追及应用题,此类题的解答方法是根据“追及路程÷速度差=追及时间”,代入数值,计算即可。
49.弟弟和哥哥跑步,如果弟弟先跑20米,哥哥跑10秒可以追上,如果弟弟先跑4秒,那么哥哥8秒可以追上.求弟弟和哥哥的速度.
【答案】见试题解答内容
【分析】根据如果弟弟先跑4秒,那么哥哥8秒可以追上,可知同样的路程,弟弟和哥哥所用时间的比是(4+8):8=3:2,所以弟弟先跑20米,哥哥跑10秒可以追上,此时弟弟所用时间是10÷2×3=15秒,也就是弟弟先跑20米,用时5秒,据此求出弟弟的速度,再求出弟弟15秒走的路程,除以哥哥所用时间,即可求出哥哥的速度,据此即可解答.
【解答】解:弟弟和哥哥所用时间的比是(4+8):8=3:2,
10÷2×3=15(秒)
20÷(15﹣10)
=20÷5
=4(米)
4×15÷10
=60÷10
=6(米)
答:弟弟每秒跑4米,哥哥每秒跑6米.
【点评】解答本题的关键是求出相同路程哥哥与弟弟所用的时间比是一定的.
50.A、B两城相距650km,有甲、乙两车都从A城开往B城。已知甲车的速度为72千米/时,甲、乙两车的速度比是3:4,甲车比乙车早出发一小时,乙车能在2小时内追上甲车吗?假如不能,需要多少小时才能追上呢?
【答案】不能,3。
【分析】根据甲乙两车的速度比可得乙车的速度,再用相距路程除以速度差可得追及时间,再作判断。
【解答】解:设乙车的速度为x千米/时,则
72:x=3:4
3x=72×4
x=96
72÷(96﹣72)
=72÷24
=3(小时)
答:乙车不能在2小时内追上甲车,需要3小时才能追上。
【点评】明确追及问题数量间的关系是解决本题的关键。
51.甲、乙两人沿着300米的环形跑道跑步,他们同时从一地出发、同向而行,甲每分钟跑260米,乙每分钟跑220米,乙刚出发就发现鞋带松了,他系鞋带用了0.5分钟。甲从出发到第一次追上乙经过多少分钟?
【答案】4.75分钟。
【分析】第一次追上乙时甲比乙多跑一圈300米,但是乙系鞋带用了0.5分钟,因此追及路程为300﹣260×0.5=170(米),追及速度为:260﹣220=40米/分钟,根据追击时间=追及路程÷追及速度,列式解答即可。
【解答】解:(300﹣260×0.5)÷(260﹣220)+0.5
=170÷40+0.5
=4.75(分钟)
答:甲从出发到第一次追上乙经过4.75分钟。
【点评】此题属于较复杂的追及问题,关键是明确甲从出发到第一次追上乙时,甲比乙多走的路程为:300﹣220×0.5=190(米)。
52.A、B两地相距210千米,甲、乙两车分别从A、B两地同时开出,同向而行。甲车每小时行105千米,乙车每小时行80千米,多少小时后甲车能追上乙车?
【答案】8.4小时。
【分析】根据“追及时间=路程差÷速度差”代入数据求解即可。
【解答】解:210÷(105﹣80)
=210÷25
=8.4(小时)
答:8.4小时后甲车能追上乙车。
【点评】本题考查了追及问题的应用,熟练掌握路程、速度和时间三者之间的关系是解题的关键。
53.A、B两地相距250千米,甲、乙两车同时从A、B两地相向而行,1小时后相遇。甲车每小时行驶的路程是乙车的1.5倍,如果甲、乙两车同时分别从A、B两地同向行驶(乙在前,甲在后),经过多少小时甲车能追上乙车?
【答案】5小时。
【分析】用A、B两地的距离除以相遇时间,得出甲、乙两车的速度和,甲车每小时行驶的路程是乙车的1.5倍,则甲、乙两车的速度和是乙车的(1+1.5)倍,用除法计算,即可得乙车每小时行驶的路程,进而得出甲车每小时行驶的路程,再用A、B两地的距离除以甲、乙两车的速度差,即可得解。
【解答】解:250÷1÷(1+1.5)
=250÷2.5
=100(千米/时)
100×1.5=150(千米/时)
250÷(150﹣100)
=250÷50
=5(小时)
答:经过5小时甲车能追上乙车。
【点评】本题主要考查了相遇及追及问题,关键是求出甲、乙车每小时行驶的路程。
54.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是270米/分,乙的速度是230米/分。经过多少分钟甲第一次追上乙?
【答案】10分钟。
【分析】甲的速度比乙的速度快,甲第一次追上乙时,甲比乙多跑了一圈,即追及路程是400米,根据“追及时间=追及路程÷速度差”即可求解。
【解答】解:400÷(270﹣230)
=400÷40
=10(分钟)
答:经过10分钟甲第一次追上乙。
【点评】本题考查了行程中的追及问题。
55.小明8:00从A地骑车出发,11:00到达B地,小华开车从A地出发,速度是小明的3倍;追上小明后,速度增加为小明的4倍。如果小华9:30到达B地,那么小华是在什么时候出发的?
【答案】8:40。
【分析】小明从A地到B地用时(11时﹣8时),假设全程是180,利用速度=路程÷时间,计算小明速度,小华的速度,设小华比小明晚2t分钟出发,计算小华追及时间,开车的时间,利用追上小明之间的路程+加速后行驶的路程=全程列方程计算即可。
【解答】解:11时﹣8时=3时,3时=180分钟,9时30分﹣8时=1时30分,1时30分即90分。
假设全程是180,小明速度:180÷180=1,小华速度:3×1=3,4×1=4。
设小华比小明晚2t分钟出发,则小华追及时间为:1×2t÷(3﹣1)=t(分),开车时间:90﹣2t﹣t=90﹣3t(分)
3t+4×(90﹣3t)=180
9t=180
t=20
20×2=40(分)
8时+40分=8时40分,即8:40
答:小华是在8:40出发的。
【点评】本题考查的是追及问题的应用。
56.一天早晨,莉莉从家出发前往学校,每分钟走60米,莉莉走了10分钟后,爸爸发现她没有带数学书,便立刻骑自行车从家出发去追莉莉,在离家900米处追上了她。爸爸骑自行车每分钟行多少米?
【答案】180米。
【分析】爸爸在距离家900米的地方遇到可可,由此可得追及的路程为900米,莉莉10分钟走了10×60=600(米),爸爸出发到追上莉莉的时间,就是莉莉从600米到900米所用的时间,即(900﹣600)÷60=5(分钟),再根据追及路程÷追及时间=速度差,由此解答即可。
【解答】解:10×60=600(米)
900÷[(900﹣600)÷60]
=900÷[300÷60]
=900÷5
=180(米)
答:爸爸骑自行车每分钟行180米。
【点评】此题考查追及问题。根据追及路程÷追及时间=速度差解答。
57.甲、乙两人同时从A地出发去B地,5分钟后,甲返回A地去取东西,没有停留,继续步行去B地,如果从两人同时出发开始计时,那么35分钟后两人同时到达,已知甲每分钟所走路程比乙每分钟所走路程的2倍少30米,求A、B两地的距离为多少米?
【答案】1750米。
【分析】设乙每分钟行驶的路程为x米,表示出甲每分钟行驶的路程,根据题意列出方程,求出方程的解即可得到乙的速度,再用乙的速度乘35即可求出A、B两地的距离。
【解答】解:设乙每分钟行驶的路程为x米,则甲每分钟行驶的路程为(2x﹣30)米。
35x+5×2×(2x﹣30)=35(2x﹣30)
35x+10(2x﹣30)=70x﹣1050
35x+20x﹣300=70x﹣1050
70x﹣35x﹣20x=1050﹣300
15x=750
x=50
35×50=1750(米)
答:A、B两地的距离为1750米。
【点评】此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解。
58.一列客车每分钟行2000m,一列货车每分钟行1500m,货车比客车的车身长135m。两车在平行的轨道上同向行驶,当客车从后面超过货车时,两车交叉的时间是45秒。这列货车和这列客车的车身各长多少米?
【答案】255米;120米。
【分析】根据题意,客车从车头接近货车车尾到两车分离所行的路程长度相当于两车总长度,根据两车交叉的时间是45秒可以得出两车车身长度和,再根据“货车比客车的车身长135m”利用“和差关系”即可分别求出两车车身分别有多长,依此解答即可。
【解答】解:45秒分
(2000﹣1500)375(米)
货车:(375+135)÷2=255(米)
客车:255﹣135=120(米)
答:货车车身长255米;客车车身长120米。
【点评】本题属于比较简单的追及应用题,此类题的解答方法是根据“(速度差)×追及(拉开)时间=追及(拉开)路程”,代入数值,结合“和差问题”的方法计算即可。
59.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是290米/分,乙的速度是250米/分。经过多少分钟甲第二次追上乙?(提示:可以画图思考)
【答案】20分钟。
【分析】当甲第二次追上乙时,甲比乙多行了两圈跑道的长度,再根据追及时间=路程差÷速度差,列式计算。
【解答】解:400×2÷(290﹣250)
=800÷40
=20(分钟)
答:经过20分钟甲第二次追上乙。
【点评】本题解题关键是理解“当甲第二次追上乙时,甲比乙多行了两圈跑道的长度”,再根据追及时间=路程差÷速度差,列式计算。
60.“大三峡 大巴山”2023重庆万州环湖马拉松比赛于12月10日举行。本次比赛吸引了八个国家近万名运动员参赛,比赛项目包括全程马拉松(42.195千米)、半程马拉松(21.0975千米)和迷你马拉松(约4.5千米)。规划参赛总人数1万人,其中半程马拉松3000人,迷你马拉松人数是全程马拉松人数的2.5倍。王叔叔和张叔叔都报名参加了全程马拉松项目,8:30他们从起点同时出发,已知张叔叔的平均速度为200米/分,经过30分钟后,王叔叔落后张叔叔600米。这时,王叔叔奋起直追,将平均速度提高到250米/分,终于追上了张叔叔,取得了较好的比赛成绩。
(1)张叔叔跑完全程大约要用多少分钟?(得数保留整数)
(2)规划参加全程马拉松和迷你马拉松各多少人?
(3)前30分钟,王叔叔的平均速度是每分钟多少米?
(4)王叔叔用了多少分钟追上了张叔叔?
【答案】(1)211分钟;(2)全程马拉松人数2000人,迷你马拉松人数5000人;(3)180米;(4)12分钟。
【分析】(1)根据题意可知,张叔叔参加的是全程马拉松项目,路程42.195千米,根据“时间=路程÷速度”即可解答张叔叔跑完全程大约要用的时间;
(2)规划参赛总人数1万人,其中半程马拉松3000人,则全程马拉松和迷你马拉松人数之和为(10000﹣3000)人,把全程马拉松人数看作1份,则迷你马拉松人数是2.5份,用全程马拉松和迷你马拉松人数之和除以份数之和即为1份量,即全程马拉松人数,再用1份量乘2.5即是迷你马拉松人数,据此计算;
(3)根据“路程=时间×速度”求出前30分钟张叔叔跑的路程,根据30分钟后王叔叔落后张叔叔600米,即可求出王叔叔前30分钟跑的路程,再根据“速度=路程÷时间”即可求出王叔叔前30分钟的平均速度是多少;
(4)根据“时间=路程差÷速度差”代入数据即可计算。
【解答】解:(1)42.195×1000=42195(米)
42195÷200≈211(分钟)
答:张叔叔跑完全程大约要用211分钟。
(2)(10000﹣3000)÷(1+2.5)
=7000÷3.5
=2000(人)
2000×2.5=5000(人)
答:规划参加全程马拉松人数2000人,迷你马拉松人数5000人。
(3)(30×200﹣600)÷30
=5400÷30
=180(米/分)
答:前30分钟,王叔叔的平均速度是每分钟180米。
(4)600÷(250﹣200)
=600÷50
=12(分钟)
答:王叔叔用了12分钟追上了张叔叔。
【点评】本题考查了行程问题的应用,熟练掌握路程、时间、速度三者之间的关系是解题的关键。
21世纪教育网(www.21cnjy.com)
同课章节目录
