期末检测卷(含答案)---2024-2025学年六年级数学下册真题重组检测卷(北京版)
文档属性
| 名称 | 期末检测卷(含答案)---2024-2025学年六年级数学下册真题重组检测卷(北京版) |

|
|
| 格式 | docx | ||
| 文件大小 | 607.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 09:53:43 | ||
图片预览



文档简介
保密★启用前
2024-2025学年六年级下册期末检测卷(北京版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.(2024六下·西城期末)x和y是两种相关联的量,它们的关系可以用下面的图象表示。那么,这个图象可能表示的是( )的关系。
A.看一本书,看了的页数和没看的页数
B.正方形的面积和边长
C.圆柱的高一定,体积和底面积
D.平行四边形的面积一定,底和高
2.(2024六下·延庆期末)一个直角三角形,两条直角边分别是4cm和 3cm。以下面两种方式旋转得到立体图形(每条旋转轴垂直于底边),旋转后图1的体积是图2体积的( )
A. B. C. D.
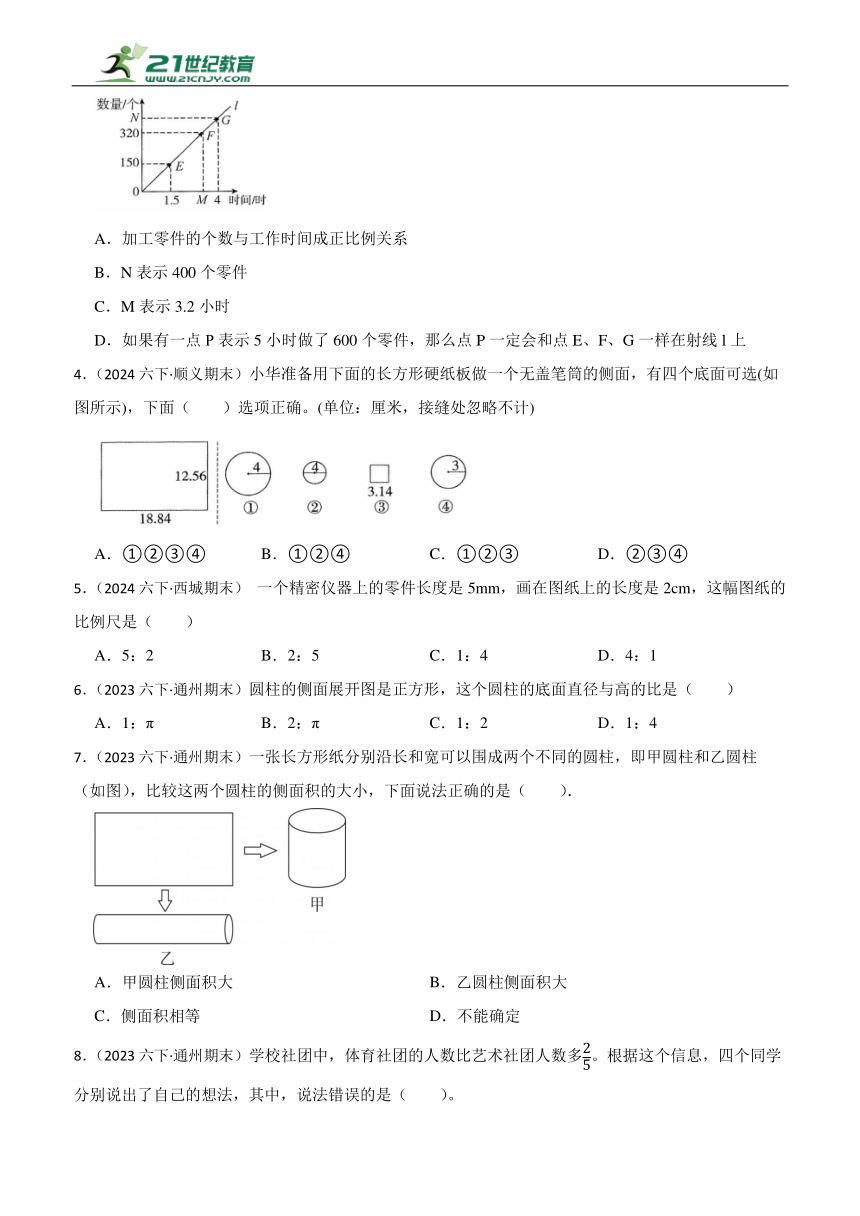
3.(2024六下·顺义期末)小李加工一批零件,工作时间与加工零件的个数的关系(如下图),下列说法错误的是( )
A.加工零件的个数与工作时间成正比例关系
B.N表示400个零件
C.M表示3.2小时
D.如果有一点Р表示5小时做了600个零件,那么点P一定会和点E、F、G一样在射线l上
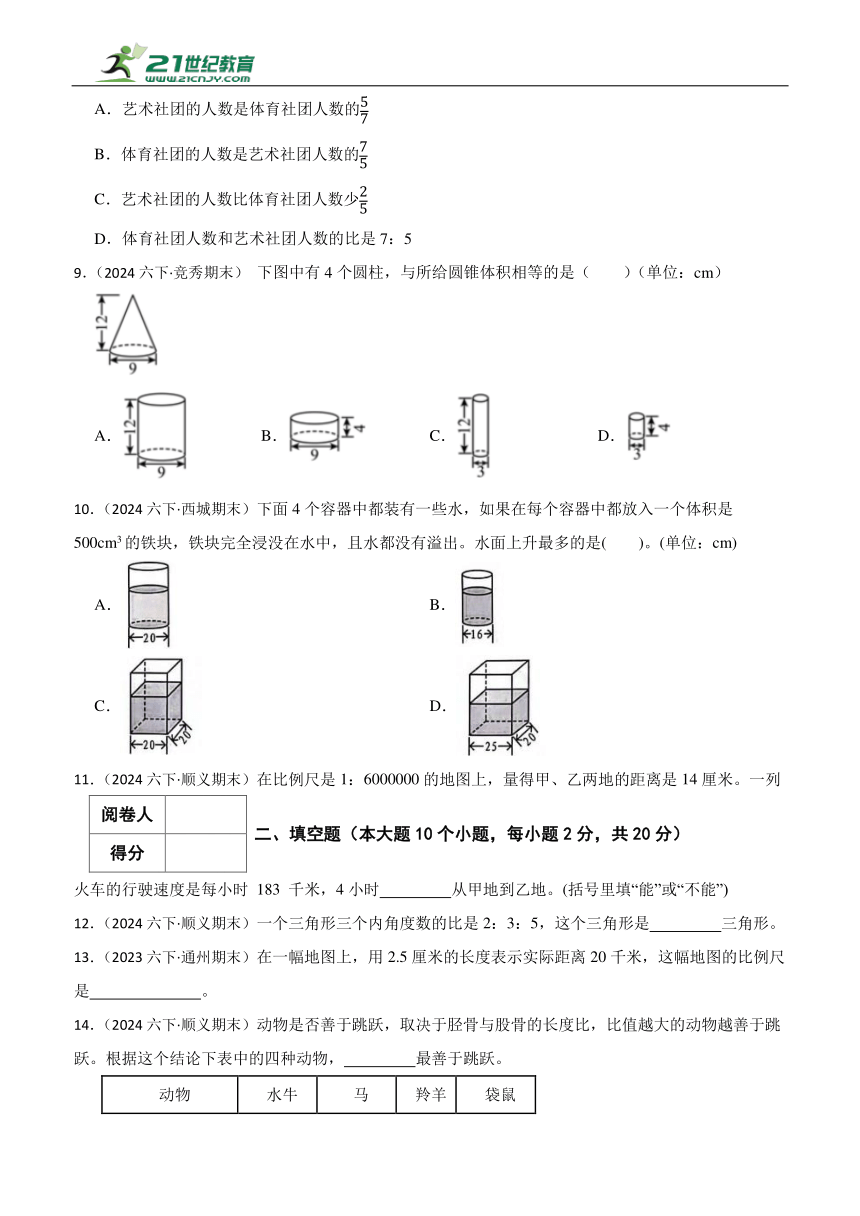
4.(2024六下·顺义期末)小华准备用下面的长方形硬纸板做一个无盖笔筒的侧面,有四个底面可选(如图所示),下面( )选项正确。(单位:厘米,接缝处忽略不计)
A.①②③④ B.①②④ C.①②③ D.②③④
5.(2024六下·西城期末) 一个精密仪器上的零件长度是5mm,画在图纸上的长度是2cm,这幅图纸的比例尺是( )
A.5:2 B.2:5 C.1:4 D.4:1
6.(2023六下·通州期末)圆柱的侧面展开图是正方形,这个圆柱的底面直径与高的比是( )
A.1:π B.2:π C.1:2 D.1:4
7.(2023六下·通州期末)一张长方形纸分别沿长和宽可以围成两个不同的圆柱,即甲圆柱和乙圆柱(如图),比较这两个圆柱的侧面积的大小,下面说法正确的是( ).
A.甲圆柱侧面积大 B.乙圆柱侧面积大
C.侧面积相等 D.不能确定
8.(2023六下·通州期末)学校社团中,体育社团的人数比艺术社团人数多。根据这个信息,四个同学分别说出了自己的想法,其中,说法错误的是( )。
A.艺术社团的人数是体育社团人数的
B.体育社团的人数是艺术社团人数的
C.艺术社团的人数比体育社团人数少
D.体育社团人数和艺术社团人数的比是7:5
9.(2024六下·竞秀期末) 下图中有4个圆柱,与所给圆锥体积相等的是( )(单位:cm)
A. B. C. D.
10.(2024六下·西城期末)下面4个容器中都装有一些水,如果在每个容器中都放入一个体积是 500cm3的铁块,铁块完全浸没在水中,且水都没有溢出。水面上升最多的是( )。(单位:cm)
A. B.
C. D.
阅卷人 二、填空题(本大题10个小题,每小题2分,共20分)
得分
11.(2024六下·顺义期末)在比例尺是1:6000000的地图上,量得甲、乙两地的距离是14厘米。一列火车的行驶速度是每小时 183 千米,4小时 从甲地到乙地。(括号里填“能”或“不能”)
12.(2024六下·顺义期末)一个三角形三个内角度数的比是2:3:5,这个三角形是 三角形。
13.(2023六下·通州期末)在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 。
14.(2024六下·顺义期末)动物是否善于跳跃,取决于胫骨与股骨的长度比,比值越大的动物越善于跳跃。根据这个结论下表中的四种动物, 最善于跳跃。
动物 水牛 马 羚羊 袋鼠
胫骨与股骨的比
15.(2024六下·顺义期末)把一个圆柱形木料削成一个最大的圆锥,削去部分的体积是 25.12立方厘米。原来圆柱形木料的体积是 立方厘米,削成的圆锥形木料的体积是 立方厘米。
16.(2024六下·西城期末) :16=0.75=15÷ = %= (填最简分数)
17.(2024六下·延庆期末)含糖率是10%的糖水,糖与水的比是 ,一杯 250 毫升的糖水,含糖 毫升。
18.(2024六下·延庆期末)下图表示一辆汽车行驶的路程和耗油量之间的关系。汽车行驶的路程和耗油量成 比例,汽车行驶 20千米,耗油 升。
19.(2024六下·延庆期末)下图中,涂色部分用分数表示是 ,用百分数表示是 ,用比表示是 ,用小数表示是 。
20.(2023六下·通州期末)一个等腰三角形的顶角和一个底角的比是4:1,那么这个三角形的顶角是 度,这个三角形按角分类是 三角形。
阅卷人 三、计算题(23分)
得分
21.(2024六下·延庆期末)解方程
⑴ ⑵
22.(2024六下·顺义期末)解比例2.5:×=8:
阅卷人 四、操作题(12分)
得分
23.(2024六下·西城期末)画一画、算一算。(π取3)
(1)王丽想用卡纸制作一个无盖的圆柱形笔筒。她用一张长是 24cm,宽是 18cm 的长方形卡纸做出笔筒的侧面(粘合处忽略不计)。请你在方格纸中用圆规画出笔筒底面的图形。(画出一种即可。)
(2)按照上面的方法制作出圆柱形笔筒,一共要用 cm2的卡纸。
阅卷人 五、解决问题(本大题6个小题,共35分)
得分
24.(2024六下·西城期末)阅读下面资料,解决问题,
生物在进化过程中,为了求得生存,动物的骨、植物的茎等都是空心的,而且内圆直径和外圆直径之比大约都是8:11。研究表明,当一根空心管子底面的内圆直径和外圆直径之比是8:11时最不容易弯曲。根据这个研究,人们制成了空心零件、自行车的车身架等,以达到耗费最少材料而使其最坚固的目的。
(1)按照上面的研究,工人师传制作了一种塑料零件(如下图)。这个零件底面的内圆直径是多少厘米?
(2)做这种塑料零件需要多少立方厘米的塑料?(π取3)
25.(2023·西城期末) 《考工记》是我国春秋战国时期的一部文献,记述了官营手工业各工种规范和制造工艺。馎(bó)是当时的一种重要农具,制造馎所需铜和锡的比是5:1,如果制造一件需要锡820克,需要铜多少克?
26.(2023六下·通州期末)沙漏是两个完全相同的圆锥形容器的组合体,单个圆锥容器高5厘米,漏口每秒可漏细沙0.05立方厘米,漏完全部细沙用时5分钟,这个沙漏的底面积是多少平方厘米?(细沙恰好装满单个圆锥)
27.(2023·西城期末) 工人准备在道路一侧安装栅栏,定制了500个大小相同的圆柱形木块。(π取3)
(1)如果给一个圆柱形木块的表面刷漆,需要刷漆的面积是多少平方分米?
(2)做这些圆柱形木块一共需要多少立方米的木料?(损耗忽略不计)
(3)将这些木块装箱,箱子的形状是一个正方体,从里面量棱长为8dm,这个箱最多能装多少个这样的圆柱形木块?
28.(2024六下·顺义期末)明明做一个实验。
步骤1:准备一个底面积是12平方厘米的圆柱形空水杯。
步骤2:放入一块底面积是9平方厘米,高是6厘米的圆锥形铅锤。
步骤3:向水杯里倒水,水面没(mò)过铅锤即可。(不倒满)
步骤 4:取出铅锤,水面下降
你能算出水面下降了多少厘米吗
29.(2024六下·顺义期末)一个工厂有三个车间,已知第一车间有 36 人,并且人数最多。
(1)以下三个关于车间人数的信息只有一个是准确的,准确的信息是( )。
A.第一车间人数比第三车间人数的少2人.
B.第一车间、第二车间、第三车间人数的比是4:2:3.
C.第一车间的人数占三个车间总人数的 30%。
(2)根据以上信息算一算,这个工厂三个车间共有多少人?
答案解析部分
1.C
解:A项:看一本书,看了的页数和没看的页数,不成比例;
B项:正方形的面积÷边长=边长,正方形的面积和边长,不成比例;
C项:圆柱的体积÷底面积=高(一定),圆柱的高一定,体积和底面积成正比例;
D项:底×高=平行四边形的面积(一定),平行四边形的面积一定,底和高成反比例。
故答案为:C。
观察图像是成正比例关系;判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
2.B
解:π×32×4÷3
=3×4×π
=12π
π×32×4-π×32×4÷3
=36π-12π
=24π
12π÷24π=12÷24=。
故答案为:B。
图1的体积=π×半径2×高÷3,图2的体积=π×半径2×高-π×半径2×高÷3,然后写出比,并且依据比的基本性质化简比。
3.D
解:A项:150÷1.5=100(个)(一定)加工零件的个数与工作时间成正比例关系,原题干说法正确;
B项:4×100=400(个),原题干说法正确;
C项:320÷100=3.2(小时),原题干说法正确;
D项:600÷5=120(个),120>100,点P不和点E、F、G一样在射线上,原题干说法错误。
故答案为:D。
A项:点O、E、F、G一样在同一条射线上,说明加工零件的个数与工作时间成正比例关系;
B项:N表示加工零件的个数=平均每小时加工零件的个数×加工的时间;
C项:M表示的时间= 加工零件的总个数÷平均每小时加工零件的个数;
D项:平均每小时加工零件的个数不是120,说明点P不和点E、F、G一样在射线上。
4.B
解:18.84÷3.14÷2
=6÷2
=3(厘米)
12.56÷3.14=4(厘米),可以选择①②④。
故答案为:B。
当12.84为底面周长时,底面半径=底面周长÷π÷2=3厘米,当12.56为底面周长时,底面直径=底面周长÷π=4厘米,所以可以选择①②④。
5.D
解:2cm=20mm,所以这幅图纸的比例尺是20mm:5mm=4:1。
故答案为:D。
先把单位进行换算,即2cm=20mm,所以这幅图纸的比例尺=图上距离:实际距离。
6.A
圆柱的侧面展开图是正方形,则底面周长=高,πd=h,
d:h=d:πd=(d÷d):(πd÷d)=1:π。
故答案为:A。
此题主要考查了圆柱侧面展开图的知识,圆柱的侧面展开图是一个长方形或正方形,当圆柱的侧面展开图是正方形,圆柱的底面周长与高相等,据此求出这个圆柱的底面直径与高的比。
7.C
甲圆柱的侧面积=乙圆柱的侧面积=长方形的面积。
故答案为:C。
用一张长方形纸分别沿长和宽可以围成两个不同的圆柱,两个圆柱的侧面积都是长方形的面积,据此解答。
8.C
把艺术社团的人数看作单位“1”,则体育社团的人数是1+=,
艺术社团比体育社团少:(-1)÷=。
故答案为:C。
根据条件“ 体育社团的人数比艺术社团人数多 ”可知,把艺术社团的人数看作单位“1”,则体育社团的人数是1+=,艺术社团的人数是体育社团人数的,体育社团人数和艺术社团人数的比是7:5,据此判断。
9.B
解:12÷3=4(cm),所以与圆锥体积相等的是B项中的圆锥。
故答案为:B。
等底等体积的圆柱和圆锥,圆锥的高是圆柱高的3倍;
等高等体积的圆柱和圆锥,圆锥的底面积是圆柱底面积的3倍。
10.B
解:A项:π×(20÷2)2=100π=314(平方厘米);
B项:π×(16÷2)2=64π=200.96(平方厘米);
C项:20×20=400(平方厘米);
D项:25×20=500(平方厘米);
500>400>314>200.96,则B项水面上升最多。
故答案为:B。
水面上升最多的容器底面积最少,所以分别计算出底面积,然后再比较大小;其中,圆柱的底面积=π×半径2,长方体的底面积=长×宽,正方体的底面积=棱长×棱长。
11.不能
解:14÷÷100000
=84000000÷100000
=840(千米)
183×4=732(千米)
840>732,那么4小时不能从甲地到乙地。
故答案为:不能。
甲地到乙地的路程=图上距离÷比例尺,一列火车4小时行驶的路程=火车的速度×行驶的时间,然后和总路程比较大小。
12.直角
解:180÷(2+3+5)×5
=180÷10×5
=18×5
=90(度),这个三角形是直角三角形。
故答案为:直角。
这个三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数,有一个角是直角的三角形是直角三角形。
13.1:800000
解:20千米=2000000厘米,比例尺是2.5:2000000=1:800000。
故答案为:1:800000。
先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可。
14.袋鼠
解:19:20=19÷20=0.95;
23:25=23÷25=0.92;
5:4=5÷4=1.25;
43:25=43÷25=1.72
1.72>1.25>0.95>0.92,袋鼠最善于跳跃。
故答案为:袋鼠。
求比值=比的前项÷比的后项,然后比较大小。
15.37.68;12.56
解:25.12÷2=12.56(立方厘米)
12.56×3=37.68(立方厘米)。
故答案为:37.68;12.56。
削成圆锥形木料的体积=削去部分的体积÷2,原来圆柱形木料的体积=削成圆锥形木料的体积×3。
16.12;20;75;
解:0.75×16=12;
15÷0.75=20;
0.75=75%==;
所以12:16=0.75=15÷20=75%=。
故答案为:12;20;75;。
比的前项=比的后项×比值;除数=被除数÷商;
小数化成分数,一位小数化成分母是10的分数,两位小数化成分母是100的分数,三位小数化成分母是1000的分数······,能约分的要约成最简分数;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号。
17.1:9;25
解:假设含糖率是10%的糖水的糖是1,则水是9,糖:水=1:9;
250×10%=25(毫升)。
故答案为:1:9;25。
假设含糖率是10%的糖水的糖是1,则水是9,糖:水=1:9;糖的体积=糖水的体积×含糖率。
18.正;2
解:10÷1=10(升),20÷2=10(升)(一定),汽车行驶的路程和耗油量成正比例;
汽车行驶 20千米,耗油2升。
故答案为:正;2。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;观察统计图可知:汽车行驶 20千米,耗油2升。
19.;25%;1:4;0.25
解:2÷8=;
=0.25=25%;
2÷8=2:8=1:4。
故答案为:;25%;1:4;0.25。
涂色部分占的分率=涂色部分的个数÷总个数=;
分数化成小数用分数的分子除以分母,
小数化成百分数,把小数的小数点向右移动两位,再加上百分号。
20.120;钝角
180°×=120°;
这个三角形按角分类是钝角三角形。
故答案为:120;钝角。
等腰三角形的两个底角相等,三角形的内角和是180°,三角形的内角和×顶角占三角形内角和的分率=顶角的度数;
三角形按角分类,可以分为锐角三角形、直角三角形、钝角三角形。有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形;三个角都是锐角的三角形是锐角三角形,据此解答。
21.解:(1)+6x=
6x=-
6x=
x=÷6
x=
(2):=x:0.9
解:x=0.9×
x=
x=÷
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先应用等式的性质1,等式两边同时减去,然后应用等式的性质2,等式两边同时除以6;
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质解比例。
22.解:2.5:x=8:
8x=2.5×
8x=2
x=2÷8
x=
比例的基本性质:在比例里,两个内项积等于两个外项积;依据比例的基本性质解比例。
23.(1)解:24÷2÷3
=12÷3
=4(厘米)
(2)480
解:(2)24×18+3×42
=432+48
=480(平方厘米)。
故答案为:(2)480。
(1)所画圆的半径=底面周长÷π÷2,即画一个底面半径4厘米的圆形;
(2)一共要用卡纸的面积=侧面长方形的长×宽+π×半径2。
24.(1)解:22÷11×8
=2×8
=16(厘米)
答:这个零件底面的内圆直径是16厘米。
(2)解:22÷2=11(厘米)
16÷2=8(厘米)
3×(112-82)×40
=3×57×40
=171×40
=6840(立方厘米)
答:做这种塑料零件需要6840立方厘米的塑料。
(1)这个零件底面的内圆直径=外圆直径÷外圆占的份数×内圆占的份数;
(2)做这种塑料零件需要塑料的体积=π×(R2-r2)×这个塑料零件的高。
25.解:820÷1×5
=820×5
=4100(克)
答:需要铜4100克。
需要铜的克数=锡的克数÷制造馎所需锡占的份数×制造馎所需铜占的份数,据此代入数值作答即可。
26.解:5分钟=300秒
0.05×300=15(立方厘米)
15×3÷5
=45÷5
=9(平方厘米)
答:这个沙漏的底面积是9平方厘米。
根据1分钟=60秒,先将分化成秒,然后用每秒可漏细沙的体积×时间=一共漏沙的体积,也就是圆锥容器的容积,圆锥容器的容积×3÷高=底面积,据此列式解答。
27.(1)解:(1.6÷2)2×3+1.6×3×4
=0.64×3+4.8×4
=1.92+19.2
=21.12(平方分米)
答:需要刷漆的面积是21.12平方分米。
(2)解:(1.6÷2)2×3×4
=0.64×12
=7.68
7.68×500=3840(立方分米)
3840立方分米=3.84立方米
答:做这些圆柱形木块一共需要3.84立方米的木料。
(3)解:8÷1.6=5(个)
8÷4=2(个)
5×5×2
=25×2
=50(个)
答:这个箱最多能装50个这样的圆柱形木块。
(1)需要刷漆的面积=底面积+侧面积,其中底面积=(底面直径÷2)2×π,侧面积=底面直径×π×高,据此代入数值作答即可;
(2)做1个圆柱形木块需要木材的体积=(底面直径÷2)2×π×高,那么做这些木块一共需要木材的体积=做1个圆柱形木块需要木材的体积×一共定制的个数,然后进行单位换算,即1立方米=1000立方分米;
(3)箱子的一条棱里面有圆柱底面直径的个数=正方体箱子的棱长÷底面直径,箱子的一条棱里面有圆柱高的个数=正方体箱子的棱长÷圆柱的高,那么这个箱最多能装圆柱形木块的个数=箱子的一条棱里面有圆柱底面直径的个数×箱子的一条棱里面有圆柱底面直径的个数×箱子的一条棱里面有圆柱高的个数。
28.解:×9×6÷12
=18÷12
=1.5(厘米)
答:水面下降了1.5厘米。
下降水的体积等于圆锥的体积,圆锥的体积=底面积×高×,然后除以圆柱的底面积,就是下降水的高度。
29.(1)B
(2)解:36÷4×(4+2+3)
=9×9
=81(人)
答:这个工厂三个车间共有81人。
解:(1)A项:(36+2)÷
=38÷
=95(人),因为一车间的人数最多,则这个信息不准确;
B项:信息准确;
C项:1-30%=70%,不一定是第一车间的人数最多,则这个信息不准确。
故答案为:B。
(1)A项:第三车间的人数=(第一车间的人数+2)÷,得到的人数比第一车间的人数多,所以错误;
B项:正确;
C项:不一定是第一车间的人数最多,则这个信息不准确。
(2) 这个工厂三个车间共有的人数=第一车间的人数÷所占的份数×总份数。
2024-2025学年六年级下册期末检测卷(北京版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
1.(2024六下·西城期末)x和y是两种相关联的量,它们的关系可以用下面的图象表示。那么,这个图象可能表示的是( )的关系。
A.看一本书,看了的页数和没看的页数
B.正方形的面积和边长
C.圆柱的高一定,体积和底面积
D.平行四边形的面积一定,底和高
2.(2024六下·延庆期末)一个直角三角形,两条直角边分别是4cm和 3cm。以下面两种方式旋转得到立体图形(每条旋转轴垂直于底边),旋转后图1的体积是图2体积的( )
A. B. C. D.
3.(2024六下·顺义期末)小李加工一批零件,工作时间与加工零件的个数的关系(如下图),下列说法错误的是( )
A.加工零件的个数与工作时间成正比例关系
B.N表示400个零件
C.M表示3.2小时
D.如果有一点Р表示5小时做了600个零件,那么点P一定会和点E、F、G一样在射线l上
4.(2024六下·顺义期末)小华准备用下面的长方形硬纸板做一个无盖笔筒的侧面,有四个底面可选(如图所示),下面( )选项正确。(单位:厘米,接缝处忽略不计)
A.①②③④ B.①②④ C.①②③ D.②③④
5.(2024六下·西城期末) 一个精密仪器上的零件长度是5mm,画在图纸上的长度是2cm,这幅图纸的比例尺是( )
A.5:2 B.2:5 C.1:4 D.4:1
6.(2023六下·通州期末)圆柱的侧面展开图是正方形,这个圆柱的底面直径与高的比是( )
A.1:π B.2:π C.1:2 D.1:4
7.(2023六下·通州期末)一张长方形纸分别沿长和宽可以围成两个不同的圆柱,即甲圆柱和乙圆柱(如图),比较这两个圆柱的侧面积的大小,下面说法正确的是( ).
A.甲圆柱侧面积大 B.乙圆柱侧面积大
C.侧面积相等 D.不能确定
8.(2023六下·通州期末)学校社团中,体育社团的人数比艺术社团人数多。根据这个信息,四个同学分别说出了自己的想法,其中,说法错误的是( )。
A.艺术社团的人数是体育社团人数的
B.体育社团的人数是艺术社团人数的
C.艺术社团的人数比体育社团人数少
D.体育社团人数和艺术社团人数的比是7:5
9.(2024六下·竞秀期末) 下图中有4个圆柱,与所给圆锥体积相等的是( )(单位:cm)
A. B. C. D.
10.(2024六下·西城期末)下面4个容器中都装有一些水,如果在每个容器中都放入一个体积是 500cm3的铁块,铁块完全浸没在水中,且水都没有溢出。水面上升最多的是( )。(单位:cm)
A. B.
C. D.
阅卷人 二、填空题(本大题10个小题,每小题2分,共20分)
得分
11.(2024六下·顺义期末)在比例尺是1:6000000的地图上,量得甲、乙两地的距离是14厘米。一列火车的行驶速度是每小时 183 千米,4小时 从甲地到乙地。(括号里填“能”或“不能”)
12.(2024六下·顺义期末)一个三角形三个内角度数的比是2:3:5,这个三角形是 三角形。
13.(2023六下·通州期末)在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 。
14.(2024六下·顺义期末)动物是否善于跳跃,取决于胫骨与股骨的长度比,比值越大的动物越善于跳跃。根据这个结论下表中的四种动物, 最善于跳跃。
动物 水牛 马 羚羊 袋鼠
胫骨与股骨的比
15.(2024六下·顺义期末)把一个圆柱形木料削成一个最大的圆锥,削去部分的体积是 25.12立方厘米。原来圆柱形木料的体积是 立方厘米,削成的圆锥形木料的体积是 立方厘米。
16.(2024六下·西城期末) :16=0.75=15÷ = %= (填最简分数)
17.(2024六下·延庆期末)含糖率是10%的糖水,糖与水的比是 ,一杯 250 毫升的糖水,含糖 毫升。
18.(2024六下·延庆期末)下图表示一辆汽车行驶的路程和耗油量之间的关系。汽车行驶的路程和耗油量成 比例,汽车行驶 20千米,耗油 升。
19.(2024六下·延庆期末)下图中,涂色部分用分数表示是 ,用百分数表示是 ,用比表示是 ,用小数表示是 。
20.(2023六下·通州期末)一个等腰三角形的顶角和一个底角的比是4:1,那么这个三角形的顶角是 度,这个三角形按角分类是 三角形。
阅卷人 三、计算题(23分)
得分
21.(2024六下·延庆期末)解方程
⑴ ⑵
22.(2024六下·顺义期末)解比例2.5:×=8:
阅卷人 四、操作题(12分)
得分
23.(2024六下·西城期末)画一画、算一算。(π取3)
(1)王丽想用卡纸制作一个无盖的圆柱形笔筒。她用一张长是 24cm,宽是 18cm 的长方形卡纸做出笔筒的侧面(粘合处忽略不计)。请你在方格纸中用圆规画出笔筒底面的图形。(画出一种即可。)
(2)按照上面的方法制作出圆柱形笔筒,一共要用 cm2的卡纸。
阅卷人 五、解决问题(本大题6个小题,共35分)
得分
24.(2024六下·西城期末)阅读下面资料,解决问题,
生物在进化过程中,为了求得生存,动物的骨、植物的茎等都是空心的,而且内圆直径和外圆直径之比大约都是8:11。研究表明,当一根空心管子底面的内圆直径和外圆直径之比是8:11时最不容易弯曲。根据这个研究,人们制成了空心零件、自行车的车身架等,以达到耗费最少材料而使其最坚固的目的。
(1)按照上面的研究,工人师传制作了一种塑料零件(如下图)。这个零件底面的内圆直径是多少厘米?
(2)做这种塑料零件需要多少立方厘米的塑料?(π取3)
25.(2023·西城期末) 《考工记》是我国春秋战国时期的一部文献,记述了官营手工业各工种规范和制造工艺。馎(bó)是当时的一种重要农具,制造馎所需铜和锡的比是5:1,如果制造一件需要锡820克,需要铜多少克?
26.(2023六下·通州期末)沙漏是两个完全相同的圆锥形容器的组合体,单个圆锥容器高5厘米,漏口每秒可漏细沙0.05立方厘米,漏完全部细沙用时5分钟,这个沙漏的底面积是多少平方厘米?(细沙恰好装满单个圆锥)
27.(2023·西城期末) 工人准备在道路一侧安装栅栏,定制了500个大小相同的圆柱形木块。(π取3)
(1)如果给一个圆柱形木块的表面刷漆,需要刷漆的面积是多少平方分米?
(2)做这些圆柱形木块一共需要多少立方米的木料?(损耗忽略不计)
(3)将这些木块装箱,箱子的形状是一个正方体,从里面量棱长为8dm,这个箱最多能装多少个这样的圆柱形木块?
28.(2024六下·顺义期末)明明做一个实验。
步骤1:准备一个底面积是12平方厘米的圆柱形空水杯。
步骤2:放入一块底面积是9平方厘米,高是6厘米的圆锥形铅锤。
步骤3:向水杯里倒水,水面没(mò)过铅锤即可。(不倒满)
步骤 4:取出铅锤,水面下降
你能算出水面下降了多少厘米吗
29.(2024六下·顺义期末)一个工厂有三个车间,已知第一车间有 36 人,并且人数最多。
(1)以下三个关于车间人数的信息只有一个是准确的,准确的信息是( )。
A.第一车间人数比第三车间人数的少2人.
B.第一车间、第二车间、第三车间人数的比是4:2:3.
C.第一车间的人数占三个车间总人数的 30%。
(2)根据以上信息算一算,这个工厂三个车间共有多少人?
答案解析部分
1.C
解:A项:看一本书,看了的页数和没看的页数,不成比例;
B项:正方形的面积÷边长=边长,正方形的面积和边长,不成比例;
C项:圆柱的体积÷底面积=高(一定),圆柱的高一定,体积和底面积成正比例;
D项:底×高=平行四边形的面积(一定),平行四边形的面积一定,底和高成反比例。
故答案为:C。
观察图像是成正比例关系;判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
2.B
解:π×32×4÷3
=3×4×π
=12π
π×32×4-π×32×4÷3
=36π-12π
=24π
12π÷24π=12÷24=。
故答案为:B。
图1的体积=π×半径2×高÷3,图2的体积=π×半径2×高-π×半径2×高÷3,然后写出比,并且依据比的基本性质化简比。
3.D
解:A项:150÷1.5=100(个)(一定)加工零件的个数与工作时间成正比例关系,原题干说法正确;
B项:4×100=400(个),原题干说法正确;
C项:320÷100=3.2(小时),原题干说法正确;
D项:600÷5=120(个),120>100,点P不和点E、F、G一样在射线上,原题干说法错误。
故答案为:D。
A项:点O、E、F、G一样在同一条射线上,说明加工零件的个数与工作时间成正比例关系;
B项:N表示加工零件的个数=平均每小时加工零件的个数×加工的时间;
C项:M表示的时间= 加工零件的总个数÷平均每小时加工零件的个数;
D项:平均每小时加工零件的个数不是120,说明点P不和点E、F、G一样在射线上。
4.B
解:18.84÷3.14÷2
=6÷2
=3(厘米)
12.56÷3.14=4(厘米),可以选择①②④。
故答案为:B。
当12.84为底面周长时,底面半径=底面周长÷π÷2=3厘米,当12.56为底面周长时,底面直径=底面周长÷π=4厘米,所以可以选择①②④。
5.D
解:2cm=20mm,所以这幅图纸的比例尺是20mm:5mm=4:1。
故答案为:D。
先把单位进行换算,即2cm=20mm,所以这幅图纸的比例尺=图上距离:实际距离。
6.A
圆柱的侧面展开图是正方形,则底面周长=高,πd=h,
d:h=d:πd=(d÷d):(πd÷d)=1:π。
故答案为:A。
此题主要考查了圆柱侧面展开图的知识,圆柱的侧面展开图是一个长方形或正方形,当圆柱的侧面展开图是正方形,圆柱的底面周长与高相等,据此求出这个圆柱的底面直径与高的比。
7.C
甲圆柱的侧面积=乙圆柱的侧面积=长方形的面积。
故答案为:C。
用一张长方形纸分别沿长和宽可以围成两个不同的圆柱,两个圆柱的侧面积都是长方形的面积,据此解答。
8.C
把艺术社团的人数看作单位“1”,则体育社团的人数是1+=,
艺术社团比体育社团少:(-1)÷=。
故答案为:C。
根据条件“ 体育社团的人数比艺术社团人数多 ”可知,把艺术社团的人数看作单位“1”,则体育社团的人数是1+=,艺术社团的人数是体育社团人数的,体育社团人数和艺术社团人数的比是7:5,据此判断。
9.B
解:12÷3=4(cm),所以与圆锥体积相等的是B项中的圆锥。
故答案为:B。
等底等体积的圆柱和圆锥,圆锥的高是圆柱高的3倍;
等高等体积的圆柱和圆锥,圆锥的底面积是圆柱底面积的3倍。
10.B
解:A项:π×(20÷2)2=100π=314(平方厘米);
B项:π×(16÷2)2=64π=200.96(平方厘米);
C项:20×20=400(平方厘米);
D项:25×20=500(平方厘米);
500>400>314>200.96,则B项水面上升最多。
故答案为:B。
水面上升最多的容器底面积最少,所以分别计算出底面积,然后再比较大小;其中,圆柱的底面积=π×半径2,长方体的底面积=长×宽,正方体的底面积=棱长×棱长。
11.不能
解:14÷÷100000
=84000000÷100000
=840(千米)
183×4=732(千米)
840>732,那么4小时不能从甲地到乙地。
故答案为:不能。
甲地到乙地的路程=图上距离÷比例尺,一列火车4小时行驶的路程=火车的速度×行驶的时间,然后和总路程比较大小。
12.直角
解:180÷(2+3+5)×5
=180÷10×5
=18×5
=90(度),这个三角形是直角三角形。
故答案为:直角。
这个三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数,有一个角是直角的三角形是直角三角形。
13.1:800000
解:20千米=2000000厘米,比例尺是2.5:2000000=1:800000。
故答案为:1:800000。
先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可。
14.袋鼠
解:19:20=19÷20=0.95;
23:25=23÷25=0.92;
5:4=5÷4=1.25;
43:25=43÷25=1.72
1.72>1.25>0.95>0.92,袋鼠最善于跳跃。
故答案为:袋鼠。
求比值=比的前项÷比的后项,然后比较大小。
15.37.68;12.56
解:25.12÷2=12.56(立方厘米)
12.56×3=37.68(立方厘米)。
故答案为:37.68;12.56。
削成圆锥形木料的体积=削去部分的体积÷2,原来圆柱形木料的体积=削成圆锥形木料的体积×3。
16.12;20;75;
解:0.75×16=12;
15÷0.75=20;
0.75=75%==;
所以12:16=0.75=15÷20=75%=。
故答案为:12;20;75;。
比的前项=比的后项×比值;除数=被除数÷商;
小数化成分数,一位小数化成分母是10的分数,两位小数化成分母是100的分数,三位小数化成分母是1000的分数······,能约分的要约成最简分数;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号。
17.1:9;25
解:假设含糖率是10%的糖水的糖是1,则水是9,糖:水=1:9;
250×10%=25(毫升)。
故答案为:1:9;25。
假设含糖率是10%的糖水的糖是1,则水是9,糖:水=1:9;糖的体积=糖水的体积×含糖率。
18.正;2
解:10÷1=10(升),20÷2=10(升)(一定),汽车行驶的路程和耗油量成正比例;
汽车行驶 20千米,耗油2升。
故答案为:正;2。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;观察统计图可知:汽车行驶 20千米,耗油2升。
19.;25%;1:4;0.25
解:2÷8=;
=0.25=25%;
2÷8=2:8=1:4。
故答案为:;25%;1:4;0.25。
涂色部分占的分率=涂色部分的个数÷总个数=;
分数化成小数用分数的分子除以分母,
小数化成百分数,把小数的小数点向右移动两位,再加上百分号。
20.120;钝角
180°×=120°;
这个三角形按角分类是钝角三角形。
故答案为:120;钝角。
等腰三角形的两个底角相等,三角形的内角和是180°,三角形的内角和×顶角占三角形内角和的分率=顶角的度数;
三角形按角分类,可以分为锐角三角形、直角三角形、钝角三角形。有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形;三个角都是锐角的三角形是锐角三角形,据此解答。
21.解:(1)+6x=
6x=-
6x=
x=÷6
x=
(2):=x:0.9
解:x=0.9×
x=
x=÷
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先应用等式的性质1,等式两边同时减去,然后应用等式的性质2,等式两边同时除以6;
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质解比例。
22.解:2.5:x=8:
8x=2.5×
8x=2
x=2÷8
x=
比例的基本性质:在比例里,两个内项积等于两个外项积;依据比例的基本性质解比例。
23.(1)解:24÷2÷3
=12÷3
=4(厘米)
(2)480
解:(2)24×18+3×42
=432+48
=480(平方厘米)。
故答案为:(2)480。
(1)所画圆的半径=底面周长÷π÷2,即画一个底面半径4厘米的圆形;
(2)一共要用卡纸的面积=侧面长方形的长×宽+π×半径2。
24.(1)解:22÷11×8
=2×8
=16(厘米)
答:这个零件底面的内圆直径是16厘米。
(2)解:22÷2=11(厘米)
16÷2=8(厘米)
3×(112-82)×40
=3×57×40
=171×40
=6840(立方厘米)
答:做这种塑料零件需要6840立方厘米的塑料。
(1)这个零件底面的内圆直径=外圆直径÷外圆占的份数×内圆占的份数;
(2)做这种塑料零件需要塑料的体积=π×(R2-r2)×这个塑料零件的高。
25.解:820÷1×5
=820×5
=4100(克)
答:需要铜4100克。
需要铜的克数=锡的克数÷制造馎所需锡占的份数×制造馎所需铜占的份数,据此代入数值作答即可。
26.解:5分钟=300秒
0.05×300=15(立方厘米)
15×3÷5
=45÷5
=9(平方厘米)
答:这个沙漏的底面积是9平方厘米。
根据1分钟=60秒,先将分化成秒,然后用每秒可漏细沙的体积×时间=一共漏沙的体积,也就是圆锥容器的容积,圆锥容器的容积×3÷高=底面积,据此列式解答。
27.(1)解:(1.6÷2)2×3+1.6×3×4
=0.64×3+4.8×4
=1.92+19.2
=21.12(平方分米)
答:需要刷漆的面积是21.12平方分米。
(2)解:(1.6÷2)2×3×4
=0.64×12
=7.68
7.68×500=3840(立方分米)
3840立方分米=3.84立方米
答:做这些圆柱形木块一共需要3.84立方米的木料。
(3)解:8÷1.6=5(个)
8÷4=2(个)
5×5×2
=25×2
=50(个)
答:这个箱最多能装50个这样的圆柱形木块。
(1)需要刷漆的面积=底面积+侧面积,其中底面积=(底面直径÷2)2×π,侧面积=底面直径×π×高,据此代入数值作答即可;
(2)做1个圆柱形木块需要木材的体积=(底面直径÷2)2×π×高,那么做这些木块一共需要木材的体积=做1个圆柱形木块需要木材的体积×一共定制的个数,然后进行单位换算,即1立方米=1000立方分米;
(3)箱子的一条棱里面有圆柱底面直径的个数=正方体箱子的棱长÷底面直径,箱子的一条棱里面有圆柱高的个数=正方体箱子的棱长÷圆柱的高,那么这个箱最多能装圆柱形木块的个数=箱子的一条棱里面有圆柱底面直径的个数×箱子的一条棱里面有圆柱底面直径的个数×箱子的一条棱里面有圆柱高的个数。
28.解:×9×6÷12
=18÷12
=1.5(厘米)
答:水面下降了1.5厘米。
下降水的体积等于圆锥的体积,圆锥的体积=底面积×高×,然后除以圆柱的底面积,就是下降水的高度。
29.(1)B
(2)解:36÷4×(4+2+3)
=9×9
=81(人)
答:这个工厂三个车间共有81人。
解:(1)A项:(36+2)÷
=38÷
=95(人),因为一车间的人数最多,则这个信息不准确;
B项:信息准确;
C项:1-30%=70%,不一定是第一车间的人数最多,则这个信息不准确。
故答案为:B。
(1)A项:第三车间的人数=(第一车间的人数+2)÷,得到的人数比第一车间的人数多,所以错误;
B项:正确;
C项:不一定是第一车间的人数最多,则这个信息不准确。
(2) 这个工厂三个车间共有的人数=第一车间的人数÷所占的份数×总份数。
同课章节目录
