期末检测卷(含答案)---2024-2025学年五年级数学下册真题重组检测卷(北京版)
文档属性
| 名称 | 期末检测卷(含答案)---2024-2025学年五年级数学下册真题重组检测卷(北京版) |

|
|
| 格式 | docx | ||
| 文件大小 | 568.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 00:00:00 | ||
图片预览



文档简介
保密★启用前
2024-2025学年五年级下册期末检测卷(北京版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
期末检测卷---2024-2025学年五年级数学下册真题重组检测卷(北京版)
一、单选题
1.(2023五下·东城期末)小明用27个1cm3的小正方体拼成一个大正方体,小利从大正方体上拿走一个1cm3的小正方体,形成新几何体的表面积可能比原来的大正方体( )。
A.少了2cm2 B.少了4cm2 C.多了3cm2 D.多了4cm2
2.(2024五下·门头沟期末)的分子加上5,要使分数大小不变,分母( )
A.应加上5 B.应加上6 C.应不变 D.无法确定
3.(2024五下·昌平期末)下图是一个长方体纸盒的上面,这个长方体纸盒有两个相对的面是正方形。这个长方体纸盒的棱长总和最大是( )cm。(可以先画一画长方体,再解决问题)
A.36 B.56 C.76 D.96
4.(2024五下·昌平期末)歌德巴赫猜想被誉为“数学皇冠上的明珠",这一猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中能反映这个猜想的是( )。
A.4=1+3 B.13=2+11 C.54 =3+51 D.36 =7+29
5.(2024五下·朝阳期末)下面提供的材料正好能拼成长方体的是( )
A. B.
C. D.
6.(2024五下·朝阳期末)秦始皇陵及兵马俑被誉为“世界第八大奇迹”,其中二号兵马俑坑第三单元有 264个步兵佣。用下面的方法数这些兵马俑,不能正好数完的是( )
A.2个2个地数 B.4个4个地数 C.3个3个地数 D.5个5个地数
7.(2024五下·东城期末)五年级的同学们准备去郊外春游,老师要求每位同学都要带足够的水。小明的妈妈给他准备了一瓶2升的矿泉水,为了携带方便小明需要把水分装到小瓶中,如果每个小瓶装550毫升,那么他至少需要( )个这样的小瓶。
A.2 B.3 C.4 D.5
8.(2024五下·房山期末)以下问题中,可以用算式解决的是( )
A.某城市九月雨天天数占全月的,晴天天数比雨天天数多全月的,雨天和晴天的天数共占全月的几分之儿?
B.一瓶2升的果汁,第一次喝了这瓶果汁的,第二次喝了了升,两次共喝这瓶果汁的几分之几?
C.君一本书,第一天看全书的,第二天看全书的,还剩下全书的几分之几没看?
D.一批货物,第一次运走吨,第二次运走吨,两次共运走多少吨?
9.(2024五下·房山期末)把分数的分子加上6、要使分数的大小不变、分母应( )
A.加上6 B.加上16 C.乘2 D.乘6
10.(2024五下·房山期末)芳芳将一个正方体盒子(如下图)完全展开,得到的展开图不可能是( )
A. B.
C. D.
阅卷人 二、填空题(本大题10个小题,每小题2分,共20分)
得分
11.(2024五下·门头沟期末)典典在文献阅读的过程中,遇到了一些表达年龄称谓的词,如“花甲”、“古稀”、“耄(mào)耋(dié)”……经过查阅,典典了解到:六十岁为“花甲”,七十岁为“古稀”,八九十岁为“耄(mào)耋(dié)”。典典)岁。的爷爷已过古稀,未及耄,且年龄既是2的倍数又有因数3,典典的爷爷最小 岁。
12.(2024五下·昌平期末)中国灯笼是一种古老的传统工艺品。乐乐用一根24dm长的铁丝了一个正方体灯笼框架,这个正方体灯笼的棱长是 dm,如果给这个灯笼的四周围上灯笼布 (上下面空着),至少需要 平方分米的灯笼布。
13.(2024五下·门头沟期末)0.32m3= dm3 300毫升= 升 40秒= 分
14.(2024五下·朝阳期末)一杯纯果汁,小亮喝了半杯后,兑满水又喝了杯,他一共喝水 杯。
15.(2024五下·朝阳期末)端午节是每年的农历五月初五,是我国首个入选非遗的节日。端午节前夕,圆圆家一共包了 24 个蛋黄粽和 36 个蜜枣粽,他们想把粽子分装成礼盒送给亲朋好友品尝。如果每盒里都有这两种口味的粽子,且分完后都没有剩余,他们最多能分装出 个同样的粽子礼盒。
16.(2024五下·东城期末)为了弘扬中华传统文化,少年宫开设了古诗词鉴资班。王红每3天上一次唐诗鉴赏班,张亮每隔5天上一次宋词鉴资班。2024年4月1日是两人同一天学习古诗词的日子,4月里他们共有 次同一天学习古诗词。
17.(2024五下·丰台期末)学校门厅有一个长 20分米,宽12分米的长方形宣传栏。如果把同学们用完全相同的正方形纸完成的书画作品,既不重叠、也无缝隙地正好贴满宣传栏,正方形纸的边长最大是 分米。
18.(2024五下·丰台期末)一瓶矿泉水的净含量是 600mL,相当于 L,可以写成 dm3
19.(2024五下·丰台期末)比5小的质数有 和 。
20.(2024五下·顺义期末)把一张正方形纸连续剪6次,依次剪下它的,还剩下这张正方形纸的 。
阅卷人 三、计算题(23分)
得分
21.(2024五下·昌平期末)口算
22.(2024五下·东城期末)脱式计算下面各题。
23.
阅卷人 四、操作题(12分)
得分
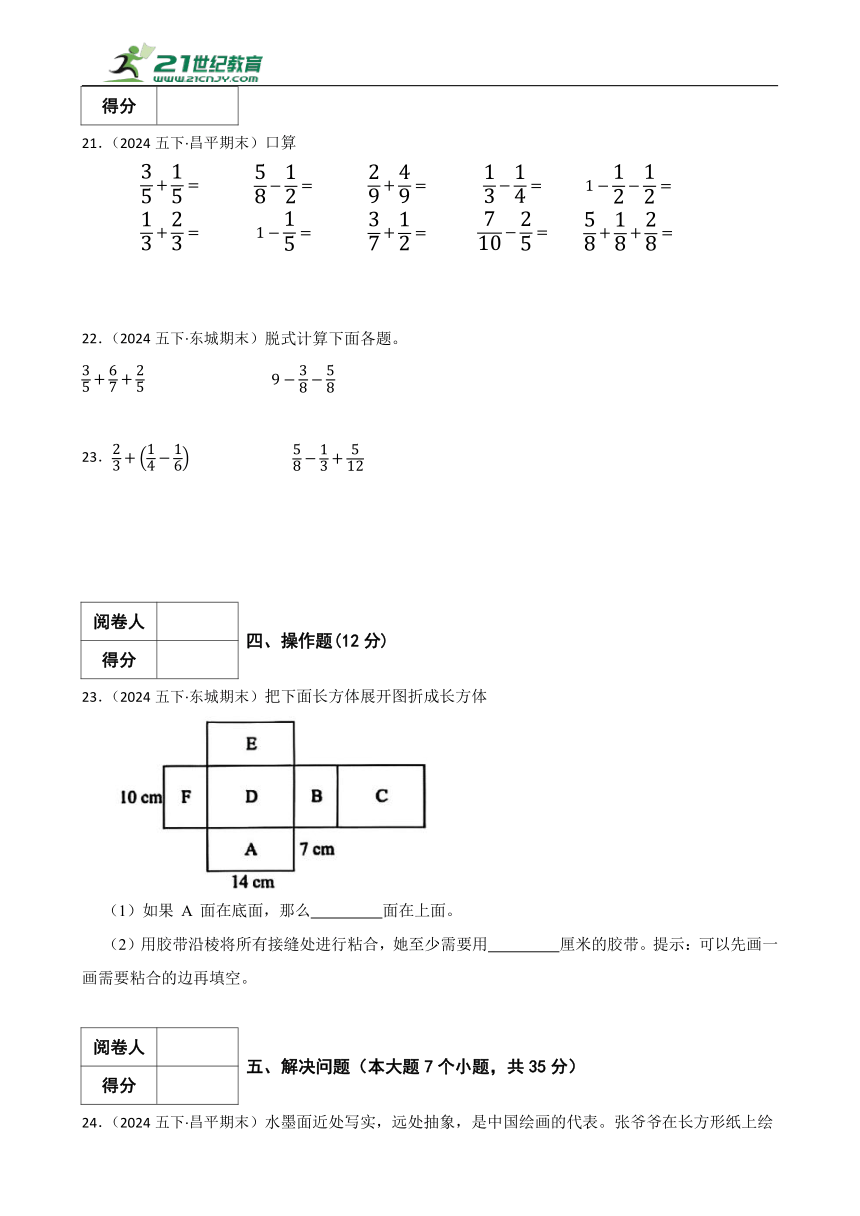
23.(2024五下·东城期末)把下面长方体展开图折成长方体
(1)如果 A 面在底面,那么 面在上面。
(2)用胶带沿棱将所有接缝处进行粘合,她至少需要用 厘米的胶带。提示:可以先画一画需要粘合的边再填空。
阅卷人 五、解决问题(本大题7个小题,共35分)
得分
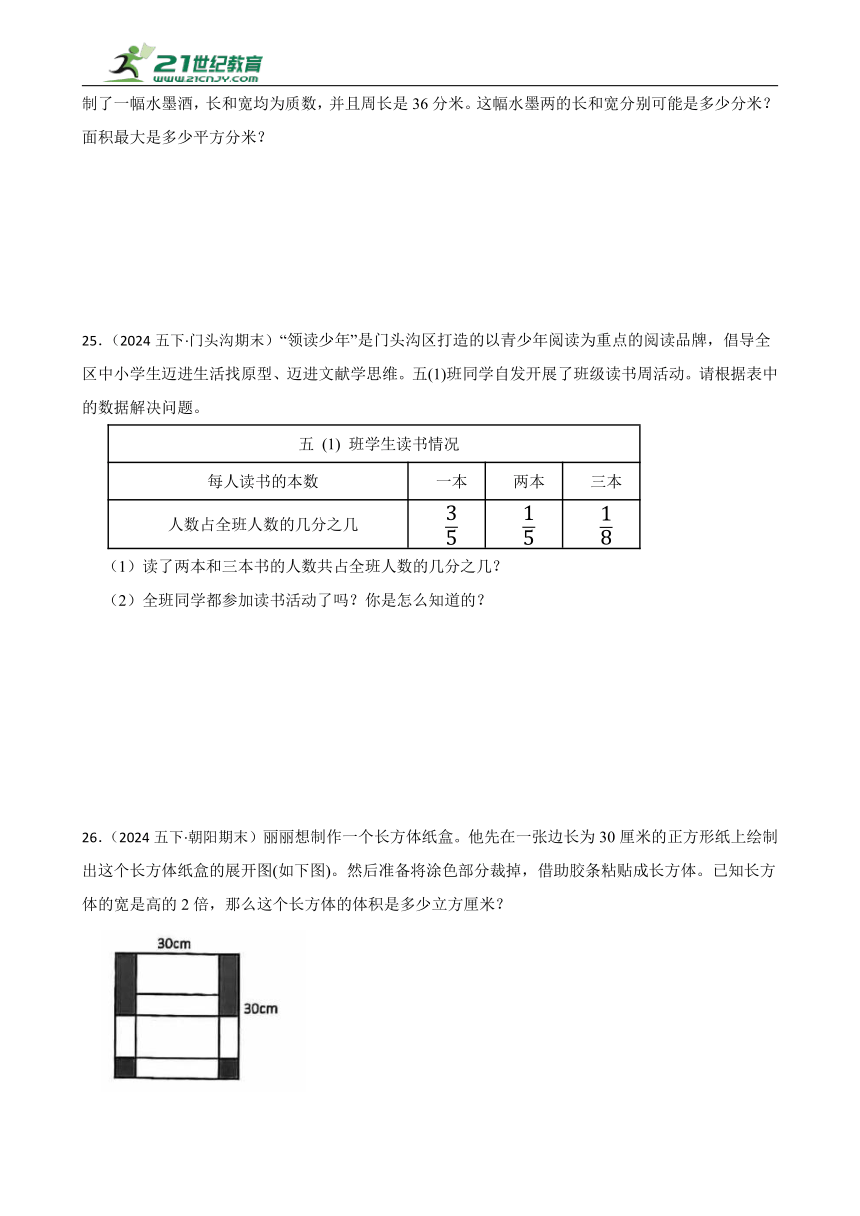
24.(2024五下·昌平期末)水墨面近处写实,远处抽象,是中国绘画的代表。张爷爷在长方形纸上绘制了一幅水墨酒,长和宽均为质数,并且周长是36分米。这幅水墨两的长和宽分别可能是多少分米?面积最大是多少平方分米?
25.(2024五下·门头沟期末)“领读少年”是门头沟区打造的以青少年阅读为重点的阅读品牌,倡导全区中小学生迈进生活找原型、迈进文献学思维。五(1)班同学自发开展了班级读书周活动。请根据表中的数据解决问题。
五 (1) 班学生读书情况
每人读书的本数 一本 两本 三本
人数占全班人数的几分之几
(1)读了两本和三本书的人数共占全班人数的几分之几?
(2)全班同学都参加读书活动了吗?你是怎么知道的?
26.(2024五下·朝阳期末)丽丽想制作一个长方体纸盒。他先在一张边长为30厘米的正方形纸上绘制出这个长方体纸盒的展开图(如下图)。然后准备将涂色部分裁掉,借助胶条粘贴成长方体。已知长方体的宽是高的2倍,那么这个长方体的体积是多少立方厘米?
27.(2024五下·朝阳期末)
(1)根据统计图,2014-2023年全国生活用水量呈 趋势。
(2)比前一年的用水量增加最多的年份是 年。
(3)请你预测 2024 年全国生活用水量,并写出理由。
28.(2024五下·东城期末)四月份有18天晴天,5天阴天,其余的是雨天。晴天的天数占这个月总天数的几分之几?
29.(2024五下·丰台期末)肥胖影响青少年的身心健康。在常规体检中,乐乐和强强的健康状况为“超重”,体检医生提示他们需要加强体育锻炼、注意健康饮食。为此,乐乐和强强每天进行了至少一小时的体育运动,并将一月至五月每天的各类食物摄入量和阶段性的体重监测情况进行了记录,如下面两幅统计图所示:
(1)乐乐和强强每天摄入 类食物相差最多。
(2)乐乐每天肉类的摄入量是强强的 。
(3)请你结合两幅图中的数据判断谁的体重下降的比较快,并分析可能的原因。
30.(2024五下·密云期末)工人要将长15厘米,宽和高都是3厘米的长方体牙盒装人纸箱中。纸箱里面的尺寸如图,(单位:厘米)。这个纸箱最多能装多少个这种牙膏盒?
答案解析部分
1.D
1×1×4
=1×4
=4(cm2)
故答案为:D。
根据题意可知,小明用27个1cm3的小正方体拼成一个大正方体,正方体的棱长是3cm,如果拿正中间的,表面积会比原来的大正方体多4个侧面的面积,据此列式解答。
2.B
解:(5+5)÷5
=10÷5
=2
6×2-6
=12-6
=6,分母应加上6。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
3.C
解:(8+3+3)×4
=14×4
=56(厘米)
(8+8+3)×4
=19×4
=76(厘米)
76>56。
故答案为:C。
这个长方体纸盒的棱长总和最大时,底面边长是8厘米,也就是长方体的长8厘米、宽8厘米、高3厘米,棱长和=(长+宽+高) ×4。
4.D
解:A项:1不是质数,猜想错误;
B项:13不是偶数,猜想错误;
C项:51不是质数,猜想错误;
D项:36是偶数,7和29都是质数,猜想正确。
故答案为:D。
个位上是0、2、4、6、8的数是偶数;个位上是1、3、5、7、9的数是奇数;
一个数只有1和它本身两个因数,这个数就是质数;一个数除了1和它本身两个因数,还有别的因数,这个数就是合数。据此选择。
5.B
解:A项:不能拼成长方体,3厘米的还差1根;
B项:可以拼成长3厘米、宽3厘米、高4厘米的长方体;
C项:不能拼成长方体;
D项:不能拼成长方体。
故答案为:B。
长方体有6个面,相对的面完全相同,12条棱中4条长、4条宽、4条高分别相等,或者特殊情况项相对的两个面是正方形时,其余8条棱长度相等。
6.D
解:A项:264个位数字是4,是2的倍数;
B项:264÷4=66,是4的倍数;
C项:2+6+4=12,是3的倍数;
D项:264不是5的倍数,则5个5个地数,不能正好数完。
故答案为:D。
个位上是0、2、4、6、8的数是2的倍数;个位上是0或者5的数是5的倍数;一个数各个数位上的数的和是3的倍数,这个数就是3的倍数;是这个数倍数的,就能正好数完,否则不能正好数完。
7.C
解:2升=2000毫升
2000÷550=3(个)······350(毫升)
3+1=4(个)。
故答案为:C。
先单位换算2升=2000毫升,他至少需要这样小瓶的个数=矿泉水的总体积÷平均每个小瓶最多装的体积,如果有余数,瓶子的个数再加1个。
8.D
解:A项:++;
B项:÷2+;
C项:1--;
D项:+。
故答案为:D。
A项:雨天和晴天的天数共占全月的分率=雨天占全月的分率+晴天占全月的分率;其中,晴天占全月的分率=雨天占全月的分率+多的分率;
B项:两次共喝这瓶果汁的分率=第一次喝的分率+ 第二次喝的分率;其中,第二次喝的分率=第二次喝的体积÷总体积;
C项:还剩下全书的分率=1-第一天看全书的分率- 第二天看全书的分率;
D项:两次共运走的质量=第一次运的质量+第二次运的质量。
9.B
解:(3+6)÷3
=9÷3
=3
8×3-8
=24-8
=16,分母应加上16。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
10.D
解:A项:是正方体展开图的“1-4-1”型;
B项:是正方体展开图的“1-4-1”型;
C项:是正方体展开图的“1-4-1”型;
D项:不是正方体的展开图。
故答案为:D。
展开后得到的图形不可能是 ,因为它不是正方体的展开图。
11.72
解:在71岁到79岁的范围内,既是2的倍数又是3的倍数的年龄是72岁。因为72岁既是偶数(2的倍数),同时72也能被3整除(7+2=9,9可以被3整除)。所以,根据题目的条件,典典的爷爷最小可能是72岁。
故答案为:72。
根据题干信息,典典的爷爷已过古稀,即年龄大于70岁;且未及耄耋,即年龄小于80岁。因此,爷爷的年龄范围是71岁到79岁。同时,题目要求爷爷的年龄既是2的倍数又是3的倍数。这就需要我们在这一个年龄范围内,找出同时满足这两个条件的年龄。
12.2;16
解:24÷12=2(分米)
2×2×4
=4×4
=16(平方分米)。
故答案为:2;16。
这个正方体灯笼的棱长=铁丝的长÷12,至少需要灯笼布的面积=棱长×棱长×4。
13.320;;
解:0.32×1000=320(立方分米);
300÷1000=(升);
40÷60=(分)。
故答案为:320;;。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
14.
解:1-=(杯),杯的是杯。
故答案为:。
一杯纯果汁,小亮喝了半杯后,则兑水1-=杯,然后他喝的水是杯的即杯。
15.12
解:24和36的最大公因数是2×2×3=12。
故答案为:12。
他们最多能分装出同样粽子礼盒的个数=24和36的最大公因数,用短除法求出。
16.2
解:3×5=15(天)
1+15=16(日),共2次。
故答案为:2。
先求出3和5的最小公倍数是3×5=15天,也就是王红和张亮最少每隔15天同时上一次宋词鉴赏班,4月有30天,4月1日是第一次,4月16日是第二次,第三次就是5月1日了,所以4月里他们共有2次同一天学习古诗词。
17.4
解:20和12的最大公因数是2×2=4,则正方形纸的边长最大是4分米。
故答案为:4。
正方形纸的边长最大是20和12的最大公因数,可以用短除法求出。
18.0.6;
解:600÷1000=0.6(升)
0.6升=升=立方分米。
故答案为:0.6;。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
19.2;3
解:比5小的质数有2、3。
故答案为:2;3。
依据100以内的质数表填空。
20.
解:1------
=-----
=----
=---
=--
=-
=。
故答案为:。
还剩下这张正方形纸的分率=1-分别剪去的分率。
21.
0
1 1
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
22.解:
=++
=1+
=
=9-(+)
=9-1
=8
=+
=
=+
=
应用加法交换律,交换后面两个加数的位置,先计算+,然后再加上;
一个数连续减去两个数,等于这个数减去后面两个数的和;
先算小括号里面的,再算括号外面的;
分数加减混合运算,按照从左到右的顺序计算。
23.(1)E
(2)75
解:(1)A和E相对,A在底面,则E在上面;
(2)
14×2+7×4+10
=28+28+10
=66(厘米)
故答案为:(1)E;(2)66。
(1)正方体相对的面不相邻,A和E相对,B和F相对,C和D相对;A在底面,则E在上面;
(2)用胶带粘合的时候,粘合在一起的两条棱只需要一条胶带,所以她至少需要用胶带的长度=长×2+高×4+宽。
24.解:36÷2=18(分米)
18=11+7=13+5
11×7=77(平方分米)
13×5=65(平方分米)
77>65
答:最大面积为 77 平方分米。
长与宽的和=周长÷2=18分米,然后写出两个质数相加等于18的数,得到18=11+7=13+5,分别用长×宽计算出面积后再比较大小。
25.(1)解:+=
答:读了两本和三本书的人数共占全班人数的。
(2)解:+=
<1
答:不是全班同学都参加了读书活动。
(1)读了两本和三本书的人数共占全班人数的分率=读两本的人数占全班人数的分率+读三本的人数占全班人数的分率;
(2)参加读书活动共占的分率=读一本的人数占全班人数的分率+读两本的人数占全班人数的分率+读三本的人数占全班人数的分率,然后和单位“1”比较,小于单位“1”,说明不是全班同学都参加了读书活动。
26.解:设长方体的高是x厘米,则宽是=(15-x)厘米。
15-x=2x
15=3x
x=15÷3
x=5
5×2=10(厘米)
20×10×5
=200×5
=1000(立方厘米)
答:这个长方体的体积是1000立方厘米。
这个长方体的体积=长×宽×高,设长方体的高是x厘米,则宽是=(15-x)厘米。依据高×2=宽,列方程求出高是5厘米,宽=高×2=10厘米,长是20厘米。
27.(1)上升
(2)2021
(3)解:全国生活用水量呈上升趋势,则2024 年全国生活用水量可能是915亿立方米。
解:(1)根据统计图,2014-2023年全国生活用水量呈上升趋势;
(2)比前一年的用水量增加最多的年份是2021年。
故答案为:(1)上升;(2)2021。
(1)2014-2023年全国生活用水量呈上升趋势;
(2)2021年较前一年的直条最陡峭,则说明这一年增加最多;
(3)全国生活用水量呈上升趋势,则2024 年全国生活用水量可能是915亿立方米。
28.解:4月=30天
18÷30=
答:晴天的天数占这个月总天数的。
晴天的天数占这个月总天数的分率=晴天的天数÷这个月的总天数。
29.(1)蔬菜
(2)
(3)解:乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
解:(1)乐乐和强强每天摄入蔬菜类食物相差最多;
(2)100÷300=。
故答案为:(1)蔬菜;(2)。
(1)乐乐和强强每天摄入蔬菜类食物的直条相差最远,则说明蔬菜类相差最多;
(2)乐乐每天肉类的摄入量是强强的分率=乐乐每天肉类的摄入量÷强强每天肉类的摄入量;
(3)乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
30.解:60÷15=4(个)
30÷3=10(个)
32÷3=10(个)······2(厘米)
4×10×10
=40×10
=400(个)
答:这个纸箱最多能装400个这种牙膏盒。
这个纸箱最多能装这种牙膏盒的个数=长边最多装的个数×宽边最多装的个数×高边最多装的个数。
2024-2025学年五年级下册期末检测卷(北京版)
数学
(时间:90分钟 满分:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 单选题(本大题10个小题,每小题1分,共10分)
得分
期末检测卷---2024-2025学年五年级数学下册真题重组检测卷(北京版)
一、单选题
1.(2023五下·东城期末)小明用27个1cm3的小正方体拼成一个大正方体,小利从大正方体上拿走一个1cm3的小正方体,形成新几何体的表面积可能比原来的大正方体( )。
A.少了2cm2 B.少了4cm2 C.多了3cm2 D.多了4cm2
2.(2024五下·门头沟期末)的分子加上5,要使分数大小不变,分母( )
A.应加上5 B.应加上6 C.应不变 D.无法确定
3.(2024五下·昌平期末)下图是一个长方体纸盒的上面,这个长方体纸盒有两个相对的面是正方形。这个长方体纸盒的棱长总和最大是( )cm。(可以先画一画长方体,再解决问题)
A.36 B.56 C.76 D.96
4.(2024五下·昌平期末)歌德巴赫猜想被誉为“数学皇冠上的明珠",这一猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中能反映这个猜想的是( )。
A.4=1+3 B.13=2+11 C.54 =3+51 D.36 =7+29
5.(2024五下·朝阳期末)下面提供的材料正好能拼成长方体的是( )
A. B.
C. D.
6.(2024五下·朝阳期末)秦始皇陵及兵马俑被誉为“世界第八大奇迹”,其中二号兵马俑坑第三单元有 264个步兵佣。用下面的方法数这些兵马俑,不能正好数完的是( )
A.2个2个地数 B.4个4个地数 C.3个3个地数 D.5个5个地数
7.(2024五下·东城期末)五年级的同学们准备去郊外春游,老师要求每位同学都要带足够的水。小明的妈妈给他准备了一瓶2升的矿泉水,为了携带方便小明需要把水分装到小瓶中,如果每个小瓶装550毫升,那么他至少需要( )个这样的小瓶。
A.2 B.3 C.4 D.5
8.(2024五下·房山期末)以下问题中,可以用算式解决的是( )
A.某城市九月雨天天数占全月的,晴天天数比雨天天数多全月的,雨天和晴天的天数共占全月的几分之儿?
B.一瓶2升的果汁,第一次喝了这瓶果汁的,第二次喝了了升,两次共喝这瓶果汁的几分之几?
C.君一本书,第一天看全书的,第二天看全书的,还剩下全书的几分之几没看?
D.一批货物,第一次运走吨,第二次运走吨,两次共运走多少吨?
9.(2024五下·房山期末)把分数的分子加上6、要使分数的大小不变、分母应( )
A.加上6 B.加上16 C.乘2 D.乘6
10.(2024五下·房山期末)芳芳将一个正方体盒子(如下图)完全展开,得到的展开图不可能是( )
A. B.
C. D.
阅卷人 二、填空题(本大题10个小题,每小题2分,共20分)
得分
11.(2024五下·门头沟期末)典典在文献阅读的过程中,遇到了一些表达年龄称谓的词,如“花甲”、“古稀”、“耄(mào)耋(dié)”……经过查阅,典典了解到:六十岁为“花甲”,七十岁为“古稀”,八九十岁为“耄(mào)耋(dié)”。典典)岁。的爷爷已过古稀,未及耄,且年龄既是2的倍数又有因数3,典典的爷爷最小 岁。
12.(2024五下·昌平期末)中国灯笼是一种古老的传统工艺品。乐乐用一根24dm长的铁丝了一个正方体灯笼框架,这个正方体灯笼的棱长是 dm,如果给这个灯笼的四周围上灯笼布 (上下面空着),至少需要 平方分米的灯笼布。
13.(2024五下·门头沟期末)0.32m3= dm3 300毫升= 升 40秒= 分
14.(2024五下·朝阳期末)一杯纯果汁,小亮喝了半杯后,兑满水又喝了杯,他一共喝水 杯。
15.(2024五下·朝阳期末)端午节是每年的农历五月初五,是我国首个入选非遗的节日。端午节前夕,圆圆家一共包了 24 个蛋黄粽和 36 个蜜枣粽,他们想把粽子分装成礼盒送给亲朋好友品尝。如果每盒里都有这两种口味的粽子,且分完后都没有剩余,他们最多能分装出 个同样的粽子礼盒。
16.(2024五下·东城期末)为了弘扬中华传统文化,少年宫开设了古诗词鉴资班。王红每3天上一次唐诗鉴赏班,张亮每隔5天上一次宋词鉴资班。2024年4月1日是两人同一天学习古诗词的日子,4月里他们共有 次同一天学习古诗词。
17.(2024五下·丰台期末)学校门厅有一个长 20分米,宽12分米的长方形宣传栏。如果把同学们用完全相同的正方形纸完成的书画作品,既不重叠、也无缝隙地正好贴满宣传栏,正方形纸的边长最大是 分米。
18.(2024五下·丰台期末)一瓶矿泉水的净含量是 600mL,相当于 L,可以写成 dm3
19.(2024五下·丰台期末)比5小的质数有 和 。
20.(2024五下·顺义期末)把一张正方形纸连续剪6次,依次剪下它的,还剩下这张正方形纸的 。
阅卷人 三、计算题(23分)
得分
21.(2024五下·昌平期末)口算
22.(2024五下·东城期末)脱式计算下面各题。
23.
阅卷人 四、操作题(12分)
得分
23.(2024五下·东城期末)把下面长方体展开图折成长方体
(1)如果 A 面在底面,那么 面在上面。
(2)用胶带沿棱将所有接缝处进行粘合,她至少需要用 厘米的胶带。提示:可以先画一画需要粘合的边再填空。
阅卷人 五、解决问题(本大题7个小题,共35分)
得分
24.(2024五下·昌平期末)水墨面近处写实,远处抽象,是中国绘画的代表。张爷爷在长方形纸上绘制了一幅水墨酒,长和宽均为质数,并且周长是36分米。这幅水墨两的长和宽分别可能是多少分米?面积最大是多少平方分米?
25.(2024五下·门头沟期末)“领读少年”是门头沟区打造的以青少年阅读为重点的阅读品牌,倡导全区中小学生迈进生活找原型、迈进文献学思维。五(1)班同学自发开展了班级读书周活动。请根据表中的数据解决问题。
五 (1) 班学生读书情况
每人读书的本数 一本 两本 三本
人数占全班人数的几分之几
(1)读了两本和三本书的人数共占全班人数的几分之几?
(2)全班同学都参加读书活动了吗?你是怎么知道的?
26.(2024五下·朝阳期末)丽丽想制作一个长方体纸盒。他先在一张边长为30厘米的正方形纸上绘制出这个长方体纸盒的展开图(如下图)。然后准备将涂色部分裁掉,借助胶条粘贴成长方体。已知长方体的宽是高的2倍,那么这个长方体的体积是多少立方厘米?
27.(2024五下·朝阳期末)
(1)根据统计图,2014-2023年全国生活用水量呈 趋势。
(2)比前一年的用水量增加最多的年份是 年。
(3)请你预测 2024 年全国生活用水量,并写出理由。
28.(2024五下·东城期末)四月份有18天晴天,5天阴天,其余的是雨天。晴天的天数占这个月总天数的几分之几?
29.(2024五下·丰台期末)肥胖影响青少年的身心健康。在常规体检中,乐乐和强强的健康状况为“超重”,体检医生提示他们需要加强体育锻炼、注意健康饮食。为此,乐乐和强强每天进行了至少一小时的体育运动,并将一月至五月每天的各类食物摄入量和阶段性的体重监测情况进行了记录,如下面两幅统计图所示:
(1)乐乐和强强每天摄入 类食物相差最多。
(2)乐乐每天肉类的摄入量是强强的 。
(3)请你结合两幅图中的数据判断谁的体重下降的比较快,并分析可能的原因。
30.(2024五下·密云期末)工人要将长15厘米,宽和高都是3厘米的长方体牙盒装人纸箱中。纸箱里面的尺寸如图,(单位:厘米)。这个纸箱最多能装多少个这种牙膏盒?
答案解析部分
1.D
1×1×4
=1×4
=4(cm2)
故答案为:D。
根据题意可知,小明用27个1cm3的小正方体拼成一个大正方体,正方体的棱长是3cm,如果拿正中间的,表面积会比原来的大正方体多4个侧面的面积,据此列式解答。
2.B
解:(5+5)÷5
=10÷5
=2
6×2-6
=12-6
=6,分母应加上6。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
3.C
解:(8+3+3)×4
=14×4
=56(厘米)
(8+8+3)×4
=19×4
=76(厘米)
76>56。
故答案为:C。
这个长方体纸盒的棱长总和最大时,底面边长是8厘米,也就是长方体的长8厘米、宽8厘米、高3厘米,棱长和=(长+宽+高) ×4。
4.D
解:A项:1不是质数,猜想错误;
B项:13不是偶数,猜想错误;
C项:51不是质数,猜想错误;
D项:36是偶数,7和29都是质数,猜想正确。
故答案为:D。
个位上是0、2、4、6、8的数是偶数;个位上是1、3、5、7、9的数是奇数;
一个数只有1和它本身两个因数,这个数就是质数;一个数除了1和它本身两个因数,还有别的因数,这个数就是合数。据此选择。
5.B
解:A项:不能拼成长方体,3厘米的还差1根;
B项:可以拼成长3厘米、宽3厘米、高4厘米的长方体;
C项:不能拼成长方体;
D项:不能拼成长方体。
故答案为:B。
长方体有6个面,相对的面完全相同,12条棱中4条长、4条宽、4条高分别相等,或者特殊情况项相对的两个面是正方形时,其余8条棱长度相等。
6.D
解:A项:264个位数字是4,是2的倍数;
B项:264÷4=66,是4的倍数;
C项:2+6+4=12,是3的倍数;
D项:264不是5的倍数,则5个5个地数,不能正好数完。
故答案为:D。
个位上是0、2、4、6、8的数是2的倍数;个位上是0或者5的数是5的倍数;一个数各个数位上的数的和是3的倍数,这个数就是3的倍数;是这个数倍数的,就能正好数完,否则不能正好数完。
7.C
解:2升=2000毫升
2000÷550=3(个)······350(毫升)
3+1=4(个)。
故答案为:C。
先单位换算2升=2000毫升,他至少需要这样小瓶的个数=矿泉水的总体积÷平均每个小瓶最多装的体积,如果有余数,瓶子的个数再加1个。
8.D
解:A项:++;
B项:÷2+;
C项:1--;
D项:+。
故答案为:D。
A项:雨天和晴天的天数共占全月的分率=雨天占全月的分率+晴天占全月的分率;其中,晴天占全月的分率=雨天占全月的分率+多的分率;
B项:两次共喝这瓶果汁的分率=第一次喝的分率+ 第二次喝的分率;其中,第二次喝的分率=第二次喝的体积÷总体积;
C项:还剩下全书的分率=1-第一天看全书的分率- 第二天看全书的分率;
D项:两次共运走的质量=第一次运的质量+第二次运的质量。
9.B
解:(3+6)÷3
=9÷3
=3
8×3-8
=24-8
=16,分母应加上16。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
10.D
解:A项:是正方体展开图的“1-4-1”型;
B项:是正方体展开图的“1-4-1”型;
C项:是正方体展开图的“1-4-1”型;
D项:不是正方体的展开图。
故答案为:D。
展开后得到的图形不可能是 ,因为它不是正方体的展开图。
11.72
解:在71岁到79岁的范围内,既是2的倍数又是3的倍数的年龄是72岁。因为72岁既是偶数(2的倍数),同时72也能被3整除(7+2=9,9可以被3整除)。所以,根据题目的条件,典典的爷爷最小可能是72岁。
故答案为:72。
根据题干信息,典典的爷爷已过古稀,即年龄大于70岁;且未及耄耋,即年龄小于80岁。因此,爷爷的年龄范围是71岁到79岁。同时,题目要求爷爷的年龄既是2的倍数又是3的倍数。这就需要我们在这一个年龄范围内,找出同时满足这两个条件的年龄。
12.2;16
解:24÷12=2(分米)
2×2×4
=4×4
=16(平方分米)。
故答案为:2;16。
这个正方体灯笼的棱长=铁丝的长÷12,至少需要灯笼布的面积=棱长×棱长×4。
13.320;;
解:0.32×1000=320(立方分米);
300÷1000=(升);
40÷60=(分)。
故答案为:320;;。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
14.
解:1-=(杯),杯的是杯。
故答案为:。
一杯纯果汁,小亮喝了半杯后,则兑水1-=杯,然后他喝的水是杯的即杯。
15.12
解:24和36的最大公因数是2×2×3=12。
故答案为:12。
他们最多能分装出同样粽子礼盒的个数=24和36的最大公因数,用短除法求出。
16.2
解:3×5=15(天)
1+15=16(日),共2次。
故答案为:2。
先求出3和5的最小公倍数是3×5=15天,也就是王红和张亮最少每隔15天同时上一次宋词鉴赏班,4月有30天,4月1日是第一次,4月16日是第二次,第三次就是5月1日了,所以4月里他们共有2次同一天学习古诗词。
17.4
解:20和12的最大公因数是2×2=4,则正方形纸的边长最大是4分米。
故答案为:4。
正方形纸的边长最大是20和12的最大公因数,可以用短除法求出。
18.0.6;
解:600÷1000=0.6(升)
0.6升=升=立方分米。
故答案为:0.6;。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
19.2;3
解:比5小的质数有2、3。
故答案为:2;3。
依据100以内的质数表填空。
20.
解:1------
=-----
=----
=---
=--
=-
=。
故答案为:。
还剩下这张正方形纸的分率=1-分别剪去的分率。
21.
0
1 1
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
22.解:
=++
=1+
=
=9-(+)
=9-1
=8
=+
=
=+
=
应用加法交换律,交换后面两个加数的位置,先计算+,然后再加上;
一个数连续减去两个数,等于这个数减去后面两个数的和;
先算小括号里面的,再算括号外面的;
分数加减混合运算,按照从左到右的顺序计算。
23.(1)E
(2)75
解:(1)A和E相对,A在底面,则E在上面;
(2)
14×2+7×4+10
=28+28+10
=66(厘米)
故答案为:(1)E;(2)66。
(1)正方体相对的面不相邻,A和E相对,B和F相对,C和D相对;A在底面,则E在上面;
(2)用胶带粘合的时候,粘合在一起的两条棱只需要一条胶带,所以她至少需要用胶带的长度=长×2+高×4+宽。
24.解:36÷2=18(分米)
18=11+7=13+5
11×7=77(平方分米)
13×5=65(平方分米)
77>65
答:最大面积为 77 平方分米。
长与宽的和=周长÷2=18分米,然后写出两个质数相加等于18的数,得到18=11+7=13+5,分别用长×宽计算出面积后再比较大小。
25.(1)解:+=
答:读了两本和三本书的人数共占全班人数的。
(2)解:+=
<1
答:不是全班同学都参加了读书活动。
(1)读了两本和三本书的人数共占全班人数的分率=读两本的人数占全班人数的分率+读三本的人数占全班人数的分率;
(2)参加读书活动共占的分率=读一本的人数占全班人数的分率+读两本的人数占全班人数的分率+读三本的人数占全班人数的分率,然后和单位“1”比较,小于单位“1”,说明不是全班同学都参加了读书活动。
26.解:设长方体的高是x厘米,则宽是=(15-x)厘米。
15-x=2x
15=3x
x=15÷3
x=5
5×2=10(厘米)
20×10×5
=200×5
=1000(立方厘米)
答:这个长方体的体积是1000立方厘米。
这个长方体的体积=长×宽×高,设长方体的高是x厘米,则宽是=(15-x)厘米。依据高×2=宽,列方程求出高是5厘米,宽=高×2=10厘米,长是20厘米。
27.(1)上升
(2)2021
(3)解:全国生活用水量呈上升趋势,则2024 年全国生活用水量可能是915亿立方米。
解:(1)根据统计图,2014-2023年全国生活用水量呈上升趋势;
(2)比前一年的用水量增加最多的年份是2021年。
故答案为:(1)上升;(2)2021。
(1)2014-2023年全国生活用水量呈上升趋势;
(2)2021年较前一年的直条最陡峭,则说明这一年增加最多;
(3)全国生活用水量呈上升趋势,则2024 年全国生活用水量可能是915亿立方米。
28.解:4月=30天
18÷30=
答:晴天的天数占这个月总天数的。
晴天的天数占这个月总天数的分率=晴天的天数÷这个月的总天数。
29.(1)蔬菜
(2)
(3)解:乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
解:(1)乐乐和强强每天摄入蔬菜类食物相差最多;
(2)100÷300=。
故答案为:(1)蔬菜;(2)。
(1)乐乐和强强每天摄入蔬菜类食物的直条相差最远,则说明蔬菜类相差最多;
(2)乐乐每天肉类的摄入量是强强的分率=乐乐每天肉类的摄入量÷强强每天肉类的摄入量;
(3)乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
30.解:60÷15=4(个)
30÷3=10(个)
32÷3=10(个)······2(厘米)
4×10×10
=40×10
=400(个)
答:这个纸箱最多能装400个这种牙膏盒。
这个纸箱最多能装这种牙膏盒的个数=长边最多装的个数×宽边最多装的个数×高边最多装的个数。
同课章节目录
