宁夏银川市第六中学2024-2025学年高一下学期月考一数学试题(含解析)
文档属性
| 名称 | 宁夏银川市第六中学2024-2025学年高一下学期月考一数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 572.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 00:00:00 | ||
图片预览



文档简介
宁夏银川市第六中学2024 2025学年高一下学期月考一数学试题
一、单选题(本大题共8小题)
1.( )
A. B. C. D.
2.已知是第一象限角,,则的值是( )
A. B. C. D.
3.函数 的最大值为( )
A.2 B. C. D.1
4.( )
A. B. C. D.
5.中国象棋是中国发明的一种古老的棋类游戏,大约有两千年的历史,是中华文明非物质文化的经典产物,如图,棋盘由边长为1的正方形方格组成,已知“马”“帅”“炮”“兵”分别位于A,B,C,D四点,则( )
A. B. C. D.3
6.设,是两个不共线的向量,若向量与向量共线,则( )
A. B. C. D.
7.已知,,则( )
A. B. C. D.
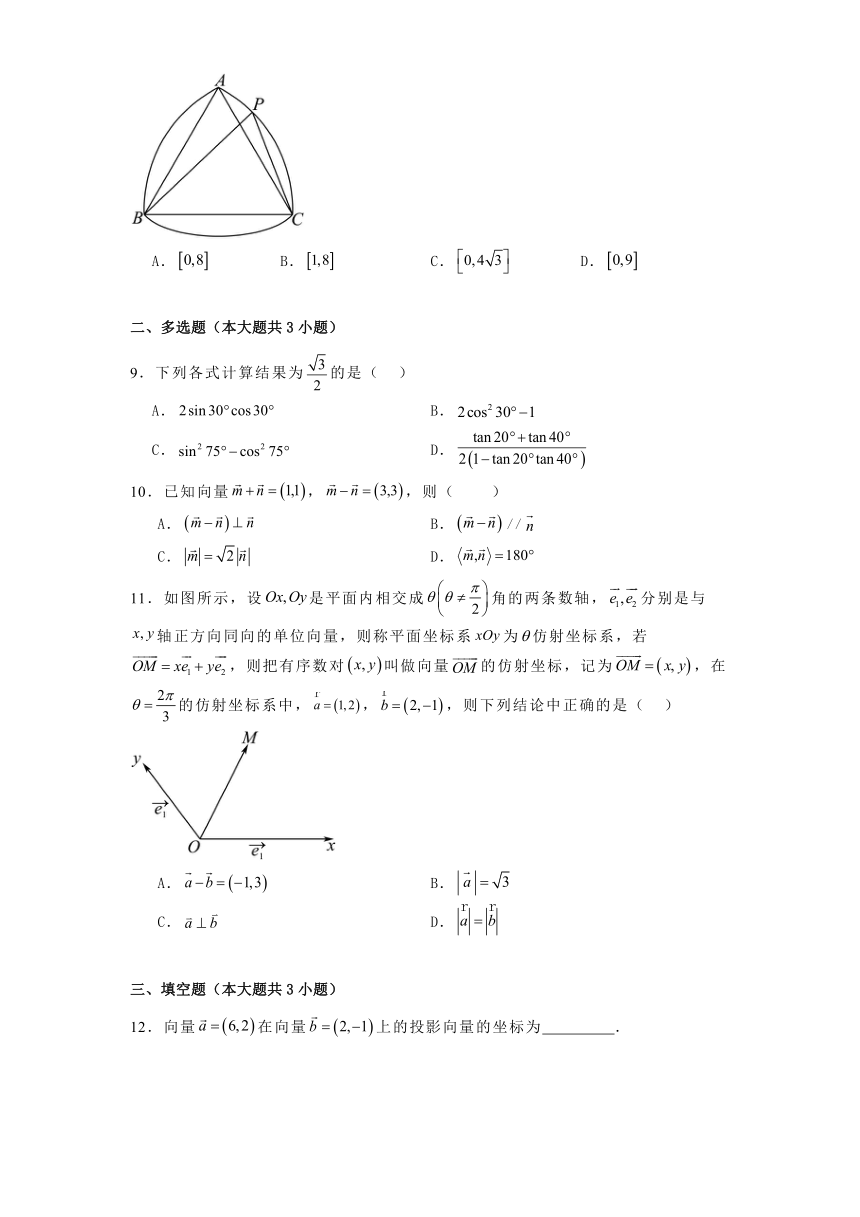
8.勒洛三角形是一种典型的定宽曲线,以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形就是勒洛三角形;在如图所示的勒洛三角形中,已知,P为弧AC(含端点)上的一点,则的范围为( )
A. B. C. D.
二、多选题(本大题共3小题)
9.下列各式计算结果为的是( )
A. B.
C. D.
10.已知向量,,则( )
A. B.
C. D.
11.如图所示,设是平面内相交成角的两条数轴,分别是与轴正方向同向的单位向量,则称平面坐标系为仿射坐标系,若,则把有序数对叫做向量的仿射坐标,记为,在的仿射坐标系中,,,则下列结论中正确的是( )
A. B.
C. D.
三、填空题(本大题共3小题)
12.向量在向量上的投影向量的坐标为 .
13.将函数的图象向左平移个单位后,得到的图象,则的最小值为 .
14.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为,若, .
四、解答题(本大题共5小题)
15.已知,为第二象限角.
(1)求的值;
(2)求的值.
16.设向量,,.
(1)求;
(2)若,,求的值;
(3)若,,,求证:A,,三点共线.
17.已知,.
(1)求的值;
(2)若,且,求的值.
18.如图,在直角三角形中,.点分别是线段上的点,满足.
(1)求的取值范围;
(2)是否存在实数,使得?若存在,求出的值;若不存在,请说明理由.
19.在平行四边形中,,为中点.
(1)若,且满足,求的长;
(2)若,求的最大值.
参考答案
1.【答案】B
【详解】,
故选B
2.【答案】D
【详解】因为是第一象限角,所以,
所以,
当时,,所以是第三象限角;
当时,,所以是第一象限角;
又,所以是第三象限角,所以,
所以.
故选D.
3.【答案】A
【详解】因为,
当,即时,函数取到最大值2.
故选A.
4.【答案】B
【详解】.
故选B
5.【答案】A
【详解】由题得.
故选A.
6.【答案】D
【详解】因为,是两个不共线的向量,且向量与向量共线,
所以,即,
所以,解得.
故选D.
7.【答案】A
【详解】,
因为,即,,
解得又,,
所以.
故选A.
8.【答案】A
【详解】取中点为,连接,显然,
所以
.
故选A
9.【答案】ACD
【详解】对A:,故A满足;
对B:,故B不满足;
对C:,故C满足;
对D:,故D满足.
故选ACD
10.【答案】BD
【详解】因为,,
所以,
选项A,因为,所以与不垂直,所以A错误,
选项B,因为,,所以,所以,所以B正确,
选项C,因为,所以,所以,所以C错误,
选项D,因为,所以,所以,所以D正确.
故选BD
11.【答案】AB
【详解】,,故A正确,
,故B正确,
,故C错误,
,故D错误,
故选AB
12.【答案】
【详解】向量在向量上的投影向量为.
13.【答案】
【详解】的图象向左平移个单位后,得到,
从而,解得,
又,故当时,取得最小值,最小值为.
14.【答案】2
【详解】因为,,所以.
15.【答案】(1)
(2)
【详解】(1),为第二象限角,
,
则;
(2).
16.【答案】(1)1
(2)2
(3)证明见解析
【详解】(1),;
(2),所以,解得:,所以;
(3)因为,所以,所以A,,三点共线.
17.【答案】(1)
(2)
【详解】(1)因为,解得,
所以.
(2)因为,则,
则,可得,
所以,
则,
又因为,则,
所以.
18.【答案】(1)
(2)存在,
【详解】(1)在直角三角形中,.
∴,,
,
∵,∴.
(2)
令,得或(舍).
∴存在实数,使得.
19.【答案】(1);(2).
【详解】解:(1)因为为中点,
因为四边形为平行四边形,
所以,
因为,
因为,,
所以,
,
解得,
所以,
(2)因为,
所以,
,
所以,
所以,当且仅当,即时取等号,
所以,
所以的最大值为
一、单选题(本大题共8小题)
1.( )
A. B. C. D.
2.已知是第一象限角,,则的值是( )
A. B. C. D.
3.函数 的最大值为( )
A.2 B. C. D.1
4.( )
A. B. C. D.
5.中国象棋是中国发明的一种古老的棋类游戏,大约有两千年的历史,是中华文明非物质文化的经典产物,如图,棋盘由边长为1的正方形方格组成,已知“马”“帅”“炮”“兵”分别位于A,B,C,D四点,则( )
A. B. C. D.3
6.设,是两个不共线的向量,若向量与向量共线,则( )
A. B. C. D.
7.已知,,则( )
A. B. C. D.
8.勒洛三角形是一种典型的定宽曲线,以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形就是勒洛三角形;在如图所示的勒洛三角形中,已知,P为弧AC(含端点)上的一点,则的范围为( )
A. B. C. D.
二、多选题(本大题共3小题)
9.下列各式计算结果为的是( )
A. B.
C. D.
10.已知向量,,则( )
A. B.
C. D.
11.如图所示,设是平面内相交成角的两条数轴,分别是与轴正方向同向的单位向量,则称平面坐标系为仿射坐标系,若,则把有序数对叫做向量的仿射坐标,记为,在的仿射坐标系中,,,则下列结论中正确的是( )
A. B.
C. D.
三、填空题(本大题共3小题)
12.向量在向量上的投影向量的坐标为 .
13.将函数的图象向左平移个单位后,得到的图象,则的最小值为 .
14.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为,若, .
四、解答题(本大题共5小题)
15.已知,为第二象限角.
(1)求的值;
(2)求的值.
16.设向量,,.
(1)求;
(2)若,,求的值;
(3)若,,,求证:A,,三点共线.
17.已知,.
(1)求的值;
(2)若,且,求的值.
18.如图,在直角三角形中,.点分别是线段上的点,满足.
(1)求的取值范围;
(2)是否存在实数,使得?若存在,求出的值;若不存在,请说明理由.
19.在平行四边形中,,为中点.
(1)若,且满足,求的长;
(2)若,求的最大值.
参考答案
1.【答案】B
【详解】,
故选B
2.【答案】D
【详解】因为是第一象限角,所以,
所以,
当时,,所以是第三象限角;
当时,,所以是第一象限角;
又,所以是第三象限角,所以,
所以.
故选D.
3.【答案】A
【详解】因为,
当,即时,函数取到最大值2.
故选A.
4.【答案】B
【详解】.
故选B
5.【答案】A
【详解】由题得.
故选A.
6.【答案】D
【详解】因为,是两个不共线的向量,且向量与向量共线,
所以,即,
所以,解得.
故选D.
7.【答案】A
【详解】,
因为,即,,
解得又,,
所以.
故选A.
8.【答案】A
【详解】取中点为,连接,显然,
所以
.
故选A
9.【答案】ACD
【详解】对A:,故A满足;
对B:,故B不满足;
对C:,故C满足;
对D:,故D满足.
故选ACD
10.【答案】BD
【详解】因为,,
所以,
选项A,因为,所以与不垂直,所以A错误,
选项B,因为,,所以,所以,所以B正确,
选项C,因为,所以,所以,所以C错误,
选项D,因为,所以,所以,所以D正确.
故选BD
11.【答案】AB
【详解】,,故A正确,
,故B正确,
,故C错误,
,故D错误,
故选AB
12.【答案】
【详解】向量在向量上的投影向量为.
13.【答案】
【详解】的图象向左平移个单位后,得到,
从而,解得,
又,故当时,取得最小值,最小值为.
14.【答案】2
【详解】因为,,所以.
15.【答案】(1)
(2)
【详解】(1),为第二象限角,
,
则;
(2).
16.【答案】(1)1
(2)2
(3)证明见解析
【详解】(1),;
(2),所以,解得:,所以;
(3)因为,所以,所以A,,三点共线.
17.【答案】(1)
(2)
【详解】(1)因为,解得,
所以.
(2)因为,则,
则,可得,
所以,
则,
又因为,则,
所以.
18.【答案】(1)
(2)存在,
【详解】(1)在直角三角形中,.
∴,,
,
∵,∴.
(2)
令,得或(舍).
∴存在实数,使得.
19.【答案】(1);(2).
【详解】解:(1)因为为中点,
因为四边形为平行四边形,
所以,
因为,
因为,,
所以,
,
解得,
所以,
(2)因为,
所以,
,
所以,
所以,当且仅当,即时取等号,
所以,
所以的最大值为
同课章节目录
