江苏省扬州市七校联盟2024-2025学年高二下学期5月联考数学试题(含详解)
文档属性
| 名称 | 江苏省扬州市七校联盟2024-2025学年高二下学期5月联考数学试题(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 692.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 00:00:00 | ||
图片预览





文档简介
七校联盟2024~2025学年第二学期第一次联考
高二数学
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1.若,则( )
A. 5 B. 6 C. 7 D. 8
2.2025年U-20男足亚洲杯足球赛于2月份在深圳举行,东道主中国所在的A组共有四支球队,四支球队之间进行单循环比赛,共进行的比赛的场数为 ( )
A. 4 B. 6 C. 8 D. 10
3.已知,,不共面,若,,且三点共线,则( )
A. B.1 C.2 D.3
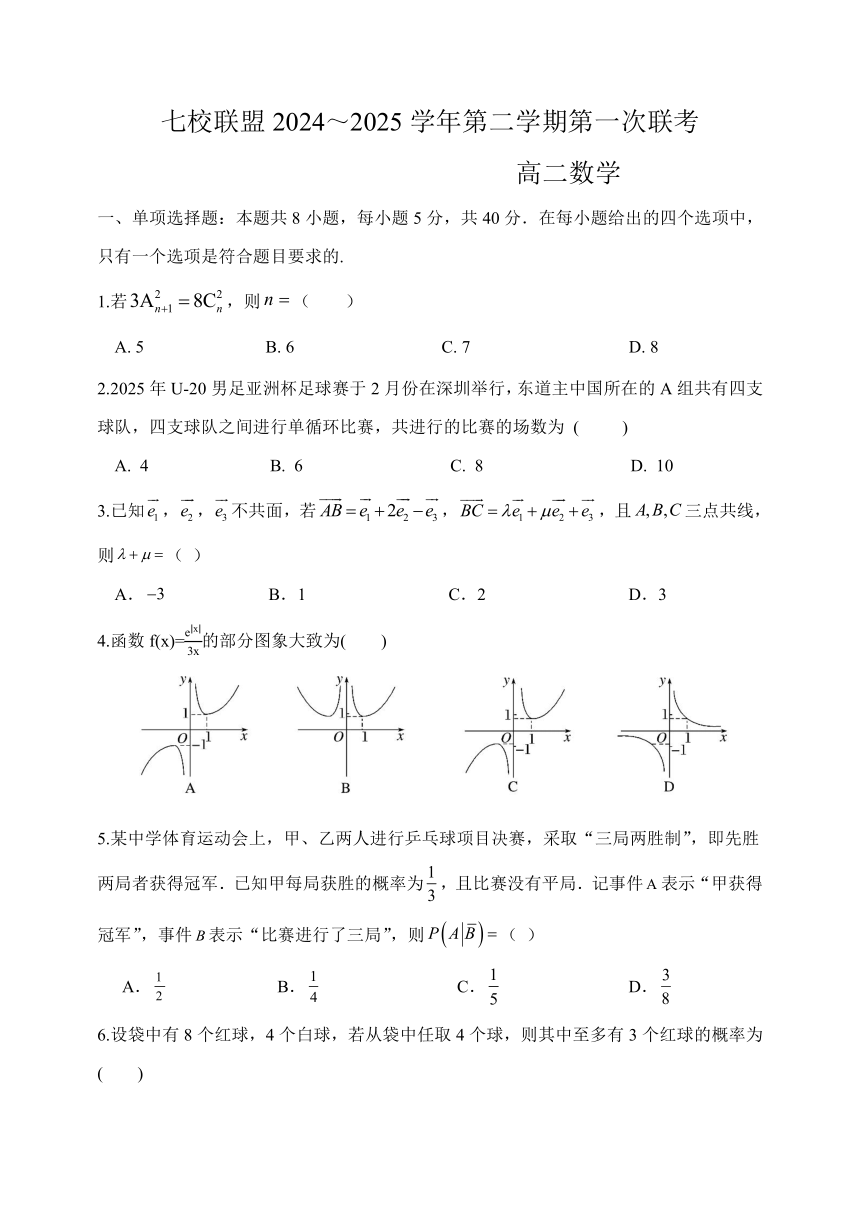
4.函数f(x)=的部分图象大致为( )
5.某中学体育运动会上,甲、乙两人进行乒乓球项目决赛,采取“三局两胜制”,即先胜两局者获得冠军.已知甲每局获胜的概率为,且比赛没有平局.记事件表示“甲获得冠军”,事件表示“比赛进行了三局”,则( )
A. B. C. D.
6.设袋中有8个红球,4个白球,若从袋中任取4个球,则其中至多有3个红球的概率为( )
7.已知平行六面体中,棱两两的夹角均为,,E为中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
8.我们约定:若两个函数的极值点个数相同,并且图象从左到右看,极大值点和极小值点分布的顺序相同,则称这两个函数的图象“相似”.已知,则下列给出的函数其图象与的图象“相似”的是( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得2分或3分或4分,有选错的得0分.
9.若函数在上单调递减,则实数的值可能为( )
A. B. C.3 D.4
10.已知二项式 的展开式中各二项式系数和为64,则下列说法正确的是( )
A.展开式共有6项 B.二项式系数最大的项是第4项
C.展开式的常数项为120 D.展开式中各项的系数和为1
11.已知为随机试验的样本空间,事件A,B满足,,则下列说法正确的是( )
A.若,且,,则
B.若,且,,则
C.若,,则
D.若,,,则
三、填空题:本题共3小题,每小题5分,共15分.
12.已知函数,则______.
13.学校公园计划在小路的一侧种植丹桂、金桂、银桂、四季桂4棵桂花树,垂乳银杏、金带银杏2棵银杏树,要求2棵银杏树必须相邻,则不同的种植方法共有________种.
14.已知梯形如图1所示,其中,A为线段的中点,四边形为正方形,现沿进行折叠,使得平面⊥平面,得到如图2所示的几何体.已知当点F满足时,平面平面,则λ的值为 .
图1 图2
四.解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 已知函数其图象在点(1,4)处的切线方程为.
(1)求函数的解析式;
(2)求函数在区间上的最值.
16.在的展开式中,求.
(1)含项的系数;
(2)求展开式中所有的有理项.
17.甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.
①求甲学校获得冠军的概率;
②用X表示乙学校的总得分,求X的分布列与期望.
18.如图,在四棱锥中,,底面为正方形,分别为的中点.
(1)求证:∥平面;
(2)求直线与平面所成角的正弦值;
(3)求点到平面的距离.
19.为更好的发挥高考的育才作用,部分新高考数学试卷采用了多选题这一题型.教育部考试中心通过科学测量分析,指出该题型扩大了试卷考点的覆盖面,有利于提高试卷的区分度,也有利于提高学生的得分率.多选题评分规则如下:对于多选题,每个小题给出的四个选项中,有两项或三项是正确的,满分6分.全部选对得6分,有错选或全不选得0分,正确答案为两项时,选对1个得3分;正确答案为三项时,选对1个得2分,选对2个得4分.多选题正确答案是两个选项的概率为p,正确答案是三个选项的概率为(其中).
(1)在一次模拟考试中,学生甲对某个多选题完全不会,决定随机选择一个选项,若,求学生甲该题得2分的概率;
(2)针对某道多选题,学生甲完全不会,此时他有三种答题方案:
Ⅰ:随机选一个选项; Ⅱ:随机选两个选项; Ⅲ:随机选三个选项.
(i)若,且学生甲选择方案Ⅰ,求本题得分的数学期望;
(ii)以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好
七校联盟2024~2025学年第二学期第一次联考答案
单项选择题
1. 【答案】C
【详解】由得:,
故选:C
2.【答案】 B
【详解】四支球队之间进行单循环比赛,共进行的比赛的场数为
故选:B
3.【答案】A
【详解】因为三点共线,
所以,
即,
所以,解得,
所以,
故选:A
4.【答案】C
【详解】[f(x)=,定义域为(-∞,0)∪(0,+∞),
∵f(-x)=-=-f(x),
∴f(x)为奇函数,图象关于原点对称,故排除B;
f(1)=<1,故排除A;
∵当x>0时,f'(x)=,
又当x>1时,f'(x)>0,
∴f(x)在(1,+∞)上单调递增,故排除D.
5.【答案】C
【详解】由题意可知,事件为“比赛进行两局,甲获得冠军”,所以,,
,
由条件概率公式可得.
故选:C.
6.【答案】 D
【详解】至多有3个红球的概率为
故选: D.
7.【答案】D
【详解】根据题意以为基底表示出可得:
,,
又棱两两的夹角均为,不妨取,则;
所以;
;
又
;
所以,
因此异面直线与所成角的余弦值为.
故选:D
8. 【答案】C
【详解】,则,
令,则,
如图,作出函数的图象,
由图可知函数的图象有两个交点,
即函数有两个零点,且,
令,则或,令,则,
所以在上单调递增,在上单调递减,
所以的极大值点为,极小值点为.
对于A,函数在上单调递减,在单调递增,
所以函数有极小值点,无极大值点,故A选项不符;
对于B,函数在上单调递增,在单调递减,
所以函数有极大值点,无极小值点,故B选项不符;
对于C,,
当或时,,当时,,
所以函数的极大值点为,极小值点为,故C选项符合题意;
对于D,,
则函数的极小值点为,极大值点为,故D选项不符.
故选:C.
二、多项选择题
9.【答案】BCD
【详解】根据题意可得函数的定义域为,
又,
若函数在上单调递减,可得在上恒成立;
即在上恒成立,所以,
根据对勾函数性质可得在上单调递增,
当时,当时,所以,
所以,
结合选择可知B、C、D符合题意.
故选:BCD
10.【答案】 BD
【详解】由题知 ,得到n=6,所以展开式共有7项,故选项A错误,对于选项B,因为n=6,由二项式系数的性质知二项式系数最大的项是第4项,所以选项B正角,
对于选项C,二项式 的展开式的通项公式为
由6-2r=0,得到r=3,所以展开式的常数项为 所以选项C错误,
对于选项D, 令x=1, 则 所以展开式中各项的系数和为1,故选项D正确,
故选: BD.
11.【答案】ACD
【详解】对于A,由,则与互斥,所以,故A正确;
对于B,由,则,所以,故B错误;
对于C,由,则,即与相互独立,
所以,故C正确;
对于D,由,且,,
可得,即,
解得,故D正确.
故选:ACD.
三、填空题
12.【答案】 ##0.6
【详解】因为,则,
令,可得,解得.
故答案为:.
13. 【答案】 240
【详解】分两步完成:
第一步,将2棵银杏树看成一个元素,考虑其顺序,有种种植方法;
第二步,将银杏树与4棵桂花树全排列,有种种植方法.
由分步乘法计数原理得,不同的种植方法共有·=240(种).
14.【答案】/
【解析】如图,以A为坐标原点,
所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
∴
则,
若是平面的一个法向量,
则
可得,
若是平面的一个法向量,
则可得
由平面平面,得,
即,
解得.
故答案为:.
四.解答题
15.已知函数其图象在点(1,4)处的切线方程为.
(1)求函数的解析式;
(2)求函数在区间上的最值
【详解】解:(1)由f(x)=x3+ax2+bx(a∈R,b∈R)可得:f′(x)=3x2+2ax+b,
所以f(x)在点(1,4)处切线的斜率为k=f′(1)=3+2a+b,
因为f(x)在点(1,4)处切线方程为y=4,
所以切线的斜率为0,且f(1)=4,
所以,即,
解得a=﹣6,b=9,
所以f(x)=x3﹣6x2+9x;
(2)由(1)知f(x)=x3﹣6x2+9x,
则f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3),
令f′(x)=0得x=1或3,
所以在上f′(x)>0,f(x)单调递增,
在(1,3)上f′(x)<0,f(x)单调递减,
在(3,5)上f′(x)>0,f(x)单调递增,
在x=1处,f(x)取得极大值f(1)=4,在x=3处f(x)取得极小值f(3)=0,
又因为,f(5)=53﹣6×52+9×5=20>f(1),
所以f(x)在上的最大值为20,最小值为0.
16.在的展开式中,求.
(1) 含项的系数;
(2)求展开式中所有的有理项.
【详解】(1)由题知展开式的通项为,
,
令,解得,
所以展开式中含项为
所以展开式中含项的系数为60.
(2) 令,.
∴
当时,
当时,
当时,
当时,
17.甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.
①求甲学校获得冠军的概率;
②用X表示乙学校的总得分,求X的分布列与期望.
【详解】①设甲学校获得冠军的事件为A,则甲学校必须获胜2场或者3场.
P(A)=0.5×0.4×0.8+(1-0.5)×0.4×0.8+0.5×(1-0.4)×0.8+0.5×0.4×(1-0.8)=0.6.
故甲学校获得冠军的概率为 0.6.
②X的取值可以为0,10,20,30.
P(X=0)=0.5×0.4×0.8=0.16,
P(X=10)=(1-0.5)×0.4×0.8+0.5×(1-0.4)×0.8+0.5×0.4×(1-0.8)=0.44,
P(X=20)=(1-0.5)×(1-0.4)×0.8+0.5×(1-0.4)×(1-0.8)+(1-0.5)×0.4×(1-0.8)=0.34,
P(X=30)=(1-0.5)×(1-0.4)×(1-0.8)=0.06.
所以X的分布列为
X 0 10 20 30
P 0.16 0.44 0.34 0.06
所以E(X)=0×0.16+10×0.44+20×0.34+30×0.06=13.
18.如图,在四棱锥中,,底面为正方形,分别为的中点.
(1)求证:∥平面;
(2)求直线与平面所成角的正弦值;
(3)求点到平面的距离.
【详解】(1)证明:因为,分别为,的中点,
所以,
又平面,平面,
故平面;
(2)由于平面,
所以平面,
以点为坐标原点,建立空间直角坐标系如图所示,
则,1,,,1,,,0,,,0,,,0,,
所以,
设平面的法向量为,
则,令,则,,
故,
设直线与平面所成角为,
则,
故直线与平面所成角的正弦值为;
(3)因为,
又平面的法向量为,
所以点到平面的距离为.
19.为更好的发挥高考的育才作用,部分新高考数学试卷采用了多选题这一题型.教育部考试中心通过科学测量分析,指出该题型扩大了试卷考点的覆盖面,有利于提高试卷的区分度,也有利于提高学生的得分率.多选题评分规则如下:对于多选题,每个小题给出的四个选项中,有两项或三项是正确的,满分6分.全部选对得6分,有错选或全不选得0分,正确答案为两项时,选对1个得3分;正确答案为三项时,选对1个得2分,选对2个得4分.多选题正确答案是两个选项的概率为p,正确答案是三个选项的概率为(其中).
(1)在一次模拟考试中,学生甲对某个多选题完全不会,决定随机选择一个选项,若,求学生甲该题得2分的概率;
(2)针对某道多选题,学生甲完全不会,此时他有三种答题方案:
Ⅰ:随机选一个选项; Ⅱ:随机选两个选项; Ⅲ:随机选三个选项.
(i)若,且学生甲选择方案Ⅰ,求本题得分的数学期望;
(ii)以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好
【详解】
(1)记事件为“正确答案选两个选项”,事件为“学生甲得分”.
,
即学生甲该题得分的概率为.
(2)(i)记为“从四个选项中随机选择一个选项的得分”,则可以取,,,
, ,
,
所以的分布列为
则数学期望.
(ⅱ)记为“从四个选项中随机选择一个选项的得分”,
则,
,
,
所以
记为“从四个选项中随机选择两个选项的得分”,
则,
,
,
所以
记为“从四个选项中随机选择三个选项的得分”,
则,
,
所以.
要使唯独选择方案Ⅰ最好,则,解得:,
故的取值范围为.
高二数学
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1.若,则( )
A. 5 B. 6 C. 7 D. 8
2.2025年U-20男足亚洲杯足球赛于2月份在深圳举行,东道主中国所在的A组共有四支球队,四支球队之间进行单循环比赛,共进行的比赛的场数为 ( )
A. 4 B. 6 C. 8 D. 10
3.已知,,不共面,若,,且三点共线,则( )
A. B.1 C.2 D.3
4.函数f(x)=的部分图象大致为( )
5.某中学体育运动会上,甲、乙两人进行乒乓球项目决赛,采取“三局两胜制”,即先胜两局者获得冠军.已知甲每局获胜的概率为,且比赛没有平局.记事件表示“甲获得冠军”,事件表示“比赛进行了三局”,则( )
A. B. C. D.
6.设袋中有8个红球,4个白球,若从袋中任取4个球,则其中至多有3个红球的概率为( )
7.已知平行六面体中,棱两两的夹角均为,,E为中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
8.我们约定:若两个函数的极值点个数相同,并且图象从左到右看,极大值点和极小值点分布的顺序相同,则称这两个函数的图象“相似”.已知,则下列给出的函数其图象与的图象“相似”的是( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得2分或3分或4分,有选错的得0分.
9.若函数在上单调递减,则实数的值可能为( )
A. B. C.3 D.4
10.已知二项式 的展开式中各二项式系数和为64,则下列说法正确的是( )
A.展开式共有6项 B.二项式系数最大的项是第4项
C.展开式的常数项为120 D.展开式中各项的系数和为1
11.已知为随机试验的样本空间,事件A,B满足,,则下列说法正确的是( )
A.若,且,,则
B.若,且,,则
C.若,,则
D.若,,,则
三、填空题:本题共3小题,每小题5分,共15分.
12.已知函数,则______.
13.学校公园计划在小路的一侧种植丹桂、金桂、银桂、四季桂4棵桂花树,垂乳银杏、金带银杏2棵银杏树,要求2棵银杏树必须相邻,则不同的种植方法共有________种.
14.已知梯形如图1所示,其中,A为线段的中点,四边形为正方形,现沿进行折叠,使得平面⊥平面,得到如图2所示的几何体.已知当点F满足时,平面平面,则λ的值为 .
图1 图2
四.解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 已知函数其图象在点(1,4)处的切线方程为.
(1)求函数的解析式;
(2)求函数在区间上的最值.
16.在的展开式中,求.
(1)含项的系数;
(2)求展开式中所有的有理项.
17.甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.
①求甲学校获得冠军的概率;
②用X表示乙学校的总得分,求X的分布列与期望.
18.如图,在四棱锥中,,底面为正方形,分别为的中点.
(1)求证:∥平面;
(2)求直线与平面所成角的正弦值;
(3)求点到平面的距离.
19.为更好的发挥高考的育才作用,部分新高考数学试卷采用了多选题这一题型.教育部考试中心通过科学测量分析,指出该题型扩大了试卷考点的覆盖面,有利于提高试卷的区分度,也有利于提高学生的得分率.多选题评分规则如下:对于多选题,每个小题给出的四个选项中,有两项或三项是正确的,满分6分.全部选对得6分,有错选或全不选得0分,正确答案为两项时,选对1个得3分;正确答案为三项时,选对1个得2分,选对2个得4分.多选题正确答案是两个选项的概率为p,正确答案是三个选项的概率为(其中).
(1)在一次模拟考试中,学生甲对某个多选题完全不会,决定随机选择一个选项,若,求学生甲该题得2分的概率;
(2)针对某道多选题,学生甲完全不会,此时他有三种答题方案:
Ⅰ:随机选一个选项; Ⅱ:随机选两个选项; Ⅲ:随机选三个选项.
(i)若,且学生甲选择方案Ⅰ,求本题得分的数学期望;
(ii)以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好
七校联盟2024~2025学年第二学期第一次联考答案
单项选择题
1. 【答案】C
【详解】由得:,
故选:C
2.【答案】 B
【详解】四支球队之间进行单循环比赛,共进行的比赛的场数为
故选:B
3.【答案】A
【详解】因为三点共线,
所以,
即,
所以,解得,
所以,
故选:A
4.【答案】C
【详解】[f(x)=,定义域为(-∞,0)∪(0,+∞),
∵f(-x)=-=-f(x),
∴f(x)为奇函数,图象关于原点对称,故排除B;
f(1)=<1,故排除A;
∵当x>0时,f'(x)=,
又当x>1时,f'(x)>0,
∴f(x)在(1,+∞)上单调递增,故排除D.
5.【答案】C
【详解】由题意可知,事件为“比赛进行两局,甲获得冠军”,所以,,
,
由条件概率公式可得.
故选:C.
6.【答案】 D
【详解】至多有3个红球的概率为
故选: D.
7.【答案】D
【详解】根据题意以为基底表示出可得:
,,
又棱两两的夹角均为,不妨取,则;
所以;
;
又
;
所以,
因此异面直线与所成角的余弦值为.
故选:D
8. 【答案】C
【详解】,则,
令,则,
如图,作出函数的图象,
由图可知函数的图象有两个交点,
即函数有两个零点,且,
令,则或,令,则,
所以在上单调递增,在上单调递减,
所以的极大值点为,极小值点为.
对于A,函数在上单调递减,在单调递增,
所以函数有极小值点,无极大值点,故A选项不符;
对于B,函数在上单调递增,在单调递减,
所以函数有极大值点,无极小值点,故B选项不符;
对于C,,
当或时,,当时,,
所以函数的极大值点为,极小值点为,故C选项符合题意;
对于D,,
则函数的极小值点为,极大值点为,故D选项不符.
故选:C.
二、多项选择题
9.【答案】BCD
【详解】根据题意可得函数的定义域为,
又,
若函数在上单调递减,可得在上恒成立;
即在上恒成立,所以,
根据对勾函数性质可得在上单调递增,
当时,当时,所以,
所以,
结合选择可知B、C、D符合题意.
故选:BCD
10.【答案】 BD
【详解】由题知 ,得到n=6,所以展开式共有7项,故选项A错误,对于选项B,因为n=6,由二项式系数的性质知二项式系数最大的项是第4项,所以选项B正角,
对于选项C,二项式 的展开式的通项公式为
由6-2r=0,得到r=3,所以展开式的常数项为 所以选项C错误,
对于选项D, 令x=1, 则 所以展开式中各项的系数和为1,故选项D正确,
故选: BD.
11.【答案】ACD
【详解】对于A,由,则与互斥,所以,故A正确;
对于B,由,则,所以,故B错误;
对于C,由,则,即与相互独立,
所以,故C正确;
对于D,由,且,,
可得,即,
解得,故D正确.
故选:ACD.
三、填空题
12.【答案】 ##0.6
【详解】因为,则,
令,可得,解得.
故答案为:.
13. 【答案】 240
【详解】分两步完成:
第一步,将2棵银杏树看成一个元素,考虑其顺序,有种种植方法;
第二步,将银杏树与4棵桂花树全排列,有种种植方法.
由分步乘法计数原理得,不同的种植方法共有·=240(种).
14.【答案】/
【解析】如图,以A为坐标原点,
所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
∴
则,
若是平面的一个法向量,
则
可得,
若是平面的一个法向量,
则可得
由平面平面,得,
即,
解得.
故答案为:.
四.解答题
15.已知函数其图象在点(1,4)处的切线方程为.
(1)求函数的解析式;
(2)求函数在区间上的最值
【详解】解:(1)由f(x)=x3+ax2+bx(a∈R,b∈R)可得:f′(x)=3x2+2ax+b,
所以f(x)在点(1,4)处切线的斜率为k=f′(1)=3+2a+b,
因为f(x)在点(1,4)处切线方程为y=4,
所以切线的斜率为0,且f(1)=4,
所以,即,
解得a=﹣6,b=9,
所以f(x)=x3﹣6x2+9x;
(2)由(1)知f(x)=x3﹣6x2+9x,
则f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3),
令f′(x)=0得x=1或3,
所以在上f′(x)>0,f(x)单调递增,
在(1,3)上f′(x)<0,f(x)单调递减,
在(3,5)上f′(x)>0,f(x)单调递增,
在x=1处,f(x)取得极大值f(1)=4,在x=3处f(x)取得极小值f(3)=0,
又因为,f(5)=53﹣6×52+9×5=20>f(1),
所以f(x)在上的最大值为20,最小值为0.
16.在的展开式中,求.
(1) 含项的系数;
(2)求展开式中所有的有理项.
【详解】(1)由题知展开式的通项为,
,
令,解得,
所以展开式中含项为
所以展开式中含项的系数为60.
(2) 令,.
∴
当时,
当时,
当时,
当时,
17.甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.
①求甲学校获得冠军的概率;
②用X表示乙学校的总得分,求X的分布列与期望.
【详解】①设甲学校获得冠军的事件为A,则甲学校必须获胜2场或者3场.
P(A)=0.5×0.4×0.8+(1-0.5)×0.4×0.8+0.5×(1-0.4)×0.8+0.5×0.4×(1-0.8)=0.6.
故甲学校获得冠军的概率为 0.6.
②X的取值可以为0,10,20,30.
P(X=0)=0.5×0.4×0.8=0.16,
P(X=10)=(1-0.5)×0.4×0.8+0.5×(1-0.4)×0.8+0.5×0.4×(1-0.8)=0.44,
P(X=20)=(1-0.5)×(1-0.4)×0.8+0.5×(1-0.4)×(1-0.8)+(1-0.5)×0.4×(1-0.8)=0.34,
P(X=30)=(1-0.5)×(1-0.4)×(1-0.8)=0.06.
所以X的分布列为
X 0 10 20 30
P 0.16 0.44 0.34 0.06
所以E(X)=0×0.16+10×0.44+20×0.34+30×0.06=13.
18.如图,在四棱锥中,,底面为正方形,分别为的中点.
(1)求证:∥平面;
(2)求直线与平面所成角的正弦值;
(3)求点到平面的距离.
【详解】(1)证明:因为,分别为,的中点,
所以,
又平面,平面,
故平面;
(2)由于平面,
所以平面,
以点为坐标原点,建立空间直角坐标系如图所示,
则,1,,,1,,,0,,,0,,,0,,
所以,
设平面的法向量为,
则,令,则,,
故,
设直线与平面所成角为,
则,
故直线与平面所成角的正弦值为;
(3)因为,
又平面的法向量为,
所以点到平面的距离为.
19.为更好的发挥高考的育才作用,部分新高考数学试卷采用了多选题这一题型.教育部考试中心通过科学测量分析,指出该题型扩大了试卷考点的覆盖面,有利于提高试卷的区分度,也有利于提高学生的得分率.多选题评分规则如下:对于多选题,每个小题给出的四个选项中,有两项或三项是正确的,满分6分.全部选对得6分,有错选或全不选得0分,正确答案为两项时,选对1个得3分;正确答案为三项时,选对1个得2分,选对2个得4分.多选题正确答案是两个选项的概率为p,正确答案是三个选项的概率为(其中).
(1)在一次模拟考试中,学生甲对某个多选题完全不会,决定随机选择一个选项,若,求学生甲该题得2分的概率;
(2)针对某道多选题,学生甲完全不会,此时他有三种答题方案:
Ⅰ:随机选一个选项; Ⅱ:随机选两个选项; Ⅲ:随机选三个选项.
(i)若,且学生甲选择方案Ⅰ,求本题得分的数学期望;
(ii)以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好
【详解】
(1)记事件为“正确答案选两个选项”,事件为“学生甲得分”.
,
即学生甲该题得分的概率为.
(2)(i)记为“从四个选项中随机选择一个选项的得分”,则可以取,,,
, ,
,
所以的分布列为
则数学期望.
(ⅱ)记为“从四个选项中随机选择一个选项的得分”,
则,
,
,
所以
记为“从四个选项中随机选择两个选项的得分”,
则,
,
,
所以
记为“从四个选项中随机选择三个选项的得分”,
则,
,
所以.
要使唯独选择方案Ⅰ最好,则,解得:,
故的取值范围为.
同课章节目录
