广东省佛山市顺德区江义初级中学北师大版七年级数学下册课件:4.3探索三角形全等的条件(1) (共18张PPT)
文档属性
| 名称 | 广东省佛山市顺德区江义初级中学北师大版七年级数学下册课件:4.3探索三角形全等的条件(1) (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-13 16:39:46 | ||
图片预览


文档简介
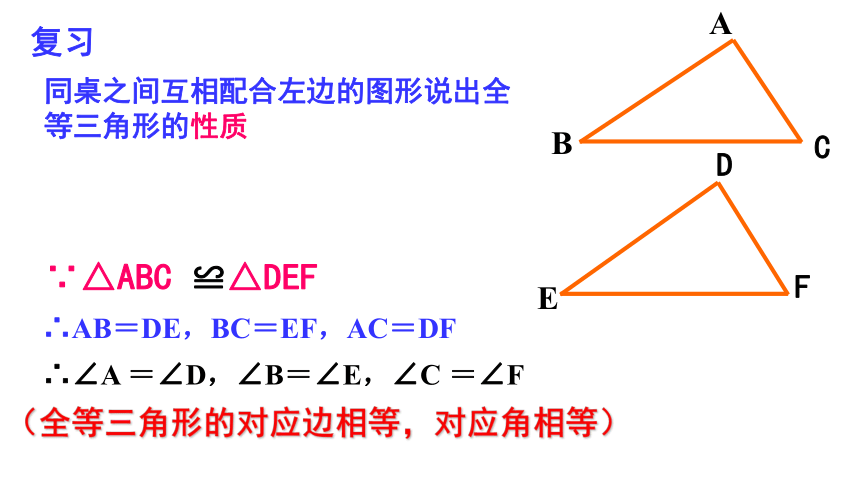
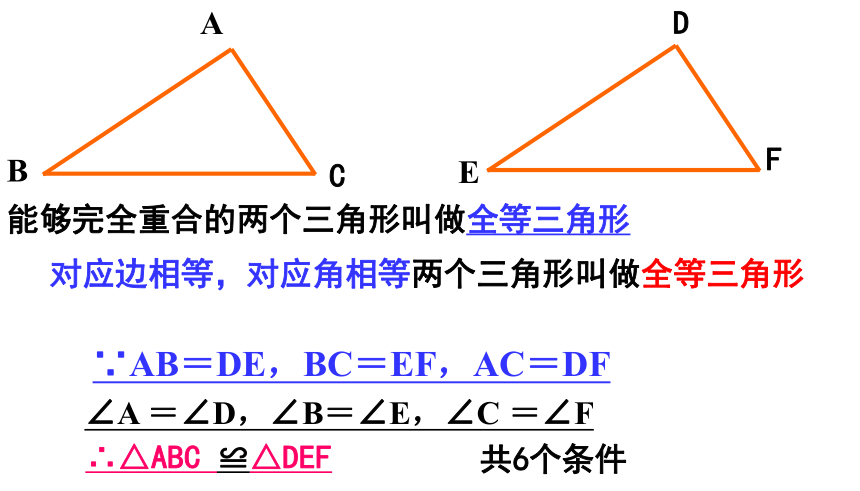
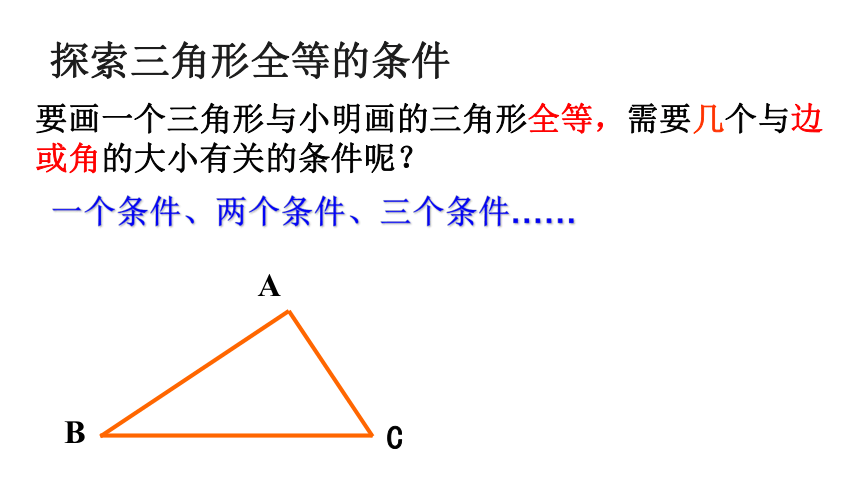
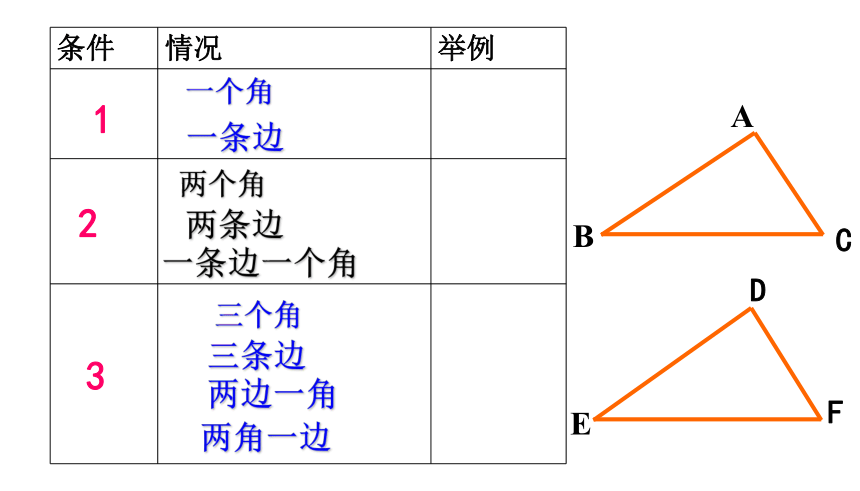
课件18张PPT。4.3探索三角形全等的条件∵△ABC ≌△DEF∴∠A =∠D,∠B=∠E,∠C =∠F ∴AB=DE,BC=EF,AC=DF(全等三角形的对应边相等,对应角相等)同桌之间互相配合左边的图形说出全等三角形的性质复习2、掌握用“边边边”的条件判断三角形全等,并能进一步它进行说明线段或角相等.学习目标1、了解探索三角形全等条件的方法。能够完全重合的两个三角形叫做全等三角形对应边相等,对应角相等两个三角形叫做全等三角形∠A =∠D,∠B=∠E,∠C =∠F∵AB=DE,BC=EF,AC=DF∴△ABC ≌△DEF共6个条件要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件、两个条件、三个条件……探索三角形全等的条件123一个角一条边两个角两条边一条边一个角三个角三条边两边一角两角一边A、只给一个条件时,大家画出的三角形一定全等吗?
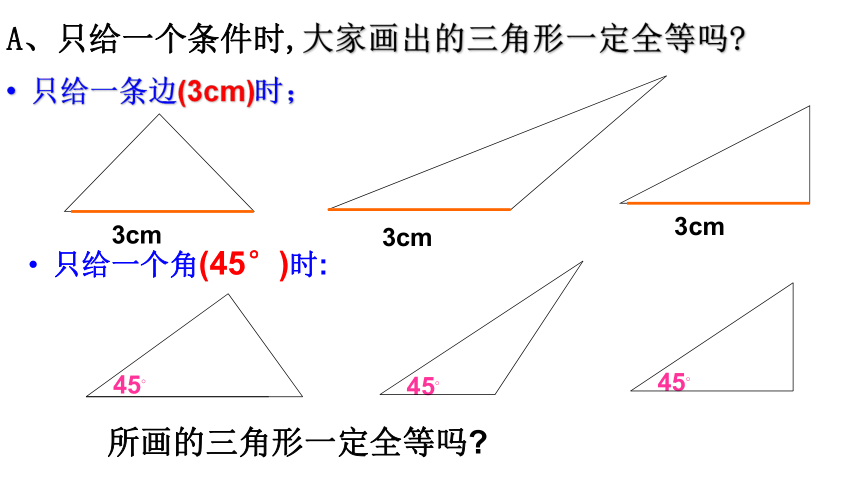
只给一条边(3cm)时;只给一个角(45°)时:所画的三角形一定全等吗? 导学一:
完成课本P97做一做中的第二个问题.
尝试画出相应图形加以说明.1、三角形的一个内角为30° ,一条边为3cm两个条件时,所画的三角形一定全等吗?B、给出两个条件呢?B、给出两个条件呢?2、三角形的两个内角分别是30 °、50°时3、如果三角形的两边分别为4cm,6cm 时C、给出三个条件呢?1、 已知一个三角形的三个内角分别为30° ,60 °,90° 它们一定全等吗? 2、 已知一个三角形的三条边分别为 4cm、5cm、7cm 。它们一定全等吗?△ABC≌ △ DEF (SSS) AB=DE
AC=DF
BC=EF三边对应相等的两个三角形全等.我们的结论是:简写为“边边边”或“SSS”AB=DEBC=EFAC=DF(SSS)数学表达式:在△ABC和△DEF中ABC ≌ DEF∴(SSS)例:如图,在四边形ABCD中,AB=CD,AD=CB,
则∠A=∠C.请说明理由。AB=CD (已知)AD=CB (已知)BD=DB (公共边)∴ ∠A= ∠C
(全等三角形的对应角相等)例题∴△ABC ≌ ( ) SSS 1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 解: △ABC≌△DCB
在△ABC和△DCB中
AB = CD
AC = DB
=
△DCB动手做一做2.如图,D,F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,还需要条件________________
AE B D F C
BF=CD 或 BD=CF 导学二
阅读课本P98中间一段,了解什么
是三角形的稳定性?并举例.
完成课本P97做一做中的第二个问题.
尝试画出相应图形加以说明.1、三角形的一个内角为30° ,一条边为3cm两个条件时,所画的三角形一定全等吗?B、给出两个条件呢?B、给出两个条件呢?2、三角形的两个内角分别是30 °、50°时3、如果三角形的两边分别为4cm,6cm 时C、给出三个条件呢?1、 已知一个三角形的三个内角分别为30° ,60 °,90° 它们一定全等吗? 2、 已知一个三角形的三条边分别为 4cm、5cm、7cm 。它们一定全等吗?△ABC≌ △ DEF (SSS) AB=DE
AC=DF
BC=EF三边对应相等的两个三角形全等.我们的结论是:简写为“边边边”或“SSS”AB=DEBC=EFAC=DF(SSS)数学表达式:在△ABC和△DEF中ABC ≌ DEF∴(SSS)例:如图,在四边形ABCD中,AB=CD,AD=CB,
则∠A=∠C.请说明理由。AB=CD (已知)AD=CB (已知)BD=DB (公共边)∴ ∠A= ∠C
(全等三角形的对应角相等)例题∴△ABC ≌ ( ) SSS 1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 解: △ABC≌△DCB
在△ABC和△DCB中
AB = CD
AC = DB
=
△DCB动手做一做2.如图,D,F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,还需要条件________________
AE B D F C
BF=CD 或 BD=CF 导学二
阅读课本P98中间一段,了解什么
是三角形的稳定性?并举例.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
