人教版五年级数学上册第六单元 组合图形和不规则图形的面积练习课 课件(共18张PPT)
文档属性
| 名称 | 人教版五年级数学上册第六单元 组合图形和不规则图形的面积练习课 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 11:26:15 | ||
图片预览




文档简介
(共18张PPT)
组合图形和不规则图形的面积
练习课
人教版五年级数学上册
第6单元 多边形的面积
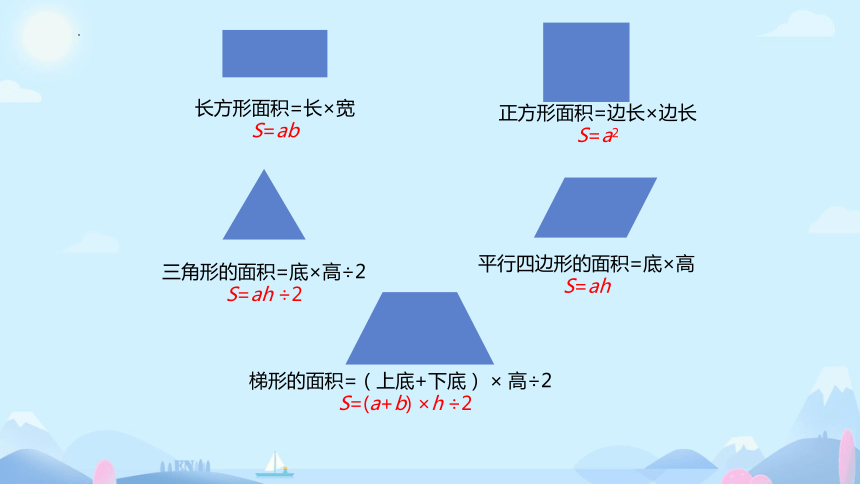
长方形面积=长×宽
S=ab
正方形面积=边长×边长
S=a2
三角形的面积=底×高÷2
S=ah ÷2
平行四边形的面积=底×高
S=ah
梯形的面积=(上底+下底) × 高÷2
S=(a+b) ×h ÷2
由几个简单的图形组合而成的图形叫组合图形。
什么是组合图形?
求组合图形面积的方法:
观察、分析组合图形可分割或添补哪些学过的基本图形,再找出计算基本图形面积需要的条件,然后利用合理的方法,先计算出基本图形的面积,再利用基本图形的面积和或差计算出组合图形的面积。
1. 借助方格图数格子估算不规则图形的面积,也可
以把不规则图形看成近似于规则的图形估算面积。
2. 用数格子估计不规则图形面积的方法:分别数出整格数和不完整格数;再根据整格数和所有格数确定面积大小的范围;最后把不完整格按半格计算加上整格数,估算出面积。
估算不规则图形的面积
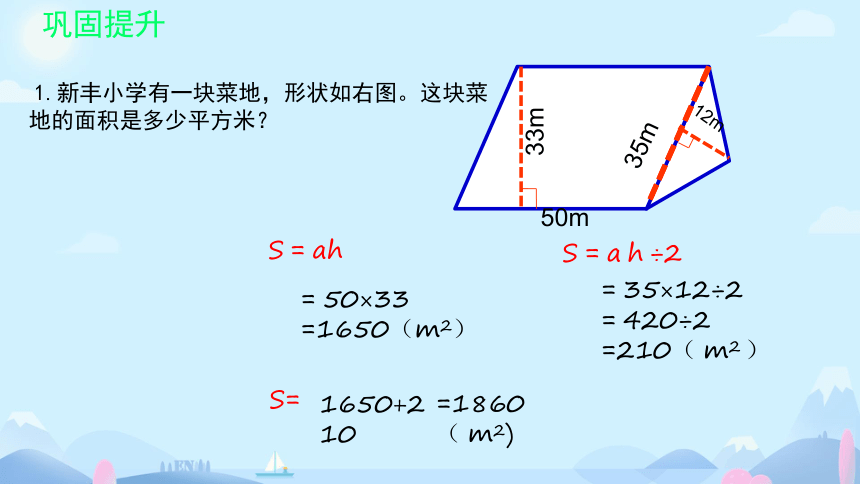
12m
35m
33m
50m
S = ah
= 50×33
=1650(m2)
S = a h ÷2
= 35×12÷2
= 420÷2
=210( m2 )
S=
1650+210
=1860( m2)
1.新丰小学有一块菜地,形状如右图。这块菜地的面积是多少平方米?
巩固提升
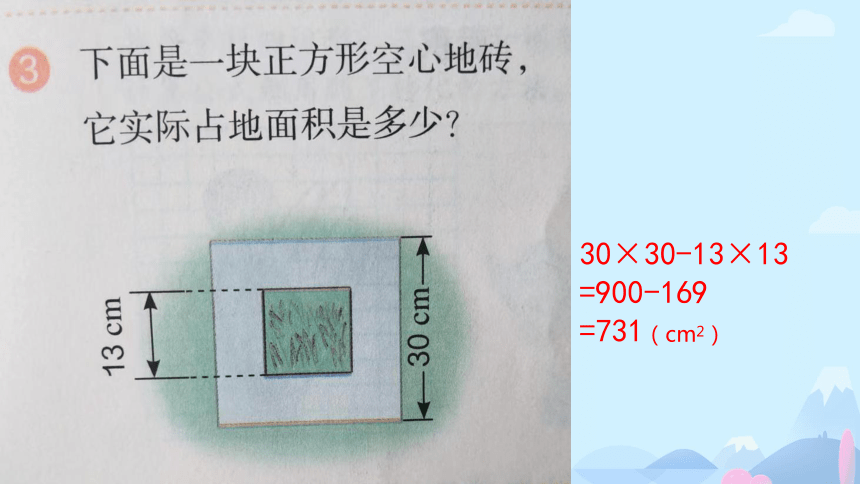
30×30-13×13
=900-169
=731(cm2)
4.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
(70+40)×30÷2-30×15
=110×30÷2-450
=3300÷2-450
=1650-450
=1200(m2)
答:草地的面积是多少平方米?
5.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
(2+10)×12÷2-3×4÷2-(4+6)×4÷2
=72-6-20
=46(cm2)
答:它的面积是46cm2。
20×10+20×10÷2
=200+100
=300(cm2)
S = ah
=43×20.1
=864.3
864(平方米)
答:这块地的面积约是864平方米
8.图中每个小方格的面积是1cm2,计算阴影部分的面积。
(2+5)×4÷2+5×4÷2
=28÷2+20÷2
=14+10
=24(cm2)
8×4=32(cm2)
9.图中每个小方格的面积为1 m2,请你估计这个池塘的面积 。
估计这个池塘的面积是12×8=96 m2 。
7×5=35(平方厘米)
5*.学校校园里有一块长方形的地,想种上红花、黄花和绿草。一种设计方案如左图。你能分别算出红花、黄花、绿草的种植面积吗?请你也设计一种方案,用上我们学过的图形,并求一求每种植物的种植面积。
=9x6÷2x4=108( m2 )
=(18x12-108)÷2
=108÷2
=54( m2 )
20
10
16
1.求下列图形的面积。(单位:cm)
12
(10+16) ×12÷2
20×(16-10) ÷2
+
=156+60
=216(cm2)
拓展提高
(4+8)x4÷2
=12x4÷2
=48÷2
=24(c㎡)
答:阴影部分面积是24c㎡。
2.计算下面图形中阴影部分的面积。
拓展提高
课后作业
课本101页第2题,102页第1题。
组合图形和不规则图形的面积
练习课
人教版五年级数学上册
第6单元 多边形的面积
长方形面积=长×宽
S=ab
正方形面积=边长×边长
S=a2
三角形的面积=底×高÷2
S=ah ÷2
平行四边形的面积=底×高
S=ah
梯形的面积=(上底+下底) × 高÷2
S=(a+b) ×h ÷2
由几个简单的图形组合而成的图形叫组合图形。
什么是组合图形?
求组合图形面积的方法:
观察、分析组合图形可分割或添补哪些学过的基本图形,再找出计算基本图形面积需要的条件,然后利用合理的方法,先计算出基本图形的面积,再利用基本图形的面积和或差计算出组合图形的面积。
1. 借助方格图数格子估算不规则图形的面积,也可
以把不规则图形看成近似于规则的图形估算面积。
2. 用数格子估计不规则图形面积的方法:分别数出整格数和不完整格数;再根据整格数和所有格数确定面积大小的范围;最后把不完整格按半格计算加上整格数,估算出面积。
估算不规则图形的面积
12m
35m
33m
50m
S = ah
= 50×33
=1650(m2)
S = a h ÷2
= 35×12÷2
= 420÷2
=210( m2 )
S=
1650+210
=1860( m2)
1.新丰小学有一块菜地,形状如右图。这块菜地的面积是多少平方米?
巩固提升
30×30-13×13
=900-169
=731(cm2)
4.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
(70+40)×30÷2-30×15
=110×30÷2-450
=3300÷2-450
=1650-450
=1200(m2)
答:草地的面积是多少平方米?
5.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
(2+10)×12÷2-3×4÷2-(4+6)×4÷2
=72-6-20
=46(cm2)
答:它的面积是46cm2。
20×10+20×10÷2
=200+100
=300(cm2)
S = ah
=43×20.1
=864.3
864(平方米)
答:这块地的面积约是864平方米
8.图中每个小方格的面积是1cm2,计算阴影部分的面积。
(2+5)×4÷2+5×4÷2
=28÷2+20÷2
=14+10
=24(cm2)
8×4=32(cm2)
9.图中每个小方格的面积为1 m2,请你估计这个池塘的面积 。
估计这个池塘的面积是12×8=96 m2 。
7×5=35(平方厘米)
5*.学校校园里有一块长方形的地,想种上红花、黄花和绿草。一种设计方案如左图。你能分别算出红花、黄花、绿草的种植面积吗?请你也设计一种方案,用上我们学过的图形,并求一求每种植物的种植面积。
=9x6÷2x4=108( m2 )
=(18x12-108)÷2
=108÷2
=54( m2 )
20
10
16
1.求下列图形的面积。(单位:cm)
12
(10+16) ×12÷2
20×(16-10) ÷2
+
=156+60
=216(cm2)
拓展提高
(4+8)x4÷2
=12x4÷2
=48÷2
=24(c㎡)
答:阴影部分面积是24c㎡。
2.计算下面图形中阴影部分的面积。
拓展提高
课后作业
课本101页第2题,102页第1题。
