2025中考数学考前15天:第9天 平行四边形(含答案)
文档属性
| 名称 | 2025中考数学考前15天:第9天 平行四边形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 129.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 11:27:11 | ||
图片预览




文档简介
平行四边形
易错易混
1.注意区分中位线与中线.
2.平行四边形的判定:
误用“一组对边相等,一组对角相等”.
忽略“同一组”对边(平行且相等必须是同一组).
方法技巧
1.(1)一组对边平行,另一组对边相等点拨的四边形不一定是平行四边形.例如:等腰梯形.
(2)一组对边平行,一组对角相等的四边形是平行四边形.
2.注意平行线之间的距离和平行线之间的平行线段是不同的概念,不能混为一谈.
3.(1)平行四边形的邻边之和等于平行四边形周长的一半.
(2)平行四边形被对角线分成四个小三角形,相邻两个小三角形周长之差等于两邻边之差.
4.中点四边形的形状的方法
顺次连接四边形各边的中点得到的四边形叫做中点四边形.连接原四边形的一条对角线,得到两组三角形的中位线,利用一组对边平行且相等这一判定定理可得中点四边形是平行四边形.
5.遇到中点想中位线
如果在三角形中遇到一个中点或一条中线,那么应当考虑是否还存在另一个中点,是否隐含了三角形的中位线,这种方法就是常说的“遇到中点想中位线”.特别是出现“线段相等十垂直”或“角平分线十垂直”模型时,往往存在另一个中点.
6.平行四边形的判定与性质
复杂图形中先拆分出基本平行四边形.
对角线性质常用于求线段长度或交点坐标.
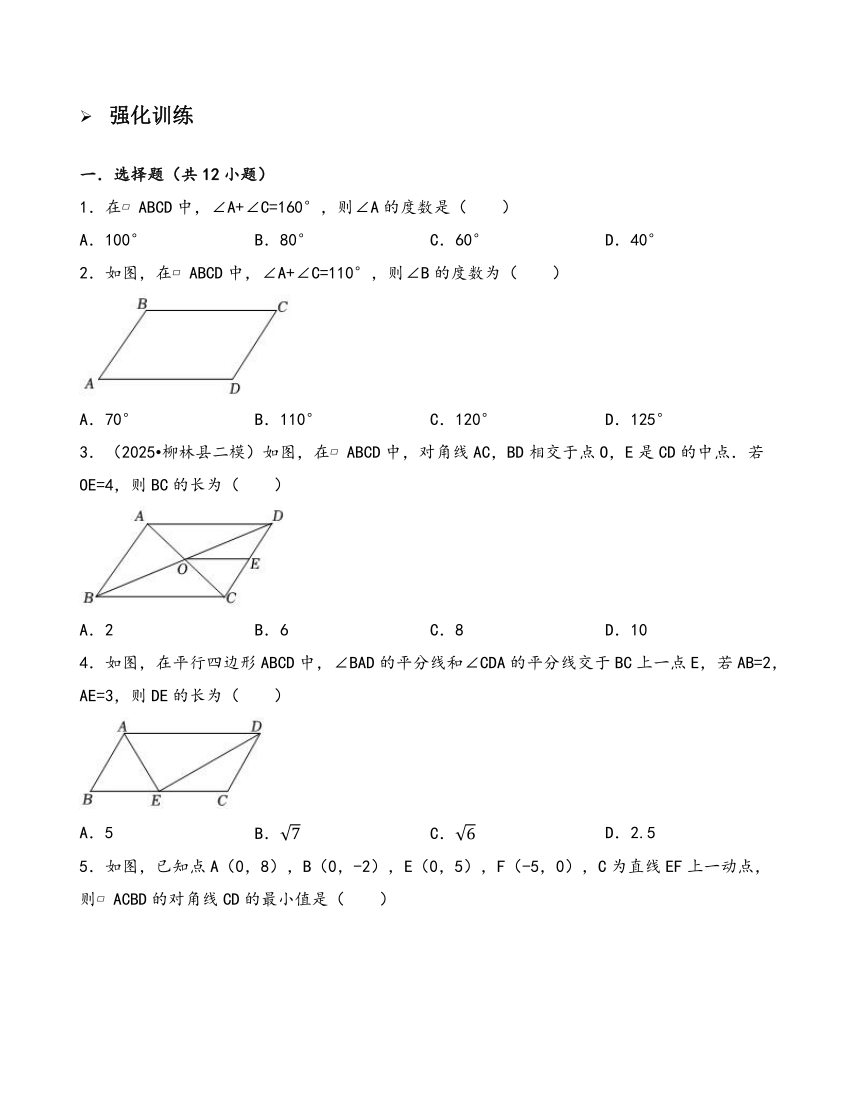
强化训练
一.选择题(共12小题)
1.在 ABCD中,∠A+∠C=160°,则∠A的度数是( )
A.100° B.80° C.60° D.40°
2.如图,在 ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.70° B.110° C.120° D.125°
3.(2025 柳林县二模)如图,在 ABCD中,对角线AC,BD相交于点O,E是CD的中点.若OE=4,则BC的长为( )
A.2 B.6 C.8 D.10
4.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=2,AE=3,则DE的长为( )
A.5 B. C. D.2.5
5.如图,已知点A(0,8),B(0,-2),E(0,5),F(-5,0),C为直线EF上一动点,则 ACBD的对角线CD的最小值是( )
A. B.4 C.5 D.
6.如图,平行四边形ABCD的对角线交于点O,点E为BC的中点,若CD=6,则OE的长度为( )
A.1 B.2 C.3 D.4
7.如图,在 ABCD中,AE⊥BC,AF⊥CD,若AE:AF=2:3, ABCD的周长为40,则AB的长为( )
A.8 B.9 C.12 D.13
8. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
9.如图,在 ABCD中,点E是BC延长线上一点,AE=AB.设AB=x,AC=y,当AD CE为定值时,无论x,y的值如何变化,下列代数式的值不变的是( )
A.x+y B.x2-y2 C.xy D.x2+y2
10.如图,在 ABCD中,∠C=120°,AB=8,AD>AB,H、G分别是CD、BC上的动点,连接AH、GH,E、F分别为AH、GH的中点,则EF的最小值是( )
A.4 B.5 C. D.
11.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=BC=1,则△APO的面积为是( )
A. B. C. D.
12.如图,△ABC为等边三角形,D、E分别是边BC、AC上的点,且满足BD=CE=BC,P是边AB上的动点,以P、D、E为顶点,DE为对角线构造 PDQE,若AB=10,则BQ的最小值为( )
A. B. C. D.10
二.填空题(共5小题)
13.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为 ______.
14.如图, ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=______.
15.如图, ABCD的对角线AC,BD相交于点O,点E是AD的中点.若AB=8,AD=12,则OE的长为 ______.
16.(2025春 鹿城区校级期中)如图,在△ABC中,BD垂直平分AC,点F在BC,连结AF,E为AF的中点,连结DE,若AB=9,BF=DE,则DE的长为 ______.
17.如图所示:四边形ABCD是平行四边形,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②FC平分∠BCE;③点E,F,B,C为顶点的四边形的面积=;④△PFC是等边三角形,其中正确的有 ______.(填序号)
三.解答题(共5小题)
18.如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)求证:BC=CF.
(2)若∠BAF=90°,AD=2,AE=,求AB的长.
19.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)若AB=10,AC=4,求BF的长.
20.如图,在平行四边形ABCD中,AE⊥BC于点E,点E为BC的中点,AE=2BE.点P在BE上,作EF⊥DP于点F,连接AF.
(1)若AD=4,求AB的长;
(2)求证:.
21.如图,E、F是 ABCD对角线AC上两点,且AE=CF.
(1)求证:四边形BFDE是平行四边形.
(2)如果把条件AE=CF改为BE⊥AC,DF⊥AC,试问四边形BFDE是平行四边形吗?为什么?
(3)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?
22.如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形.
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:BR=RD;
(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件?
第9天 平行四边形
(参考答案)
一.选择题(共12小题)
1、B 2、D 3、C 4、B 5、A 6、C 7、A 8、C 9、B 10、D 11、B 12、A
二.填空题(共5小题)
13、10; 14、135°; 15、4; 16、3; 17、①②③;
三.解答题(共5小题)
18、(1)证明:∵点E是平行四边形ABCD的边CD的中点,
∴AB∥CD,AD∥BC,AD=BC,CE=DE,
∴∠D=∠DCF,∠DAE=∠F,
∴△ADE≌△FCE,
∴AE=EF,
∵AB∥CD,
∴,
∴BC=CF;
(2)解:由(1)得:AE=EF,AD=BC=CF,
∴,AD=BC=CF=2,
∴,BF=4,
∵∠BAF=90°,
∴.
19、(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵EF∥BC,
∴四边形BDEF是平行四边形.
(2)解:∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB-AG)=(AB-AC)=(10-4)=3.
20、(1)解:∵点E为BC的中点,
∴BC=2BE,
由条件可知AE=BC,
∵四边形ABCD是平行四边形,AD=4,
∴AD=BC=4,
∴AE=AD=4,,
∵AE⊥BC,
∴AB==2;
(2)证明:过点A作AH⊥AF交DP于点H,
则∠DAE=∠FAH=90°,
∴∠DAE-∠EAH=∠FAH-∠EAH,
即∠DAH=∠EAF,
∵∠1+∠EAD+∠ADP=180°,∠2+∠EFD+∠AEF=180°,
且∠1=∠2,∠DAE=∠EFD=90°,
∴∠AEF=∠ADF,
∵∠DAH=∠EAF,AD=AE,
∴△AEF≌△ADH(ASA),
∴DH=EF,AF=AH,
在Rt△AFH中,∠FAH=90°,
由勾股定理得:,
∵DF=FH+HD,
∴,
∴.
21、(1)证法一:∵ABCD是平行四边形
∴AB=CD 且AB∥CD(平行四边形的对边平行且相等)
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF(SAS)
∴BE=DF,∠AEB=∠CFD
∴∠BEF=180°-∠AEB∠DFE=180°-∠CFD
即:∠BEF=∠DFE
∴BE∥DF,而BE=DF
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
证法二:连接BD,交AC于点O.
∵ABCD是平行四边形
∴OA=OC OB=OD(平行四边形的对角线互相平分)
又∵AE=CF
∴OA-AE=OC-CF,即OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
(2)四边形BFDE是平行四边形
∵ABCD是平行四边形
∴AB=CD 且AB∥CD(平行四边形的对边平行且相等)
∴∠BAE=∠DCF
∵BE⊥AC,DF⊥AC
∴∠BEA=∠DFC=90°,BE∥DF
∴△BAE≌△DCF(AAS)
∴BE=DF
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
(3)四边形BFDE不是平行四边形
因为把条件AE=CF改为BE=DF后,不能证明△BAE与△DCF全等.
22、(1)证明:∵∠ABD=90°,AB∥RC,
∴CR⊥BD.
∵BC=CD,
∴∠BCR=∠DCR.
∵四边形ABCR是平行四边形,
∴∠BCR=∠BAR.
∴∠BAR=∠DCR.
又∵AB=CR,AR=BC=CD,
∴△ABR≌△CRD(SAS).
(2)解:由PS∥QR,PS∥RD(四边形PRDS为平行四边形)知,点R在QD上,
又∵PS∥BC,PS∥RD,
故BC∥AD.
又由AB=CD知∠A=∠CDA,
因为SR∥PQ∥BA,
所以∠SRD=∠A=∠CDA,
∵从而SR=SD,
由PS∥BC,
∴△DCB∽△DSP,
∵BC=CD,
∴SP=SD.
∵SP=DR,
所以SR=SD=RD,
故∠CDA=60°.
因此四边形ABCD还应满足BC∥AD,∠CDA=60°.
(注:若推出的条件为BC∥AD,∠BAD=60°或BC∥AD,∠BCD=120°等亦可).
易错易混
1.注意区分中位线与中线.
2.平行四边形的判定:
误用“一组对边相等,一组对角相等”.
忽略“同一组”对边(平行且相等必须是同一组).
方法技巧
1.(1)一组对边平行,另一组对边相等点拨的四边形不一定是平行四边形.例如:等腰梯形.
(2)一组对边平行,一组对角相等的四边形是平行四边形.
2.注意平行线之间的距离和平行线之间的平行线段是不同的概念,不能混为一谈.
3.(1)平行四边形的邻边之和等于平行四边形周长的一半.
(2)平行四边形被对角线分成四个小三角形,相邻两个小三角形周长之差等于两邻边之差.
4.中点四边形的形状的方法
顺次连接四边形各边的中点得到的四边形叫做中点四边形.连接原四边形的一条对角线,得到两组三角形的中位线,利用一组对边平行且相等这一判定定理可得中点四边形是平行四边形.
5.遇到中点想中位线
如果在三角形中遇到一个中点或一条中线,那么应当考虑是否还存在另一个中点,是否隐含了三角形的中位线,这种方法就是常说的“遇到中点想中位线”.特别是出现“线段相等十垂直”或“角平分线十垂直”模型时,往往存在另一个中点.
6.平行四边形的判定与性质
复杂图形中先拆分出基本平行四边形.
对角线性质常用于求线段长度或交点坐标.
强化训练
一.选择题(共12小题)
1.在 ABCD中,∠A+∠C=160°,则∠A的度数是( )
A.100° B.80° C.60° D.40°
2.如图,在 ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.70° B.110° C.120° D.125°
3.(2025 柳林县二模)如图,在 ABCD中,对角线AC,BD相交于点O,E是CD的中点.若OE=4,则BC的长为( )
A.2 B.6 C.8 D.10
4.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=2,AE=3,则DE的长为( )
A.5 B. C. D.2.5
5.如图,已知点A(0,8),B(0,-2),E(0,5),F(-5,0),C为直线EF上一动点,则 ACBD的对角线CD的最小值是( )
A. B.4 C.5 D.
6.如图,平行四边形ABCD的对角线交于点O,点E为BC的中点,若CD=6,则OE的长度为( )
A.1 B.2 C.3 D.4
7.如图,在 ABCD中,AE⊥BC,AF⊥CD,若AE:AF=2:3, ABCD的周长为40,则AB的长为( )
A.8 B.9 C.12 D.13
8. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
9.如图,在 ABCD中,点E是BC延长线上一点,AE=AB.设AB=x,AC=y,当AD CE为定值时,无论x,y的值如何变化,下列代数式的值不变的是( )
A.x+y B.x2-y2 C.xy D.x2+y2
10.如图,在 ABCD中,∠C=120°,AB=8,AD>AB,H、G分别是CD、BC上的动点,连接AH、GH,E、F分别为AH、GH的中点,则EF的最小值是( )
A.4 B.5 C. D.
11.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=BC=1,则△APO的面积为是( )
A. B. C. D.
12.如图,△ABC为等边三角形,D、E分别是边BC、AC上的点,且满足BD=CE=BC,P是边AB上的动点,以P、D、E为顶点,DE为对角线构造 PDQE,若AB=10,则BQ的最小值为( )
A. B. C. D.10
二.填空题(共5小题)
13.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为 ______.
14.如图, ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=______.
15.如图, ABCD的对角线AC,BD相交于点O,点E是AD的中点.若AB=8,AD=12,则OE的长为 ______.
16.(2025春 鹿城区校级期中)如图,在△ABC中,BD垂直平分AC,点F在BC,连结AF,E为AF的中点,连结DE,若AB=9,BF=DE,则DE的长为 ______.
17.如图所示:四边形ABCD是平行四边形,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②FC平分∠BCE;③点E,F,B,C为顶点的四边形的面积=;④△PFC是等边三角形,其中正确的有 ______.(填序号)
三.解答题(共5小题)
18.如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)求证:BC=CF.
(2)若∠BAF=90°,AD=2,AE=,求AB的长.
19.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)若AB=10,AC=4,求BF的长.
20.如图,在平行四边形ABCD中,AE⊥BC于点E,点E为BC的中点,AE=2BE.点P在BE上,作EF⊥DP于点F,连接AF.
(1)若AD=4,求AB的长;
(2)求证:.
21.如图,E、F是 ABCD对角线AC上两点,且AE=CF.
(1)求证:四边形BFDE是平行四边形.
(2)如果把条件AE=CF改为BE⊥AC,DF⊥AC,试问四边形BFDE是平行四边形吗?为什么?
(3)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?
22.如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形.
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:BR=RD;
(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件?
第9天 平行四边形
(参考答案)
一.选择题(共12小题)
1、B 2、D 3、C 4、B 5、A 6、C 7、A 8、C 9、B 10、D 11、B 12、A
二.填空题(共5小题)
13、10; 14、135°; 15、4; 16、3; 17、①②③;
三.解答题(共5小题)
18、(1)证明:∵点E是平行四边形ABCD的边CD的中点,
∴AB∥CD,AD∥BC,AD=BC,CE=DE,
∴∠D=∠DCF,∠DAE=∠F,
∴△ADE≌△FCE,
∴AE=EF,
∵AB∥CD,
∴,
∴BC=CF;
(2)解:由(1)得:AE=EF,AD=BC=CF,
∴,AD=BC=CF=2,
∴,BF=4,
∵∠BAF=90°,
∴.
19、(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵EF∥BC,
∴四边形BDEF是平行四边形.
(2)解:∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB-AG)=(AB-AC)=(10-4)=3.
20、(1)解:∵点E为BC的中点,
∴BC=2BE,
由条件可知AE=BC,
∵四边形ABCD是平行四边形,AD=4,
∴AD=BC=4,
∴AE=AD=4,,
∵AE⊥BC,
∴AB==2;
(2)证明:过点A作AH⊥AF交DP于点H,
则∠DAE=∠FAH=90°,
∴∠DAE-∠EAH=∠FAH-∠EAH,
即∠DAH=∠EAF,
∵∠1+∠EAD+∠ADP=180°,∠2+∠EFD+∠AEF=180°,
且∠1=∠2,∠DAE=∠EFD=90°,
∴∠AEF=∠ADF,
∵∠DAH=∠EAF,AD=AE,
∴△AEF≌△ADH(ASA),
∴DH=EF,AF=AH,
在Rt△AFH中,∠FAH=90°,
由勾股定理得:,
∵DF=FH+HD,
∴,
∴.
21、(1)证法一:∵ABCD是平行四边形
∴AB=CD 且AB∥CD(平行四边形的对边平行且相等)
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF(SAS)
∴BE=DF,∠AEB=∠CFD
∴∠BEF=180°-∠AEB∠DFE=180°-∠CFD
即:∠BEF=∠DFE
∴BE∥DF,而BE=DF
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
证法二:连接BD,交AC于点O.
∵ABCD是平行四边形
∴OA=OC OB=OD(平行四边形的对角线互相平分)
又∵AE=CF
∴OA-AE=OC-CF,即OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
(2)四边形BFDE是平行四边形
∵ABCD是平行四边形
∴AB=CD 且AB∥CD(平行四边形的对边平行且相等)
∴∠BAE=∠DCF
∵BE⊥AC,DF⊥AC
∴∠BEA=∠DFC=90°,BE∥DF
∴△BAE≌△DCF(AAS)
∴BE=DF
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
(3)四边形BFDE不是平行四边形
因为把条件AE=CF改为BE=DF后,不能证明△BAE与△DCF全等.
22、(1)证明:∵∠ABD=90°,AB∥RC,
∴CR⊥BD.
∵BC=CD,
∴∠BCR=∠DCR.
∵四边形ABCR是平行四边形,
∴∠BCR=∠BAR.
∴∠BAR=∠DCR.
又∵AB=CR,AR=BC=CD,
∴△ABR≌△CRD(SAS).
(2)解:由PS∥QR,PS∥RD(四边形PRDS为平行四边形)知,点R在QD上,
又∵PS∥BC,PS∥RD,
故BC∥AD.
又由AB=CD知∠A=∠CDA,
因为SR∥PQ∥BA,
所以∠SRD=∠A=∠CDA,
∵从而SR=SD,
由PS∥BC,
∴△DCB∽△DSP,
∵BC=CD,
∴SP=SD.
∵SP=DR,
所以SR=SD=RD,
故∠CDA=60°.
因此四边形ABCD还应满足BC∥AD,∠CDA=60°.
(注:若推出的条件为BC∥AD,∠BAD=60°或BC∥AD,∠BCD=120°等亦可).
同课章节目录
