华东师大版八年级下 第18章 平行四边形 单元巩固卷(含答案)
文档属性
| 名称 | 华东师大版八年级下 第18章 平行四边形 单元巩固卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 00:00:00 | ||
图片预览



文档简介
华东师大版八年级下 第18章 平行四边形 单元巩固卷
一.选择题(共12小题)
1.(2025春 道外区期中)如图,G、E分别为 ABCD的边CD,DA的中点,则△BGE和 ABCD的面积比为( )
A.1:4 B.1:3 C.3:8 D.7:16
2.如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,∠BAD=135°,∠ACD=80°,∠CBD=20°,则∠COD的度数为( )
A.75° B.53° C.85° D.90°
3.如图是一个由4张直角三角形纸片和1张正方形纸片拼成的平行四边形,相邻纸片之间无缝隙且不重叠,其中两张等腰直角三角形纸片的面积都为S1=1,则这个平行四边形的面积为( )
A.3 B.4 C.5 D.6
4.在平行四边形ABCD中,对角线AC、BD相交于点O,AC=6,BD=12,则边AD的长度x的取值范围是( )
A.2<x<6 B.3<x<9 C.1<x<9 D.2<x<8
5.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=3,AE=2,则DE的长为( )
A. B. C.5 D.6
6.如图, ABCD的周长是24cm,对角线相交于点O,且EO⊥BD,则△ABE的周长为( )
A.24 B.15 C.12 D.10
7.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD=BC B.AB=BC,AD=CD
C.AB∥DC,AB=DC D.AD=BC,AO=CO
8.如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当AD=CD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
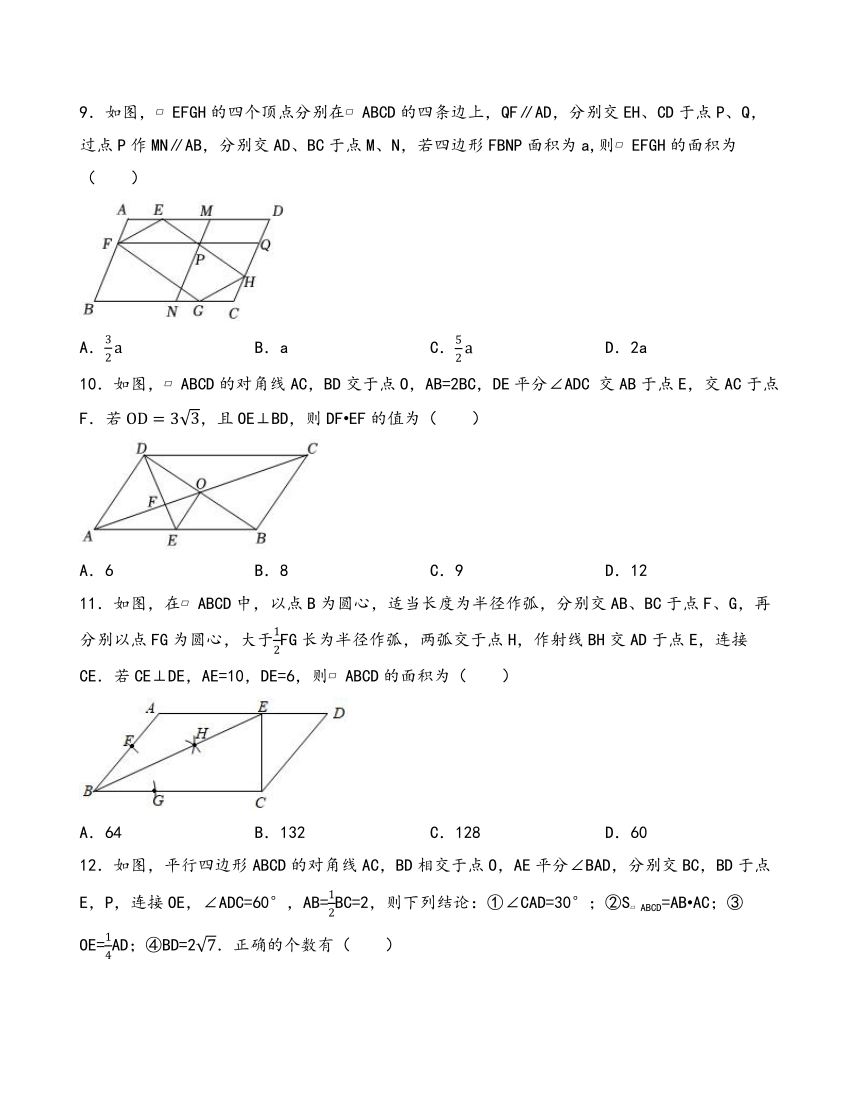
9.如图, EFGH的四个顶点分别在 ABCD的四条边上,QF∥AD,分别交EH、CD于点P、Q,过点P作MN∥AB,分别交AD、BC于点M、N,若四边形FBNP面积为a,则 EFGH的面积为( )
A. B.a C. D.2a
10.如图, ABCD的对角线AC,BD交于点O,AB=2BC,DE平分∠ADC 交AB于点E,交AC于点F.若,且OE⊥BD,则DF EF的值为( )
A.6 B.8 C.9 D.12
11.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB、BC于点F、G,再分别以点FG为圆心,大于FG长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥DE,AE=10,DE=6,则 ABCD的面积为( )
A.64 B.132 C.128 D.60
12.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E,P,连接OE,∠ADC=60°,AB=BC=2,则下列结论:①∠CAD=30°;②S ABCD=AB AC;③OE=AD;④BD=2.正确的个数有( )
A.1 B.2 C.3 D.4
二.填空题(共5小题)
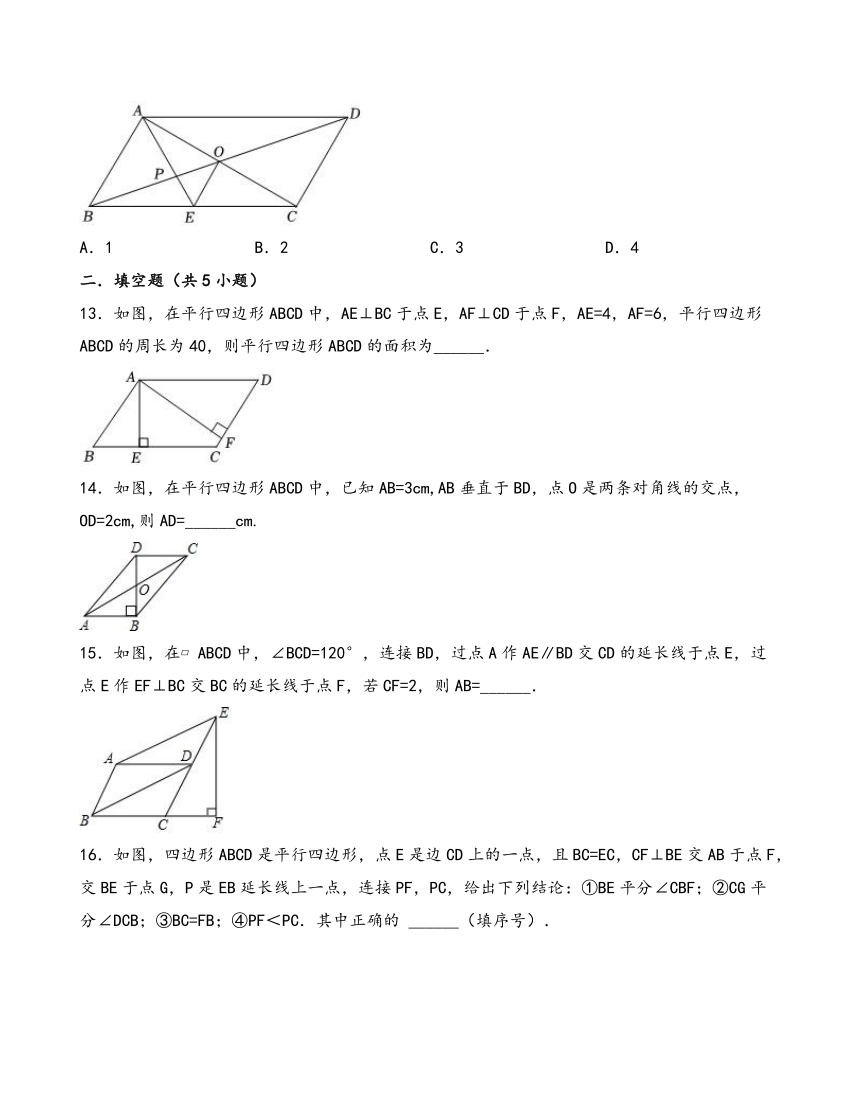
13.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积为______.
14.如图,在平行四边形ABCD中,已知AB=3cm,AB垂直于BD,点O是两条对角线的交点,OD=2cm,则AD=______cm.
15.如图,在 ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=______.
16.如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,交BE于点G,P是EB延长线上一点,连接PF,PC,给出下列结论:①BE平分∠CBF;②CG平分∠DCB;③BC=FB;④PF<PC.其中正确的 ______(填序号).
17.如图,平行四边形ABCD中,O为对角线交点,DP平分∠ADC,CP平分∠BCD,AB=7,AD=10,则OP=______.
三.解答题(共5小题)
18.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长;
(3)若AC⊥AB,BD=2AC,当AC=4时,求 ABCD的面积.
19.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=8,求四边形AECD的周长.
20.已知△ABC和△ADE均为等边三角形,点F、D分别在AC、BC上,AF=CD,连接BF、EF.求证:
(1)AD=BF;
(2)四边形BFED为平行四边形.
21.如图, ABCD的对角线AC,BD相交于点O,点E在AD上,点F在BC上,连结EF使EF恰好经过点O.
(1)求证:ED=FB.
(2)若AC⊥BD,ED+CF=5,AC=6,求BD的长.
22.如图,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA.
(2)当AE⊥AF时,求∠EBH的度数.
华东师大版八年级下 第18章 平行四边形 单元巩固卷
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、B 4、B 5、B 6、C 7、C 8、C 9、B 10、B 11、C 12、D
二.填空题(共5小题)
13、48; 14、5; 15、2; 16、①②③; 17、1.5;
三.解答题(共5小题)
18、(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,AO=CO,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF;
(2)解:∵AE=EF=4,OE=OF,
∴EO=OF=2,
∴AO===2,
∴AC=2AO=4;
(3)解:∵BD=2AC,AC=4,
∴BD=8,
∴BO=4,AO=2,
∵AC⊥AB,
∴AB===2,
∴ ABCD的面积=AB AC=2×4=8.
19、(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
由(1)知:四边形AECD是平行四边形,
∴四边形AECD是菱形,
∴四边形AECD的周长=4CD=4×8=32.
20、证明:(1)∵△ABC和△ADE均为等边三角形,
∴AB=AC,∠BAF=∠C=60°,
又∵AF=CD,
∴△ABF≌△CAD(SAS),
∴AD=BF;
(2)如图,设AC与DE相交于点H,
由(1)知,BF=AD,
∵△ADE是等边三角形,
∴AD=DE,
∴BF=DE,
∵∠C=∠AED=60°,∠DHC=∠AHE,
∴∠CDH=∠CAE,
∵∠CAE+∠DAC=∠CBF+∠ABF=60°,∠ABF=∠DAC,
∴∠CBF=∠CAE,
∴∠CBD=∠CDH,
∴BF∥DE,
∴四边形BFED为平行四边形.
21、(1)证明:∵四边形ABCD是平行四边形,
∴OD=OB,AD∥BC,
∴∠EDO=∠FBO,∠DEO=∠BFO,
在△DEO和△BFO中,
,
∴△DEO和△BFO(AAS),
∴DE=BF.
(2)由(1)知BF=DE,
∵ED+CF=5,
∴BF+CF=BC=5,
∵四边形ABCD是平行四边形,
∴CO=AC=×6=3,BD=2OB,
∵AC⊥BD,
∴∠BOC=90°,
∴OB==4,
∴BD=2×4=8.
22、(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠ABC=∠ADC,
∵BE=BC,DF=DC,∠EBC=∠CDF,
∴AB=FD,EB=AD,∠ABE=∠FDA,
在△ABE和△FDA中,
,
∴△ABE≌△FDA(SAS);
(2)∵△ABE≌△FDA,
∴∠AEB=∠DAF,
∵AE⊥AF,∠BAD=32°,
∴∠EAB+∠DAF=90°-∠BAD=58°,
∴∠EBH=∠EAB+∠AEB=∠EAB+∠DAF=58°.
一.选择题(共12小题)
1.(2025春 道外区期中)如图,G、E分别为 ABCD的边CD,DA的中点,则△BGE和 ABCD的面积比为( )
A.1:4 B.1:3 C.3:8 D.7:16
2.如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,∠BAD=135°,∠ACD=80°,∠CBD=20°,则∠COD的度数为( )
A.75° B.53° C.85° D.90°
3.如图是一个由4张直角三角形纸片和1张正方形纸片拼成的平行四边形,相邻纸片之间无缝隙且不重叠,其中两张等腰直角三角形纸片的面积都为S1=1,则这个平行四边形的面积为( )
A.3 B.4 C.5 D.6
4.在平行四边形ABCD中,对角线AC、BD相交于点O,AC=6,BD=12,则边AD的长度x的取值范围是( )
A.2<x<6 B.3<x<9 C.1<x<9 D.2<x<8
5.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=3,AE=2,则DE的长为( )
A. B. C.5 D.6
6.如图, ABCD的周长是24cm,对角线相交于点O,且EO⊥BD,则△ABE的周长为( )
A.24 B.15 C.12 D.10
7.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD=BC B.AB=BC,AD=CD
C.AB∥DC,AB=DC D.AD=BC,AO=CO
8.如图,△ABC的面积为24,点D为AC边上的一点,延长BD交BC的平行线AG于点E,连结EC,以DE、EC为邻边作平行四边形DECF,DF交BC边于点H,连结AH,当AD=CD时,则△AHC的面积为( )
A.4 B.6 C.8 D.12
9.如图, EFGH的四个顶点分别在 ABCD的四条边上,QF∥AD,分别交EH、CD于点P、Q,过点P作MN∥AB,分别交AD、BC于点M、N,若四边形FBNP面积为a,则 EFGH的面积为( )
A. B.a C. D.2a
10.如图, ABCD的对角线AC,BD交于点O,AB=2BC,DE平分∠ADC 交AB于点E,交AC于点F.若,且OE⊥BD,则DF EF的值为( )
A.6 B.8 C.9 D.12
11.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB、BC于点F、G,再分别以点FG为圆心,大于FG长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥DE,AE=10,DE=6,则 ABCD的面积为( )
A.64 B.132 C.128 D.60
12.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E,P,连接OE,∠ADC=60°,AB=BC=2,则下列结论:①∠CAD=30°;②S ABCD=AB AC;③OE=AD;④BD=2.正确的个数有( )
A.1 B.2 C.3 D.4
二.填空题(共5小题)
13.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积为______.
14.如图,在平行四边形ABCD中,已知AB=3cm,AB垂直于BD,点O是两条对角线的交点,OD=2cm,则AD=______cm.
15.如图,在 ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=______.
16.如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,交BE于点G,P是EB延长线上一点,连接PF,PC,给出下列结论:①BE平分∠CBF;②CG平分∠DCB;③BC=FB;④PF<PC.其中正确的 ______(填序号).
17.如图,平行四边形ABCD中,O为对角线交点,DP平分∠ADC,CP平分∠BCD,AB=7,AD=10,则OP=______.
三.解答题(共5小题)
18.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长;
(3)若AC⊥AB,BD=2AC,当AC=4时,求 ABCD的面积.
19.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=8,求四边形AECD的周长.
20.已知△ABC和△ADE均为等边三角形,点F、D分别在AC、BC上,AF=CD,连接BF、EF.求证:
(1)AD=BF;
(2)四边形BFED为平行四边形.
21.如图, ABCD的对角线AC,BD相交于点O,点E在AD上,点F在BC上,连结EF使EF恰好经过点O.
(1)求证:ED=FB.
(2)若AC⊥BD,ED+CF=5,AC=6,求BD的长.
22.如图,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA.
(2)当AE⊥AF时,求∠EBH的度数.
华东师大版八年级下 第18章 平行四边形 单元巩固卷
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、B 4、B 5、B 6、C 7、C 8、C 9、B 10、B 11、C 12、D
二.填空题(共5小题)
13、48; 14、5; 15、2; 16、①②③; 17、1.5;
三.解答题(共5小题)
18、(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,AO=CO,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF;
(2)解:∵AE=EF=4,OE=OF,
∴EO=OF=2,
∴AO===2,
∴AC=2AO=4;
(3)解:∵BD=2AC,AC=4,
∴BD=8,
∴BO=4,AO=2,
∵AC⊥AB,
∴AB===2,
∴ ABCD的面积=AB AC=2×4=8.
19、(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
由(1)知:四边形AECD是平行四边形,
∴四边形AECD是菱形,
∴四边形AECD的周长=4CD=4×8=32.
20、证明:(1)∵△ABC和△ADE均为等边三角形,
∴AB=AC,∠BAF=∠C=60°,
又∵AF=CD,
∴△ABF≌△CAD(SAS),
∴AD=BF;
(2)如图,设AC与DE相交于点H,
由(1)知,BF=AD,
∵△ADE是等边三角形,
∴AD=DE,
∴BF=DE,
∵∠C=∠AED=60°,∠DHC=∠AHE,
∴∠CDH=∠CAE,
∵∠CAE+∠DAC=∠CBF+∠ABF=60°,∠ABF=∠DAC,
∴∠CBF=∠CAE,
∴∠CBD=∠CDH,
∴BF∥DE,
∴四边形BFED为平行四边形.
21、(1)证明:∵四边形ABCD是平行四边形,
∴OD=OB,AD∥BC,
∴∠EDO=∠FBO,∠DEO=∠BFO,
在△DEO和△BFO中,
,
∴△DEO和△BFO(AAS),
∴DE=BF.
(2)由(1)知BF=DE,
∵ED+CF=5,
∴BF+CF=BC=5,
∵四边形ABCD是平行四边形,
∴CO=AC=×6=3,BD=2OB,
∵AC⊥BD,
∴∠BOC=90°,
∴OB==4,
∴BD=2×4=8.
22、(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠ABC=∠ADC,
∵BE=BC,DF=DC,∠EBC=∠CDF,
∴AB=FD,EB=AD,∠ABE=∠FDA,
在△ABE和△FDA中,
,
∴△ABE≌△FDA(SAS);
(2)∵△ABE≌△FDA,
∴∠AEB=∠DAF,
∵AE⊥AF,∠BAD=32°,
∴∠EAB+∠DAF=90°-∠BAD=58°,
∴∠EBH=∠EAB+∠AEB=∠EAB+∠DAF=58°.
