华东师大版九年级下 第26章 二次函数 单元巩固卷(含答案)
文档属性
| 名称 | 华东师大版九年级下 第26章 二次函数 单元巩固卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 135.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 11:44:42 | ||
图片预览



文档简介
华东师大版九年级下 第26章 二次函数 单元巩固卷
一.选择题(共12小题)
1.抛物线y=(x+2)2+3的对称轴是直线( )
A.x=2 B.x=-2 C.x=3 D.x=-3
2.已知二次函数y=x2-4x图象上有两点A(-4,y1),B(1,y2),则y1与y2的大小关系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.无法确定
3.将抛物线y=3x2向下平移2个单位,得到的抛物线是( )
A.y=3(x-2)2 B.y=3(x+2)2 C.y=3x2-2 D.y=3x2+2
4.将抛物线y=2x2经过怎样的平移可得到抛物线y=2(x+3)2+4( )
A.先向左平移3个单位,再向上平移4个单位
B.先向左平移3个单位,再向下平移4个单位
C.先向右平移3个单位,再向上平移4个单位
D.先向右平移3个单位,再向下平移4个单位
5.若二次函数y=x2-4x+k的图象经过点(-1,y1),(3,y2),则y1与y2的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
6.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象过点(3,-1),图象的对称轴是直线x=1,且c<-1,则下列结论正确的是( )
A.a<0 B.b>0 C.b2<4ac D.a-b+c=-1
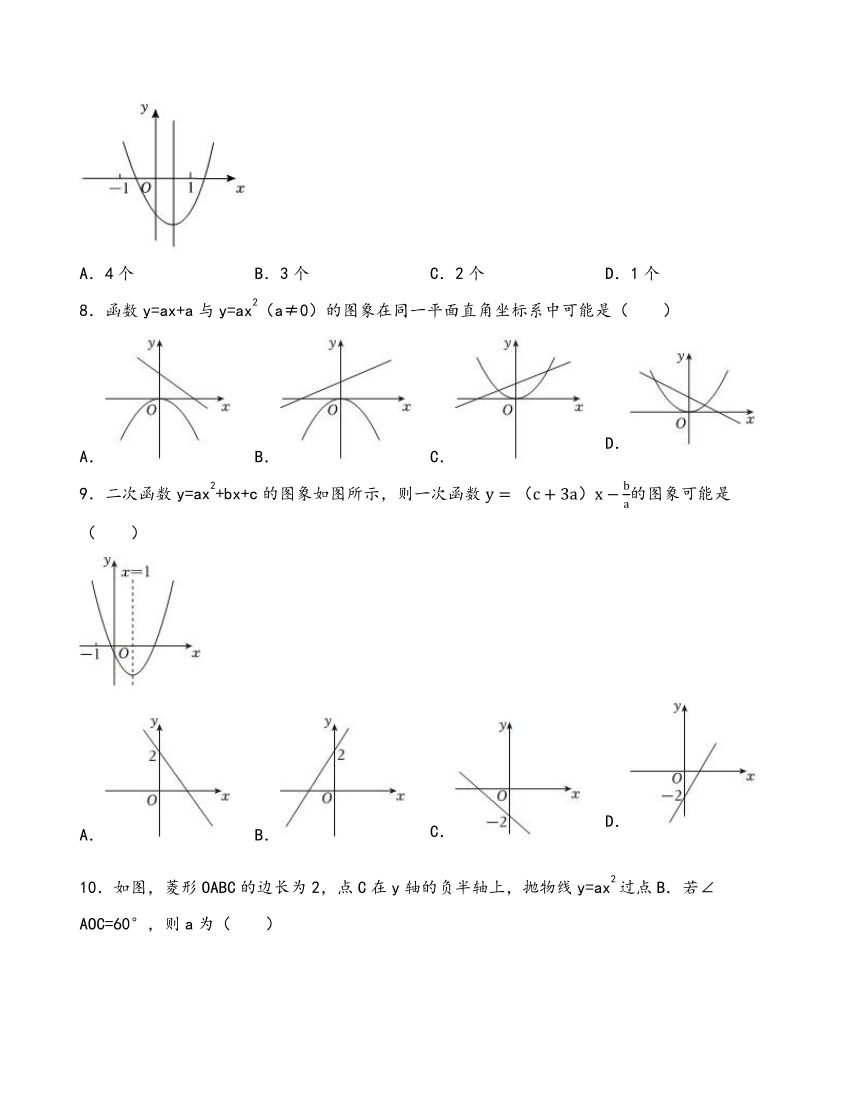
7.二次函数y=ax2+bx+c的图象如图所示,则b,c,b2-4ac,a+b+c这四个式子中,值为正数的有( )
A.4个 B.3个 C.2个 D.1个
8.函数y=ax+a与y=ax2(a≠0)的图象在同一平面直角坐标系中可能是( )
A. B. C. D.
9.二次函数y=ax2+bx+c的图象如图所示,则一次函数的图象可能是( )
A. B. C. D.
10.如图,菱形OABC的边长为2,点C在y轴的负半轴上,抛物线y=ax2过点B.若∠AOC=60°,则a为( )
A.-1 B.-2 C. D.1
11.如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,经过点(1,0),且与y轴的交点在点(0,-2)与(0,-3)之间,函数图象的对称轴为直线x=-1.下列判断正确的是( )
A.b2<4ac B.2a+b=0 C.a-3b+c>0 D.
12.如图,抛物线与交于点B(1,-2),且分别与y轴交于点D,E.过点B作x轴的平行线,交抛物线于点A,C.则以下结论错误的是( )
A.无论x取何值,y2总是负数
B.抛物线y2可由抛物线y1向右平移3个单位,再向下平移3个单位得到
C.当-3<x<1时,随着x的增大,y1-y2的值先增大后减小
D.若依次连接AE、EC、CD、DA,则四边形AECD为正方形
二.填空题(共5小题)
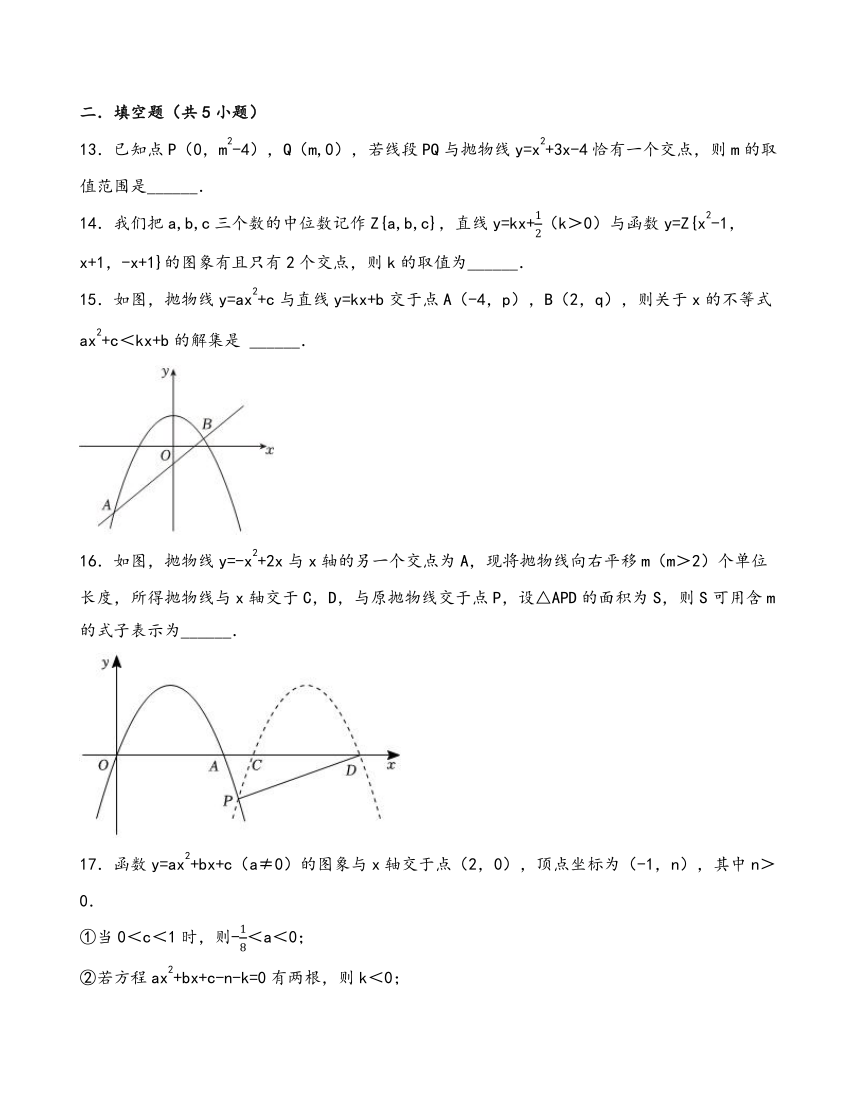
13.已知点P(0,m2-4),Q(m,0),若线段PQ与抛物线y=x2+3x-4恰有一个交点,则m的取值范围是______.
14.我们把a,b,c三个数的中位数记作Z{a,b,c},直线y=kx+(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,则k的取值为______.
15.如图,抛物线y=ax2+c与直线y=kx+b交于点A(-4,p),B(2,q),则关于x的不等式ax2+c<kx+b的解集是 ______.
16.如图,抛物线y=-x2+2x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△APD的面积为S,则S可用含m的式子表示为______.
17.函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0),顶点坐标为(-1,n),其中n>0.
①当0<c<1时,则-<a<0;
②若方程ax2+bx+c-n-k=0有两根,则k<0;
③点P1(x1,y1),P2(x2,y2)是抛物线上不同于A,B的两个点,当|x1+1|>|x2+1|>3时,y1<y2;
④函数y=kx+1的图象与y=ax2+bx+c(a≠0)的函数图象总有两个不同交点.
以上结论正确的序号是 ______.
三.解答题(共5小题)
18.已知:抛物线y=ax2-(a+3)x+1.
(1)求证:抛物线与x轴总有两个交点;
(2)若点A(a-1,m),点B(a+1,m)是该抛物线上两点,求代数式2a3-a2-3a+1的值.
19.(2025春 玄武区校级期中)在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的公共点中有整点?若存在,求所有整数a的值;若不存在,请说明理由.
20.已知二次函数y=x2-(m-1)x-1(m是常数)的图象过点(m,2m).
(1)求m的值;
(2)设抛物线y=x2-(m-1)x-1与x轴的交点为(k,0),设,请判断S>0,S=0,S<0哪个成立?并说明理由.
21.在节假日期间,濮阳龙湖论语广场的音乐喷泉上演了绚丽的灯光秀.随着音乐的节拍,喷泉的水线起伏跳跃,勾勒出迷人的抛物线图案.假设喷泉的出水口为坐标原点,出水口离岸边18米.随着音乐的变化,抛物线的顶点在直线y=kx(k≠0)上变动,从而产生一组不同的抛物线,设这组抛物线的统一形式为y=ax2+bx(a<0).
(1)若,
①若喷出的水恰好达到岸边,则此时喷出的抛物线形水线最大高度是多少米?
②若喷出的抛物线形水线最大高度为4m,求a、b的值;
(2)当音乐节奏加快,抛物线的顶点在直线y=x上,喷出的水不能触及岸边.请直接写出此时a的取值范围.
22.在平面直角坐标系中,抛物线y=ax2+bx+c经过点A(-1,0),B(4,0),C(0,4)三点,与y轴交于点C,点P是抛物线上一动点,且在直线BC的上方.
(1)求抛物线的表达式.
(2)如图1,过点P作PD⊥x轴,交直线BC于点E,连接PB若,求点P的坐标.
(3)如图2,连接AC,PC,AP,AP与BC交于点G,过点P作PF∥AC交BC于点F.记△ACG,△PCG,△PGF的面积分别为S1,S2,S3.求的最小值.
华东师大版九年级下 第26章 二次函数 单元巩固卷
(参考答案)
一.选择题(共12小题)
1、B 2、A 3、C 4、A 5、A 6、D 7、D 8、C 9、B 10、A 11、D 12、C
二.填空题(共5小题)
13、m=0或m≥1或m≤-4; 14、<k≤1或k=; 15、x<-4或x>2; 16、-1; 17、①③;
三.解答题(共5小题)
18、(1)证明:当ax2-(a+3)x+1=0时,
Δ=[-(a+3)]2-4a
=a2+2a+9
=(a+1)2+8,
∵(a+1)2≥0,
∴(a+1)2+8>0,即Δ>0;
∴抛物线与x轴总有两个交点;
(2)解:∵点A(a-1,m),点B(a+1,m)是抛物线上关于对称轴对称的两个点,
∴,
∴,
∴2a2-a=3,
∴2a3-a2-3a+1=a(2a2-a)-3a+1=3a-3a+1=1.
19、解:当时,函数表达式为y=12x+6,令y=0,得,不符合题意,
当时,在y=(4a+2)x2+(9-6a)x-4a+4中,令y=0,得0=(4a+2)x2+(9-6a)x-4a+4,
解得或,
∵,a是整数,
∴当2a+1是6的因数时,是整数,
∴2a+1=-6或2a+1=-3或2a+1=-2或2a+1=-1或2a+1=1或2a+1=2或2a+1=3或2a+1=6,
解得或a=-2或或a=-1或a=0或或a=1或,
∵a是整数,
∴a=-2或a=-1或a=0或a=1.
20、解:(1)把点(m,2m)代入,得:
m2-m(m-1)-1=2m,
解得:m=-1;
(2)S=0,理由如下:
由(1)得y=x2+2x-1,
因为抛物线与x轴的交点为(k,0),
∴k2+2k-1=0,
从而可得k2+2k=1,k2=1-2k,,
∴,
,
=
=
=
=.
=
=
=
∴S=0.
21、解:(1)由条件可知,
①∵喷出的水恰好达到岸边,
∴抛物线过(18,0),
∵抛物线过原点(0,0),
∴抛物线的对称轴是直线,
∵抛物线的顶点在直线上,
∴当x=9时,,
∴抛物线水线最大高度是米;
②由条件可知抛物线顶点的纵坐标为4m,
当 y=4时,,
解得:x=8,
∴抛物线的顶点是(8,4),
∴y=ax2+bx=a(x-8)2+4,
∵抛物线过原点(0,0),
∴64a+4=0,
解得,
∴,
∴,b=1.
(2)∵,
∴抛物线的顶点坐标为,
∵抛物线的顶点在直线y=x上,
∴,
解得:b=2,
由条件可知,即,
解得.
22、解:(1)由题意得:,
解得,
∴y=-x2+3x+4;
(2)设直线BC的解析式为y=kx+b,则有:
,解得:,
∴直线BC的解析式为:y=-x+4,
设点P(m,-m2+3m+4),
∵PD⊥x轴,
∴PD∥y轴,
∴E(m,-m+4),D(m,0),
∴PE=-m2+3m+4-(-m+4)=-m2+4m,ED=-m+5,
∵,,
∴3PE=4ED,
∴3(-m2+4m)=4(-m+4),
解得:,m2=4(此时B,P重合,不合题意舍去),
∴;
(3)∵PF∥AC,
∴△ACG∽△PFG,
∴,,
∴,
作AN∥BC交y轴于N,作PQ∥y轴交BC于Q,
∵直线BC的解析式为y=-x+4,AN∥BC,
∴直线AN的解析式为y=-x+n,
由条件可得n=-1,
∴直线AN的解析式为y=-x-1,
当x=0时,y=-1,
∴N(0,-1),
∴ON=1,CN=OC+ON=5,
由条件可知∠PQF=∠NCB=∠ANC,∠PFC=∠ACF,
∵∠PFC=∠FPQ+∠PQF,∠ACF=∠NCB+∠ACN,∠PQF=∠NCB=45°,
∴∠FPQ=∠ACN,
∴△CAN∽△PFQ,
∴,
设P(t,-t2+3t+4),则Q(t,-t+4),PQ=-t2+4t,
∴,
∴,
∴当t=2时,有最小值.
一.选择题(共12小题)
1.抛物线y=(x+2)2+3的对称轴是直线( )
A.x=2 B.x=-2 C.x=3 D.x=-3
2.已知二次函数y=x2-4x图象上有两点A(-4,y1),B(1,y2),则y1与y2的大小关系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.无法确定
3.将抛物线y=3x2向下平移2个单位,得到的抛物线是( )
A.y=3(x-2)2 B.y=3(x+2)2 C.y=3x2-2 D.y=3x2+2
4.将抛物线y=2x2经过怎样的平移可得到抛物线y=2(x+3)2+4( )
A.先向左平移3个单位,再向上平移4个单位
B.先向左平移3个单位,再向下平移4个单位
C.先向右平移3个单位,再向上平移4个单位
D.先向右平移3个单位,再向下平移4个单位
5.若二次函数y=x2-4x+k的图象经过点(-1,y1),(3,y2),则y1与y2的大小关系为( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
6.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象过点(3,-1),图象的对称轴是直线x=1,且c<-1,则下列结论正确的是( )
A.a<0 B.b>0 C.b2<4ac D.a-b+c=-1
7.二次函数y=ax2+bx+c的图象如图所示,则b,c,b2-4ac,a+b+c这四个式子中,值为正数的有( )
A.4个 B.3个 C.2个 D.1个
8.函数y=ax+a与y=ax2(a≠0)的图象在同一平面直角坐标系中可能是( )
A. B. C. D.
9.二次函数y=ax2+bx+c的图象如图所示,则一次函数的图象可能是( )
A. B. C. D.
10.如图,菱形OABC的边长为2,点C在y轴的负半轴上,抛物线y=ax2过点B.若∠AOC=60°,则a为( )
A.-1 B.-2 C. D.1
11.如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,经过点(1,0),且与y轴的交点在点(0,-2)与(0,-3)之间,函数图象的对称轴为直线x=-1.下列判断正确的是( )
A.b2<4ac B.2a+b=0 C.a-3b+c>0 D.
12.如图,抛物线与交于点B(1,-2),且分别与y轴交于点D,E.过点B作x轴的平行线,交抛物线于点A,C.则以下结论错误的是( )
A.无论x取何值,y2总是负数
B.抛物线y2可由抛物线y1向右平移3个单位,再向下平移3个单位得到
C.当-3<x<1时,随着x的增大,y1-y2的值先增大后减小
D.若依次连接AE、EC、CD、DA,则四边形AECD为正方形
二.填空题(共5小题)
13.已知点P(0,m2-4),Q(m,0),若线段PQ与抛物线y=x2+3x-4恰有一个交点,则m的取值范围是______.
14.我们把a,b,c三个数的中位数记作Z{a,b,c},直线y=kx+(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,则k的取值为______.
15.如图,抛物线y=ax2+c与直线y=kx+b交于点A(-4,p),B(2,q),则关于x的不等式ax2+c<kx+b的解集是 ______.
16.如图,抛物线y=-x2+2x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△APD的面积为S,则S可用含m的式子表示为______.
17.函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0),顶点坐标为(-1,n),其中n>0.
①当0<c<1时,则-<a<0;
②若方程ax2+bx+c-n-k=0有两根,则k<0;
③点P1(x1,y1),P2(x2,y2)是抛物线上不同于A,B的两个点,当|x1+1|>|x2+1|>3时,y1<y2;
④函数y=kx+1的图象与y=ax2+bx+c(a≠0)的函数图象总有两个不同交点.
以上结论正确的序号是 ______.
三.解答题(共5小题)
18.已知:抛物线y=ax2-(a+3)x+1.
(1)求证:抛物线与x轴总有两个交点;
(2)若点A(a-1,m),点B(a+1,m)是该抛物线上两点,求代数式2a3-a2-3a+1的值.
19.(2025春 玄武区校级期中)在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的公共点中有整点?若存在,求所有整数a的值;若不存在,请说明理由.
20.已知二次函数y=x2-(m-1)x-1(m是常数)的图象过点(m,2m).
(1)求m的值;
(2)设抛物线y=x2-(m-1)x-1与x轴的交点为(k,0),设,请判断S>0,S=0,S<0哪个成立?并说明理由.
21.在节假日期间,濮阳龙湖论语广场的音乐喷泉上演了绚丽的灯光秀.随着音乐的节拍,喷泉的水线起伏跳跃,勾勒出迷人的抛物线图案.假设喷泉的出水口为坐标原点,出水口离岸边18米.随着音乐的变化,抛物线的顶点在直线y=kx(k≠0)上变动,从而产生一组不同的抛物线,设这组抛物线的统一形式为y=ax2+bx(a<0).
(1)若,
①若喷出的水恰好达到岸边,则此时喷出的抛物线形水线最大高度是多少米?
②若喷出的抛物线形水线最大高度为4m,求a、b的值;
(2)当音乐节奏加快,抛物线的顶点在直线y=x上,喷出的水不能触及岸边.请直接写出此时a的取值范围.
22.在平面直角坐标系中,抛物线y=ax2+bx+c经过点A(-1,0),B(4,0),C(0,4)三点,与y轴交于点C,点P是抛物线上一动点,且在直线BC的上方.
(1)求抛物线的表达式.
(2)如图1,过点P作PD⊥x轴,交直线BC于点E,连接PB若,求点P的坐标.
(3)如图2,连接AC,PC,AP,AP与BC交于点G,过点P作PF∥AC交BC于点F.记△ACG,△PCG,△PGF的面积分别为S1,S2,S3.求的最小值.
华东师大版九年级下 第26章 二次函数 单元巩固卷
(参考答案)
一.选择题(共12小题)
1、B 2、A 3、C 4、A 5、A 6、D 7、D 8、C 9、B 10、A 11、D 12、C
二.填空题(共5小题)
13、m=0或m≥1或m≤-4; 14、<k≤1或k=; 15、x<-4或x>2; 16、-1; 17、①③;
三.解答题(共5小题)
18、(1)证明:当ax2-(a+3)x+1=0时,
Δ=[-(a+3)]2-4a
=a2+2a+9
=(a+1)2+8,
∵(a+1)2≥0,
∴(a+1)2+8>0,即Δ>0;
∴抛物线与x轴总有两个交点;
(2)解:∵点A(a-1,m),点B(a+1,m)是抛物线上关于对称轴对称的两个点,
∴,
∴,
∴2a2-a=3,
∴2a3-a2-3a+1=a(2a2-a)-3a+1=3a-3a+1=1.
19、解:当时,函数表达式为y=12x+6,令y=0,得,不符合题意,
当时,在y=(4a+2)x2+(9-6a)x-4a+4中,令y=0,得0=(4a+2)x2+(9-6a)x-4a+4,
解得或,
∵,a是整数,
∴当2a+1是6的因数时,是整数,
∴2a+1=-6或2a+1=-3或2a+1=-2或2a+1=-1或2a+1=1或2a+1=2或2a+1=3或2a+1=6,
解得或a=-2或或a=-1或a=0或或a=1或,
∵a是整数,
∴a=-2或a=-1或a=0或a=1.
20、解:(1)把点(m,2m)代入,得:
m2-m(m-1)-1=2m,
解得:m=-1;
(2)S=0,理由如下:
由(1)得y=x2+2x-1,
因为抛物线与x轴的交点为(k,0),
∴k2+2k-1=0,
从而可得k2+2k=1,k2=1-2k,,
∴,
,
=
=
=
=.
=
=
=
∴S=0.
21、解:(1)由条件可知,
①∵喷出的水恰好达到岸边,
∴抛物线过(18,0),
∵抛物线过原点(0,0),
∴抛物线的对称轴是直线,
∵抛物线的顶点在直线上,
∴当x=9时,,
∴抛物线水线最大高度是米;
②由条件可知抛物线顶点的纵坐标为4m,
当 y=4时,,
解得:x=8,
∴抛物线的顶点是(8,4),
∴y=ax2+bx=a(x-8)2+4,
∵抛物线过原点(0,0),
∴64a+4=0,
解得,
∴,
∴,b=1.
(2)∵,
∴抛物线的顶点坐标为,
∵抛物线的顶点在直线y=x上,
∴,
解得:b=2,
由条件可知,即,
解得.
22、解:(1)由题意得:,
解得,
∴y=-x2+3x+4;
(2)设直线BC的解析式为y=kx+b,则有:
,解得:,
∴直线BC的解析式为:y=-x+4,
设点P(m,-m2+3m+4),
∵PD⊥x轴,
∴PD∥y轴,
∴E(m,-m+4),D(m,0),
∴PE=-m2+3m+4-(-m+4)=-m2+4m,ED=-m+5,
∵,,
∴3PE=4ED,
∴3(-m2+4m)=4(-m+4),
解得:,m2=4(此时B,P重合,不合题意舍去),
∴;
(3)∵PF∥AC,
∴△ACG∽△PFG,
∴,,
∴,
作AN∥BC交y轴于N,作PQ∥y轴交BC于Q,
∵直线BC的解析式为y=-x+4,AN∥BC,
∴直线AN的解析式为y=-x+n,
由条件可得n=-1,
∴直线AN的解析式为y=-x-1,
当x=0时,y=-1,
∴N(0,-1),
∴ON=1,CN=OC+ON=5,
由条件可知∠PQF=∠NCB=∠ANC,∠PFC=∠ACF,
∵∠PFC=∠FPQ+∠PQF,∠ACF=∠NCB+∠ACN,∠PQF=∠NCB=45°,
∴∠FPQ=∠ACN,
∴△CAN∽△PFQ,
∴,
设P(t,-t2+3t+4),则Q(t,-t+4),PQ=-t2+4t,
∴,
∴,
∴当t=2时,有最小值.
