北师大版九年级下 第2章 二次函数 单元巩固卷(含答案)
文档属性
| 名称 | 北师大版九年级下 第2章 二次函数 单元巩固卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 55.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-24 21:52:22 | ||
图片预览



文档简介
北师大版九年级下 第2章 二次函数 单元巩固卷
一.选择题(共12小题)
1.将抛物线y=2x2+1向右平移3个单位后所得图象对应的函数解析式为( )
A.y=2x2+4 B.y=2x2-2
C.y=2(x+3)2+1 D.y=2(x-3)2+1
2.关于x的二次函数y=(a+1)x2+ax+a2-1的图象过原点,则a的值为( ).
A.1 B.-1 C.±1 D.0
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则点(a,c)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在二次函数y=ax2+bx+c中,如果a>0,b<0,c>0,那么它的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.下列函数中,一定是二次函数的是( )
A.(其中m是常数)
B.y=ax2+bx+c(其中a、b、c是常数)
C.y=(2x-1)x
D.y=(x+4)2-x2
6.已知点A(-3,y1),B(-1,y2),C(3,y3)在函数y=-x2-2x+b的图象上,则y1、y2、y3的大小关系为( )
A.y3<y1<y2 B.y2<y1<y3 C.y3<y2<y1 D.y1<y3<y2
7.在平面直角坐标系xOy中,如果点都在抛物线上,那么( )
A.a<b<c B.c<a<b C.b<c<a D.b<a<c
8.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象过点(3,-1),图象的对称轴是直线x=1,且c<-1,则下列结论正确的是( )
A.a<0 B.b>0 C.b2<4ac D.a-b+c=-1
9.如图,抛物线y=ax2+bx+c(a,b,c为常数)关于直线x=1对称.以下结论中:①ac>0;②关于x的一元二次方程ax2+bx+c=0一定有一个根x2满足2<x2<3;③3a+c>0;④am2+bm+a>0(m为实数).其中正确的有( )
A.①④ B.②③ C.②③④ D.①②③④
10.抛物线y=-7(x+3)2+1可以由抛物线y=-7x2平移得到,则下列平移过程正确的是( )
A.先向左平移3个单位,再向上平移1个单位
B.先向右平移3个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移3个单位
D.先向右平移1个单位,再向下平移3个单位
11.已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为A(m,0),0<m<1,下列结论中:①abc>0;②3a+c>0;③若t为任意实数,则有a-bt≤at2+b;④当此抛物线经过点时,方程ax2+bx+c-2=0的两根为x1,x2(x1<x2),可求得x1+2x2=-2.正确结论的序号为( )
A.①②③ B.②③ C.③④ D.②③④
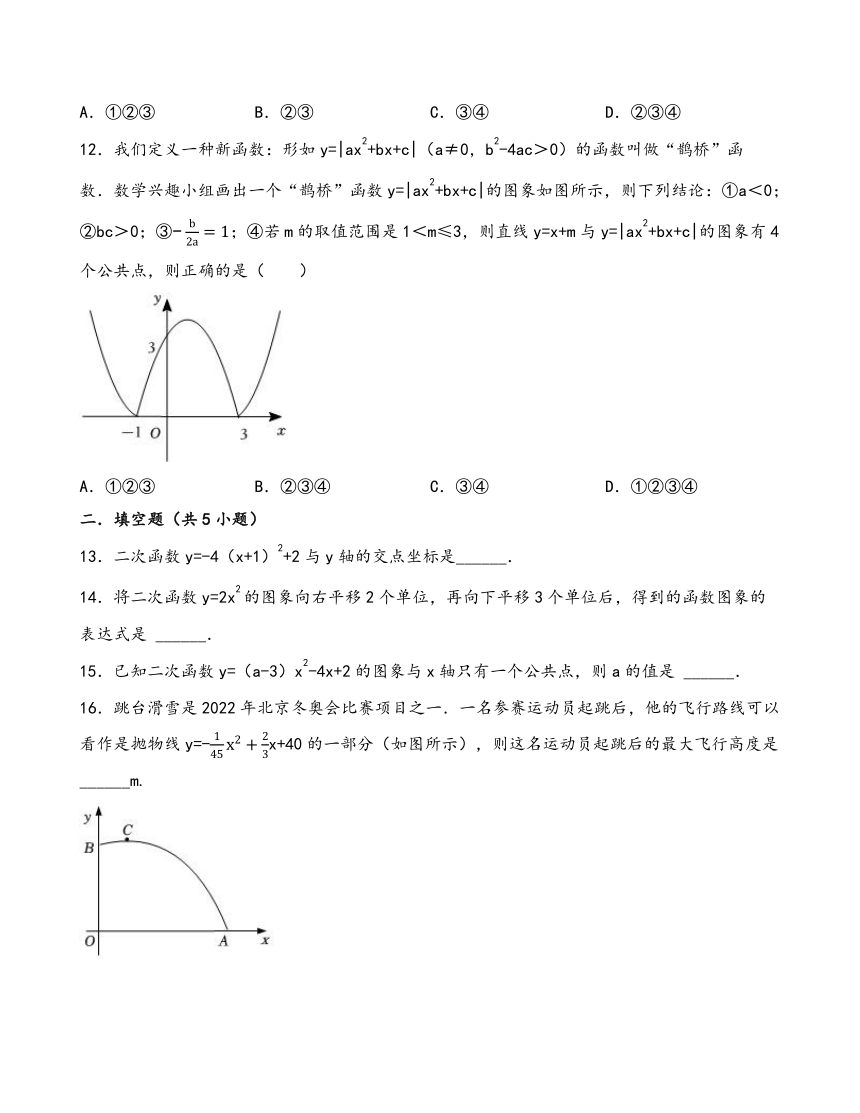
12.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2-4ac>0)的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数y=|ax2+bx+c|的图象如图所示,则下列结论:①a<0;②bc>0;③;④若m的取值范围是1<m≤3,则直线y=x+m与y=|ax2+bx+c|的图象有4个公共点,则正确的是( )
A.①②③ B.②③④ C.③④ D.①②③④
二.填空题(共5小题)
13.二次函数y=-4(x+1)2+2与y轴的交点坐标是______.
14.将二次函数y=2x2的图象向右平移2个单位,再向下平移3个单位后,得到的函数图象的表达式是 ______.
15.已知二次函数y=(a-3)x2-4x+2的图象与x轴只有一个公共点,则a的值是 ______.
16.跳台滑雪是2022年北京冬奥会比赛项目之一.一名参赛运动员起跳后,他的飞行路线可以看作是抛物线y=-x+40的一部分(如图所示),则这名运动员起跳后的最大飞行高度是 ______m.
17.对于三个实数a,b,c,用F{a,b}表示这两个数的平方差,用max{a,b,c}表示这三个数中最大的数,例如:F{1,2}=12-22=1-4=-3,max{1,2,-1}=2.若F{a-2,-3}<max{a2,a2+1,-3},则负整数a的值是______.
三.解答题(共5小题)
18.已知二次函数y=x2-(m-2)x-m(m为常数).
(1)求证:函数与x轴有两个交点;
(2)若当x≥3时,y随x的增大而增大,求m的取值范围.
19.已知函数y=(m+1)x2+2x-1.
(1)若函数图象经过点(1,2),求m的值;
(2)若函数图象与x轴只有一个交点A,求点A的坐标;
(3)若函数y=(m+1)x2+2x-1满足x>-1时,y随x的增大而增大;x<-1时,y随x的增大而减小,且图象与x轴的两个交点为(a,0),(b,0).求证:b8=1155-34a4.
20.冰糖心苹果是阿克苏的特色农产品,它色泽光亮自然,水分足,果肉脆,口味甜,深受市民喜爱.上市时,王经理按市场价格6元/千克收购了2000千克苹果放入冷库中.据预测,苹果的市场价格每天每千克将上涨0.2元,但冷库存放这批苹果每天需要支出各种费用160元,而且苹果在冷库中最多可以保存50天,同时,每天有10千克的苹果损坏不能出售.
(1)若存放x天后,将这批苹果一次性出售,设这批苹果的销售总金额为y元,试写出y与x之间的函数解析式;
(2)王经理想获得3850元的利润,需将这批苹果存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)王经理将这批苹果存放多少天后出售可获得最大利润?最大利润是多少?
21.某班级一次课外活动中设计了一个弹珠投箱子的游戏(长方体无盖箱子放在水平面上).同学受游戏启发,将弹珠抽象为一个点,并建立了如图所示的平面直角坐标系(x轴经过箱子底面中心,并与其一组对边平行,矩形DEFG为箱子的截面示意图).某同学将弹珠从A(1,0)处抛出,弹珠的飞行轨迹为抛物线(单位长度为1m)的一部分,且当弹珠的高度为时,对应的两个位置的水平距离为2m,已知DE=1m,,DA=4.7m.
(1)求抛物线L的解析式和顶点坐标;
(2)该同学抛出的弹珠能否投入箱子?请通过计算说明.
22.如图①,在平面直角坐标系中,二次函数y=-x2+bx+c的图象交x轴于A,B两点,交y轴于点C(0,4),若点B的坐标为(4,0),点D是该二次函数图象上的一个动点,且在第一象限.
(1)求二次函数的表达式;
(2)连接BC,过点D作DE⊥x轴于点E,交线段BC于点F,当点D运动到什么位置时,线段DF有最大值?请求出点D的坐标和DF的最大值;
(3)连接OD,CD,若△OCD关于y轴的对称图形是△OCD′,是否存在点D,使得四边形ODCD′为菱形?若存在,求出点D的坐标,若不存在,请说明理由.
北师大版九年级下 第2章 二次函数 单元巩固卷
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、B 4、C 5、C 6、A 7、A 8、D 9、B 10、A 11、B 12、C
二.填空题(共5小题)
13、(0,-2); 14、y=2(x-2)2-3; 15、5; 16、45; 17、-1;
三.解答题(共5小题)
18、(1)证明:∵判别式Δ=[-(m-2)]2-4×1×(-m)=m2+4,
又∵m2≥0,
∴m2+4>0,
∴二次函数y=x2-(m-2)x-m与x轴有两个交点.
(2)解:∵二次函数y=x2-(m-2)x-m的对称轴为x=,开口向上,
又∵y随x的增大而增大,
∴≤3,
解得:m≤8,
∴当x≥3时,y随x的增大而增大,m的取值范围是m≤8.
19、(1)解:由题意得,把点(1,2)代入y=(m+1)x2+2x-1,
得,m+1+2-1=2,
解得:m=0;
(2)解:当m+1=0时,y=2x-1,
则当y=0,2x-1=0,
解得:,
∴;
当m+1≠0时,则Δ=22-4(m+1)×(-1)=0,
解得:m=-2,
∴函数y=-x2+2x-1,
则当y=0,-x2+2x-1=0,
解得:x1=x2=1,
∴A(1,0),
综上:A(1,0)或;
(3)证明:由题意得,对称轴为,
解得:m=0,
∴函数为:y=x2+2x-1,
∵图象与x轴的两个交点为(a,0),(b,0),
∴当y=0,则x2+2x-1=0,则a2+2a-1=0,a+b=-2,
∴a2=1-2a,b2=1-2b,
∴a4=(a2)2=(1-2a)2=4a2-4a+1=4(1-2a)-4a+1=-12a+5,
∴1155-34a4=1155-34(-12a+5)=985+408a,
同理b4=-12b+5,
∴b8=(b4)2=(-12b+5)2=144b2-120b+25=144(1-2b)-120b+25=-408b+169,
∵a+b=-2,
∴b=-2-a,
∴b8=-408b+169=-408×(-2-a)+169=985+408a,
∴b8=1155-34a4.
20、解:(1)由题意y与x之间的函数关系式为:y=(6+0.2x)(2000-10x)=-2x2+340x+12000(1≤x≤50,且x为整数);
(2)由题意得:
-2x2+340x+12000-6×2000-160x=3850,
解方程得:x1=35,x2=55(不合题意,舍去),
王经理想获得 3850 元的利润,需将这批苹果存放35天后出售;
(3)设利润为w,由题意得:
w=-2x2+340x+12000-6×2000-160x=-2(x-45)2+4050,
∵-2<0,
∴抛物线开口方向向下,
∴x=45时,w最大=4050,
45<50,符合题意,
∴王经理将这批苹果存放45天后出售可获得最大利润,最大利润是4050元.
21、解:(1)由抛物线可知,当x=0时,,
又当弹珠的高度为时,对应的两个位置的水平距离为2m,由图可知另一点坐标为,
把点A(1,0),代入得:,
解得:,
∴抛物线L的解析式为,
∵,
∴顶点坐标为(-1,2);
(2)∵A(1,0),
∴OA=1m,
∵DA=4.7m,
∴DO=3.7m,即点D(-3.7,0),
∵DE=1m,,
∴OE=2.7m,
∴点,,
当时,,
解得:,
∵,
∴该同学抛出的弹珠能投入箱子.
22、解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=-x2+3x+4;
(2)由抛物线的表达式知,点B(3,0),
由点B、C的坐标得,直线BC的表达式为:y=-x+4,
设点D(x,-x2+3x+4),则点F(x,-x+4),
则DF=-x2+4x=-(x-2)2+4≤4,
即DF的最大值为4,此时,点D(2,6);
(3)存在,理由:
∵四边形ODCD′为菱形,则OD=CD,
则点D在OC的中垂线上,即yD=CO=2=-x2+3x+4,
解得:x=,
即点D(,2).
一.选择题(共12小题)
1.将抛物线y=2x2+1向右平移3个单位后所得图象对应的函数解析式为( )
A.y=2x2+4 B.y=2x2-2
C.y=2(x+3)2+1 D.y=2(x-3)2+1
2.关于x的二次函数y=(a+1)x2+ax+a2-1的图象过原点,则a的值为( ).
A.1 B.-1 C.±1 D.0
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则点(a,c)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在二次函数y=ax2+bx+c中,如果a>0,b<0,c>0,那么它的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.下列函数中,一定是二次函数的是( )
A.(其中m是常数)
B.y=ax2+bx+c(其中a、b、c是常数)
C.y=(2x-1)x
D.y=(x+4)2-x2
6.已知点A(-3,y1),B(-1,y2),C(3,y3)在函数y=-x2-2x+b的图象上,则y1、y2、y3的大小关系为( )
A.y3<y1<y2 B.y2<y1<y3 C.y3<y2<y1 D.y1<y3<y2
7.在平面直角坐标系xOy中,如果点都在抛物线上,那么( )
A.a<b<c B.c<a<b C.b<c<a D.b<a<c
8.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象过点(3,-1),图象的对称轴是直线x=1,且c<-1,则下列结论正确的是( )
A.a<0 B.b>0 C.b2<4ac D.a-b+c=-1
9.如图,抛物线y=ax2+bx+c(a,b,c为常数)关于直线x=1对称.以下结论中:①ac>0;②关于x的一元二次方程ax2+bx+c=0一定有一个根x2满足2<x2<3;③3a+c>0;④am2+bm+a>0(m为实数).其中正确的有( )
A.①④ B.②③ C.②③④ D.①②③④
10.抛物线y=-7(x+3)2+1可以由抛物线y=-7x2平移得到,则下列平移过程正确的是( )
A.先向左平移3个单位,再向上平移1个单位
B.先向右平移3个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移3个单位
D.先向右平移1个单位,再向下平移3个单位
11.已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为A(m,0),0<m<1,下列结论中:①abc>0;②3a+c>0;③若t为任意实数,则有a-bt≤at2+b;④当此抛物线经过点时,方程ax2+bx+c-2=0的两根为x1,x2(x1<x2),可求得x1+2x2=-2.正确结论的序号为( )
A.①②③ B.②③ C.③④ D.②③④
12.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2-4ac>0)的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数y=|ax2+bx+c|的图象如图所示,则下列结论:①a<0;②bc>0;③;④若m的取值范围是1<m≤3,则直线y=x+m与y=|ax2+bx+c|的图象有4个公共点,则正确的是( )
A.①②③ B.②③④ C.③④ D.①②③④
二.填空题(共5小题)
13.二次函数y=-4(x+1)2+2与y轴的交点坐标是______.
14.将二次函数y=2x2的图象向右平移2个单位,再向下平移3个单位后,得到的函数图象的表达式是 ______.
15.已知二次函数y=(a-3)x2-4x+2的图象与x轴只有一个公共点,则a的值是 ______.
16.跳台滑雪是2022年北京冬奥会比赛项目之一.一名参赛运动员起跳后,他的飞行路线可以看作是抛物线y=-x+40的一部分(如图所示),则这名运动员起跳后的最大飞行高度是 ______m.
17.对于三个实数a,b,c,用F{a,b}表示这两个数的平方差,用max{a,b,c}表示这三个数中最大的数,例如:F{1,2}=12-22=1-4=-3,max{1,2,-1}=2.若F{a-2,-3}<max{a2,a2+1,-3},则负整数a的值是______.
三.解答题(共5小题)
18.已知二次函数y=x2-(m-2)x-m(m为常数).
(1)求证:函数与x轴有两个交点;
(2)若当x≥3时,y随x的增大而增大,求m的取值范围.
19.已知函数y=(m+1)x2+2x-1.
(1)若函数图象经过点(1,2),求m的值;
(2)若函数图象与x轴只有一个交点A,求点A的坐标;
(3)若函数y=(m+1)x2+2x-1满足x>-1时,y随x的增大而增大;x<-1时,y随x的增大而减小,且图象与x轴的两个交点为(a,0),(b,0).求证:b8=1155-34a4.
20.冰糖心苹果是阿克苏的特色农产品,它色泽光亮自然,水分足,果肉脆,口味甜,深受市民喜爱.上市时,王经理按市场价格6元/千克收购了2000千克苹果放入冷库中.据预测,苹果的市场价格每天每千克将上涨0.2元,但冷库存放这批苹果每天需要支出各种费用160元,而且苹果在冷库中最多可以保存50天,同时,每天有10千克的苹果损坏不能出售.
(1)若存放x天后,将这批苹果一次性出售,设这批苹果的销售总金额为y元,试写出y与x之间的函数解析式;
(2)王经理想获得3850元的利润,需将这批苹果存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)王经理将这批苹果存放多少天后出售可获得最大利润?最大利润是多少?
21.某班级一次课外活动中设计了一个弹珠投箱子的游戏(长方体无盖箱子放在水平面上).同学受游戏启发,将弹珠抽象为一个点,并建立了如图所示的平面直角坐标系(x轴经过箱子底面中心,并与其一组对边平行,矩形DEFG为箱子的截面示意图).某同学将弹珠从A(1,0)处抛出,弹珠的飞行轨迹为抛物线(单位长度为1m)的一部分,且当弹珠的高度为时,对应的两个位置的水平距离为2m,已知DE=1m,,DA=4.7m.
(1)求抛物线L的解析式和顶点坐标;
(2)该同学抛出的弹珠能否投入箱子?请通过计算说明.
22.如图①,在平面直角坐标系中,二次函数y=-x2+bx+c的图象交x轴于A,B两点,交y轴于点C(0,4),若点B的坐标为(4,0),点D是该二次函数图象上的一个动点,且在第一象限.
(1)求二次函数的表达式;
(2)连接BC,过点D作DE⊥x轴于点E,交线段BC于点F,当点D运动到什么位置时,线段DF有最大值?请求出点D的坐标和DF的最大值;
(3)连接OD,CD,若△OCD关于y轴的对称图形是△OCD′,是否存在点D,使得四边形ODCD′为菱形?若存在,求出点D的坐标,若不存在,请说明理由.
北师大版九年级下 第2章 二次函数 单元巩固卷
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、B 4、C 5、C 6、A 7、A 8、D 9、B 10、A 11、B 12、C
二.填空题(共5小题)
13、(0,-2); 14、y=2(x-2)2-3; 15、5; 16、45; 17、-1;
三.解答题(共5小题)
18、(1)证明:∵判别式Δ=[-(m-2)]2-4×1×(-m)=m2+4,
又∵m2≥0,
∴m2+4>0,
∴二次函数y=x2-(m-2)x-m与x轴有两个交点.
(2)解:∵二次函数y=x2-(m-2)x-m的对称轴为x=,开口向上,
又∵y随x的增大而增大,
∴≤3,
解得:m≤8,
∴当x≥3时,y随x的增大而增大,m的取值范围是m≤8.
19、(1)解:由题意得,把点(1,2)代入y=(m+1)x2+2x-1,
得,m+1+2-1=2,
解得:m=0;
(2)解:当m+1=0时,y=2x-1,
则当y=0,2x-1=0,
解得:,
∴;
当m+1≠0时,则Δ=22-4(m+1)×(-1)=0,
解得:m=-2,
∴函数y=-x2+2x-1,
则当y=0,-x2+2x-1=0,
解得:x1=x2=1,
∴A(1,0),
综上:A(1,0)或;
(3)证明:由题意得,对称轴为,
解得:m=0,
∴函数为:y=x2+2x-1,
∵图象与x轴的两个交点为(a,0),(b,0),
∴当y=0,则x2+2x-1=0,则a2+2a-1=0,a+b=-2,
∴a2=1-2a,b2=1-2b,
∴a4=(a2)2=(1-2a)2=4a2-4a+1=4(1-2a)-4a+1=-12a+5,
∴1155-34a4=1155-34(-12a+5)=985+408a,
同理b4=-12b+5,
∴b8=(b4)2=(-12b+5)2=144b2-120b+25=144(1-2b)-120b+25=-408b+169,
∵a+b=-2,
∴b=-2-a,
∴b8=-408b+169=-408×(-2-a)+169=985+408a,
∴b8=1155-34a4.
20、解:(1)由题意y与x之间的函数关系式为:y=(6+0.2x)(2000-10x)=-2x2+340x+12000(1≤x≤50,且x为整数);
(2)由题意得:
-2x2+340x+12000-6×2000-160x=3850,
解方程得:x1=35,x2=55(不合题意,舍去),
王经理想获得 3850 元的利润,需将这批苹果存放35天后出售;
(3)设利润为w,由题意得:
w=-2x2+340x+12000-6×2000-160x=-2(x-45)2+4050,
∵-2<0,
∴抛物线开口方向向下,
∴x=45时,w最大=4050,
45<50,符合题意,
∴王经理将这批苹果存放45天后出售可获得最大利润,最大利润是4050元.
21、解:(1)由抛物线可知,当x=0时,,
又当弹珠的高度为时,对应的两个位置的水平距离为2m,由图可知另一点坐标为,
把点A(1,0),代入得:,
解得:,
∴抛物线L的解析式为,
∵,
∴顶点坐标为(-1,2);
(2)∵A(1,0),
∴OA=1m,
∵DA=4.7m,
∴DO=3.7m,即点D(-3.7,0),
∵DE=1m,,
∴OE=2.7m,
∴点,,
当时,,
解得:,
∵,
∴该同学抛出的弹珠能投入箱子.
22、解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=-x2+3x+4;
(2)由抛物线的表达式知,点B(3,0),
由点B、C的坐标得,直线BC的表达式为:y=-x+4,
设点D(x,-x2+3x+4),则点F(x,-x+4),
则DF=-x2+4x=-(x-2)2+4≤4,
即DF的最大值为4,此时,点D(2,6);
(3)存在,理由:
∵四边形ODCD′为菱形,则OD=CD,
则点D在OC的中垂线上,即yD=CO=2=-x2+3x+4,
解得:x=,
即点D(,2).
